The Overview of Human Localization and Vital Sign Signal Measurement Using Handheld IR-UWB Through-Wall Radar
Abstract
1. Introduction
2. The Development of the Human Target Signal Model of IR-UWB Through-Wall Radar
2.1. The Development of IR-UWB Through-Wall Radar
2.2. The Human Return Signal Model of the IR-UWB Through-Wall Radar
3. The Pre-Processing of Radar Signals before Human Information Is Obtained
3.1. The Clutter Removal Methods
3.1.1. Pulse Cancelling
3.1.2. Cumulative Average Background Cancellation
3.1.3. Exponentially Weighted Cancellation
3.2. The Signal Enhancement Algorithms
3.2.1. Propagation Time Gain
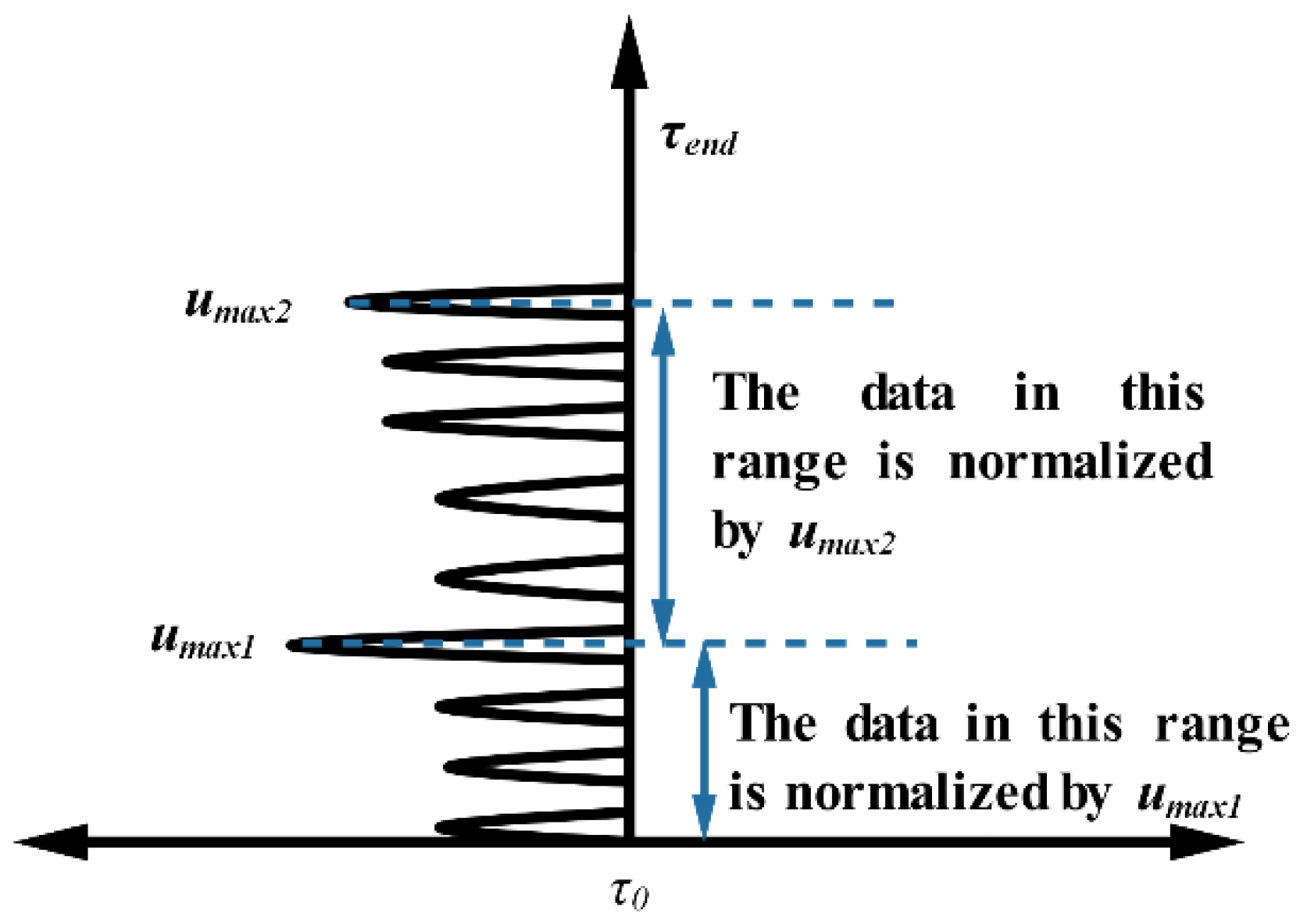
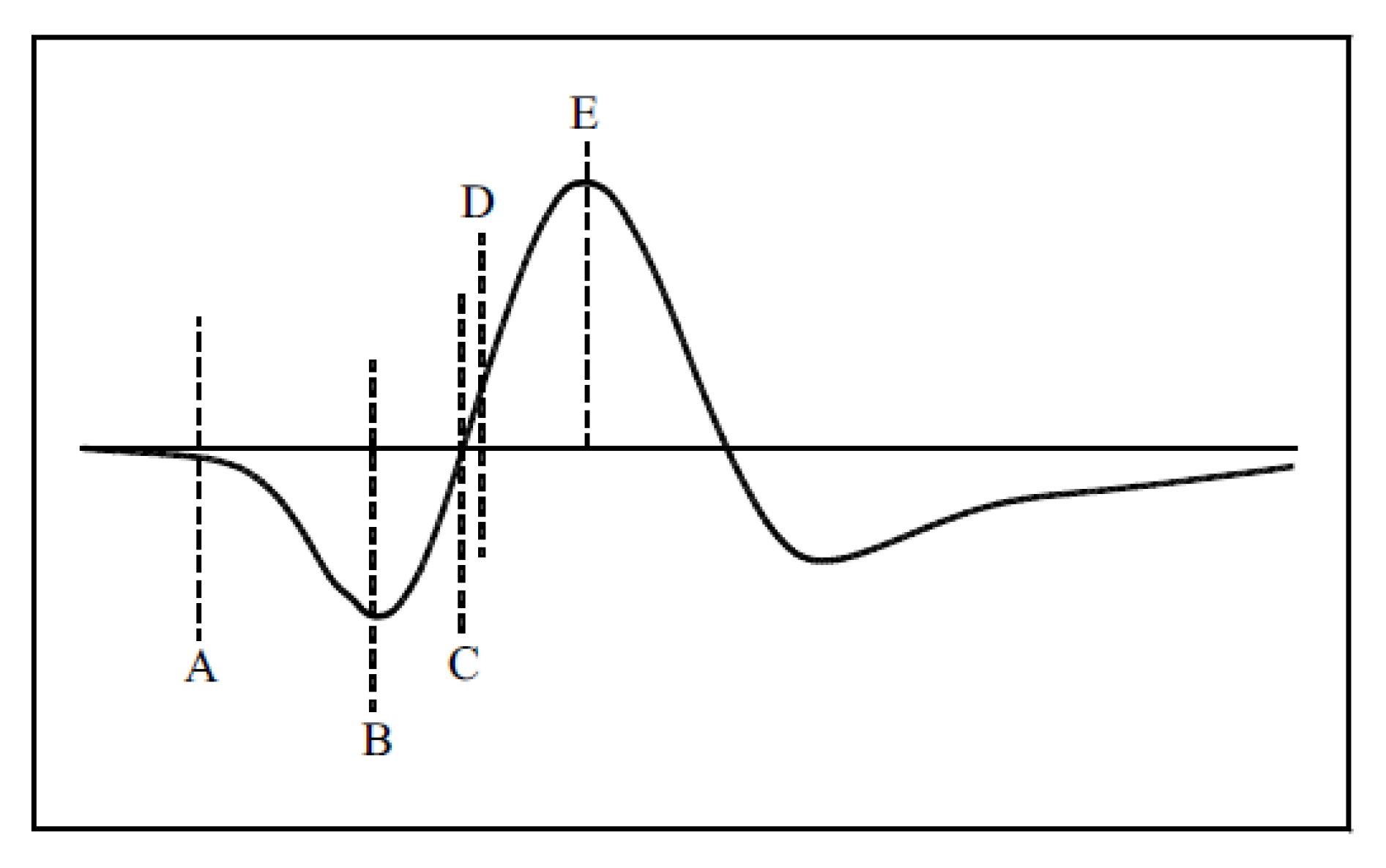
3.2.2. Advance Normalization
| Algorithm 1 Advance1 normalization |
| Input: Raw signal |
| Output: Enhanced signal |
| While do |
| If then |
| Else |
| End if |
| For |
| End |
| End while |
| End |
3.2.3. Automatic Gain Control
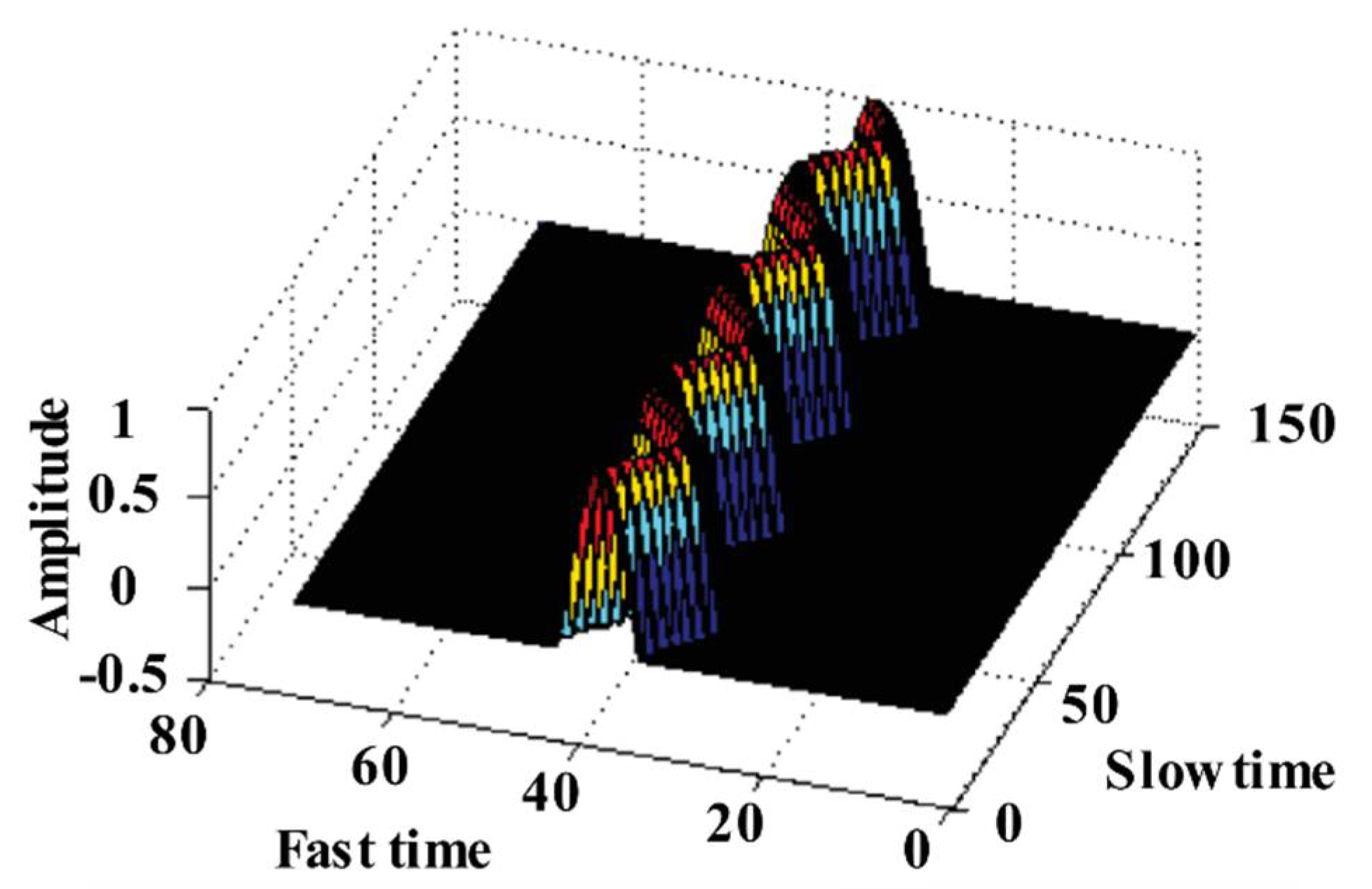
3.2.4. Verification Based on Real-World Measured Data
3.3. The Method for Reference True Time Zero Search and Time-Delay Calibration
| Algorithm 2 Multi-channel time delay calibration method based on the reference zero time |
| Input: |
| The distance of transmitting and receiving antenna set: |
| The first positive peak position of each receive channel set: |
| Output: |
| The time delay with reference channel: . |
| 1. Setting the receive channel closest to the transmitting channel as the reference channel, namely the No.1 channel; |
| 2. Calculate the delay of each channel by (14) (15); the channel delay set can then be obtained: ; |
| 3. Calculate the delay shift between each channel and the reference channel: ; |
| For to |
| If then |
| Find the corresponding return signal, with zero padding from the starting position of the signal; |
| The padding number is ; |
| Else |
| Find the corresponding return signal and discard the data from the starting position of the signal; |
| The discard number is ; |
| End if |
| End |
| End |
3.4. The Wall Parameter Estimation Method
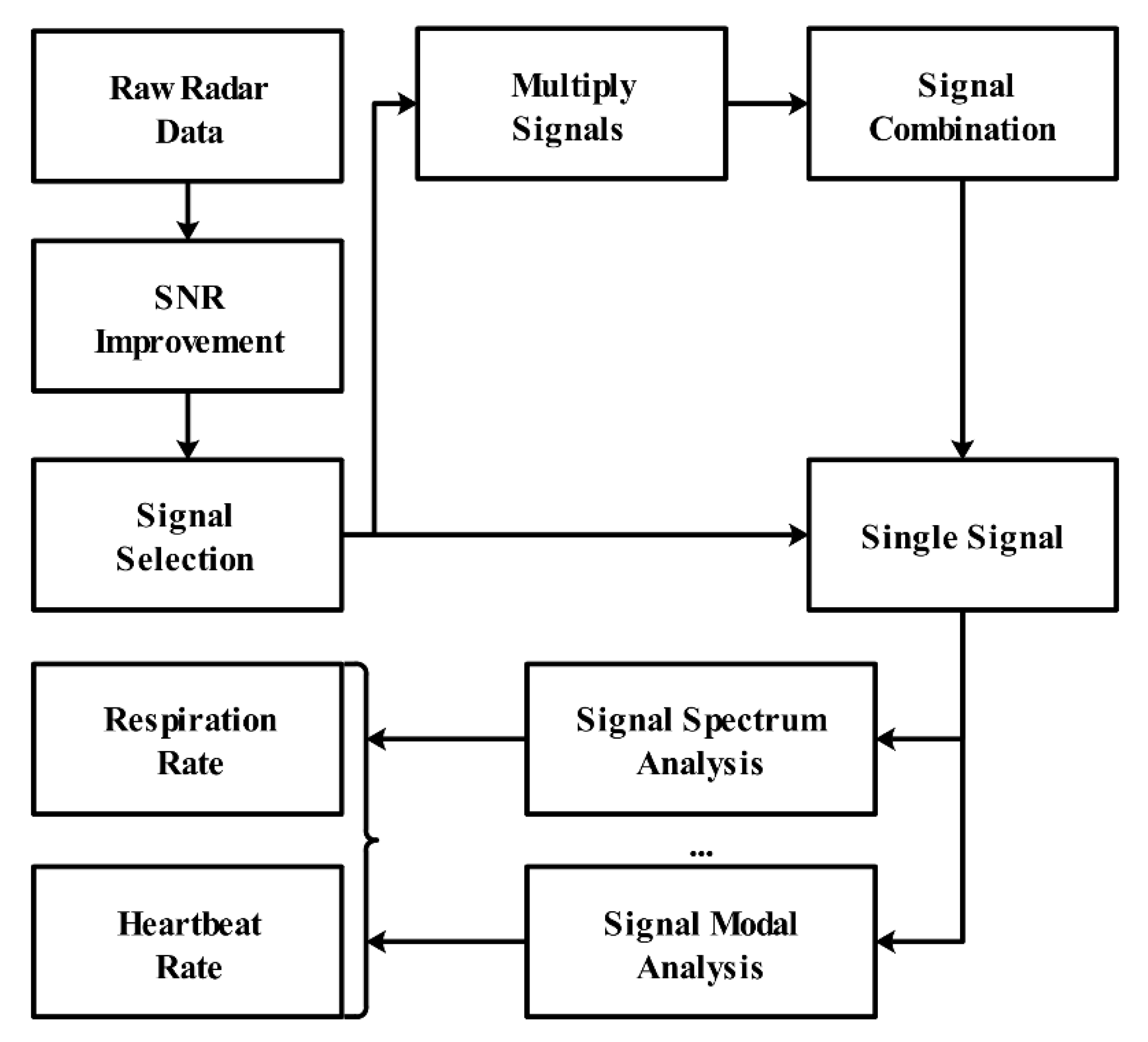
4. Obtaining Human Information
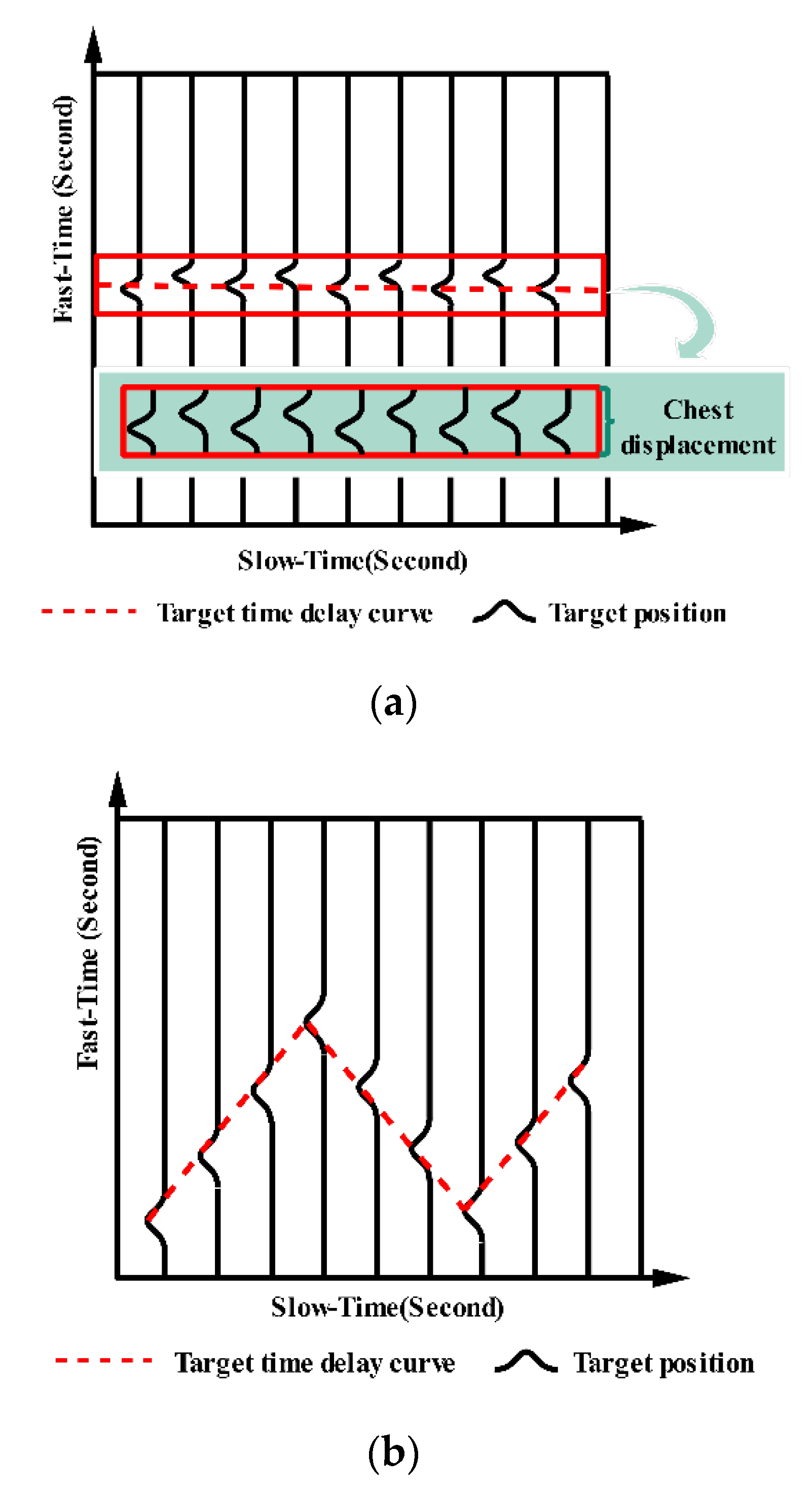
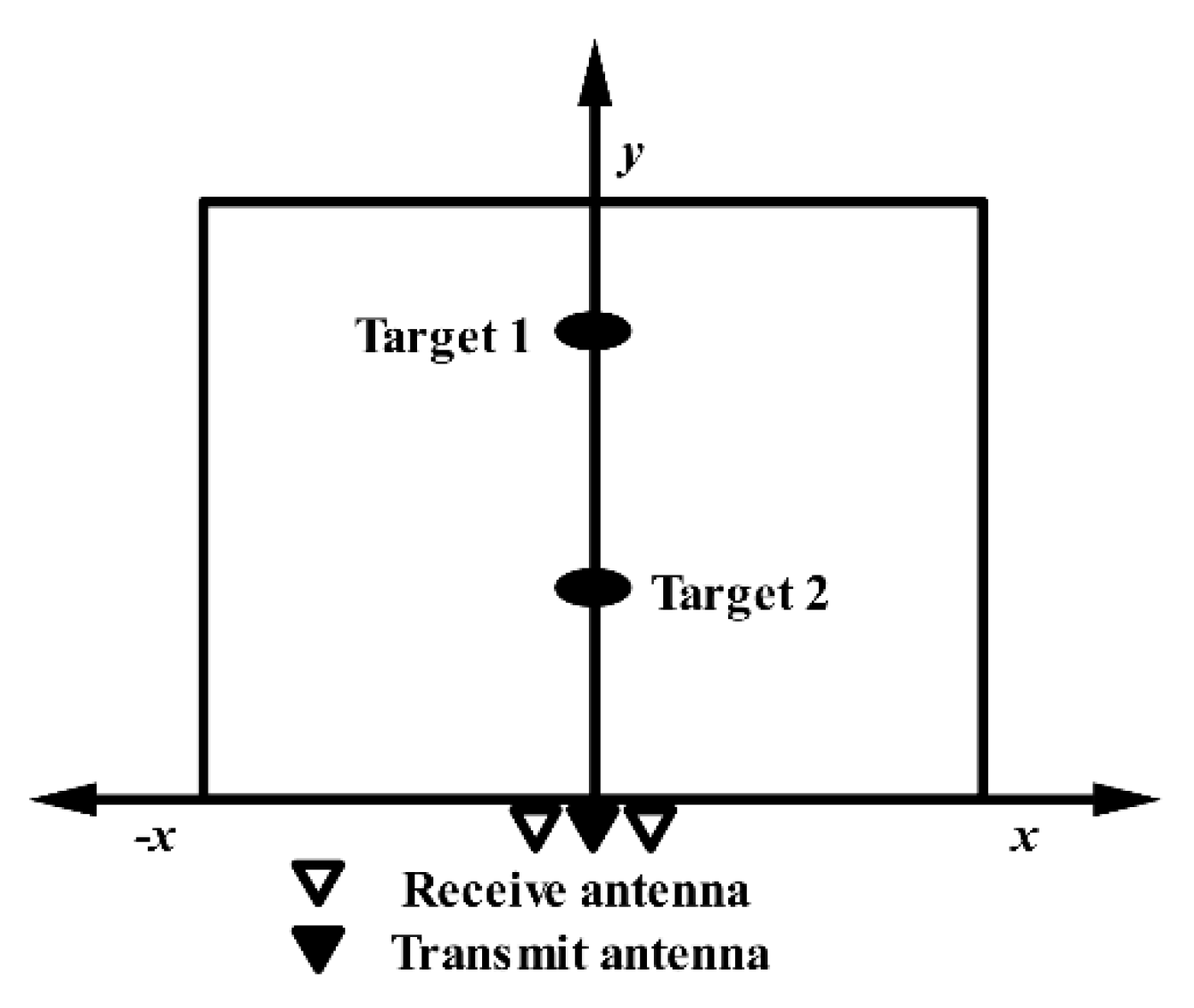
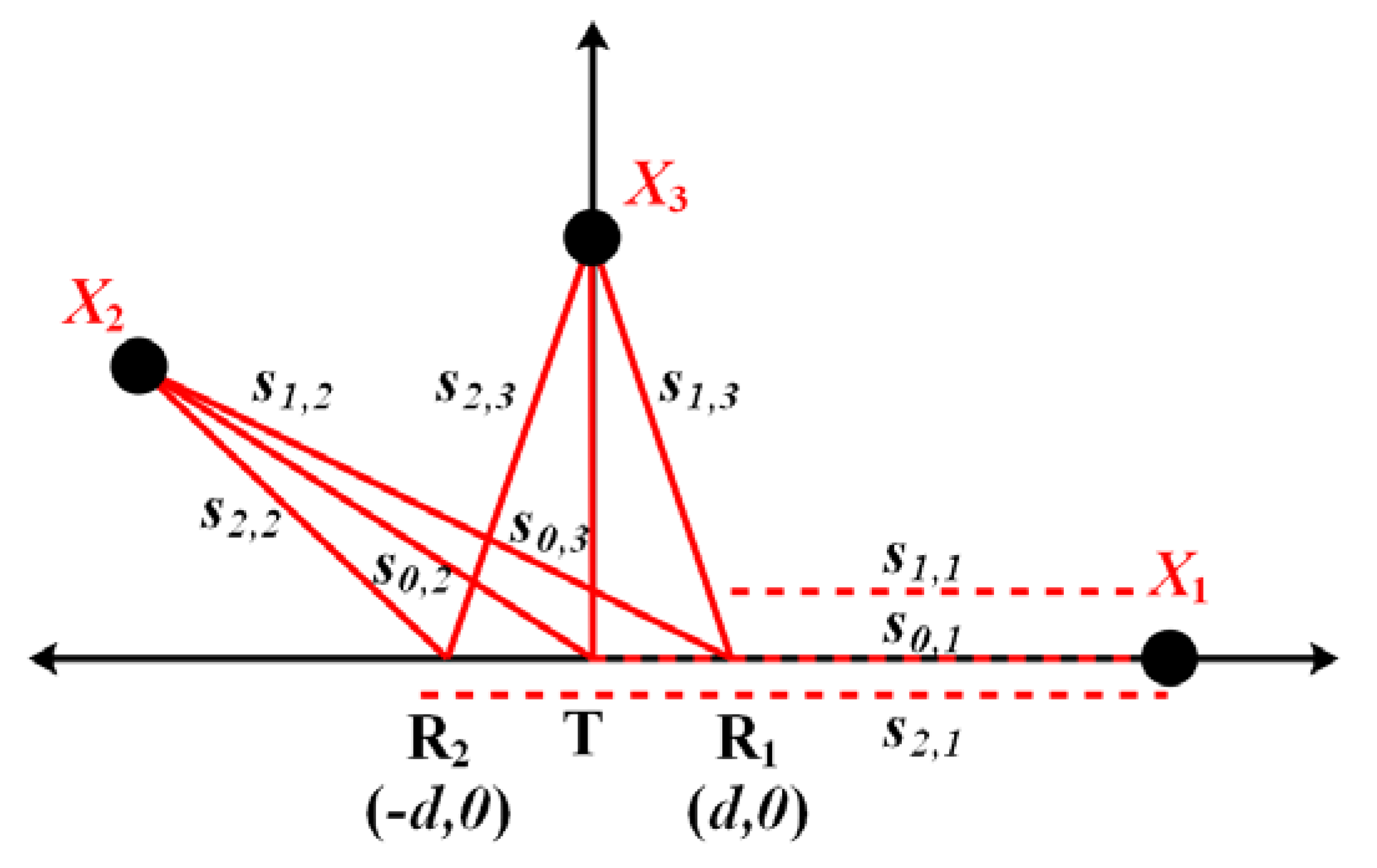
4.1. Basic Theory of Human Localization
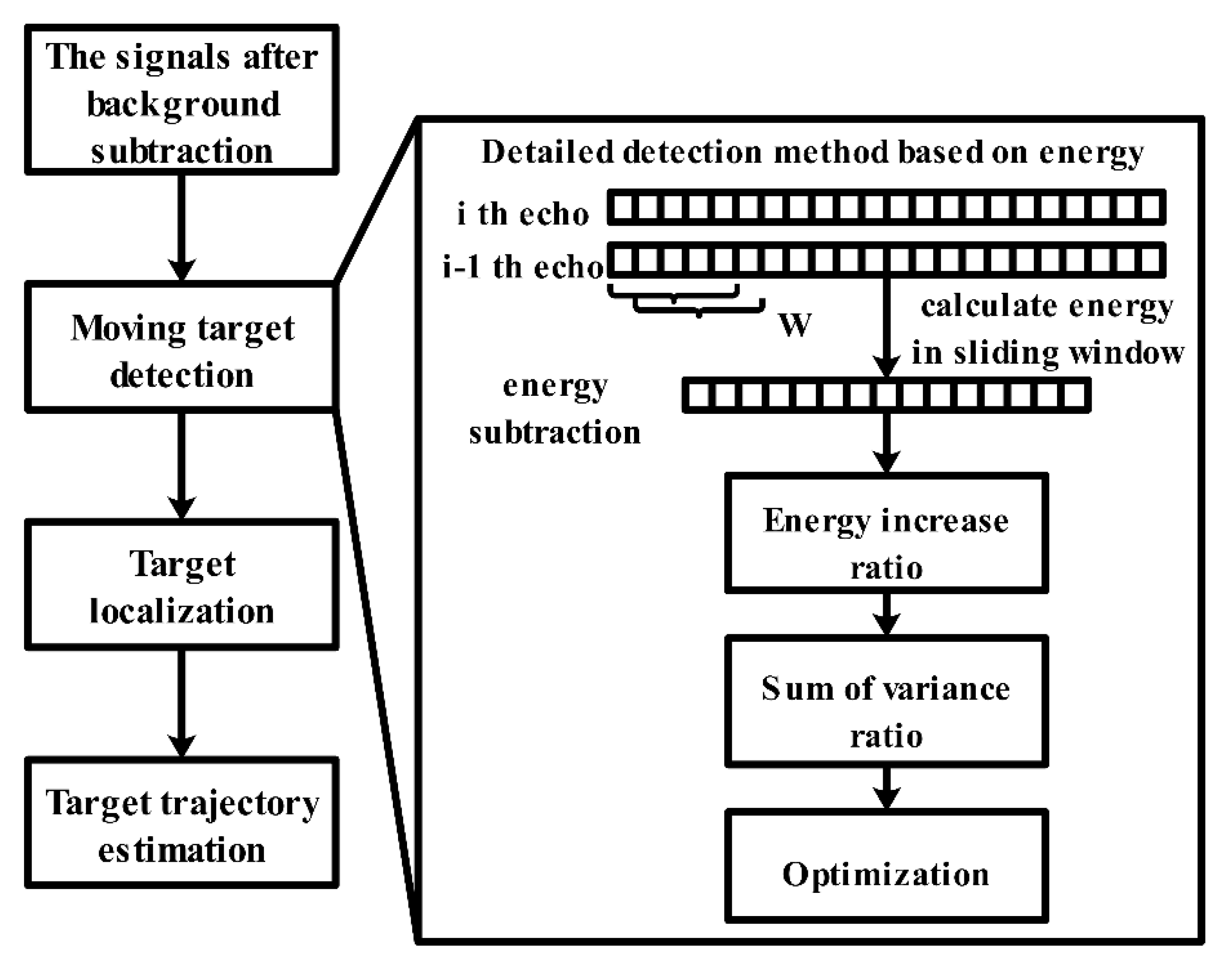
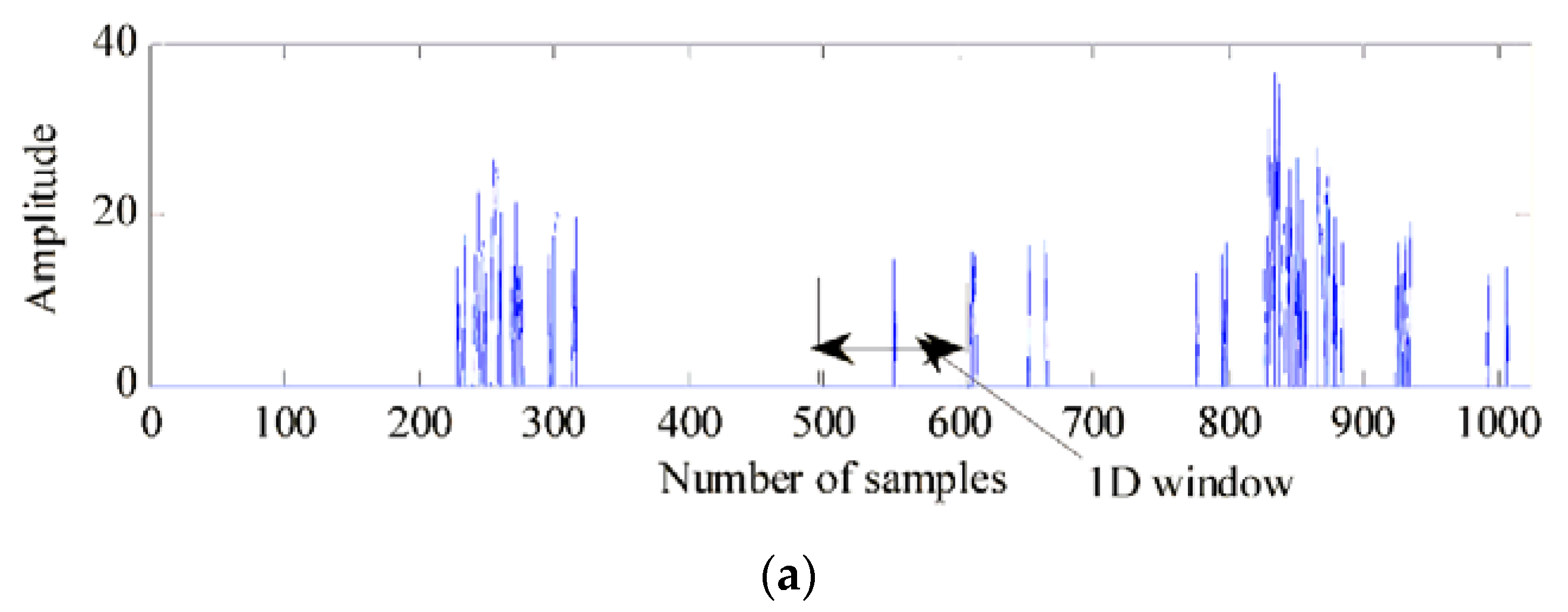
4.2. Moving Human Detection
| Algorithm 3 The steps of the CLEAN algorithm |
| Input: |
| The waveform shape |
| The detection threshold |
| Output: |
| The estimated amplitude |
| The estimated time delay |
| 1. Set the initial residual waveform and the initial counter ; |
| 2. Calculate the cross-correlation between and ; the time-index associated with the maximum amplitude of is the estimated TOA: |
| . |
| The cross-correlation at is the estimated amplitude: |
| . |
| If the path magnitude below the detection threshold is , stop and record the TOA and amplitude. |
| 3. Increase the iteration counter: . |
| 4. Update the residual waveform: |
| . |
| 5. Iterate: Go to step.2. |
| * The waveform shape $s(t)$ can be approximated by the radar transmitted signal in free space or an anechoic chamber. |
| End |
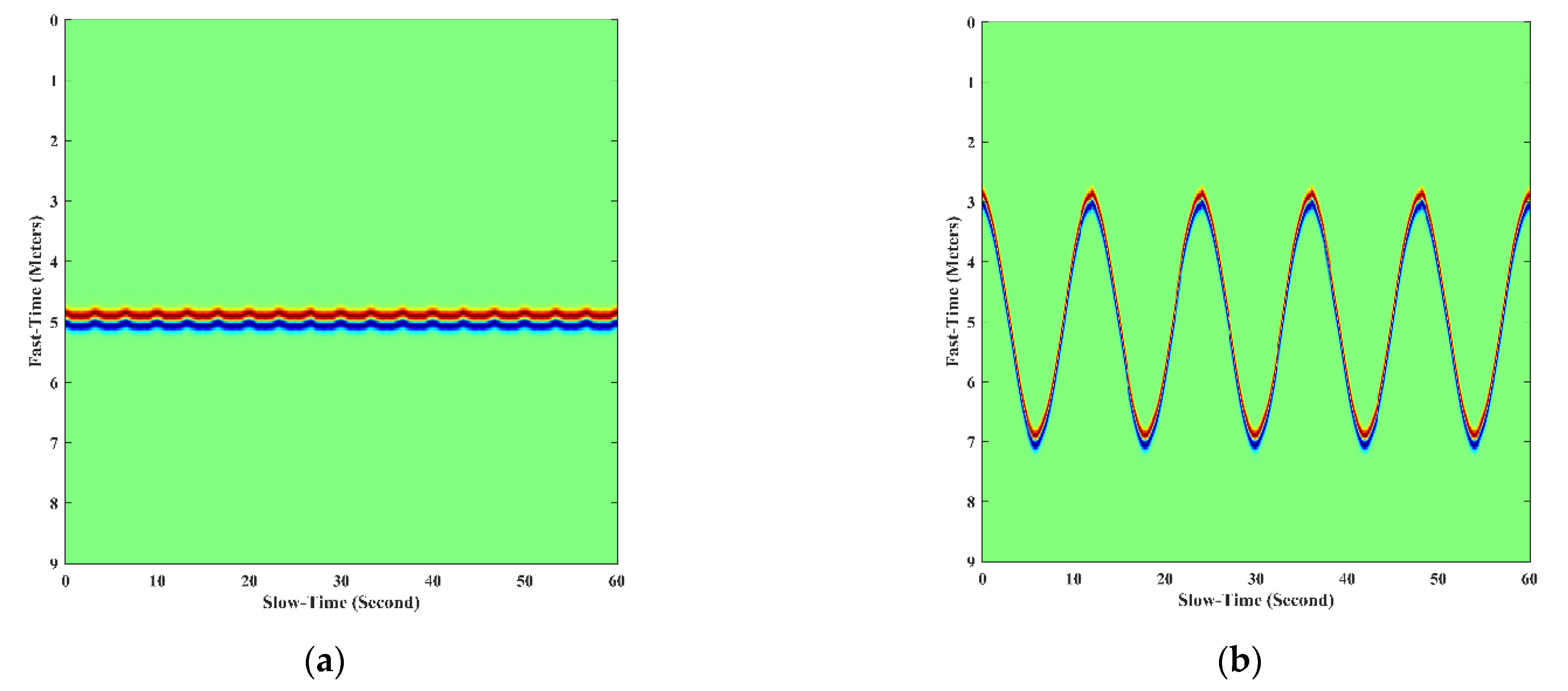
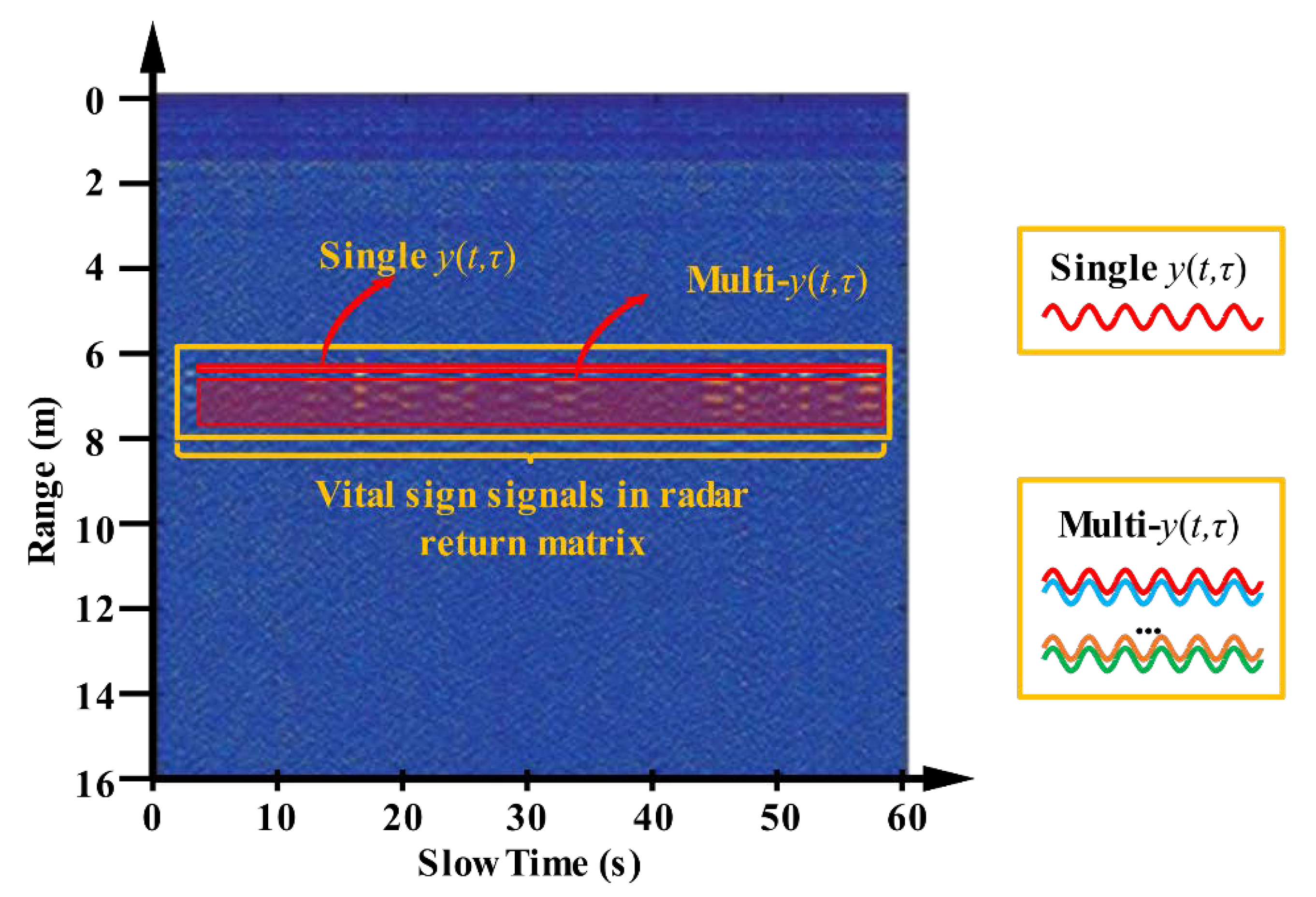
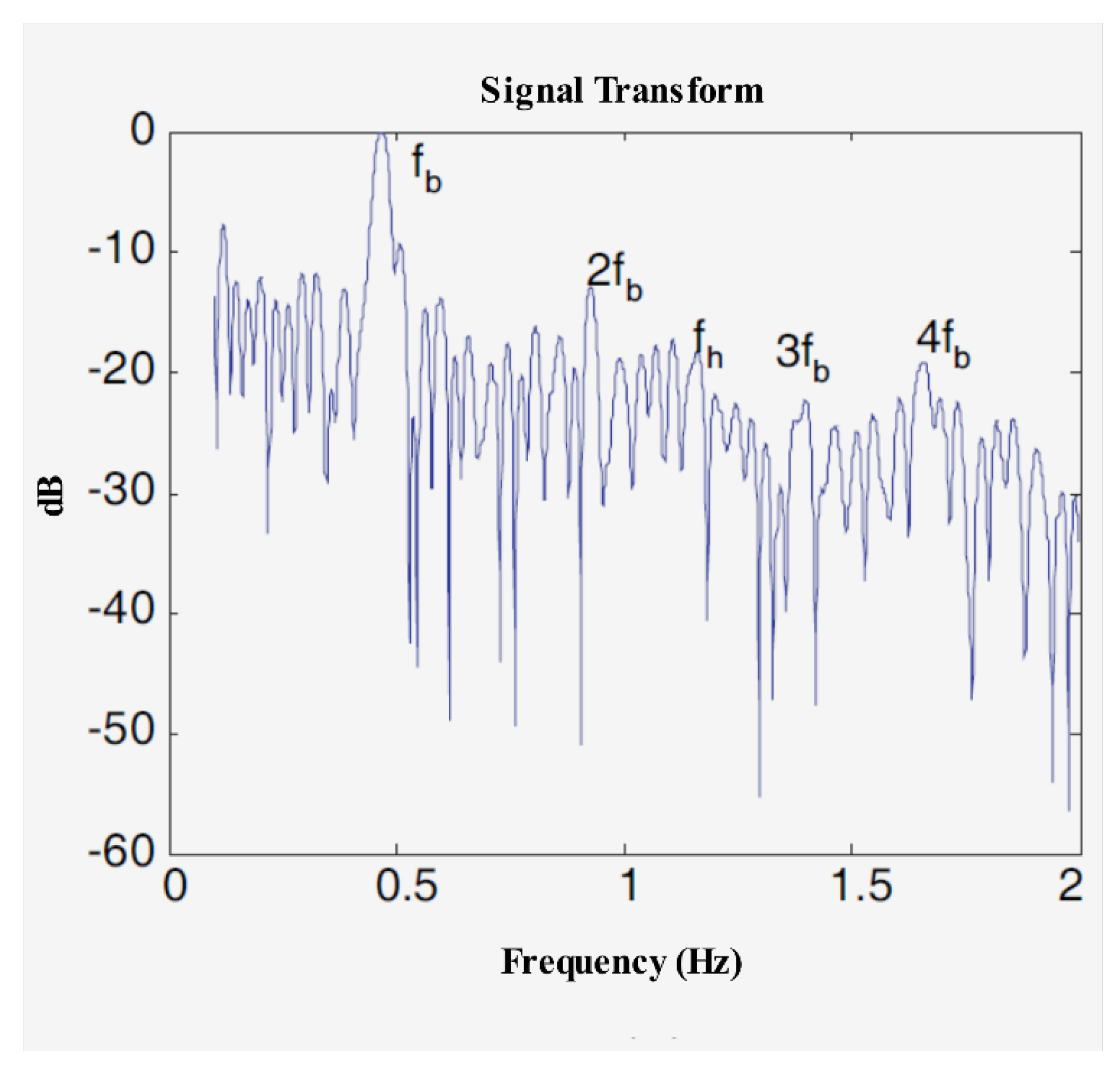
4.3. Vital Sign Signal Measurement
5. Conclusions and Future Prospects
- (1)
- Research on the cognitive detection of penetrating media. The most important task of through-wall radar is to detect a target behind non-metallic obstacles, as the physical characteristics of obstacles lead to target position distortion. At present, the parameter estimation method for through-wall radar is mainly based on SFCW UWB radar. For IR-UWB through-wall radar, determining how to recognize the parameters of obstacles in real-time is a problem worthy of further study.
- (2)
- Research on the UWB radar general integrated system. According to the particularities of the scene used by UWB radar, in addition to through-wall radar, ground penetrating radar and life detector radar can also be used. In fact, the design architectures of these three radar types are largely the same, and their signal processing algorithms also tend to be the same. Therefore, it should be determined whether these three kinds of radar can be integrated in a general system. Based on cognitive radar theory and artificial intelligence, a general system can be enabled to complete adaptive optimal detection based on a complex real-world environment.
- (3)
- Research on environment modeling. At present, many UWB through-wall radar systems have only been tested under ideal experimental conditions. However, if applied in real-world scenes, such radar solutions may face many unpredictable problems. Therefore, the gap between real-world and lab environments is worthy of attention.
- (4)
- Research on UWB radar networking. The performance of a single radar is limited in complex environments. Multiplying through-wall radar could effectively enhance the ability of environmental perception and target information acquisition. Thus, the protocol of radar networking needs to be studied.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- FC Commission. Revision of Part 15 of the Commission’s Rules Regarding Ultra-Wideband Transmission Systems; First report and order; FCC: Washington, DC, USA, 2002; pp. 2–48. [Google Scholar]
- Yarovoy, A.G.; Zhuge, X.; Savelyev, T.G.; Ligthart, L.P. Comparison of UWB Technologies for Human Being Detection with Radar. In Proceedings of the 4th European Radar Conference, Munich, Germany, 10–12 October 2007; p. 4. [Google Scholar]
- Taylor, J.D. (Ed.) Advanced Ultrawideband Radar: Signals, Targets, and Applications; CRC Press: Boca Raton, FL, USA, 2017; ISBN 978-1-4665-8657-4. [Google Scholar]
- Khan, F.; Ghaffar, A.; Khan, N.; Cho, S.H. An Overview of Signal Processing Techniques for Remote Health Monitoring Using Impulse Radio UWB Transceiver. Sensors 2020, 20, 2479. [Google Scholar] [CrossRef]
- Kebe, M.; Gadhafi, R.; Mohammad, B.; Sanduleanu, M.; Saleh, H.; Qutayri, M. Human Vital Signs Detection Methods and Potential Using Radars: A Review. Sensors 2020, 20, 1454. [Google Scholar] [CrossRef]
- Zhang, Y.; Qi, F.; Lv, H.; Liang, F.; Wang, J. Bioradar Technology: Recent Research and Advancements. IEEE Microw. 2019, 20, 58–73. [Google Scholar] [CrossRef]
- Thi, P.V.N.; Tang, L.; Demir, V.; Hasan, S.F.; Duc, M.N.; Mukhopadhyay, S. Review-Microwave Radar Sensing Systems for Search and Rescue Purposes. Sensors 2019, 19, 2879. [Google Scholar] [CrossRef]
- Jin, T.; Song, Y. Review on human target detection using through-wall radar. Chin. J. Radio Sci. 2020, 35, 486–495. [Google Scholar]
- Barnes, M.A. Covert Range Gated Wall Penetrating Motion Sensor Provides Benefits for Surveillance and Forced Entries; Time Domain Corp: Huntsville, AL, USA, 1999. [Google Scholar]
- Gaugue, A.C.; Politano, J.L. Overview of Current Technologies for Through-the-Wall Surveillance. In Proceedings of the European Symposium on Optics and Photonics for Defence and Security, Bruges, Belgium, 26–28 September 2005; p. 59891H. [Google Scholar] [CrossRef]
- Nag, S.; Barnes, M.A.; Payment, T.; Holladay, G.W. An Ultra-Wideband Through-Wall Radar for Detecting the Motion of People in Real Time. Radar Sens. Technol. Data Vis. 2002, 4744, 48–57. [Google Scholar]
- Borek, S.E. An Overview of Through the Wall Surveillance for Homeland Security. In Proceedings of the 34th Applied Imagery and Pattern Recognition Workshop (AIPR’05), Washington, DC, USA, 19 October–21 December 2009; pp. 42–47. [Google Scholar]
- Burchett, H. Advances in through Wall Radar for Search, Rescue and Security Applications. In Proceedings of the IET Conference on Crime and Security, London, UK, 13–14 June 2006; Volume 2006, pp. 511–525. [Google Scholar]
- Beeri, A.; Daisy, R. High-Resolution through-Wall Imaging. In Proceedings of the Defense and Security Symposium, Kissimmee, FL, USA, 17–21 April 2006; p. 62010J. [Google Scholar]
- Ziqi, Z.; Yang, Z.; Fugui, Q.; Miao, L.; Pengfei, W.; Yue, Y.; Gang, S.; Wang, J. Two Dimensional Localization Algorithm of Bio-Radar Based on Hyperbolic Model. China Med. Devices 2017, 32, 25–29. [Google Scholar]
- Yi, D. Recent Progress of Human Body Detection Using Through-Wall Radar. Telecommun. Eng. 2009, 10, 93–97. [Google Scholar]
- Novasky Electronic Technology Company. Novasky Products. Available online: http://novasky.cn/product.html (accessed on 30 August 2020).
- LSJ Technoogy. LSJ Technoogy Products. Available online: http://www.lsjkj.com/prolist.aspx (accessed on 30 June 2020).
- Special Equipment Network Life Detector Linked to Life Signals at the Collapsed Hotel in Quanzhou. Available online: https://news.tezhongzhuangbei.com/Qydt_date_141745.Html (accessed on 11 March 2020).
- Fei, Y. Ultra Wideband Radar Theory and Technology; Nation Defense Industry Press: Beijing, China, 2010. [Google Scholar]
- Chang, S.; Mitsumoto, N.; Burdick, J.W. An Algorithm for UWB Radar-Based Human Detection. In Proceedings of the 2009 IEEE Radar Conference, Pasadena, CA, USA, 4–8 May 2009; pp. 1–6. [Google Scholar]
- Chang, S.; Sharan, R.; Wolf, M.; Mitsumoto, N.; Burdick, J.W. People Tracking with UWB Radar Using a Multiple-Hypothesis Tracking of Clusters (MHTC) Method. Int. J. Soc. Robot. 2010, 2, 3–18. [Google Scholar] [CrossRef]
- Tsao, J.; Porrat, D.; Tse, D. Prediction and Modeling for the Time-Evolving Ultra-Wideband Channel. IEEE J. Sel. Top. Signal. Process. 2007, 1, 340–356. [Google Scholar] [CrossRef]
- Hashemi, H. Impulse Response Modeling of Indoor Radio Propagation Channels. IEEE J. Sel. Areas Commun. 1993, 11, 967–978. [Google Scholar] [CrossRef]
- Liang, X.; Deng, J.; Zhang, H.; Gulliver, T.A. Ultra-Wideband Impulse Radar Through-Wall Detection of Vital Signs. Sci. Rep. 2018, 8, 13367. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Qiao, D.; Li, Y.; Dai, H. A Novel Through-Wall Respiration Detection Algorithm Using UWB Radar. In Proceedings of the 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Osaka, Japan, 3–7 July 2013; pp. 1013–1016. [Google Scholar]
- Mark, A. Richards Fundamentals of Radar Signal. Processing, 2nd ed.; McGraw-Hill Education: New York, NY, USA, 2014. [Google Scholar]
- Zetik, R.; Crabbe, S.; Krajnak, J.; Peyerl, P.; Sachs, J.; Thomä, R. Detection and Localization of Persons behind Obstacles Using M-Sequence through-the-Wall Radar. In Proceedings of the Defense and Security Symposium, Kissimmee, FL, USA, 17–21 April 2006; p. 62010I. [Google Scholar]
- Tivive, F.H.C.; Bouzerdoum, A.; Amin, M.G. A Subspace Projection Approach for Wall Clutter Mitigation in Through-the-Wall Radar Imaging. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2108–2122. [Google Scholar] [CrossRef]
- Ahmad, F.; Amin, M.G. Multi-Location Wideband Synthetic Aperture Imaging for Urban Sensing Applications. J. Frankl. Inst. 2008, 345, 618–639. [Google Scholar] [CrossRef]
- Yeo, S.Y.; Amin, M.G. Spatial Filtering for Wall-Clutter Mitigation in Through-the-Wall Radar Imaging. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3192–3208. [Google Scholar] [CrossRef]
- Zhu, Z.; Wakin, M.B. Wall Clutter Mitigation and Target Detection Using Discrete Prolate Spheroidal Sequences. In Proceedings of the 2015 3rd International Workshop on Compressed Sensing Theory and its Applications to Radar, Sonar and Remote Sensing (CoSeRa), Pisa, Italy, 17–19 June 2015; pp. 41–45. [Google Scholar]
- Ahmad, F.; Amin, M.G.; Dogaru, T. Partially Sparse Imaging of Stationary Indoor Scenes. EURASIP J. Adv. Signal. Process. 2014, 2014, 100. [Google Scholar] [CrossRef][Green Version]
- He, F.; Zhu, G.; Mou, M.; Zhou, Z. Experiment study of life locomotion detection based on ultra-wideband through wall radar. Modem Radar 2010, 32, 29–33. [Google Scholar]
- Verma, P.K.; Gaikwad, A.N.; Singh, D.; Nigam, M.J. Analysis of clutter reduction techniques for through WALL imaging in uwb range. PIER B 2009, 17, 29–48. [Google Scholar] [CrossRef]
- Singh, S.; Liang, Q.; Chen, D.; Sheng, L. Sense through Wall Human Detection Using UWB Radar. J. Wirel. Com Netw. 2011, 2011, 20. [Google Scholar] [CrossRef]
- Rovnakova, J.; Kocur, D. Weak Signal Enhancement in Radar Signal Processing. In Proceedings of the 20th International Conference Radioelektronika 2010, Brno, Czech Republic, 19–21 April 2010; pp. 1–4. [Google Scholar]
- Kocur, D.; Rovnakova, J.; Urdzik, D. Mutual Shadowing Effect of People Tracked by the Short-Range UWB Radar. In Proceedings of the 2011 34th International Conference on Telecommunications and Signal Processing (TSP), Budapest, Hungary, 18–20 August 2011; pp. 302–306. [Google Scholar]
- Hanseok, K.; Arozullah, M. Background Noise Suppression for Signal Enhancement by Novelty Filtering. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 102–113. [Google Scholar] [CrossRef]
- Wu, X.; Jiang, Z.; Repperger, D.; Guo, Y. Nonlinear Enhancement of Weak Signals Using Optimization Theory. In Proceedings of the 2006 International Conference on Mechatronics and Automation, Luoyang, China, 25–28 June 2006; pp. 66–71. [Google Scholar]
- Tzanis, A. MatGPR Release 2: A Freeware MATLAB® Package for the Analysis & Interpretation of Common and Single Offset GPR Data. FastTimes 2010, 15, 17–43. [Google Scholar]
- Zhu, Z.; Liang, B.; Yang, D.; Zhao, R. Research, Fabrication and Application of IR-UWB through Wall Radar System. Transducer Microsyst. Technol. 2020, 39, 103–106. [Google Scholar]
- Yelf, R. Where Is True Time Zero? In Proceedings of the Tenth International Conference on Grounds Penetrating Radar, Delft, The Netherlands, 21 June 2004; Volume 1, pp. 279–282. [Google Scholar]
- Wang, G.; Amin, M.G. Imaging Through Unknown Walls Using Different Standoff Distances. IEEE Trans. Signal. Process. 2006, 54, 4015–4025. [Google Scholar] [CrossRef]
- Dehmollaian, M.; Sarabandi, K. Refocusing Through Building Walls Using Synthetic Aperture Radar. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1589–1599. [Google Scholar] [CrossRef]
- Muqaibel, A.H.; Safaai, J.A. A New Formulation for Characterization of Materials Based on Measured Insertion Transfer Function. IEEE Trans. Microw. Theory Techn. 2003, 51, 1946–1951. [Google Scholar] [CrossRef]
- Muqaibel, A.; Safaai, J.A.; Bayram, A.; Riad, S.M. Ultra Wideband Material Characterization for Indoor Propagation. In Proceedings of the IEEE Antennas and Propagation Society International Symposium, Digest. Held in conjunction with: USNC/CNC/URSI North American Radio Sci. Meeting (Cat. No.03CH37450), Columbus, OH, USA, 22–27 June 2003; Volume 4, pp. 623–626. [Google Scholar]
- Wang, G.; Amin, M.G.; Zhang, Y. New Approach for Target Locations in the Presence of Wall Ambiguities. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 301–315. [Google Scholar] [CrossRef]
- Zhang, H.M.; Zhang, Y.R.; Wang, F.F.; An, J.L. Application of Support Vector Machines for Estimating Wall Parameters in Through-Wall Radar Imaging. Int. J. Antennas Propag. 2015, 2015, 1–8. [Google Scholar] [CrossRef]
- Qu, L. Sparse Blind Deconvolution Method for Wall Parameters Estimation. IEEE Geosci. Remote Sens. Lett. 2020, 1–5. [Google Scholar] [CrossRef]
- Li, X.; An, D.; Huang, X.; Peng, S. Estimation of Wall Parameters Based on Range Profiles. Sci. China Inf. Sci. 2011, 54, 2178–2189. [Google Scholar] [CrossRef]
- Warren, C.; Giannopoulos, A.; Giannakis, I. GprMax: Open Source Software to Simulate Electromagnetic Wave Propagation for Ground Penetrating Radar. Comput. Phys. Commun. 2016, 209, 163–170. [Google Scholar] [CrossRef]
- Thajudeen, C.; Hoorfar, A. A Hybrid Bistatic–Monostatic Radar Technique for Calibration-Free Estimation of Lossy Wall Parameters. Antennas Wirel. Propag. Lett. 2017, 16, 1249–1252. [Google Scholar] [CrossRef]
- Mu, K.; Luan, T.H.; Zhu, L.; Cai, L.X.; Gao, L. A Survey of Handy See-Through Wall Technology. IEEE Access 2020, 8, 82951–82971. [Google Scholar] [CrossRef]
- Rovňáková, J.; Kocur, D. TOA Estimation and Data Association for Through-Wall Tracking of Moving Targets. J. Wirel. Com. Netw. 2010, 2010, 420767. [Google Scholar] [CrossRef]
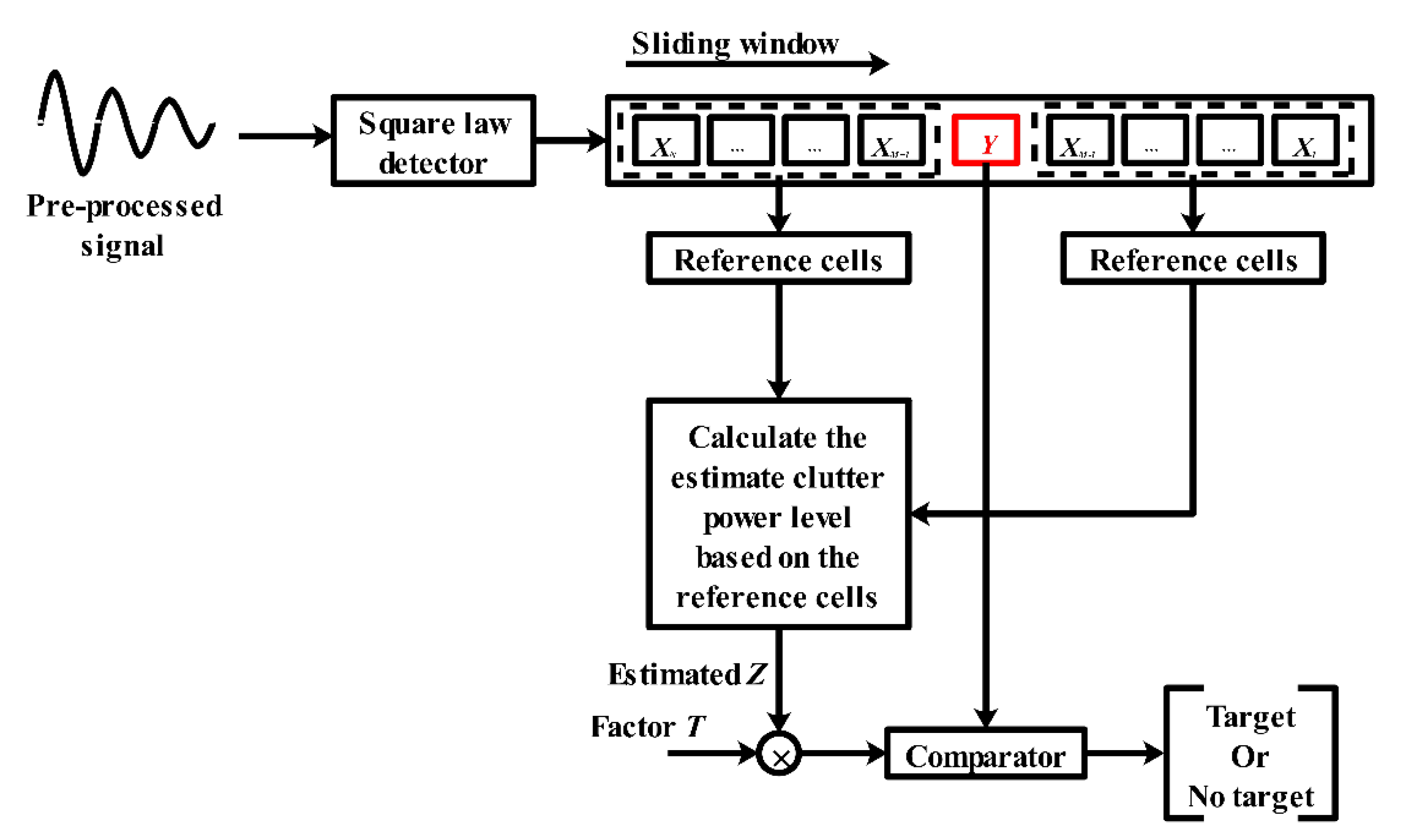
- Rohling, H. Radar CFAR Thresholding in Clutter and Multiple Target Situations. IEEE Trans. Aerosp. Electron. Syst. 1983, 19, 608–621. [Google Scholar] [CrossRef]
- Liang, X.; Lv, T.; Zhang, H.; Gao, Y.; Fang, G. Through-Wall Human Being Detection Using UWB Impulse Radar. J. Wirel. Com. Netw. 2018, 2018, 46. [Google Scholar] [CrossRef]
- Yan, J.; Hong, H.; Zhao, H.; Li, Y.; Gu, C.; Zhu, X. Through-Wall Multiple Targets Vital Signs Tracking Based on VMD Algorithm. Sensors 2016, 16, 1293. [Google Scholar] [CrossRef] [PubMed]
- Liang, S.D. Sense-through-Wall Human Detection Based on UWB Radar Sensors. Signal. Process. 2016, 126, 117–124. [Google Scholar] [CrossRef]
- Liang, X.; Zhang, H.; Ye, S.; Gulliver, T.A. An Improved Algorithm for Through-Wall Target Detection Using Ultra-Wideband Impulse Radar. IEEE Access 2017, 5, 18. [Google Scholar] [CrossRef]
- In, C.; Lim, D.W.; Kang, J.M.; Lee, J.H.; Kim, H.M.; Kim, S.; Kim, C. Human Detection Based on the Condition Number in the Non-Stationary Clutter Environment Using UWB Impulse Radar. In Proceedings of the 2013 Asia-Pacific Microwave Conference Proceedings (APMC), Seoul, Korea, 5–8 November 2013; pp. 1006–1008. [Google Scholar]
- Xue, H.; Liu, M.; Zhang, Y.; Liang, F.; Qi, F.; Chen, F.; Lv, H.; Wang, J.; Zhang, Y. An Algorithm Based Wavelet Entropy for Shadowing Effect of Human Detection Using Ultra-Wideband Bio-Radar. Sensors 2017, 17, 2255. [Google Scholar] [CrossRef]
- Wu, S.; Fang, G. Detection and Tracking of Moving Target behind Wall Using UWB Through-Wall Radar. In Proceedings of the 2010 International Conference on Intelligent System Design and Engineering Application, Changsha, China, 13–14 October 2010; pp. 605–608. [Google Scholar]
- Liang, X.; Zhang, H. Remotely Detectable Signs of Life Based on Impulse UWB Radar. Multimed. Tools Appl. 2019, 78, 10583–10599. [Google Scholar] [CrossRef]
- Liang, X.; Deng, J. Detection of Stationary Human Target via Contactless Radar Networks. J. Ambient Intell. Hum. Comput. 2019, 10, 3193–3200. [Google Scholar] [CrossRef]
- Urdzik, D.; Kocur, D. CFAR Detectors for through Wall Tracking of Moving Targets by M-Sequence UWB Radar. In Proceedings of the 20th International Conference Radioelektronika 2010, Brno, Czech Republic, 19–21 April 2010; pp. 1–4. [Google Scholar]
- Liu, J. Human Target Detection and Tracking with Ultra-Wideband Radar; National University of Defense Technology: Changsha, China, 2014. [Google Scholar]
- Nguyen, V.H.; Pyun, J.Y. Location Detection and Tracking of Moving Targets by a 2D IR-UWB Radar System. Sensors 2015, 15, 6740–6762. [Google Scholar] [CrossRef] [PubMed]
- Khan, F.; Cho, S. A Detailed Algorithm for Vital Sign Monitoring of a Stationary/Non-Stationary Human through IR-UWB Radar. Sensors 2017, 17, 290. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Liu, Z.; Barrowes, B.E. Through-Wall Bio-Radiolocation with UWB Impulse Radar: Observation, Simulation and Signal Extraction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 791–798. [Google Scholar] [CrossRef]
- Lazaro, A.; Girbau, D.; Villarino, R. Analysis of vital signs monitoring using an IR-UWB radar. PIER 2010, 100, 265–284. [Google Scholar] [CrossRef]
- Singh, M.; Ramachandran, G. Reconstruction of Sequential Cardiac In-Plane Displacement Patterns on the Chest Wall by Laser Speckle Interferometry. IEEE Trans. Biomed. Eng. 1991, 38, 483–489. [Google Scholar] [CrossRef]
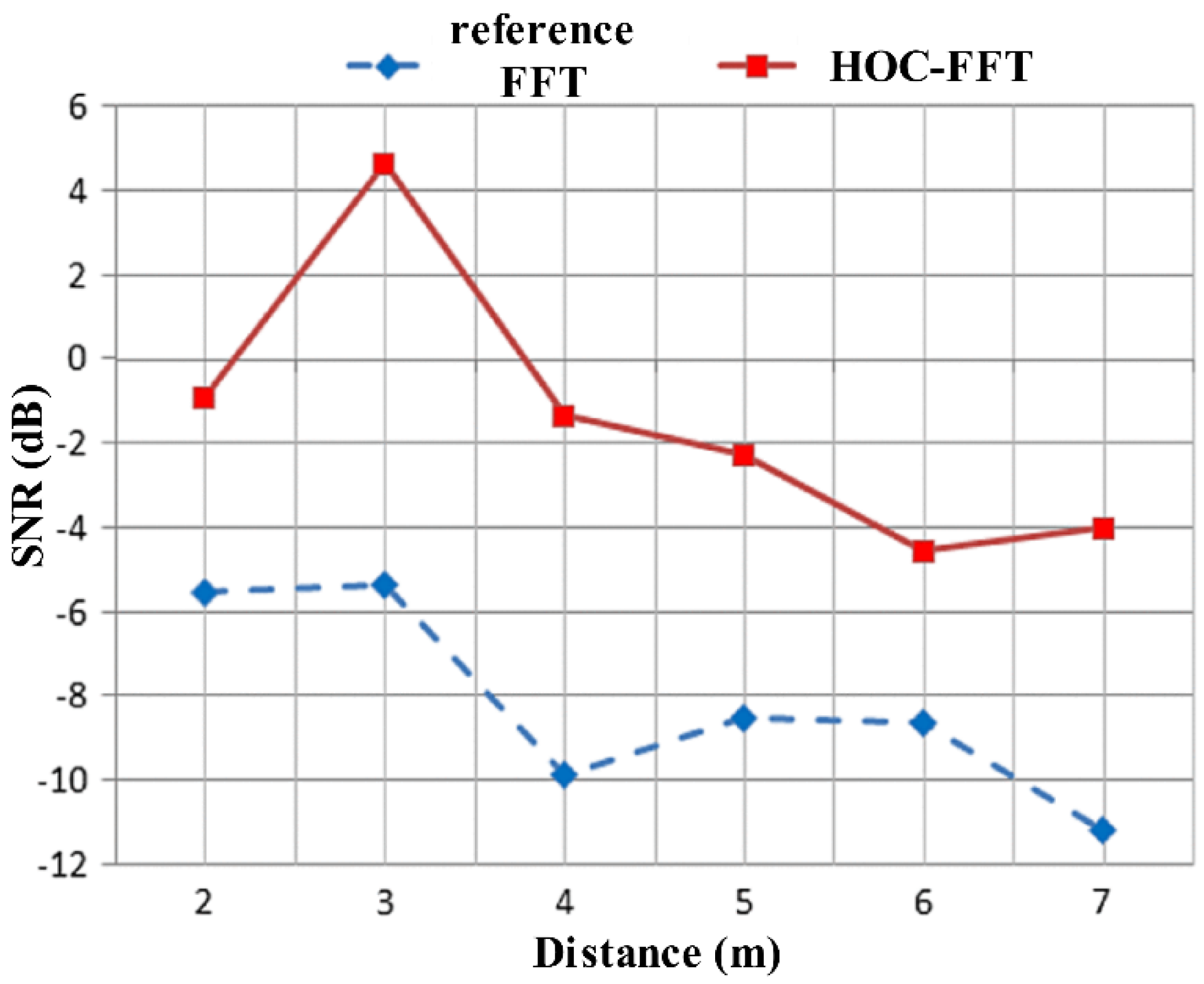
- Xu, Y.; Dai, S.; Wu, S.; Chen, J.; Fang, G. Vital Sign Detection Method Based on Multiple Higher Order Cumulant for Ultrawideband Radar. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1254–1265. [Google Scholar] [CrossRef]
- Li, J.; Zeng, Z.; Sun, J.; Liu, F. Through-Wall Detection of Human Being’s Movement by UWB Radar. IEEE Geosci. Remote Sens. Lett. 2012, 9, 1079–1083. [Google Scholar] [CrossRef]
- Baboli, M.; Ghorashi, S.A.; Saniei, N.; Ahmadian, A. A New Wavelet Based Algorithm for Estimating Respiratory Motion Rate Using UWB Radar. In Proceedings of the 2009 International Conference on Biomedical and Pharmaceutical Engineering, Singapore, 2–4 December 2009; pp. 1–3. [Google Scholar]
- Le, M.; Le, D.K.; Lee, J. Multivariate Singular Spectral Analysis for Heartbeat Extraction in Remote Sensing of Uwb Impulse Radar. Sens. Actuators A Phys. 2020, 306, 111968. [Google Scholar] [CrossRef]
- Liu, L.; Liu, Z.; Xie, H.; Barrowes, B.; Bagtzoglou, C.A. Numerical Simulation of UWB Impulse Radar Vital Sign Detection at an Earthquake Disaster Site. Ad Hoc Netw. 2014, 13, 34–41. [Google Scholar] [CrossRef]
- Shyu, K.K.; Chiu, L.J.; Lee, P.L.; Tung, T.H.; Yang, S.H. Detection of Breathing and Heart Rates in UWB Radar Sensor Data Using FVPIEF-Based Two-Layer EEMD. IEEE Sens. J. 2019, 19, 774–784. [Google Scholar] [CrossRef]
- Feng, J.; Pan, S. Extraction Algorithm of Vital Signals Based on Empirical Mode Decomposition. J. China Univ. Technol. (Nat. Sci. Ed.) 2010, 38, 1–6. [Google Scholar]
- Zhang, C.; Zhang, C.; Zhang, Q. Applications of EEMD in Vital Signal Detection for UWB Radar. Electron. Meas. Technol. 2012, 35, 76–80. [Google Scholar]
- Gouveia, C.; Vieira, J.; Pinho, P. A Review on Methods for Random Motion Detection and Compensation in Bio-Radar Systems. Sensors 2019, 19, 604. [Google Scholar] [CrossRef] [PubMed]
- Lazaro, A.; Girbau, D.; Villarino, R. Techniques for Clutter Suppression in the Presence of Body Movements during the Detection of Respiratory Activity through UWB Radars. Sensors 2014, 14, 2595–2618. [Google Scholar] [CrossRef] [PubMed]
- Liang, B.; Jin, Y.; Yang, D.; Zhao, D.; Zhang, Y. An Accelerated Algorithm for Detecting Micro-Moving Objects of Radar Life Detector of Smart Campus Based on Block Data Analysis. IEEE Access 2018, 6, 57994–58003. [Google Scholar] [CrossRef]
- Yang, D.; Zhu, Z.; Liang, B. Vital Sign Signal Extraction Method Based on Permutation Entropy and EEMD Algorithm for Ultra-Wideband Radar. IEEE Access 2019, 7, 128879–178890. [Google Scholar] [CrossRef]












| Thickness (cm) | Relative Permittivity | Conductivity (S/m) | ||||
|---|---|---|---|---|---|---|
| Actual | Error | Actual | Error | Actual | Error | |
| Proposed method | 10 | 2.2% | 6 | 3.8% | 0.01 | 15.5% |
| ESPRIT method | 19.5% | 66.7% | 40.7% | |||
| Proposed method | 20 | 0.39% | 0.5% | 20.4% | ||
| ESPRIT method | 3.15% | 6.2% | 24.1% | |||
| Proposed method | 30 | 0.07% | 0.33% | 22.9% | ||
| ESPRIT method | 0.67% | 1% | 21.8% | |||
| SNE(dB) | Thickness (cm) | Relative Permittivity | Conductivity (S/m) | |||
|---|---|---|---|---|---|---|
| Estimated | Actual | Estimated | Actual | Estimated | Actual | |
| 0 | 20.73 | 20 | 5.60 | 6 | 0.0048 | 0.01 |
| 5 | 20.33 | 5.83 | 0.0068 | |||
| 10 | 19.65 | 6.22 | 0.0085 | |||
| 15 | 19.83 | 6.11 | 0.0112 | |||
| 20 | 20.19 | 5.91 | 0.0108 | |||
| 25 | 20.08 | 5.97 | 0.0110 | |||
| 30 | 20.08 | 5.97 | 0.0108 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, D.; Zhu, Z.; Zhang, J.; Liang, B. The Overview of Human Localization and Vital Sign Signal Measurement Using Handheld IR-UWB Through-Wall Radar. Sensors 2021, 21, 402. https://doi.org/10.3390/s21020402
Yang D, Zhu Z, Zhang J, Liang B. The Overview of Human Localization and Vital Sign Signal Measurement Using Handheld IR-UWB Through-Wall Radar. Sensors. 2021; 21(2):402. https://doi.org/10.3390/s21020402
Chicago/Turabian StyleYang, Degui, Zhengliang Zhu, Junchao Zhang, and Buge Liang. 2021. "The Overview of Human Localization and Vital Sign Signal Measurement Using Handheld IR-UWB Through-Wall Radar" Sensors 21, no. 2: 402. https://doi.org/10.3390/s21020402
APA StyleYang, D., Zhu, Z., Zhang, J., & Liang, B. (2021). The Overview of Human Localization and Vital Sign Signal Measurement Using Handheld IR-UWB Through-Wall Radar. Sensors, 21(2), 402. https://doi.org/10.3390/s21020402







