A New Algebraic Solution for Acoustic Emission Source Localization without Premeasuring Wave Velocity
Abstract
:1. Introduction
2. Related Works
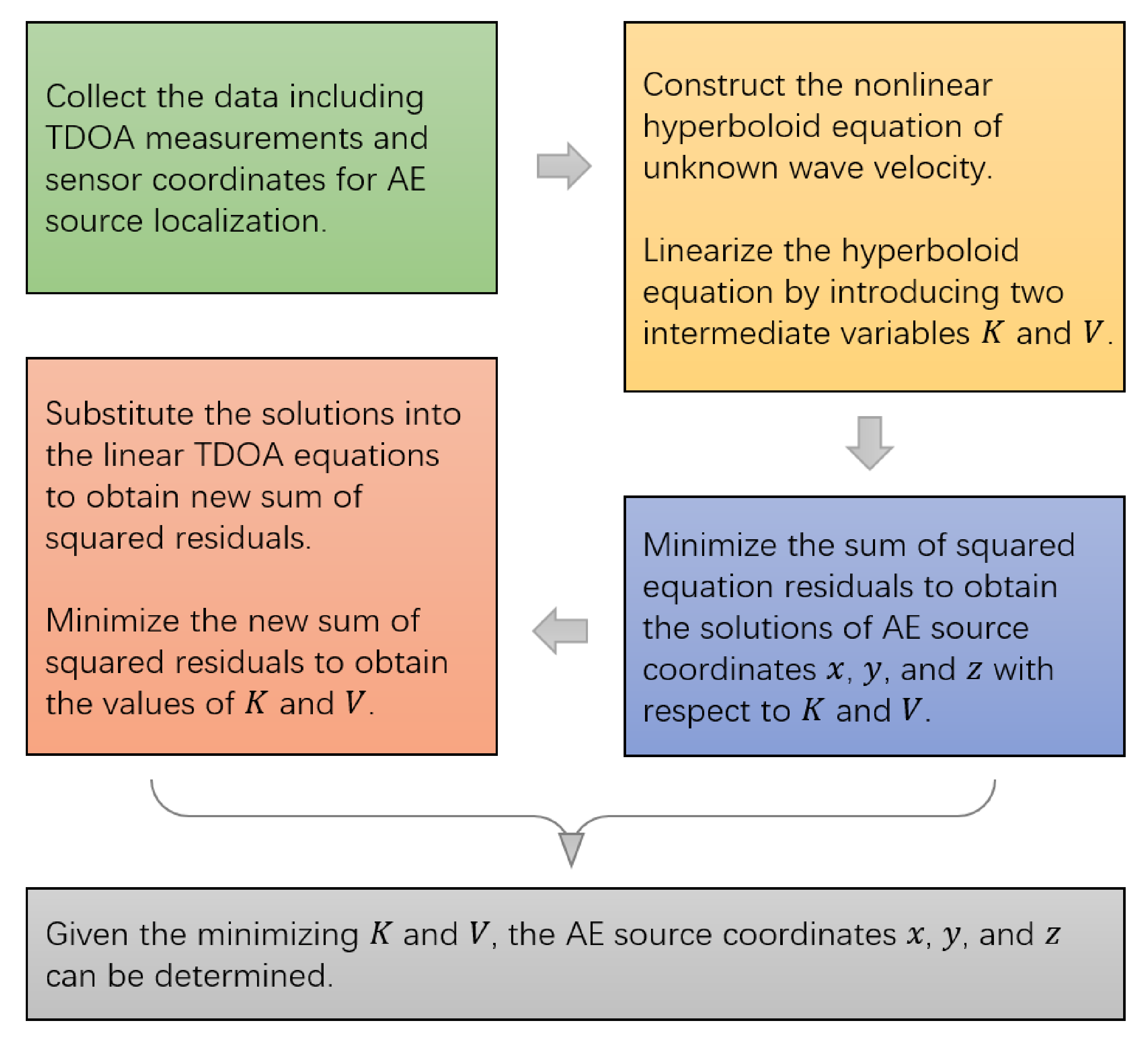
3. Theory of the Proposed Method
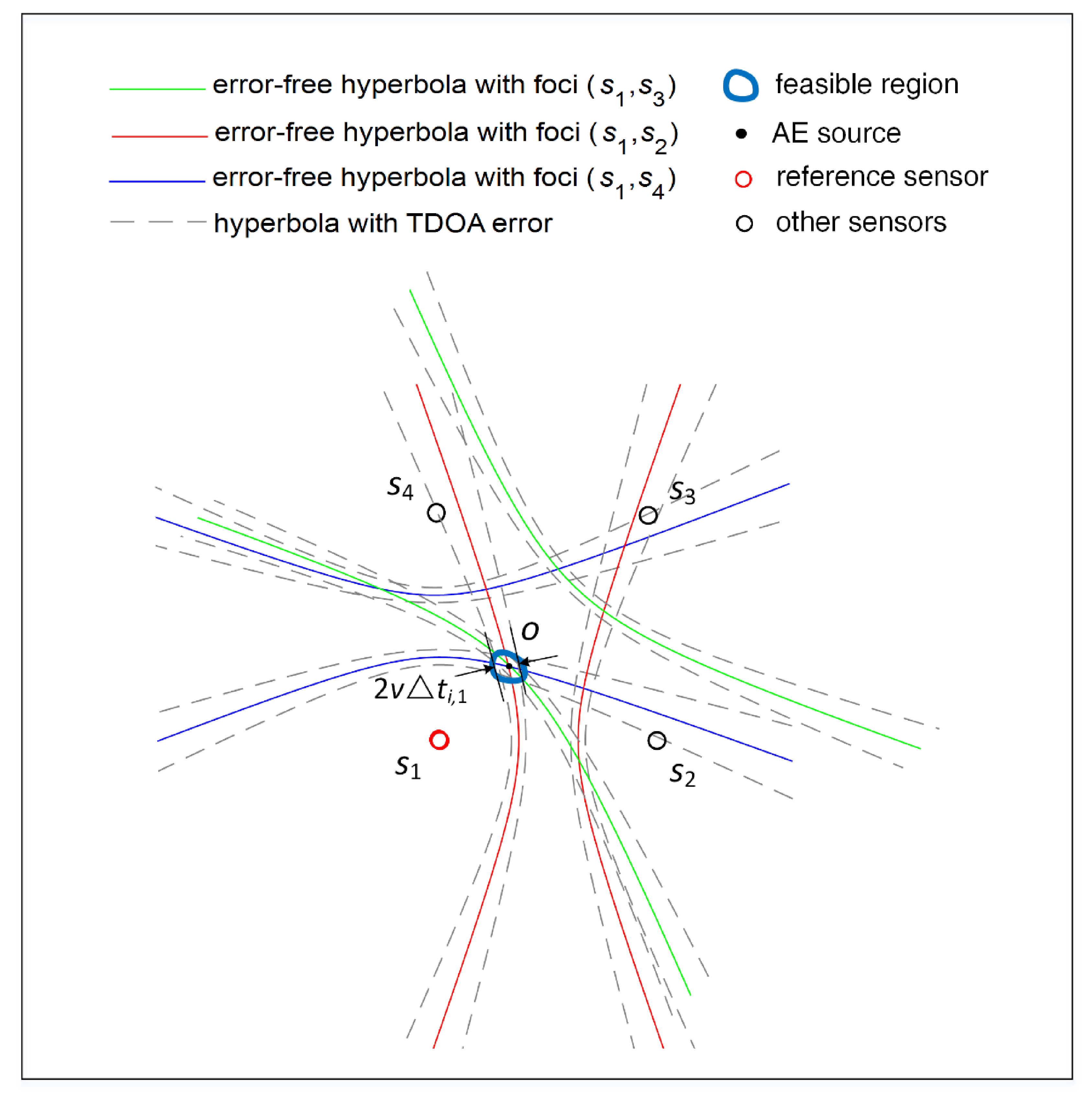
3.1. Transform the Nonlinear Hyperboloid Equations into Linear Ones
3.2. Minimize Sum of Squared Residuals with Respect to x, y, and z
3.3. Minimize Sum of Squared Residuals with Respect to K and V
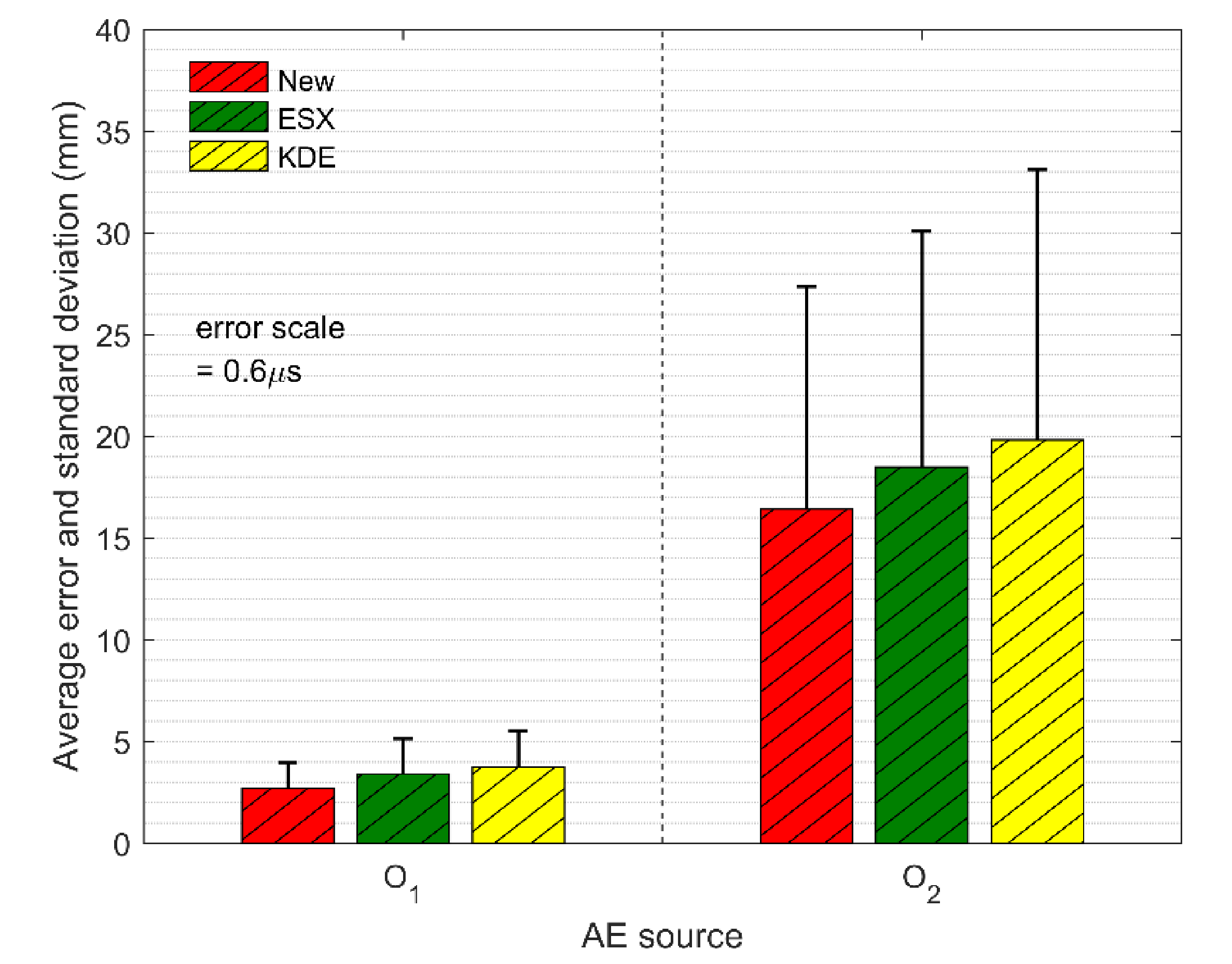
4. The Experiment of Pencil-Lead Breaks
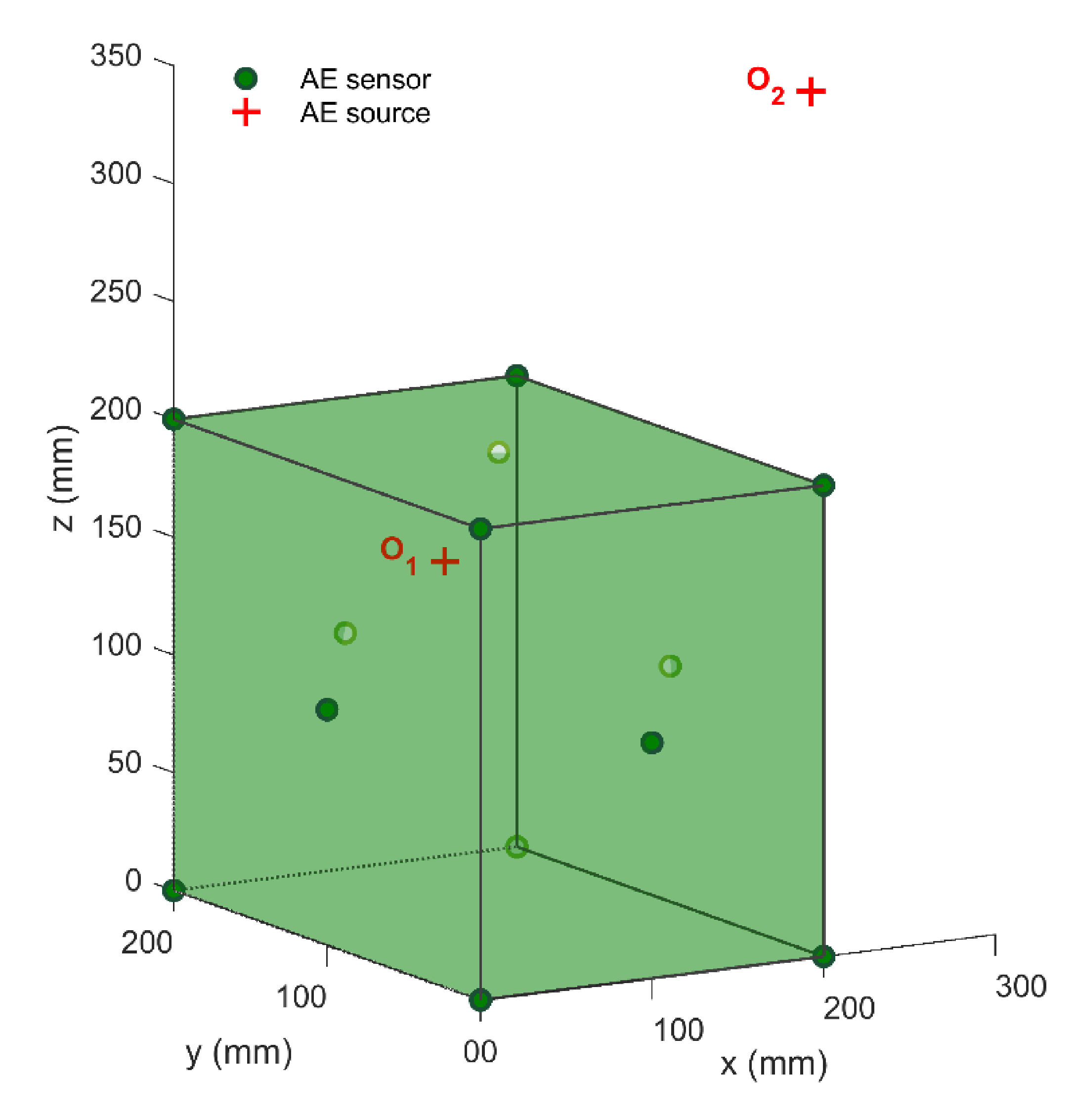
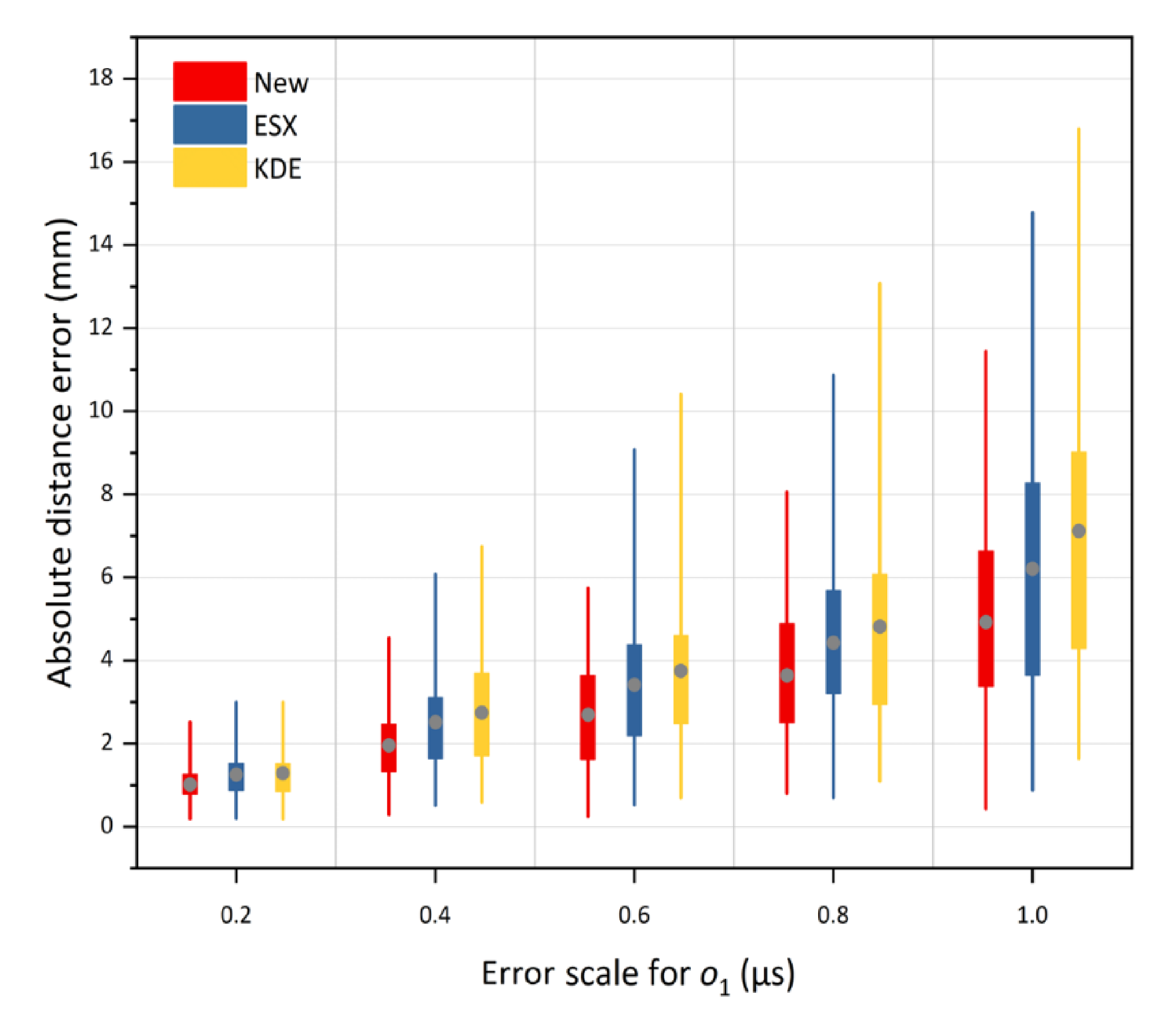
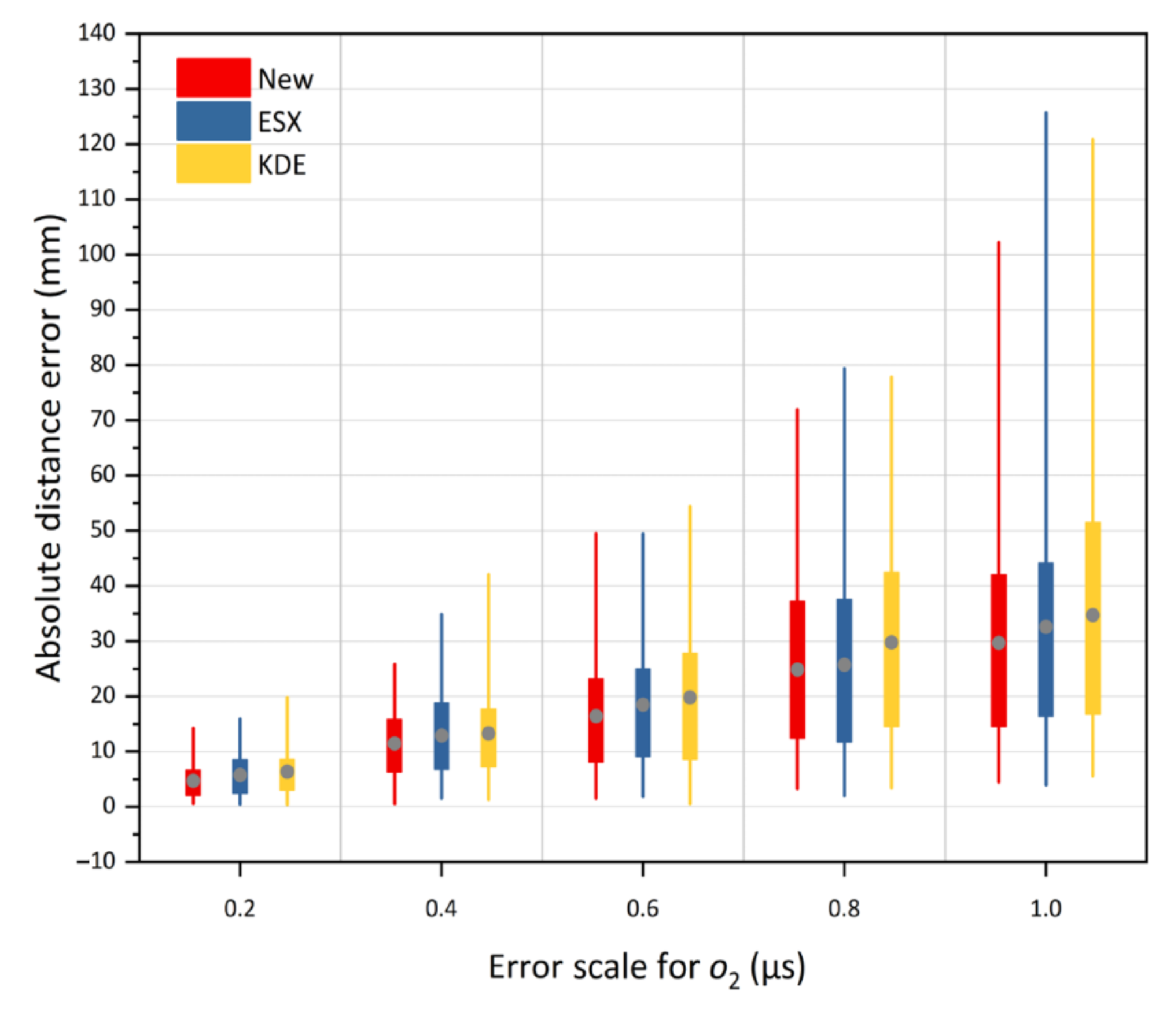
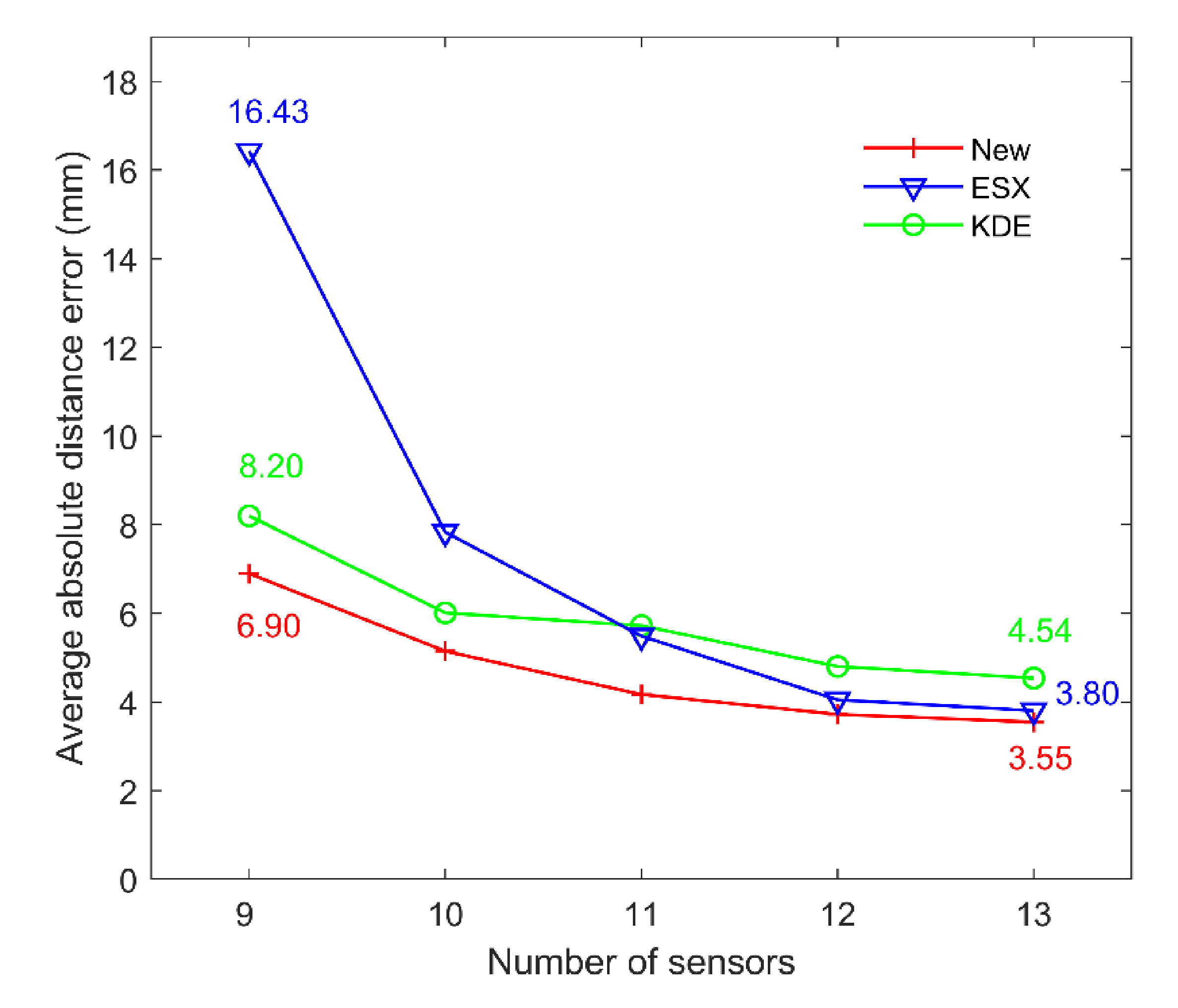
5. Simulation Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Grosse, C.U.; Ohtsu, M. Acoustic Emission Testing; Springer Science & Business Media: Heidelberg, Germany, 2008. [Google Scholar]
- Cai, X.; Zhou, Z.; Tan, L.; Zang, H.; Song, Z. Water Saturation Effects on Thermal Infrared Radiation Features of Rock Materials During Deformation and Fracturing. Rock Mech. Rock Eng. 2020, 53, 1–18. [Google Scholar]
- Du, K.; Li, X.; Tao, M.; Wang, S. Experimental study on acoustic emission (AE) characteristics and crack classification during rock fracture in several basic lab tests. Int. J. Rock Mech. Min. Sci. 2020, 133, 104411. [Google Scholar] [CrossRef]
- Wang, Y.; Han, J.Q.; Li, C.H. Acoustic emission and CT investigation on fracture evolution of granite containing two flaws subjected to freeze—Thaw and cyclic uniaxial increasing-amplitude loading conditions. Constr. Build. Mater. 2020, 260, 119769. [Google Scholar] [CrossRef]
- Holford, K.M.; Carter, D.C. Acoustic Emission Source Location. Key Eng. Mater. 1999, 167–168, 162–171. [Google Scholar] [CrossRef]
- Stoica, P.; Li, J. Source Localization from Range-Difference Measurements. IEEE Signal Process. Mag. 2006, 23, 63–66. [Google Scholar] [CrossRef]
- Yue, J.G.; Kunnath, S.K.; Xiao, Y. Uniaxial concrete tension damage evolution using acoustic emission monitoring. Constr. Build. Mater. 2020, 232, 117281. [Google Scholar] [CrossRef]
- Dou, L.; Lu, C.; Mu, Z.; Gao, M. Prevention and forecasting of rock burst hazards in coal mines. Min. Sci. Technol. 2009, 19, 585–591. [Google Scholar] [CrossRef]
- Li, L.; Yang, K.; Bian, X.; Liu, Q.; Yang, Y.; Ma, F. A Gas Leakage Localization Method Based on a Virtual Ultrasonic Sensor Array. Sensors 2019, 19, 3152. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peng, P.; Jiang, Y.; Wang, L.; He, Z. Microseismic event location by considering the influence of the empty area in an excavated tunnel. Sensors 2020, 20, 574. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, Z.; Rui, Y.; Zhou, J.; Dong, L.; Cai, X. Locating an Acoustic Emission Source in Multilayered Media Based on the Refraction Path Method. IEEE Access 2018, 6, 25090–25099. [Google Scholar] [CrossRef]
- Inglada, V. The calculation of the stove coordinates of a Nahbebens. Gerlands Beitrage Zur Geophys. 1928, 19, 73–98. [Google Scholar]
- Abel, J.S.; Smith, J.O. Spherical Interpolation Method for Closed-Form Passive Source Localization Using Range Difference Measurements. ICASSP IEEE Int. Conf. Acoust. Speech Signal Process. Proc. 1987, 12, 471–474. [Google Scholar]
- Schau, H.C.; Robinson, A.Z. Passive Source Localization Employing Intersecting Spherical Surfaces from Time-of-Arrival Differences. IEEE Trans. Acoust. 1987, 35, 1223–1225. [Google Scholar] [CrossRef]
- Schmidt, R.O. New Approach to Geometry of Range Difference Location. IEEE Trans. Aerosp. Electron. Syst. 1972, 8, 821–835. [Google Scholar] [CrossRef]
- Zhou, Z.; Rui, Y.; Zhou, J.; Dong, L.; Chen, L.; Cai, X.; Cheng, R. A new closed-form solution for acoustic emission source location in the presence of outliers. Appl. Sci. 2018, 8, 949. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Dong, L.; Li, X.; Yin, Z.; Liu, X. Effects of sonic speed on location accuracy of acoustic emission source in rocks. Trans. Nonferrous Met. Soc. China 2011, 21, 2719–2726. [Google Scholar] [CrossRef]
- Reuschlé, T.; Haore, S.G.; Darot, M. The effect of heating on the microstructural evolution of La Peyratte granite deduced from acoustic velocity measurements. Earth Planet. Sci. Lett. 2006, 243, 692–700. [Google Scholar] [CrossRef]
- Stanchits, S.; Vinciguerra, S.; Dresen, G. Ultrasonic velocities, acoustic emission characteristics and crack damage of basalt and granite. Pure Appl. Geophys. 2006, 163, 974–993. [Google Scholar] [CrossRef]
- Dong, L.; Shu, W.; Li, X.; Han, G.; Zou, W. Three Dimensional Comprehensive Analytical Solutions for Locating Sources of Sensor Networks in Unknown Velocity Mining System. IEEE Access 2017, 5, 11337–11351. [Google Scholar] [CrossRef]
- Dong, L.; Zou, W.; Li, X.; Shu, W.; Wang, Z. Collaborative localization method using analytical and iterative solutions for microseismic/acoustic emission sources in the rockmass structure for underground mining. Eng. Fract. Mech. 2019, 210, 95–112. [Google Scholar] [CrossRef]
- Dong, L.; Li, X.; Tang, L.; Gong, F. Mathematical functions and parameters for microseismic source location without pre-measuring speed. Chin. J. Rock Mech. Eng. 2011, 30, 2057–2067. [Google Scholar]
- Dong, L.; Zou, W.; Sun, D.; Tong, X.; Li, X.; Shu, W. Some Developments and New Insights for Microseismic/Acoustic Emission Source Localization. Shock Vib. 2019, 2019. [Google Scholar] [CrossRef] [Green Version]
- Ciampa, F.; Meo, M. A new algorithm for acoustic emission localization and flexural group velocity determination in anisotropic structures. Compos. Part A Appl. Sci. Manuf. 2010, 41, 1777–1786. [Google Scholar] [CrossRef]
- Dehghan Niri, E.; Salamone, S. A probabilistic framework for acoustic emission source localization in plate-like structures. Smart Mater. Struct. 2012, 21, 035009. [Google Scholar] [CrossRef]
- Chan, Y.T.; Ho, K.C. A Simple and Efficient Estimator for Hyperbolic Location. IEEE Trans. Signal Process. 1994, 42, 1905–1915. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Z.; Rui, Y.; Cai, X.; Lan, R.; Cheng, R. A closed-form method of acoustic emission source location for velocity-free system using complete tdoa measurements. Sensors 2020, 20, 3553. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Rui, Y.; Cai, X.; Cheng, R.; Du, X.; Lu, J. A weighted linear least squares location method of an acoustic emission source without measuring wave velocity. Sensors 2020, 20, 3191. [Google Scholar] [CrossRef]
- Kundu, T.; Nakatani, H.; Takeda, N. Acoustic source localization in anisotropic plates. Ultrasonics 2012, 52, 740–746. [Google Scholar] [CrossRef]
- Li, X.; Dong, L. An efficient closed-form solution for acoustic emission source location in three-dimensional structures. AIP Adv. 2014, 4, 27110. [Google Scholar] [CrossRef]
- Annibale, P.; Rabenstein, R. Closed-form estimation of the speed of propagating waves from time measurements. Multidimens. Syst. Signal Process. 2014, 25, 361–378. [Google Scholar] [CrossRef]
- Fang, W.; Liu, L.; Yang, J.; Shui, A. A Non-iterative AE Source Localization Algorithm with Unknown Velocity. J. Logist. Eng. Univ. 2016, 32, 1–7. [Google Scholar]
- Smith, J.; Abel, J. Closed-form least-squares source location estimation from range-difference measurements. IEEE Trans. Acoust. 1987, 35, 1661–1669. [Google Scholar] [CrossRef]
- Bestagini, P.; Compagnoni, M.; Antonacci, F.; Sarti, A.; Tubaro, S. TDOA-based acoustic source localization in the space-range reference frame. Multidimens. Syst. Signal Process. 2014, 25, 337–359. [Google Scholar] [CrossRef]
- Dong, L.; Li, X.; Ma, J.; Tang, L. Three-dimensional analytical comprehensive solutions for acoustic emission/microseismic sources of unknown velocity system. Chin. J. Rock Mech. Eng. 2017, 36, 186–197. [Google Scholar]
- Zhou, Z.; Lan, R.; Rui, Y.; Zhou, J.; Dong, L.; Cheng, R.; Cai, X. A New Acoustic Emission Source Location Method Using Tri-Variate Kernel Density Estimator. IEEE Access 2019, 7, 158379–158388. [Google Scholar] [CrossRef]
- Ge, M. Analysis of source location algorithms Part I: Overview and non-iterative methods. J. Acoust. Emiss. 2003, 21, 14–28. [Google Scholar]
- Das, A.K.; Lai, T.T.; Chan, C.W.; Leung, C.K.Y. A new non-linear framework for localization of acoustic sources. Struct. Heal. Monit. 2019, 18, 590–601. [Google Scholar] [CrossRef]
- Dong, L.; Shu, W.; Han, G.; Li, X.; Wang, J. A Multi-Step Source Localization Method with Narrowing Velocity Interval of Cyber-Physical Systems in Buildings. IEEE Access 2017, 5, 20207–20219. [Google Scholar] [CrossRef]
- Li, N.; Wang, E.; Li, B.; Wang, X.; Chen, D. Research on the influence law and mechanisms of sensors network layouts for the source location. J. China Univ. Min. Technol. 2017, 46, 229–236. [Google Scholar]



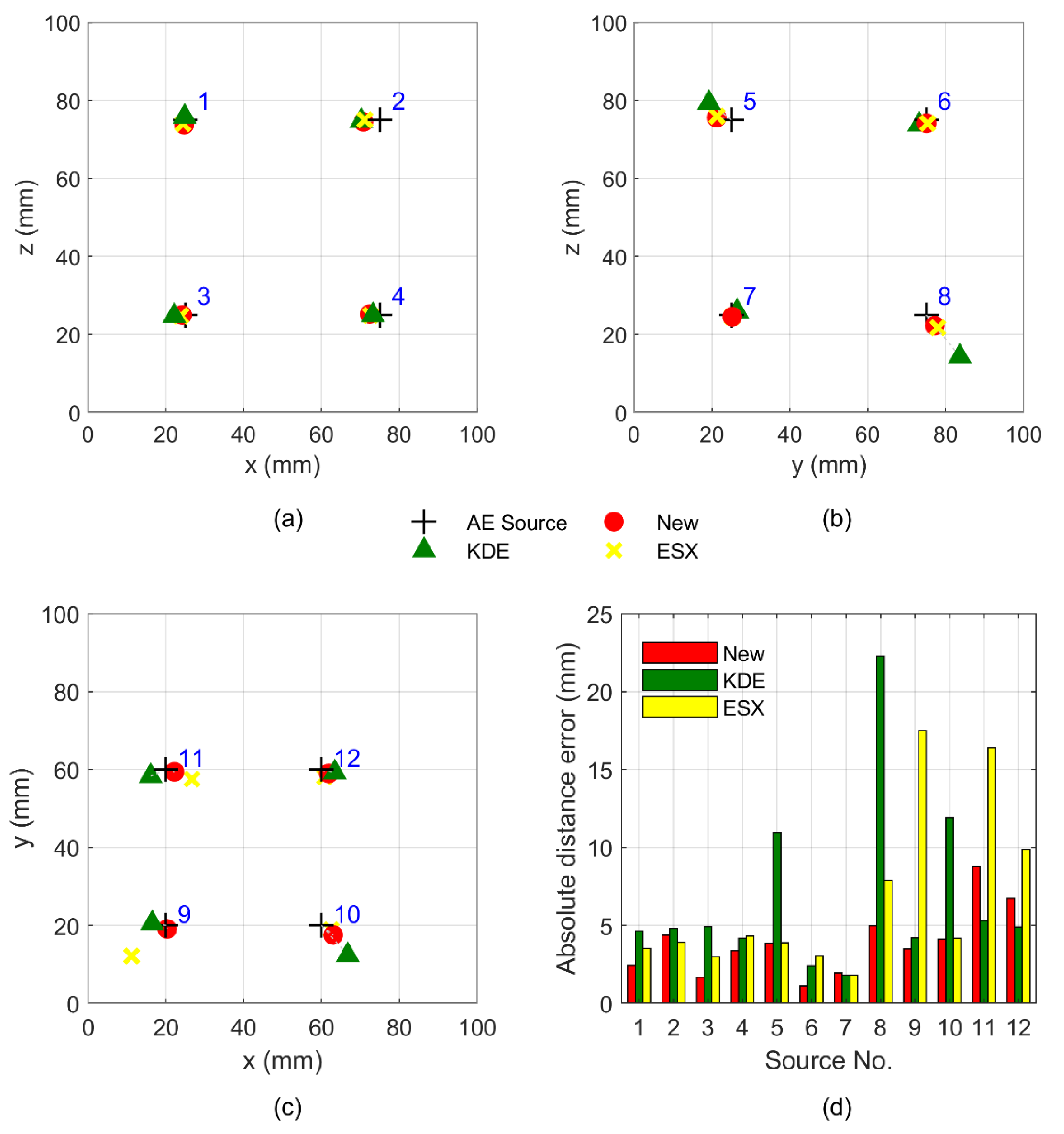

| Source No. | Method | Coordinates | Error | Source No. | Method | Coordinates | Error | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| X | Y | Z | X | Y | Z | ||||||
| 1 | true | 25.00 | 0.00 | 75.00 | - | 7 | true | 100.00 | 25.00 | 25.00 | - |
| New | 24.71 | −2.09 | 73.77 | 2.44 | New | 101.87 | 25.21 | 24.52 | 1.94 | ||
| ESX | 24.46 | −3.33 | 74.02 | 3.51 | ESX | 101.73 | 25.23 | 24.55 | 1.80 | ||
| KDE | 24.84 | −4.56 | 75.80 | 4.63 | KDE | 99.40 | 26.46 | 25.90 | 1.82 | ||
| 2 | true | 75.00 | 0.00 | 75.00 | - | 8 | true | 100.00 | 75.00 | 25.00 | - |
| New | 70.76 | 0.89 | 74.46 | 4.37 | New | 103.49 | 77.22 | 22.24 | 4.97 | ||
| ESX | 71.09 | 0.14 | 74.96 | 3.91 | ESX | 106.54 | 78.00 | 21.75 | 7.89 | ||
| KDE | 70.20 | 0.32 | 74.72 | 4.82 | KDE | 117.52 | 83.66 | 14.32 | 22.27 | ||
| 3 | true | 25.00 | 0.00 | 25.00 | - | 9 | true | 20.00 | 20.00 | 100.00 | - |
| New | 24.18 | −1.44 | 24.96 | 1.66 | New | 20.31 | 19.10 | 96.63 | 3.50 | ||
| ESX | 23.83 | −2.74 | 24.76 | 2.99 | ESX | 11.15 | 12.16 | 112.88 | 17.49 | ||
| KDE | 22.15 | −3.99 | 24.70 | 4.91 | KDE | 16.49 | 20.56 | 102.23 | 4.20 | ||
| 4 | true | 75.00 | 0.00 | 25.00 | - | 10 | true | 60.00 | 20.00 | 100.00 | - |
| New | 72.35 | −2.09 | 25.19 | 3.38 | New | 63.02 | 17.52 | 98.66 | 4.13 | ||
| ESX | 72.61 | −3.60 | 24.92 | 4.33 | ESX | 62.52 | 18.82 | 96.87 | 4.19 | ||
| KDE | 73.18 | −3.75 | 24.93 | 4.17 | KDE | 66.74 | 12.38 | 106.22 | 11.93 | ||
| 5 | true | 100.00 | 25.00 | 75.00 | - | 11 | true | 20.00 | 60.00 | 100.00 | - |
| New | 99.54 | 21.20 | 75.57 | 3.87 | New | 22.18 | 59.41 | 91.54 | 8.76 | ||
| ESX | 101.02 | 21.35 | 75.90 | 3.89 | ESX | 26.64 | 57.57 | 85.21 | 16.39 | ||
| KDE | 108.20 | 19.25 | 79.35 | 10.92 | KDE | 16.05 | 58.31 | 96.88 | 5.31 | ||
| 6 | true | 100.00 | 75.00 | 75.00 | - | 12 | true | 60.00 | 60.00 | 100.00 | - |
| New | 100.68 | 75.1 | 74.12 | 1.12 | New | 61.86 | 58.99 | 93.61 | 6.73 | ||
| ESX | 102.84 | 75.42 | 74.07 | 3.02 | ESX | 60.82 | 58.13 | 90.33 | 9.88 | ||
| KDE | 98.92 | 73.24 | 73.79 | 2.40 | KDE | 63.42 | 59.25 | 96.60 | 4.88 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Lan, R.; Rui, Y.; Dong, L.; Cai, X. A New Algebraic Solution for Acoustic Emission Source Localization without Premeasuring Wave Velocity. Sensors 2021, 21, 459. https://doi.org/10.3390/s21020459
Zhou Z, Lan R, Rui Y, Dong L, Cai X. A New Algebraic Solution for Acoustic Emission Source Localization without Premeasuring Wave Velocity. Sensors. 2021; 21(2):459. https://doi.org/10.3390/s21020459
Chicago/Turabian StyleZhou, Zilong, Riyan Lan, Yichao Rui, Longjun Dong, and Xin Cai. 2021. "A New Algebraic Solution for Acoustic Emission Source Localization without Premeasuring Wave Velocity" Sensors 21, no. 2: 459. https://doi.org/10.3390/s21020459





