Estimation of Human Center of Mass Position through the Inertial Sensors-Based Methods in Postural Tasks: An Accuracy Evaluation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Subjects
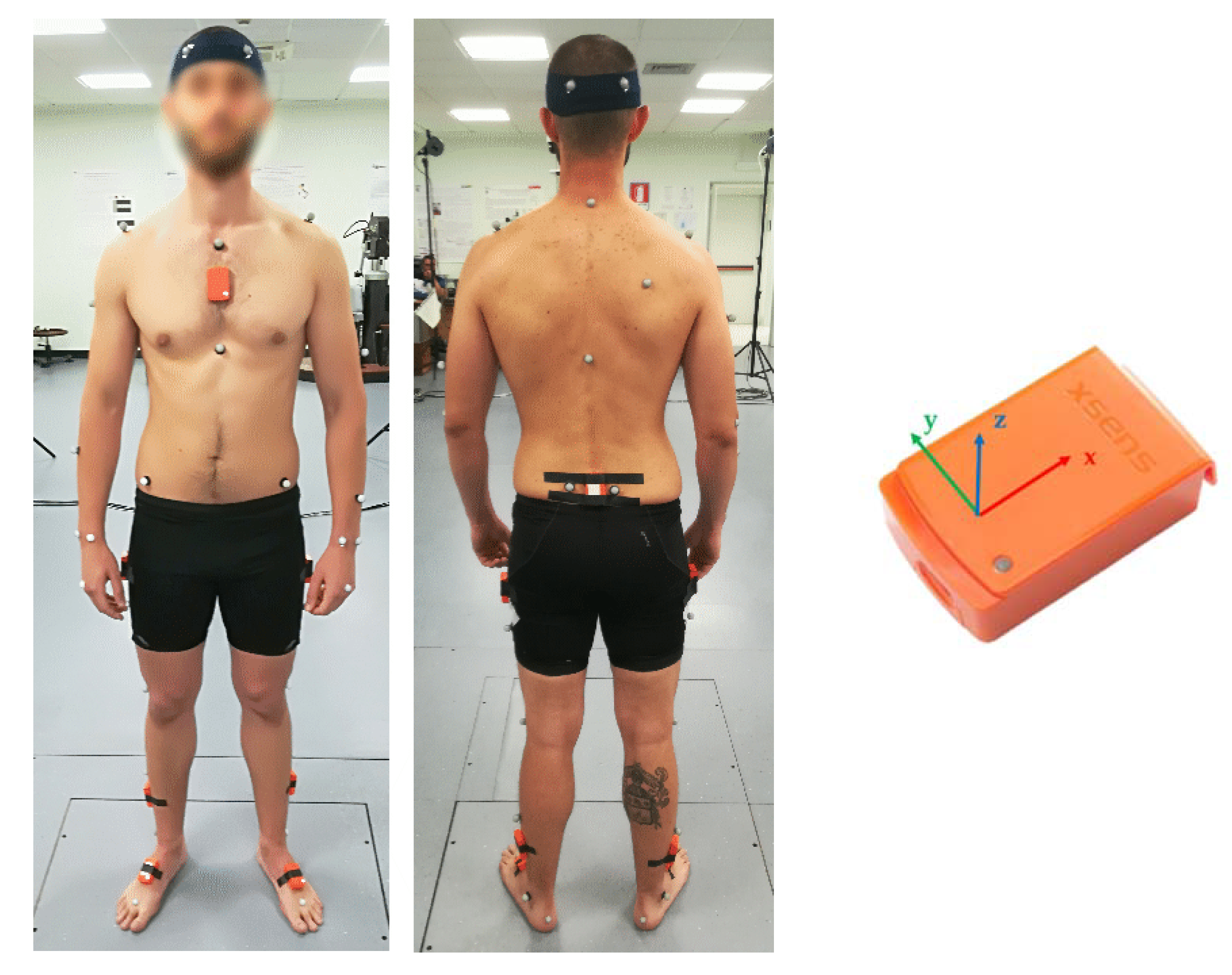
2.2. Experimental Setup
2.3. Experimental Procedure
2.4. Data Processing
2.4.1. First Method: Inertial Sensor Network
2.4.2. Second Method: Strapdown Integration
2.5. Statistical Analysis
3. Results
3.1. Comparison of the Root Mean Square Errors of the Investigated Methods
3.2. Comparison of the Errors Introduced in the Estimation of Postural Variables
3.3. Correlation Analysis
4. Discussion
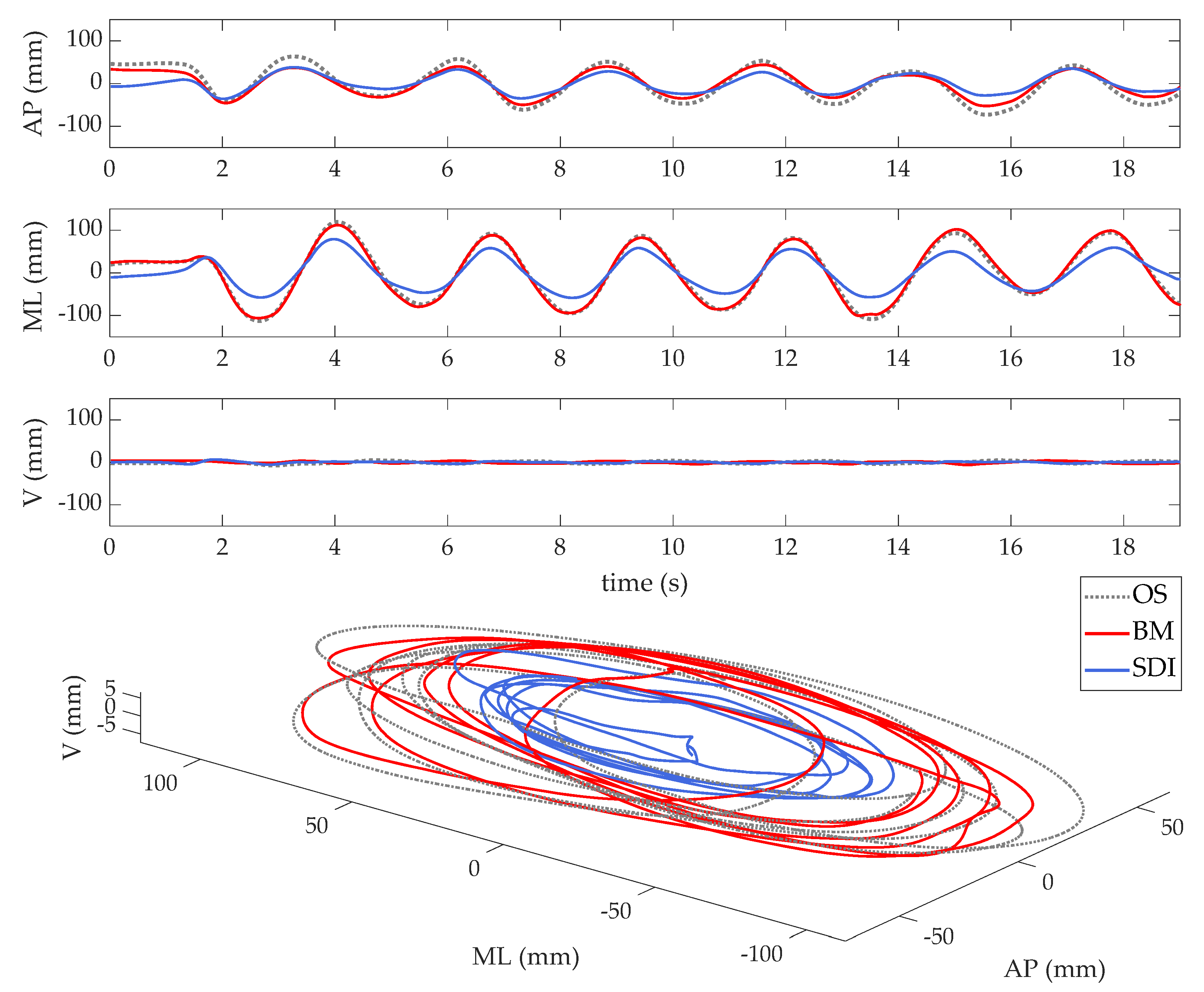
4.1. Accuracy of CoM Displacement Estimation
4.2. Accuracy of Kinematic Postural Parameters Estimation
4.3. Limits
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Huang, C.; Kim, W.; Zhang, Y.; Xiong, S. Development and validation of a wearable inertial sensors-based automated system for assessing work-related musculoskeletal disorders in the workspace. Int. J. Environ. Res. Public Health 2020, 17, 50. [Google Scholar] [CrossRef]
- Conforti, I.; Ilaria, M.; Zaccaria, D.P.; Eduardo, P. Measuring Biomechanical Risk in Lifting Load Tasks Machine-Learning Approach. Sensors 2020, 20, 1557. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ranavolo, A.; Varrecchia, T.; Rinaldi, M.; Silvetti, A.; Serrao, M.; Conforto, S.; Draicchio, F. Mechanical lifting energy consumption in work activities designed by means of the “revised NIOSH lifting equation”. Ind. Health 2017, 55, 444–454. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pavei, G.; Seminati, E.; Cazzola, D.; Minetti, A.E. On the Estimation Accuracy of the 3D Body Center of Mass Trajectory during Human Locomotion: Inverse vs. Forward Dynamics. Front. Physiol. 2017, 8, 129. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Myklebust, H.; Gløersen, Ø.; Hallén, J. Validity of ski skating center-of-mass displacement measured by a single inertial measurement unit. J. Appl. Biomech. 2015, 31, 492–498. [Google Scholar] [CrossRef] [PubMed]
- Reenalda, J.; Maartens, E.; Homan, L.; Buurke, J.H. Continuous three dimensional analysis of running mechanics during a marathon by means of inertial magnetic measurement units to objectify changes in running mechanics. J. Biomech. 2016, 49, 3362–3367. [Google Scholar] [CrossRef] [PubMed]
- Schepers, H.M.; Van Asseldonk, E.H.F.; Buurke, J.H.; Veltink, P.H. Ambulatory estimation of center of mass displacement during walking. IEEE Trans. Biomed. Eng. 2009, 56, 1189–1195. [Google Scholar] [CrossRef]
- Maki, B.E.; McIlroy, W.E. Postural control in the older adult. Clin. Geriatr. Med. 1996, 12, 635–658. [Google Scholar] [CrossRef]
- Najafi, B.; Horn, D.; Marclay, S.; Crews, R.T.; Wu, S.; Wrobel, J.S. Assessing postural control and postural control strategy in diabetes patients using innovative and wearable technology. J. Diabetes Sci. Technol. 2010, 4, 780–791. [Google Scholar] [CrossRef] [Green Version]
- Mileti, I.; Taborri, J.; Rossi, S.; Del Prete, Z.; Paoloni, M.; Suppa, A.; Palermo, E. Reactive postural responses to continuous yaw perturbations in healthy humans: The effect of aging. Sensors 2020, 20, 63. [Google Scholar] [CrossRef] [Green Version]
- Cenciarini, M.; Loughlin, P.J.; Sparto, P.J.; Redfern, M.S. Stiffness and Damping in Postural Control Increase with Age. IEEE Trans. Biomed. Eng. 2010, 57, 267–275. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ivanenko, Y.; Gurfinkel, V.S. Human postural control. Front. Neurosci. 2018, 12, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Rasman, B.G.; Forbes, P.A.; Tisserand, R.; Blouin, J.S. Sensorimotor manipulations of the balance control loop-beyond imposed external perturbations. Front. Neurol. 2018, 9, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Horak, F.B.; Nashner, L.M. Central programming of postural movements: Adaptation to altered support-surface configurations. J. Neurophysiol. 1986, 55, 1369–1381. [Google Scholar] [CrossRef] [PubMed]
- Woollacott, M.H.; Tang, P.F. Balance control during walking in the older adult: Research and its implications. Phys. Ther. 1997, 77, 646–660. [Google Scholar] [CrossRef]
- Mummolo, C.; Cursi, F.; Kim, J.H. Balanced and falling states for biped systems: Applications to robotic versus human walking stability. In Proceedings of the 2016 IEEE-RAS 16th International Conference on Humanoid Robots (Humanoids), Cancun, Mexico, 15–17 November 2016; pp. 1155–1160. [Google Scholar]
- Vallabhajosula, S.; Buckley, T.A.; Tillman, M.D.; Hass, C.J. Age and Parkinson’s disease related kinematic alterations during multi-directional gait initiation. Gait Posture 2013, 37, 280–286. [Google Scholar] [CrossRef]
- Nardone, A.; Schieppati, M. Balance in Parkinson’s disease under static and dynamic conditions. Mov. Disord. 2006, 21, 1515–1520. [Google Scholar] [CrossRef]
- Cole, M.H.; Silburn, P.A.; Wood, J.M.; Worringham, C.J.; Kerr, G.K. Falls in Parkinson’s disease: Kinematic evidence for impaired head and trunk control. Mov. Disord. 2010, 25, 2369–2378. [Google Scholar] [CrossRef] [Green Version]
- Mileti, I.; Zampogna, A.; Santuz, A.; Asci, F.; Del Prete, Z.; Arampatzis, A.; Palermo, E.; Suppa, A. Muscle Synergies in Parkinson’s Disease. Sensors 2020, 20, 3209. [Google Scholar] [CrossRef]
- Taborri, J.; Mileti, I.; Del Prete, Z.; Rossi, S.; Palermo, E. Yaw Postural Perturbation Through Robotic Platform: Aging Effects on Muscle Synergies. In Proceedings of the 2018 7th IEEE International Conference on Biomedical Robotics and Biomechatronics (Biorob), Enschede, The Netherlands, 26–29 August 2018; pp. 916–921. [Google Scholar]
- Reaz, M.B.I.; Hussain, M.S.; Mohd-Yasin, F. Techniques of EMG signal analysis: Detection, processing, classification and applications. Biol. Proced. Online 2006, 8, 11–35. [Google Scholar] [CrossRef] [Green Version]
- Alberto, R.; Draicchio, F.; Varrecchia, T.; Silvetti, A.; Iavicoli, S. Wearable monitoring devices for biomechanical risk assessment at work: Current status and future challenges—A systematic review. Int. J. Environ. Res. Public Health 2018, 15, 2001. [Google Scholar] [CrossRef] [Green Version]
- Tsao, L.; Li, L.; Ma, L. Human work and status evaluation based on wearable sensors in human factors and ergonomics: A review. IEEE Trans. Human-Machine Syst. 2019, 49, 72–84. [Google Scholar] [CrossRef]
- Camomilla, V.; Bergamini, E.; Fantozzi, S.; Vannozzi, G. Trends supporting the in-field use of wearable inertial sensors for sport performance evaluation: A systematic review. Sensors 2018, 18, 873. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Taborri, J.; Keogh, J.; Kos, A.; Santuz, A.; Umek, A.; Urbanczyk, C.; van der Kruk, E.; Rossi, S. Sport biomechanics applications using inertial, force, and EMG sensors: A literature overview. Appl. Bionics Biomech. 2020, 2020. [Google Scholar] [CrossRef]
- Najafi, B.; Lee-Eng, J.; Wrobel, J.S.; Goebel, R. Estimation of center of mass trajectory using wearable sensors during golf swing. J. Sport. Sci. Med. 2015, 14, 354–363. [Google Scholar]
- Majumder, S.; Mondal, T.; Deen, M.J. Wearable sensors for remote health monitoring. Sensors 2017, 17, 130. [Google Scholar] [CrossRef]
- Zampogna, A.; Mileti, I.; Palermo, E.; Celletti, C.; Paoloni, M.; Manoni, A.; Mazzetta, I.; Costa, G.D.; Carlos, P.; Camerota, F.; et al. Fifteen Years of Wireless Sensors for Balance Assessment in Neurological Disorders. Sensors 2020, 20, 3247. [Google Scholar] [CrossRef]
- Na, E.; Hwang, H.; Woo, Y. Study of acceleration of center of mass during sit-to-stand and stand-to-sit in patients with stroke. J. Phys. Ther. Sci. 2016, 28, 2457–2460. [Google Scholar] [CrossRef] [Green Version]
- Mohamed Refai, M.I.; van Beijnum, B.-J.F.; Buurke, J.H.; Veltink, P.H. Portable Gait Lab: Instantaneous centre of mass velocity using three inertial measurement units. In Proceedings of the 2020 IEEE SENSORS, Rotterdam, The Netherlands, 25–28 October 2020; pp. 1–4. [Google Scholar]
- Shin, S.-S.; Yoo, W.-G.; An, D.-H. Effects of task velocity and center of mass acceleration during Y-Balance Test in elderly females with good and poor visual acuity. J. Phys. Ther. Sci. 2018, 30, 879–882. [Google Scholar] [CrossRef]
- Mancini, M.; Salarian, A.; Carlson-Kuhta, P.; Zampieri, C.; King, L.; Chiari, L.; Horak, F.B. ISway: A sensitive, valid and reliable measure of postural control. J. Neuroeng. Rehabil. 2012, 9, 59. [Google Scholar] [CrossRef] [Green Version]
- Floor-Westerdijk, M.J.; Schepers, H.M.; Veltink, P.H.; Van Asseldonk, E.H.F.; Buurke, J.H. Use of inertial sensors for ambulatory assessment of center-of-mass displacements during walking. IEEE Trans. Biomed. Eng. 2012, 59, 2080–2084. [Google Scholar] [CrossRef] [PubMed]
- Cardarelli, S.; Mengarelli, A.; Tigrini, A.; Strazza, A.; Di Nardo, F.; Fioretti, S.; Verdini, F. Single IMU Displacement and Orientation Estimation of Human Center of Mass: A Magnetometer-Free Approach. IEEE Trans. Instrum. Meas. 2020, 69, 5629–5639. [Google Scholar] [CrossRef]
- Fasel, B.; Spörri, J.; Schütz, P.; Lorenzetti, S.; Aminian, K. An inertial sensor-based method for estimating the athlete’s relative joint center positions and center of mass kinematics in alpine ski racing. Front. Physiol. 2017, 8, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Roetenberg, D.; Luinge, H.; Slycke, P. Xsens MVN: Full 6DOF Human Motion Tracking Using Miniature Inertial Sensors. Xsens Motion Technol. BV Tech. Rep. 2009, 1–7. [Google Scholar]
- Pavei, G.; Salis, F.; Cereatti, A.; Bergamini, E. Body center of mass trajectory and mechanical energy using inertial sensors: A feasible stride? Gait Posture 2020, 80, 199–205. [Google Scholar] [CrossRef]
- Guo, L.; Xiong, S. Accuracy of Base of Support Using an Inertial Sensor Based Motion Capture System. Sensors 2017, 17, 2091. [Google Scholar] [CrossRef] [Green Version]
- Xsens MVN: Consistent Tracking of Human Motion Using Inertial Sensing. Available online: https://www.researchgate.net/publication/324007368_Xsens_MVN_Consistent_Tracking_of_Human_Motion_Using_Inertial_Sensing (accessed on 13 January 2021).
- Guaitolini, M.; Aprigliano, F.; Mannini, A.; Micera, S.; Monaco, V.; Sabatini, A.M. Ambulatory Assessment of the Dynamic Margin of Stability Using an Inertial Sensor Network. Sensors 2019, 19, 4117. [Google Scholar] [CrossRef] [Green Version]
- Choi, A.; Jung, H.; Mun, J.H. Single inertial sensor-based neural networks to estimate COM-COP inclination angle during walking. Sensors 2019, 19, 2974. [Google Scholar] [CrossRef] [Green Version]
- Ghislieri, M.; Gastaldi, L.; Pastorelli, S.; Tadano, S.; Agostini, V. Wearable Inertial Sensors to Assess Standing Balance: A Systematic Review. Sensors 2019, 19, 4075. [Google Scholar] [CrossRef] [Green Version]
- van der Straaten, R.; Wesseling, M.; Jonkers, I.; Vanwanseele, B.; Bruijnes, A.K.B.D.; Malcorps, J.; Bellemans, J.; Truijen, J.; de Baets, L.; Timmermans, A. Discriminant validity of 3D joint kinematics and centre of mass displacement measured by inertial sensor technology during the unipodal stance task. PLoS ONE 2020, 15. [Google Scholar] [CrossRef]
- Davis, R.B.; Õunpuu, S.; Tyburski, D.; Gage, J.R. A gait analysis data collection and reduction technique. Hum. Mov. Sci. 1991, 10, 575–587. [Google Scholar] [CrossRef]
- Palermo, E.; Rossi, S.; Marini, F.; Patanè, F.; Cappa, P. Experimental evaluation of accuracy and repeatability of a novel body-to-sensor calibration procedure for inertial sensor-based gait analysis. MEASUREMENT 2014, 52, 145–155. [Google Scholar] [CrossRef]
- Pacilli, A.; Mileti, I.; Germanotta, M.; Di Sipio, E.; Imbimbo, I.; Aprile, I.; Padua, L.; Rossi, S.; Palermo, E.; Cappa, P. A wearable setup for auditory cued gait analysis in patients with Parkinson’s Disease. In Proceedings of the 2016 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Benevento, Italy, 15–18 May 2016; pp. 1–6. [Google Scholar]
- Erra, C.; Mileti, I.; Germanotta, M.; Petracca, M.; Imbimbo, I.; De Biase, A.; Rossi, S.; Ricciardi, D.; Pacilli, A.; Di Sipio, E.; et al. Immediate effects of rhythmic auditory stimulation on gait kinematics in Parkinson’s disease ON/OFF medication. Clin. Neurophysiol. 2019, 130, 1789–1797. [Google Scholar] [CrossRef] [PubMed]
- Savage, P.G. Strapdown inertial navigation integration algorithm design part 1: Attitude algorithms. J. Guid. Control. Dyn. 1998, 21, 19–28. [Google Scholar] [CrossRef]
- Savage, P.G. Strapdown inertial navigation integration algorithm design part 2: Velocity and position algorithms. J. Guid. Control. Dyn. 1998, 21, 208–221. [Google Scholar] [CrossRef]
- Bellusci, G.; Dijkstra, F.; Slycke, P. Xsens MTw: Miniature Wireless Inertial Motion Tracker for Highly Accurate 3D Kinematic Applications. Xsens Technol. 2013, 1–9. [Google Scholar]
- Walther, B.A.; Moore, J.L. The concepts of bias, precision and accuracy, and their use in testing the performance of species richness estimators, with a literature review of estimator performance. Ecography 2005, 28, 815–829. [Google Scholar] [CrossRef]
- Guilford, J.P. Fundamental Statistics in Psychology and Education. New York (330 West 42nd Street): McGraw-Hill Book Company, 1956. 565 P. $6.25. Sci. Educ. 1957, 41, 244. [Google Scholar] [CrossRef]
- Argent, R.; Drummond, S.; Remus, A.; O’Reilly, M.; Caulfield, B. Evaluating the use of machine learning in the assessment of joint angle using a single inertial sensor. J. Rehabil. Assist. Technol. Eng. 2019, 6. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Zhang, J.; Zhang, Y.; Zhu, R. A wearable motion capture device able to detect dynamic motion of human limbs. Nat. Commun. 2020, 11, 5615. [Google Scholar] [CrossRef]




| Task | Component | BM RMSE | SDI RMSE | Difference | p-Value | ||
|---|---|---|---|---|---|---|---|
| Mean (SD) | Range | Mean (SD) | Range | Mean (SD) | |||
| Double Leg Stance | AP (mm) | 6.5 (3.0) | 1.8–19.8 | 6.1 (1.8) | 3.3–13.2 | 0.4 (3.6) | 0.514 |
| ML (mm) | 2.5 (0.9) | 1.2–4.7 | 1.9 (1.6) | 0.9–9.1 | 0.5 (1.4) | 0.045 | |
| V (mm) | 0.9 (0.3) | 0.5–1.6 | 0.3 (0.1) | 0.2–0.8 | 0.6 (0.3) | <0.001 | |
| mod (mm) | 5.4 (2.6) | 3.5–18.0 | 4.5 (1.3) | 3.2–10.2 | 0.9 (3.1) | 0.129 | |
| Single-Leg Stance | AP (mm) | 26.2 (15.1) | 5.6–63.9 | 11.0 (5.0) | 4.6–29.3 | 15.2 (15.1) | <0.001 |
| ML (mm) | 12.0 (10.1) | 0.0–42.7 | 8.7 (8.7) | 2.6–36.3 | 3.8 (10.6) | 0.066 | |
| V (mm) | 4.0 (3.1) | 1.1–13.9 | 2.0 (1.4) | 0.8–6.5 | 2.0 (3.5) | 0.005 | |
| mod (mm) | 23.8 (19.3) | 3.3–68.7 | 9.8 (7.2) | 3.8–35.4 | 14.0 (21.0) | 0.001 | |
| AP sway | AP (mm) | 18.9 (7.5) | 9.1–38.2 | 32.0 (17.6) | 15.8–90.8 | −13.1 (17.0) | <0.001 |
| ML (mm) | 7.6 (2.3) | 4.5–12.4 | 6.1 (2.2) | 3.2–14.9 | 1.4 (2.5) | 0.004 | |
| V (mm) | 8.9 (2.5) | 4.5–12.8 | 5.5 (3.1) | 1.5–14.5 | 3.3 (3.5) | <0.001 | |
| mod (mm) | 17.1 (5.6) | 9.2–29.8 | 24.5 (4.2) | 13.1–31.8 | −7.4 (4.9) | <0.001 | |
| ML sway | AP (mm) | 6.3 (1.3) | 4.6–9.1 | 10.5 (3.6) | 4.8–17.8 | −4.1 (3.8) | <0.001 |
| ML (mm) | 23.9 (25.2) | 6.8–133.3 | 48.6 (42.2) | 13.4–171.4 | −24.7 (33.0) | <0.001 | |
| V (mm) | 8.4 (4.1) | 2.5–16.6 | 3.0 (1.6) | 1.3–8.8 | 5.3 (3.9) | <0.001 | |
| mod (mm) | 18.4 (11.7) | 6.2–44.7 | 36.9 (14.2) | 13.7–72.5 | −18.5 (14.2) | <0.001 | |
| Free sway | AP (mm) | 15.8 (7.8) | 5.4–34.8 | 26.9 (17.7) | 10.6–84.7 | −11.1 (15.9) | 0.001 |
| ML (mm) | 23.9 (14.2) | 7.2–59.3 | 44.1 (26.8) | 16.2–124.3 | −20.2 (23.2) | <0.001 | |
| V (mm) | 11.4 (4.6) | 3.7–20.5 | 4.9 (2.6) | 1.8–12.8 | 6.5 (4.2) | <0.001 | |
| mod (mm) | 18.5 (9.3) | 7.7–44.5 | 35.3 (10.3) | 21.8–56.9 | −16.8 (11.3) | <0.001 | |
| Squat | AP (mm) | 17.0 (10.9) | 4.2–52.4 | 41.9 (17.4) | 7.3–72.6 | −24.9 (19.0) | <0.001 |
| ML (mm) | 9.7 (5.0) | 3.4–23.5 | 6.5 (2.6) | 2.1–13.0 | 3.3 (5.7) | 0.004 | |
| V (mm) | 24.4 (11.4) | 5.9–48.5 | 79.5 (30.3) | 33.5–153.7 | −55.1 (28.2) | <0.001 | |
| mod (mm) | 22.3 (9.7) | 6.3–43.9 | 84.7 (32.0) | 41.8–159.5 | −62.4 (29.8) | <0.001 | |
| Task | Kinematic Parameter | Pearson’s Correlation Coefficient (p Value) between OS and BM | Pearson’s Correlation Coefficient (p Value) between OS and SDI |
|---|---|---|---|
| Double Leg Stance | AP Sway | 0.579 (0.001) | 0.238 (0.204) |
| ML Sway | 0.779 (<0.001) | 0.466 (0.009) | |
| 95% Sway Area | 0.331 (0.074) | 0.154 (0.418) | |
| Mean Sway Velocity | 0.838 (<0.001) | 0.514 (0.004) | |
| Single Leg Stance | AP Sway | 0.692 (<0.001) | 0.501 (0.006) |
| ML Sway | 0.892 (<0.001) | 0.806 (<0.001) | |
| 95% Sway Area | 0.904 (0.001) | 0.811 (0.552) | |
| Mean Sway Velocity | 0.869 (<0.001) | 0.922 (<0.001) | |
| AP Sway | AP Sway | 0.831 (<0.001) | 0.688 (<0.001) |
| ML Sway | 0.699 (<0.001) | 0.287 (0.124) | |
| 95% Sway Area | 0.703 (<0.001) | 0.557 (0.001) | |
| Mean Sway Velocity | 0.942 (<0.001) | 0.962 (<0.001) | |
| ML Sway | AP Sway | 0.822 (<0.001) | 0.416 (0.025) |
| ML Sway | 0.930 (<0.001) | 0.630 (<0.001) | |
| 95% Sway Area | 0.810 (<0.001) | 0.535 (0.003) | |
| Mean Sway Velocity | 0.935 (<0.001) | 0.873 (<0.001) | |
| Free Sway | AP Sway | 0.919 (<0.001) | 0.806 (<0.001) |
| ML Sway | 0.962 (<0.001) | 0.521 (0.003) | |
| 95% Sway Area | 0.946 (<0.001) | 0.708 (<0.001) | |
| Mean Sway Velocity | 0.980 (<0.001) | 0.873 (<0.001) | |
| Squat | AP Sway | 0.917 (<0.001) | 0.437 (0.016) |
| ML Sway | 0.586 (0.001) | 0.293 (0.116) | |
| 95% Sway Area | 0.677 (<0.001) | 0.388 (0.034) | |
| Mean Sway Velocity | 0.933 (<0.001) | 0.675 (<0.001) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Germanotta, M.; Mileti, I.; Conforti, I.; Del Prete, Z.; Aprile, I.; Palermo, E. Estimation of Human Center of Mass Position through the Inertial Sensors-Based Methods in Postural Tasks: An Accuracy Evaluation. Sensors 2021, 21, 601. https://doi.org/10.3390/s21020601
Germanotta M, Mileti I, Conforti I, Del Prete Z, Aprile I, Palermo E. Estimation of Human Center of Mass Position through the Inertial Sensors-Based Methods in Postural Tasks: An Accuracy Evaluation. Sensors. 2021; 21(2):601. https://doi.org/10.3390/s21020601
Chicago/Turabian StyleGermanotta, Marco, Ilaria Mileti, Ilaria Conforti, Zaccaria Del Prete, Irene Aprile, and Eduardo Palermo. 2021. "Estimation of Human Center of Mass Position through the Inertial Sensors-Based Methods in Postural Tasks: An Accuracy Evaluation" Sensors 21, no. 2: 601. https://doi.org/10.3390/s21020601
APA StyleGermanotta, M., Mileti, I., Conforti, I., Del Prete, Z., Aprile, I., & Palermo, E. (2021). Estimation of Human Center of Mass Position through the Inertial Sensors-Based Methods in Postural Tasks: An Accuracy Evaluation. Sensors, 21(2), 601. https://doi.org/10.3390/s21020601








