Sensor Faults Isolation in Networked Control Systems: Application to Mobile Robot Platoons
Abstract
:1. Introduction
- How can we develop such sensor faults isolation method for each robot of the platoons using only conventional sensors (GPS, velocity sensor, radar) and network communication?
- How to compensate faults propagation effect in the communication network from one robot to the others so that it does not affect the sensor faults isolation process?
- How to implement the sensor faults isolation in a distributed way?
- We have developed a model for sensor faults diagnosis purposes for the robotics platoon.
- We have proposed a general UIO-based distributed sensor faults isolation approach for a network of linear control systems.
- Based on these two results, we have solved the weak sensor faults isolation problem in such robotics platoon that use conventional sensors: GPS-based localization; velocity sensor; and radar sensor.
2. UIO-Based Sensor Faults Isolation
2.1. General Model of Unknown Input Observer (UIO)
2.2. UIO for Sensor Faults Isolation
3. Sensor Faults Isolation in Networks of Control Systems
3.1. Sensor Faults in Networked Control Systems
3.2. UIO for Sensor Faults Isolation in Networked Control Systems
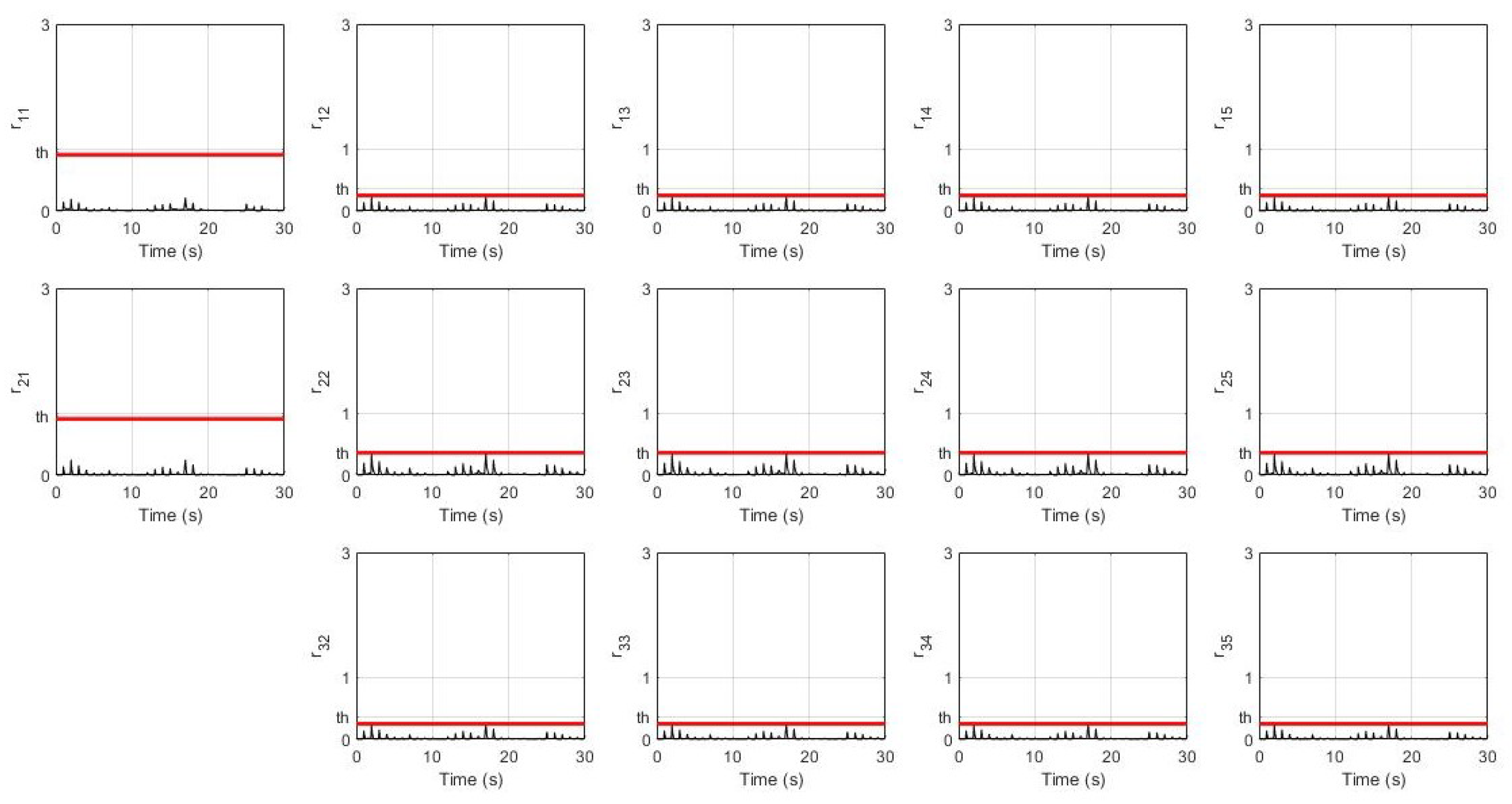
3.3. Threshold Computation for Fault Isolation
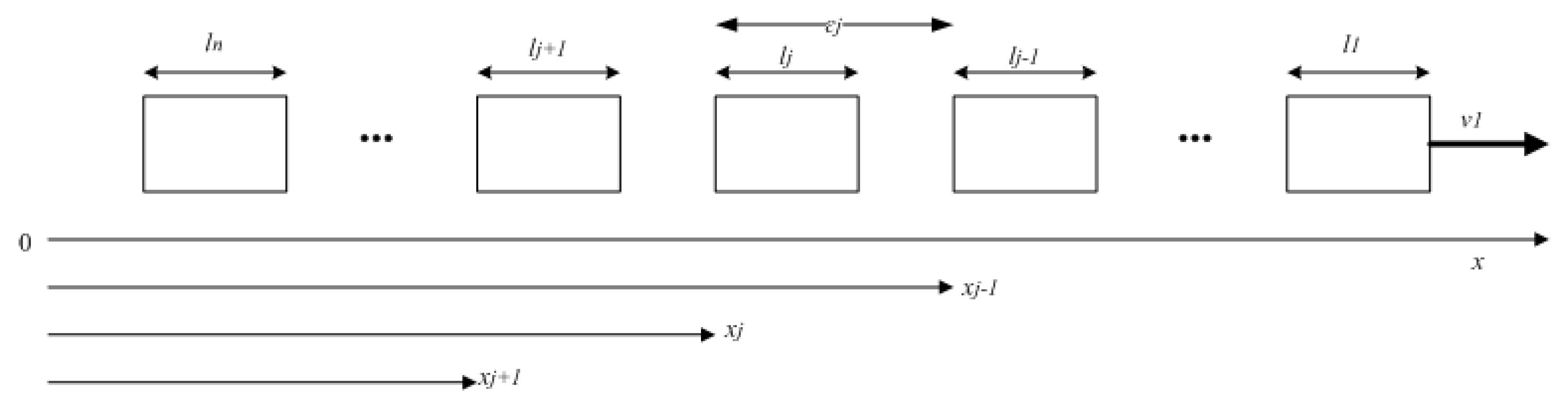
4. Modelling of Controlled Robots Platoon
4.1. Fault Free Model of Controlled Robots Platoon
4.2. Model of Controlled Robots Platoon with Sensor Faults
- is a position measurement to obtain the state using a GPS-based sensor (S1).
- is a velocity measurement obtained from the same GPS-based sensor. For GPS-based velocity measurement, please refer to [33].
- is a velocity measurement by using the wheel-mounted velocity sensor (S2) on the robot to obtain the state.
- is an inter-vehicle distance measurement to obtain the state using a radar-based sensor (S3).
4.3. Special Case: The Leader Robot
4.4. Model of the Leader Robot with Sensor Faults
- is a GPS-based position measurement to obtain the state.
- is a velocity measurement based on the same GPS sensor.
- is a velocity measurement by using the wheel-mounted velocity sensor on the robot to obtain the state.
5. Sensor Faults Isolation in Controlled Robots Platoon
5.1. Sensor Faults Isolation in the Follower Robots
5.2. Sensor Faults Isolation in the Leader Robot
6. Results and Discussion
6.1. Simulation Method
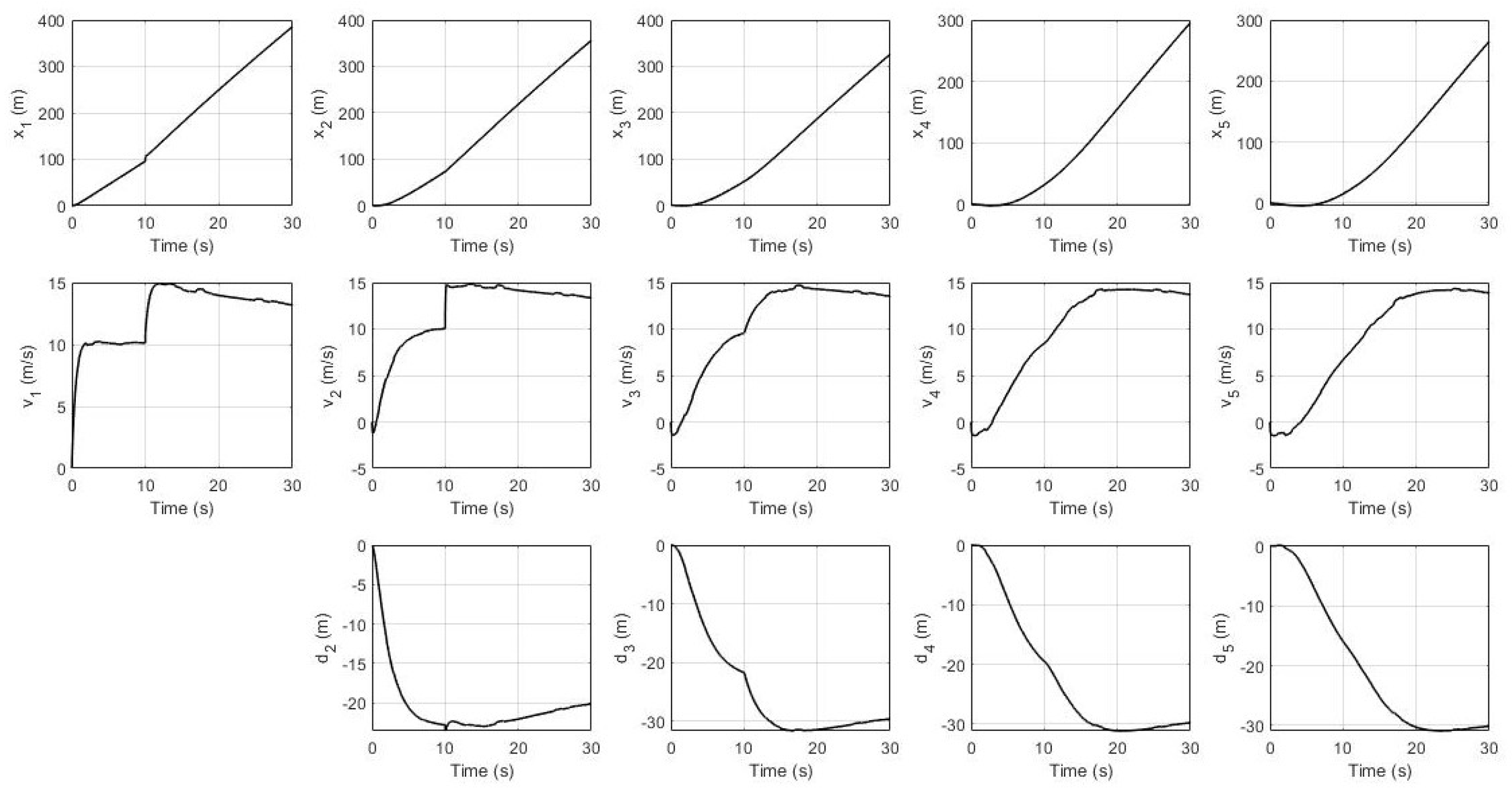
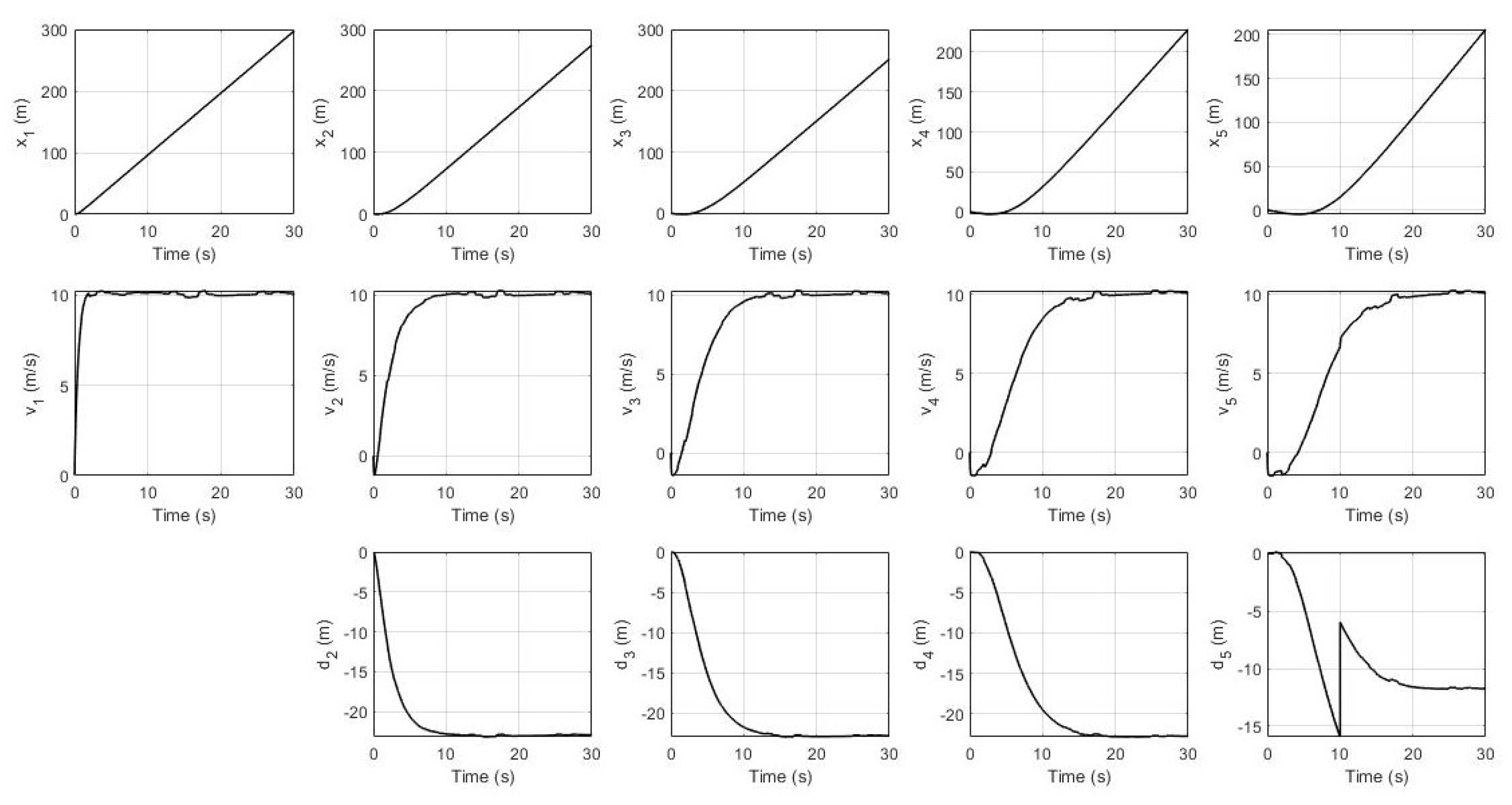
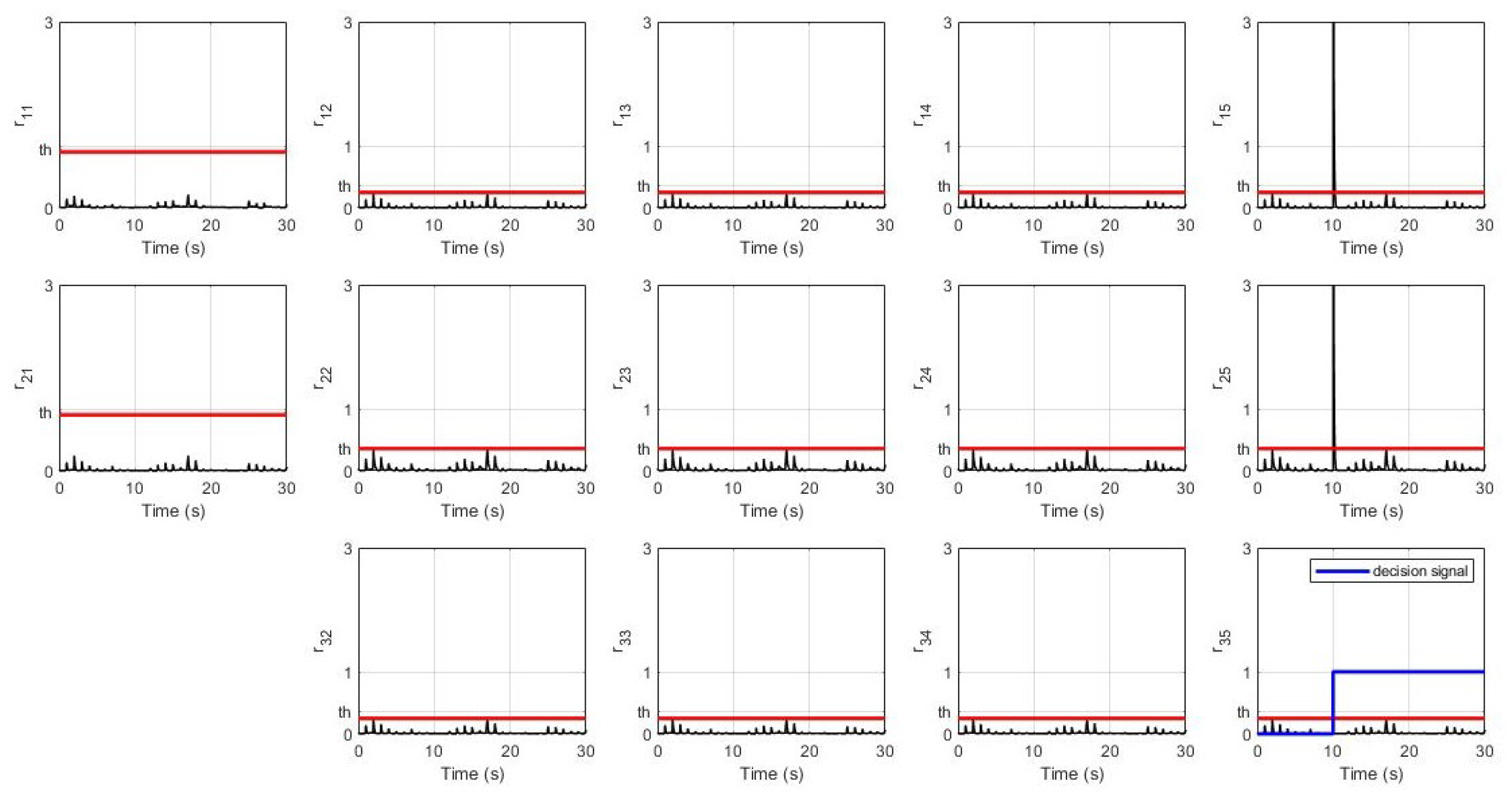
6.2. Simulation Results
6.3. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mohamed, N.; Al-Jaroodi, J.; Jawhar, I. A review of middleware for networked robots. Int. J. Comput. Sci. Netw. Secur. 2009, 9, 139–148. [Google Scholar]
- Roveda, L.; Spahiu, B.; Terkaj, W. On the Proposal of a Unified Safety Framework for Industry 4.0 Multi-Robot Scenario. In Proceedings of the SEBD, Grosseto, Italy, 16–19 June 2019. [Google Scholar]
- Gonzalez-Ruiz, A.; Ghaffarkhah, A.; Mostofi, Y. A comprehensive overview and characterization of wireless channels for networked robotic and control systems. J. Robot. 2011, 2011, 340372. [Google Scholar] [CrossRef] [Green Version]
- Fehér, Á.; Márton, L. Transient Behaviour Analysis and Design for Platoons with Communication Delay. IFAC-PapersOnLine 2019, 52, 13–18. [Google Scholar] [CrossRef]
- Blanke, M.; Kinnaert, M.; Lunze, J.; Staroswiecki, M.; Schröder, J. Diagnosis and Fault-Tolerant Control; Springer: Berlin/Heidelberg, Germany, 2006; Volume 2. [Google Scholar]
- Varga, A. Solving fault diagnosis problems. Studies in Systems, Decision and Control, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Pózna, A.I.; Fodor, A.; Hangos, K.M. Model-based fault detection and isolation of non-technical losses in electrical networks. Math. Comput. Model. Dyn. Syst. 2019, 25, 397–428. [Google Scholar] [CrossRef]
- Gertler, J. Fault detection and isolation using parity relations. Control Eng. Pract. 1997, 5, 653–661. [Google Scholar] [CrossRef]
- Song, T.; Collins, E.G., Jr. Robust H estimation with application to robust fault detection. J. Guid. Control Dyn. 2000, 23, 1067–1071. [Google Scholar] [CrossRef] [Green Version]
- Niemann, H.; Saberi, A.; Stoorvogel, A.A.; Sannuti, P. Optimal fault estimation. IFAC Proc. Vol. 2000, 33, 267–272. [Google Scholar] [CrossRef]
- Menke, T.E.; Maybeck, P.S. Sensor/actuator failure detection in the Vista F-16 by multiple model adaptive estimation. IEEE Trans. Aerosp. Electron. Syst. 1995, 31, 1218–1229. [Google Scholar] [CrossRef] [Green Version]
- White, N.A.; Maybeck, P.S.; DeVilbiss, S.L. MMAE detection of interference/jamming and spoofing in a DGPS-aided inertial system. In Proceedings of the 11th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1998), Nashville, TN, USA, 15–18 September 1998; pp. 905–914. [Google Scholar]
- Simani, S.; Fantuzzi, C.; Patton, R.J. Model-based fault diagnosis techniques. In Model-based Fault Diagnosis in Dynamic Systems Using Identification Techniques; Springer: Berlin/Heidelberg, Germany, 2003; pp. 19–60. [Google Scholar]
- Michail, K.; Deliparaschos, K.M.; Tzafestas, S.G.; Zolotas, A.C. AI-based actuator/sensor fault detection with low computational cost for industrial applications. IEEE Trans. Control Syst. Technol. 2015, 24, 293–301. [Google Scholar] [CrossRef] [Green Version]
- Nasiri, S.; Khosravani, M.R.; Weinberg, K. Fracture mechanics and mechanical fault detection by artificial intelligence methods: A review. Eng. Fail. Anal. 2017, 81, 270–293. [Google Scholar] [CrossRef]
- Xiao, S.; Yao, J.; Chen, Y.; Li, D.; Zhang, F.; Wu, Y. Fault Detection and Isolation Methods in Subsea Observation Networks. Sensors 2020, 20, 5273. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Wang, Y.; Wang, J.; Wang, C.; Duan, Y. Recent advances in sensor fault diagnosis: A review. Sensors Actuators A Phys. 2020, 309, 111990. [Google Scholar] [CrossRef]
- Chen, J.; Patton, R.J. Robust Model-Based Fault Diagnosis for Dynamic Systems; Springer: Berlin/Heidelberg, Germany, 2012; Volume 3. [Google Scholar]
- Chakrabarty, A.; Corless, M.J.; Buzzard, G.T.; Żak, S.H.; Rundell, A.E. State and Unknown Input Observers for nonlinear systems with bounded exogenous inputs. IEEE Trans. Autom. Control 2017, 62, 5497–5510. [Google Scholar] [CrossRef]
- Chakrabarty, A.; Fridman, E.; Żak, S.H.; Buzzard, G.T. State and Unknown Input Observers for nonlinear systems with delayed measurements. Automatica 2018, 95, 246–253. [Google Scholar] [CrossRef]
- Xu, F.; Tan, J.; Wang, X.; Puig, V.; Liang, B.; Yuan, B. A novel design of Unknown Input Observers using set-theoretic methods for robust fault detection. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 5957–5961. [Google Scholar]
- Zuo, L.; Yao, L.; Kang, Y. UIO Based Sensor Fault Diagnosis and Compensation for Quadrotor UAV. In Proceedings of the 2020 Chinese Control And Decision Conference (CCDC), Hefei, China, 21–23 May 2020; pp. 4052–4057. [Google Scholar]
- Taha, A.F.; Elmahdi, A.; Panchal, J.H.; Sun, D. Unknown input observer design and analysis for networked control systems. Int. J. Control 2015, 88, 920–934. [Google Scholar] [CrossRef]
- Shames, I.; Teixeira, A.M.; Sandberg, H.; Johansson, K.H. Distributed fault detection for interconnected second-order systems. Automatica 2011, 47, 2757–2764. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Saif, M. Unknown input observer design for a class of nonlinear systems: An LMI approach. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; pp. 834–838. [Google Scholar]
- Chakrabarty, A.; Sundaram, S.; Corless, M.J.; Buzzard, G.T.; Żak, S.H.; Rundell, A.E. Distributed Unknown Input Observers for interconnected nonlinear systems. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 101–106. [Google Scholar]
- Liu, X.; Gao, X.; Han, J. Robust Unknown Input Observer based fault detection for high-order multi-agent systems with disturbances. ISA Trans. 2016, 61, 15–28. [Google Scholar] [CrossRef] [PubMed]
- Shames, I.; Teixeira, A.M.; Sandberg, H.; Johansson, K.H. Distributed fault detection and isolation with imprecise network models. In Proceedings of the 2012 American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 5906–5911. [Google Scholar]
- Zhang, K.; Liu, G.; Jiang, B. Robust Unknown Input Observer-based fault estimation of leader–follower linear multi-agent systems. Circuits Syst. Signal Process. 2017, 36, 525–542. [Google Scholar] [CrossRef]
- Rajamani, R. Vehicle Dynamics and Control; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Chen, C. Linear System Theory and Design. Available online: http://ebadi.profcms.um.ac.ir/imagesm/474/stories/modern_control/chen%20c%20-t%20linear%20system%20theory%20and%20design.pdf (accessed on 18 August 2021).
- Xiao, L.; Gao, F. A comprehensive review of the development of adaptive cruise control systems. Veh. Syst. Dyn. 2010, 48, 1167–1192. [Google Scholar] [CrossRef]
- Serrano, L.; Kim, D.; Langley, R.B.; Itani, K.; Ueno, M. A GPS velocity sensor: How accurate can it be?… A first look. In Proceedings of the 2004 National Technical Meeting of The Institute of Navigation, Long Beach, CA, USA, 16–19 May 2004; pp. 875–885. [Google Scholar]
- Fehér, Á.; Márton, L.; Pituk, M. Approximation of a linear autonomous differential equation with small delay. Symmetry 2019, 11, 1299. [Google Scholar] [CrossRef] [Green Version]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kurniawan, W.; Marton, L. Sensor Faults Isolation in Networked Control Systems: Application to Mobile Robot Platoons. Sensors 2021, 21, 6702. https://doi.org/10.3390/s21206702
Kurniawan W, Marton L. Sensor Faults Isolation in Networked Control Systems: Application to Mobile Robot Platoons. Sensors. 2021; 21(20):6702. https://doi.org/10.3390/s21206702
Chicago/Turabian StyleKurniawan, Wijaya, and Lorinc Marton. 2021. "Sensor Faults Isolation in Networked Control Systems: Application to Mobile Robot Platoons" Sensors 21, no. 20: 6702. https://doi.org/10.3390/s21206702
APA StyleKurniawan, W., & Marton, L. (2021). Sensor Faults Isolation in Networked Control Systems: Application to Mobile Robot Platoons. Sensors, 21(20), 6702. https://doi.org/10.3390/s21206702





