Advanced Kidney Volume Measurement Method Using Ultrasonography with Artificial Intelligence-Based Hybrid Learning in Children
Abstract
:1. Introduction
2. Materials and Methods
2.1. Subject Analysis
2.2. Statistical Analysis
2.3. Kidney Volume Measurement
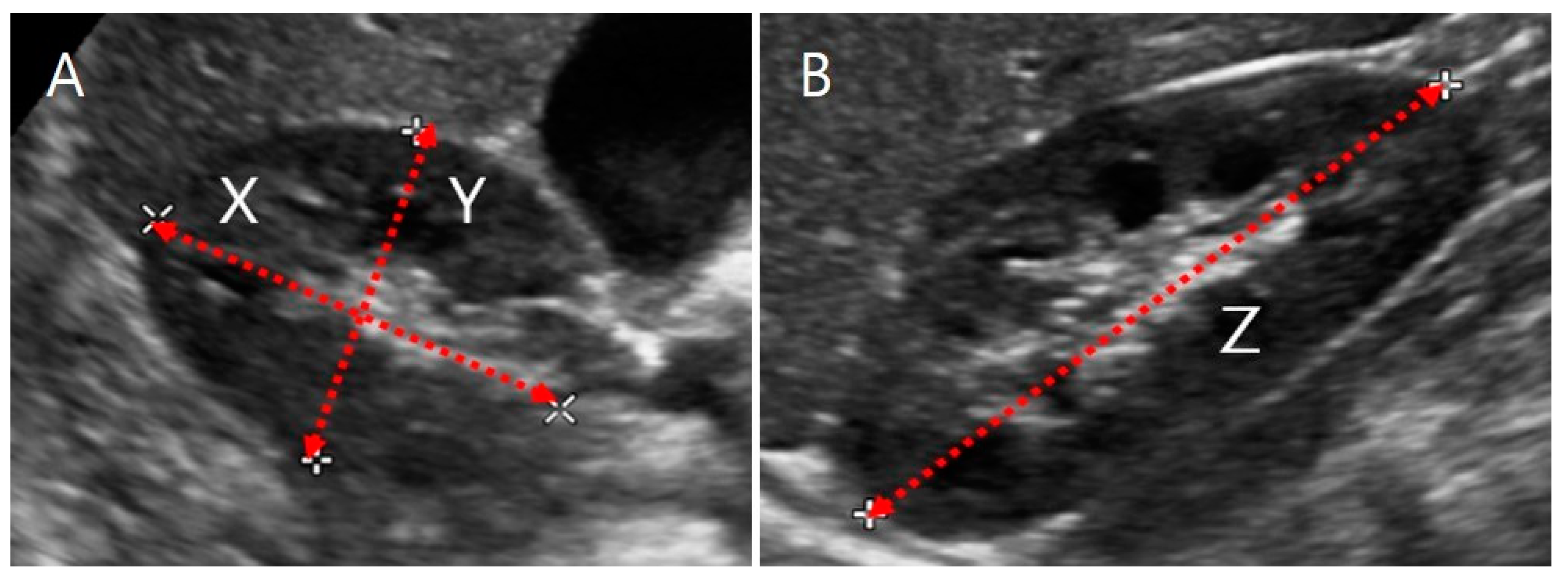
2.3.1. US Images and Ellipsoidal Method
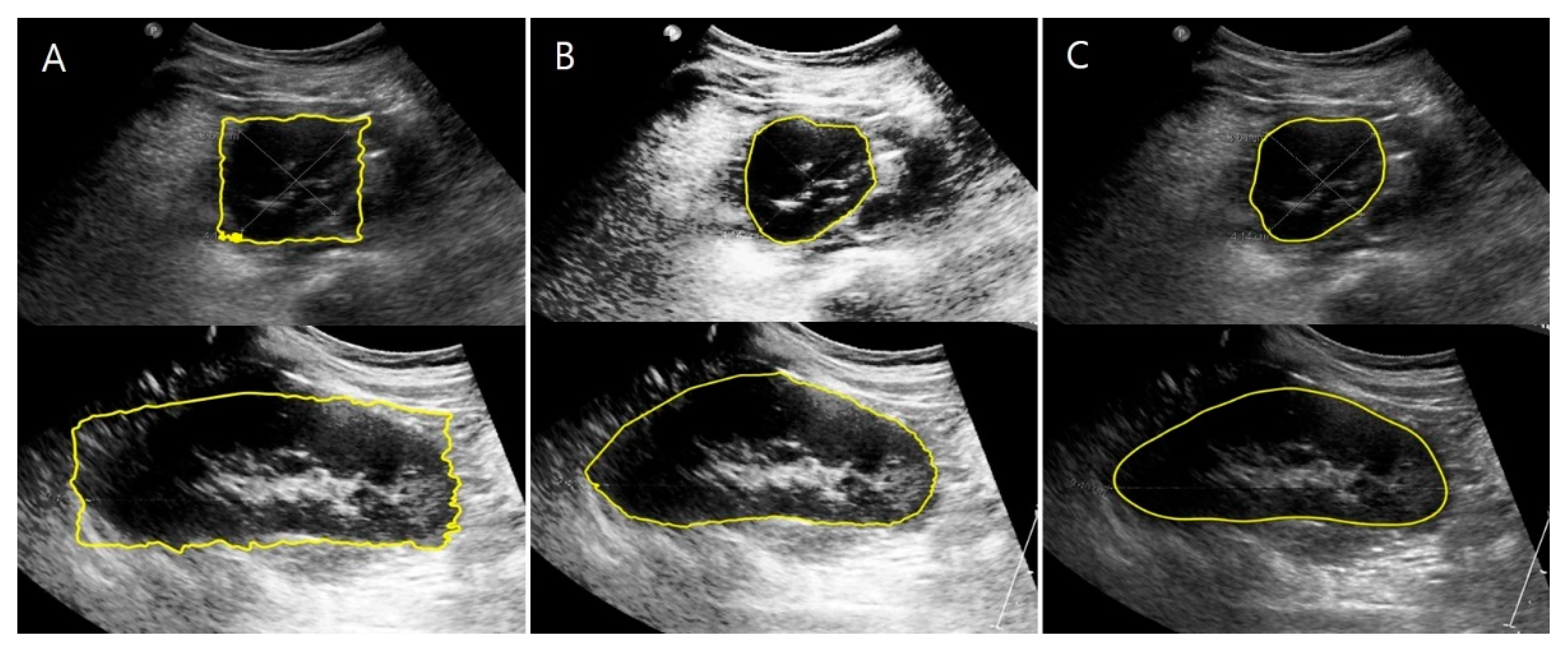
2.3.2. US Images and Image Processing Program
2.3.3. CT Images and Volume Calculation
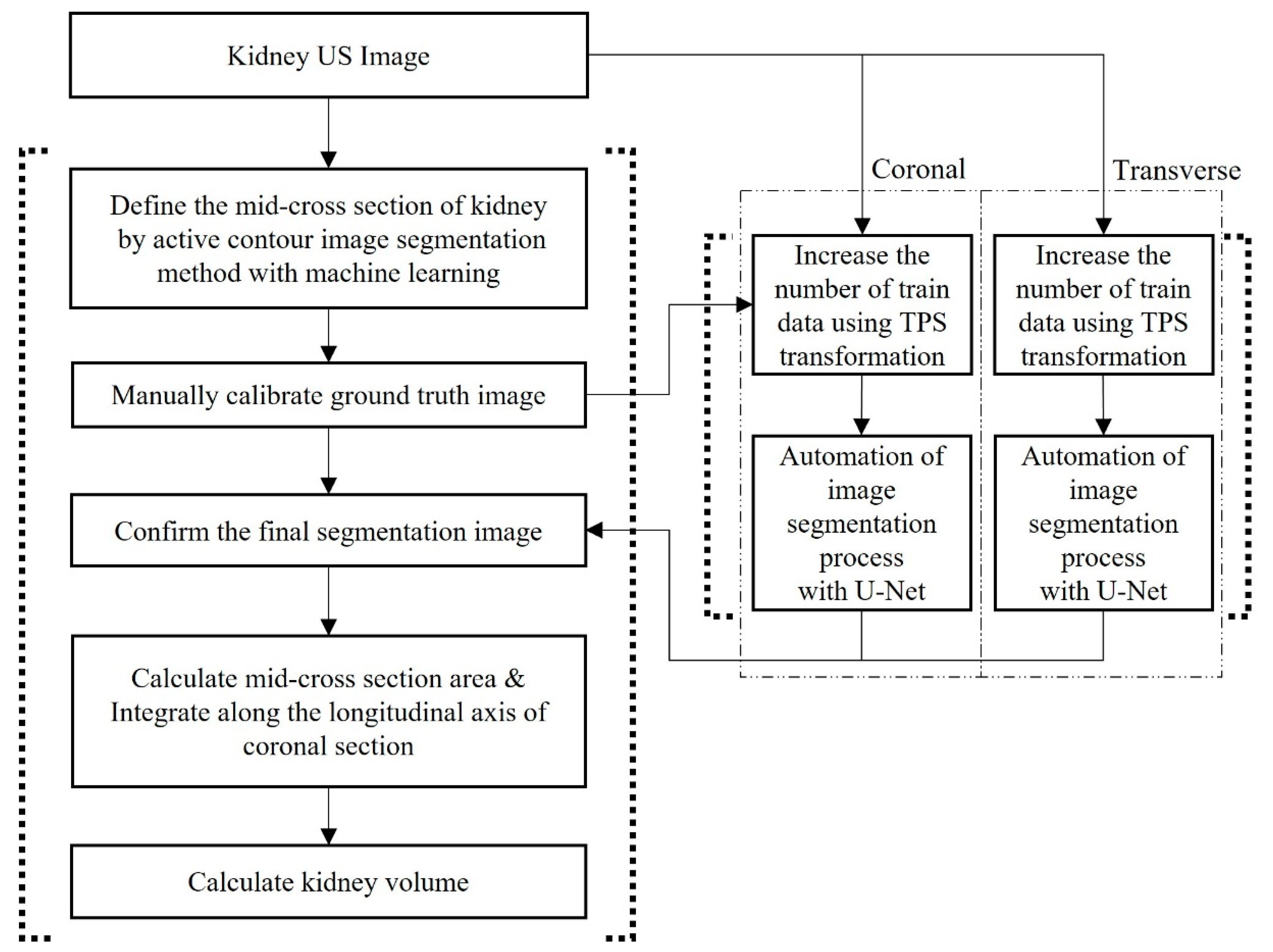
2.4. Automation of Volume Measurement by Hybrid Learning
2.4.1. Datasets
2.4.2. Data Augmentation Using Thin-Plate Spline Transformation
2.4.3. Deep Learning Network and Loss Function
3. Results
3.1. Comparison of Kidney Volumes Based on Sex, Age, and Position of the Kidney
3.2. Correlation between Age and Kidney Volume Measured by Different Methods
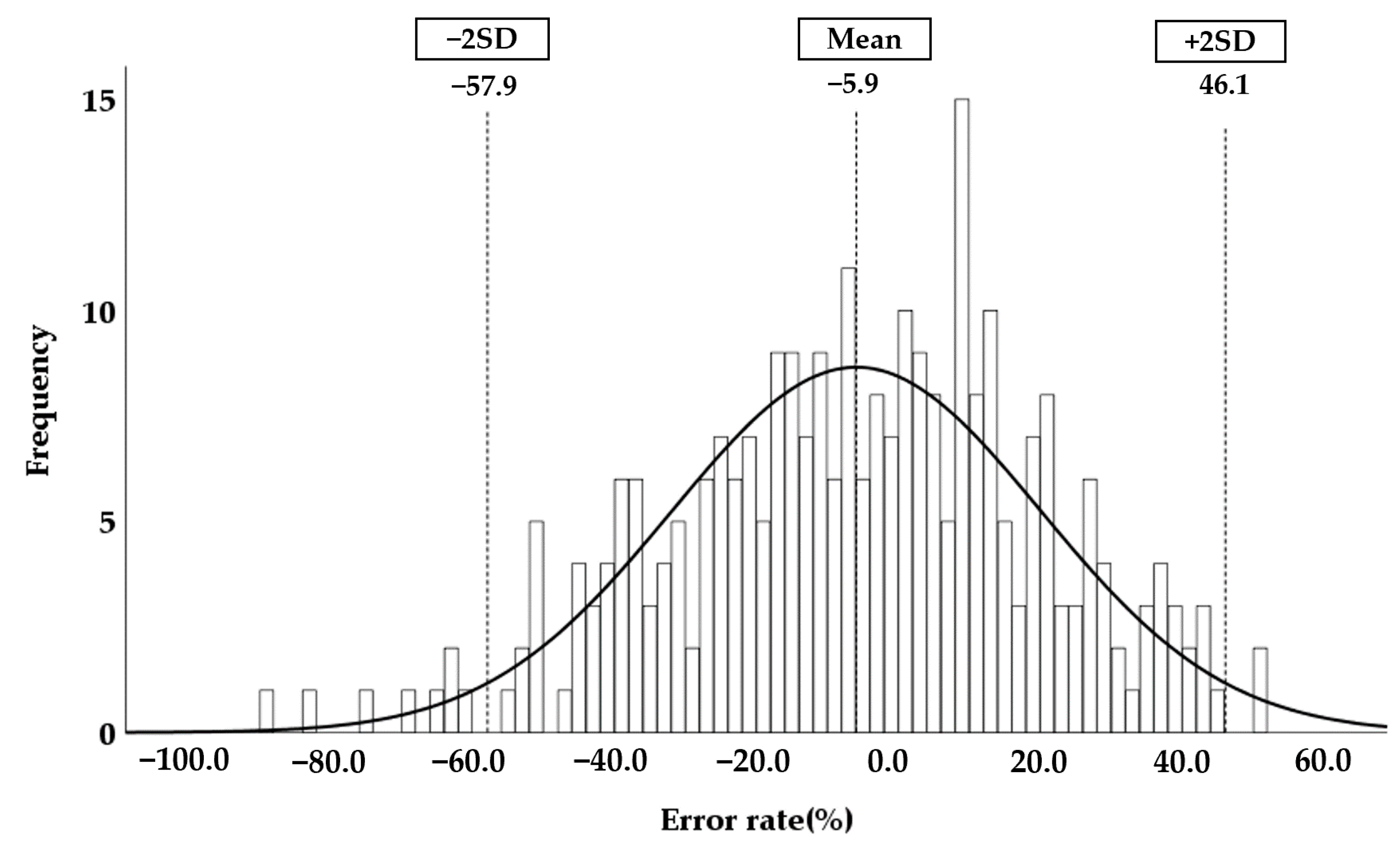
3.3. Degree of Agreement with the Reference Kidney Volume
3.4. Factors Affecting Changes in Kidney Volume
3.5. Accuracy of the Automatically Measured Kidney Volume Using Hybrid Learning
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schmidt, I.M.; Main, K.M.; Damgaard, I.N.; Mau, C.; Haavisto, A.M.; Chellakooty, M.; Boisen, K.A.; Petersen, J.H.; Sheike, T.; Olgaard, K. Kidney Growth in 717 Healthy Children Aged 0–18 Months: A Longitudinal Cohort Study. Pediatr. Nephrol. 2004, 19, 992–1003. [Google Scholar] [CrossRef]
- O’Neill, W.C. Sonographic Evaluation of Renal Failure. Am. J. Kidney Dis. 2000, 35, 1021–1038. [Google Scholar] [CrossRef]
- Kariyanna, S.S.; Light, R.P.; Agarwal, R. A Longitudinal Study of Kidney Structure and Function in Adults. Nephrol. Dial. Transplant. 2010, 25, 1120–1126. [Google Scholar] [CrossRef] [Green Version]
- Cain, J.E.; Di Giovanni, V.; Smeeton, J.; Rosenblum, N.D. Genetics of Renal Hypoplasia: Insights into the Mechanisms Controlling Nephron Endowment. Pediatr. Res. 2010, 68, 91–98. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vegar Zubović, S.; Kristić, S.; Pašić, I.S. Odnos Ultrazvučno Određenog Volumena Bubrega i Progresije Hronične Bubrežne Bolesti. Med. Glas. 2016, 13, 90–94. [Google Scholar] [CrossRef]
- Sharma, K.; Caroli, A.; Van Quach, L.; Petzold, K.; Bozzetto, M.; Serra, A.L.; Remuzzi, G.; Remuzzi, A. Kidney Volume Measurement Methods for Clinical Studies on Autosomal Dominant Polycystic Kidney Disease. PLoS ONE 2017, 12, e0178488. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oh, M.S.; Hwang, G.; Han, S.; Kang, H.S.; Kim, S.H.; Kim, Y.D.; Kang, K.S.; Shin, K.S.; Lee, M.S.; Choi, G.M.; et al. Sonographic Growth Charts for Kidney Length in Normal Korean Children: A Prospective Observational Study. J. Korean Med. Sci. 2016, 31, 1089–1093. [Google Scholar] [CrossRef] [PubMed]
- Shi, B.; Yang, Y.; Li, S.X.; Ju, H.; Ren, W.D. Ultrasonographic Renal Volume in Chinese Children: Results of 1683 Cases. J. Pediatr. Surg. 2015, 50, 1914–1918. [Google Scholar] [CrossRef]
- Han, B.K.; Babcock, D.S. Sonographic Measurements and Appearance of Normal Kidneys in Children. Am. J. Roentgenol. 1985, 145, 611–616. [Google Scholar] [CrossRef]
- Cheung, C.M.; Chrysochou, C.; Shurrab, A.E.; Buckley, D.L.; Cowie, A.; Kalra, P.A. Effects of Renal Volume and Single-Kidney Glomerular Filtration Rate on Renal Functional Outcome in Atherosclerotic Renal Artery Stenosis. Nephrol. Dial. Transplant. 2010, 25, 1133–1140. [Google Scholar] [CrossRef] [Green Version]
- Cheung, C.M.; Shurrab, A.E.; Buckley, D.L.; Hegarty, J.; Middleton, R.J.; Mamtora, H.; Kalra, P.A. MR-Derived Renal Morphology and Renal Function in Patients with Atherosclerotic Renovascular Disease. Kidney Int. 2006, 69, 715–722. [Google Scholar] [CrossRef] [Green Version]
- Widjaja, E.; Oxtoby, J.W.; Hale, T.L.; Jones, P.W.; Harden, P.N.; McCall, I.W. Ultrasound Measured Renal Length versus Low Dose CT Volume in Predicting Single Kidney Glomerular Filtration Rate. Br. J. Radiol. 2004, 77, 759–764. [Google Scholar] [CrossRef]
- Magistroni, R.; Corsi, C.; Martí, T.; Torra, R. A Review of the Imaging Techniques for Measuring Kidney and Cyst Volume in Establishing Autosomal Dominant Polycystic Kidney Disease Progression. Am. J. Nephrol. 2018, 48, 67–78. [Google Scholar] [CrossRef]
- Hwang, H.S.; Yoon, H.E.; Park, J.H.; Chun, H.J.; Park, C.W.; Yang, C.W.; Kim, Y.S.; Choi, B.S. Noninvasive and Direct Measures of Kidney Size in Kidney Donors. Am. J. Kidney Dis. 2011, 58, 266–271. [Google Scholar] [CrossRef]
- Bakker, J.; Olree, M.; Kaatee, R.; De Lange, E.E.; Moons, K.G.M.; Beutler, J.J.; Beek, F.J.A. Renal Volume Measurements: Accuracy and Repeatability of US Compared with That of MR Imaging. Radiology 1999, 211, 623–628. [Google Scholar] [CrossRef] [PubMed]
- Back, S.J.; Acharya, P.T.; Bellah, R.D.; Cohen, H.L.; Darge, K.; Deganello, A.; Harkanyi, Z.; Ključevšek, D.; Ntoulia, A.; Paltiel, H.J.; et al. Contrast-Enhanced Ultrasound of the Kidneys and Adrenals in Children. Pediatr. Radiol. 2021. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.H.; Kim, M.J.; Lim, S.H.; Kim, J.; Lee, M.J. Length and Volume of Morphologically Normal Kidneys in Korean Children: Ultrasound Measurement and Estimation Using Body Size. Korean J. Radiol. 2013, 14, 677–682. [Google Scholar] [CrossRef] [PubMed]
- Janki, S.; Kimenai, H.J.A.N.; Dijkshoorn, M.L.; Looman, C.W.N.; Dwarkasing, R.S.; Ijzermans, J.N.M. Validation of Ultrasonographic Kidney Volume Measurements: A Reliable Imaging Modality. Exp. Clin. Transplant. 2018, 16, 16–22. [Google Scholar] [CrossRef]
- Rasmussen, S.N.; Haase, L.; Kjeldsen, H.; Hancke, S. Determination of Renal Volume by Ultrasound Scanning. J. Clin. Ultrasound 1978, 6, 160–164. [Google Scholar] [CrossRef]
- Benjamin, A.; Chen, M.; Li, Q.; Chen, L.; Dong, Y.; Carrascal, C.A.; Xie, H.; Samir, A.E.; Anthony, B.W. Renal Volume Estimation Using Freehand Ultrasound Scans: An Ex Vivo Demonstration. Ultrasound Med. Biol. 2020, 46, 1769–1782. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Qin, W.; Xie, Y.; Wen, T.; Gu, J. A Shape-Optimized Framework for Kidney Segmentation in Ultrasound Images Using NLTV Denoising and DRLSE. Biomed. Eng. Online 2012, 11, 82. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zheng, Q.; Warner, S.; Tasian, G.; Fan, Y. A Dynamic Graph Cuts Method with Integrated Multiple Feature Maps for Segmenting Kidneys in 2D Ultrasound Images. Acad. Radiol. 2018, 25, 1136–1145. [Google Scholar] [CrossRef] [PubMed]
- Mendoza, C.S.; Kang, X.; Safdar, N.; Myers, E.; Martin, A.D.; Grisan, E.; Peters, C.A.; Linguraru, M.G. Automatic Analysis of Pediatric Renal Ultrasound Using Shape, Anatomical and Image Acquisition Priors. In Proceedings of the 16th International Conference, Nagoya, Japan, 22–26 September 2013; pp. 259–266. [Google Scholar] [CrossRef] [Green Version]
- Yin, S.; Peng, Q.; Li, H.; Zhang, Z.; You, X.; Furth, S.L.; Tasian, G.E.; Fan, Y. Automatic kidney segmentation in ultrasound images using subsequent boundary distance regression and pixelwise classification networks. Med. Image Anal. 2020, 60, 101602. [Google Scholar] [CrossRef] [PubMed]
- Torres, H.R.; Queirós, S.; Morais, P.; Oliveira, B.; Fonseca, J.C.; Vilaça, J.L. Kidney Segmentation in Ultrasound, Magnetic Resonance and Computed Tomography Images: A Systematic Review. Comput. Methods Programs Biomed. 2018, 157, 49–67. [Google Scholar] [CrossRef] [PubMed]
- Chu, Y.S.; An, H.G.; Oh, B.H.; Yang, S. Artificial Intelligence in Cutaneous Oncology. Front. Med. 2020, 7, 318. [Google Scholar] [CrossRef] [PubMed]
- Zakhari, N.; Blew, B.; Shabana, W. Simplified Method to Measure Renal Volume: The Best Correction Factor for the Ellipsoid Formula Volume Calculation in Pretransplant Computed Tomographic Live Donor. Urology 2014, 83, 1444.e15–1444.e19. [Google Scholar] [CrossRef] [PubMed]
- Mcandrew, A. An Introduction to Digital Image Processing with Matlab Notes for SCM2511 Image. Sch. Comput. Sci. Math. Vic. Univ. Technol. 2004, 264, 1–264. [Google Scholar]
- Lankton, S.; Member, S.; Tannenbaum, A. Localizing Region-Based Active Contours. IEEE Trans. Image Process. 2008, 17, 2029–2039. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gray, H. Anatomy of the Human Body, 20th ed.; Lea & Febiger: Philadelphia, PA, USA, 1918; p. 1219. [Google Scholar]
- Schuhmacher, P.; Kim, E.; Hahn, F.; Sekula, P.; Jilg, C.A.; Leiber, C.; Neumann, H.P.; Schultze-Seemann, W.; Walz, G.; Zschiedrich, S. Growth Characteristics and Therapeutic Decision Markers in von Hippel-Lindau Disease Patients with Renal Cell Carcinoma. Orphanet J. Rare Dis. 2019, 14, 235. [Google Scholar] [CrossRef]
- Iliuta, I.A.; Shi, B.; Pourafkari, M.; Akbari, P.; Bruni, G.; Hsiao, R.; Stella, S.F.; Khalili, K.; Shlomovitz, E.; Pei, Y. Foam Sclerotherapy for Cyst Volume Reduction in Autosomal Dominant Polycystic Kidney Disease: A Prospective Cohort Study. Kidney Med. 2019, 1, 366–375. [Google Scholar] [CrossRef] [Green Version]
- Lodewick, T.M.; Arnoldussen, C.W.K.P.; Lahaye, M.J.; van Mierlo, K.M.C.; Neumann, U.P.; Beets-Tan, R.G.; Dejong, C.H.C.; van Dam, R.M. Fast and Accurate Liver Volumetry Prior to Hepatectomy. Hpb 2016, 18, 764–772. [Google Scholar] [CrossRef] [Green Version]
- Gopal, A.; Grayburn, P.A.; Mack, M.; Chacon, I.; Kim, R.; Montenegro, D.; Phan, T.; Rudolph, J.; Filardo, G.; Mack, M.J.; et al. Noncontrast 3D CMR Imaging for Aortic Valve Annulus Sizing in TAVR. JACC Cardiovasc. Imaging 2015, 8, 375–378. [Google Scholar] [CrossRef] [PubMed]
- Szarvas, M.; Yoshizawa, A.; Yamamoto, M.; Ogata, J. Pedestrian Detection with Convolutional Neural Networks. IEEE Intell. Veh. Symp. Proc. 2005, 2005, 224–229. [Google Scholar] [CrossRef]
- O’Mahony, N.; Campbell, S.; Carvalho, A.; Harapanahalli, S.; Hernandez, G.V.; Krpalkova, L.; Riordan, D.; Walsh, J. Deep Learning vs. Traditional Computer Vision. Adv. Intell. Syst. Comput. 2020, 943, 128–144. [Google Scholar] [CrossRef] [Green Version]
- Donato, G.; Belongie, S. Approximate Thin Plate Spline Mappings. In European Conference on Computer Vision; Lecture Notes in Computer Science Book Series; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2352, pp. 21–31. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Lecture Notes in Computer Science Book Series; Springer: Cham, Switzerland, 2015; Volume 9351, pp. 234–241. [Google Scholar] [CrossRef] [Green Version]
- Zhang, M.; Li, W.; Chen, D. Blood Vessel Segmentation in Fundus Images Based on Improved Loss Function. In Proceedings of the 2019 Chinese Automation Congress (CAC), Hangzhou, China, 22–24 November 2019; pp. 4017–4021. [Google Scholar] [CrossRef]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollar, P. Focal Loss for Dense Object Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 318–327. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kistler, A.D.; Poster, D.; Krauer, F.; Weishaupt, D.; Raina, S.; Senn, O.; Binet, I.; Spanaus, K.; Wüthrich, R.P.; Serra, A.L. Increases in Kidney Volume in Autosomal Dominant Polycystic Kidney Disease Can Be Detected within 6 Months. Kidney Int. 2009, 75, 235–241. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Muñoz Agel, F.; Varas Lorenzo, M.J. Tridimensional (3D) Ultrasonography. Rev. Esp. Enferm. Dig. 2005, 97, 125–134. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Riccabona, M.; Fritz, G.; Ring, E. Potential Applications of Three-Dimensional Ultrasound in the Pediatric Urinary Tract: Pictorial Demonstration Based on Preliminary Results. Eur. Radiol. 2003, 13, 2680–2687. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Wang, Y.; Yang, X.; Lei, B.; Liu, L.; Li, S.X.; Ni, D.; Wang, T. Deep Learning in Medical Ultrasound Analysis: A Review. Engineering 2019, 5, 261–275. [Google Scholar] [CrossRef]
- Radiol, P.; Statistics, M. Pediatric Radiology Sonographical Growth Charts for Kidney Length and Volume *’**. Statistics 1985, 2, 38–43. [Google Scholar]
- Hope, J.W. Pediatric Radiology. Am. J. Roentgenol. Radium Ther. Nucl. Med. 1962, 88, 589–591. [Google Scholar] [PubMed]
- Chitty, L.S.; Altman, D.G. Charts of Fetal Size: Kidney and Renal Pelvis Measurements. Prenat. Diagn. 2003, 23, 891–897. [Google Scholar] [CrossRef] [PubMed]
- Barbosa, R.M.; Souza, R.T.; Silveira, C.; Andrade, K.C.; Almeida, C.M.; Bortoleto, A.G.; Oliveira, P.F.; Cecatti, J.G. Reference Ranges for Ultrasound Measurements of Fetal Kidneys in a Cohort of Low-Risk Pregnant Women. Arch. Gynecol. Obstet. 2019, 299, 585–591. [Google Scholar] [CrossRef]
- Hu, Y.; Guo, Y.; Wang, Y.; Yu, J.; Li, J.; Zhou, S.; Chang, C. Automatic Tumor Segmentation in Breast Ultrasound Images Using a Dilated Fully Convolutional Network Combined with an Active Contour Model. Med. Phys. 2019, 46, 215–228. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ataloglou, D.; Dimou, A.; Zarpalas, D.; Daras, P. Fast and Precise Hippocampus Segmentation through Deep Convolutional Neural Network Ensembles and Transfer Learning. Neuroinformatics 2019, 17, 563–582. [Google Scholar] [CrossRef] [PubMed]





| Group | No. of Subjects | (%) | |
|---|---|---|---|
| Sex | Boys | 83 | (58.9) |
| Girls | 58 | (41.1) | |
| Total | 141 | (100.0) | |
| Age group (years) | 0–5 | 69 | (48.9) |
| 6–12 | 46 | (32.6) | |
| 13–18 | 26 | (18.4) | |
| Total | 141 | (100.0) | |
| Imaging study | US only | 112 | (79.4) |
| CT + US | 29 | (20.6) | |
| Total | 141 | (100.0) |
| Coronal Plane | Transverse Plane | |||
|---|---|---|---|---|
| No. of Data Points | No. of Subjects | No. of Data Points | No. of Subjects | |
| Train | 255 | 137 | 256 | 139 |
| Validation | 36 | 18 | 36 | 18 |
| Test | 35 | 18 | 35 | 18 |
| Total | 326 | 173 | 327 | 175 |
| Age Group (years) | IMGSEG_Vol | p-Value | |
| Right Kidney | Left Kidney | ||
| Mean (Error Measure) | Mean (Error Measure) | ||
| 0–5 | 44.8 ± 23.0 † | 45.6 ± 22.7 † | 0.526 † |
| 6–12 | 109.0 ± 36.9 ‡ | 108.7 ± 36.6 ‡ | 0.932 ‡ |
| 13–18 | 170.3 ± 49.6 †† | 161.3 ± 49.1 †† | 0.636 †† |
| Position of Kidney | IMGSEG_Vol | p-Value | |
| Boys | Girls | ||
| Mean (Error Measure) | Mean (Error Measure) | ||
| Right | 92.1 ± 63.1 ∥ | 84.3 ± 52.2 ∥ | 0.135 ∥ |
| Left | 90.8 ± 57.6 ¶ | 82.8 ±53.8 ¶ | 0.402 ¶ |
| Kidney Volume | ICC * | 95% CI ** | p-Value |
|---|---|---|---|
| IMGSEG_Vol | 0.909 | 0.847–0.946 | p < 0.05 |
| ELLIP_Vol | 0.805 | 0.327–0.919 |
| Independent Variables | Intercept | B * | Standard Error | Standardized Coefficient (β) | p-Value | |
|---|---|---|---|---|---|---|
| Weight | 20.599 | 2.467 | 0.079 | 0.899 | p < 0.001 | 0.809 |
| BSA | −2.878 | 106.281 | 3.277 | 0.890 | p < 0.001 | 0.792 |
| Height | −46.459 | 1.220 | 0.045 | 0.851 | p < 0.001 | 0.724 |
| Age | 34.881 | 8.468 | 0.339 | 0.831 | p < 0.001 | 0.690 |
| BMI | −76.77 | 9.751 | 0.740 | 0.621 | p < 0.001 | 0.386 |
| Independent Variables | Intercept | B * | Standard Error (SE) | Standardized Coefficient (β) | p-Value | VIF ** | |
|---|---|---|---|---|---|---|---|
| Weight Height | 5.138 | 2.220 0.252 | 0.198 0.094 | 0.737 0.175 | p < 0.001 p < 0.05 | 6.273 | 0.810 |
| Coronal Plane | Transverse Plane | |||||
|---|---|---|---|---|---|---|
| Recall | Precision | F1 Score | Recall | Precision | F1 Score | |
| Validation | 0.9211 | 0.9716 | 0.9441 | 0.8617 | 0.9382 | 0.8808 |
| Test | 0.9310 | 0.9801 | 0.9538 | 0.8858 | 0.9224 | 0.8940 |
| Method | ICC * | 95%CI ** | p-Value |
|---|---|---|---|
| HYBRID_Vol | 0.925 ‡, ¶ | 0.872–0.956 | p = 0.59 ‡ |
| IMGSEG_Vol | 0.909 ‡, ∮ | 0.847–0.946 | p < 0.01 ¶ |
| ELLIP_Vol | 0.805 ¶, ∮ | 0.327–0.919 | p < 0.05 ∮ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, D.-W.; Ahn, H.-G.; Kim, J.; Yoon, C.-S.; Kim, J.-H.; Yang, S. Advanced Kidney Volume Measurement Method Using Ultrasonography with Artificial Intelligence-Based Hybrid Learning in Children. Sensors 2021, 21, 6846. https://doi.org/10.3390/s21206846
Kim D-W, Ahn H-G, Kim J, Yoon C-S, Kim J-H, Yang S. Advanced Kidney Volume Measurement Method Using Ultrasonography with Artificial Intelligence-Based Hybrid Learning in Children. Sensors. 2021; 21(20):6846. https://doi.org/10.3390/s21206846
Chicago/Turabian StyleKim, Dong-Wook, Hong-Gi Ahn, Jeeyoung Kim, Choon-Sik Yoon, Ji-Hong Kim, and Sejung Yang. 2021. "Advanced Kidney Volume Measurement Method Using Ultrasonography with Artificial Intelligence-Based Hybrid Learning in Children" Sensors 21, no. 20: 6846. https://doi.org/10.3390/s21206846
APA StyleKim, D.-W., Ahn, H.-G., Kim, J., Yoon, C.-S., Kim, J.-H., & Yang, S. (2021). Advanced Kidney Volume Measurement Method Using Ultrasonography with Artificial Intelligence-Based Hybrid Learning in Children. Sensors, 21(20), 6846. https://doi.org/10.3390/s21206846







