Investigations on Practical Issues in Solid Immersion Lens Based Sub-Wavelength Terahertz Imaging Technique: System Stability Verification and Interference Pattern Removal
Abstract
:1. Introduction
2. Experimental System Characterization
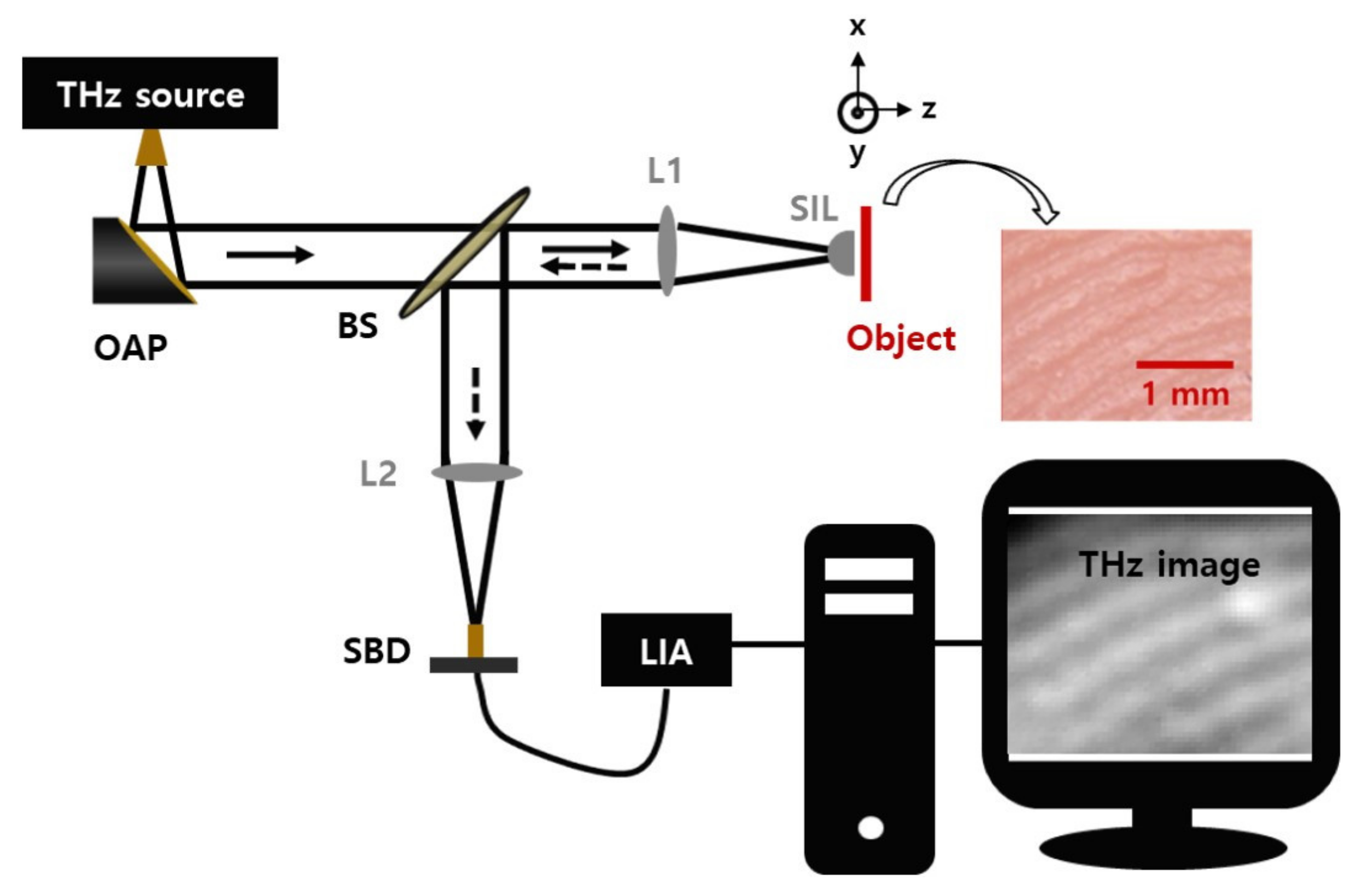
2.1. Experimental Setup
2.2. System Stability Verification
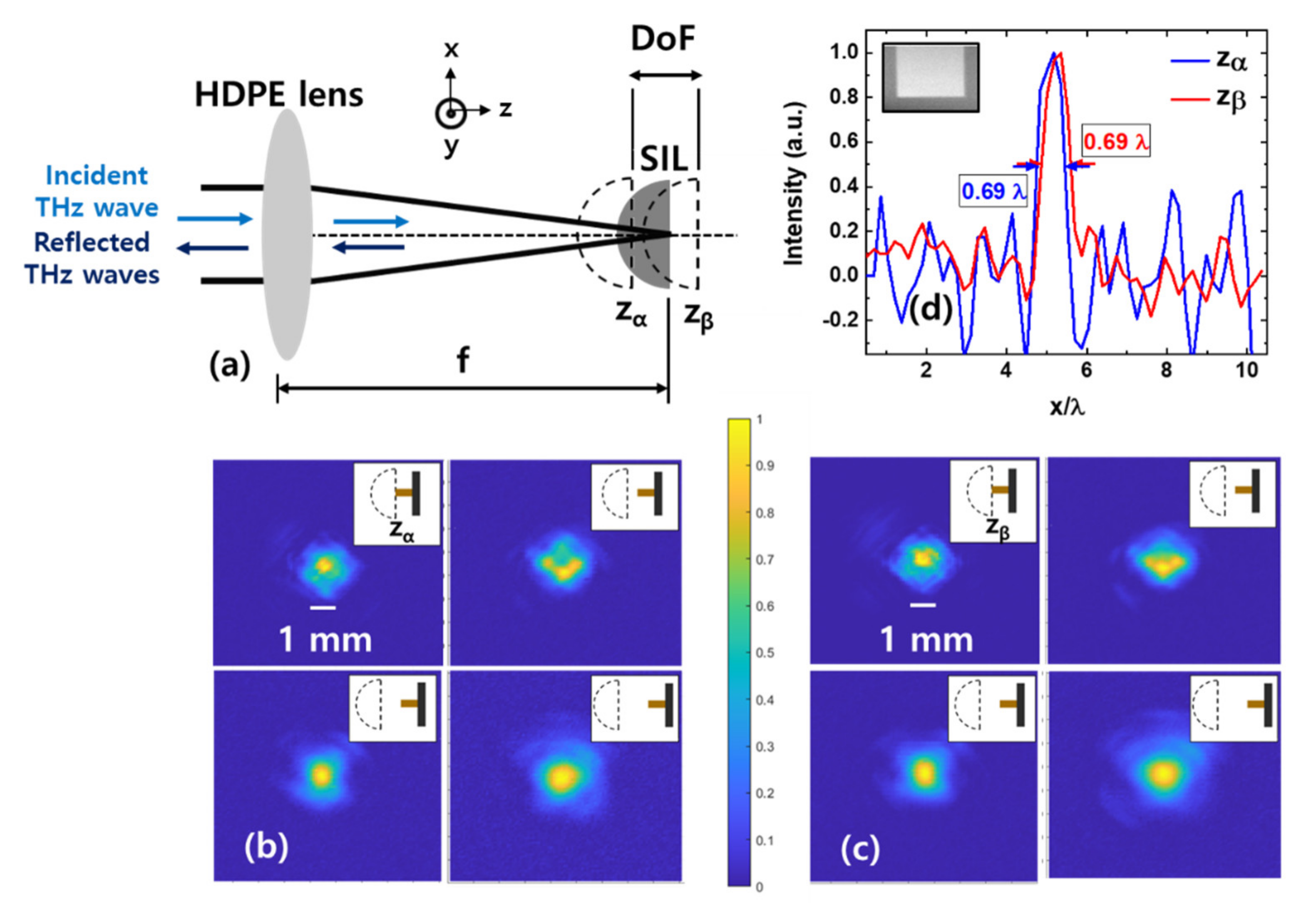
2.2.1. DoF Determination
2.2.2. Experimental Verification of System Stability
3. Contact-Free Sub-Wavelength Imaging
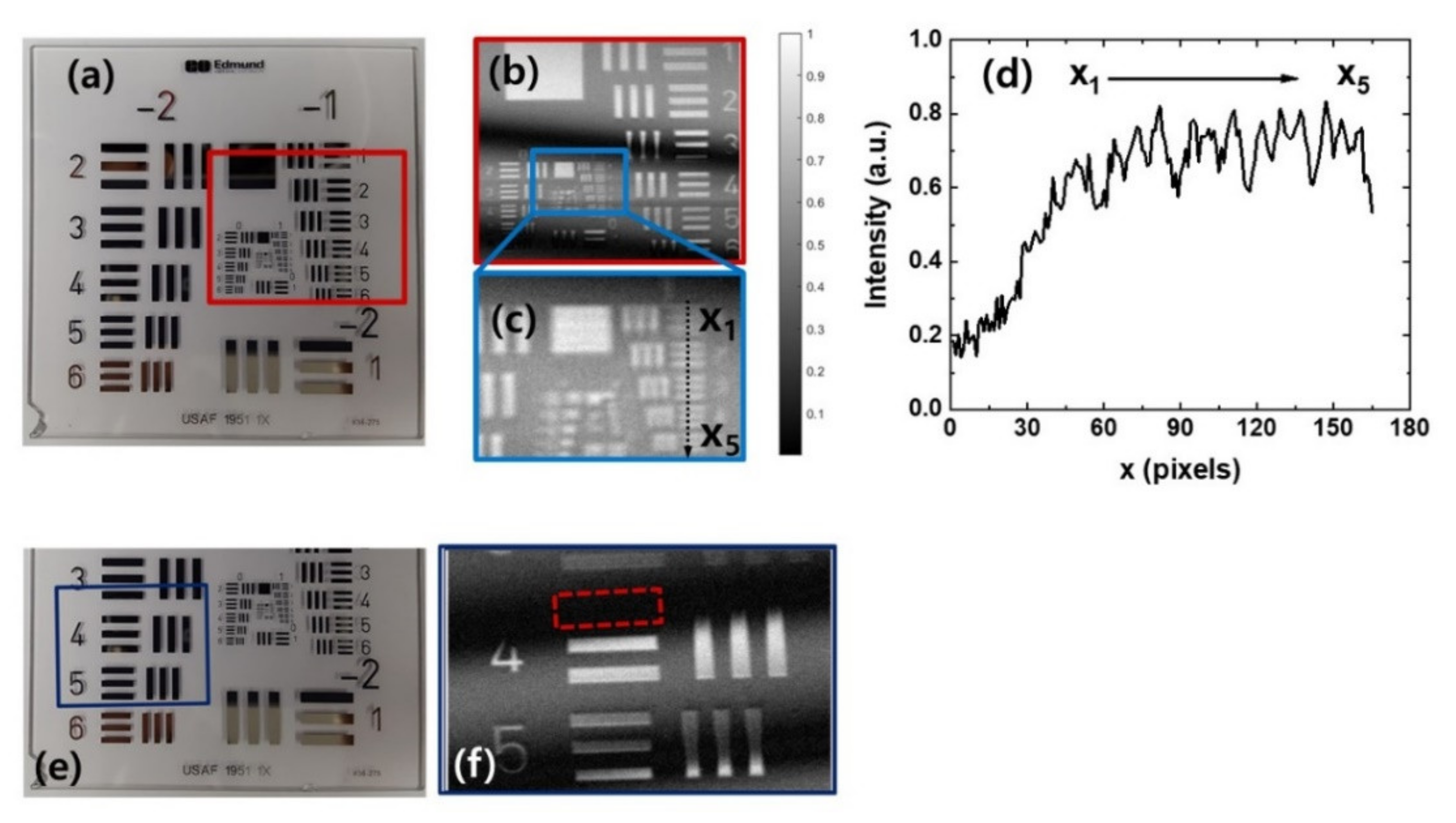
3.1. Imaging Examples and Limitations by Interference
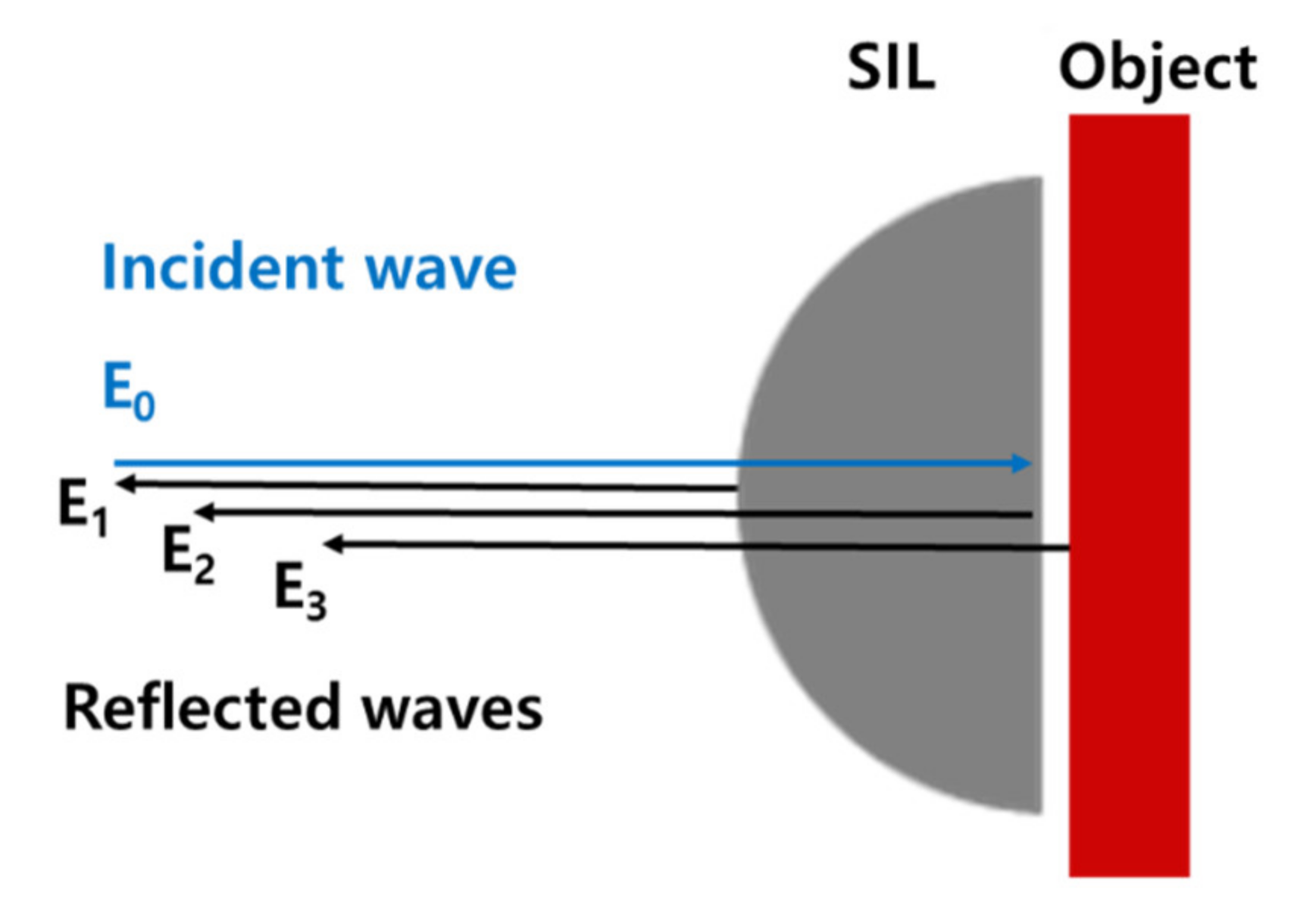
3.2. Theoretical and Experimental Investigations on Interference Pattern Removal
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dhillon, S.S.; Vitiello, M.S.; Linfield, E.H.; Davies, A.G.; Hoffmann, M.C.; Booske, J.; Paoloni, C.; Gensch, M.; Weightman, P.; Williams, G.P.; et al. The 2017 terahertz science and technology roadmap. J. Phys. D Appl. Phys. 2017, 50, 043001. [Google Scholar] [CrossRef]
- Stoik, C.; Bohn, M.; Blackshire, J. Nondestructive evaluation of aircraft composites using reflective terahertz time domain spectroscopy. NDT Int. 2010, 43, 106–115. [Google Scholar] [CrossRef] [Green Version]
- Krimi, S.; Klier, J.; Jonuscheit, J.; von Freymann, G.; Urbansky, R.; Beigang, R. Highly accurate thickness measurement of multi-layered automotive paints using terahertz technology. Appl. Phys. Lett. 2016, 109, 021105. [Google Scholar] [CrossRef]
- Yasui, T.; Yasuda, T.; Sawanaka, K.; Araki, T. Terahertz paintmeter for noncontact monitoring of thickness and drying progress in paint film. Appl. Opt. 2005, 44, 6849–6856. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abraham, E.; Younus, A.; Delagnes, J.C.; Mounaix, P. Non-invasive investigation of art paintings by terahertz imaging. Appl. Phys. A 2010, 100, 585–590. [Google Scholar] [CrossRef]
- Cosentino, A. Terahertz and cultural heritage science: Examination of art and archaeology. Technologies 2016, 4, 6. [Google Scholar] [CrossRef]
- Wang, J.; Sun, Q.; Stantchev, R.I.; Chiu, T.W.; Ahuja, A.T.; Pickwell-MacPherson, E. In vivo terahertz imaging to evaluate scar treatment strategies: Silicone gel sheeting. Biomed. Opt. Express 2019, 10, 3584–3590. [Google Scholar] [CrossRef]
- Taylor, Z.D.; Singh, R.S.; Bennett, D.B.; Tewari, P.; Kealey, C.P.; Bajwa, N.; Culjat, M.O.; Stojadinovic, A.; Lee, H.; Hubschman, J.-P.; et al. THz medical imaging: In vivo hydration sensing. IEEE Trans. THz Sci. Technol. 2011, 1, 201–218. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Stantchev, R.I.; Sun, Q.; Chiu, T.W.; Ahuja, A.T.; MacPherson, E.P. THz in vivo measurements: The effects of pressure on skin reflectivity. Biomed. Opt. Express 2018, 9, 6467–6476. [Google Scholar] [CrossRef] [Green Version]
- Sun, Q.; Parrott, E.P.; He, Y.; Pickwell-MacPherson, E. In vivo THz imaging of human skin: Accounting for occlusion effects. J. Biophotonics 2018, 11, e201700111. [Google Scholar] [CrossRef]
- Huber, A.J.; Keilmann, F.; Wittborn, J.; Aizpurua, J.; Hillenbrand, R. Terahertz Near-Field Nanoscopy of Mobile Carriers in Single Semiconductor Nanodevices. Nano Lett. 2008, 8, 3766–3770. [Google Scholar] [CrossRef]
- Chen, H.T.; Kersting, R.; Cho, G.C. Terahertz imaging with nanometer resolution. Appl. Phys. Lett. 2003, 83, 3009–3011. [Google Scholar] [CrossRef]
- Giordano, M.C.; Mastel, S.; Liewald, C.; Columbo, L.L.; Brambilla, M.; Viti, L.; Politano, A.; Zhang, K.; Li, L.; Davies, A.G.; et al. Phase-resolved terahertz self-detection near-field microscopy. Opt. Express 2018, 26, 18423–18435. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pham, H.H.N.; Hisatake, S.; Minin, O.V.; Nagatsuma, T.; Minin, I.V. Enhancement of spatial resolution of terahertz imaging systems based on terajet generation by dielectric cube. APL Photonics 2017, 2, 056106. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Liu, H.; Yang, M.; Cui, B.; Zhang, W. Dielectric sphere-coupled THz super-resolution imaging. Appl. Phys. Lett. 2018, 113, 031105. [Google Scholar] [CrossRef]
- Mansfield, S.M.; Kino, G.S. Solid immersion microscope. Appl. Phys. Lett. 1990, 57, 2615–2616. [Google Scholar] [CrossRef]
- Terris, B.D.; Mamin, H.J.; Rugar, D.; Studenmund, W.R.; Kino, G.S. Near-field optical data storage using a solid immersion lens. Appl. Phys. Lett. 1994, 65, 388–390. [Google Scholar] [CrossRef]
- Wang, L.; Bateman, B.; Zanetti-Domingues, L.C.; Moores, A.N.; Astbury, S.; Spindloe, C.; Darrow, M.C.; Romano, M.; Needham, S.R.; Beis, K.; et al. Solid immersion microscopy images cells under cryogenic conditions with 12 nm resolution. Commun. Biol. 2019, 2, 1–11. [Google Scholar] [CrossRef]
- Pimenov, A.; Loidl, A. Focusing of millimeter-wave radiation beyond the Abbe barrier. Appl. Phys. Lett. 2003, 83, 4122–4124. [Google Scholar] [CrossRef]
- Gompf, B.; Gerull, M.; Müller, T.; Dressel, M. THz-micro-spectroscopy with backward-wave oscillators. Infrared Phys. Technol. 2006, 49, 128–132. [Google Scholar] [CrossRef]
- Chernomyrdin, N.V.; Kucheryavenko, A.S.; Kolontaeva, G.S.; Katyba, G.M.; Dolganova, I.N.; Karalkin, P.A.; Ponomarev, D.S.; Kurlov, V.N.; Reshetov, I.V.; Skorobogatiy, M.; et al. Reflection-mode continuous-wave 0.15 λ-resolution terahertz solid immersion microscopy of soft biological tissues. Appl. Phys. Lett. 2018, 113, 111102. [Google Scholar] [CrossRef]
- Chernomyrdin, N.V.; Schadko, A.O.; Lebedev, S.P.; Tolstoguzov, V.L.; Kurlov, V.N.; Reshetov, I.V.; Spektor, I.E.; Skorobogatiy, M.; Yurchenko, S.O.; Zaytsev, K.I. Solid immersion terahertz imaging with sub-wavelength resolution. Appl. Phys. Lett. 2017, 110, 221109. [Google Scholar] [CrossRef] [Green Version]
- Dai, J.; Zhang, J.; Zhang, W.; Grischkowsky, D. Terahertz time-domain spectroscopy characterization of the far-infrared absorption and index of refraction of high-resistivity, float-zone silicon. J. Opt. Soc. Am. B 2004, 21, 1379–1386. [Google Scholar] [CrossRef] [Green Version]
- Chernomyrdin, N.V.; Zhelnov, V.A.; Kucheryavenko, A.S.; Dolganova, I.N.; Katyba, G.M.; Karasik, V.E.; Reshetov, I.V.; Zaytsev, K.I. Numerical analysis and experimental study of terahertz solid immersion microscopy. Opt. Eng. 2019, 59, 061605. [Google Scholar] [CrossRef]
- Subbarao, M.; Tyan, J.-K. Selecting the optimal focus measure for autofocusing and depth-from-focus. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 864–870. [Google Scholar] [CrossRef] [Green Version]
- Geusebroek, J.-M.; Cornelissen, F.; Smeulders, A.W.M.; Geerts, H. Robust autofocusing in microscopy. Cytom. A 2000, 39, 1–9. [Google Scholar] [CrossRef]
- Hurtado-Pérez, R.; Toxqui-Quitl, C.; Padilla-Vivanco, A.; Aguilar-Valdez, J.F.; Ortega-Mendoza, G. Focus measure method based on the modulus of the gradient of the color planes for digital microscopy. Opt. Eng. 2018, 57, 023106. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.; Wang, D.; Rong, L.; Panezai, S.; Zhang, D.; Qiu, P.; Gao, L.; Gao, H.; Zheng, H.; Zheng, Z. Continuous-wave off-axis and in-line terahertz digital holography with phase unwrapping and phase autofocusing. Opt. Comm. 2018, 426, 612–622. [Google Scholar] [CrossRef]
- Groen, F.C.A.; Young, I.T.; Ligthart, G. A Comparison of Different Focus Functions for Use in Autofocus Algorithms. Cytometry 1985, 6, 81–91. [Google Scholar] [CrossRef] [Green Version]
- Young, I.T.; Zagers, R.; van Vliet, L.J.; Mullikin, J.; Boddeke, F.; Netten, H. Depth-of-Focus in microscopy. In Proceedings of the 8th Scandinavian Conference on Image Analysis, Tromso, Norway, 25–28 May 1993; pp. 493–498. [Google Scholar]
- Perraud, J.-B.; Guillet, J.-P.; Redon, O.; Hamdi, M.; Simoens, F.; Mounaix, P. Shape-from-focus for real-time terahertz 3D imaging. Opt. Lett. 2019, 44, 483–486. [Google Scholar] [CrossRef]
- Fitzgerald, A.J.; Berry, E.; Miles, R.E.; Zinovev, N.N.; Smith, M.A.; Chamberlain, J.M. Evaluation of image quality in terahertz pulsed imaging using test objects. Phys. Med. Biol. 2002, 47, 3865–3873. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, L.; Chen, T.; Xu, D.; Shi, J.; Ren, Y.; Li, C.; Zhang, C.; Liu, H.; Wu, L.; et al. Interference elimination in terahertz imaging based on inverse image processing. J. Phys. D Appl. Phys. 2018, 51, 325101. [Google Scholar] [CrossRef]
- Ning, W.; Qi, F.; Liu, Z.; Wang, Y.; Wang, J. Origin of interference fringes and its countermeasures in coherent terahertz imaging. Microw. Opt. Technol. Lett. 2018, 60, 2492–2496. [Google Scholar] [CrossRef]
- Farina, A.; Kovacs-Vajna, Z.M.; Leone, A. Fingerprint minutiae extraction from skeletonized binary images. Pattern Recognit. 1999, 32, 877–889. [Google Scholar] [CrossRef]
- Choi, D.-H.; Lee, I.-M.; Moon, K.; Park, D.W.; Lee, E.S.; Park, K.H. Terahertz continuous wave system using phase shift interferometry for measuring the thickness of sub-100-μm-thick samples without frequency sweep. Opt. Express 2019, 27, 14695–14704. [Google Scholar] [CrossRef] [PubMed]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, D.-H.; Shin, J.-H.; Lee, I.-M.; Park, K.H. Investigations on Practical Issues in Solid Immersion Lens Based Sub-Wavelength Terahertz Imaging Technique: System Stability Verification and Interference Pattern Removal. Sensors 2021, 21, 6990. https://doi.org/10.3390/s21216990
Choi D-H, Shin J-H, Lee I-M, Park KH. Investigations on Practical Issues in Solid Immersion Lens Based Sub-Wavelength Terahertz Imaging Technique: System Stability Verification and Interference Pattern Removal. Sensors. 2021; 21(21):6990. https://doi.org/10.3390/s21216990
Chicago/Turabian StyleChoi, Da-Hye, Jun-Hwan Shin, Il-Min Lee, and Kyung Hyun Park. 2021. "Investigations on Practical Issues in Solid Immersion Lens Based Sub-Wavelength Terahertz Imaging Technique: System Stability Verification and Interference Pattern Removal" Sensors 21, no. 21: 6990. https://doi.org/10.3390/s21216990
APA StyleChoi, D.-H., Shin, J.-H., Lee, I.-M., & Park, K. H. (2021). Investigations on Practical Issues in Solid Immersion Lens Based Sub-Wavelength Terahertz Imaging Technique: System Stability Verification and Interference Pattern Removal. Sensors, 21(21), 6990. https://doi.org/10.3390/s21216990




