Secure Cognitive Radio-Enabled Vehicular Communications under Spectrum-Sharing Constraints
Abstract
:1. Introduction
1.1. Related Works
1.2. Motivation
- In [44], the authors considered the following assumptions while analyzing the secrecy performance of CRVNs; (i) single-power constraint of the interference on the primary receiver, and (ii) Nakagami-m fading. In addition, the system’s performance was evaluated in terms of secrecy outage probability (SOP).
- In [45], the authors considered the following assumptions while investigating the PHY-security performance of CRVNs; (i) single-power constraint of the interference on the primary receiver, (ii) cascaded Rayleigh fading for the main channel (between secondary source and secondary receiver), and Rayleigh fading for both the wiretap channel (between secondary source and secondary eavesdropper) and interference channel (between secondary source and primary receiver). However, for evaluating the system’s performance, the cascaded Rayleigh fading was transformed into a Nakagami-m fading approximation, and assumed statistical independence among the channel gains. In addition, the performance was evaluated in terms of SOP, intercept probability, and probability of non-zero secrecy capacity.
- Different from [44,45], in this paper, we adopt the following: (i) two power control strategies at the secondary transmitter, i.e., Strategy I: single-power constraint of the interference on the primary receiver, and Strategy II: combined power constraint of the interference on the primary receiver and the maximum transmission power at the secondary transmitter, (ii) double-Rayleigh fading for all the links, and (iii) statistical dependency among the channel gains. In addition, we evaluate the secrecy performance in terms of exact SOP, asymptotic SOP, and ergodic secrecy capacity (ESC), under Strategies I and II.
- In this work, we consider the channel between the moving vehicles to be quasistationary for a short duration (i.e., one fading block time), where the distance between the nodes is much greater than the scattering radii. Consequently, assuming the radio propagation between two moving vehicles undergoes independent double scattering events, the channel can be modeled as double-Rayleigh fading. By contrast, the works presented in [46,47] considered the scenario where the symbol period of the detected signal is larger than the coherence time of the channel, and hence, the system fading links can be characterized as time-selective. Particularly, the works [46,47] considered Rayleigh fading channels and Nakagami-m fading channels, respectively.
- In [46], the authors considered a single-power constraint of the interference on the primary receiver, whereas in [47], the authors adopted a combined power constraint of the interference on the primary receiver and the maximum transmission power at the secondary transmitter. Different from [46,47], this paper adopts both single-power- and combined-power-based control strategies for managing interference at the primary receiver.
- In [46], the authors evaluated the SOP and intercept probability expressions over Rayleigh fading channels, while in [47], the authors derived the expressions for the SOP and ESC over Nakagami-m fading channels. In this paper, we derived the SOP and ESC expressions over double-Rayleigh fading channels.
1.3. Contributions
- We deduce the exact SOP expressions over double-Rayleigh fading channels in order to investigate the secrecy performance under two considered power control strategies. These SOP expressions enable us to effectively determine the impact of key system/channel parameters on the system’s secrecy performance.
- We further present the asymptotic SOP expressions for Strategy I and Strategy II over double-Rayleigh fading channels. These asymptotic expressions provide us some important insights related to the system’s achievable secrecy diversity order. Based on these asymptotic results, it is observed that the system can achieve a secrecy diversity order of 1, when the average channel gain of the main link goes to infinity and the average channel gain of the wiretap link is fixed. However, the convergence of achieving the asymptotical secrecy diversity order of 1 is very slow, due the involvement of double-Rayleigh fading channels. In addition, the secrecy diversity order reduces to zero when the average channel gains of the main and wiretap links go to infinity.
- Using the derived exact SOP expression under Strategy II, we demonstrate the impact of maximum tolerable interference level and maximum secondary transmitter power on the secrecy performance. Specifically, we analyze two cases, viz., (1) when maximum tolerable interference level is proportional to maximum secondary transmitter power, and (2) when maximum tolerable interference level is not related to maximum secondary transmitter power. It is revealed from these two cases that the SOP performance saturates when maximum secondary transmitter power is large enough, which results into a zero system’ secrecy diversity gain.
- Further, we deduce novel ESC expressions for Strategy I and Strategy II under double-Rayleigh fading, in order to analyze the impact of interference threshold, maximum transmit power, and average channel gains on the secrecy performance. We also present two key observations irrespective of two power control strategies, when the average channel gains of main and wiretap links are very large, i.e., (1) there exists a ceiling of ESC, and (2) the ESC follows a scaling law of , where and are the average channel gains of main and wiretap links, respectively.
- We finally verify our analytical and theoretical findings via simulation studies. Our results show the impact of involved network parameters on the system’s SOP and ESC performances under Strategy I and Strategy II.
1.4. Organization
2. System and Channel Models
2.1. Statistical Background: The Double-Rayleigh Distribution
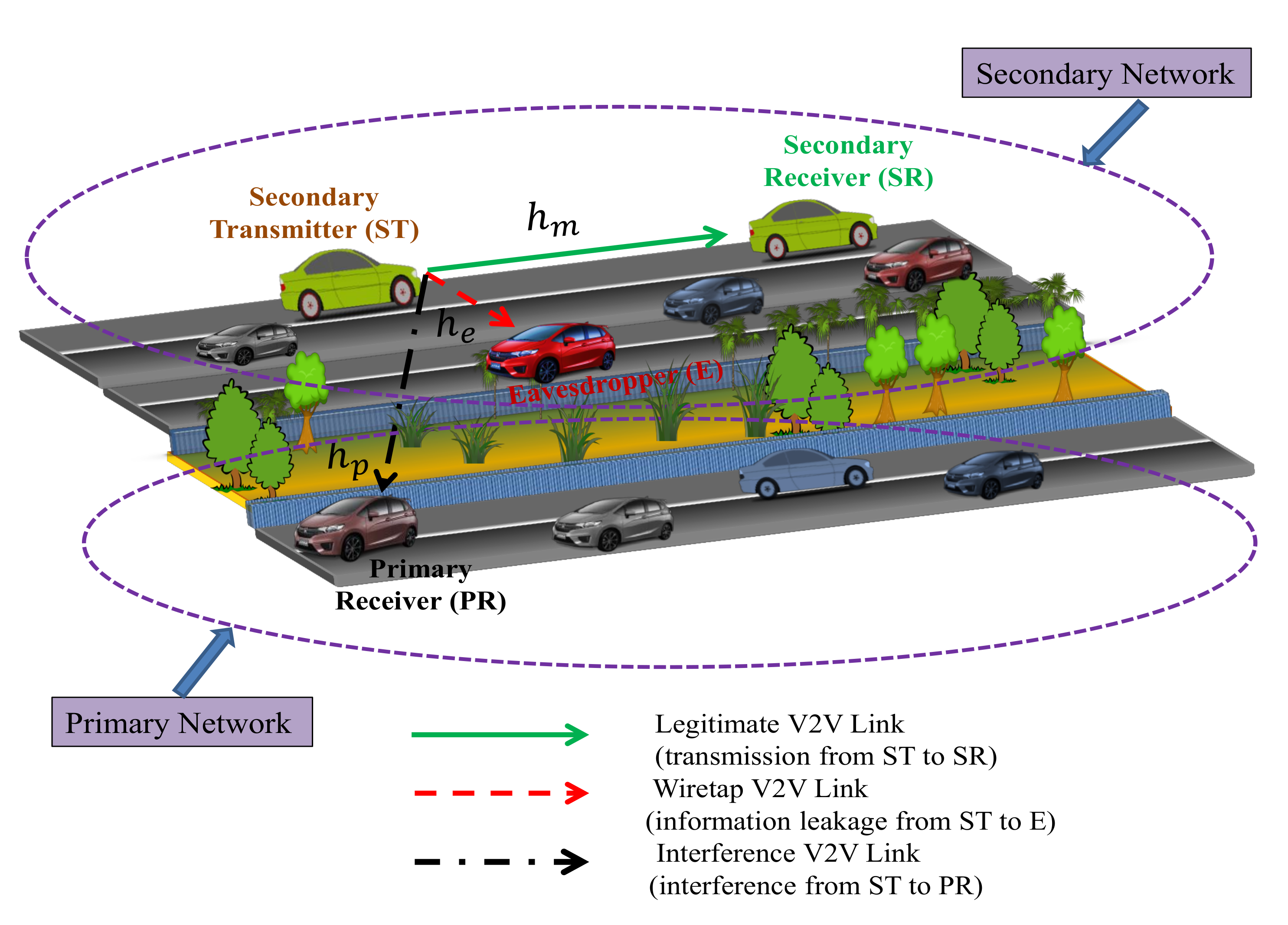
2.2. Cognitive Radio Vehicular System
2.3. Instantaneous End-to-End Signal-to-Noise Ratio
2.4. Practical Applicability
- The proposed analysis under Strategy I can be more appropriate under the practical scenario when the service provided by the primary user has an instantaneous QoS requirement.
- The proposed analysis under Strategy II is suitable under the practical scenario when there is a stringent requirement of protecting QoS of primary user and maximizing secondary user throughput simultaneously.
- The proposed analysis under double-Rayleigh fading assumption is practically applicable for vehicular communication scenarios in rush-hour urban traffic.
- The proposed analysis is also applicable for the scenario when one mobile terminal is located indoors in low-ascent building, and the another mobile terminal is placed outdoors, as the cascaded fading envelope distribution is found suitable under such scenario.
- The proposed analysis can be applied to the scenario when the mobile nodes are located in a relatively dense scattering (e.g., vegetation) environment, as the channel between them will be a good fit for cascaded fading distribution.
3. Exact and Asymptotic SOP Analyses under Strategies I and II
3.1. Strategy I: Single-Power Constraint of the Interference on the PR
3.1.1. Exact Analysis for SOP
3.1.2. Asymptotic Analysis for SOP
3.2. Strategy II: Combined Power Constraint of the Interference at the PR and Maximum Transmit Power at the ST
3.2.1. Exact Analysis for SOP
3.2.2. Asymptotic Analysis for SOP
3.2.3. Impact of Maximum Tolerable Interference Level and Maximum Secondary Transmitter Power Q
4. ESC Analysis under Strategies I and II
4.1. Strategy I: Single-Power Constraint of the Interference on the PR
4.2. Strategy II: Combined Power Constraint of the Interference at the PR and Maximum Transmit Power at the ST
5. Numerical Results and Discussion
5.1. SOP Performance under Strategies I and II
5.2. ESC Performance under Strategies I and II
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Proof of Theorem 1
Appendix B
Proof of Theorem 3
Appendix C
Proof of Theorem 4
Appendix D
Proof of Theorem 5
References
- Zhou, H.; Xu, W.; Chen, J.; Weng, W. Evolutionary V2X technologies toward the Internet of vehicles: Challenges and opportunities. Proc. IEEE. 2020, 108, 308–320. [Google Scholar] [CrossRef]
- Fallgren, M. 5GCAR: Executive Summary. 2019. Available online: https://5gcar.eu/wp-content/uploads/2019/12/5GCAR-Executive-Summary-White-Paper.pdf (accessed on 18 October 2021).
- Wong, V.W.; Schober, R.; Ng, D.W.K.; Wang, L.C. Key Technologies for 5G Wireless Systems; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Kaiwartya, O.; Kumar, S. Enhanced caching for geocast routing in vehicular Ad Hoc network. In Intelligent Computing, Networking, and Informatics; Advances in Intelligent Systems and Computing; Springer: New Delhi, India, 2014; Volume 243, pp. 213–220. [Google Scholar]
- Mumtaz, S.; Huq, K.M.S.; Ashraf, M.I.; Rodriguez, J.; Monteiro, V.; Politis, C. Cognitive vehicular communication for 5G. IEEE Commun. Mag. 2015, 53, 109–117. [Google Scholar] [CrossRef]
- Eze, J.; Zhang, S.; Liu, E.; Eze, E. Cognitive radio-enabled Internet of Vehicles: A cooperative spectrum sensing and allocation for vehicular communication. IET Netw. 2018, 7, 190–199. [Google Scholar] [CrossRef] [Green Version]
- Di Felice, M.; Doost-Mohammady, R.; Chowdhury, K.R.; Bononi, L. Smart Radios for Smart Vehicles: Cognitive Vehicular Networks. IEEE Veh. Technol. Mag. 2012, 7, 26–33. [Google Scholar] [CrossRef]
- Zou, Y.; Zhu, J.; Yang, L.; Liang, Y.C.; Yao, Y.D. Securing physical-layer communications for cognitive radio networks. IEEE Commun. Mag. 2015, 53, 48–54. [Google Scholar] [CrossRef] [Green Version]
- Shu, Z.; Qian, Y.; Ci, S. On physical layer security for cognitive radio networks. IEEE Netw. 2013, 27, 28–33. [Google Scholar]
- Zou, Y.; Zhu, J.; Wang, X.; Hanzo, L. A survey on wireless security: Technical challenges, recent advances, and future trends. Proc. IEEE. 2016, 104, 1727–1765. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Yang, L.; Hasna, M.O.; Alouini, M.S.; Zhang, J. Amount of secrecy loss: A novel metric for physical layer security analysis. IEEE Commun. Lett. 2020, 24, 1626–1630. [Google Scholar] [CrossRef]
- Chen, X.; Ng, D.W.K.; Gerstacker, W.H.; Chen, H.H. A survey on multiple-antenna techniques for physical layer security. IEEE Commun. Surv. Tut. 2017, 19, 1027–1053. [Google Scholar] [CrossRef]
- Moualeu, J.M.; da Costa, D.B.; Lopez-Martinez, F.J.; Hamouda, W.; Nkouatchah, T.M.; Dias, U.S. Transmit antenna selection in secure MIMO systems over α-μ fading channels. IEEE Trans. Commun. 2019, 67, 6483–6498. [Google Scholar] [CrossRef]
- Park, J.; Yun, S.; Kim, I.; Ha, J. Secure communications with a full-duplex relay network under residual self-interference. IEEE Commun. Lett. 2020, 24, 496–500. [Google Scholar] [CrossRef]
- Le, K.N.; Bao, V.N.Q. Secrecy under Rayleigh-dual correlated Rician fading employing opportunistic relays and an adaptive encoder. IEEE Trans. Veh. Technol. 2020, 69, 5179–5192. [Google Scholar] [CrossRef]
- Yang, L.; Chen, J.; Jiang, H.; Vorobyov, S.A.; Zhang, H. Optimal relay selection for secure cooperative communications with an adaptive eavesdropper. IEEE Trans. Wirel. Commun. 2017, 16, 6–42. [Google Scholar] [CrossRef]
- Fan, L.; Lei, X.; Yang, N.; Duong, T.Q.; Karagiannidis, G.K. Secrecy cooperative networks with outdated relay selection over correlated fading channels. IEEE Trans. Veh. Technol. 2017, 66, 7599–7603. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.; Liu, Z.; Yang, L.; Alouini, M.S. Secrecy analysis in DF relay over Generalized-K fading channels. IEEE Trans. Commun. 2019, 67, 7168–7182. [Google Scholar] [CrossRef] [Green Version]
- Madeira, J.; Guerreiro, J.; Dinis, R.; Carvalho, P.; Campos, L. On the physical layer security characteristics for MIMO-SVD techniques for SC-FDE schemes. Sensors 2019, 19, 4757. [Google Scholar] [CrossRef] [Green Version]
- Madeira, J.; Guerreiro, J.; Serra, H.; Dinis, R.; Carvalho, P.; Campos, L. A physical layer security technique for NOMA systems with MIMO SC-FDE schemes. Electronics 2020, 9, 240. [Google Scholar] [CrossRef] [Green Version]
- Kumar, S.; Singh, K.; Kumar, S.; Kaiwartya, O.; Cao, Y.; Zhou, H. Delimitated anti jammer scheme for Internet of Vehicle: Machine learning based security approach. IEEE Access 2019, 7, 113311–113323. [Google Scholar] [CrossRef]
- Chakraborty, P.; Prakriya, S. Secrecy outage performance of a cooperative cognitive relay network. IEEE Commun. Lett. 2017, 21, 326–329. [Google Scholar] [CrossRef]
- Nguyen, M.N.; Nguyen, N.P.; Da Costa, D.B.; Nguyen, H.K.; De Sousa, R.T. Secure cooperative half-duplex cognitive radio networks with K-th best relay selection. IEEE Access. 2017, 5, 6678–6687. [Google Scholar] [CrossRef]
- Chopra, K.; Bose, R.; Joshi, A. Secrecy performance of threshold-based cognitive relay network with diversity combining. J. Commun. Netw. 2018, 20, 383–395. [Google Scholar] [CrossRef]
- Bouabdellah, M.; Bouanani, F.E.; Alouini, M.S. A PHY layer security analysis of uplink cooperative jamming-based underlay CRNs with multi-eavesdroppers. IEEE Trans. Cog. Commun. Netw. 2020, 6, 704–717. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, A.; Maity, S.P. On residual energy maximization in cognitive relay networks with eavesdropping. IEEE Syst. J. 2019, 13, 3836–3846. [Google Scholar] [CrossRef]
- Zhang, T.; Cai, Y.; Huang, Y.; Duong, T.Q.; Yang, W. Secure transmission in cognitive MIMO relaying networks with outdated channel state information. IEEE Access 2016, 4, 8212–8224. [Google Scholar] [CrossRef] [Green Version]
- Zou, Y.; Li, X.; Liang, Y. Secrecy outage and diversity analysis of cognitive radio systems. IEEE J. Sel. Areas Commun. 2014, 32, 2222–2236. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Yin, H.; Huang, Y.; Fu, T.; Wang, Y.; Yu, R. Secrecy performance analysis in MISOSE cognitive radio networks over correlated fading. In Proceedings of the 2nd IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC 2018), Xi’an, China, 25–27 May 2018; pp. 875–879. [Google Scholar]
- Singh, A.; Bhatnagar, M.R.; Mallik, R.K. Physical layer security of a multiantenna-based CR network with single and multiple primary users. IEEE Trans. Veh. Technol. 2017, 66, 11011–11022. [Google Scholar] [CrossRef]
- Timilsina, S.; Baduge, G.A.A.; Schaefer, R.F. Secure communication in spectrum-sharing massive MIMO systems with active eavesdropping. IEEE Trans. Cog. Commun. Netw. 2018, 4, 390–405. [Google Scholar] [CrossRef]
- Lei, H.; Zhang, J.; Park, K.H.; Ansari, I.S.; Pan, G.; Alouini, M.S. Secrecy performance analysis of SIMO underlay cognitive radio systems with outdated CSI. IET Commun. 2017, 11, 1961–1969. [Google Scholar] [CrossRef]
- Andersen, J.B. Statistical distributions in mobile communications using multiple scattering. In Proceedings of the 27th URSI General Assembly, Maastricht, The Netherlands, 17–24 August 2002. [Google Scholar]
- Salo, J.; El-Sallabi, H.M.; Vainikainen, P. Statistical analysis of the multiple scattering radio channel. IEEE Trans. Antennas Propag. 2006, 54, 3114–3124. [Google Scholar] [CrossRef]
- Pandey, A.; Yadav, S. Physical layer security in cooperative AF relaying networks with direct links over mixed Rayleigh and double-Rayleigh fading channels. IEEE Trans. Veh. Technol. 2018, 67, 10615–10630. [Google Scholar] [CrossRef]
- Kovács, I.Z.; Eggers, P.C.; Olesen, K.; Petersen, L.G. Radio channel description and quality of service for TETRA direct mode operation in forest environments. In Proceedings of the IEEE 54th Vehicular Technology Conference, VTC Fall, Atlantic City, NJ, USA, 7–11 October 2001; pp. 1970–1974. [Google Scholar]
- Kovács, I.Z.; Eggers, P.C.; Olesen, K.; Petersen, L.G. Investigations of outdoor-to-indoor mobile-to-mobile radio communication channels. In Proceedings of the IEEE 56th Vehicular Technology Conference, Vancouver, BC, Canada, 24–28 September 2002; pp. 430–434. [Google Scholar]
- Zhang, J.; Pan, G. Secrecy outage analysis with Kth best relay selection in dual-hop inter-vehicle communication systems. AEU—Int. J. Electron. Commun. 2017, 71, 139–144. [Google Scholar] [CrossRef]
- Pandey, A.; Yadav, S. Secrecy analysis of cooperative vehicular relaying networks over double-Rayleigh fading Channels. Wirel. Pers. Commun. 2020, 114, 2733–2753. [Google Scholar] [CrossRef]
- Pandey, A.; Yadav, S. Physical layer security in cooperative amplify-and-forward relay networks over mixed Nakagami-M Double Nakagami-m Fading Channels: Perform. Eval. Optimisation. IET Commun. 2020, 14, 95–104. [Google Scholar] [CrossRef]
- Ahn, N.; Lee, D.; Oh, S. Vehicle Communication Using Secrecy Capacity. In Proceeding FTC; Arai, K., Bhatia, R., Kapoor, S., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 158–172. [Google Scholar]
- Duy, T.T.; Alexandropoulos, G.C.; Tung, V.T.; Son, V.N.; Duong, T.Q. Outage performance of cognitive cooperative networks with relay selection over double-Rayleigh fading channels. IET Commun. 2016, 10, 57–64. [Google Scholar] [CrossRef]
- Lee, J.; Lee, J.H.; Bahk, S. Performance analysis for multi-hop cognitive radio networks over cascaded Rayleigh fading channels with imperfect channel state information. IEEE Trans. Veh. Technol. 2019, 68, 10335–10339. [Google Scholar] [CrossRef]
- Ata, S.O.; Erdogan, E. Secrecy outage probability of inter-vehicular cognitive radio networks. Int. J. Commun. Sys. 2019, 33, e4244. [Google Scholar] [CrossRef]
- Tashman, D.H.; Hamouda, W. Physical-layer security for cognitive radio networks over cascaded Rayleigh fading channels. In Proceedings of the IEEE Global Communications Conference (GLOBECOM 2020), Taipei, Taiwan, 7–11 December 2020; pp. 1–6. [Google Scholar]
- Yadav, S.; Pandey, A. Secrecy performance of cognitive vehicular radio networks: Joint impact of nodes mobility and imperfect channel estimates. In Proceedings of the IEEE International Black Sea Conference on Communications and Networking (BlackSeaCom), Odessa, Ukraine, 26–29 May 2020; pp. 1–7. [Google Scholar]
- Pandey, A.; Yadav, S. Joint impact of nodes mobility and imperfect channel estimates on the secrecy performance of cognitive radio vehicular networks over Nakagami-M Fading Channels. IEEE Open J. Veh. Technol. 2021, 2, 289–309. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Tables of Integrals, Series, and Products, 6th ed.; Academic Press: New York, NY, USA, 2000. [Google Scholar]
- The Wolfram Functions Site [Online]. Available online: Http://functions.wolfram.com (accessed on 18 October 2021).
- Patel, C.S.; Stuber, G.L.; Pratt, T.G. Simulation of Rayleigh-faded mobile-to-mobile communication channels. IEEE Trans. Commun. 2005, 53, 1876–1884. [Google Scholar] [CrossRef]
- Patzold, M.; Hogstad, B.O.; Youssef, N. Modeling, analysis, and simulation of MIMO mobile-to-mobile fading channels. IEEE Trans. Wirel. Commun. 2008, 7, 510–520. [Google Scholar] [CrossRef]
- Ghasemi, A.; Sousa, E.S. Fundamental limits of spectrum-sharing in fading environments. IEEE Trans. Wirel. Commun. 2007, 6, 649–658. [Google Scholar] [CrossRef]
- Duong, T.Q.; da Costa, D.B.; Elkashlan, M.; Bao, V.N.Q. Cognitive amplify-and-forward relay networks over Nakagami-m fading. IEEE Trans. Veh. Technol. 2012, 61, 2368–2374. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; National Bureau of Standards: Washington, DC, USA, 1972. [Google Scholar]
- Ansari, I.S.; Al-Ahmadi, S.; Yilmaz, F.; Alouini, M.S.; Yanikomeroglu, H. A new formula for the BER of binary modulations with dual-branch selection over generalized-K composite fading channels. IEEE Trans. Commun. 2011, 59, 2654–2658. [Google Scholar] [CrossRef] [Green Version]
- Lei, H.; Zhang, H.; Ansari, I.S.; Gao, C.; Guo, Y.; Pan, G.; Qaraqe, K.A. Performance analysis of physical layer security over generalized-K fading channels using a mixture Gamma distribution. IEEE Commun. Lett. 2016, 20, 408–411. [Google Scholar]










Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yadav, S.; Pandey, A.; Do, D.-T.; Lee, B.M.; Silva, A. Secure Cognitive Radio-Enabled Vehicular Communications under Spectrum-Sharing Constraints. Sensors 2021, 21, 7160. https://doi.org/10.3390/s21217160
Yadav S, Pandey A, Do D-T, Lee BM, Silva A. Secure Cognitive Radio-Enabled Vehicular Communications under Spectrum-Sharing Constraints. Sensors. 2021; 21(21):7160. https://doi.org/10.3390/s21217160
Chicago/Turabian StyleYadav, Suneel, Anshul Pandey, Dinh-Thuan Do, Byung Moo Lee, and Adão Silva. 2021. "Secure Cognitive Radio-Enabled Vehicular Communications under Spectrum-Sharing Constraints" Sensors 21, no. 21: 7160. https://doi.org/10.3390/s21217160
APA StyleYadav, S., Pandey, A., Do, D.-T., Lee, B. M., & Silva, A. (2021). Secure Cognitive Radio-Enabled Vehicular Communications under Spectrum-Sharing Constraints. Sensors, 21(21), 7160. https://doi.org/10.3390/s21217160







