A Systematic Design Optimization Approach for Multiphysics MEMS Devices Based on Combined Computer Experiments and Gaussian Process Modelling
Abstract
:1. Introduction
2. Working Principle and Structural Design of MEMS Accelerometer
3. Design and Analysis of Computer Experiments (DACE) Based Multi-Response Optimization
3.1. Gaussian Process Modelling
3.2. Design Parameters and Their Levels
3.3. Latin Hypercube Sampling (LHS) Based Space Filling Design
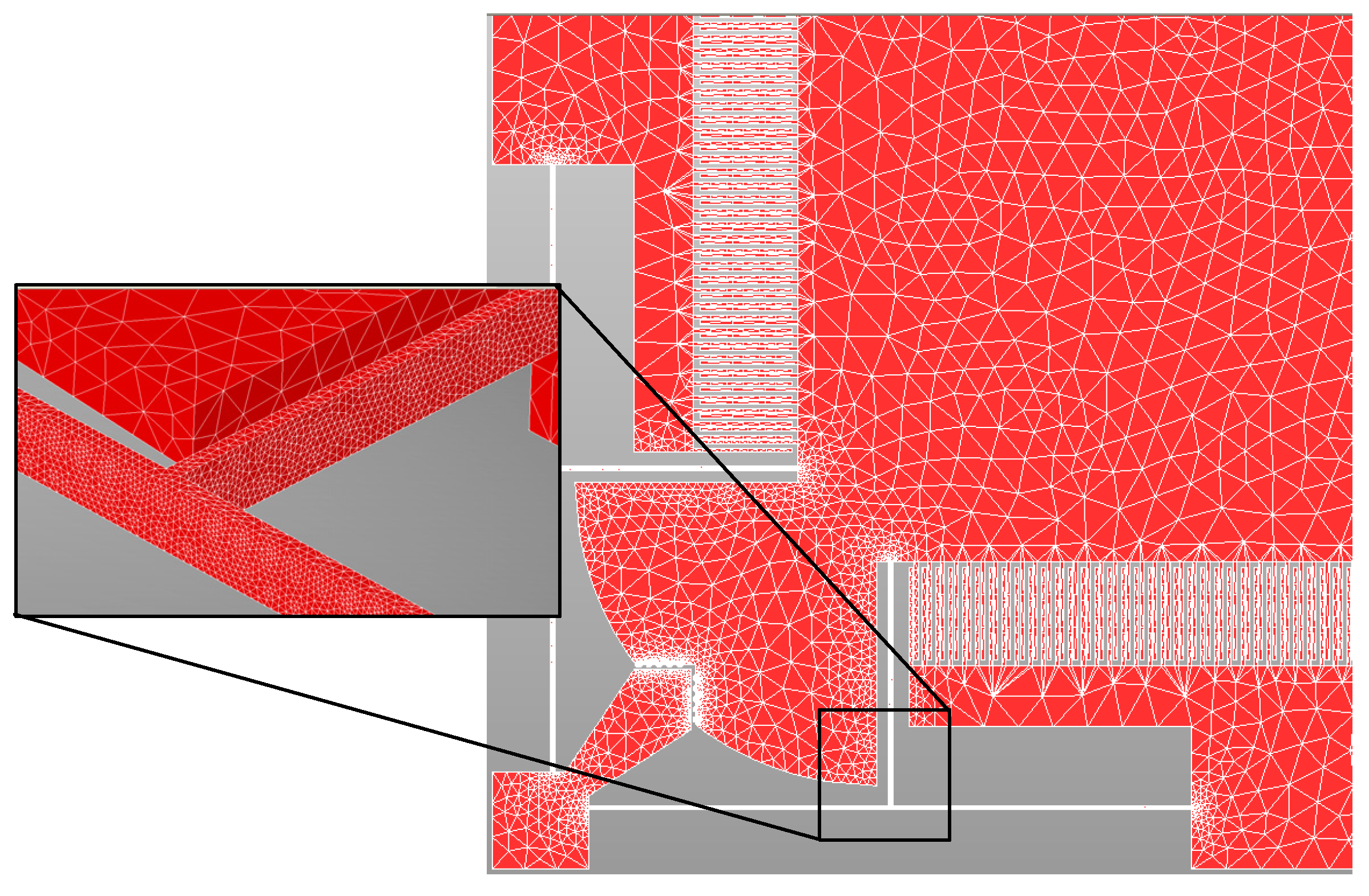
3.4. FEM Modelling of 2-DoF MEMS Accelerometer
4. Development of GP Based Metamodels for the Output Responses
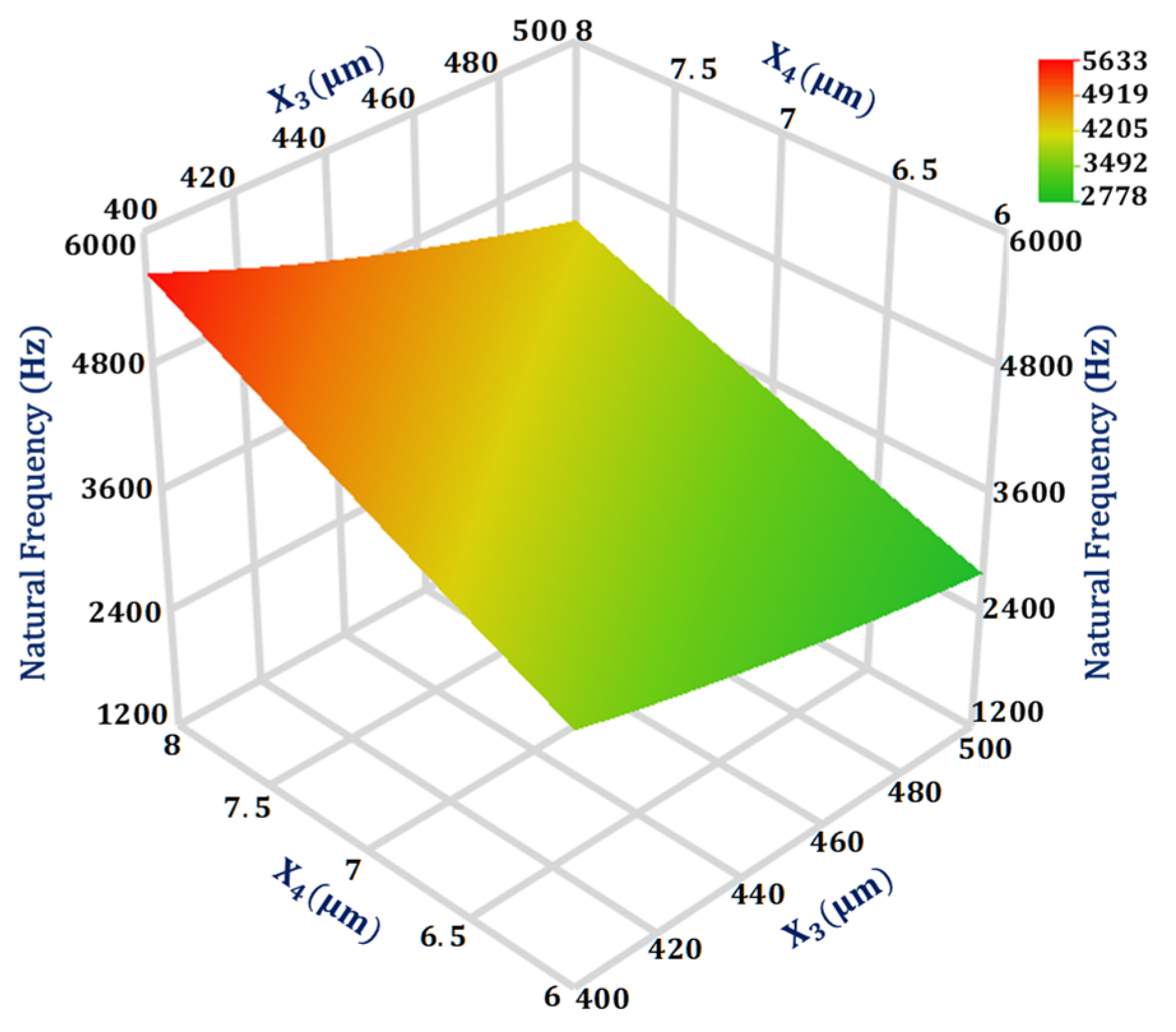
4.1. Significant Design Parameters and Interaction Analysis for Natural Frequency ()
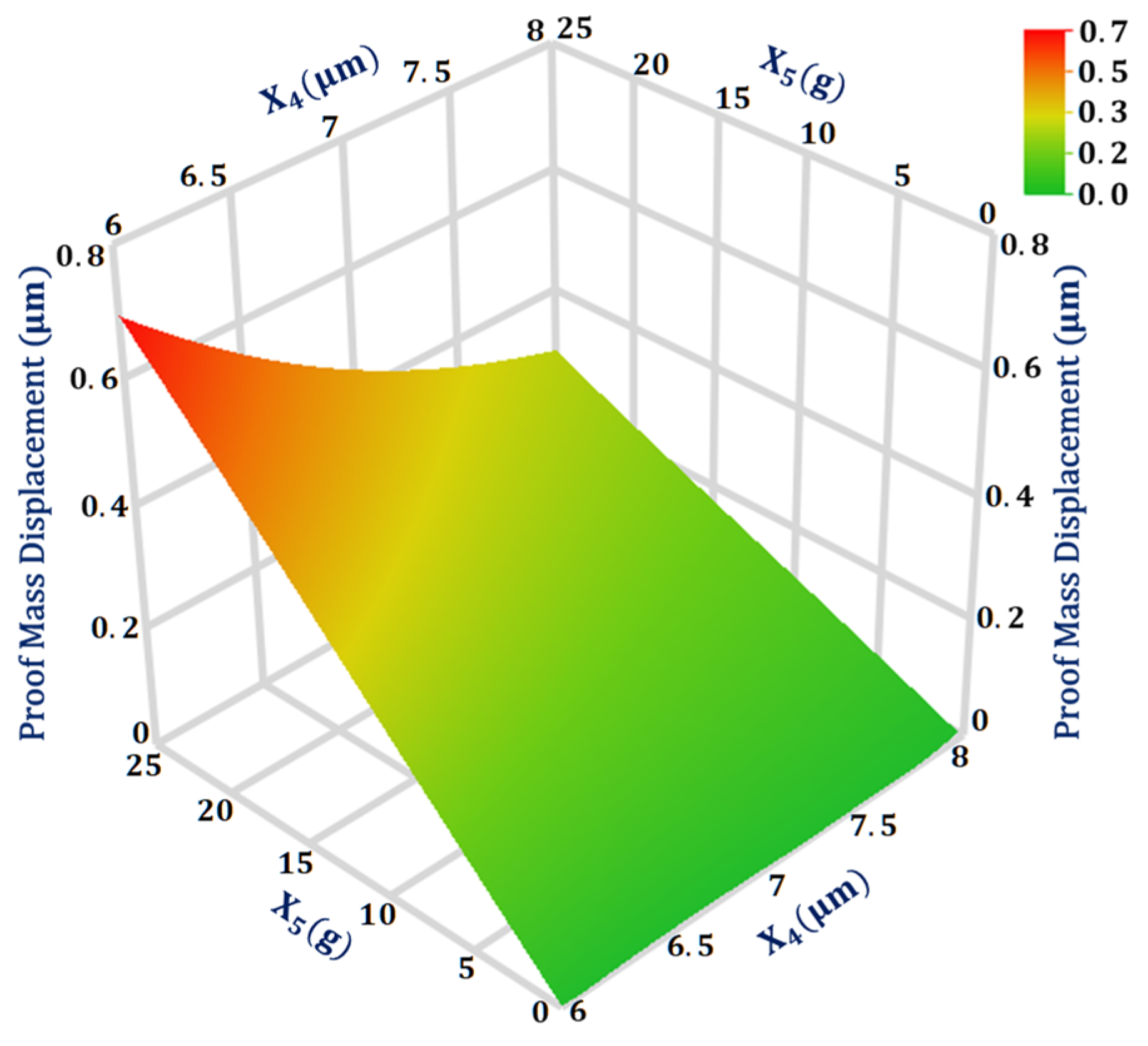
4.2. Significant Design Parameters and Interaction Analysis for Proof Mass Displacement ()
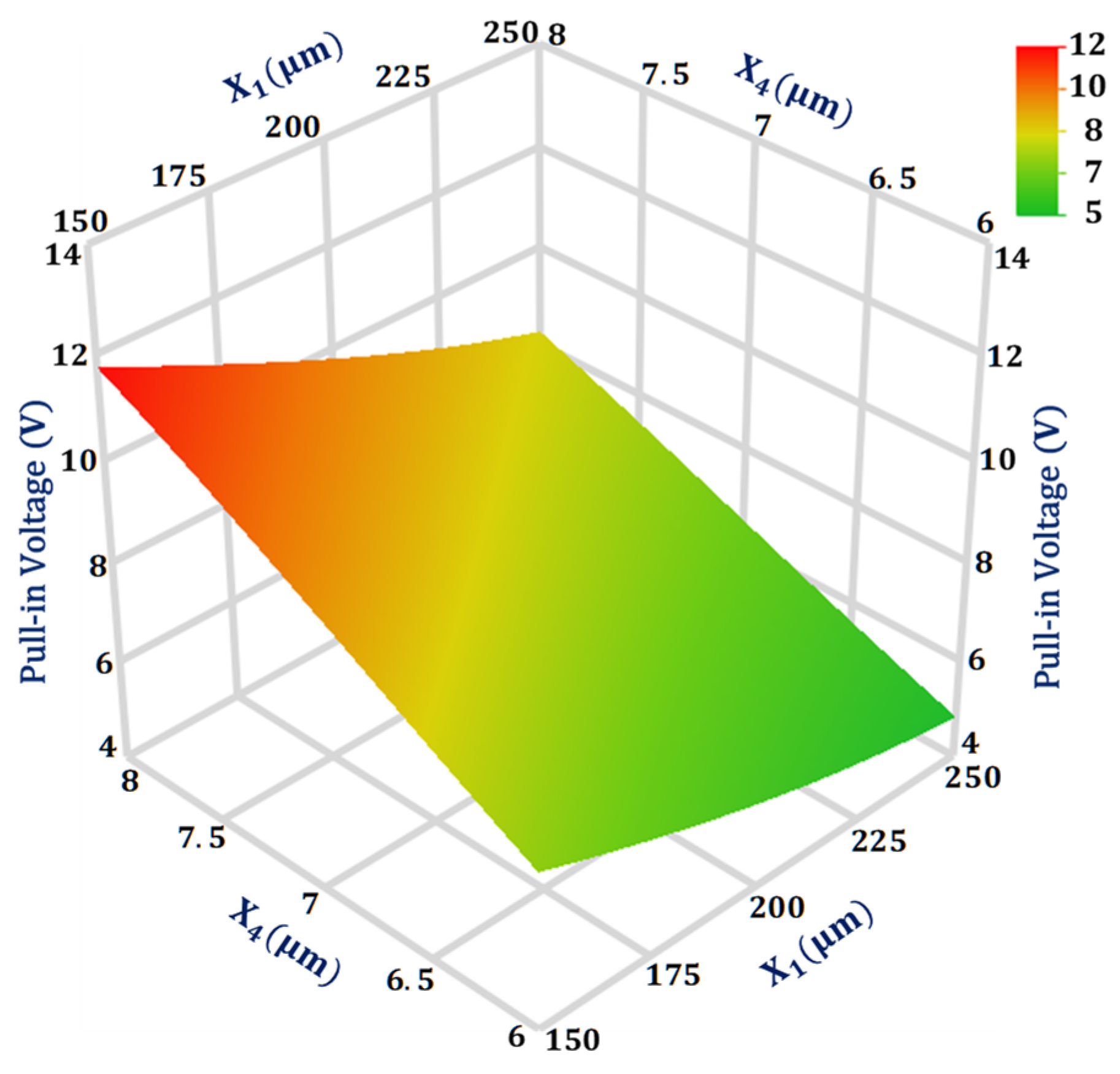
4.3. Significant Design Parameters and Interaction Analysis for Pull-In Voltage ()
4.4. Significant Design Parameters and Interaction Analysis for Capacitance Change ()
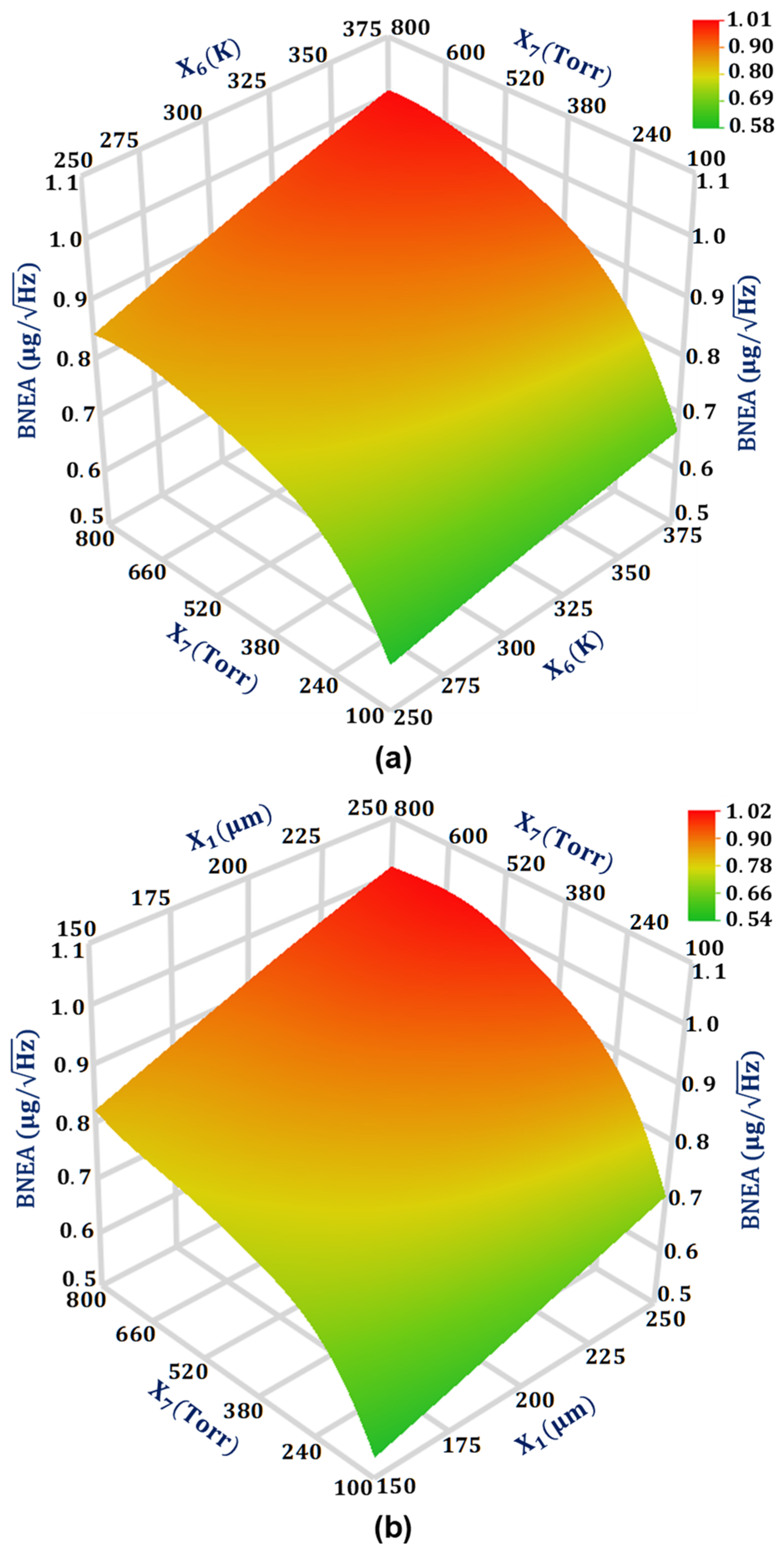
4.5. Significant Design Parameters and Interaction Analysis for BNEA ()
4.6. Prediction Accuracy of the Fitted GP Metamodels
5. Multi-Response Optimization
5.1. Optimization Objective Function
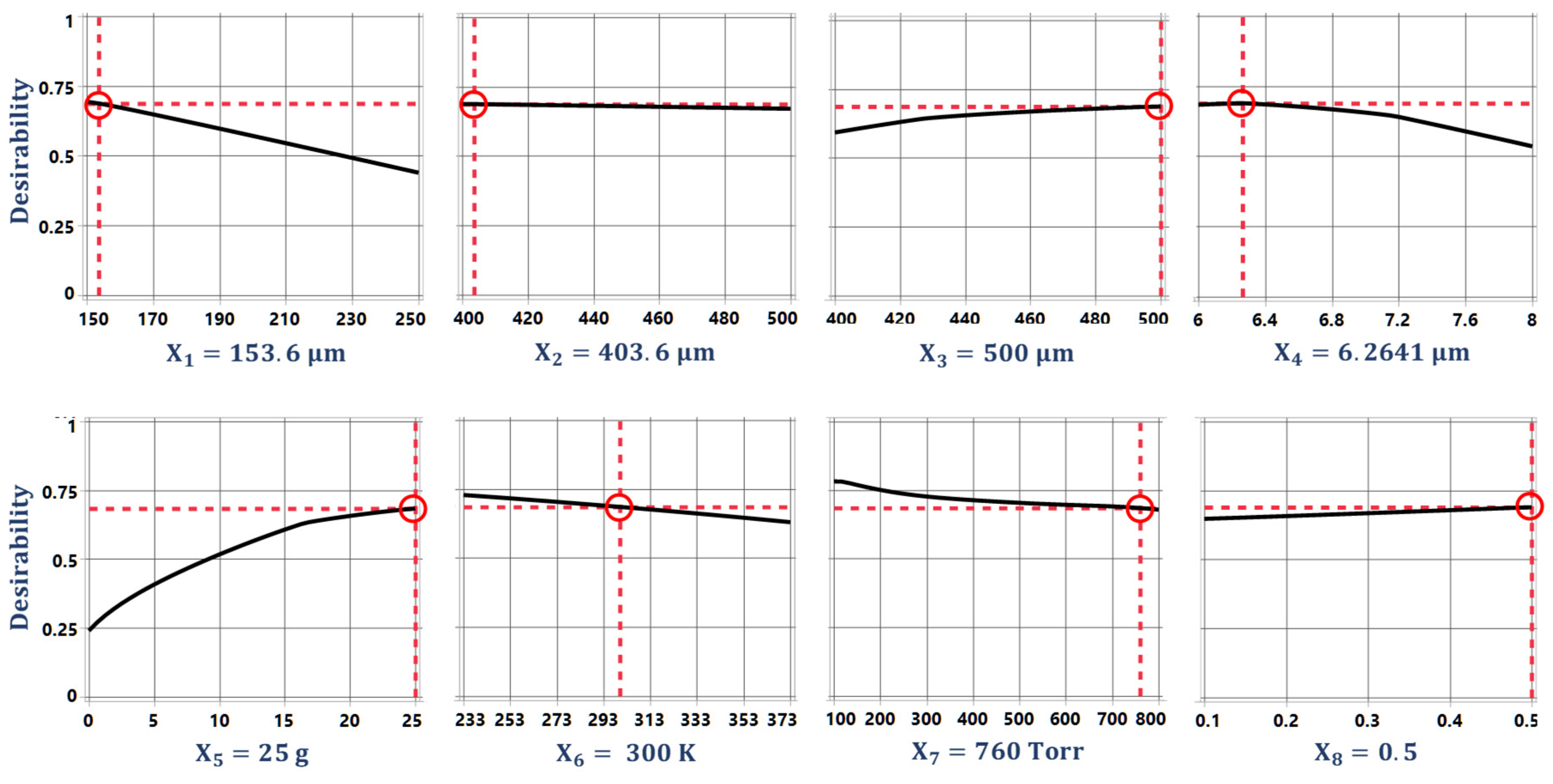
5.2. Desirability Function Based Simultaneous Multi-Response Optimization
5.3. Verification of Predicted Values for the Output Responses
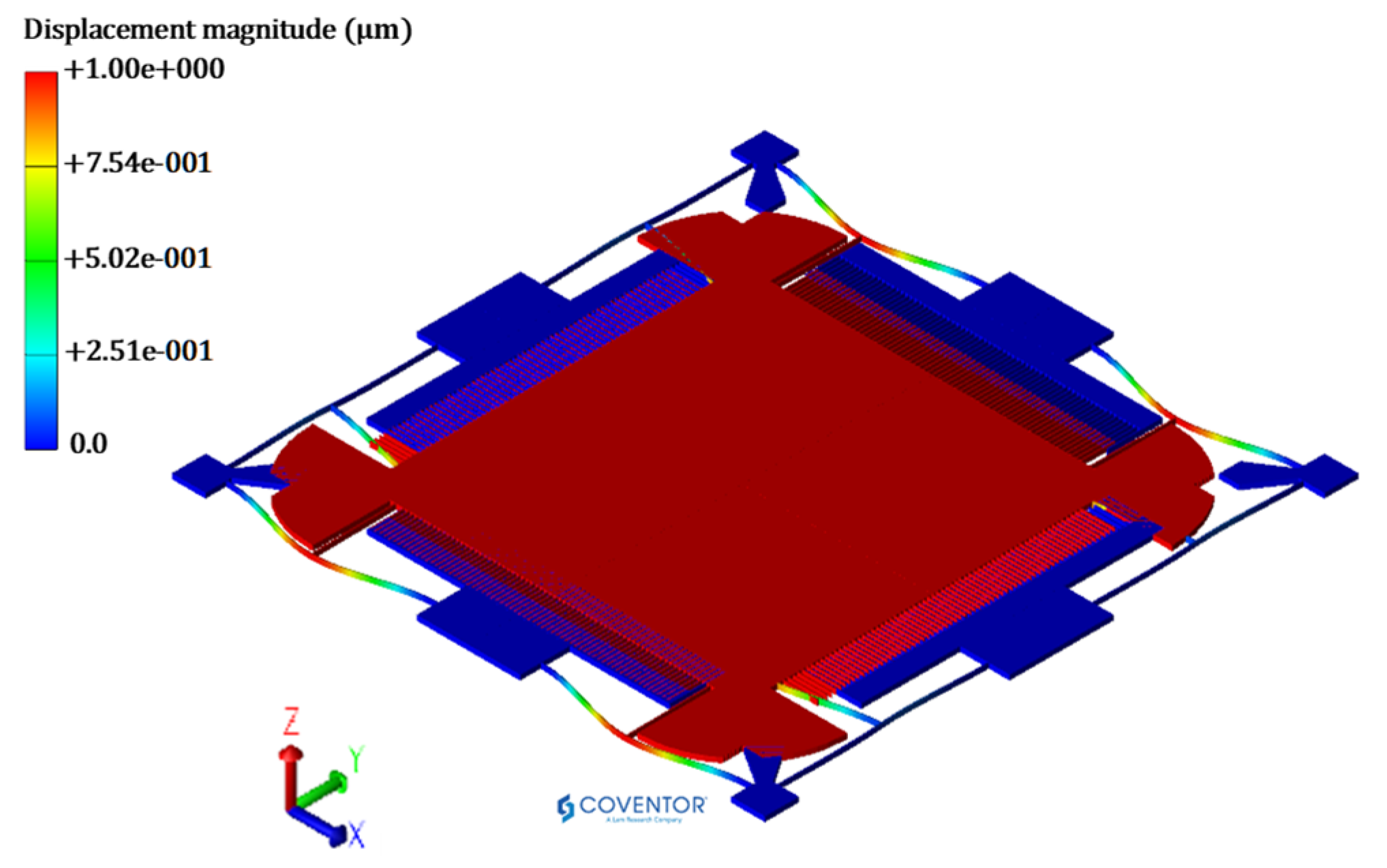
5.3.1. Natural Frequency Analysis
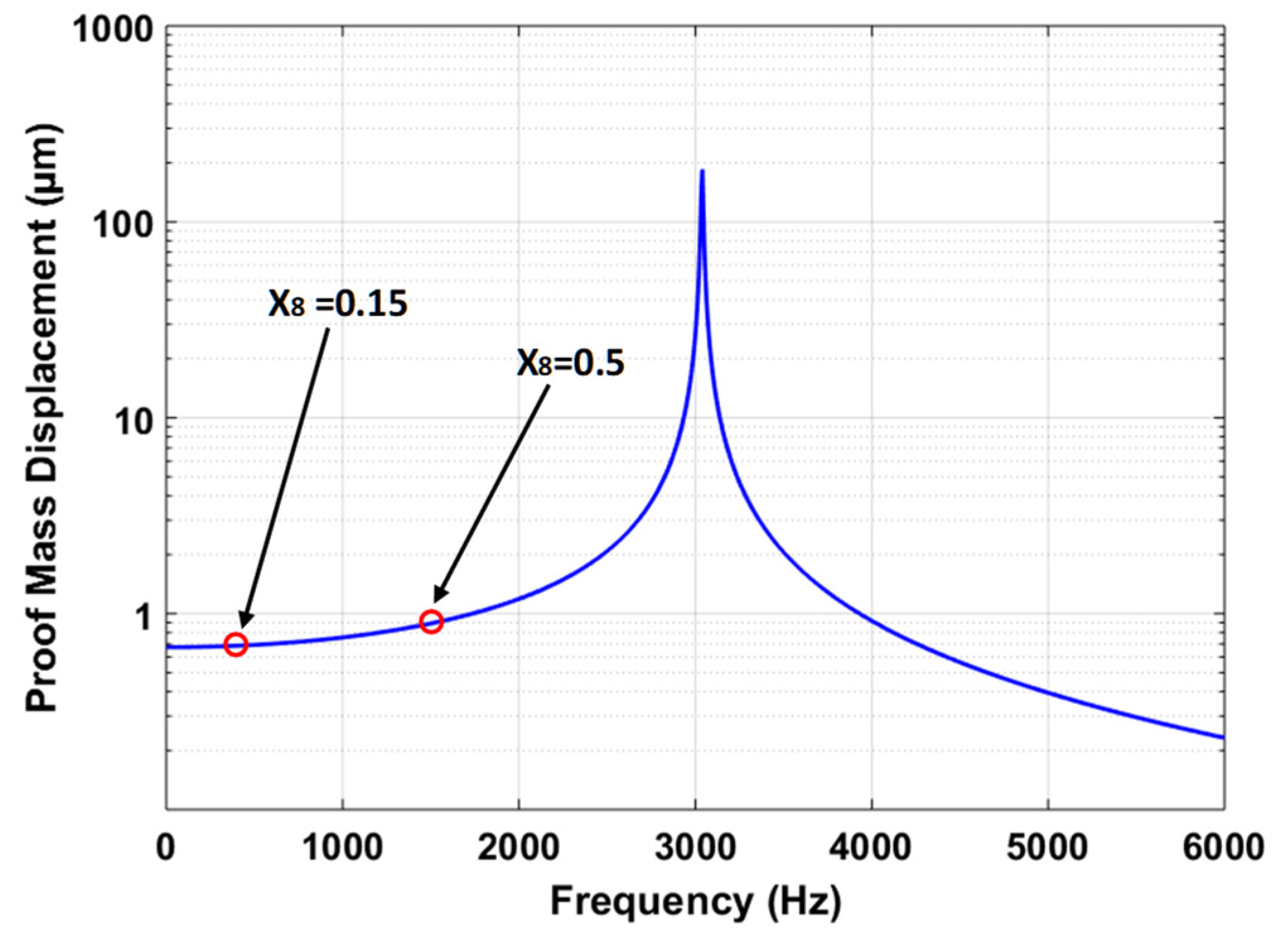
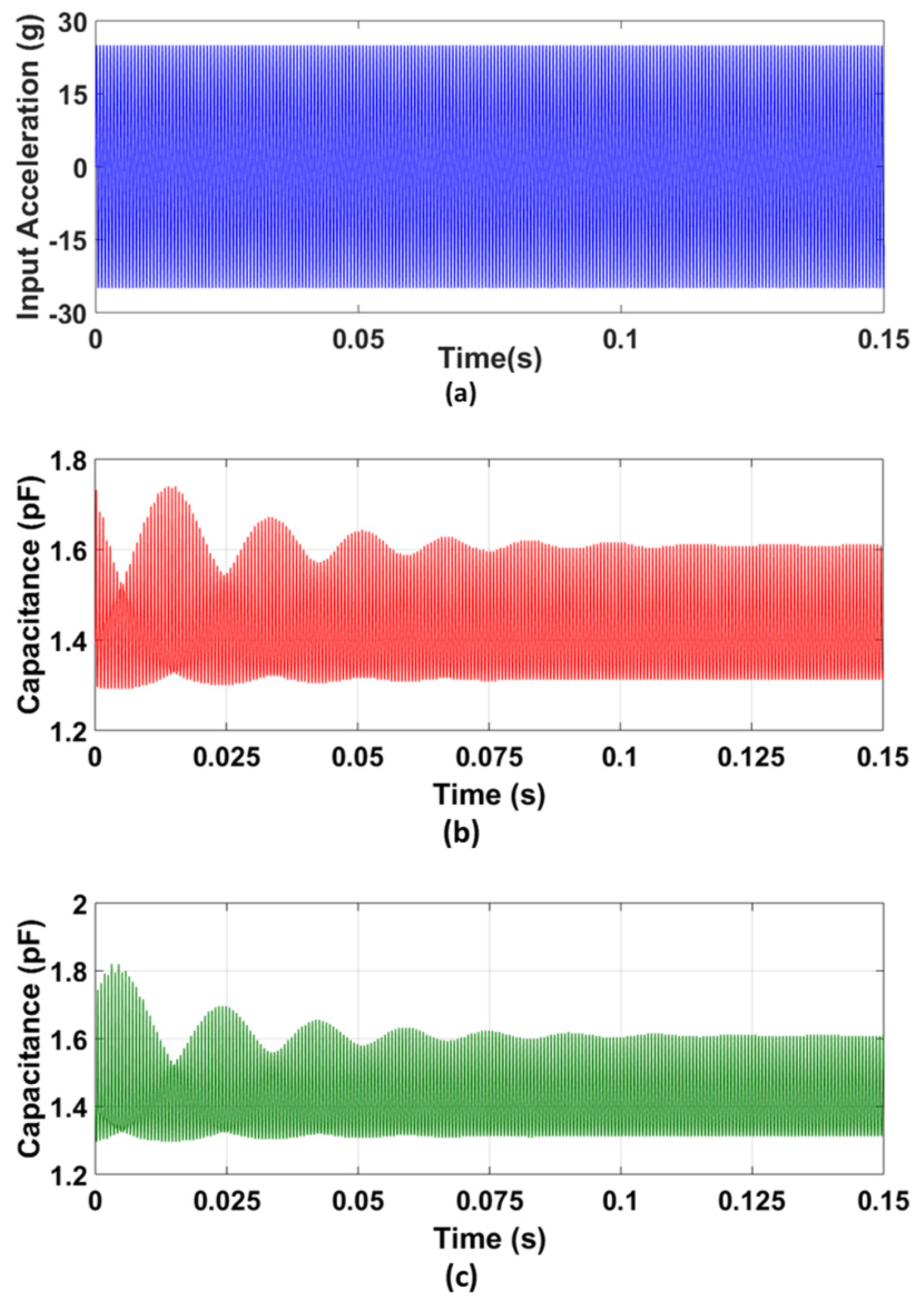
5.3.2. Frequency Response Analysis
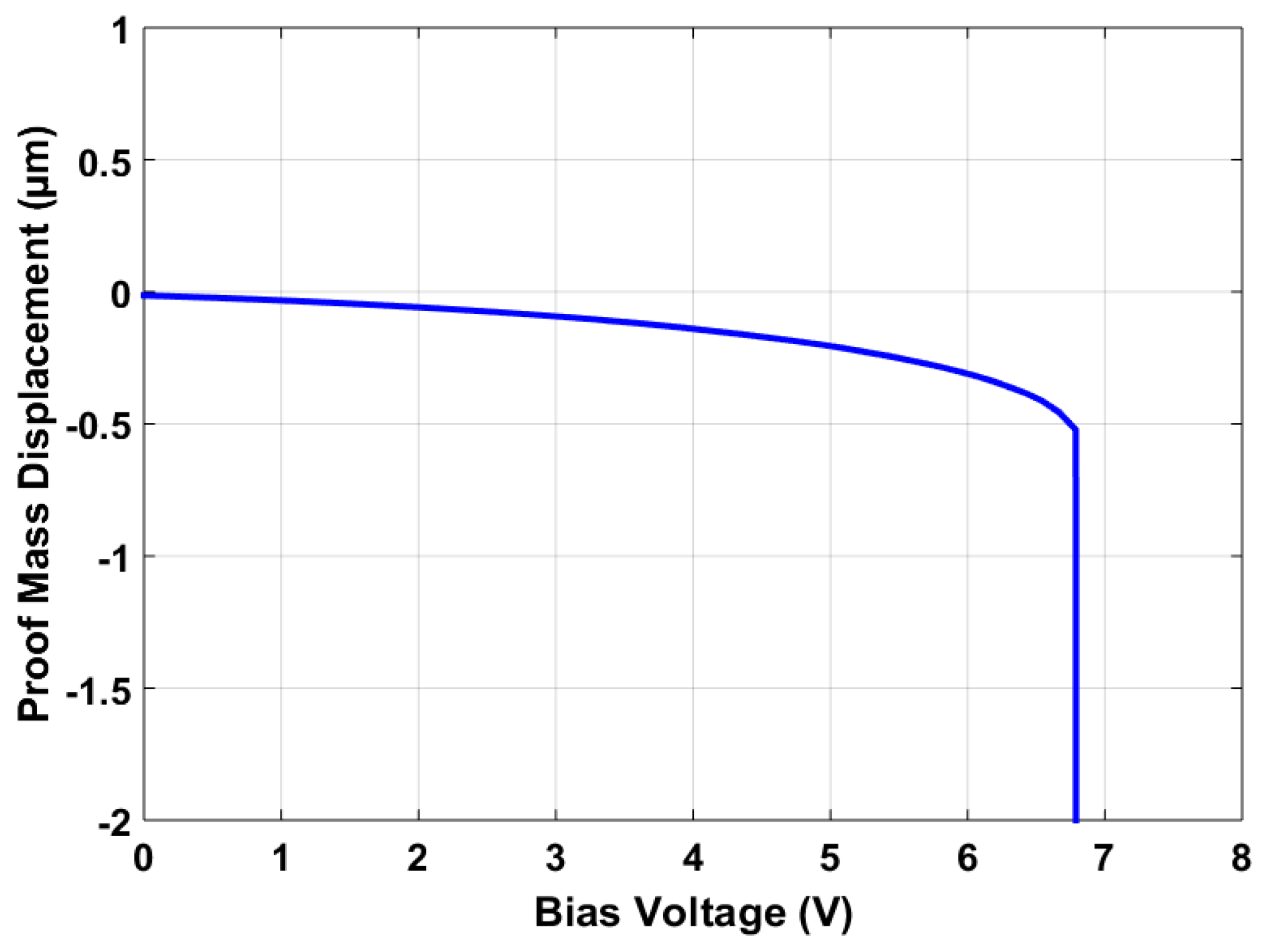
5.3.3. Pull-In Voltage Analysis
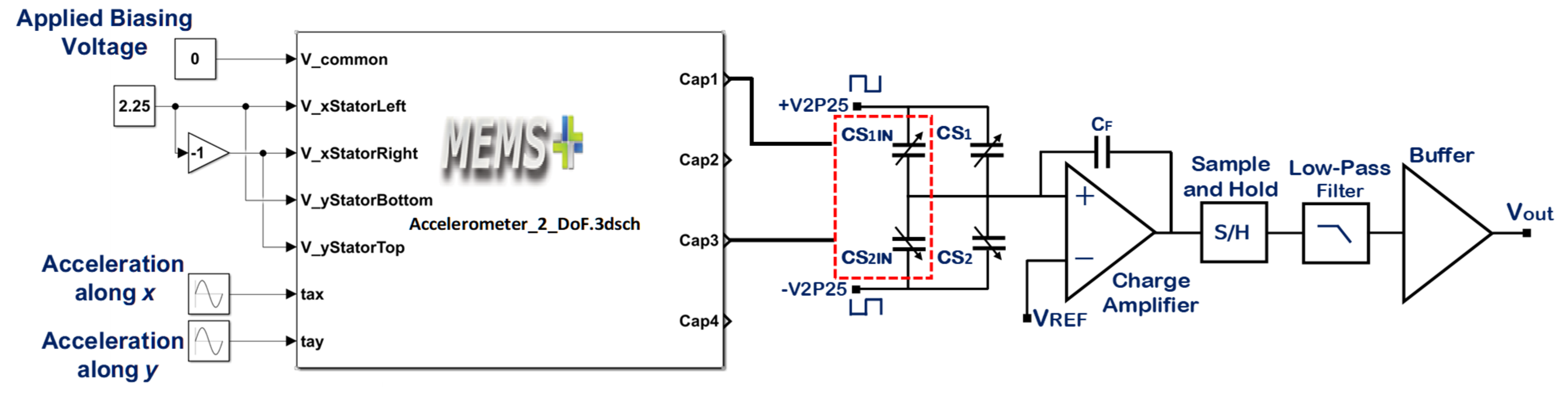
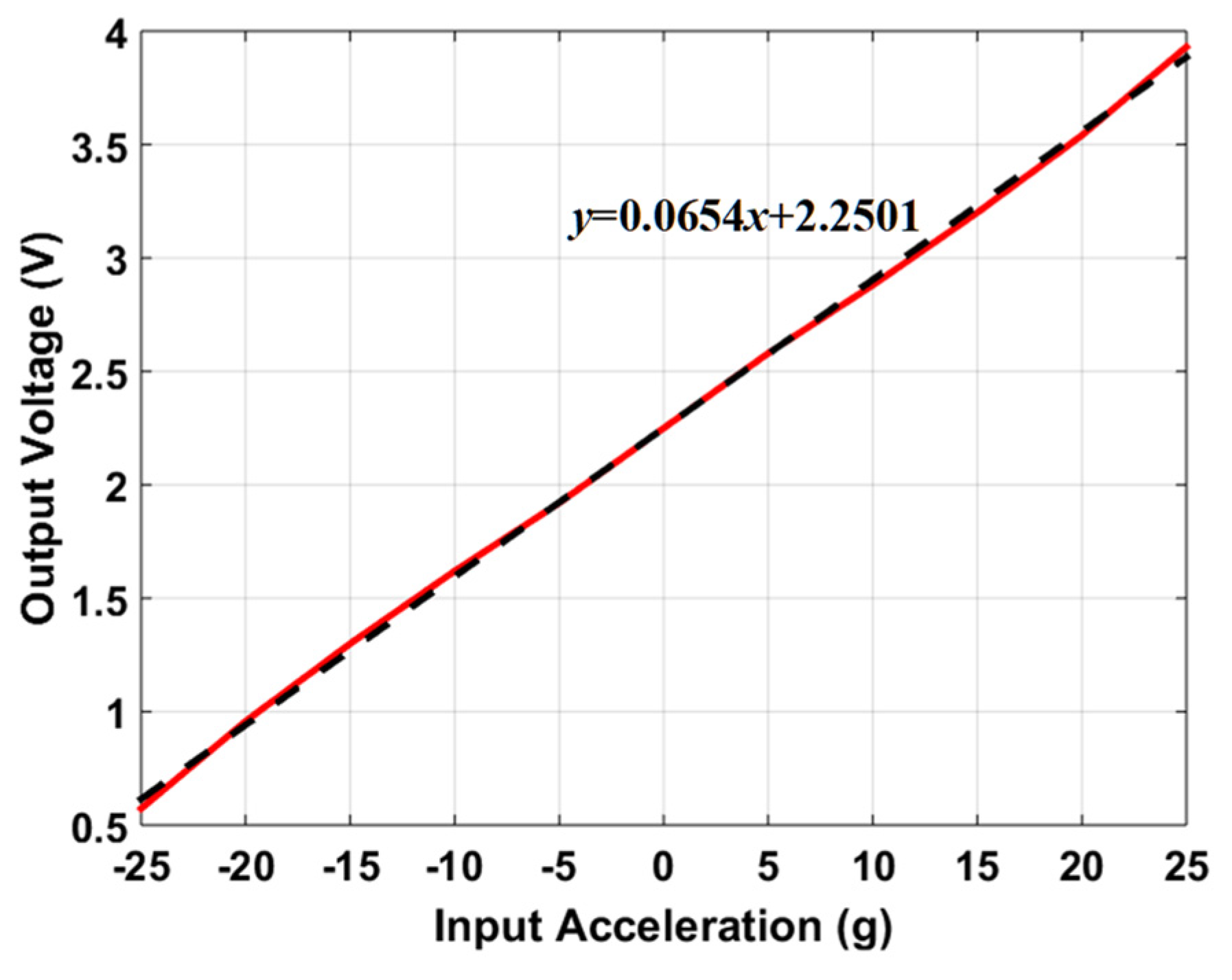
5.3.4. Capacitance Change Analysis
5.3.5. Estimation of Brownian Noise Equivalent Acceleration (BNEA)
6. Discussion
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- Venkatesh, K.A. Design of MEMS accelerometer based acceleration measurement system for automobiles. Meas. Sci. Rev. 2012, 12, 189. [Google Scholar] [CrossRef]
- Huang, C.-Y.; Chen, J.-H. Development of dual-axis MEMS accelerometers for machine tools vibration monitoring. Appl. Sci. 2016, 6, 201. [Google Scholar] [CrossRef] [Green Version]
- Varanis, M.; Silva, A.; Mereles, A.; Pederiva, R. MEMS accelerometers for mechanical vibrations analysis: A comprehensive review with applications. J. Braz. Soc. Mech. Sci. Eng. Vol. 2018, 40, 527. [Google Scholar] [CrossRef]
- Daeichin, M.; Ozdogan, M.; Towfighian, S.; Miles, R. Dynamic response of a tunable MEMS accelerometer based on repulsive force. Sens. Actuators A Phys. 2019, 289, 34–43. [Google Scholar] [CrossRef]
- Guan, L.; Xu, X.; Gao, Y.; Liu, F.; Rong, H.; Wang, M.; Noureldin, A. Micro-inertial-aided high-precision positioning method for small-diameter PIG navigation. In Advances in Human and Machine Navigation Systems; IntechOpen: London, UK, 2018. [Google Scholar]
- Roy, S.; Mandal, S.; Hanumaiah, N. MEMS accelerometer: From engineering to medicine. IEEE Potentials 2016, 35, 30–33. [Google Scholar] [CrossRef]
- Łuczak, S. Effects of misalignments of MEMS accelerometers in tilt measurements. In Mechatronics 2013; Springer: Berlin/Heidelberg, Germany, 2014; pp. 393–400. [Google Scholar]
- Rödjegård, H.; Johansson, C.; Enoksson, P.; Andersson, G. A monolithic three-axis SOI-accelerometer with uniform sensitivity. Sens. Actuators A Phys. 2005, 123, 50–53. [Google Scholar] [CrossRef]
- Tez, S.; Aykutlu, U.; Torunbalci, M.M.; Akin, T. A Bulk-Micromachined Three-Axis Capacitive MEMS Accelerometer on a Single Die. J. Microelectromechan. Syst. 2015, 24, 1264–1274. [Google Scholar] [CrossRef]
- Aydemir, A.; Terzioglu, Y.; Akin, T. A new design and a fabrication approach to realize a high performance three axes capacitive MEMS accelerometer. Sens. Actuators A Phys. 2016, 244, 324–333. [Google Scholar] [CrossRef]
- Merdassi, A.; Kezzo, M.N.; Xereas, G.; Chodavarapu, V.P. Wafer level vacuum encapsulated tri-axial accelerometer with low cross-axis sensitivity in a commercial MEMS Process. Sens. Actuators A Phys. 2015, 236, 25–37. [Google Scholar] [CrossRef]
- Yamane, D.; Matsushima, T.; Konishi, T.; Toshiyoshi, H.; Masu, K.; Machida, K. A dual-axis MEMS capacitive inertial sensor with high-density proof mass. Microsyst. Technol. 2015, 22, 459–464. [Google Scholar] [CrossRef]
- Mohammed, Z.; Dushaq, G.; Chatterjee, A.; Rasras, M. An optimization technique for performance improvement of gap-changeable MEMS accelerometers. Mechatronics 2017, 54, 203–216. [Google Scholar] [CrossRef]
- Mukherjee, T.; Iyer, S.; Feeder, G.K. Optimization-based synthesis of microresonators. Sens. Actuators A Phys. 1998, 70, 118–127. [Google Scholar] [CrossRef]
- Benmessaoud, M.; Nasreddine, M.M. Optimization of MEMS capacitive accelerometer. Microsyst. Technol. 2013, 19, 713–720. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Yang, H.Y.; Wang, G.C. Genetic Algorithm Based Multidisciplinary Design Optimization of MEMS Accelerometer. In Applied Mechanics and Materials, 2012; Trans Tech Publications: Bäch SZ, Switzerland, 2012; pp. 530–533. [Google Scholar]
- Giannini, D.; Braghin, F.; Aage, N. Topology optimization of 2D in-plane single mass MEMS gyroscopes. Struct. Multidiscip. Optim. 2020, 62, 2069–2089. [Google Scholar] [CrossRef]
- Rao, K.S.; Chand, C.G.; Sravani, K.G.; Prathyusha, D.; Naveena, P.; Lakshmi, G.S.; Kumar, P.A.; Narayana, T.L. Design, Modeling and Analysis of Perforated RF MEMS Capacitive Shunt Switch. IEEE Access 2019, 7, 74869–74878. [Google Scholar] [CrossRef]
- Lyu, M.; Zhao, J.; Kacem, N.; Tang, B.; Liu, P.; Song, J.; Zhong, H.; Huang, Y. Design and modeling of a MEMS accelerometer based on coupled mode-localized nonlinear resonators under electrostatic actuation. Commun. Nonlinear Sci. Numer. Simul. 2021, 103, 105960. [Google Scholar] [CrossRef]
- Keshavarzi, M.; Hasani, J.Y. Design and optimization of fully differential capacitive MEMS accelerometer based on surface micromachining. Microsyst. Technol. 2018, 25, 1369–1377. [Google Scholar] [CrossRef]
- Ramakrishnan, J.; Gaurav, P.R.; Chandar, N.S.; Sudharsan, N. Structural design, analysis and DOE of MEMS-based capacitive accelerometer for automotive airbag application. Microsyst. Technol. 2021, 27, 763–777. [Google Scholar] [CrossRef]
- Li, R.; Mohammed, Z.; Rasras, M.; Elfadel, I.A.M.; Choi, D. Design, modelling and characterization of comb drive MEMS gap-changeable differential capacitive accelerometer. Measurement 2021, 169, 108377. [Google Scholar] [CrossRef]
- Kim, D.-W.; Cho, M.-W.; Seo, T.-I.; Lee, E.-S. Application of Design of Experiment Method for Thrust Force Minimization in Step-feed Micro Drilling. Sensors 2008, 8, 211–221. [Google Scholar] [CrossRef] [Green Version]
- Haque, R.I.; Loussert, C.; Sergent, M.; Benaben, P.; Boddaert, X. Optimization of Capacitive Acoustic Resonant Sensor Using Numerical Simulation and Design of Experiment. Sensors 2015, 15, 8945–8967. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hoshmand, R. Design of Experiments for Agriculture and the Natural Sciences; Chapman and Hall/CRC: Boca Raton, FL, USA, 2018. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: New York, NY, USA, 2017. [Google Scholar]
- Saleem, M.; Somá, A. Design of experiments based factorial design and response surface methodology for MEMS optimization. Microsyst. Technol. 2015, 21, 263–276. [Google Scholar] [CrossRef]
- Younis, S.; Saleem, M.M.; Zubair, M.; Zaidi, S.M.T. Multiphysics design optimization of RF-MEMS switch using response surface methodology. Microelectron. J. 2018, 71, 47–60. [Google Scholar] [CrossRef]
- Welch, W.J.; Yu, T.-K.; Kang, S.M.; Sacks, J. Computer Experiments for Quality Control by Parameter Design. J. Qual. Technol. 1990, 22, 15–22. [Google Scholar] [CrossRef]
- Simpson, T.W.; Peplinski, J.; Koch, P.N.; Allen, J.K. On the Use of Statistics in Design and the Implications for Deterministic Computer Experiments. In International Design Engineering Technical Conferences and Computers and Information in Engineering Conference; American Society of Mechanical Engineers: New York, NY, USA, 1997; Paper No. V003T30A008. [Google Scholar]
- Sacks, J.; Welch, W.J.; Mitchell, T.J.; Wynn, H.P. Design and analysis of computer experiments. Stat. Sci. 1989, 4, 409–423. [Google Scholar] [CrossRef]
- Wang, M.; Lv, W.; Yang, F.; Yan, C.; Cai, W.; Zhou, D.; Zeng, X. Efficient Yield Optimization for Analog and SRAM Circuits via Gaussian Process Regression and Adaptive Yield Estimation. IEEE Trans. Comput. Des. Integr. Circuits Syst. 2017, 37, 1929–1942. [Google Scholar] [CrossRef]
- Sanabria-Borbón, A.C.; Soto-Aguilar, S.; Estrada-López, J.J.; Allaire, D.; Sánchez-Sinencio, E. Gaussian-Process-Based Surrogate for Optimization-Aided and Process-Variations-Aware Analog Circuit Design. Electronics 2020, 9, 685. [Google Scholar] [CrossRef] [Green Version]
- Akin, A.; Kahveci, H.S. An optimization study for rotorcraft avionics bay cooling. Aerosp. Sci. Technol. 2019, 90, 1–11. [Google Scholar] [CrossRef]
- Fan, X.; Wang, P.; Hao, F. Reliability-based design optimization of crane bridges using Kriging-based surrogate models. Struct. Multidiscip. Optim. 2019, 59, 993–1005. [Google Scholar] [CrossRef]
- Cowen, A.; Hames, G.; Monk, D.; Wilcenski, S.; Hardy, B. SOIMUMPs Design Handbook; MEMSCAP Inc.: Durham, NC, USA, 2011; pp. 2002–2011. [Google Scholar]
- Erickson, C.B.; Ankenman, B.E.; Sanchez, S.M. Comparison of Gaussian process modeling software. Eur. J. Oper. Res. 2018, 266, 179–192. [Google Scholar] [CrossRef] [Green Version]
- Jones, B.; Johnson, R.T. Design and analysis for the Gaussian process model. Qual. Reliab. Eng. Int. 2009, 25, 515–524. [Google Scholar] [CrossRef] [Green Version]
- Viana, F.A. A tutorial on Latin hypercube design of experiments. Qual. Reliab. Eng. Int. 2016, 32, 1975–1985. [Google Scholar] [CrossRef]
- Bukhari, S.A.R.; Saleem, M.M.; Khan, U.S.; Hamza, A.; Iqbal, J.; Shakoor, R.I. Microfabrication Process-Driven Design, FEM Analysis and System Modeling of 3-DoF Drive Mode and 2-DoF Sense Mode Thermally Stable Non-Resonant MEMS Gyroscope. Micromachines 2020, 11, 862. [Google Scholar] [CrossRef]
- Haider, S.T.; Saleem, M.M.; Ahmed, M. Effect of environmental conditions and geometric parameters on the squeeze film damping in RF-MEMS switches. Analog. Integr. Circuits Signal. Process. 2018, 100, 357–368. [Google Scholar] [CrossRef]
- Gabrielson, T.B. Mechanical-thermal noise in micromachined acoustic and vibration sensors. IEEE Trans. Electron. Devices 1993, 40, 903–909. [Google Scholar] [CrossRef] [Green Version]
- Samui, P. Utilization of Gaussian Process Regression for Determination of Soil Electrical Resistivity. Geotech. Geol. Eng. 2013, 32, 191–195. [Google Scholar] [CrossRef]
- Brantson, E.T.; Ju, B.; Ziggah, Y.Y.; Akwensi, P.H.; Sun, Y.; Wu, D.; Addo, B.J. Forecasting of Horizontal Gas Well Production Decline in Unconventional Reservoirs using Productivity, Soft Computing and Swarm Intelligence Models. Nat. Resour. Res. 2018, 28, 717–756. [Google Scholar] [CrossRef]
- Khuri, A.I.; Conlon, M. Simultaneous Optimization of Multiple Responses Represented by Polynomial Regression Functions. Technometrics 1981, 23, 363–375. [Google Scholar] [CrossRef]
- Ko, Y.-H.; Kim, K.-J.; Jun, C.-H. A New Loss Function-Based Method for Multiresponse Optimization. J. Qual. Technol. 2005, 37, 50–59. [Google Scholar] [CrossRef]
- Derringer, G.; Suich, R. Simultaneous Optimization of Several Response Variables. J. Qual. Technol. 1980, 12, 214–219. [Google Scholar] [CrossRef]
- Harrington, E.C. The desirability function. Ind. Qual. Control 1965, 21, 494–498. [Google Scholar]
- Del Castillo, E.; Montgomery, D.C.; McCarville, D.R. Modified Desirability Functions for Multiple Response Optimization. J. Qual. Technol. 1996, 28, 337–345. [Google Scholar] [CrossRef]
- Datasheet MUCRI. MS3110 Universal Capacitive ReadoutTM IC; MicroSensors, Inc.: Costa Mesa, CA, USA, 2004. [Google Scholar]
- Shi, Y.; Zhao, Y.; Feng, H.; Cao, H.; Tang, J.; Li, J.; Zhao, R.; Liu, J. Design, fabrication and calibration of a high-G MEMS accelerometer. Sens. Actuators A Phys. 2018, 279, 733–742. [Google Scholar] [CrossRef]
- Martha, P.; Kadayinti, N.; Seena, V. CMOS-MEMS Accelerometer with Stepped Suspended Gate FET Array: Design & Analysis. IEEE Trans. Electron. Devices 2021, 68, 5133–5141. [Google Scholar]




| Code | Design Parameters | Low Level | High Level |
|---|---|---|---|
| X1 | Overlap length of comb | 150 µm | 250 µm |
| X2 | Length of suspension beam 1 | 400 µm | 500 µm |
| X3 | Length of suspension beam 2 | 400 µm | 500 µm |
| X4 | Width of suspension beam | 6 µm | 8 µm |
| X5 | Input acceleration | 1 g | 25 g |
| X6 | Operating temperature | 233.15 K | 373.15 K |
| X7 | Operating pressure | 100 Torr | 760 Torr |
| X8 | Frequency ratio | 0.1 | 0.5 |
| Output Responses | Design Parameters | |||||||
|---|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | |
| Natural frequency (Y1) | 4.23 × 10−6 | 5.52 × 10−6 | 9.74 × 10−5 | 0.36 | 0 | 0 | 0 | 0 |
| Proof mass displacement (Y2) | 0 | 0 | 8.26 × 10−5 | 0.34 | 0.01 | 0 | 0 | 1.24 |
| Pull-in voltage (Y3) | 6.29 × 10−5 | 1.23 × 10−5 | 5.49 × 10−5 | 0.14 | 1.49 × 10−5 | 4.29 × 10−6 | 6.18 × 10−9 | 2.19 |
| Capacitance change (Y4) | 2.19 × 10−5 | 1.01 × 10−6 | 0.000026 | 0.1235 | 0.0018 | 7.66 × 10−7 | 3.82 × 10−8 | 0.88 |
| BNEA (Y5) | 0.000142 | 0 | 0 | 0 | 0 | 5.26 × 10−5 | 6.03 × 10−6 | 0 |
| Output Responses | Significant Design Parameters Interaction | |
|---|---|---|
| Design Parameters | Interaction Value | |
| Natural frequency (Y1) | 0.005 | |
| Proof mass displacement (Y2) | 0.031 | |
| Pull-in voltage (Y3) | 0.004 | |
| Capacitance change (Y4) | 0.038 | |
| BNEA (Y5) | , | 0.007, 0.007 |
| Output Responses | MAE | RMSE | R |
|---|---|---|---|
| Natural frequency (Y1) | 29.64 Hz | 41.19 Hz | 0.998 |
| Proof mass displacement (Y2) | 0.024 μm | 0.034 μm | 0.981 |
| Pull-in voltage (Y3) | 0.085 V | 0.134 V | 0.997 |
| Capacitance change (Y4) | 10.178 fF | 14.05 fF | 0.996 |
| BNEA (Y5) | 0.973 |
| Reference | Optimization Approach | Design Factor(s) | Output Response(s) | Simultaneous Optimization of Output Responses |
|---|---|---|---|---|
| Mohammed et al. [13] | One design factor | Geometric parameters | Differential capacitance | No |
| Keshavarzi and Hasani [20] | Two design factors | Geometric parameters | Capacitance sensitivity | No |
| Ramakrishnan et al. [21] | Traditional DOE | Geometric parameters | Mechanical displacement, stress, bandwidth | No |
| Li et al. [22] | One design factor | Geometric parameters | Capacitance sensitivity | No |
| Shi et al. [51] | Two design factors | Geometric parameters | Mechanical sensitivity, stress, natural frequency | No |
| Martha et al. [52] | Two design factors | Geometric parameters | Pull-in voltage, capacitance sensitivity | No |
| This work | Combined DACE and GP Modelling | Geometric parameters, Operating conditions | Natural frequency, mechanical displacement, capacitance sensitivity, BNEA, pull-in voltage | Yes |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saghir, S.; Saleem, M.M.; Hamza, A.; Riaz, K.; Iqbal, S.; Shakoor, R.I. A Systematic Design Optimization Approach for Multiphysics MEMS Devices Based on Combined Computer Experiments and Gaussian Process Modelling. Sensors 2021, 21, 7242. https://doi.org/10.3390/s21217242
Saghir S, Saleem MM, Hamza A, Riaz K, Iqbal S, Shakoor RI. A Systematic Design Optimization Approach for Multiphysics MEMS Devices Based on Combined Computer Experiments and Gaussian Process Modelling. Sensors. 2021; 21(21):7242. https://doi.org/10.3390/s21217242
Chicago/Turabian StyleSaghir, Shayaan, Muhammad Mubasher Saleem, Amir Hamza, Kashif Riaz, Sohail Iqbal, and Rana Iqtidar Shakoor. 2021. "A Systematic Design Optimization Approach for Multiphysics MEMS Devices Based on Combined Computer Experiments and Gaussian Process Modelling" Sensors 21, no. 21: 7242. https://doi.org/10.3390/s21217242







