Vibrational Transportation on a Platform Subjected to Sinusoidal Displacement Cycles Employing Dry Friction Control
Abstract
:1. Introduction
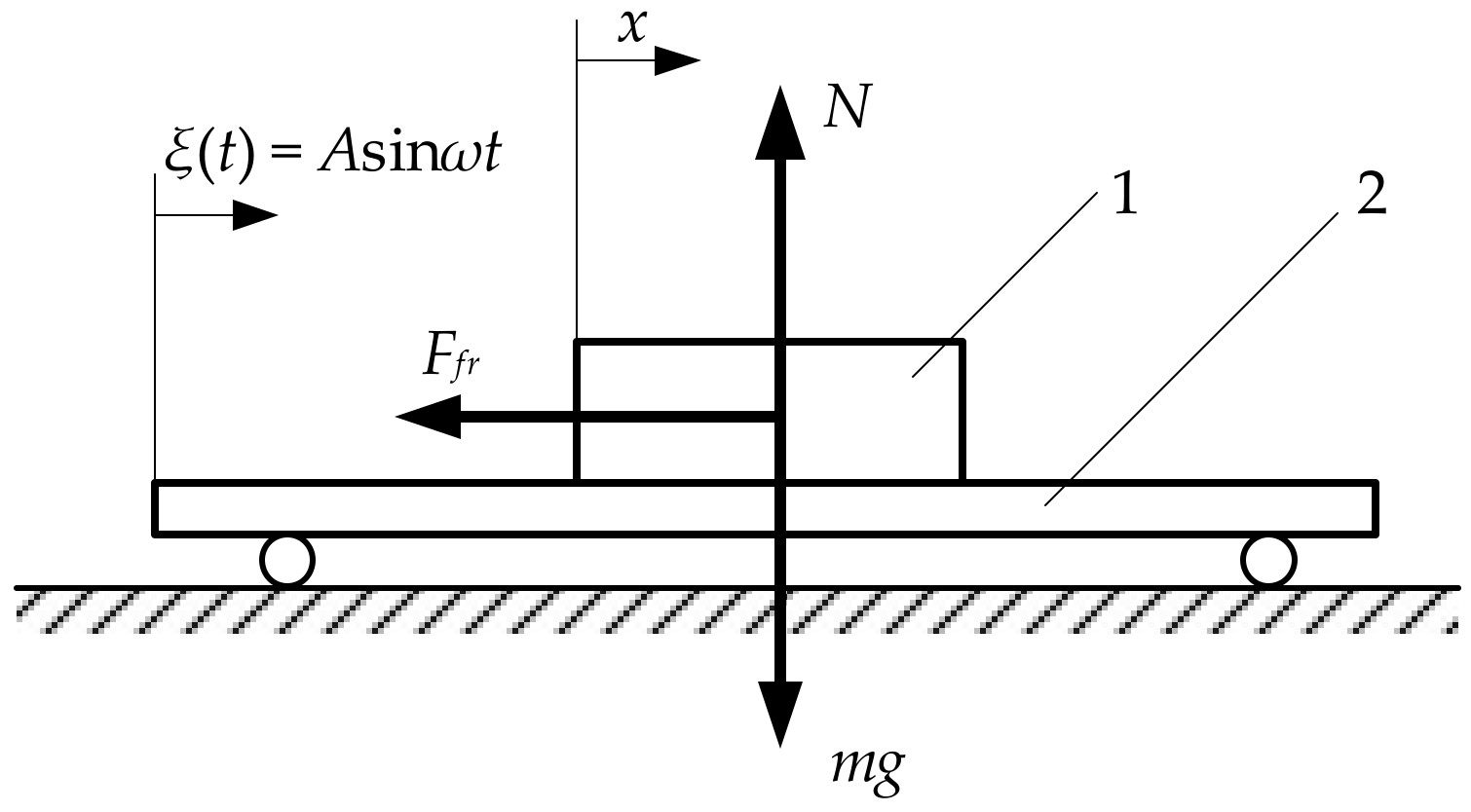
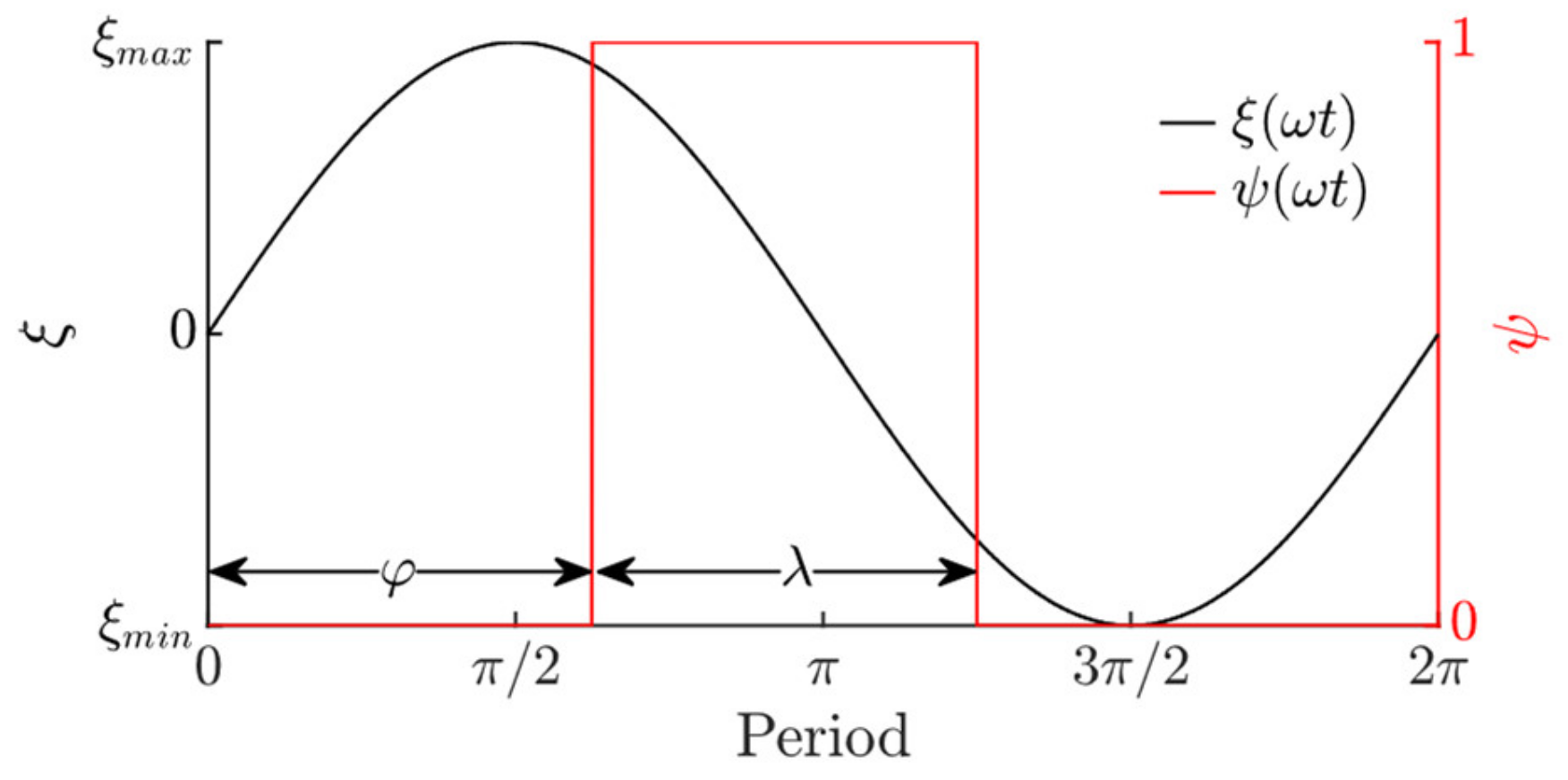
2. Theoretical Research
2.1. Mathematical Model
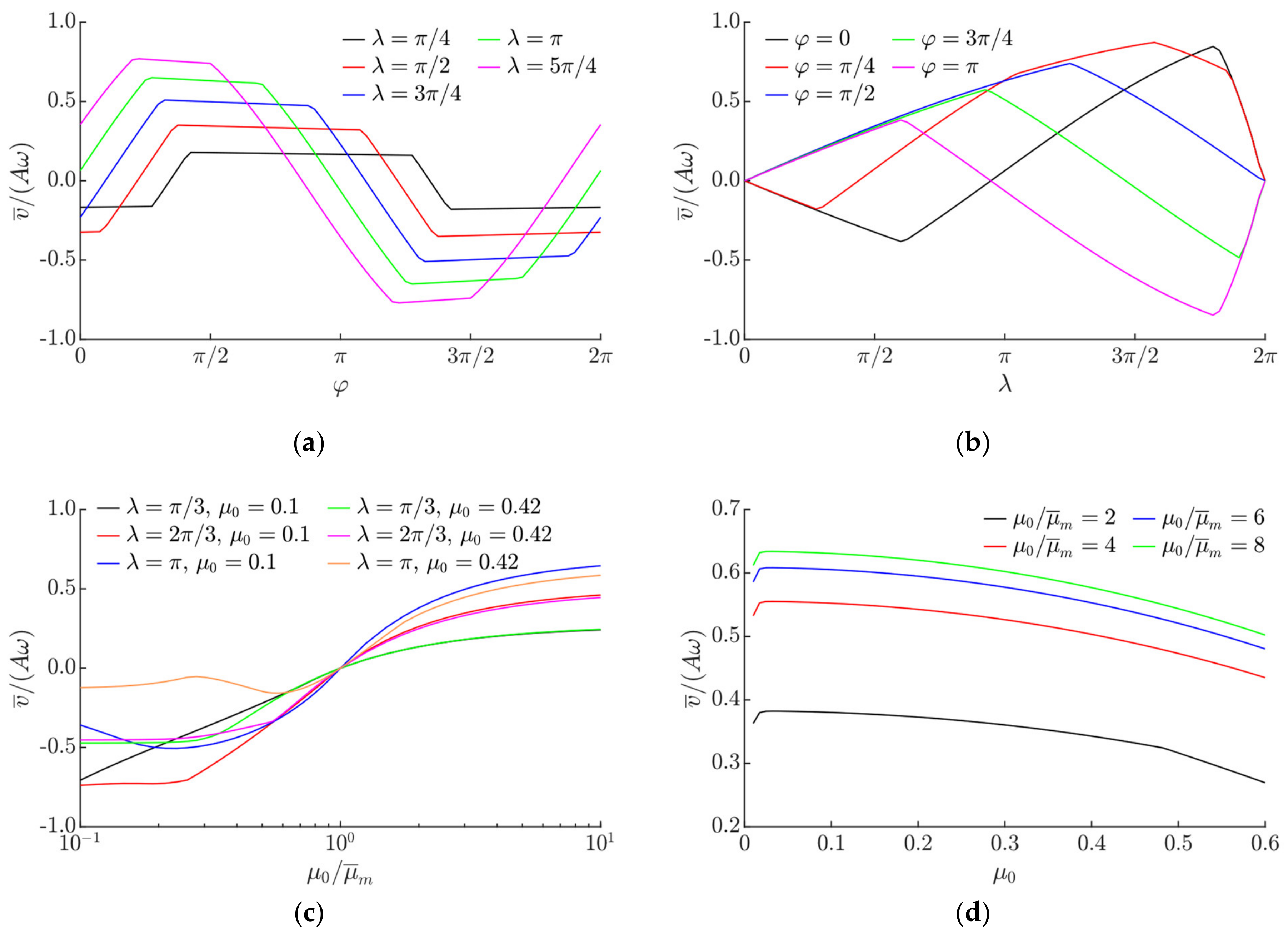
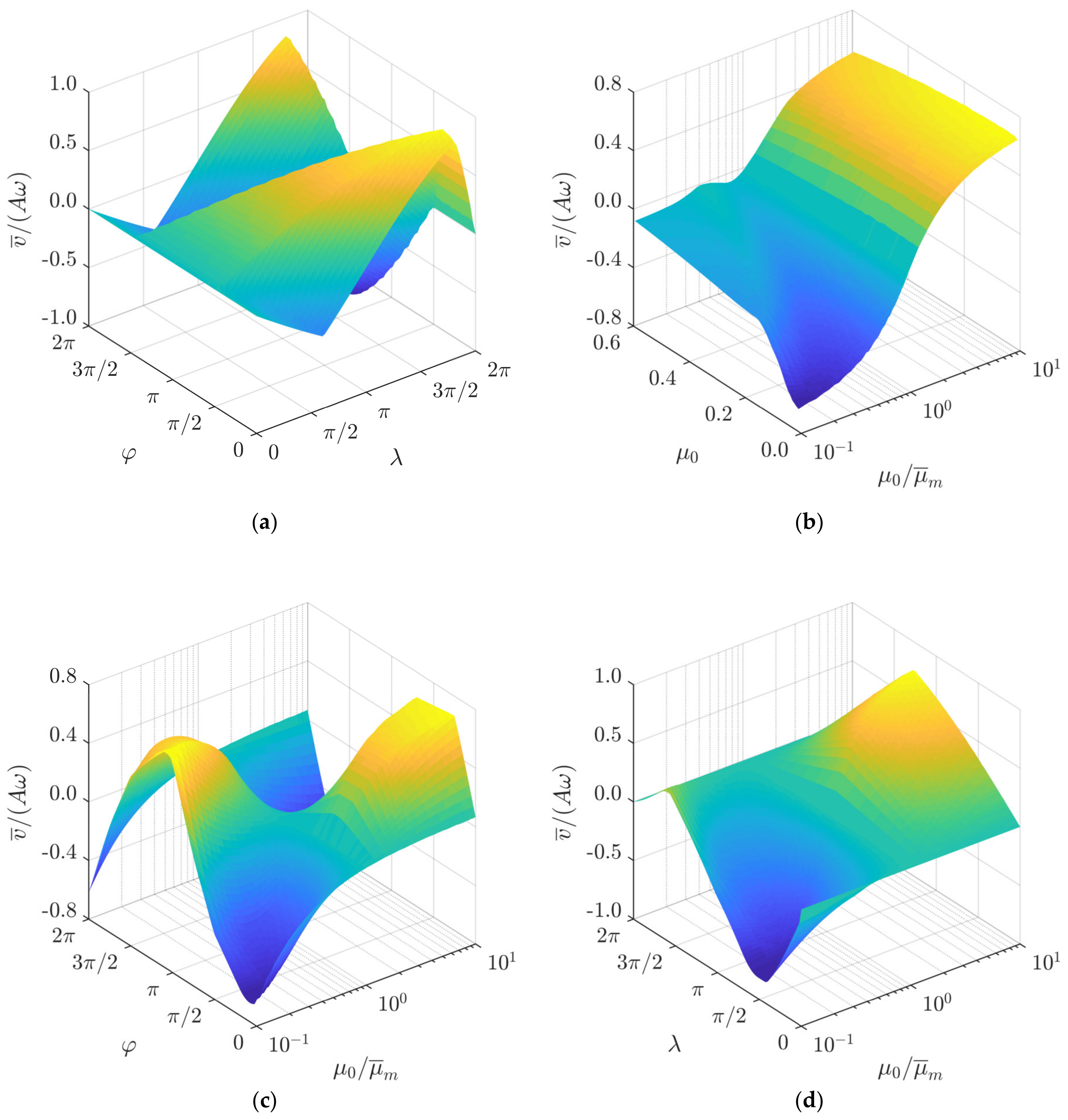
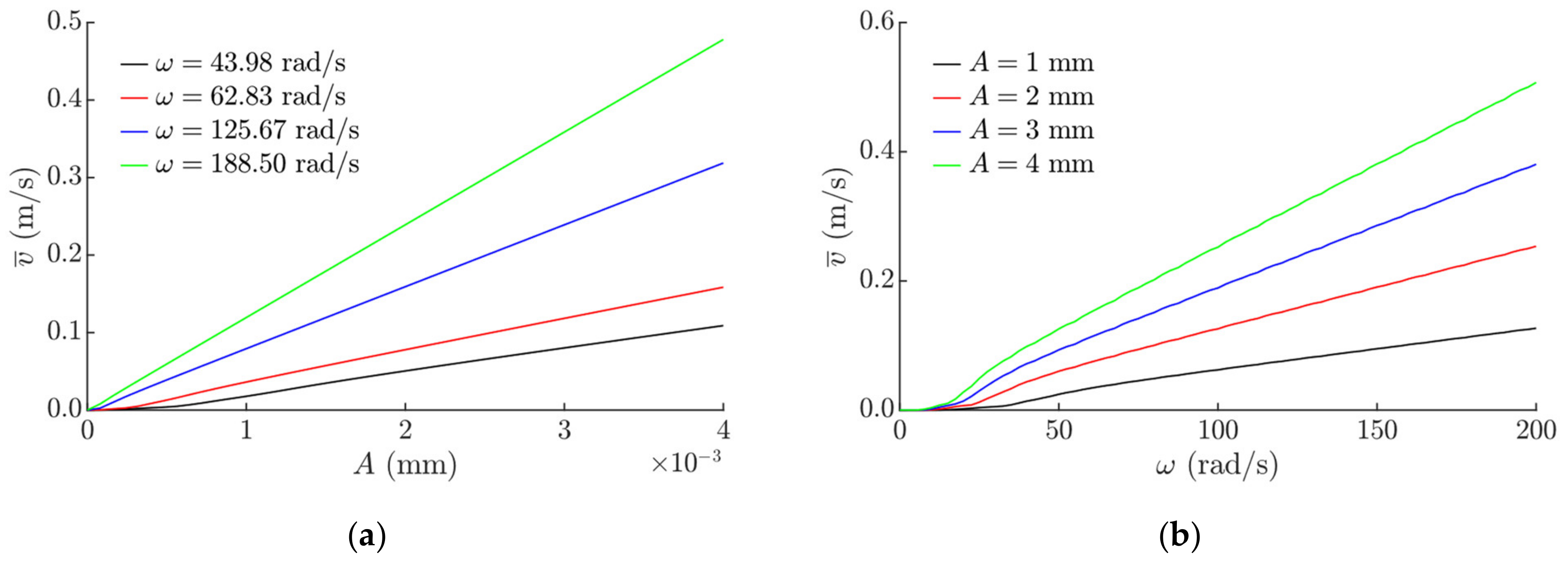
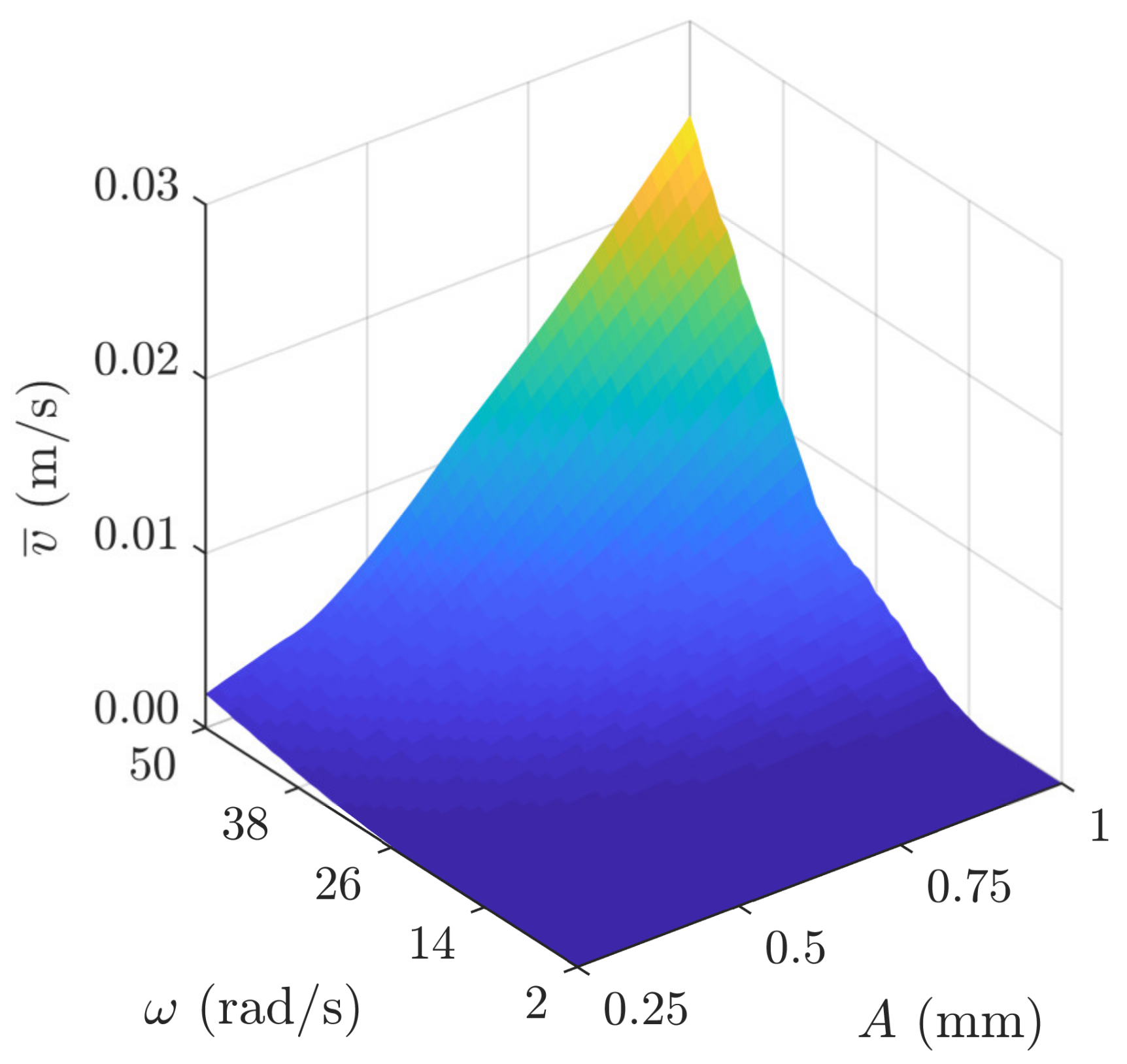
2.2. Modeling Results
3. Experimental Research
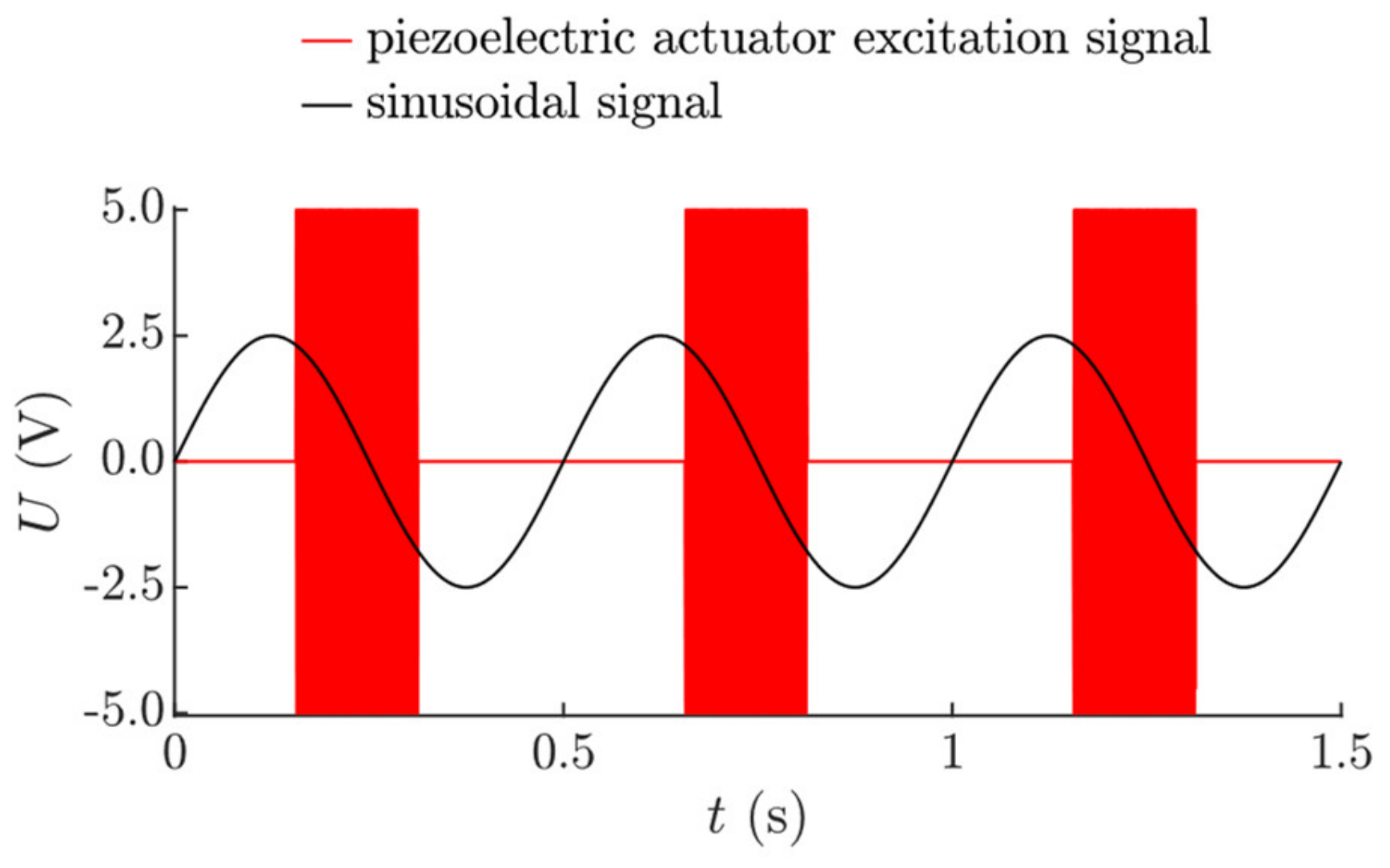
3.1. Experimental Setup and Methodology
3.2. Experimental Results and Comparison with the Model
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Huang, J.; Jiang, C.; Li, G.; Lu, Q.; Chen, H. Design and Analysis of a Light-Operated Microgripper Using an Opto-Electrostatic Repulsive Combined Actuator. Micromachines 2021, 12, 1026. [Google Scholar] [CrossRef] [PubMed]
- Rivera, P.; Valarezo Añazco, E.; Kim, T. Object Manipulation with an Anthropomorphic Robotic Hand via Deep Reinforcement Learning with a Synergy Space of Natural Hand Poses. Sensors 2021, 21, 5301. [Google Scholar] [CrossRef] [PubMed]
- Yamaguchi, K.; Higashimori, M. 1-Actuator 3-DoF Manipulation Using a Virtual Turntable Based on Differential Friction Surface. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation, Brisbane, QLD, Australia, 21–25 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 3573–3580. [Google Scholar] [CrossRef]
- Yuan, W.; Hang, K.; Kragic, D.; Wang, M.Y.; Stork, J.A. End-to-end nonprehensile rearrangement with deep reinforcement learning and simulation-to-reality transfer. Rob. Auton. Syst. 2019, 119, 119–134. [Google Scholar] [CrossRef]
- Hogan, F.R.; Rodriguez, A. Reactive planar non-prehensile manipulation with hybrid model predictive control. Int. J. Robot. Res. 2020, 39, 755–773. [Google Scholar] [CrossRef]
- Paing, M.S.; William Nshama, E.; Uchiyama, N. Motion Trajectory Estimation of a Flying Object and Optimal Reduced Impact Catching by a Planar Manipulator. In Proceedings of the 29th IEEE International Conference on Robot and Human Interactive Communication, Naples, Italy, 31 August–4 September 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 920–925. [Google Scholar] [CrossRef]
- Serra, D.; Ruggiero, F.; Lippiello, V.; Siciliano, B. A nonlinear least squares approach for nonprehensile dual-hand robotic ball juggling. IFAC PapersOnLine 2017, 50, 11485–11490. [Google Scholar] [CrossRef]
- Jiang, C.; Ueno, S. Posture maintenance control of 2-link object by nonprehensile two-cooperative-arm robot without compensating friction. IEEE CAA J. Autom. Sin. 2019, 6, 1397–1403. [Google Scholar] [CrossRef]
- Joe, H.; Lee, J.; Oh, J. Dynamic Nonprehensile Manipulation of a Moving Object Using a Batting Primitive. Appl. Sci. 2021, 11, 3920. [Google Scholar] [CrossRef]
- Ragulskis, K.; Spruogis, B.; Bogdevičius, M.; Matuliauskas, A.; Mištinas, V.; Ragulskis, L. Motion of vibration manipulators with self stopping device in one direction with interactions of two non deformable elements in one direction. Mechanika 2020, 26, 526–531. [Google Scholar] [CrossRef]
- Fomin, A.; Antonov, A.; Glazunov, V.; Rodionov, Y. Inverse and forward kinematic analysis of a 6-DOF parallel manipulator utilizing a circular guide. Robotics 2021, 10, 31. [Google Scholar] [CrossRef]
- Fomin, A.; Antonov, A.; Glazunov, V.; Carbone, G. Dimensional (Parametric) Synthesis of the Hexapod-Type Parallel Mechanism with Reconfigurable Design. Machines 2021, 9, 117. [Google Scholar] [CrossRef]
- Li, Z.; Liu, P.; Yan, P. Design and Analysis of a Novel Flexure-Based Dynamically Tunable Nanopositioner. Micromachines 2021, 12, 212. [Google Scholar] [CrossRef] [PubMed]
- Herrero, S.; Pinto, C.; Diez, M.; Zubizarreta, A. Optimization of the 2PRU-1PRS Parallel Manipulator Based on Workspace and Power Consumption Criteria. Appl. Sci. 2021, 11, 7770. [Google Scholar] [CrossRef]
- Röthlisberger, M.; Schuck, M.; Kulmer, L.; Kolar, J.W. Contactless Picking of Objects Using an Acoustic Gripper. Actuators 2021, 10, 70. [Google Scholar] [CrossRef]
- Janusas, T.; Urbaite, S.; Palevicius, A.; Nasiri, S.; Janusas, G. Biologically Compatible Lead-Free Piezoelectric Composite for Acoustophoresis Based Particle Manipulation Techniques. Sensors 2021, 21, 483. [Google Scholar] [CrossRef]
- Usadi, L.N.; Yee, S.; ElBidweihy, H.; Firebaugh, S. Manipulation of Microrobots Using Chladni Plates and Multimode Membrane Resonators. Eng. Proc. 2021, 4, 39. [Google Scholar] [CrossRef]
- Wijaya, H.; Latifi, K.; Zhou, Q. Two-dimensional manipulation in mid-air using a single transducer acoustic levitator. Micromachines 2019, 10, 257. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rizwan, M.; Shiakolas, P.S. On the optimum synthesis of a microconveyor platform for micropart translocation using differential evolution. Inverse Probl. Sci. Eng. 2013, 21, 1335–1351. [Google Scholar] [CrossRef]
- Ruggiero, F.; Lippiello, V.; Siciliano, B. Nonprehensile dynamic manipulation: A survey. IEEE Robot. Autom. Lett. 2018, 3, 1711–1718. [Google Scholar] [CrossRef]
- Reznik, D.; Canny, J.; Goldberg, K. Analysis of part motion on a longitudinally vibrating plate. In Proceedings of the 1997 IEEE/RSJ International Conference on Intelligent Robot and Systems, Grenoble, France, 11 September 1997; IEEE: Piscataway, NJ, USA, 1997; pp. 421–427. [Google Scholar] [CrossRef] [Green Version]
- Hunnekens, B.G.B.; Fey, R.H.B.; Shukla, A.; Nijmeijer, H. Vibrational self-alignment of a rigid object exploiting friction. Nonlinear Dyn. 2011, 65, 109–129. [Google Scholar] [CrossRef] [Green Version]
- Van Hoof, J.; Verhaegh, J.; Fey, R.; Van De Meerakker, P.; Nijmeijer, H. Experimental validation of object positioning via stick–slip vibrations. IEEE/ASME Trans. Mechatron. 2013, 19, 1092–1101. [Google Scholar] [CrossRef]
- Mayyas, M. Parallel Manipulation Based on Stick-Slip Motion of Vibrating Platform. Robotics 2020, 9, 86. [Google Scholar] [CrossRef]
- Mayyas, M. Modeling and analysis of vibratory feeder system based on robust stick–slip motion. J. Vibrat. Control. 2021, 10775463211009633. [Google Scholar] [CrossRef]
- Higashimori, M.; Yamaguchi, K.; Shibata, A. Omnidirectional Nonprehensile Manipulation Using Only One Actuator. Robotics 2018, 7, 34. [Google Scholar] [CrossRef] [Green Version]
- Sakashita, R.; Higashimori, M. 1-actuator 3-DoF parts feeding using hybrid joint mechanism with twisted axis layout. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA); Singapore, 29 May–3 June 2017, IEEE: Piscataway, NJ, USA, 2017; pp. 2335–2342. [Google Scholar] [CrossRef]
- Viswarupachari, C.; DasGupta, A.; Pratik Khastgir, S. Vibration induced directed transport of particles. J. Vib. Acoust. 2012, 134, 051005. [Google Scholar] [CrossRef]
- Blekhman, I.I.; Vasilkov, V.B.; Semenov, Y.A. Vibrotransporting of Bodies on a Surface with Non-Translational Rotational Oscillations. J. Mach. Manuf. Reliab. 2020, 49, 280–286. [Google Scholar] [CrossRef]
- Blekhman, I.I.; Blekhman, L.I.; Vaisberg, L.A.; Vasilkov, V.B. Energy Performance of Vibrational Transportation and Process Machines. In Proceedings of the 14th International Conference on Vibration Problems, Crete, Greece, 1–4 September 2019; Springer: Singapore, 2021; pp. 29–46. [Google Scholar] [CrossRef]
- Frei, P.U.; Wiesendanger, M.; Büchi, R.; Ruf, L. Simultaneous planar transport of multiple objects on individual trajectories using friction forces. In Distributed Manipulation; Böhringer, K.F., Choset, H., Eds.; Springer: Boston, MA, USA, 2000; pp. 49–64. [Google Scholar] [CrossRef]
- Umbanhowar, P.; Vose, T.H.; Mitani, A.; Hirai, S.; Lynch, K.M. The effect of anisotropic friction on vibratory velocity fields. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, St Paul, MN, USA, 14–19 May 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 2584–2591. [Google Scholar] [CrossRef]
- Chen, H.; Jiang, S.; Liu, R.; Zhang, W. Particle Directional Conveyance under Longitudinal Vibration by considering the Trough Surface Texture: Numerical Simulation Based on the Discrete Element Method. Shock Vibrat. 2018, 2018, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Cao, H.X.; Jung, D.; Lee, H.; Go, G.; Nan, M.; Choi, E.; Kim, C.; Park, J.; Kang, B. Micromotor Manipulation Using Ultrasonic Active Traveling Waves. Micromachines 2021, 12, 192. [Google Scholar] [CrossRef] [PubMed]
- Palencia, J.L.D. Travelling Waves Approach in a Parabolic Coupled System for Modelling the Behaviour of Substances in a Fuel Tank. Appl. Sci. 2021, 11, 5846. [Google Scholar] [CrossRef]
- Kharkongor, B.; Pohlong, S.S.; Mahato, M.C. Net transport in a periodically driven potential-free system. Phys. A Stat. Mech. Appl. 2021, 562, 125341. [Google Scholar] [CrossRef]
- Kumar, A.; DasGupta, A. Generation of circumferential harmonic travelling waves on thin circular plates. J. Sound Vib. 2020, 478, 115343. [Google Scholar] [CrossRef]
- Minikes, A.; Bucher, I. Noncontacting lateral transportation using gas squeeze film generated by flexural traveling waves—Numerical analysis. J. Acoust. Soc. Am. 2003, 113, 2464–2473. [Google Scholar] [CrossRef] [PubMed]
- Zouaghi, A.; Zouzou, N.; Dascalescu, L. Assessment of forces acting on fine particles on a traveling-wave electric field conveyor: Application to powder manipulation. Powder Technol. 2019, 343, 375–382. [Google Scholar] [CrossRef]
- Reznik, D.S.; Canny, J.F.; Alldrin, N. Leaving on a plane jet. In Proceedings of the 2001 IEEE/RSJ International Conference on Intelligent Robots and Systems, Maui, HI, USA, 29 October–3 November 2001; IEEE: Piscataway, NJ, USA, 2001; pp. 202–207. [Google Scholar] [CrossRef]
- Dunst, P.; Bornmann, P.; Hemsel, T.; Sextro, W. Vibration-Assisted Handling of Dry Fine Powders. Actuators 2018, 7, 18. [Google Scholar] [CrossRef] [Green Version]
- Kilikevičius, S.; Liutkauskienė, K.; Fedaravičius, A. Nonprehensile Manipulation of Parts on a Horizontal Circularly Oscillating Platform with Dynamic Dry Friction Control. Sensors 2021, 21, 5581. [Google Scholar] [CrossRef] [PubMed]
- Kilikevičius, S.; Fedaravičius, A.; Daukantienė, V.; Liutkauskienė, K.; Paukštaitis, L. Manipulation of Miniature and Microminiature Bodies on a Harmonically Oscillating Platform by Controlling Dry Friction. Micromachines 2021, 12, 1087. [Google Scholar] [CrossRef] [PubMed]
- Benad, J.; Nakano, K.; Popov, V.L.; Popov, M. Active control of friction by transverse oscillations. Friction 2019, 7, 74–85. [Google Scholar] [CrossRef] [Green Version]
- Popov, V.L.; Starcevic, J.; Filippov, A.E. Influence of ultrasonic in-plane oscillations on static and sliding friction and intrinsic length scale of dry friction processes. Tribol. Lett. 2010, 39, 25–30. [Google Scholar] [CrossRef]
- Teidelt, E.; Starcevic, J.; Popov, V.L. Influence of ultrasonic oscillation on static and sliding friction. Tribol. Lett. 2012, 48, 51–62. [Google Scholar] [CrossRef]
- Wang, P.; Ni, H.; Wang, R.; Li, Z.; Wang, Y. Experimental investigation of the effect of in-plane vibrations on friction for different materials. Tribol. Int. 2016, 99, 237–247. [Google Scholar] [CrossRef]
- Benad, J.; Popov, M.; Nakano, K.; Popov, V.L. Stiff and soft active control of friction by vibrations and their energy efficiency. Forsch. Ingenieurwes. 2018, 82, 331–339. [Google Scholar] [CrossRef]
- Kapelke, S.; Seemann, W. On the effect of longitudinal vibrations on dry friction: Modelling aspects and experimental investigations. Tribol. Lett. 2018, 66, 79. [Google Scholar] [CrossRef]
- Gutowski, P.; Leus, M. Computational model of friction force reduction at arbitrary direction of tangential vibrations and its experimental verification. Tribol. Int. 2020, 143, 106065. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kilikevičius, S.; Fedaravičius, A. Vibrational Transportation on a Platform Subjected to Sinusoidal Displacement Cycles Employing Dry Friction Control. Sensors 2021, 21, 7280. https://doi.org/10.3390/s21217280
Kilikevičius S, Fedaravičius A. Vibrational Transportation on a Platform Subjected to Sinusoidal Displacement Cycles Employing Dry Friction Control. Sensors. 2021; 21(21):7280. https://doi.org/10.3390/s21217280
Chicago/Turabian StyleKilikevičius, Sigitas, and Algimantas Fedaravičius. 2021. "Vibrational Transportation on a Platform Subjected to Sinusoidal Displacement Cycles Employing Dry Friction Control" Sensors 21, no. 21: 7280. https://doi.org/10.3390/s21217280
APA StyleKilikevičius, S., & Fedaravičius, A. (2021). Vibrational Transportation on a Platform Subjected to Sinusoidal Displacement Cycles Employing Dry Friction Control. Sensors, 21(21), 7280. https://doi.org/10.3390/s21217280






