A Sequential Handwriting Recognition Model Based on a Dynamically Configurable CRNN
Abstract
:1. Introduction
2. Literature Review
2.1. Handwriting Recognition Based on Deep Learning
2.2. Neuroevolutionary Methods Based on Sequence-Less Datasets
3. Swarm Evolving-Based Automatically Configured CRNN
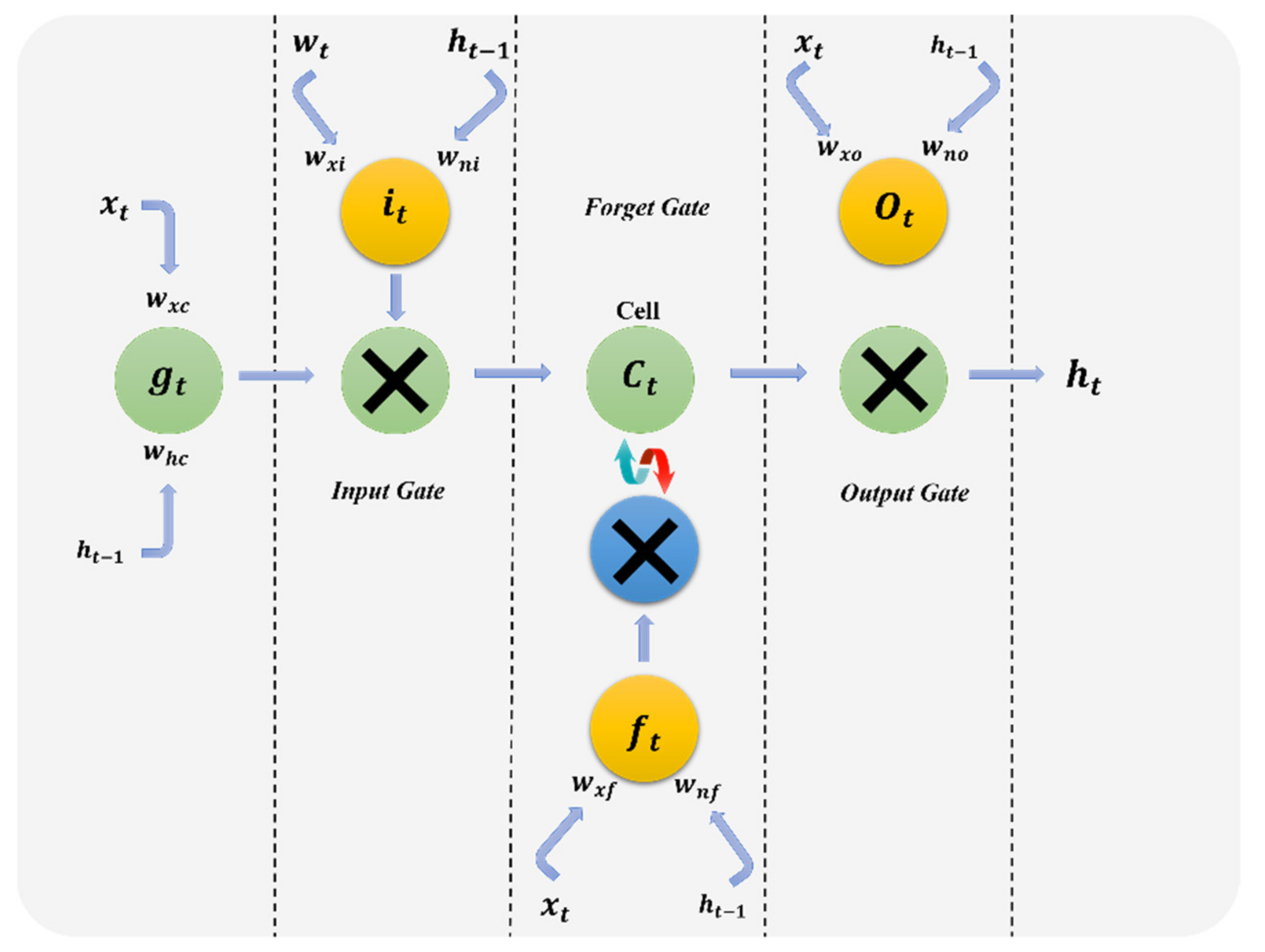
3.1. Convolutional Recurrent Neural Network (CRNN)
3.2. Solution Representation
- Batch size: The total number of training samples presented in a single batch, B ∈ (16, 32, 64, 128).
- Optimizer: The adaptive learning rate optimization algorithm is used to iteratively update the CRNN network weights based on the training data. The optimization algorithm can be any of the following: Adam, Nadam, RMSprop, Adadelta, SGD, Adagrad, Adamax.
- Learning rate: The change in the weights during training. The learning rate is represented by one decision variable in the solution, and is one of seven values: LR ∈ (1 × 10−5, 5 × 10−5, 1 × 10−4, 5 × 10−4, 1 × 10−3, 5 × 10−3, 1 × 10−2, 1 × 10−2, 5 × 10−2).
- Number of convolution layers: This decision variable determines how many convolution layers to add to our CRNN. Since handwriting recognition is considered a complex classification task, the first three layers are compulsory in all of the generated individuals (i.e., the first three convolution layers are combined as a fixed layer) to guarantee the automatic detection of the important features. However, an increase in the number of convolution layers can result in an increase in the number of weights as well as the model complexity. Consequently, we limit the convolution layers in our CRNN to 10, and that maximum number of layers can be chosen in our DC-CRNN’s search space.
- Number of LSTM layers: This decision variable determines how many LSTM layers to add to our CRNN.
- Other decision variables used to determine the remaining hyperparameters, which may vary for each convolution layer in the network, are:
- Convolution kernels (ck): The number of kernels in each convolution layer, where ck ∈ (4, 8, 16, 32, 64, 128, 265, 512).
- Convolution kernel size (cs): The kernel size used in each convolution layer, where cs ∈ (2, 3, 4, 5, 6, 7, 8, 9).
- Convolution batch normalization (cb): The use of batch normalization, which is typically utilized to enhance a neural network’s speed and performance. It is applied between the convolution layer and the nonlinearity layers, such as max pooling and ReLU. In our solution, the decision variable for batch normalization is in a binary (0, 1) range.
- Convolution activation function (ca): The usual ReLU is the default and most common activation function used in deep learning networks, especially convolutional neural networks. However, we attempt to choose a more suitable function for our network, which may be: ‘relu’, ‘linear’, ‘elu’, ‘selu’ or ‘tanh’.
- Convolution pooling size (cp): The pooling layer used to reduce the representation size of the input handwritten image, which leads to a reduction in the number of parameters and amount of computation in the network. While the use of pooling layers is important for maintaining a reasonable computation time during the optimization process that finds the optimum network structure, the overuse of pooling layers often removes important features or even reaches a representation size of (1, 1). In our decision variables, we limit the probability of using the pooling after each convolution layer to 50%, the pooling size to (2, 2) and the stride to ∈ {(2, 2), (2, 1)}.
- Skip connection (cr): The use of skip connections, which improve the convergence and performance during training.
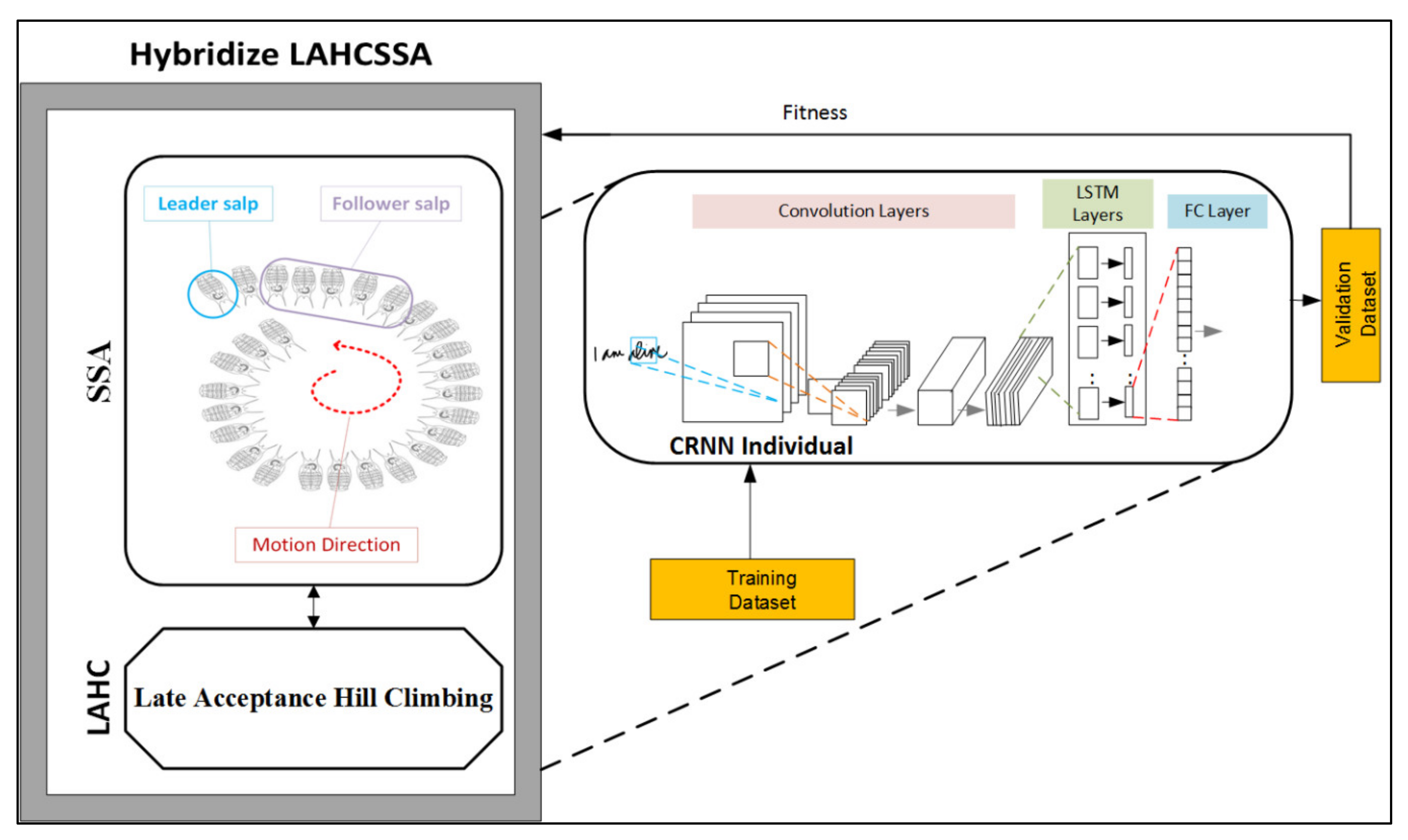
3.3. Hybrid SSA (HSSA)
| Algorithm 1: Salp Swarm Algorithm (SSA) |
| N → number of salps in the swarm. D → number of dimensions of the given problem. X → Initialize a swarm of salps with respect to lb and ub. F → The best search agent (Food source). while (Stopping criterion is not met) do Calculate the fitness of the salps c1 = 2 x e(4l=L) for i = (1 to N) do for j = (1 to D) do if i = 1 then Update the position of salps’ leader using Equation (6). else …… (See Equation (9)) for i = (1 to N) do Fit xi to its boundaries. if f(xi) < f(F) then F = xi Output: F |
| Algorithm 2: Hybridized SSA. |
| Input:Handwritten text dataset (sequence of letters and digits) N → number of salps in the swarm. D → number of dimensions of the given problem. X → Initialize a swarm of salps with respect to lb and ub. F → The best search agent (Food source). while (Stopping criterion is not met) do for each salp 2 X do Decodes the salp to a CRNN network (See Section 3.2) Train the CRNN on part of the training set. Evaluates the salp’s fitness based on part of the validation set. Update the positions of the salps. F Get the best salp. for i =(1 to N) do Fit xi to its boundaries. if f(xi) < f(F) then F = xi if rand() < lp then F local search(F) Output: Best CRNN con_guration (F) |
| Algorithm 3: Late Acceptance Hill-Climbing (LAHC) |
| X → Initial CRNN structure obtained from the SSA L → length of the list for i = 1 to L do fi = f(X). > Initialize the fitness list. X*= X. >Memorize the best solution. for i = 1 to Max_iterations do X’ = NS(X). >Move from the current solution to a new one. v = i mod L if f(X’) ≤ fv ll f(X’) ≤ f(X) then X = X0. >Accept the new solution. if X0 < X_ then X_ = X0 fv = f(X). >Insert the current cost to the fitness list. Output: X_ |
| Algorithm 4: Simulated annealing (SA) |
| X → Initial CRNN structure obtained from the SSA T → Initial temperature α → Cooling scheduler Tf → final temperature X* = X > memorize the best solution while (T > Tf) do X’ = NS(X) if f(X’) ≤ f(X) then X = X’ if X’ < X* then X* = X’ else if then X = X’ T=T*α Output: X* |
4. Experimental Design
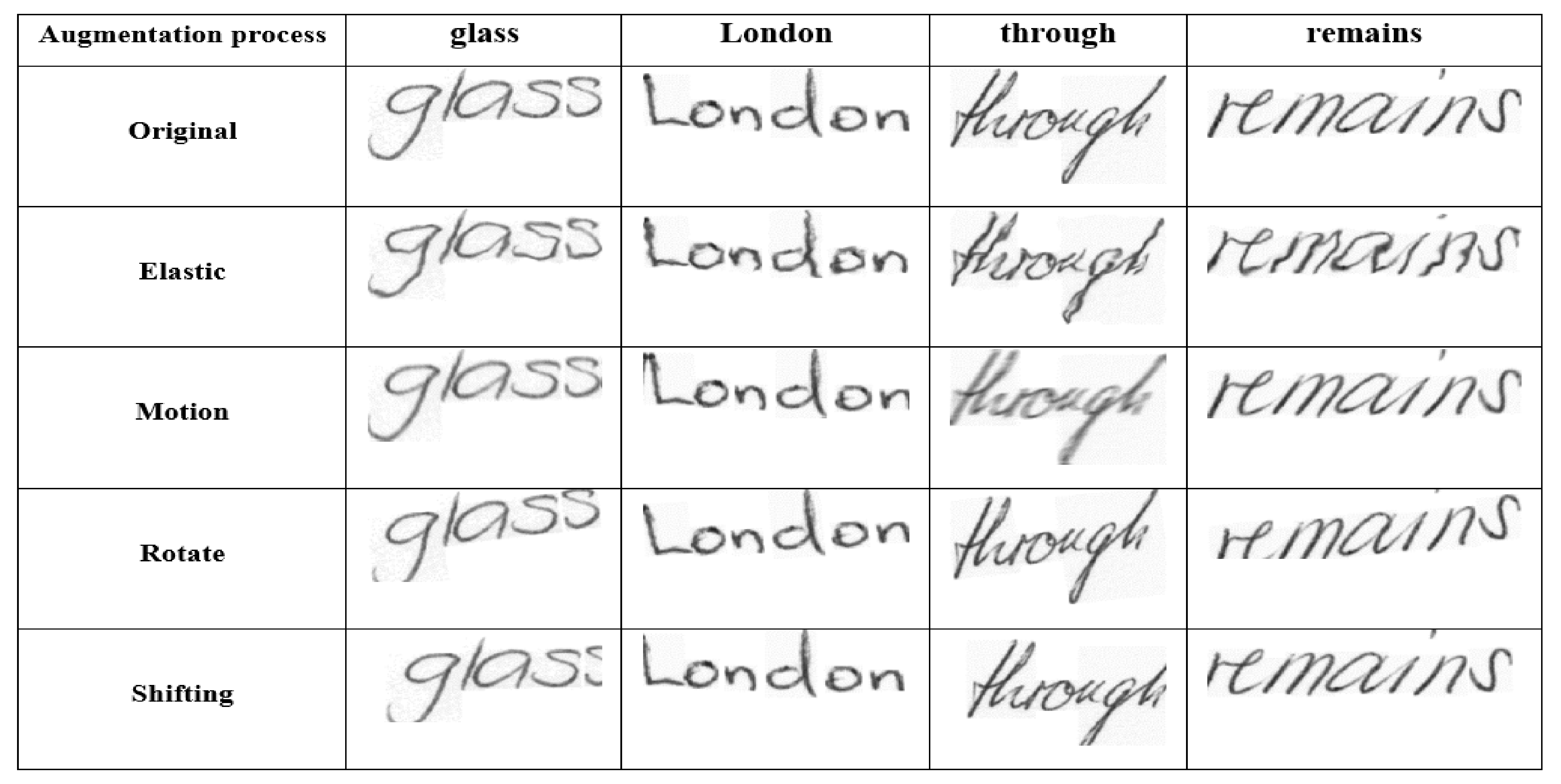
4.1. Implementation Details
4.2. Dataset
4.2.1. English Sequence Handwriting Dataset
4.2.2. Arabic Sequence Handwriting Dataset
4.3. Evaluation Metrics
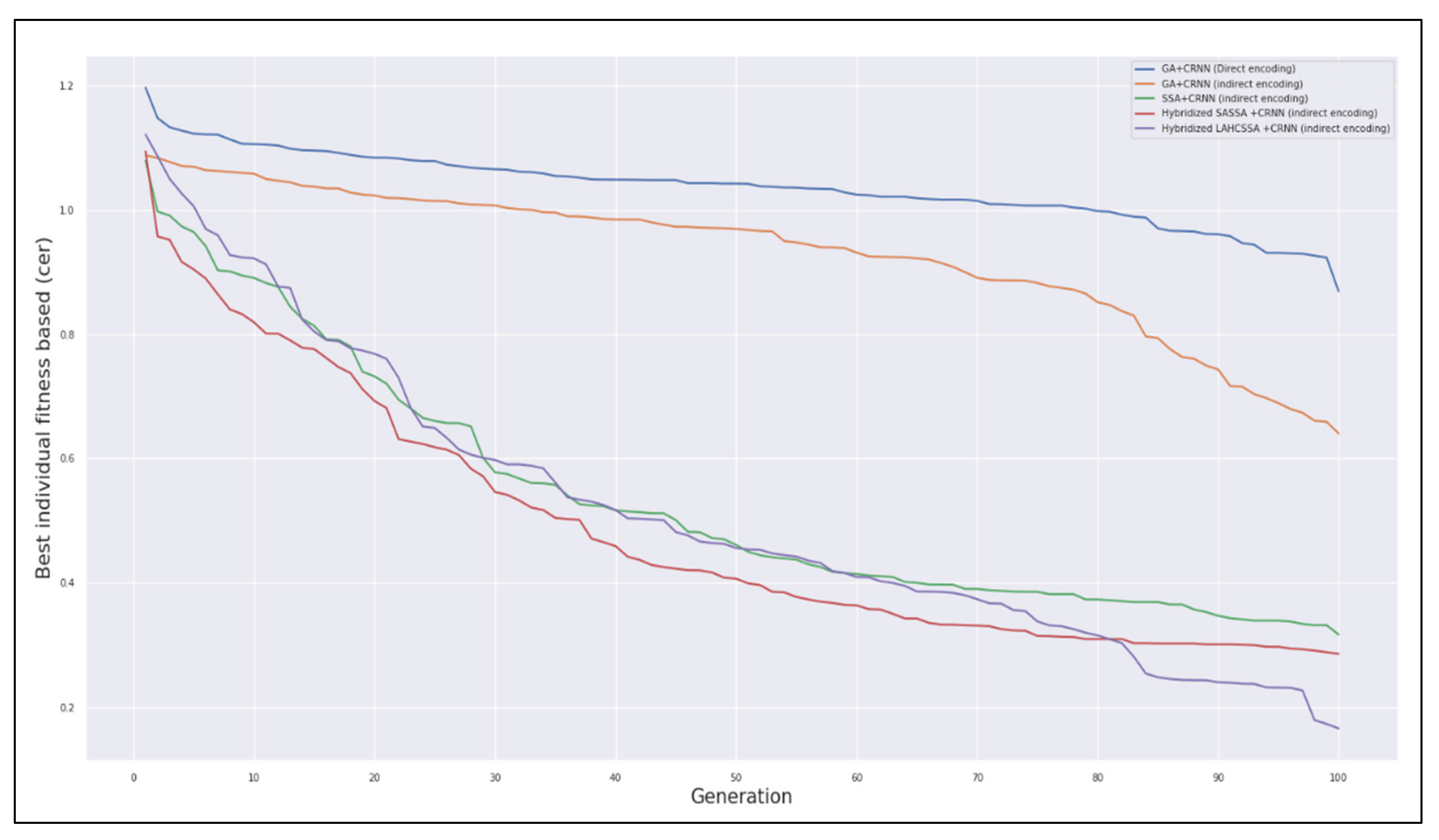
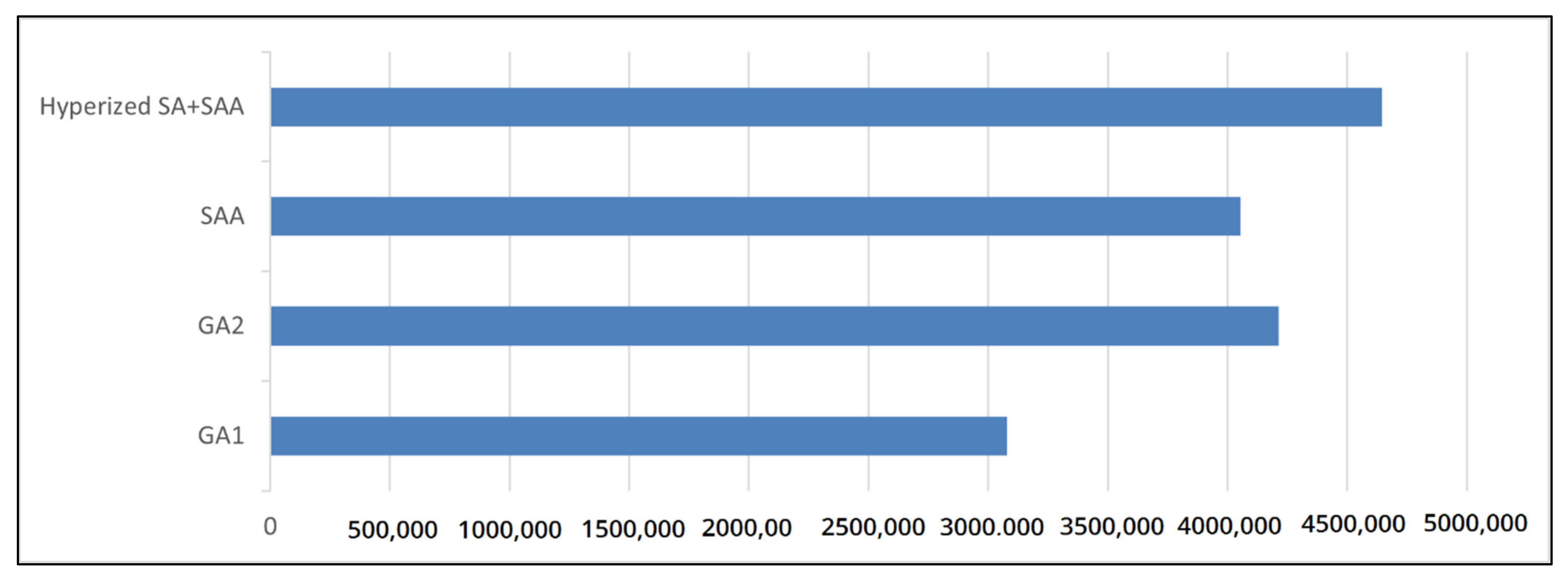
4.4. Convergence Analysis of the Proposed Method
4.5. Ablation Experiment from the Optimized CRNN
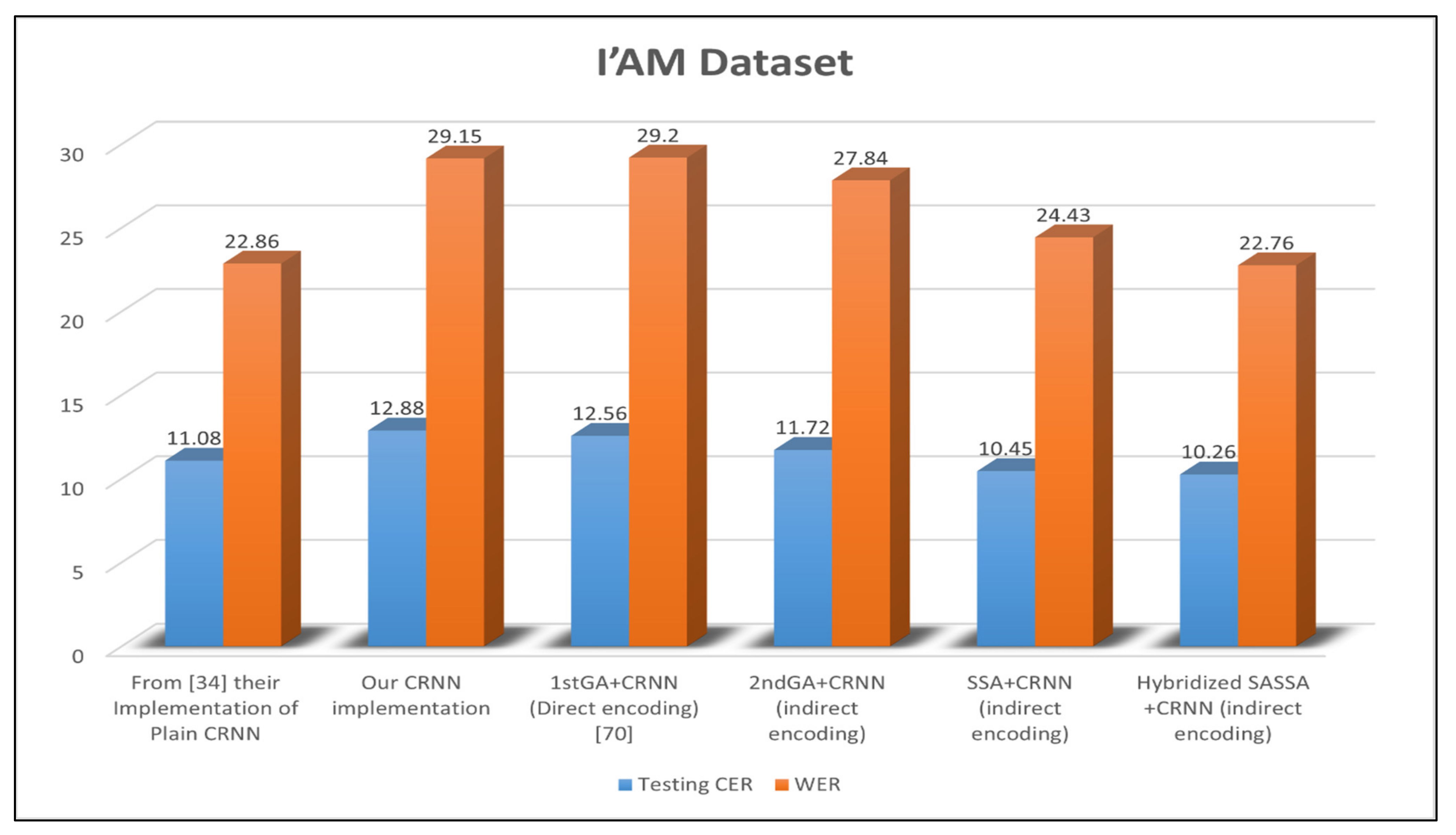
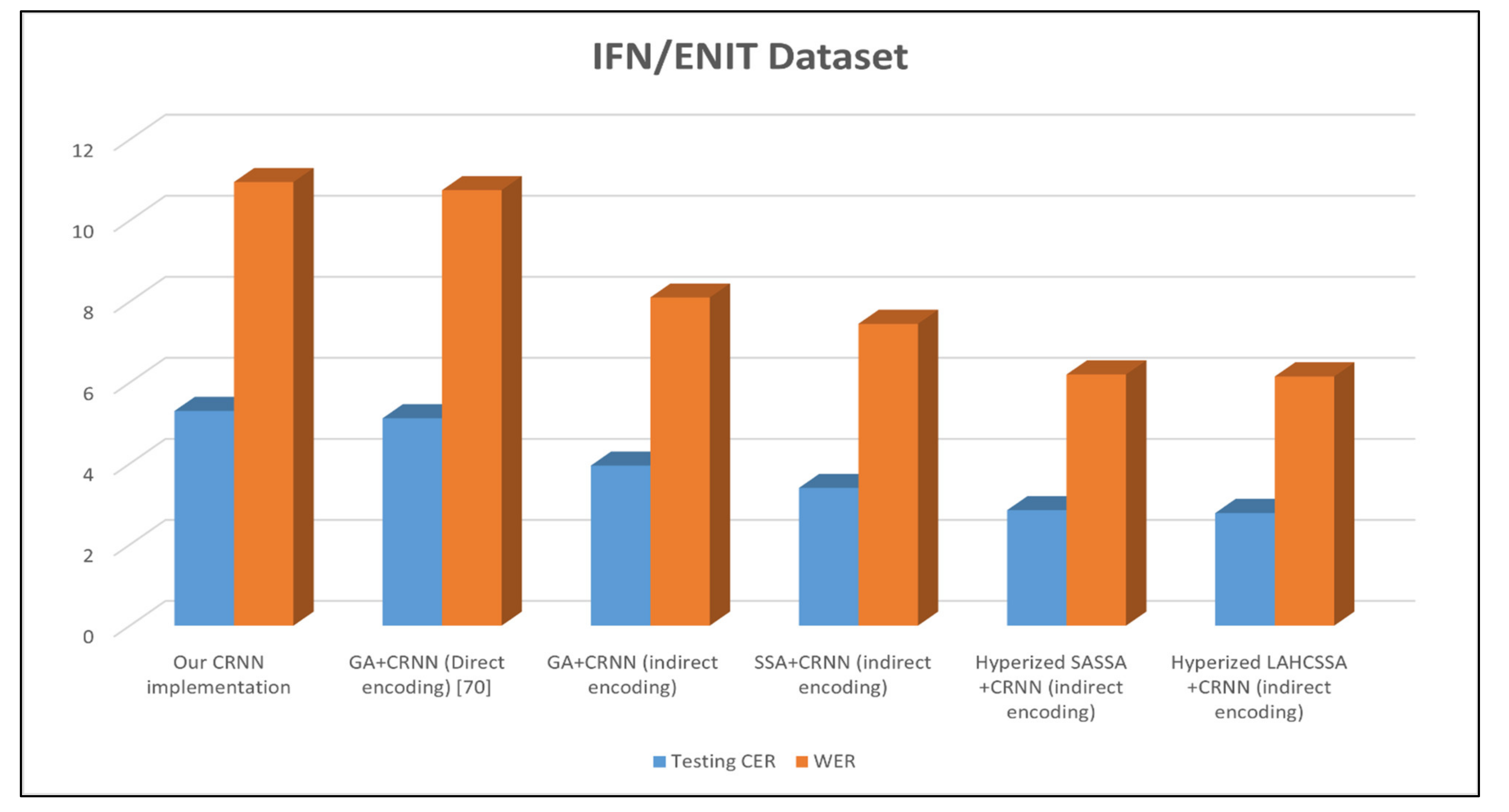
4.6. Reliability of the Proposed DC-CRNN
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| DC-CRNN | Dynamically Configurable Convolutional Recurrent Neural Network |
| SSA | Salp Swarm Optimization Algorithm |
| SA | Simulated Annealing |
| HC | Hill Climbing |
| LAHC | Late Acceptance Hill-Climbing |
| TS | Tabu Search |
| lp | Local Search Probability |
| RNNs | Recurrent Neural Networks |
| CRNNs | Convolutional Recurrent Neural Networks |
| CNNs | Convolutional Neural Networks |
| NAS | Neural Architecture Search |
| LSTM | Long Short-Term Memory |
| WFST | Weighted Finite-State Transducer |
| CTC | Connectionist Temporal Classification |
| BLSTM | Bidirectional Long Short-Term Memory |
| STN | Spatial Transformer Network |
| TL | Transfer Learning |
| seq-to-seq | Sequence-To-Sequence |
| LDN | Language Denoiser Network |
| NEAT | Neuroevolution Of Augmenting Topologies |
| PSO | Particle Swarm Optimization |
| QBPSO | Particle Swarm Optimization With Binary Encoding |
| ACO | Ant Colony Optimization |
| HSSA | Hybrid Salp Swarm Optimization Algorithm |
| IFN/ENIT | Technology/Ecole Nationale d’Ingénieurs De Tunis |
| WER | Word Error Rate |
| CER | Character Error Rate |
Appendix A
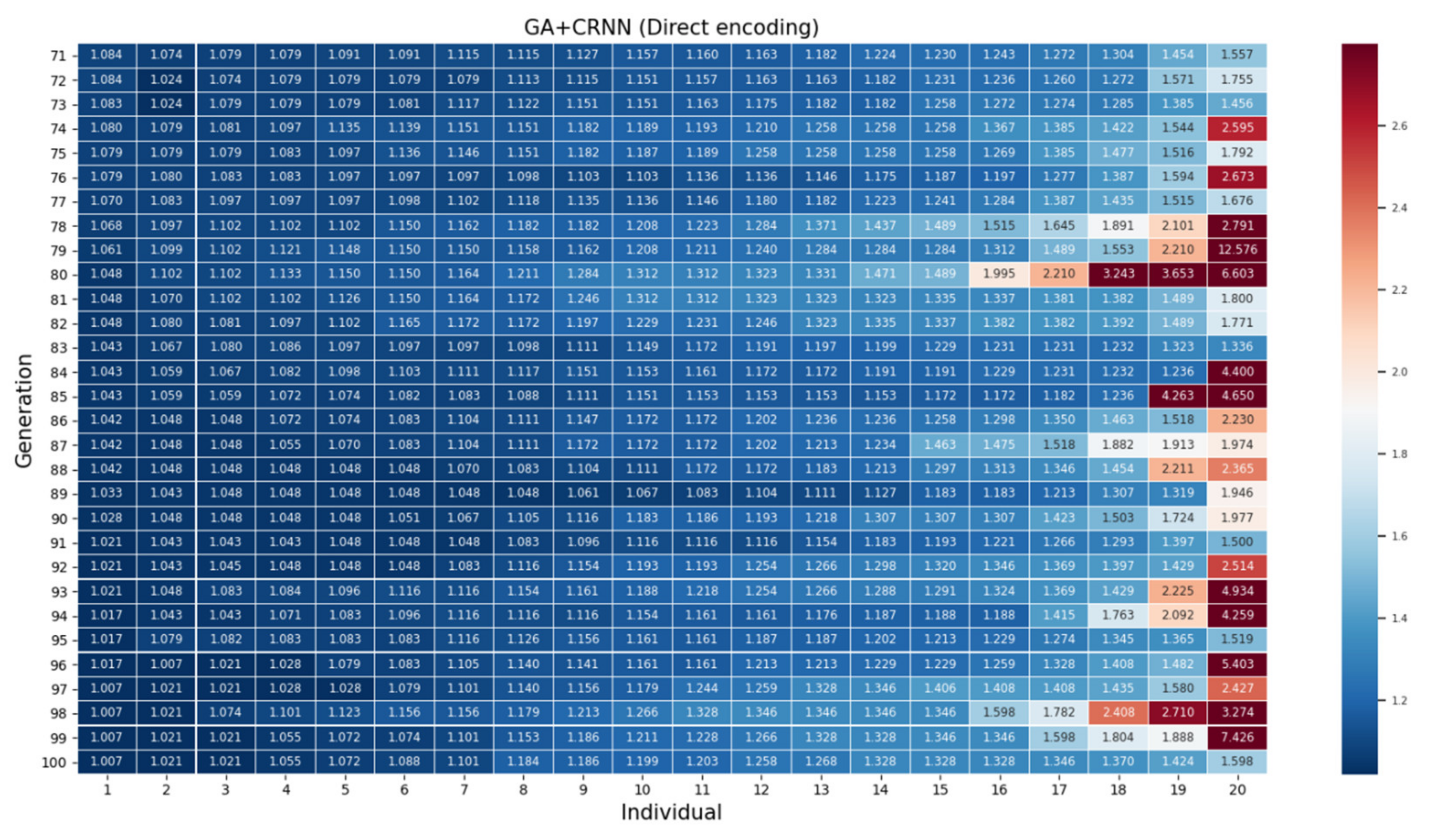
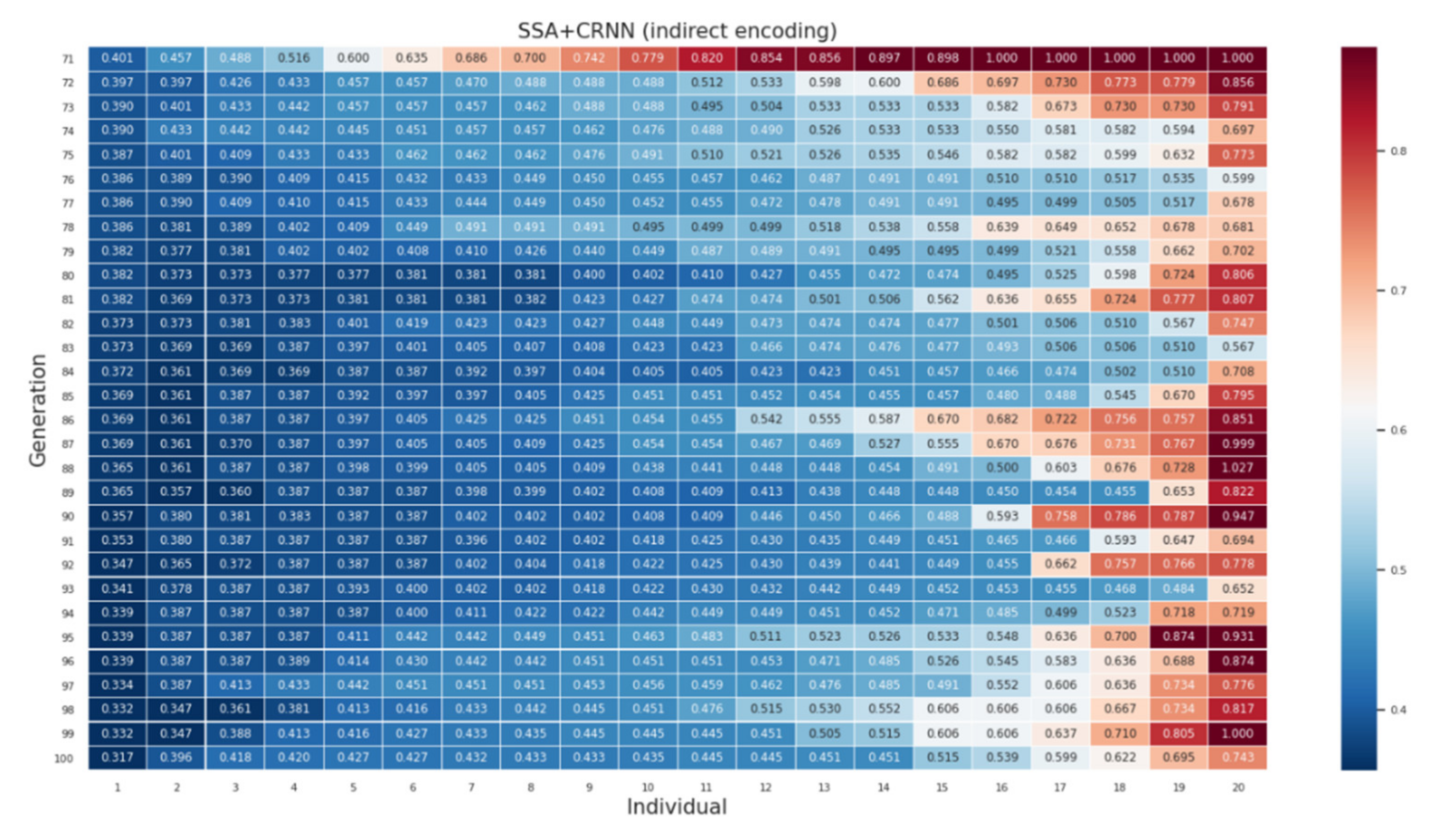
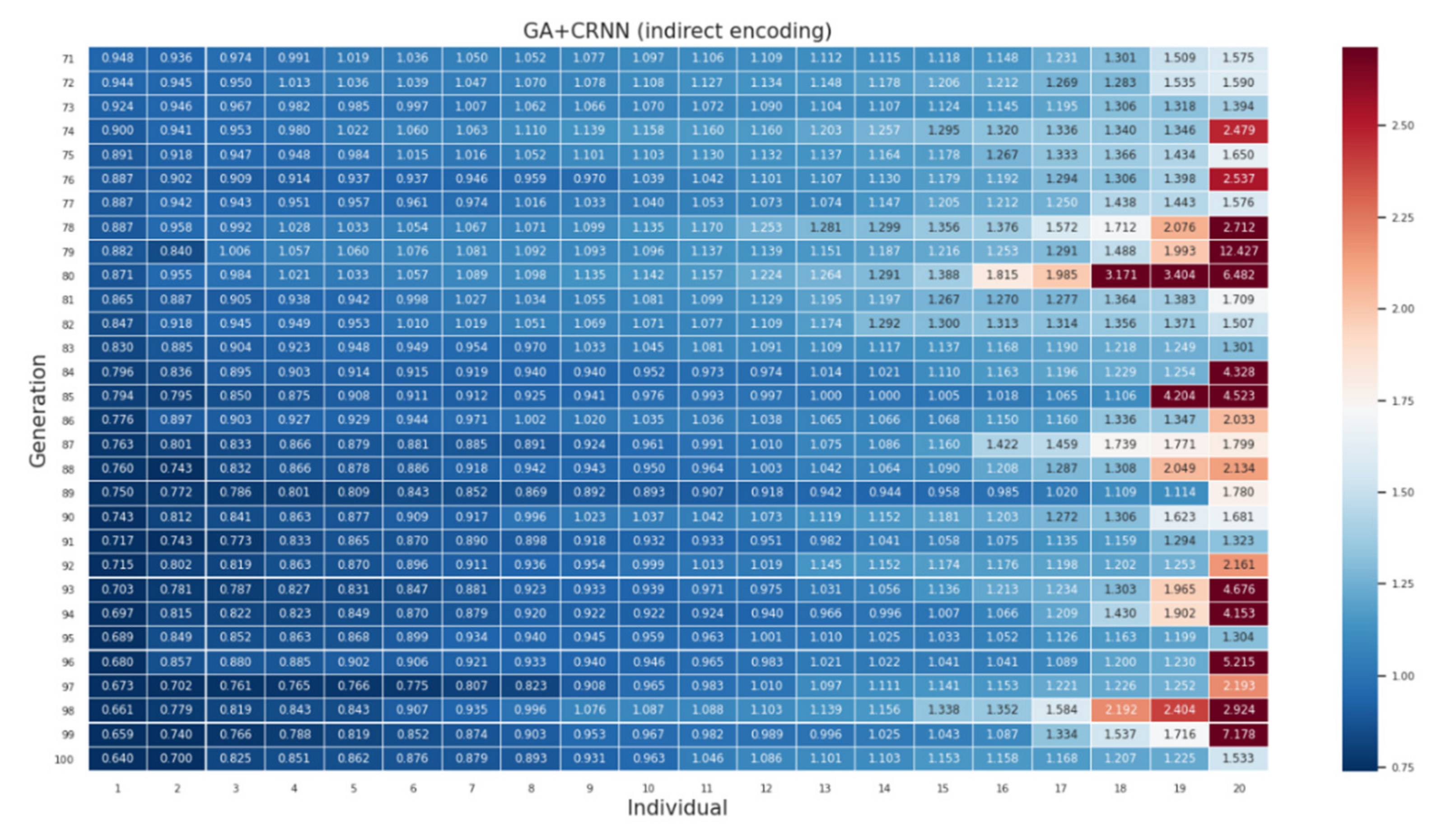
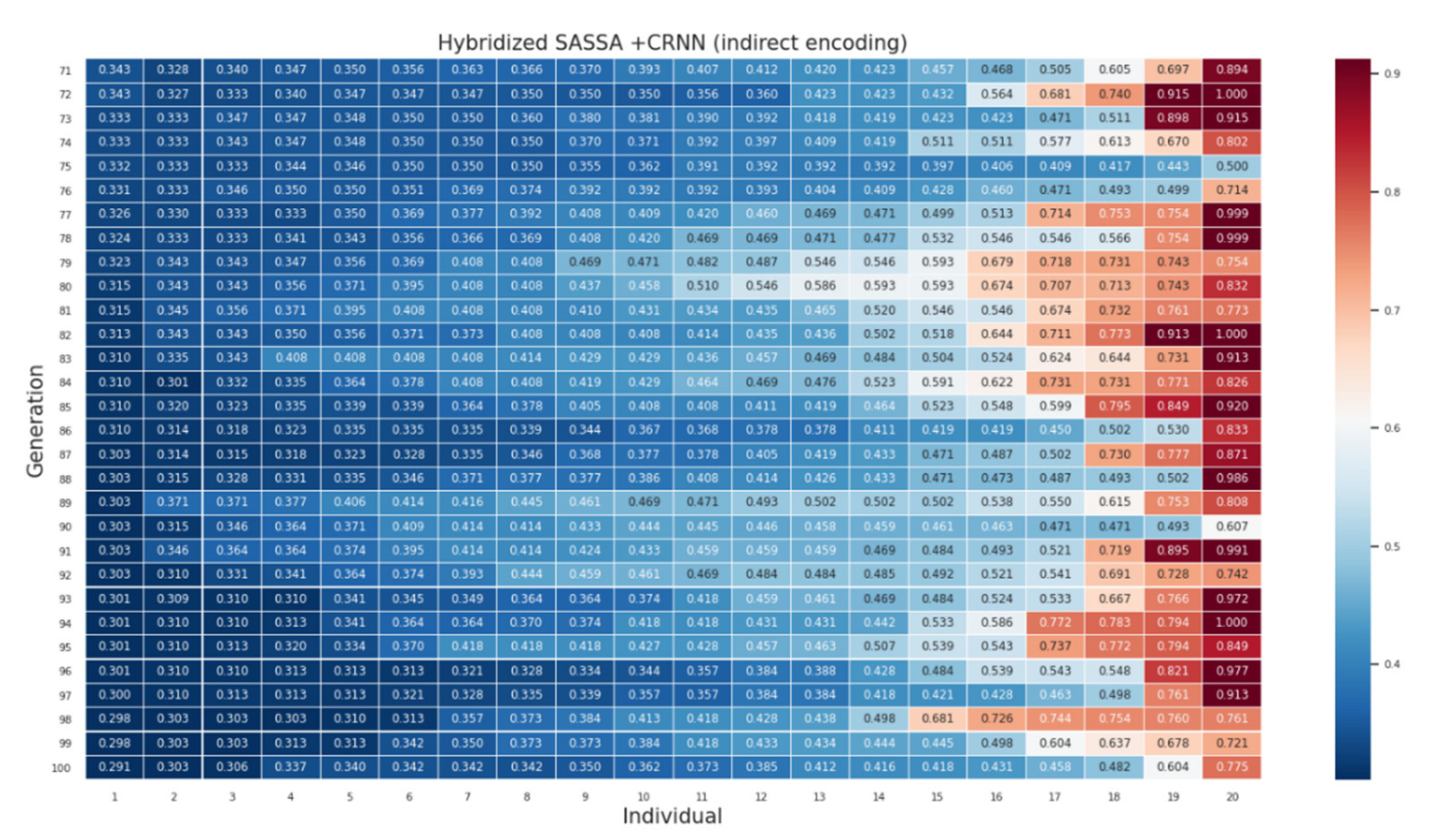
References
- Al-Saiagh, W.; Tiun, S.; Al-Saffar, A.; Awang, S.; Al-Khaleefa, A. Word sense disambiguation using hybrid swarm intelligence aroach. PLoS ONE 2018, 13, e0208695. [Google Scholar] [CrossRef] [Green Version]
- Zin, T.T.; Pwint, M.Z.; Thant, S. A Mobile Alication for Offline Handwritten Character Recognition. In Proceedings of the 2020 IEEE 9th Global Conference on Consumer Electronics (GCCE), Kobe, Japan, 13–16 October 2020; pp. 10–11. [Google Scholar]
- Hopcan, S.; Tokel, S.T. Exploring the effectiveness of a mobile writing alication for suorting handwriting acquisition of students with dysgraphia. Educ. Inf. Technol. 2021, 26, 3967–4002. [Google Scholar] [CrossRef]
- Sharma, A.; Jayagopi, D.B. Towards efficient unconstrained handwriting recognition using Dilated Temporal Convolution Network. Expert Syst. Appl. 2021, 164, 114004. [Google Scholar] [CrossRef]
- Ahmed, R.; Gogate, M.; Tahir, A.; Dashtipour, K.; Al-Tamimi, B.; Hawalah, A.; El-Affendi, M.A.; Hussain, A. Deep Neural Network-Based Contextual Recognition of Arabic Handwritten Scripts. Entropy 2021, 23, 340. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Xiao, G. Real-time chinese traffic warning signs recognition based on cascade and CNN. J. Real-Time Image Process. 2020, 18, 669–680. [Google Scholar] [CrossRef]
- Zhang, Y.-J. Alication of Image Technology. In Handbook of Image Engineering; Springer: Berlin/Heidelberg, Germany, 2021; pp. 1819–1836. [Google Scholar]
- Hwang, S.-M.; Yeom, H.-G. An Implementation of a System for Video Translation Using OCR. In Software Engineering in IoT, Big Data, Cloud and Mobile Computing; Springer: Berlin/Heidelberg, Germany, 2021; pp. 49–57. [Google Scholar]
- Zhao, B.; Tao, J.; Yang, M.; Tian, Z.; Fan, C.; Bai, Y. Deep imitator: Handwriting calligraphy imitation via deep attention networks. Pattern Recogn. 2020, 104, 107080. [Google Scholar] [CrossRef]
- Awang, S.; Azmi, N.M.A.N.; Rahman, M.A. Vehicle type classification using an enhanced sparse-filtered convolutional neural network with layer-skiing strategy. IEEE Access 2020, 8, 14265–14277. [Google Scholar] [CrossRef]
- Cakic, S.; Ismailisufi, A.; Popovic, T.; Krco, S.; Gligoric, N.; Kupresanin, S.; Maras, V. Digital Transformation and Transparency in Wine Suly Chain Using OCR and DLT. In Proceedings of the 2021 25th International Conference on Information Technology (IT), Žabljak, Montenegro, 16–20 February 2021; pp. 1–5. [Google Scholar]
- Georgieva, P.; Zhang, P. Optical Character Recognition for Autonomous Stores. In Proceedings of the 2020 IEEE 10th International Conference on Intelligent Systems (IS), Varna, Bulgaria, 26–28 June 2020; pp. 69–75. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A.; Bengio, Y. Deep Learning; MIT press: Cambridge, MA, USA, 2016; Volume 1. [Google Scholar]
- Alkhateeb, J.H. An Effective Deep Learning Approach for Improving Off-Line Arabic Handwritten Character Recognition. Int. J. Softw. Eng. Comput. Syst. 2020, 6, 53–61. [Google Scholar]
- Ball, G.R.; Srihari, S.N.; Srinivasan, H. Segmentation-based and segmentation-free methods for spotting handwritten arabic words. In Proceedings of the Tenth International Workshop on Frontiers in Handwriting Recognition, La Baule, France, 23–26 October 2006. [Google Scholar]
- Biadsy, F.; Saabni, R.; El-Sana, J. Segmentation-free online arabic handwriting recognition. Int. J. Pattern Recogn. Artif. Intell. 2011, 25, 1009–1033. [Google Scholar] [CrossRef]
- Rusinol, M.; Aldavert, D.; Toledo, R.; Lladós, J. Browsing heterogeneous document collections by a segmentation-free word spotting method. In Proceedings of the 2011 International Conference on Document Analysis and Recognition, Beijing, China, 18–21 September 2011; pp. 63–67. [Google Scholar]
- Dwivedi, A.; Saluja, R.; Sarvadevabhatla, R.K. An OCR for Classical Indic Documents Containing Arbitrarily Long Words. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 560–561. [Google Scholar]
- Carbune, V.; Gonnet, P.; Deselaers, T.; Rowley, H.A.; Daryin, A.; Calvo, M.; Wang, L.-L.; Keysers, D.; Feuz, S.; Gervais, P. Fast multi-language LSTM-based online handwriting recognition. Int. J. Doc. Anal. Recogn. 2020, 32, 89–102. [Google Scholar] [CrossRef] [Green Version]
- Bluche, T.; Messina, R. Gated convolutional recurrent neural networks for multilingual handwriting recognition. In Proceedings of the 2017 14th IAPR International Conference on Document Analysis and Recognition (ICDAR), Kyoto, Japan, 9–15 November 2017; pp. 646–651. [Google Scholar]
- Xie, Z.; Sun, Z.; Jin, L.; Feng, Z.; Zhang, S. Fully convolutional recurrent network for handwritten chinese text recognition. In Proceedings of the 2016 23rd International Conference on Pattern Recognition (ICPR), Cancun, Mexico, 4–8 December 2016; pp. 4011–4016. [Google Scholar]
- Zhan, H.; Lyu, S.; Tu, X.; Lu, Y. Residual CRNN and Its Alication to Handwritten Digit String Recognition. In Proceedings of the International Conference on Neural Information Processing, Sydney, Australia, 12–15 December 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 49–56. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing atari with deep reinforcement learning. arXiv 2013, arXiv:1312.5602 2013. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, PMLR, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Yuan, W.; Dong, B.; Wang, S.; Unoki, M.; Wang, W. Evolving Multi-Resolution Pooling CNN for Monaural Singing Voice Separation. IEEE/ACM Trans. Audio Speech Lang. Process. 2021, 29, 807–822. [Google Scholar] [CrossRef]
- Sun, D.; Wei, E.; Ma, Z.; Wu, C.; Xu, S. Optimized CNNs to Indoor Localization through BLE Sensors Using Improved PSO. Sensors 2021, 21, 1995. [Google Scholar] [CrossRef] [PubMed]
- Stanovov, V.; Akhmedova, S.; Semenkin, E. Neuroevolution of augmented topologies with difference-based mutation. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2021; p. 012075. [Google Scholar]
- Galván, E.; Mooney, P. Neuroevolution in deep neural networks: Current trends and future challenges. arXiv 2021, arXiv:2006.05415. [Google Scholar]
- Krishnan, P.; Dutta, K.; Jawahar, C. Deep feature embedding for accurate recognition and retrieval of handwritten text. In Proceedings of the 2016 15th International Conference on Frontiers in Handwriting Recognition (ICFHR), Shenzhen, China, 23–26 October 2015; pp. 289–294. [Google Scholar]
- Rawls, S.; Cao, H.; Kumar, S.; Natarajan, P. Combining convolutional neural networks and lstms for segmentation-free ocr. In Proceedings of the 2017 14th IAPR international conference on document analysis and recognition (ICDAR), Kyoto, Japan, 9–15 November 2017; pp. 155–160. [Google Scholar]
- Ptucha, R.; Such, F.P.; Pillai, S.; Brockler, F.; Singh, V.; Hutkowski, P. Intelligent character recognition using fully convolutional neural networks. Pattern Recogn. 2019, 88, 604–613. [Google Scholar] [CrossRef]
- Krishnan, P.; Dutta, K.; Jawahar, C. Word spotting and recognition using deep embedding. In Proceedings of the 2018 13th IAPR International Workshop on Document Analysis Systems (DAS), Vienna, Austria, 24–28 April 2018; pp. 1–6. [Google Scholar]
- Dutta, K.; Krishnan, P.; Mathew, M.; Jawahar, C. Improving cnn-rnn hybrid networks for handwriting recognition. In Proceedings of the 2018 16th International Conference on Frontiers in Handwriting Recognition (ICFHR), Niagara Falls, NY, USA, 5–8 August 2018; pp. 80–85. [Google Scholar]
- Jaramillo, J.C.A.; Murillo-Fuentes, J.J.; Olmos, P.M. Boosting handwriting text recognition in small databases with transfer learning. In Proceedings of the 2018 16th International Conference on Frontiers in Handwriting Recognition (ICFHR), Niagara Falls, NY, USA, 5–8 August 2018; pp. 429–434. [Google Scholar]
- Marti, U.-V.; Bunke, H. The IAM-database: An English sentence database for offline handwriting recognition. Int. J. Doc. Anal. Recognit. 2002, 5, 39–46. [Google Scholar] [CrossRef]
- Fischer, A.; Keller, A.; Frinken, V.; Bunke, H. Lexicon-free handwritten word spotting using character HMMs. Pattern Recog. Lett. 2012, 33, 934–942. [Google Scholar] [CrossRef]
- Kang, L.; Riba, P.; Villegas, M.; Fornés, A.; Rusiñol, M. Candidate fusion: Integrating language modelling into a sequence-to-sequence handwritten word recognition architecture. Pattern Recogn. 2021, 112, 107790. [Google Scholar] [CrossRef]
- Chung, J.; Delteil, T. A computationally efficient pipeline aroach to full page offline handwritten text recognition. In Proceedings of the 2019 International Conference on Document Analysis and Recognition Workshops (ICDARW), Sydney, Australia, 22–25 September 2019; pp. 35–40. [Google Scholar]
- Yao, X.; Liu, Y. A new evolutionary system for evolving artificial neural networks. IEEE Trans. Neural Netw. 1997, 8, 694–713. [Google Scholar] [CrossRef] [Green Version]
- Stanley, K.O.; Miikkulainen, R. Evolving neural networks through augmenting topologies. Evol. Comput. 2002, 10, 99–127. [Google Scholar] [CrossRef] [PubMed]
- Kassahun, Y.; Sommer, G. Efficient reinforcement learning through Evolutionary Acquisition of Neural Topologies. In Proceedings of the European Symposium On Artificial Neural Networks, Computational Intelligence and Machine Learning, ESANN, Bruges, Belgium, 27–29 April 2005; pp. 259–266. [Google Scholar]
- Stanley, K.O.; Clune, J.; Lehman, J.; Miikkulainen, R. Designing neural networks through neuroevolution. Nat. Mach. Intell. 2019, 1, 24–35. [Google Scholar] [CrossRef]
- Liu, H.; Simonyan, K.; Vinyals, O.; Fernando, C.; Kavukcuoglu, K. Hierarchical representations for efficient architecture search. arXiv 2017, arXiv:1711.00436 2017. [Google Scholar]
- Real, E.; Moore, S.; Selle, A.; Saxena, S.; Suematsu, Y.L.; Tan, J.; Le, Q.V.; Kurakin, A. Large-scale evolution of image classifiers. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 2902–2911. [Google Scholar]
- Sun, Y.; Xue, B.; Zhang, M.; Yen, G.G.; Lv, J. Automatically designing CNN architectures using the genetic algorithm for image classification. IEEE Trans. Cybern. 2020, 50, 3840–3854. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Talbi, E.-G. Automated Design of Deep Neural Networks: A Survey and Unified Taxonomy. ACM Comput. Surv. (CSUR) 2021, 54, 1–37. [Google Scholar]
- Katona, A.; Lourenço, N.; Machado, P.; Franks, D.W.; Walker, J.A. Utilizing the Untaed Potential of Indirect Encoding for Neural Networks with MetaLearning. In Proceedings of the Evostar, Virtual Event, 7–9 April 2021; Volume 2021. [Google Scholar]
- Miikkulainen, R.; Liang, J.; Meyerson, E.; Rawal, A.; Fink, D.; Francon, O.; Raju, B.; Shahrzad, H.; Navruzyan, A.; Duffy, N. Evolving deep neural networks. In Artificial Intelligence in the Age of Neural Networks and Brain Computing; Elsevier: Amsterdam, The Netherlands, 2019; pp. 293–312. [Google Scholar]
- Baldominos, A.; Saez, Y.; Isasi, P. Evolutionary convolutional neural networks: An alication to handwriting recognition. Neurocomputing 2018, 283, 38–52. [Google Scholar] [CrossRef]
- Fielding, B.; Zhang, L. Evolving image classification architectures with enhanced particle swarm optimisation. IEEE Access 2018, 6, 68560–68575. [Google Scholar] [CrossRef]
- Li, Y.; Xiao, J.; Chen, Y.; Jiao, L. Evolving deep convolutional neural networks by quantum behaved particle swarm optimization with binary encoding for image classification. Neurocomputing 2019, 362, 156–165. [Google Scholar] [CrossRef]
- Tan, T.Y.; Zhang, L.; Lim, C.P. Adaptive melanoma diagnosis using evolving clustering, ensemble and deep neural networks. Knowl.-Based Syst. 2020, 187, 104807. [Google Scholar] [CrossRef]
- Rosa, G.; Papa, J.; Marana, A.; Scheirer, W.; Cox, D. Fine-tuning convolutional neural networks using harmony search. In Proceedings of the Iberoamerican Congress on Pattern Recognition, Montevideo, Uruguay, 9–12 November 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 683–690. [Google Scholar]
- Khalifa, M.H.; Ammar, M.; Ouarda, W.; Alimi, A.M. Particle swarm optimization for deep learning of convolution neural network. In Proceedings of the 2017 Sudan Conference on Computer Science and Information Technology (SCCSIT), Khartoum, Sudan, 17–19 November 2017; pp. 1–5. [Google Scholar]
- Ororbia, A.; ElSaid, A.; Desell, T. Investigating recurrent neural network memory structures using neuro-evolution. In Proceedings of the Genetic and Evolutionary Computation Conference, Prague, Czech Republic, 13–17 July 2019; pp. 446–455. [Google Scholar]
- Bayer, J.; Wierstra, D.; Togelius, J.; Schmidhuber, J. Evolving memory cell structures for sequence learning. In Proceedings of the International Conference on Artificial Neural Networks, Limassol, Cyprus, 14–17 September 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 755–764. [Google Scholar]
- Rawal, A.; Miikkulainen, R. Evolving deep LSTM-based memory networks using an information maximization objective. In Proceedings of the Genetic and Evolutionary Computation Conference 2016, Denver, CO, USA, 20–24 July 2016; pp. 501–508. [Google Scholar]
- Chandra, R.; Chand, S. Evaluation of co-evolutionary neural network architectures for time series prediction with mobile alication in finance. Appl. Soft Comput. 2016, 49, 462–473. [Google Scholar] [CrossRef]
- Desell, T.; Clachar, S.; Higgins, J.; Wild, B. Evolving deep recurrent neural networks using ant colony optimization. In Proceedings of the European Conference on Evolutionary Computation in Combinatorial Optimization, Copenhagen, Denmark, 8–10 April 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 86–98. [Google Scholar]
- ElSaid, A.; Jamiy, F.E.; Higgins, J.; Wild, B.; Desell, T. Using ant colony optimization to optimize long short-term memory recurrent neural networks. In Proceedings of the Genetic and Evolutionary Computation Conference, Kyoto, Japan, 15–19 July 2018; pp. 13–20. [Google Scholar]
- Shi, B.; Bai, X.; Yao, C. An end-to-end trainable neural network for image-based sequence recognition and its alication to scene text recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 2298–2304. [Google Scholar] [CrossRef] [Green Version]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Glover, F. Future paths for integer programming and links to artificial intelligence. Comput. Oper. Res. 1986, 13, 533–549. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Ketkar, N. Introduction to pytorch. In Deep Learning with Python; Springer: Berlin/Heidelberg, Germany, 2017; pp. 195–208. [Google Scholar]
- El Abed, H.; Margner, V. The IFN/ENIT-database-a tool to develop Arabic handwriting recognition systems. In Proceedings of the 2007 9th International Symposium on Signal Processing and Its Alications, Sharjah, United Arab Emirates, 12–15 February 2007; pp. 1–4. [Google Scholar]
- Pechwitz, M.; Maddouri, S.S.; Märgner, V.; Ellouze, N.; Amiri, H. IFN/ENIT-database of handwritten Arabic words. In Proceedings of the CIFED, Hammamet, Tunisia, 21–23 October 2002; Citeseer: Princeton, NJ, USA, 2002; pp. 127–136. [Google Scholar]
- Yan, R.; Peng, L.; Xiao, S.; Johnson, M.T.; Wang, S. Dynamic temporal residual network for sequence modeling. Int. J. Doc. Anal. Recogn. 2019, 22, 235–246. [Google Scholar] [CrossRef]
- Yousefi, M.R.; Soheili, M.R.; Breuel, T.M.; Stricker, D. A comparison of 1D and 2D LSTM architectures for the recognition of handwritten Arabic. In Proceedings of the Document Recognition and Retrieval XXII, International Society for Optics and Photonics, San Francisco, CA, USA, 11–12 February 2015; p. 94020H. [Google Scholar]
- Maalej, R.; Kherallah, M. Improving MDLSTM for offline Arabic handwriting recognition using dropout at different positions. In Proceedings of the International Conference on Artificial Neural Networks, Vancouver, BC, Canada, 24–29 July 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 431–438. [Google Scholar]
- Elleuch, M.; Kherallah, M. Boosting of deep convolutional architectures for Arabic handwriting recognition. Int. J. Multimed. Data Eng. Manag. 2019, 10, 26–45. [Google Scholar] [CrossRef]
- Khémiri, A.; Echi, A.K.; Elloumi, M. Bayesian versus convolutional networks for Arabic handwriting recognition. Arab. J. Sci. Eng. 2019, 44, 9301–9319. [Google Scholar] [CrossRef]
- Maalej, R.; Kherallah, M. Maxout into MDLSTM for offline Arabic handwriting recognition. In Proceedings of the International Conference on Neural Information Processing, Sydney, Australia, 12–15 December 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 534–545. [Google Scholar]
- Eltay, M.; Zidouri, A.; Ahmad, I. Exploring deep learning aroaches to recognize handwritten arabic texts. IEEE Access 2020, 8, 89882–89898. [Google Scholar] [CrossRef]

| Decision Variable Sectors | Total Decision Variable Bits for Each Sector | Hyperparameters | No. of Bits for Each Hyperparameter |
|---|---|---|---|
| General parameters | 10 bits | Bs (batch size) | 2 |
| Op (optimizer) | 1 | ||
| Lr (learning rate) | 3 | ||
| Nc (number of convolution layers) | 2 | ||
| Nr (number of LSTM layers) | 2 | ||
| Convolution layer parameters × 7 | 11 bits × 7 layers = 77 bits | Ck (number of kernels) | 3 |
| Cs (kernel size) | 3 | ||
| Cb (batch normalization) | 1 | ||
| Ca (activation function) | 1 | ||
| Cp (pooling size) | 2 | ||
| Cr (skip connection or not) | 1 | ||
| Recurrent network parameters × 4 | 3 bits × 4 layers = 12 bits | Rh (size of hidden layer) | 2 |
| Rb (bidirectional) | 1 |
| No. | Recognizer Model | CER | WER |
|---|---|---|---|
| 1. | [32] | 3.72 | 6.69 |
| 2. | [33] | 4.80 | 9.30 |
| 3. | [34] | 4.70 | 8.22 |
| 4. | [35] | 6.34 | 16.19 |
| 3.50 | 9.30 | ||
| 5. | [36] | 11.08 | 22.86 |
| 4.88 | 12.61 | ||
| 6. | [37] | 3.30 Parzival | No |
| 7. | [40] | 4.27 | 8.36 |
| 8. | [41] | 8.5 | -- |
| 9. | Proposed method | 3.40 | 6.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
AL-Saffar, A.; Awang, S.; AL-Saiagh, W.; AL-Khaleefa, A.S.; Abed, S.A. A Sequential Handwriting Recognition Model Based on a Dynamically Configurable CRNN. Sensors 2021, 21, 7306. https://doi.org/10.3390/s21217306
AL-Saffar A, Awang S, AL-Saiagh W, AL-Khaleefa AS, Abed SA. A Sequential Handwriting Recognition Model Based on a Dynamically Configurable CRNN. Sensors. 2021; 21(21):7306. https://doi.org/10.3390/s21217306
Chicago/Turabian StyleAL-Saffar, Ahmed, Suryanti Awang, Wafaa AL-Saiagh, Ahmed Salih AL-Khaleefa, and Saad Adnan Abed. 2021. "A Sequential Handwriting Recognition Model Based on a Dynamically Configurable CRNN" Sensors 21, no. 21: 7306. https://doi.org/10.3390/s21217306
APA StyleAL-Saffar, A., Awang, S., AL-Saiagh, W., AL-Khaleefa, A. S., & Abed, S. A. (2021). A Sequential Handwriting Recognition Model Based on a Dynamically Configurable CRNN. Sensors, 21(21), 7306. https://doi.org/10.3390/s21217306






