Low-Cost Polyethylene Terephthalate Fluidic Sensor for Ultrahigh Accuracy Measurement of Liquid Concentration Variation
Abstract
:1. Introduction
2. Sensing Principles and Birefringent Fluidic Sensor
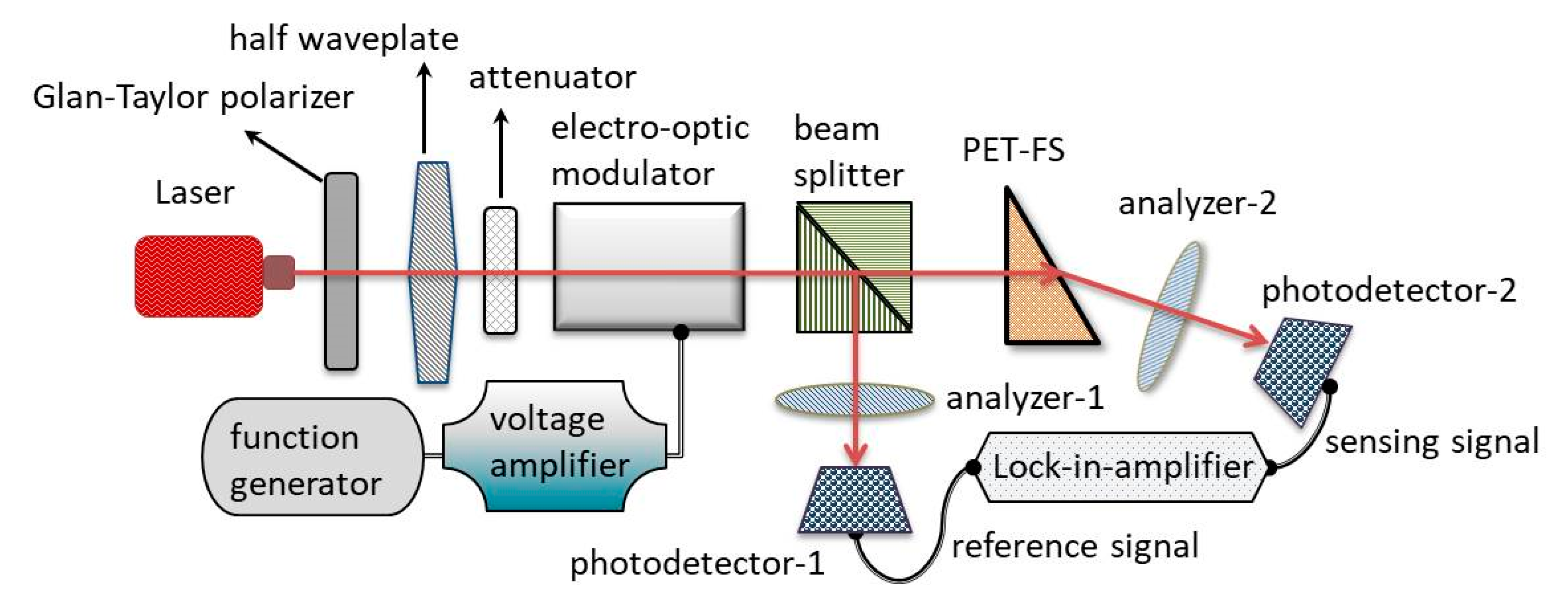
3. Measurement Setup
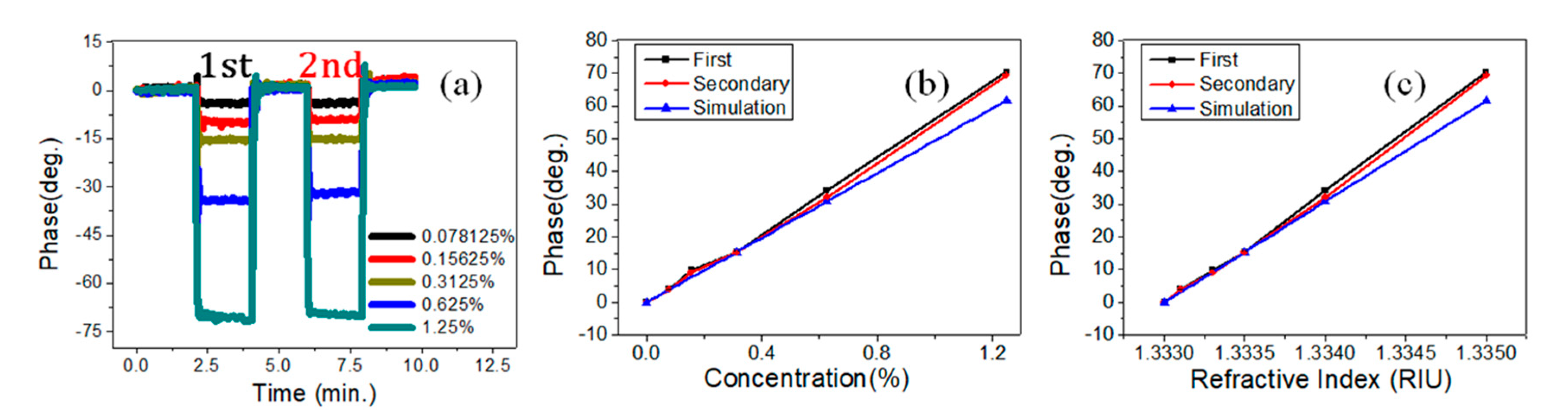
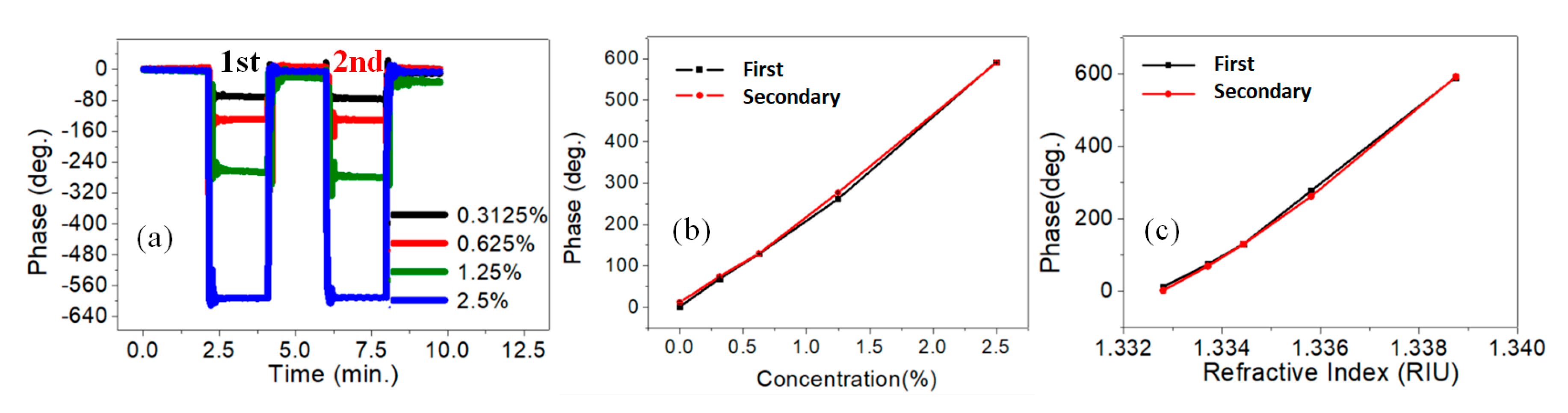
4. Results and Discussions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ling, H.; Chen, R.; Huang, Q.; Shen, F.; Wang, Y.; Wang, X. Transparent, flexible and recyclable nanopaper-based touch sensors fabricated via inkjet-printing. Green Chem. 2020, 22, 3208–3215. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, W.; Cheng, H.-M.; Silva, S.R.P. Critical review of recent progress of flexible perovskite solar cells. Mater. Today 2020, 39, 66–88. [Google Scholar] [CrossRef]
- Endo, T.; Ozawa, S.; Okuda, N.; Yanagida, Y.; Tanaka, S.; Hatsuzawa, T. Reflectometric detection of influenza virus in human saliva using nanoimprint lithography-based flexible two-dimensional photonic crystal biosensor. Sensor. Actuat. B—Chem. 2010, 148, 269–276. [Google Scholar] [CrossRef]
- Wang, M.; Hiltunen, J.; Liedert, C.; Pearce, S.; Charlton, M.; Hakalahti, L.; Karioja, P.; Myllylä, R. Highly sensitive biosensor based on UV imprinted layered polymeric–inorganic composite waveguides. Opt. Express 2012, 20, 20309–20317. [Google Scholar] [CrossRef]
- Hu, J.; Li, L.; Lin, H.; Zhang, P.; Zhou, W.; Ma, Z. Flexible integrated photonics: Where materials, mechanics and optics meet. Opt. Mater. Express 2013, 3, 1313–1331. [Google Scholar] [CrossRef]
- Chen, G.-Y.; Sun, J.-S. Design of flexible printed antenna. Electron. Lett. 2004, 40, 1034–1035. [Google Scholar] [CrossRef]
- Aikio, S.; Hiltunen, J.; Hiitola-Keinänen, J.; Hiltunen, M.; Kontturi, V.; Siitonen, S.; Karioja, P. Disposable photonic integrated circuits for evanescent wave sensors by ultra-high volume roll-to-roll method. Opt. Express 2016, 24, 2527–2541. [Google Scholar] [CrossRef]
- Hong, N.; Synowicki, R.A.; Hilfiker, J.N. Mueller matrix characterization of flexible plastic substrates. Appl. Surf. Sci. 2017, 421, 518–528. [Google Scholar] [CrossRef]
- Lim, J.-G.; Kwak, K.; Song, J.-K. Computation of refractive index and optical retardation in stretched polymer films. Opt. Express 2017, 25, 16409–16418. [Google Scholar] [CrossRef] [PubMed]
- Hsu, J.; Li, P. Direct deflection radius measurement of flexible PET substrates by using an optical interferometry. Appl. Opt. 2015, 54, 5469–5474. [Google Scholar] [CrossRef] [PubMed]
- Edmund Optics Inc. Available online: http://www.edmundoptics.com/ (accessed on 7 October 2021).
- ZEON Corporation. Available online: https://www.zeon.co.jp/en/business/enterprise/plastic/film/ (accessed on 7 October 2021).
- Choi, Y.; Jang, H.; Byun, D.; Ko, D.-H. Selective chemical wet etching of Si1-xGex versus Si in single-layer and multi-layer with HNO3/HF mixtures. Thin Solid Film. 2020, 709, 138230. [Google Scholar] [CrossRef]
- Vaisala Corporation. Available online: https://www.vaisala.com/en/industrial-measurements/products/liquid-concentration (accessed on 7 October 2021).
- Rosemount Analytical Inc. Available online: http://www.RosemountAnalytical.com (accessed on 7 October 2021).
- Ebrahimi, A.; Scott, J.; Ghorbani, K. Microwave reflective biosensor for glucose level detection in aqueous solutions. Sens. Actuators A Phys. 2020, 301, 111662. [Google Scholar] [CrossRef]
- Schäfer, R.; Carlson, J.E.; Hauptmann, P. Ultrasonic concentration measurement of aqueous solutions using PLS regression. Ultrasonics 2006, 44, e947–e950. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiménez-Márquez, F.; Vázquez, J.; Úbeda, J.; Sánchez-Rojas, J.L. Temperature dependence of grape must refractive index and its application to winemaking monitoring. Sens. Actuators B Chem. 2016, 225, 121–127. [Google Scholar] [CrossRef]
- Xu, M.; Ren, J.; Miao, R.; Zhang, Z. Nonintrusive measurement of the liquid refractive index by using properties of the cuvette wall. Appl. Opt. 2016, 55, 8101–8106. [Google Scholar] [CrossRef] [PubMed]
- Calixto, S.; Martinez-Ponce, G.; Garnica, G.; Figueroa-Gerstenmaier, S. A wavefront division polarimeter for the measurements of solute concentrations in solutions. Sensors 2017, 17, 2844. [Google Scholar] [CrossRef] [Green Version]
- Twu, R.-C.; Wang, C.-S. A Birefringent-refraction transducer for measuring angular displacement based on heterodyne interferometry. Appl. Sci. 2016, 6, 208. [Google Scholar] [CrossRef] [Green Version]
- Twu, R.-C.; Yan, N.-Y. Birefringence angle sensor for optical displacement measurements. Sens. Actuators A Phys. 2017, 267, 272–277. [Google Scholar] [CrossRef]
- Xu, S.; Chang, W.; Zhang, Y.; Yuan, X.; Huang, Y.; Ren, X. Ultrasensitive enhanced fabrication-tolerance refractometer based on PANDA-air-hole microfiber at the birefringent dispersion turning point. Opt. Express 2021, 29, 3694–3707. [Google Scholar] [CrossRef]
- Pinet, E.; Dube, S.; Vachon-Savary, M.; Cote, J.-S.; Poliquin, M. Sensitive chemical optic sensor using birefringent porous glass for the detection of volatile organic compounds. IEEE Sens. J. 2006, 6, 854–860. [Google Scholar] [CrossRef]
- Wang, I.-T.; Lee, Y.-H.; Chuang, E.-Y.; Hsiao, Y.-C. Sensitive, Color-indicating and labeling-free multi-detection cholesteric liquid crystal biosensing chips for detecting albumin. Polymers 2021, 13, 1463. [Google Scholar] [CrossRef] [PubMed]
- Hsieh, M.-C.; Liao, C.-H.; Lin, J.-Y. Optical relative humidity sensor based on a polyvinyl alcohol film and a phase-enhancement total-internal-reflection heterodyne interferometer. Sens. Actuators A Phys. 2020, 316, 112412. [Google Scholar] [CrossRef]
- Lee, J.-Y.; Su, D.-C. Improved common-path optical heterodyne interferometer for measuring small optical rotation angle of chiral medium. Opt. Commun. 2005, 256, 337–341. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Twu, R.-C.; Li, K.-H.; Lin, B.-L. Low-Cost Polyethylene Terephthalate Fluidic Sensor for Ultrahigh Accuracy Measurement of Liquid Concentration Variation. Sensors 2021, 21, 7410. https://doi.org/10.3390/s21217410
Twu R-C, Li K-H, Lin B-L. Low-Cost Polyethylene Terephthalate Fluidic Sensor for Ultrahigh Accuracy Measurement of Liquid Concentration Variation. Sensors. 2021; 21(21):7410. https://doi.org/10.3390/s21217410
Chicago/Turabian StyleTwu, Ruey-Ching, Kai-Hsuan Li, and Bo-Lin Lin. 2021. "Low-Cost Polyethylene Terephthalate Fluidic Sensor for Ultrahigh Accuracy Measurement of Liquid Concentration Variation" Sensors 21, no. 21: 7410. https://doi.org/10.3390/s21217410
APA StyleTwu, R.-C., Li, K.-H., & Lin, B.-L. (2021). Low-Cost Polyethylene Terephthalate Fluidic Sensor for Ultrahigh Accuracy Measurement of Liquid Concentration Variation. Sensors, 21(21), 7410. https://doi.org/10.3390/s21217410





