Micromechanical Force Sensor Using the Stress–Impedance Effect of Soft Magnetic FeCuNbSiB
Abstract
:1. Introduction
2. Materials and Methods
2.1. Investigation of the Properties of FeCuNbSiB
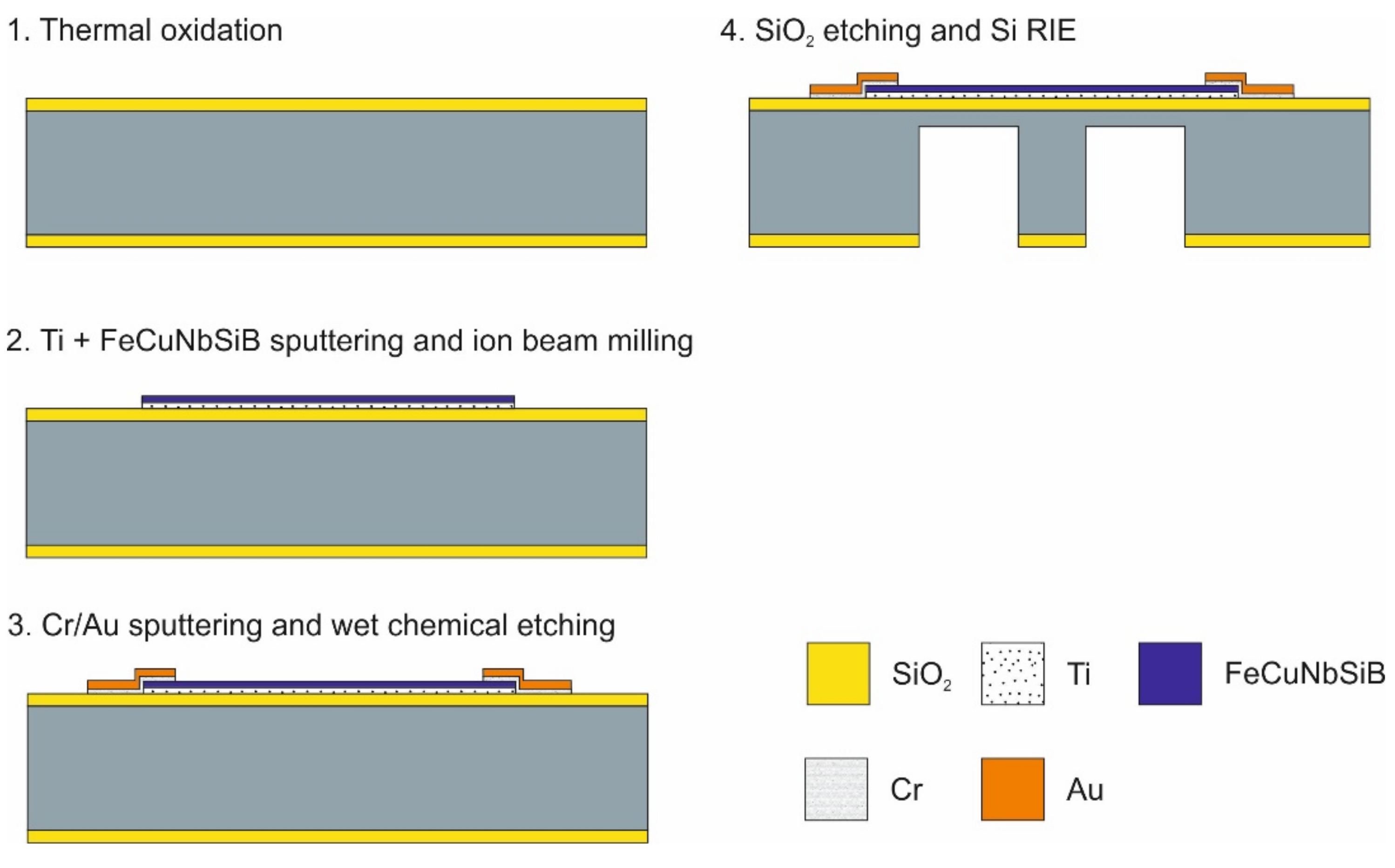
2.2. Fabrication of the Force Sensor Using FeCuNbSiB as Transducer
3. Results
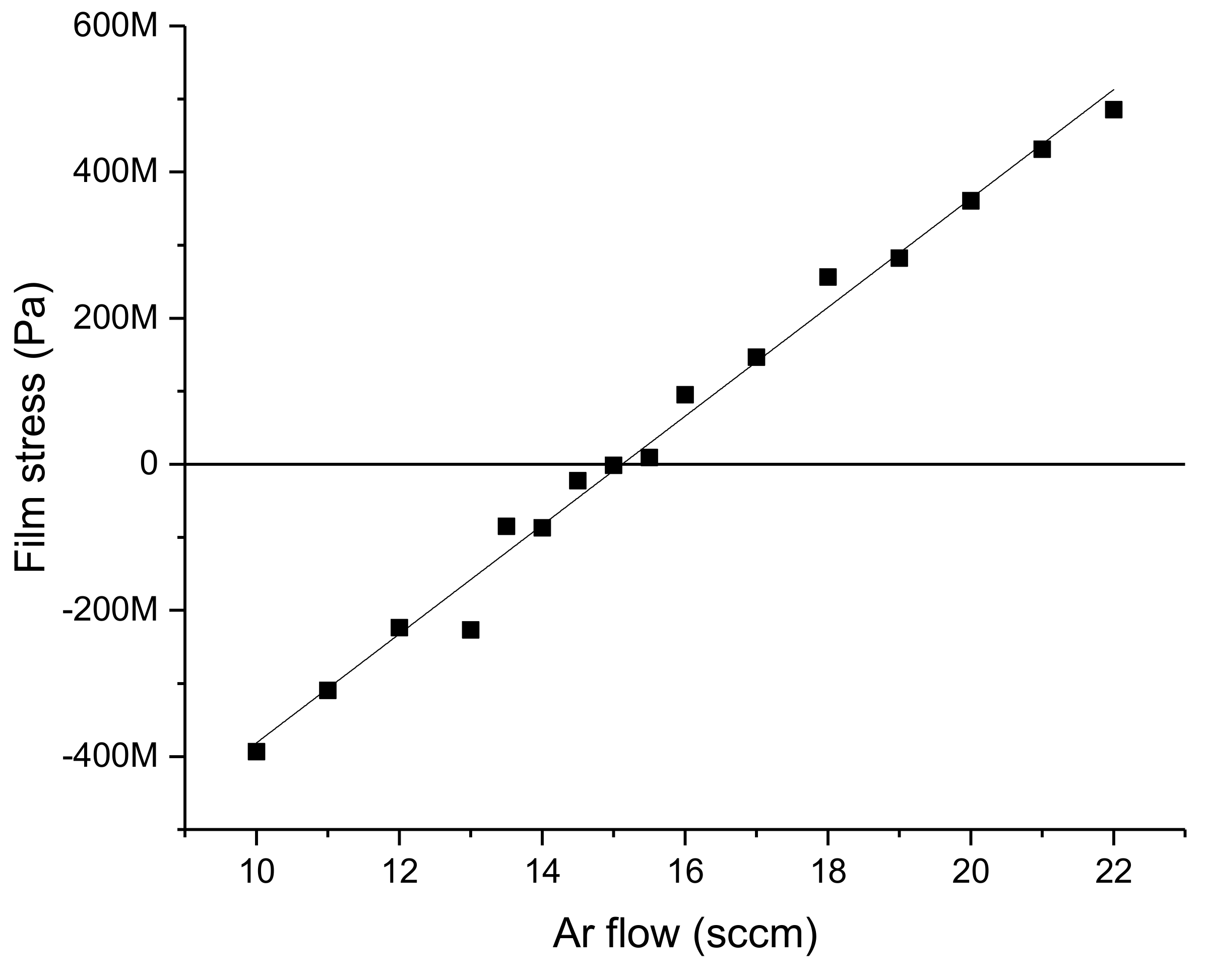
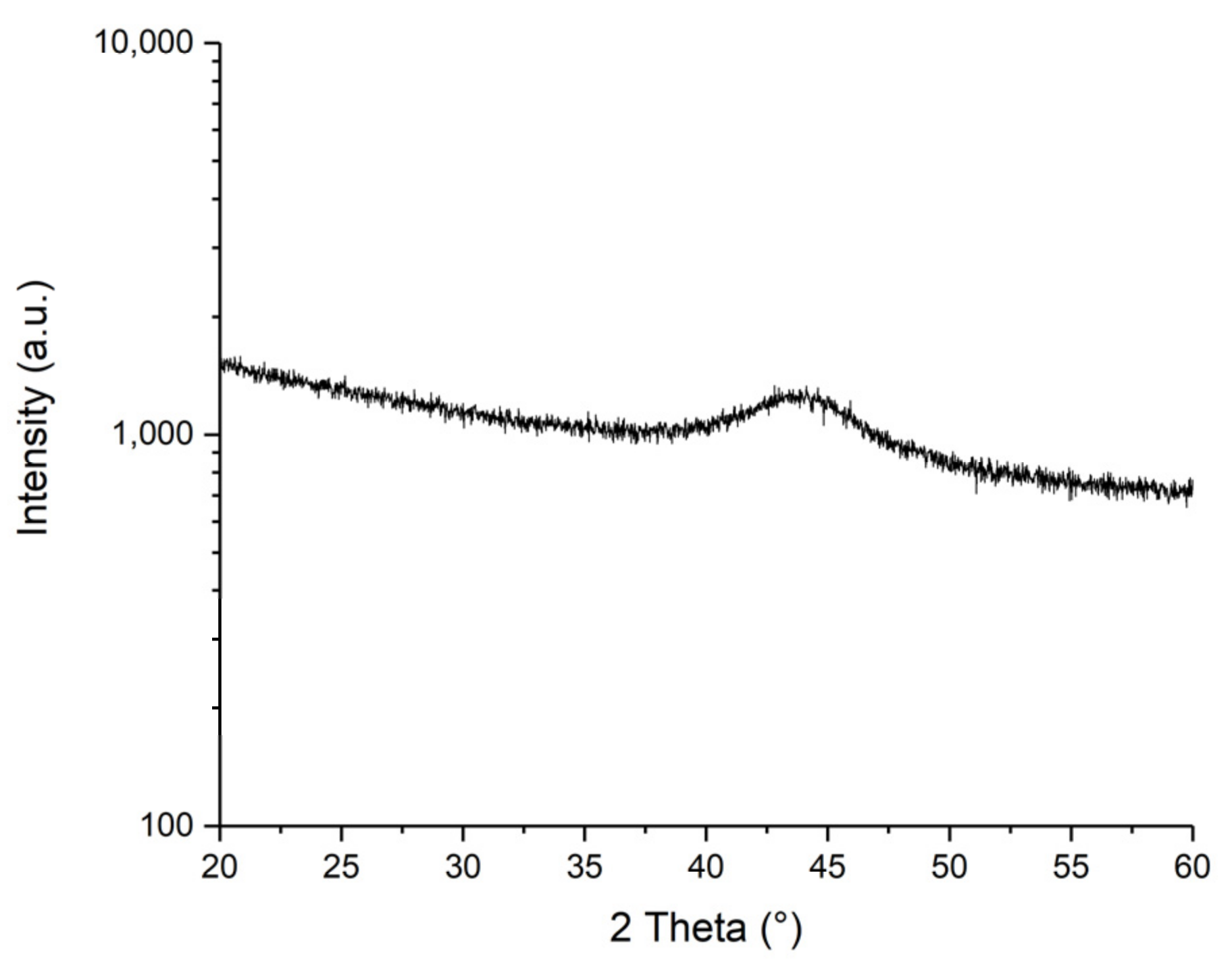
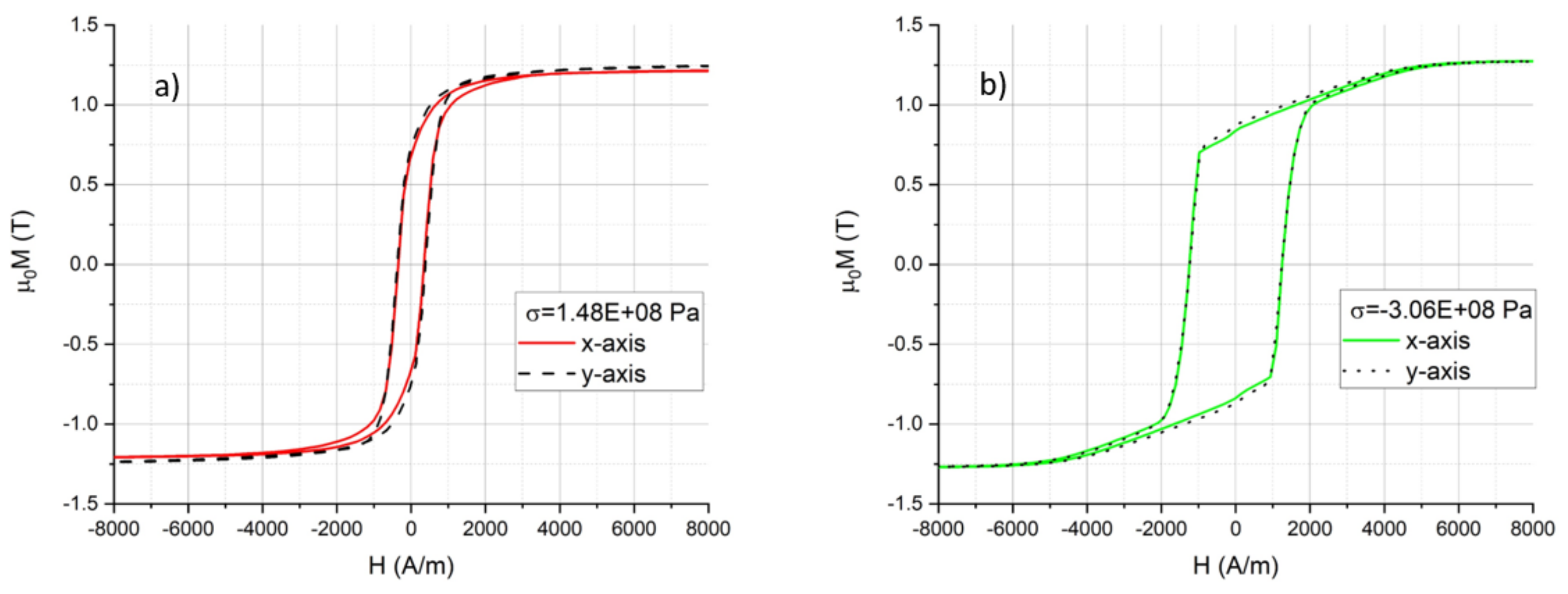
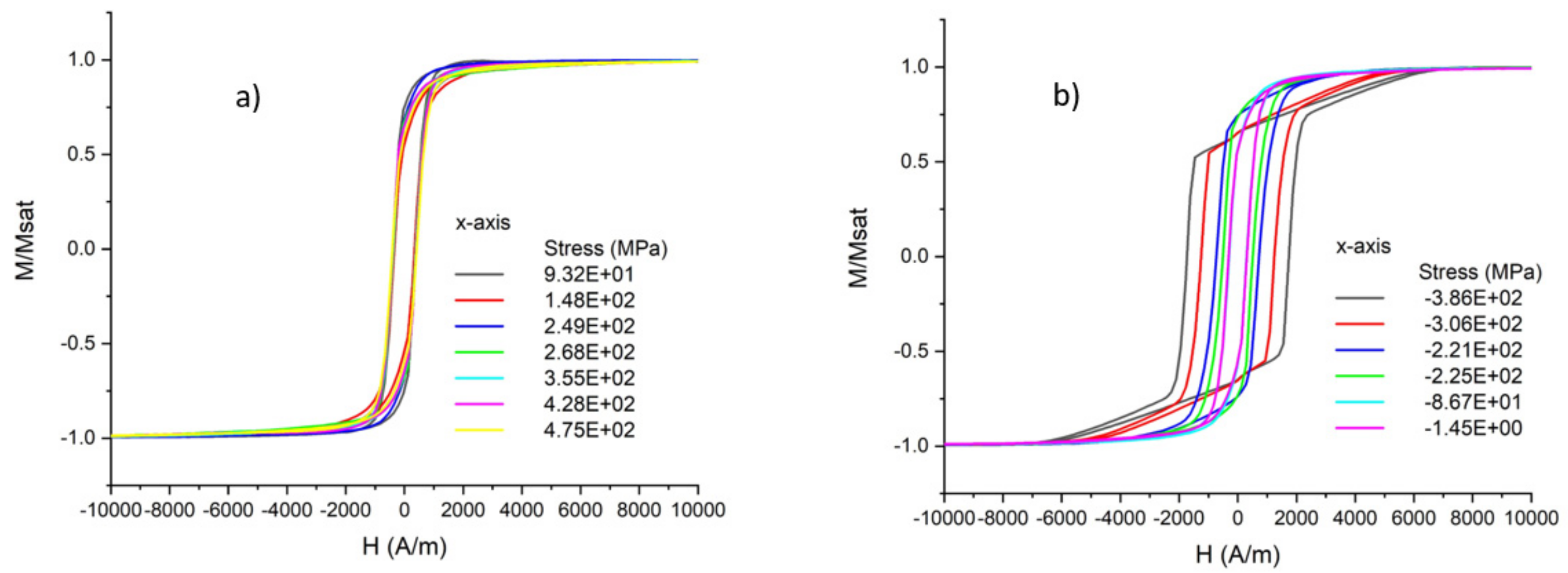
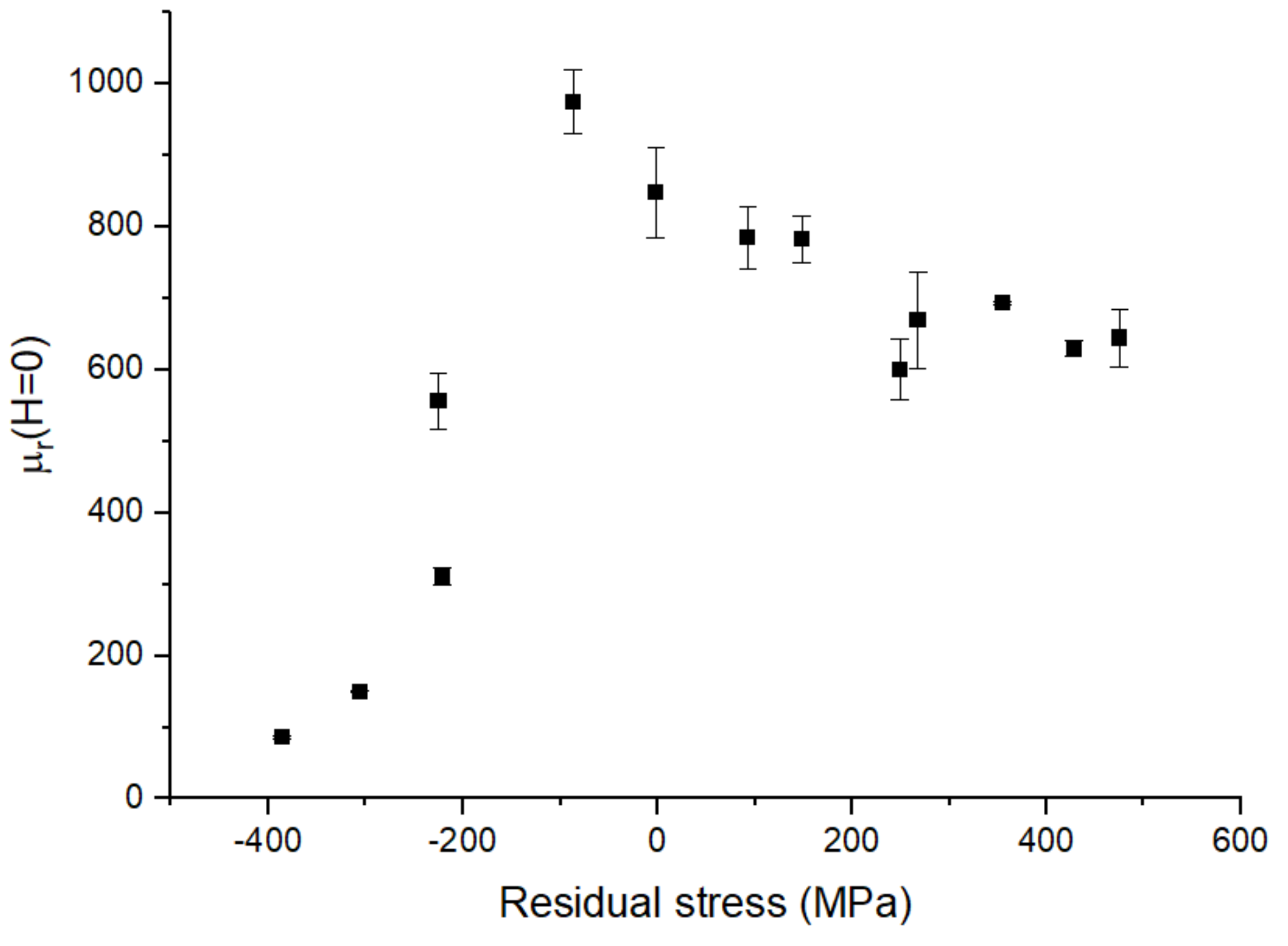
3.1. Investigation of the Properties of FeCuNbSiB
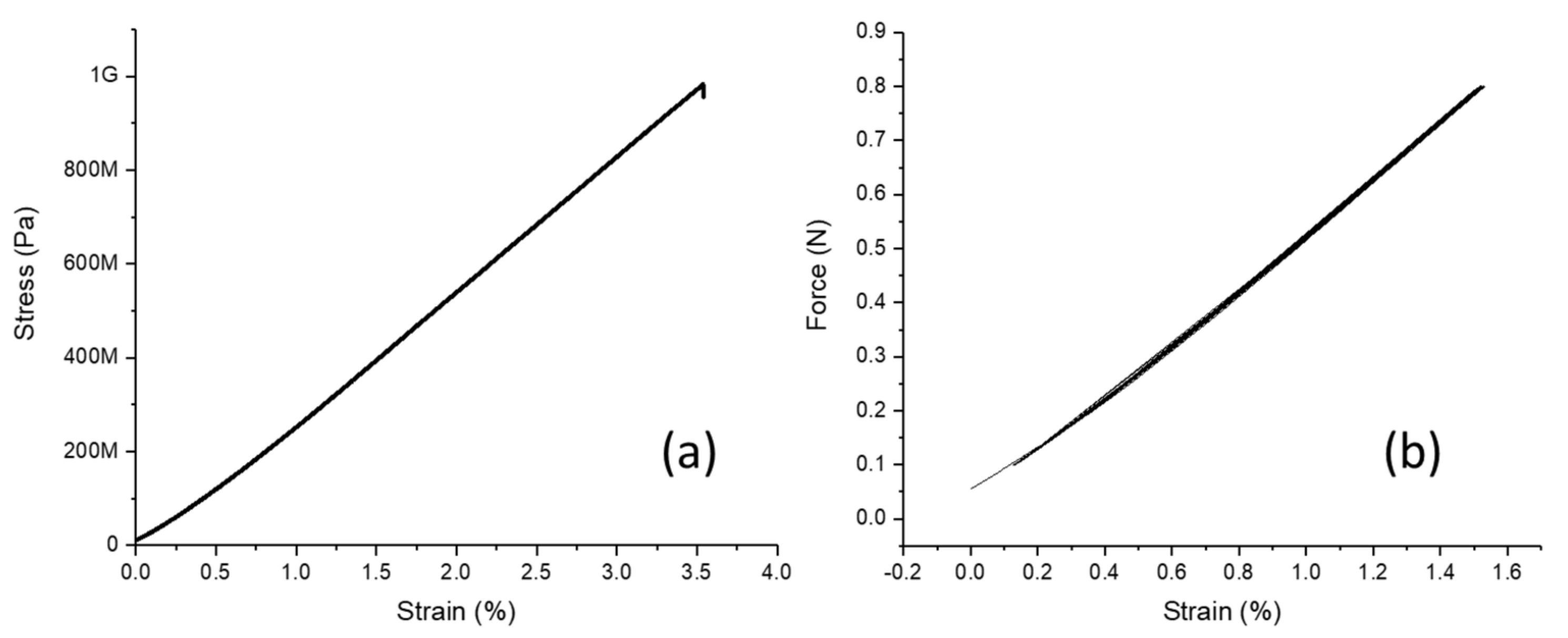
3.2. Characterization of the SI Force Sensor
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kappassov, Z.; Corrales, J.A.; Perdereau, V. Tactile sensing in dexterous robot hands—Review. Rob. Auton. Syst. 2015, 74, 195–220. [Google Scholar] [CrossRef] [Green Version]
- Asano, S.; Muroyama, M.; Nakayama, T.; Hata, Y.; Nonomura, Y.; Tanaka, S. 3-Axis Fully-Integrated Capacitive Tactile Sensor with Flip-Bonded CMOS on LTCC Interposer. Sensors 2017, 17, 2451. [Google Scholar] [CrossRef]
- Lee, H.K.; Chung, J.; Chang, S.I.; Yoon, E. Normal and shear force measurement using a flexible polymer tactile sensor with embedded multiple capacitors. J. Microelectromech. Syst. 2008, 17, 934–942. [Google Scholar] [CrossRef]
- Cutkosky, M.R.; Ulmen, J. Dynamic tactile sensing. In The Human Hand as an Inspiration for Robot Hand Development; Springer Tracts in Advanced Robotics; Springer: Cham, Switzerland, 2014; Volume 95, pp. 389–403. [Google Scholar]
- Seminara, L.; Capurro, M.; Cirillo, P.; Cannata, G.; Valle, M. Electromechanical characterization of piezoelectric PVDF polymer films for tactile sensors in robotics applications. Sens. Actuators A Phys. 2011, 169, 49–58. [Google Scholar] [CrossRef]
- Fraden, J. Handbook of Modern Sensors; Springer: New York, NY, USA, 2010. [Google Scholar]
- Yussof, H.; Ohka, M.; Suzuki, H.; Morisawa, N. Tactile sensing-based control system for dexterous robot manipulation. In Advances in Computational Algorithms and Data Analysis; Lecture Notes in Electrical Engineering; Springer: Dordrecht, The Netherlands, 2009; Volume 14, pp. 199–213. [Google Scholar]
- Villari, E. Ueber die Aenderungen des magnetischen Moments, welche der Zug und das Hindurchleiten eines galvanischen Stroms in einem Stabe von Stahl oder Eisen hervorbringen. Ann. Phys. Chem. 1865, 202, 87–122. [Google Scholar] [CrossRef] [Green Version]
- Harrison, E.P.; Rowe, H. An impedance magnetometer. Proc. Phys. Soc. 1938, 50, 176. [Google Scholar] [CrossRef]
- Lamb, H. XIII. On electrical motions in a spherical conductor. Philos. Trans. R. Soc. Lond. 1883, 174, 519–549. [Google Scholar] [CrossRef]
- Kaviraj, B.; Ghatak, S.K. Simulation of stress-impedance effects in low magnetostrictive films. J. Non-Cryst. Solids 2007, 353, 1515–1520. [Google Scholar] [CrossRef]
- Sablik, M.J.; Kwun, H.; Burkhardt, G.L.; Jiles, D.C. Model for the effect of tensile and compressive stress on ferromagnetic hysteresis. J. Appl. Phys. 1987, 61, 3799–3801. [Google Scholar] [CrossRef]
- Bieńkowski, A.; Kulikowski, J. Effect of stresses on the magnetostriction of Ni-Zn(Co) ferrites. J. Magn. Magn. Mater. 1991, 101, 122–124. [Google Scholar] [CrossRef]
- Yu, J.; Zhou, Y.; Cai, B.; Xu, D. Giant magneto-impedance effect in amorphous magnetostrictive FeSiB thin films. J. Magn. Magn. Mater. 2000, 213, 32–36. [Google Scholar] [CrossRef]
- Panina, L.V.; Mohri, K. Mechanism of the Magneto-Impedance Effect in Negative Magnetostrictive Amorphous Wires. IEEE Transl. J. Magn. Jpn. 1994, 9, 34–39. [Google Scholar] [CrossRef]
- Squire, P.T.; Atkinson, D.; Gibbs, M.R.J.; Atalay, S. Amorphous wires and their applications. J. Magn. Magn. Mater. 1994, 132, 10–21. [Google Scholar] [CrossRef]
- Machado, F.L.A.; Martins, C.S.; Rezende, S.M. Giant magnetoimpedance in the ferromagnetic alloy Co75-xFexSi15B10. Phys. Rev. B 1995, 51, 3926–3929. [Google Scholar] [CrossRef]
- Shen, L.P.; Uchiyama, T.; Mohri, K.; Kita, E.; Bushida, K. Sensitive stress-impedance micro sensor using amorphous magnetostrictive wire. IEEE Trans. Magn. 1997, 33, 3355–3357. [Google Scholar] [CrossRef]
- Mohri, K.; Uchiyama, T.; Shen, L.P.; Cai, C.M.; Panina, L.V.; Honkura, Y.; Yamamoto, M. Amorphous wire and CMOS IC-based sensitive micromagnetic sensors utilizing magnetoimpedance (MI) and stress-impedance (SI) effects. IEEE Trans. Magn. 2002, 38, 3063–3068. [Google Scholar] [CrossRef]
- Fosalau, C.; Damian, C.; Zet, C. A high performance strain gage based on the stressimpedance effect in magnetic amorphous wires. Sens. Actuators A Phys. 2013, 191, 105–110. [Google Scholar] [CrossRef]
- Tejedor, M.; Hernando, B.; Sánchez, M.; Prida, V.; Vázquez, M. Magneto-impedance effect in amorphous ribbons for stress sensor application. Sens. Actuators A Phys. 2000, 81, 98–101. [Google Scholar] [CrossRef]
- Garcia-Arribas, A.; Combarro, L.; Goiriena-Goikoetxea, M.; Kurlyandskaya, G.V.; Svalov, A.V.; Fernandez, E.; Orue, I.; Feuchtwanger, J. Thin-Film Magnetoimpedance Structures onto Flexible Substrates as Deformation Sensors. IEEE Trans. Magn. 2017, 53, 1–5. [Google Scholar] [CrossRef]
- Suwa, Y.; Agatsuma, S.; Hashi, S.; Ishiyama, K. Study on impedance change of strain sensor using magnetostrictive film. J. Magn. Soc. Jpn. 2010, 34, 342–346. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.A.; Ding, W.; Zhou, Y.; Cao, Y.; Zhou, Z.M.; Zhang, Y.M. Stress-impedance effects in sandwiched FeCuNbCrSiB/Cu/FeCuNbCrSiB films. Mater. Lett. 2006, 60, 2554–2557. [Google Scholar] [CrossRef]
- Zhou, Y.; Ding, W.; Mao, X.H.; Chen, J.A.; Zhang, Y.M.; Gao, X.Y. Stress-impedance effects in multilayered FeSiB/Cu/FeSiB films. Thin Solid Films 2005, 489, 177–180. [Google Scholar] [CrossRef]
- Vincent, J.D.S.; Rodrigues, M.; Leong, Z.; Morley, N.A. Design and Development of Magnetostrictive Actuators and Sensors for Structural Health Monitoring. Sensors 2020, 20, 711. [Google Scholar] [CrossRef] [Green Version]
- Froemel, J.; Akita, S.; Tanaka, S. Simple Device to Measure Pressure Using the Stress Impedance Effect of Amorphous Soft Magnetic Thin Film. Micromachines 2020, 11, 649. [Google Scholar] [CrossRef]
- Yamadera, H.; Nishibe, Y. Strain-impedance properties of a CoSiB/Cu/CoSiB layered film. J. Appl. Phys. 2000, 87, 5356–5358. [Google Scholar] [CrossRef]
- Mao, X.H.; Zhou, Y.; Chen, J.A.; Yu, J.Q.; Cai, B.C. Giant magnetoimpedance and stress-impedance effects in multilayered FeSiB/Cu/FeSiB films with a meander structure. J. Mater. Res. 2003, 18, 868–871. [Google Scholar] [CrossRef]
- Alben, R.; Becker, J.J.; Chi, M.C. Random anisotropy in amorphous ferromagnets. J. Appl. Phys. 1978, 49, 1653–1658. [Google Scholar] [CrossRef]
- Herzer, G. Grain Size Dependence of Coercivity and Permeability in Nanocrystalline Ferromagnets. IEEE Trans. Magn. 1990, 26, 1397–1402. [Google Scholar] [CrossRef]
- Sartorelli, M.L.; Knobel, M.; Schoenmaker, J.; Gutierrez, J.; Barandiarán, J.M. Giant magneto-impedance and its relaxation in Co-Fe-Si-B amorphous ribbons. Appl. Phys. Lett. 1997, 71, 2208–2210. [Google Scholar] [CrossRef] [Green Version]
- Marin, P.; Hernando, A. Applications of amorphous and nanocrystalline magnetic materials. J. Magn. Magn. Mater. 2000, 215, 729–734. [Google Scholar] [CrossRef]
- Prida, V.M.; Gorría, P.; Kurlyandskaya, G.V.; Sánchez, M.L.; Hernando, B.; Tejedor, M. Magneto-impedance effect in nanostructured soft ferromagnetic alloys. Nanotechnology 2003, 14, 231–238. [Google Scholar] [CrossRef]
- Stoney, G.G. The tension of metallic films deposited by electrolysis. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1909, 82, 172–175. [Google Scholar] [CrossRef] [Green Version]
- Leenaerts, D.; van der Tang, J.; Vaucher, C.S. Circuit Design for RF Transceivers; Springer US: Boston, MA, USA, 2001; ISBN 978-0-7923-7551-7. [Google Scholar]
- Garg, R.; Bahl, I.; Bozzi, M. Microstrip Lines and Slotlines, 3rd ed.; Artech House: London, UK, 2013; ISBN 978-0890067666. [Google Scholar]
- Yoshizawa, Y.; Oguma, S.; Yamauchi, K. New Fe-based soft magnetic alloys composed of ultrafine grain structure. J. Appl. Phys. 1988, 64, 6044–6046. [Google Scholar] [CrossRef]
- Livingston, J.D. Magnetomechanical properties of amorphous metals. Phys. Status Solidi 1982, 70, 591–596. [Google Scholar] [CrossRef]
- Shin, K.H.; Inoue, M.; Arai, K.I. Elastically coupled magneto-electric elements with highly magnetostrictive amorphous films and PZT substrates. Smart Mater. Struct. 2000, 9, 357–361. [Google Scholar] [CrossRef]
- Appino, C.; Fiorillo, F.; Maraner, A. Initial Susceptibility vs. Applied Stress in Amorphous Alloys with Positive and Negative Magnetostriction. IEEE Trans. Magn. 1993, 29, 3469–3471. [Google Scholar] [CrossRef]
- Saito, N.; Fujiwara, H.; Sugita, Y. A new type of magnetic domain structure in negative magnetostriction ni-fe films. J. Phys. Soc. Jpn. 1964, 19, 1116–1125. [Google Scholar] [CrossRef]
- Inoue, A.; Shen, B.L.; Chang, C.T. Fe- and Co-based bulk glassy alloys with ultrahigh strength of over 4000 MPa. Intermetallics 2006, 14, 936–944. [Google Scholar] [CrossRef]
- Javaid, S.; Hirano, H.; Tanaka, S.; Muroyama, M. Surface Covering Structure and Active Sensing with MEMS-CMOS Integrated 3-Axis Tactile Sensors for Object Slip Detection and Texture Recognition. In Proceedings of the 2021 21st International Conference on Solid-State Sensors, Actuators and Microsystems (Transducers), Orlando, FL, USA, 20–24 June 2021. [Google Scholar]
- Shao, C.; Hirano, H.; Miyaguchi, H.; Nomoto, M.; Muroyama, M.; Tanaka, S. Event-Driven Tactile Sensing System including 100 CMOS-MEMS Integrated 3-Axis Force Sensors Based on Asynchronous Serial Bus Communication. IEEE Sens. J. 2020, 20, 10159–10169. [Google Scholar] [CrossRef]
- Muroyama, M.; Hirano, H.; Shao, C.; Tanaka, S. Development of a real-time force and temperature sensing system with mems-lsi integrated tactile sensors for next-generation robots. J. Robot. Mechatron. 2020, 32, 323–332. [Google Scholar] [CrossRef]
- Muroyama, M.; Nakayama, T.; Hata, Y.; Tanaka, S. Multi-sensor platform LSI enabling different sensors to be event-driven and connected to common differental bus line. In Proceedings of the TRANSDUCERS 2017—19th International Conference on Solid-State Sensors, Actuators and Microsystems, Kaohsiung, Taiwan, 18–22 June 2017; Institute of Electrical and Electronics Engineers Inc.: Kaohsiung, Taiwan, 2017; pp. 1156–1159. [Google Scholar]






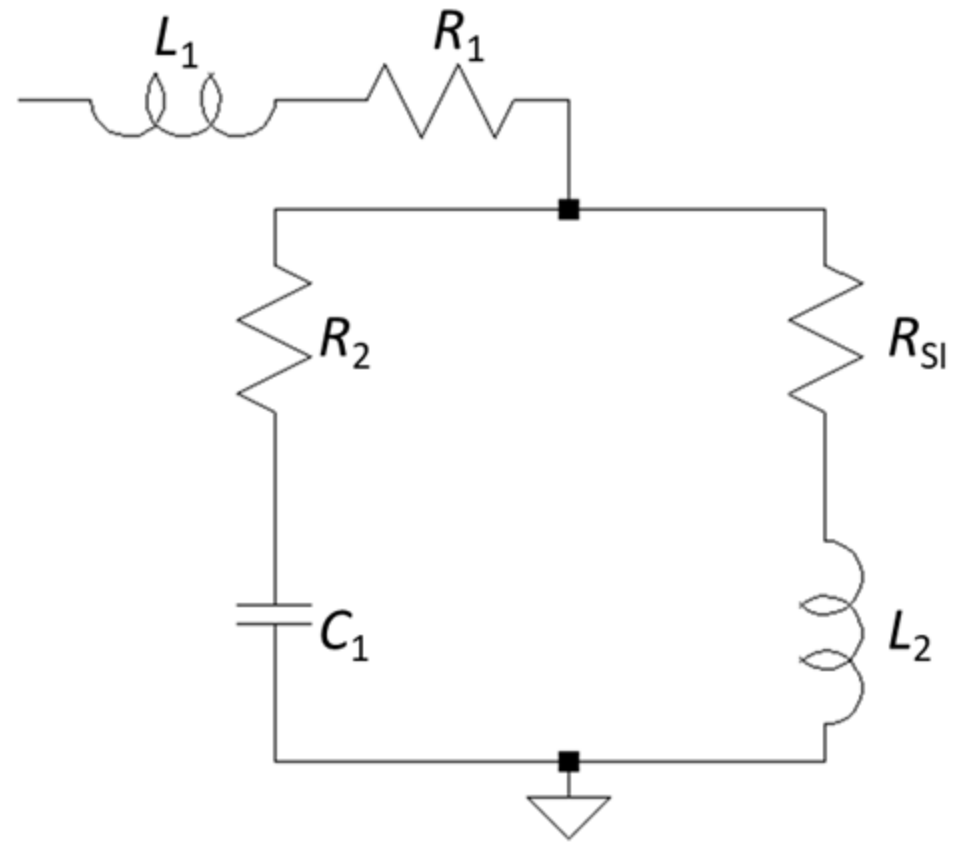
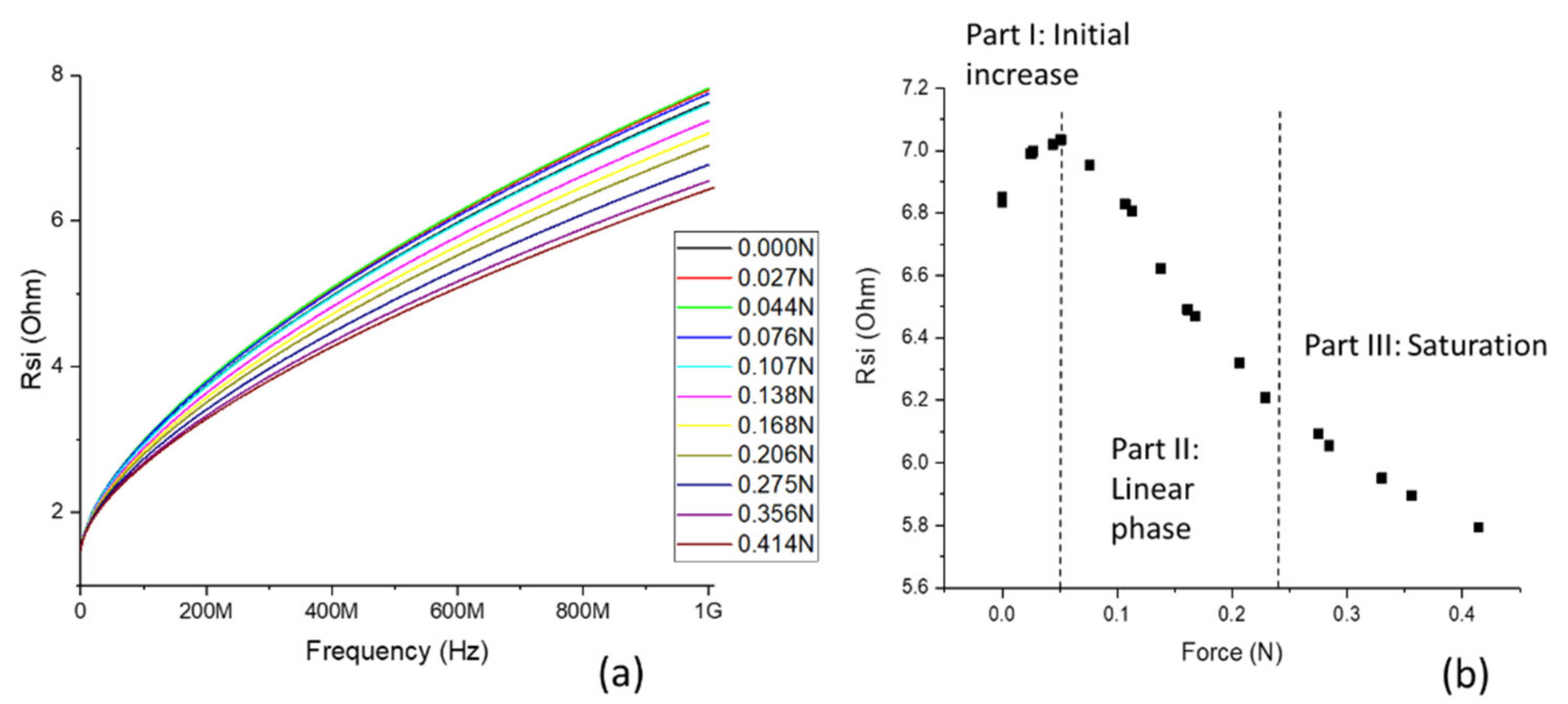
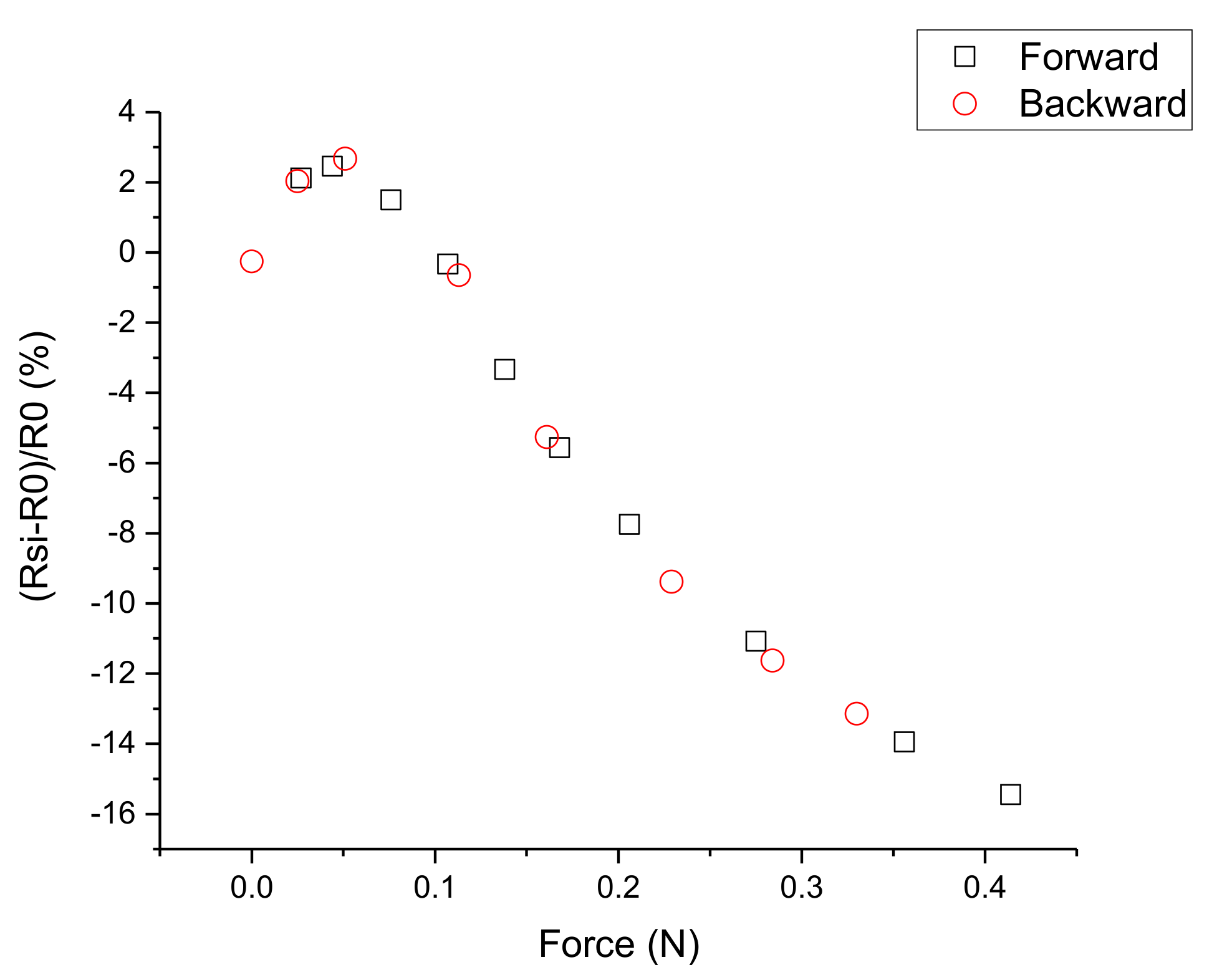
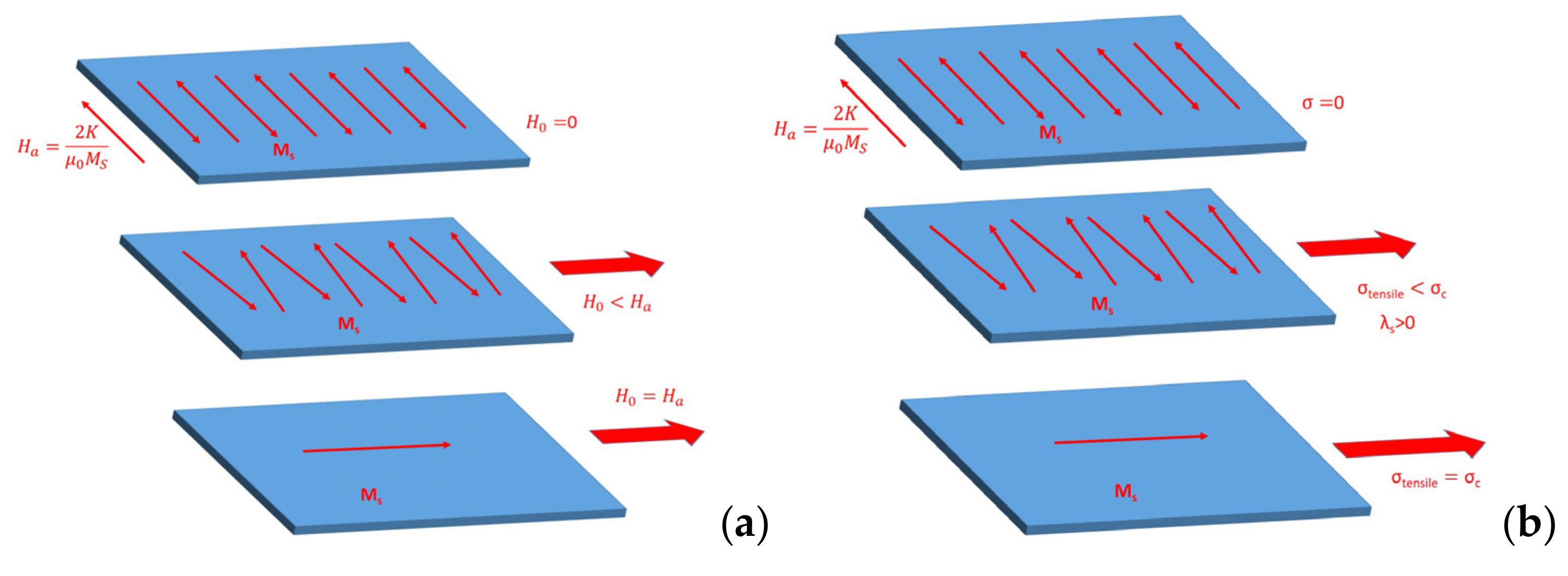
| Lumped Equivalent Circuit Element | Fitted Value |
|---|---|
| R1 | 3.98 Ω |
| R2 | 5.29 Ω |
| L1 | 1.73 nH |
| L2 | 2.87 nH |
| C1 | 2.26 pF |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Froemel, J.; Diguet, G.; Muroyama, M. Micromechanical Force Sensor Using the Stress–Impedance Effect of Soft Magnetic FeCuNbSiB. Sensors 2021, 21, 7578. https://doi.org/10.3390/s21227578
Froemel J, Diguet G, Muroyama M. Micromechanical Force Sensor Using the Stress–Impedance Effect of Soft Magnetic FeCuNbSiB. Sensors. 2021; 21(22):7578. https://doi.org/10.3390/s21227578
Chicago/Turabian StyleFroemel, Joerg, Gildas Diguet, and Masanori Muroyama. 2021. "Micromechanical Force Sensor Using the Stress–Impedance Effect of Soft Magnetic FeCuNbSiB" Sensors 21, no. 22: 7578. https://doi.org/10.3390/s21227578
APA StyleFroemel, J., Diguet, G., & Muroyama, M. (2021). Micromechanical Force Sensor Using the Stress–Impedance Effect of Soft Magnetic FeCuNbSiB. Sensors, 21(22), 7578. https://doi.org/10.3390/s21227578






