An Information-Theoretic Approach to Detect the Associations of GPS-Tracked Heifers in Pasture
Abstract
:1. Introduction
2. Materials and Methods
2.1. Animal Housing and Sensor Technology
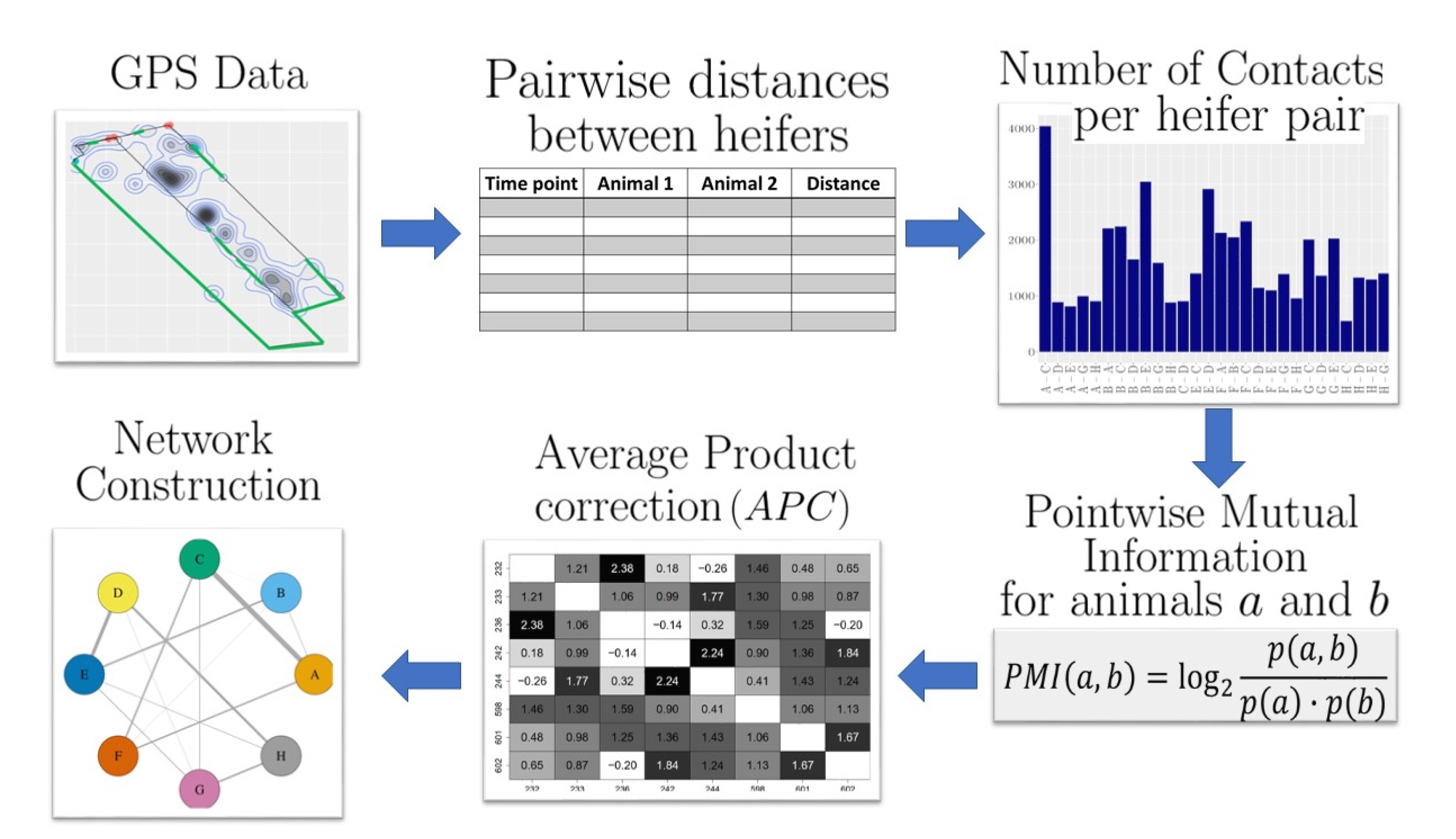
2.2. Social Network Construction
2.2.1. Pairwise Distances between Heifers
2.2.2. Contacts between Heifers
2.2.3. Pointwise Mutual Information
2.2.4. Average Product Correction
2.2.5. Network Construction
2.3. Validation of the Application
2.3.1. Influence Factors of Network Construction
2.3.2. Robustness
2.3.3. Comparison with Existing Methods
3. Results
3.1. Investigation of Animal Contacts
3.2. Investigation of Animal Activity
3.3. Investigation of the Method’s Robustness
3.4. Validation of APC Application
4. Discussion
4.1. Investigation of Different Distance Constraints
4.2. Investigation of Different Activities
4.3. Robustness and Validation
4.4. GNSS Technology
4.5. Association Measures of Animal Relationships
4.6. Heifer Social Associations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| APC | Average product correction |
| CEP | Circular error probability |
| DOP | Dilution of precision |
| GNSS | Global Navigation Satellite System |
| GPS | Global Positioning System |
| PMI | Pointwise mutual information |
| PPMI | Positive pointwise mutual information |
| RTK | Real-time kinematic |
| 2DRMS | Twice-distance root mean square |
Appendix A
Appendix A.1. Network Comparison of Different Distance Thresholds
| Dyad | 1 m | 1.5 m | 2.5 m | 5 m |
|---|---|---|---|---|
| A–C | x | x | x | x |
| A–H | x | |||
| B–A | x | x | x | x |
| B–C | x | x | x | x |
| B–E | x | x | x | x |
| D–E | x | x | x | x |
| D–G | x | x | x | x |
| D–H | x | x | x | x |
| F–A | x | x | x | x |
| F–B | x | x | x | x |
| F–C | x | x | x | x |
| F–H | x | x | ||
| G–C | x | x | x | |
| G–E | x | x | x | x |
| H–E | x | x | x | x |
| H–G | x | x | x | x |
Appendix A.2. Understanding of PMI and the APC Procedure by Example

References
- Farine, D.R.; Whitehead, H. Constructing, conducting and interpreting animal social network analysis. J. Anim. Ecol. 2015, 84, 1144–1163. [Google Scholar] [CrossRef] [Green Version]
- Koene, P.; Ipema, B. Social Networks and Welfare in Future Animal Management. Animals 2014, 4, 93–118. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wey, T.; Blumstein, D.T.; Shen, W.; Jordán, F. Social network analysis of animal behaviour: A promising tool for the study of sociality. Anim. Behav. 2008, 75, 333–344. [Google Scholar] [CrossRef]
- Chopra, K.; Hodges, H.R.; Barker, Z.E.; Vázquez Diosdado, J.A.; Amory, J.R.; Cameron, T.C.; Croft, D.P.; Bell, N.J.; Codling, E.A. Proximity Interactions in a Permanently Housed Dairy Herd: Network Structure, Consistency, and Individual Differences. Front. Vet. Sci. 2020, 7, 1040. [Google Scholar] [CrossRef]
- Vimalajeewa, D.; Balasubramaniam, S.; O’Brien, B.; Kulatunga, C.; Berry, D.P. Leveraging Social Network Analysis for Characterizing Cohesion of Human-Managed Animals. IEEE Trans. Comput. Soc. Syst. 2019, 6, 323–337. [Google Scholar] [CrossRef]
- Büttner, K.; Czycholl, I.; Mees, K.; Krieter, J. Social network analysis in pigs: Impacts of significant dyads on general network and centrality parameters. Animal 2019, 14, 1–11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Büttner, K.; Scheffler, K.; Czycholl, I.; Krieter, J. Social network analysis—Centrality parameters and individual network positions of agonistic behavior in pigs over three different age levels. Springerplus 2015, 4, 185. [Google Scholar] [CrossRef] [Green Version]
- Büttner, K.; Scheffler, K.; Czycholl, I.; Krieter, J. Network characteristics and development of social structure of agonistic behaviour in pigs across three repeated rehousing and mixing events. Appl. Anim. Behav. Sci. 2015, 168, 24–30. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Johnston, L.J.; Martin, W. Understanding Tail-Biting in Pigs through Social Network Analysis. Animals 2018, 8, 13. [Google Scholar] [CrossRef] [Green Version]
- de Freslon, I.; Martínez-López, B.; Belkhiria, J.; Strappini, A.; Monti, G. Use of social network analysis to improve the understanding of social behaviour in dairy cattle and its impact on disease transmission. Appl. Anim. Behav. Sci. 2019, 213, 47–54. [Google Scholar] [CrossRef]
- Chen, S.; Sanderson, M.W.; White, B.J.; Amrine, D.E.; Lanzas, C. Temporal-spatial heterogeneity in animal-environment contact: Implications for the exposure and transmission of pathogens. Sci. Rep. 2013, 3, 3112. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; White, B.J.; Sanderson, M.W.; Amrine, D.E.; Ilany, A.; Lanzas, C. Highly dynamic animal contact network and implications on disease transmission. Sci. Rep. 2014, 4, 4472. [Google Scholar] [CrossRef]
- Rocha, L.E.; Terenius, O.; Veissier, I.; Meunier, B.; Nielsen, P.P. Persistence of sociality in group dynamics of dairy cattle. Appl. Anim. Behav. Sci. 2020, 223, 104921. [Google Scholar] [CrossRef]
- Chen, S.; Ilany, A.; White, B.J.; Sanderson, M.W.; Lanzas, C. Spatial-Temporal Dynamics of High-Resolution Animal Networks: What Can We Learn from Domestic Animals? PLoS ONE 2015, 10, e0129253. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bolt, S.L.; Boyland, N.K.; Mlynski, D.T.; James, R.; Croft, D.P. Pair Housing of Dairy Calves and Age at Pairing: Effects on Weaning Stress, Health, Production and Social Networks. PLoS ONE 2017, 12, e0166926. [Google Scholar] [CrossRef] [PubMed]
- Gygax, L.; Neisen, G.; Wechsler, B. Socio-Spatial Relationships in Dairy Cows. Ethology 2010, 116, 10–23. [Google Scholar] [CrossRef]
- Boyland, N.K.; Mlynski, D.T.; James, R.; Brent, L.J.; Croft, D.P. The social network structure of a dynamic group of dairy cows: From individual to group level patterns. Appl. Anim. Behav. Sci. 2016, 174, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Bailey, D.W.; Trotter, M.G.; Tobin, C.; Thomas, M.G. Opportunities to Apply Precision Livestock Management on Rangelands. Front. Sustain. Food Syst. 2021, 5, 93. [Google Scholar] [CrossRef]
- Chen, C.; Zhu, W.; Liu, D.; Steibel, J.; Siegford, J.; Wurtz, K.; Han, J.; Norton, T. Detection of aggressive behaviours in pigs using a RealSence depth sensor. Comput. Electron. Agric. 2019, 166, 105003. [Google Scholar] [CrossRef]
- Drickamer, L.; Vessey, S.; Jakob, E. Animal Behavior: Mechanisms, Ecology, Evolution; McGraw-Hill: Boston, MA, USA, 2002. [Google Scholar]
- Bøe, K.E.; Ehrlenbruch, R.; Jørgensen, G.H.M.; Andersen, I.L. Individual distance during resting and feeding in age homogeneous vs. age heterogeneous groups of goats. Appl. Anim. Behav. Sci. 2013, 147, 112–116. [Google Scholar] [CrossRef]
- Keeling, L. Spacing behaviour and an ethological approach to assessing optimum space allocations for groups of laying hens. Appl. Anim. Behav. Sci. 1995, 44, 171–186. [Google Scholar] [CrossRef]
- Cairns, S.J.; Schwager, S.J. A comparison of association indices. Anim. Behav. 1987, 35, 1454–1469. [Google Scholar] [CrossRef] [Green Version]
- Davis, G.H.; Crofoot, M.C.; Farine, D.R. Estimating the robustness and uncertainty of animal social networks using different observational methods. Anim. Behav. 2018, 141, 29–44. [Google Scholar] [CrossRef]
- Farine, D.R. A guide to null models for animal social network analysis. Methods Ecol. Evol. 2017, 8, 1309–1320. [Google Scholar] [CrossRef] [Green Version]
- Bonnell, T.R.; Vilette, C. Constructing and analysing time-aggregated networks: The role of bootstrapping, permutation and simulation. Methods Ecol. Evol. 2021, 12, 114–126. [Google Scholar] [CrossRef]
- Bejder, L.; Fletcher, D.; Bräger, S. A method for testing association patterns of social animals. Anim. Behav. 1998, 56, 719–725. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dunn, S.; Wahl, L.; Gloor, G. Mutual information without the influence of phylogeny or entropy dramatically improves residue contact prediction. Bioinformatics 2007, 24, 333–340. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meckbach, C.; Tacke, R.; Hua, X.; Waack, S.; Wingender, E.; Gültas, M. PC-TraFF: Identification of potentially collaborating transcription factors using pointwise mutual information. BMC Bioinform. 2015, 16, 400. [Google Scholar] [CrossRef] [Green Version]
- Damani, O.P. Improving Pointwise Mutual Information (PMI) by Incorporating Significant Co-occurrence. arXiv 2013, arXiv:1307.0596. [Google Scholar]
- Bouma, G. Normalized (Pointwise) Mutual Information in Collocation Extraction. In Proceedings of the Biennial GSCL Conference 2009, Potsdam, Germany, 1 October 2009. [Google Scholar]
- Islam, M.A.; Inkpen, D. Second Order Co-occurrence PMI for Determining the Semantic Similarity of Words. In Proceedings of the Fifth International Conference on Language Resources and Evaluation (LREC’06), Genoa, Italy, 22–28 May 2006; European Language Resources Association (ELRA): Genoa, Italy, 2006. [Google Scholar]
- Ungar, E.; Nevo, Y.; Baram, H.; Arieli, A. Evaluation of the IceTag leg sensor and its derivative models to predict behaviour, using beef cattle on rangeland. J. Neurosci. Methods 2017, 300. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Wickham, H.; François, R.; Henry, L.; Müller, K. dplyr: A Grammar of Data Manipulation; R Package Version 1.0.7; The R Project for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Chang, W. Extrafont: Tools for Using Fonts; R Package Version 0.17; The R Project for Statistical Computing: Vienna, Austria, 2014. [Google Scholar]
- Hijmans, R.J. Geosphere: Spherical Trigonometry; R Package Version 1.5-10; The R Project for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016. [Google Scholar]
- Csardi, G.; Nepusz, T. The igraph software package for complex network research. InterJ. Complex Syst. 2006, 1695, 1–9. [Google Scholar]
- You, K. NetworkDistance: Distance Measures for Networks; R Package Version 0.3.4.; The R Project for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Klinke, S. plot.matrix: Visualizes a Matrix as Heatmap; R Package Version 1.6; The R Project for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Campitelli, E. ggnewscale: Multiple Fill and Colour Scales in ‘ggplot2’; R Package Version 0.4.5; The R Project for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Lüdecke, D. sjmisc: Data and Variable Transformation Functions. J. Open Source Softw. 2018, 3, 754. [Google Scholar] [CrossRef]
- Wickham, H. Stringr: Simple, Consistent Wrappers for Common String Operations; R Package Version 1.4.0; The R Project for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Grolemund, G.; Wickham, H. Dates and Times Made Easy with lubridate. J. Stat. Softw. 2011, 40, 1–25. [Google Scholar] [CrossRef]
- Levy, O.; Goldberg, Y.; Dagan, I. Improving Distributional Similarity with Lessons Learned from Word Embeddings. Trans. Assoc. Comput. Linguist. 2015, 3, 211–225. [Google Scholar] [CrossRef]
- Girelli, G. A Web Graphical Interface to Visualize and Analyze Tumor Evolution Networks. Ph.D. Thesis, University of Trento, Trento, Italy, 2014. [Google Scholar] [CrossRef]
- Gotelli, N.; Graves, G. Null Models in Ecology; Smithsonian Institution Press: Washington, DC, UDA, 1996. [Google Scholar]
- Patison, K.P.; Swain, D.L.; Bishop-Hurley, G.J.; Robins, G.; Pattison, P.; Reid, D.J. Changes in temporal and spatial associations between pairs of cattle during the process of familiarisation. Appl. Anim. Behav. Sci. 2010, 128, 10–17. [Google Scholar] [CrossRef]
- Sato, S.; Tarumizu, K.; Hatae, K. The influence of social factors on allogrooming in cows. Appl. Anim. Behav. Sci. 1993, 38, 235–244. [Google Scholar] [CrossRef]
- Harris, N.R.; Johnson, D.E.; McDougald, N.K.; George, M.R. Social Associations and Dominance of Individuals in Small Herds of Cattle. Rangel. Ecol. Manag. 2007, 60, 339–349. [Google Scholar] [CrossRef]
- Shiyomi, M. How are distances between individuals of grazing cows explained by a statistical model? Ecol. Model. 2004, 172, 87–94. [Google Scholar] [CrossRef]
- Reinhardt, V.; Reinhardt, A. Cohesive Relationships in a Cattle Herd (Bos indicus). Behaviour 1981, 77, 121–151. [Google Scholar] [CrossRef]
- Ma, H.; Zhao, Q.; Verhagen, S.; Psychas, D.; Liu, X. Assessing the Performance of Multi-GNSS PPP-RTK in the Local Area. Remote Sens. 2020, 12, 3343. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X.; Ren, X.; Fritsche, M.; Wickert, J.; Schuh, H. Precise positioning with current multi-constellation Global Navigation Satellite Systems: GPS, GLONASS, Galileo and BeiDou. Sci. Rep. 2015, 5, 8328. [Google Scholar] [CrossRef] [PubMed]
- Nadarajah, N.; Khodabandeh, A.; Wang, K.; Choudhury, M.; Teunissen, P.J.G. Multi-GNSS PPP-RTK: From Large- to Small-Scale Networks. Sensors 2018, 18, 1078. [Google Scholar] [CrossRef] [Green Version]
- Keshavarzi, H.; Lee, C.; Johnson, M.; Abbott, D.; Ni, W.; Campbell, D.L.M. Validation of Real-Time Kinematic (RTK) Devices on Sheep to Detect Grazing Movement Leaders and Social Networks in Merino Ewes. Sensors 2021, 21, 924. [Google Scholar] [CrossRef]
- Katzner, T.E.; Arlettaz, R. Evaluating Contributions of Recent Tracking-Based Animal Movement Ecology to Conservation Management. Front. Ecol. Evol. 2020, 7, 519. [Google Scholar] [CrossRef] [Green Version]
- Stricklin, W.R. Matrilinear Social Dominance and Spatial Relationships among Angus and Hereford Cows. J. Anim. Sci. 1983, 57, 1397–1405. [Google Scholar] [CrossRef] [PubMed]








| Animal | Age (Months (Days)) | Breed | Days b. Calving | Recordings | Mean Satellites (Mean DOP) |
|---|---|---|---|---|---|
| A | 25 (+7) | Crossbreed | 97 | 41,747 | 5.39 (1.53) |
| B | 25 (+16) | Holstein Frisian | 98 | 41,750 | 7.07 (1.51) |
| C | 25 (+4) | Crossbreed | 100 | 41,753 | 6.32 (1.52) |
| D | 24 (+28) | Holstein Frisian | 89 | 41,753 | 6.08 (1.49) |
| E | 24 (+19) | Holstein Frisian | 91 | 41,758 | 6.10 (1.49) |
| F | 22 (+24) | Holstein Frisian | 141 | 41,747 | 6.16 (1.50) |
| G | 22 (+7) | Holstein Frisian | 159 | 41,749 | 6.23 (1.50) |
| H | 22 (+3) | Holstein Frisian | 208 | 41,758 | 6.16 (1.50) |
| Pair | Sig. Contact Counts | Sig. Values | |
|---|---|---|---|
| A–C | x | x | x |
| B–E | x | x | x |
| D–E | x | x | x |
| A–F | x | x | x |
| C–F | x | x | x |
| E–G | x | x | x |
| D–G | x | x | |
| D–H | x | x | |
| G–H | x | x | |
| A–B | x | x | |
| B–C | x | x | |
| B–F | x | x | |
| C–G | x | x | |
| E–H | x | ||
| F–H | x |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meckbach, C.; Elsholz, S.; Siede, C.; Traulsen, I. An Information-Theoretic Approach to Detect the Associations of GPS-Tracked Heifers in Pasture. Sensors 2021, 21, 7585. https://doi.org/10.3390/s21227585
Meckbach C, Elsholz S, Siede C, Traulsen I. An Information-Theoretic Approach to Detect the Associations of GPS-Tracked Heifers in Pasture. Sensors. 2021; 21(22):7585. https://doi.org/10.3390/s21227585
Chicago/Turabian StyleMeckbach, Cornelia, Sabrina Elsholz, Caroline Siede, and Imke Traulsen. 2021. "An Information-Theoretic Approach to Detect the Associations of GPS-Tracked Heifers in Pasture" Sensors 21, no. 22: 7585. https://doi.org/10.3390/s21227585
APA StyleMeckbach, C., Elsholz, S., Siede, C., & Traulsen, I. (2021). An Information-Theoretic Approach to Detect the Associations of GPS-Tracked Heifers in Pasture. Sensors, 21(22), 7585. https://doi.org/10.3390/s21227585






