JOM-4S Overhauser Magnetometer and Sensitivity Estimation
Abstract
:1. Introduction
2. Physical Principles
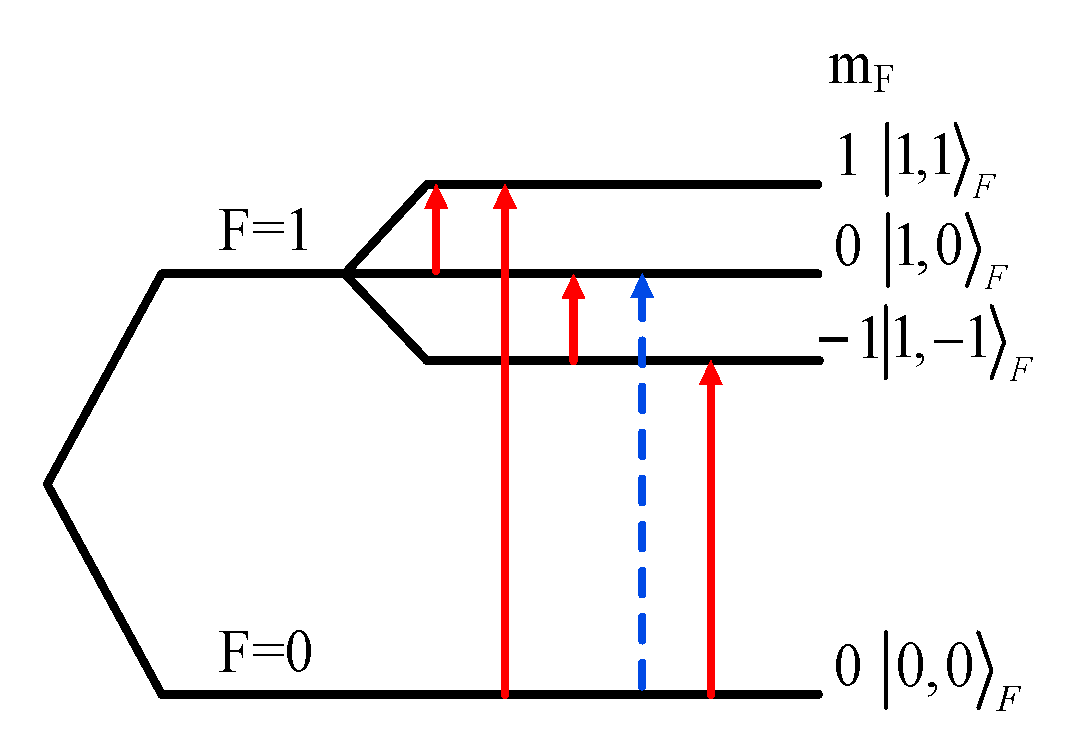
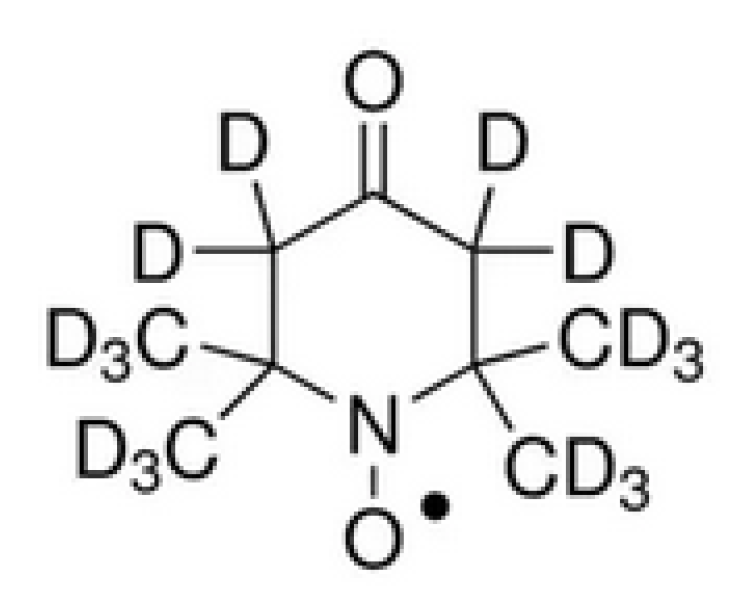
2.1. ESR
2.2. Solomon’s Equation
2.3. Lamor Precession
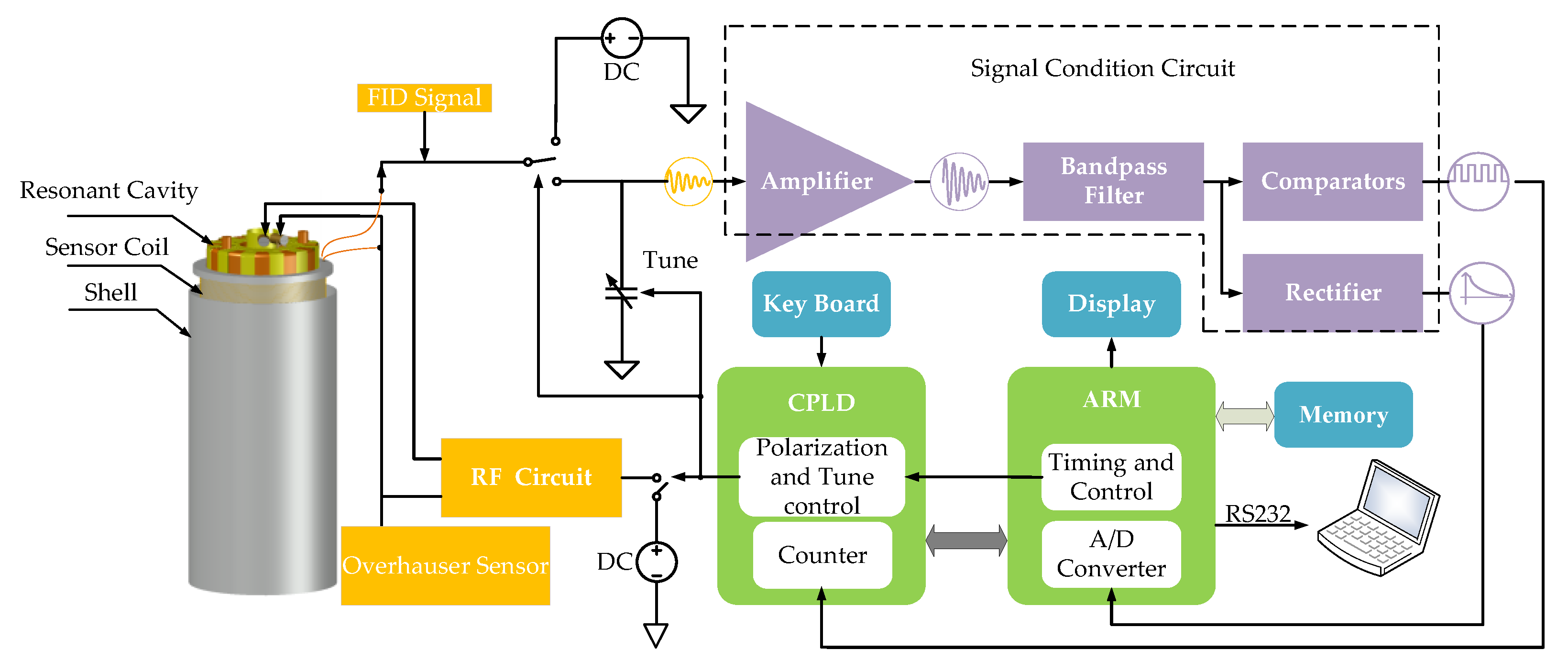
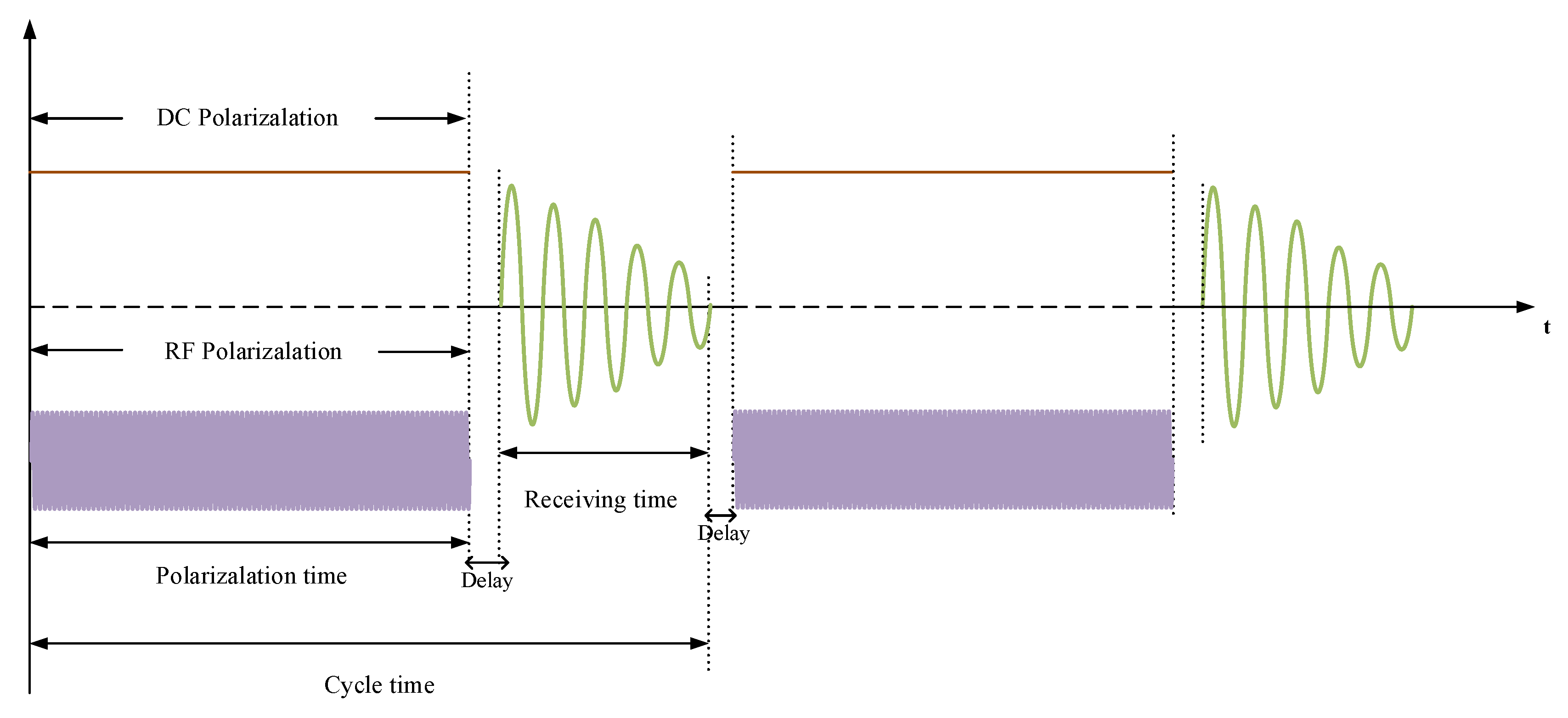
3. Construction of JOM-4S OVM
3.1. Brief Introduction of JOM-4S OVM
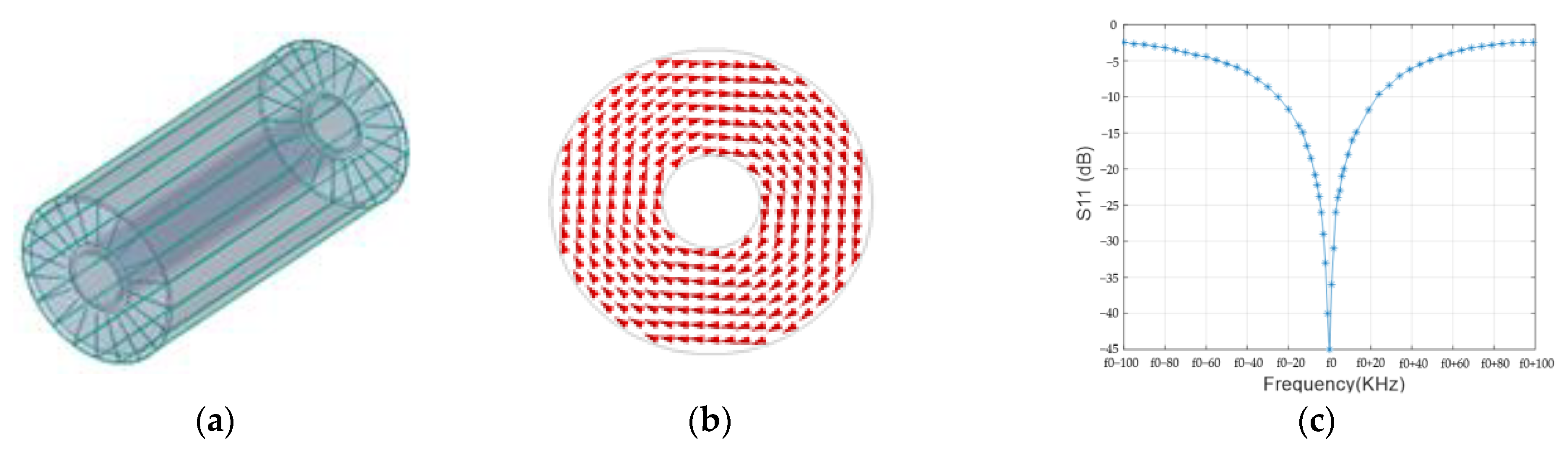
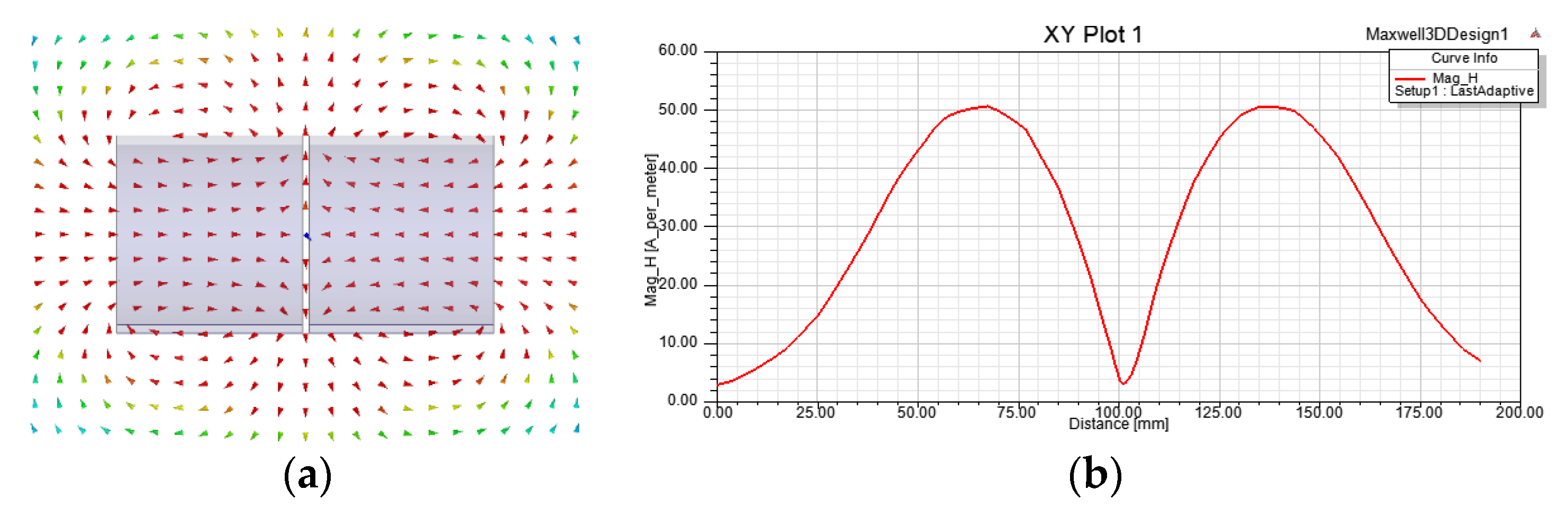
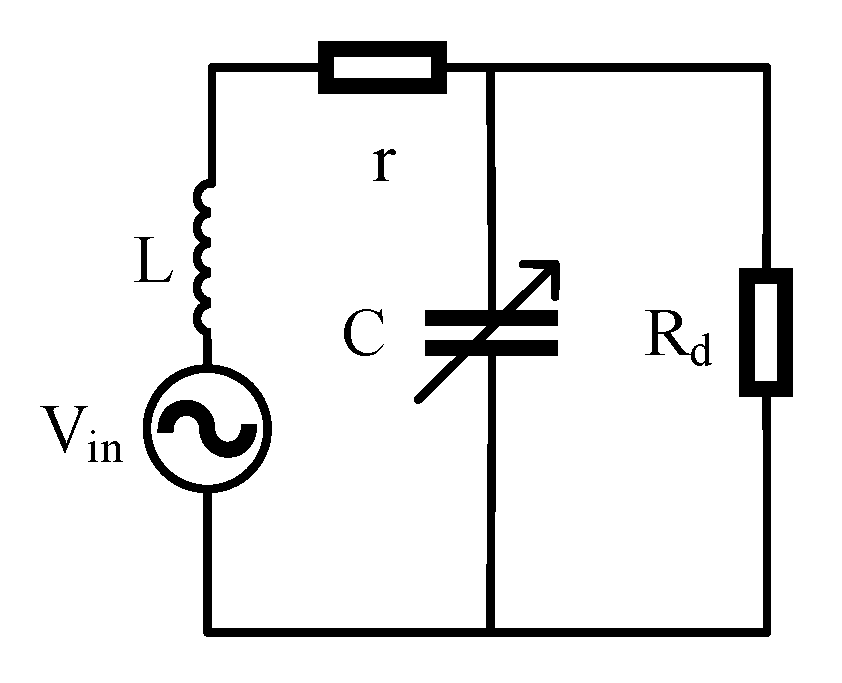
3.2. Sensor Design
3.3. Analog Circuit Designs
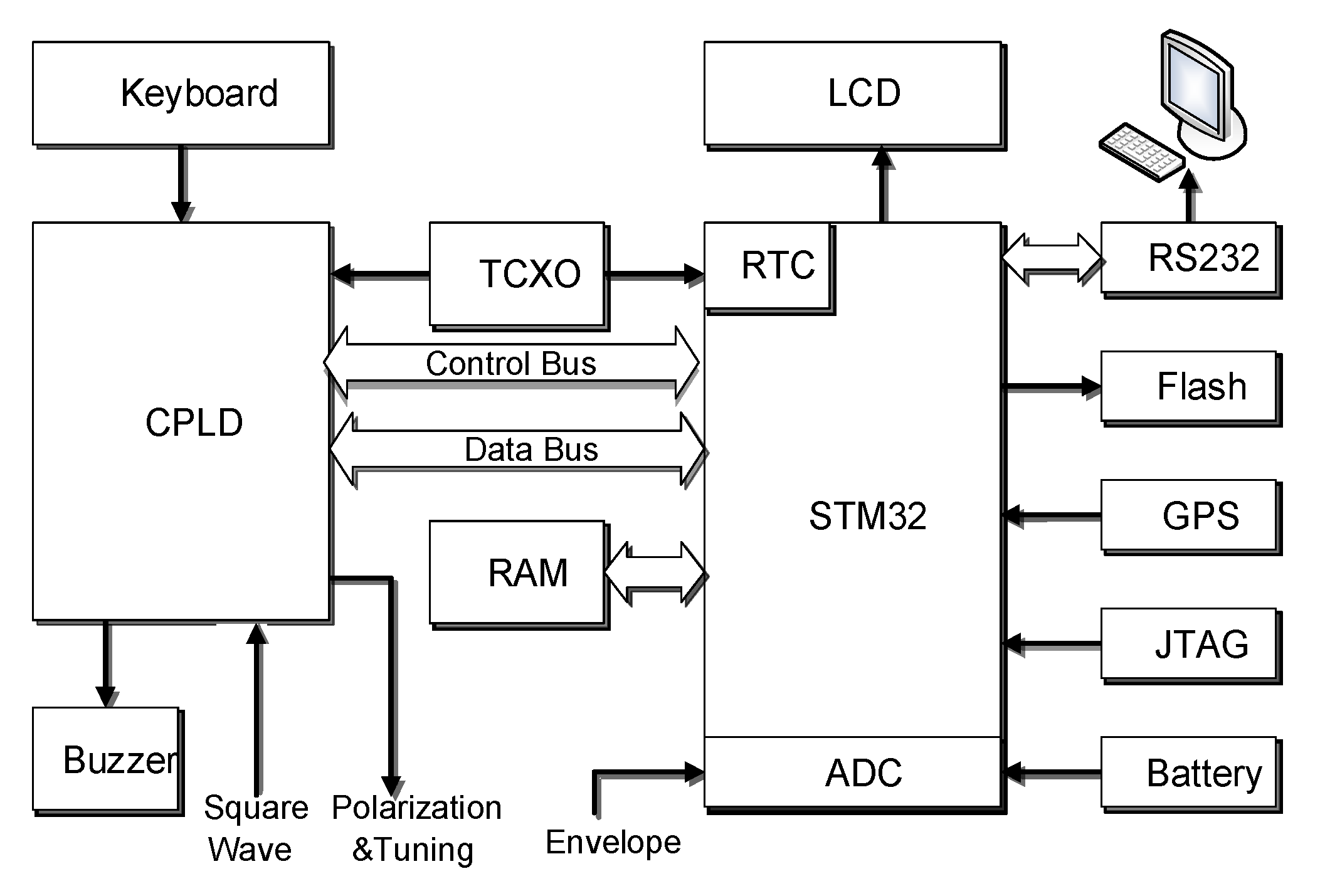
3.4. Digital Circuit Designs
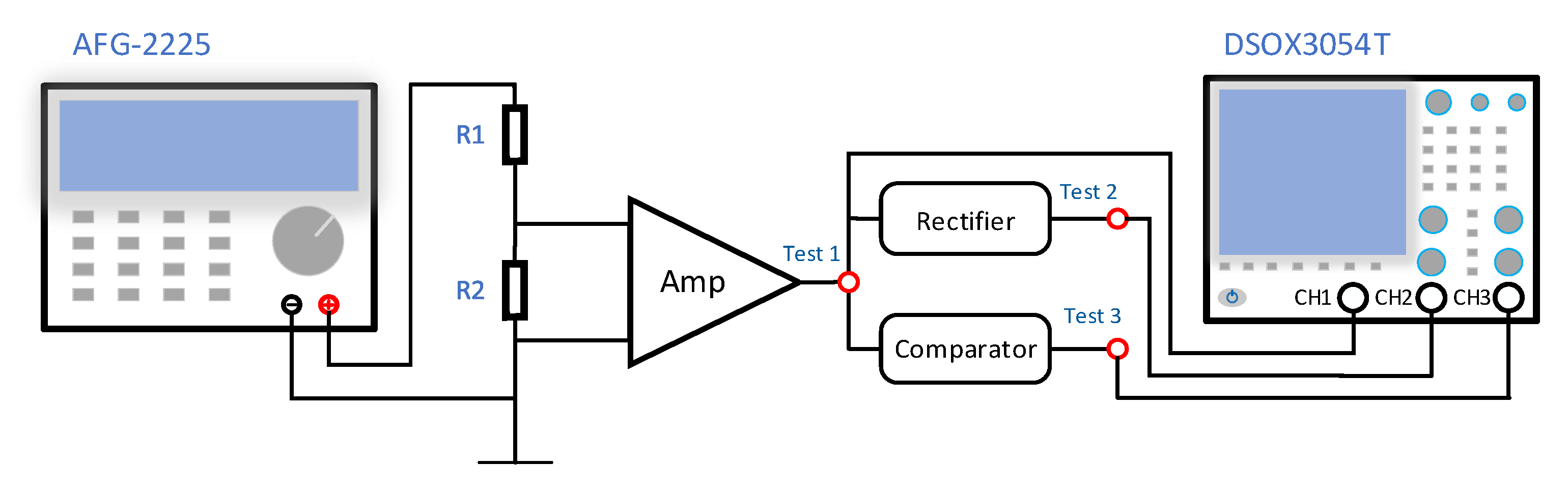
4. Sensitivity Estimation Methods
4.1. Fourth-Order Difference
4.2. Correlation Analysis
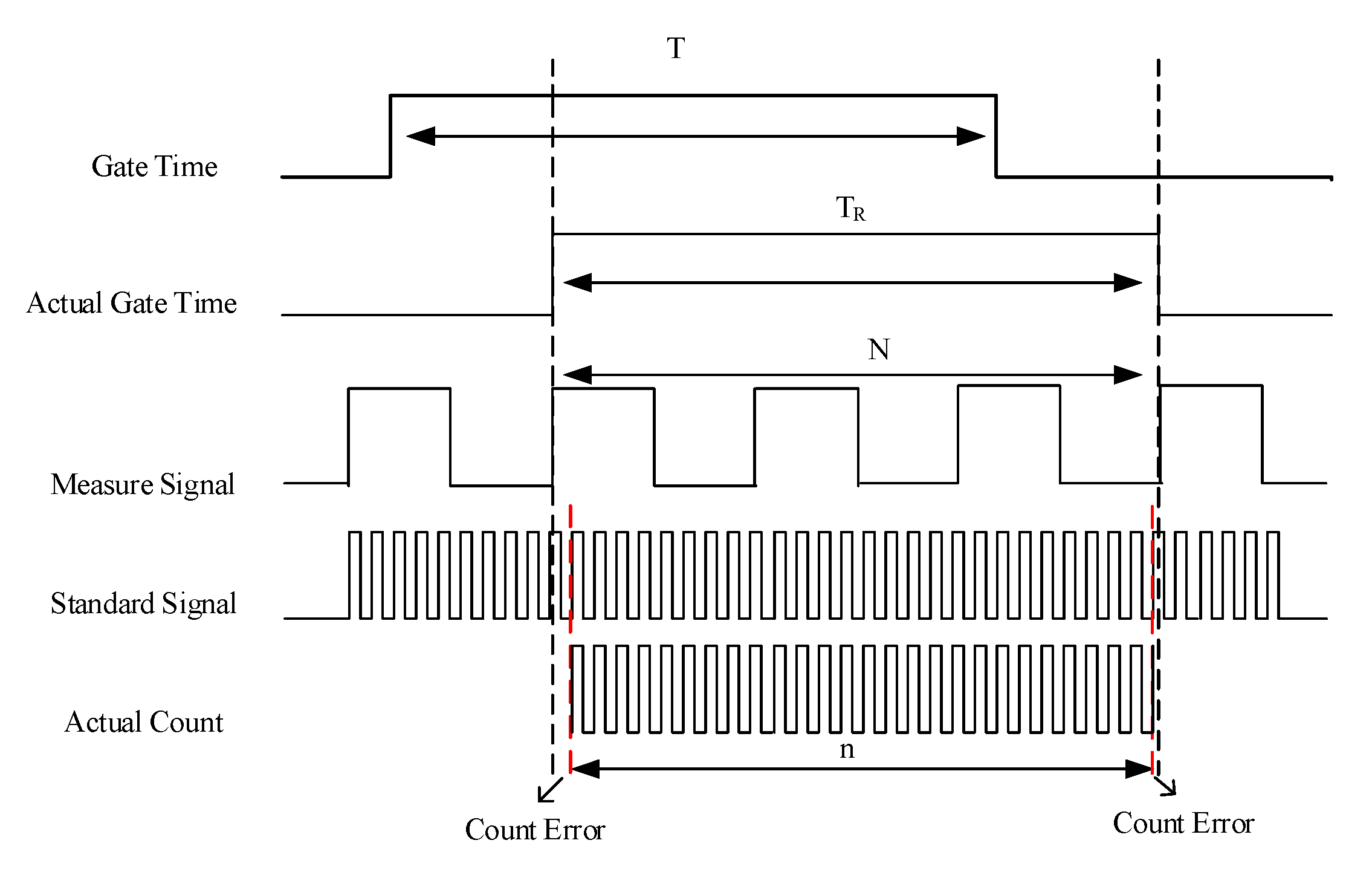
4.3. Direct Measurement Method in Time Domain
4.4. Synchronization Method in Time Domain
4.5. PSD Estimation in Frequency Domain
5. Experimental Results and Discussions
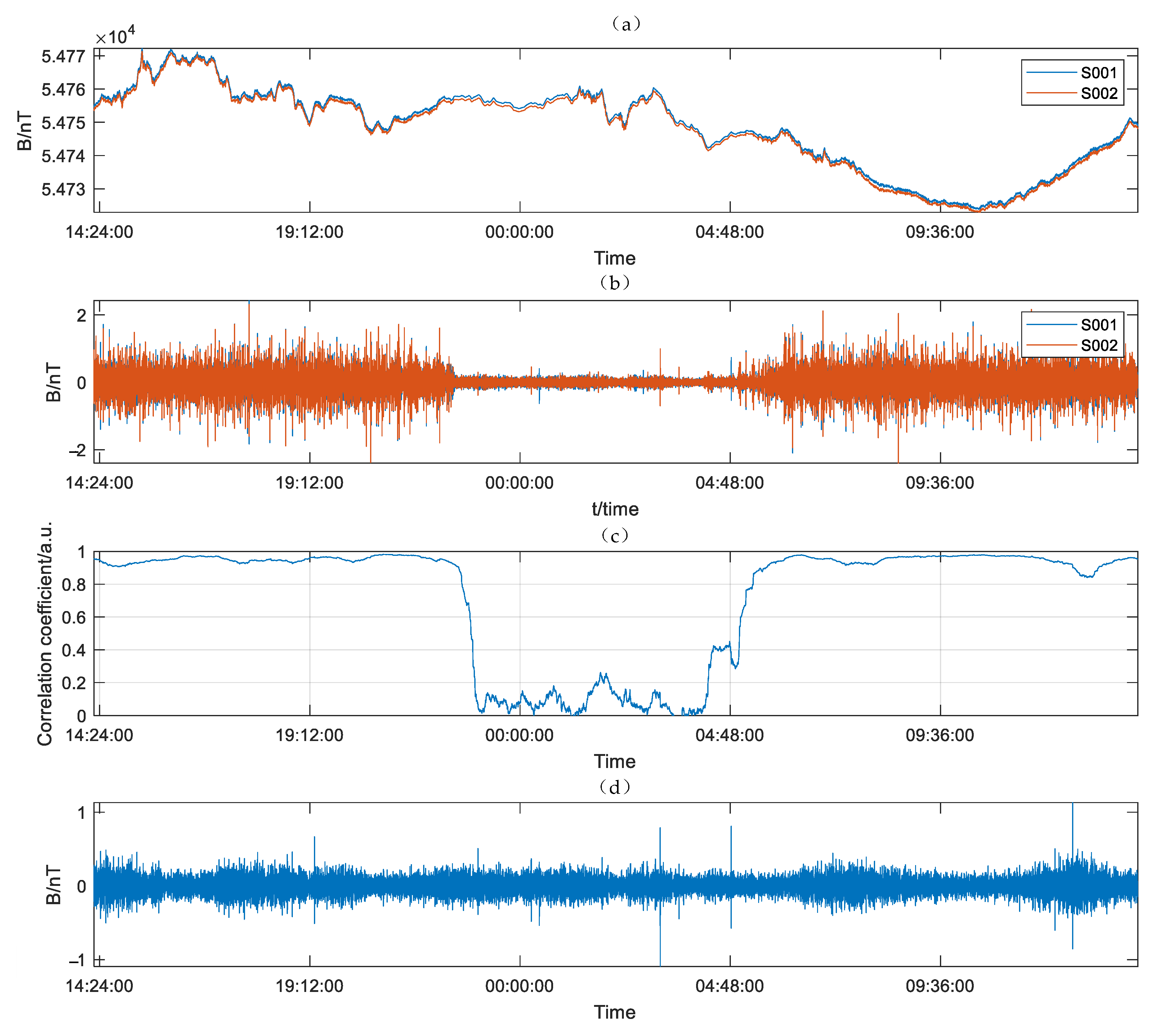
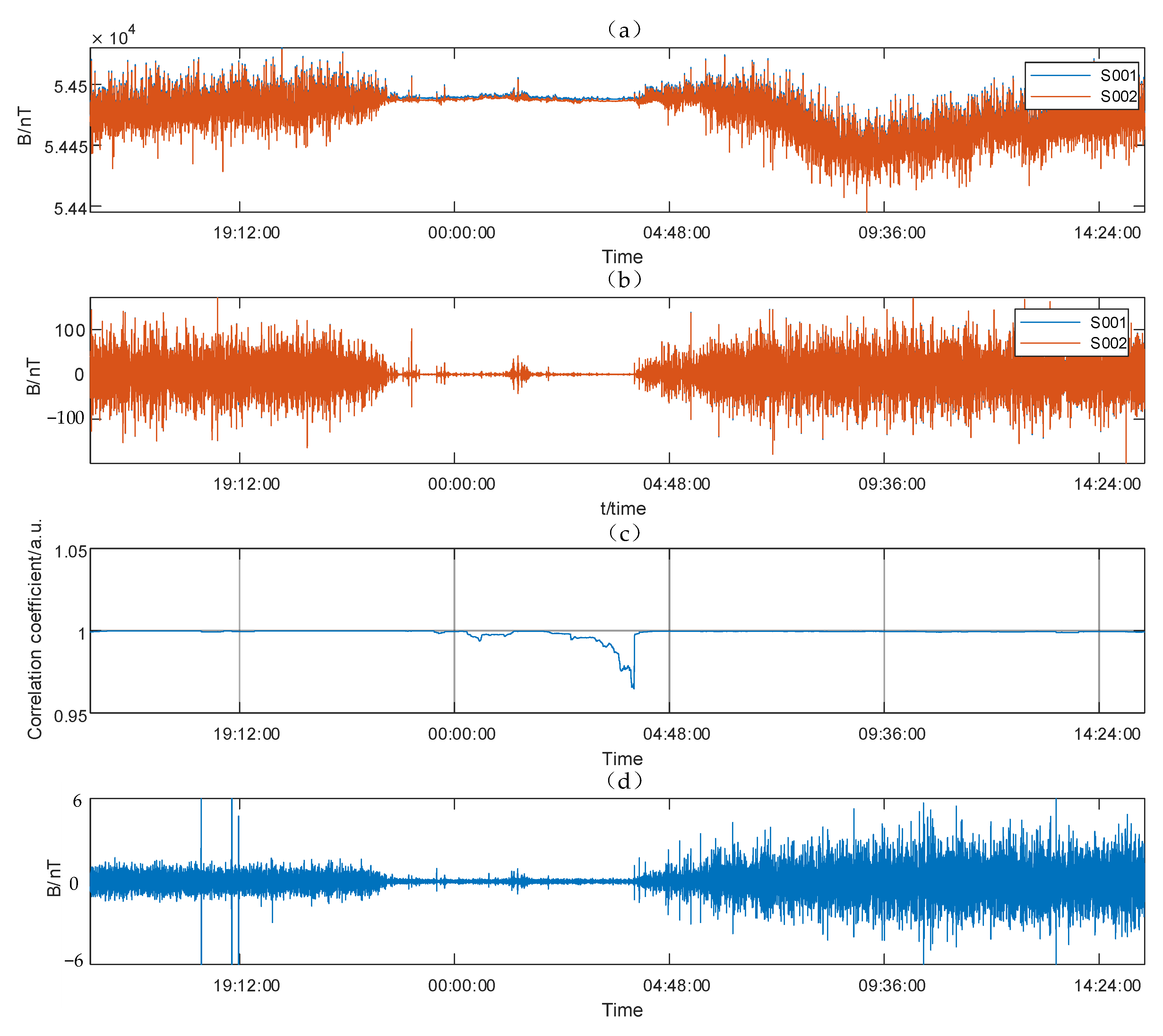
5.1. Sensitivity Estimation in Time Domain under a Quiet Environment
5.2. Sensitivity Estimation in Time Domain under a Noisy Environment
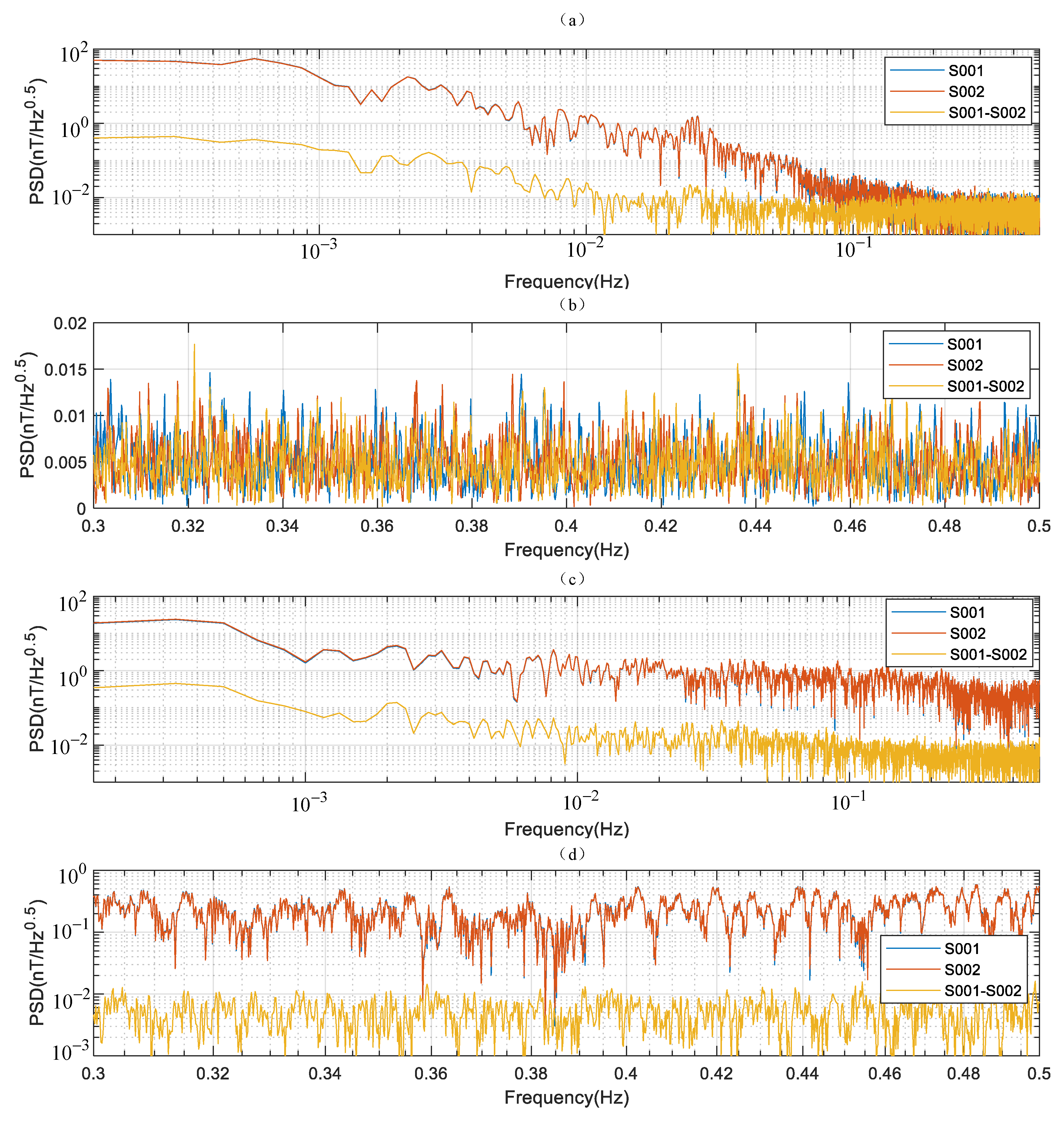
5.3. Sensitivity Estimation in Frequency Domain
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Packard, M.E. Free nuclear induction in the earth’s magnetic field. Phys. Rev. 1954, 93, 941. [Google Scholar]
- Varian, R.H. Method and Means for Correlating Nuclear Properties of Atoms and Magnetic Fields. U.S. Patent US2561490A, 24 July 1951. [Google Scholar]
- Waters, G.S. A measurement of the earth’s magnetic field by nuclear induction. Nature 1955, 4484, 691. [Google Scholar] [CrossRef]
- James, A.; Koehler, R. Proton precession magnetometers, revision 3. In Proceedings of the Industrial Control and Electronics Engineering (ICICEE), Comox, BC, Canada, 23–25 March 2012. [Google Scholar]
- Mahavarkar, P.; Singh, S.; Labde, S.; Dongre, V.; Patil, A. The low cost Proton Precession Magnetometer developed at the Indian Institute of Geomagnetism. J. Instrum. 2017, 12, T05002. [Google Scholar] [CrossRef]
- Overhauser, A.W. Polarization of nuclei in metals. Phys. Rev. 1953, 92, 411. [Google Scholar] [CrossRef]
- Abragam, A. Overhauser effect in nonmetals. Phys. Rev. 1955, 98, 1729–1735. [Google Scholar] [CrossRef]
- Solomon, I. Relaxation precesses in a system of two spins. Phys. Rev. 1955, 99, 559–565. [Google Scholar] [CrossRef]
- Halse, M.E.; Callaghan, P.T. A dynamic nuclear polarization strategy for multi-dimensional Earth’s field NMR spectroscopy. J. Magn. Reson. 2008, 195, 162–168. [Google Scholar] [CrossRef] [PubMed]
- Guiberteau, T.; Grucker, D. EPR spectroscopy by dynamic nuclear polarization in low magnetic field. J. Magn. Reson. Ser. B 1996, 110, 47–54. [Google Scholar] [CrossRef]
- Kernevez, N.; Glénat, H. Description of a high sensitivity CW scalar DNP-NMR magnetometer. IEEE Trans. Magn. 1991, 27, 5402–5404. [Google Scholar] [CrossRef]
- Duret, D.; Bonzom, J.; Brochier, M.; Frances, M.; Leger, J.M.; Odru, R.; Salvi, C.; Thomas, T.; Perret, A. Overhauser magnetometer for the Danish Oersted satellite. IEEE Trans. Magn. 1995, 31, 3197–3199. [Google Scholar] [CrossRef]
- Duret, D.; Leger, J.M. Performances of the OVH magnetometer for the Danish Oersted satellite. IEEE Trans. Magn. 1996, 32, 4935–4937. [Google Scholar] [CrossRef]
- Hrvoic, I. Overhauser Magnetometers for Measurement of the Earth’s Magnetic Field. In Proceedings of the International Workshop on Geomagnetic Observatory Data Acquisition and Processing; Finnish Meteorological Institute: Helsinki, Finland, 1990; Available online: https://www.gemsys.ca/pdf/Overhauser-Magnetometers-for-Measurement-of-the-Earth’s-Magnetic-Field.pdf (accessed on 27 October 2021).
- Sapunov, V.; Denisov, A.; Denisova, O.; Saveliev, D. Proton and Overhauser magnetometers metrology. Contrib. Geophys. Geod. 2001, 31, 119–124. [Google Scholar]
- Khomutov, S.Y.; Mandrikova, O.V.; Budilova, E.A.; Kusumita, A.; Manjula, L. Noise in raw data from magnetic observatories: DIMOVER. Earth Planets Space 2006, 58, 711–716. [Google Scholar] [CrossRef] [Green Version]
- Jian, G.; Dong, H.; Liu, H.; Yuan, Z.; Dong, H.; Zhao, Z.; Liu, Y.; Zhu, J.; Zhang, H. Overhauser geomagnetic sensor based on the dynamic nuclear polarization effect for magnetic prospecting. Sensors 2016, 16, 806. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Bai, B.; Liu, Z. Contruction of an overhauser magnetic gradiometer and the applications in geomagnetic observation and ferromagnetic target localization. J. Instrum. 2017, 12, T10008. [Google Scholar] [CrossRef]
- Liu, H.; Dong, H.; Liu, Z.; Ge, J.; Bai, B.; Zhang, C. Noise characterization for the FID signal from proton precession magnetometer. J. Instrum. 2017, 12, P07019. [Google Scholar] [CrossRef]
- Liu, H.; Dong, H.; Liu, Z.; Ge, J. Application of Hilbert-Huang decomposition to reduce noise and characterize for NMR FID signal of proton precession magnetometer. Instrum. Exp. Tech. 2018, 61, 55–64. [Google Scholar] [CrossRef] [Green Version]
- Bai, B.; Liu, H.; Ge, J.; Dong, H. Research on an improved resonant cavity for overhauser geomagnetic sensor. IEEE Sens. J. 2018, 18, 2713–2721. [Google Scholar] [CrossRef]
- Liu, H.; Dong, H.; Ge, J.; Liu, Z.; Zhu, J.; Zhang, H. Efficient performance optimization for the magnetic data readout from a proton precession magnetometer with low-rank constraint. IEEE Trans. Magn. 2019, 55, 1–4. [Google Scholar] [CrossRef]
- Acuna, M.H. Space-based magnetometers. Rev. Sci. Instrum. 2002, 73, 3717–3736. [Google Scholar] [CrossRef]
- Lenz, J.; Edelstein, S. Magnetic sensors and their applications. IEEE Sens. J. 2006, 6, 631–649. [Google Scholar] [CrossRef]
- Narkhov, E.D.; Sapunov, V.A.; Denisov, A.U.; Saveliev, D.V. Novel quantum NMR magnetometer non-contact defectoscopy and monitoring technique for the safe exploitation of gas pipelines. WIT Trans. Ecol. Environ. 2014, 186, 649–658. [Google Scholar]
- Oluwagbemi, J.E.; Olakunle, A.S.; Lawrence, O.O. A study of subsurface geological structure of Sumaje village, Nigeria. J. Geol. Min. Res. 2013, 5, 232–238. [Google Scholar] [CrossRef]
- Hatakeyama, T.; Kitahara, Y.; Yokoyama, S.; Jigena, B.; Berrocoso, M.; Torrecillas, C.; Vidfal, J.; Barbero, I.; Fernandez-Ros, A. Magnetic survey of archaeological kiln sites with Overhauser magnetometer: A case study of buried Sue ware kilns in Japan. J. Archaeol. Sci. Rep. 2018, 18, 568–576. [Google Scholar] [CrossRef]
- Gerginov, V.; Krzyzewski, S.; Knappe, S. Pulsed operation of a miniature scalar optically pumped magnetometer. J. Opt. Soc. Am. B Opt. Phys. 2017, 34, 1429–1434. [Google Scholar] [CrossRef]
- Liwei, J.; Quan, W.; Liang, Y.; Liu, J.; Duan, L.; Fang, J. Effects of pump laser power density on the hybrid optically pumped comagnetometer for rotation sensing. Opt. Express 2019, 27, 27420–27430. [Google Scholar]
- Savukov, I.; Kim, Y.J.; Shah, V.; Boshier, M.G. High-sensitivity operation of single-beam optically pumped magnetometer in a kHz frequency range. Meas. Sci. Technol. 2017, 28, 035104. [Google Scholar] [CrossRef] [Green Version]
- Jodko-Wadzińska, A.; Wildner, K.; Pako, T.; Wladzinski, M. Compensation system for biomagnetic measurements with optically pumped magnetometers inside a magnetically shielded room. Sensors 2020, 20, 4563. [Google Scholar] [CrossRef]
- Liu, L.; Lu, Y.; Zhuang, X.; Zhang, Q.; Fang, G. Noise analysis in pre-amplifier circuits associated to highly sensitive optically-pumped magnetometers for geomagnetic applications. Appl. Sci. 2020, 10, 7172. [Google Scholar] [CrossRef]
- Volkmar, S.; Bastian, S.; Rob, I.; Scholtes, T.; Woetzel, S.; Stolz, R. An optically pumped magnetometer working in the light-shift dispersed mz mode. Sensors 2017, 17, 561. [Google Scholar] [CrossRef] [Green Version]
- Gerginov, V.; Pomponio, M.; Knappe, S. Scalar magnetometry below 100 fT/Hz1/2 in a microfabricated cell. IEEE Sens. J. 2020, 20, 12684–12690. [Google Scholar] [CrossRef]
- Jaufenthaler, A.; Kornack, T.; Lebedev, V.; Limes, M.E.; Korber, R.; Liebl, M.; Baumgarten, D. Pulsed optically pumped magnetometers: Addressing dead time and bandwidth for the unshielded magnetorelaxometry of magnetic nanoparticles. Sensors 2021, 21, 1212. [Google Scholar] [CrossRef] [PubMed]
- Denisov, A.Y.; Denisova, O.V.; Sapunov, V.A.; Khomoutov, S.Y. Measurement quality estimation of proton-precession magnetometers. Earth Planets Space 2006, 58, 707–710. [Google Scholar] [CrossRef] [Green Version]
- Guiberteau, T.; Grucker, D. Dynamic nuclear polarization of water protons by saturation of σ and π EPR transitions of nitroxides. J. Magn. Reson. Ser. A 1993, 105, 98–103. [Google Scholar] [CrossRef]
- Breit, G.; Rabi, I.I. Measurement of nuclear spin. Phys. Rev. 1931, 38, 2082–2083. [Google Scholar] [CrossRef]
- Lang, K.; Moussavi, M.; Belorizky, E. New, high-performance, hydrogenated paramagnetic solution for use in earth field DNP-NMR magnetometers. J. Phys. Chem. A 1997, 101, 1662–1671. [Google Scholar] [CrossRef]
- Yamada, K.-I.; Kinoshita, Y.; Yamasaki, T.; Sadasue, H.; Mito, F.; Nagai, M.; Matsumoto, S.; Aso, M.; Suemune, H.; Sakai, K.; et al. Synthesis of nitroxyl radicals for overhauser-enhanced magnetic resonance imaging. Arch. Pharm. 2008, 341, 548–553. [Google Scholar] [CrossRef] [PubMed]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, X.; Chen, S.; Zhang, S. JOM-4S Overhauser Magnetometer and Sensitivity Estimation. Sensors 2021, 21, 7698. https://doi.org/10.3390/s21227698
Gong X, Chen S, Zhang S. JOM-4S Overhauser Magnetometer and Sensitivity Estimation. Sensors. 2021; 21(22):7698. https://doi.org/10.3390/s21227698
Chicago/Turabian StyleGong, Xiaorong, Shudong Chen, and Shuang Zhang. 2021. "JOM-4S Overhauser Magnetometer and Sensitivity Estimation" Sensors 21, no. 22: 7698. https://doi.org/10.3390/s21227698
APA StyleGong, X., Chen, S., & Zhang, S. (2021). JOM-4S Overhauser Magnetometer and Sensitivity Estimation. Sensors, 21(22), 7698. https://doi.org/10.3390/s21227698




