A New Bearing Fault Diagnosis Method Based on Capsule Network and Markov Transition Field/Gramian Angular Field
Abstract
:1. Introduction
2. Methods
2.1. Transformation Method
2.2. Capsule Network
- (1)
- The prediction vector , iteration number , input capsule , and output capsule , parameter .
- (2)
- Update the vector by Equation (8).
- (3)
- The input capsule is obtained by Equation (9) and updated with the “squashing” (Equation (7)).
- (4)
- Update by Equation (10) and return to step (2) for iterative calculation.
- (5)
- Return the final output vector after iterations.
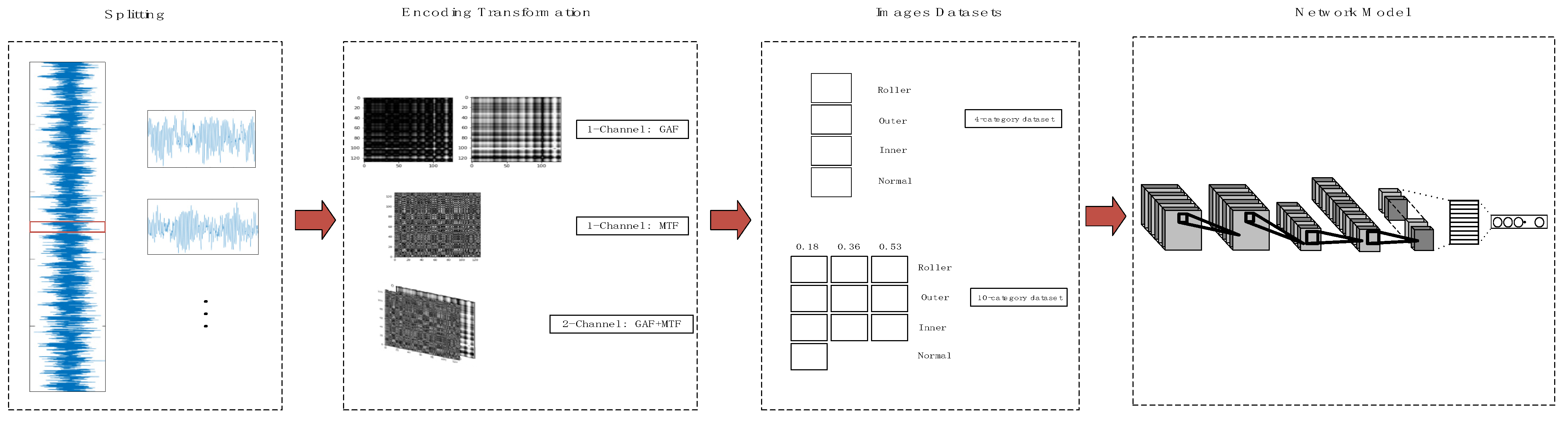
2.3. Proposed Methodology
- Splitting. The original vibration signal is divided into appropriate signal segments to make it suitable for later encoding transformation. We will experiment to determine the appropriate signal split length.
- Encoding transformation. By the above transformation method, every segment is converted into a one-channel or two-channel image. The entire original vibration signal is converted into a large number of feature images. In this step, three transformation methods are considered feasible. There is GAF for the one-channel image, MTF for the one-channel image, and GAF and MTF for the two-channel image. We will compare the diagnostic accuracy of these methods in the experiment.
- Images datasets. The feature images are classified according to the fault type of the original vibration signal to form the image dataset.
- Network model. The image dataset is fed into the configured neural network model for training and testing. The image dataset will be fed into the conventional convolutional neural network and the proposed improved capsule network. We compare and summarize the advantages of the proposed network in the following experiments.
3. Experiments and Results
3.1. Dataset and Simulation Environment
3.2. Experiment#1: GAF-Deeplearning
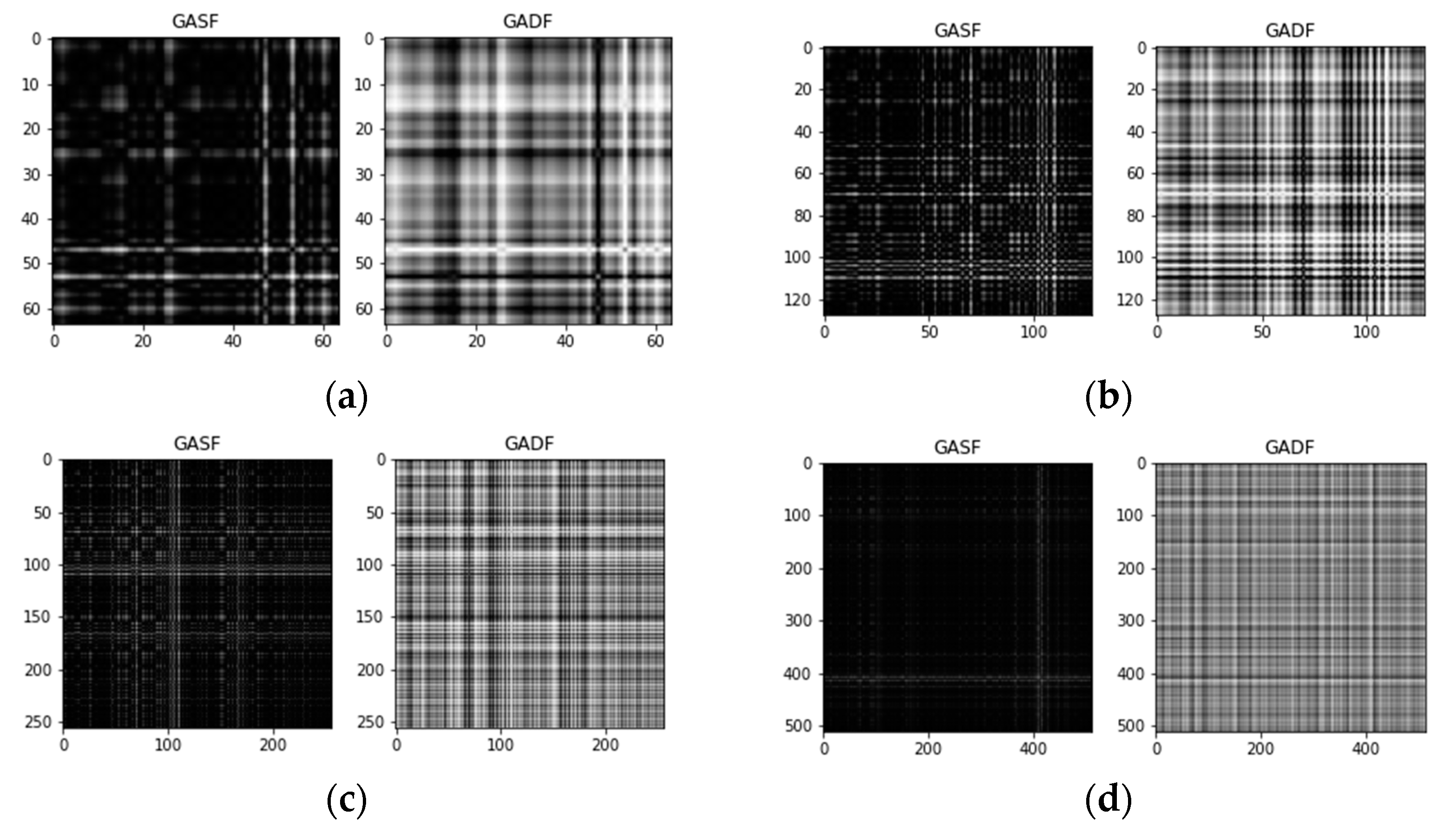
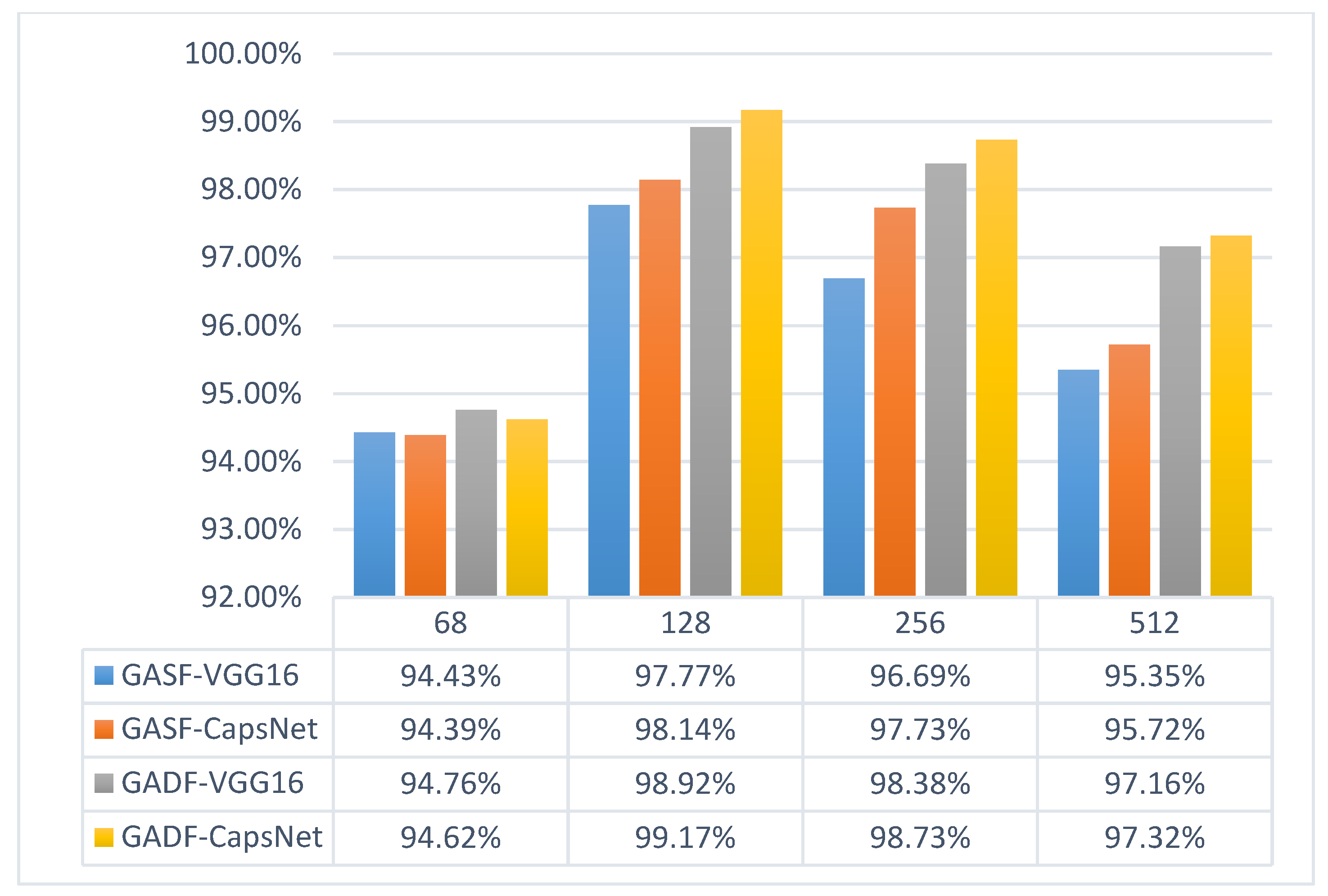
- When the size is 64, it is obvious that it is difficult to guarantee that an image contains complete information about the fault features. Images sized 128 have the best performance, and larger images contain more information but cause the network parameters to increase and make the training time of the network much longer.
- Except for the case of incomplete information at size 64, the experiments on images of other sizes show that GADF has higher accuracy than GASF.
- In the comparison between VGG and CapsNet, CapsNet performs better than VGG in most cases, but there is no significant advantage.
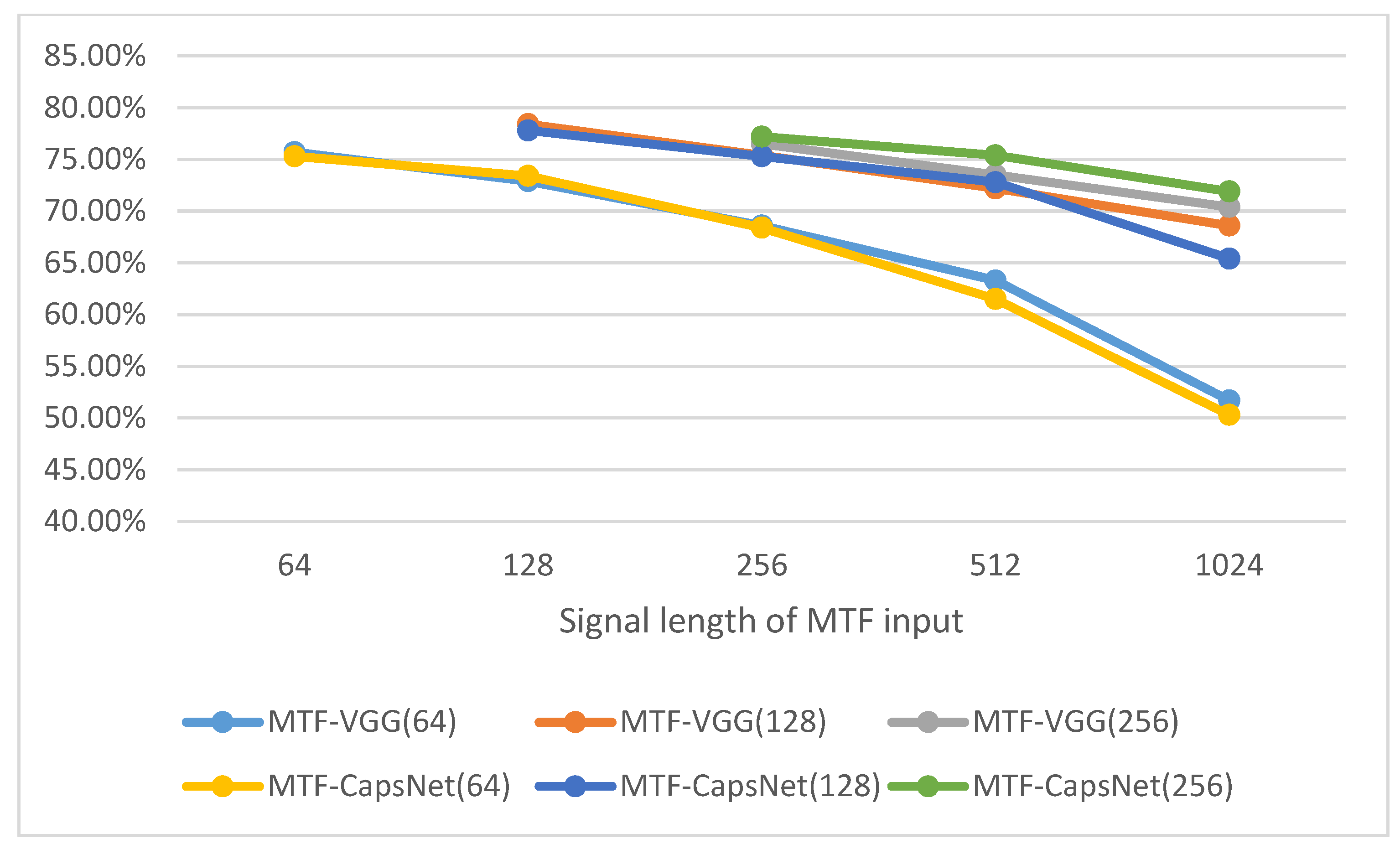
3.3. Experiment#2: MTF-Deeplearning
3.4. Experiment#3: GAFMTF-Deeplearning
4. Conclusions
- The GAF technique retains sufficient bearing failure characteristics. Neural networks more easily extract fault features and perform classification and diagnosis by GAF images. For the capsule network and VGG network, the original vibration signal cut into 128 and converted into a 128 × 128 GAF image has a better performance compared to other cut lengths. GAF-CapsNet has, at most, 99.17% accuracy in training 128 × 128 GAF images.
- For different sizes of signal cuts and output image sizes, MTF is only less than 80% accurate in CapsNet and VGG. The MTF technique loses a large number of fault characteristics, but also retains some of them. MTF retains more dynamic features and less static information than the GAF technique.
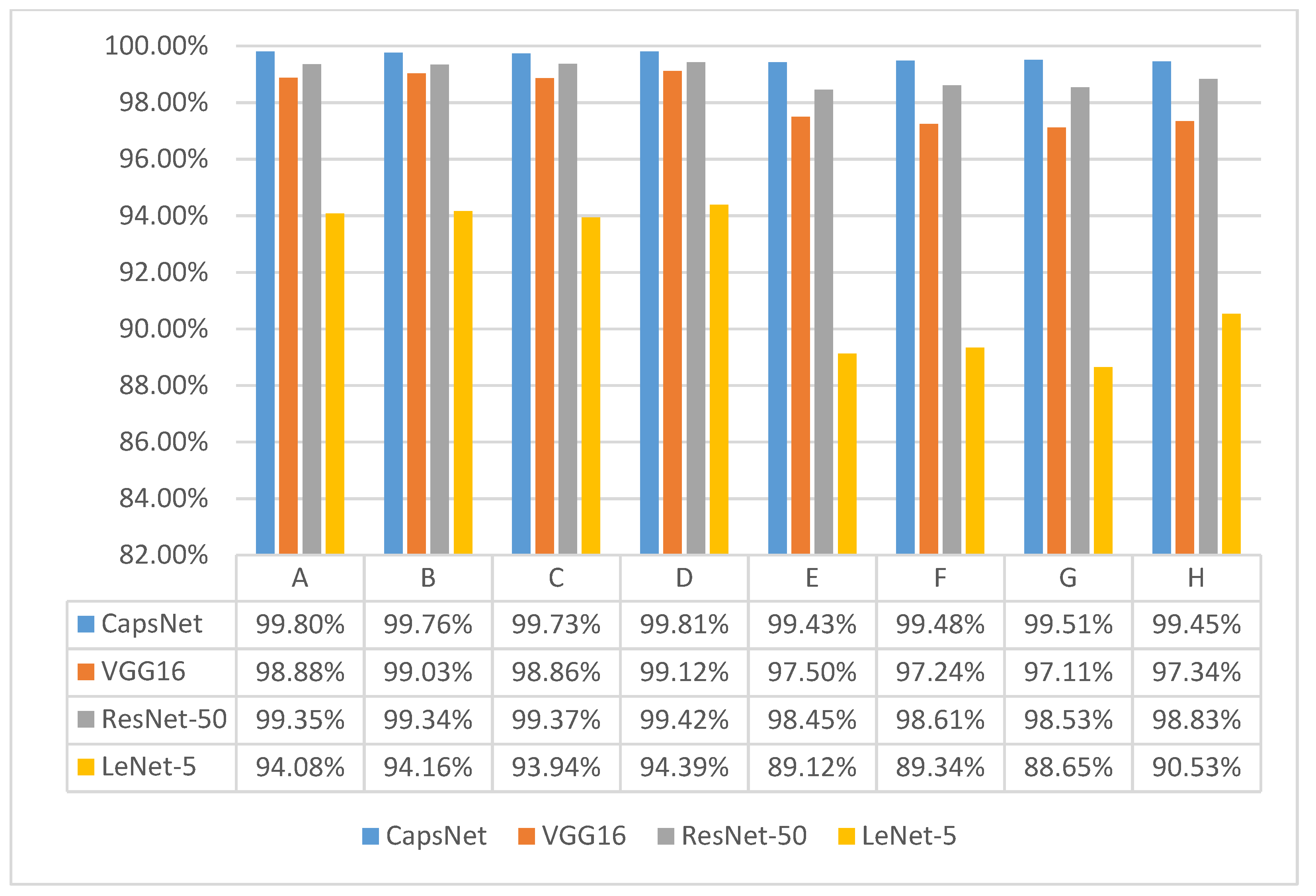
- The four-category dataset and the 10-category dataset have an average accuracy of 99.8% and 99.5% on GAFMTF-CapsNet. Using GAF and MTF images as two-channel inputs in the neural network allows the network to be trained to obtain both the static information by GAF and dynamic information by MTF for the vibration signal. For this signal processing method (GAFMTF), CapsNet has 1–2% higher diagnostic accuracy than VGG16 and ResNet-50, and 5–10% higher accuracy than LeNet-5.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, W.; Lee, H. An energy kurtosis demodulation technique for signal denoising and bearing fault detection. Meas. Sci. Technol. 2013, 24, 025601. [Google Scholar] [CrossRef]
- Yiakopoulos, C.T.; Gryllias, K.C.; Antoniadis, I.A. Rolling element bearing fault detection in industrial environments based on a K-means clustering approach. Expert Syst. Appl. 2011, 38, 2888–2911. [Google Scholar] [CrossRef]
- Fong, A.C.M.; Hui, S.C. An intelligent online machine fault diagnosis system. Comput. Control Eng. J. 2001, 12, 217–223. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, J.H.; Bi, F.R.; Lin, J.W.; Ma, W.P. A fault diagnosis approach for diesel engine valve train based on improved ITD and SDAG-RVM. Meas Sci. Technol. 2015, 26, 025003. [Google Scholar]
- Chen, B.J.; He, Z.J.; Chen, X.F.; Cao, H.R.; Cai, G.G.; Zi, Y.Y. A demodulating approach based on local mean decomposition and its applications in mechanical fault diagnosis. Meas. Sci. Technol. 2011, 22, 22. [Google Scholar] [CrossRef]
- Lei, Y.G.; He, Z.J.; Zi, Y.Y. Application of an intelligent classification method to mechanical fault diagnosis. Expert Syst. Appl. 2009, 36, 9941–9948. [Google Scholar] [CrossRef]
- Wang, D.; Tse, P.W.; Guo, W.; Miao, Q.A. Support vector data description for fusion of multiple health indicators for enhancing gearbox fault diagnosis and prognosis. Meas Sci. Technol. 2011, 22, 025102. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Zheng, Y.; Zhao, Z.Z.; Wang, J.P. Bearing Fault Diagnosis Based on Statistical Locally Linear Embedding. Sensors 2015, 15, 16225–16247. [Google Scholar] [CrossRef]
- Li, K.; Chen, P.; Wang, S.M. An Intelligent Diagnosis Method for Rotating Machinery Using Least Squares Mapping and a Fuzzy Neural Network. Sensors 2012, 12, 5919–5939. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rai, V.K.; Mohanty, A.R. Bearing fault diagnosis using FFT of intrinsic mode functions in Hilbert-Huang transform. Mech. Syst. Signal Process. 2007, 21, 2607–2615. [Google Scholar] [CrossRef]
- Pandya, D.H.; Upadhyay, S.H.; Harsha, S.P. Fault diagnosis of rolling element bearing with intrinsic mode function of acoustic emission data using APF-KNN. Expert Syst. Appl. 2013, 40, 4137–4145. [Google Scholar] [CrossRef]
- Li, B.; Chow, M.Y.; Tipsuwan, Y.; Hung, J.C. Neural-network-based motor rolling bearing fault diagnosis. IEEE Trans. Ind. Electron. 2000, 47, 1060–1069. [Google Scholar] [CrossRef] [Green Version]
- Santos, P.; Villa, L.F.; Renones, A.; Bustillo, A.; Maudes, J. An SVM-Based Solution for Fault Detection in Wind Turbines. Sensors 2015, 15, 5627–5648. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Hu, X.G.; Yang, F. Support vector machine with genetic algorithm for machinery fault diagnosis of high voltage circuit breaker. Measurement 2011, 44, 1018–1027. [Google Scholar] [CrossRef]
- Jia, F.; Lei, Y.G.; Lin, J.; Zhou, X.; Lu, N. Deep neural networks: A promising tool for fault characteristic mining and intelligent diagnosis of rotating machinery with massive data. Mech. Syst. Signal Process. 2016, 72–73, 303–315. [Google Scholar] [CrossRef]
- Guo, L.; Gao, H.L.; Huang, H.F.; He, X.; Li, S.C. Multifeatures Fusion and Nonlinear Dimension Reduction for Intelligent Bearing Condition Monitoring. Shock. Vib. 2016, 2016, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Simonyan, K.; Zisserman, A.J. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- He, K.; Ren, X.Z.S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Ince, T. Real-time broken rotor bar fault detection and classification by shallow 1D convolutional neural networks. Electr. Eng. 2019, 101, 599–608. [Google Scholar] [CrossRef]
- Abdeljaber, O.; Avci, O.; Kiranyaz, S.; Gabbouj, M.; Inman, D.J. Real-time vibration-based structural damage detection using one-dimensional convolutional neural networks. J. Sound Vib. 2017, 388, 154–170. [Google Scholar] [CrossRef]
- Ozcan, I.H.; Devecioglu, O.C.; Ince, T.; Eren, L.; Askar, M. Enhanced bearing fault detection using multichannel, multilevel 1D CNN classifier. Electr. Eng. 2021, 1–13. [Google Scholar] [CrossRef]
- He, J.; Li, X.; Chen, Y.; Chen, D.F.; Guo, J.; Zhou, Y. Deep Transfer Learning Method Based on 1D-CNN for Bearing Fault Diagnosis. Shock. Vib. 2021, 2021, 1–16. [Google Scholar] [CrossRef]
- Ding, X.X.; He, Q.B. Energy-Fluctuated Multiscale Feature Learning With Deep ConvNet for Intelligent Spindle Bearing Fault Diagnosis. IEEE Trans. Instrum. Meas. 2017, 66, 1926–1935. [Google Scholar] [CrossRef]
- Zhang, J.Q.; Sun, Y.; Guo, L.; Gao, H.L.; Hong, X.; Song, H.L. A new bearing fault diagnosis method based on modified convolutional neural networks. Chin. J. Aeronaut. 2020, 33, 439–447. [Google Scholar] [CrossRef]
- Hoang, D.T.; Kang, H.J. Rolling element bearing fault diagnosis using convolutional neural network and vibration image. Cogn. Syst. Res. 2019, 53, 42–50. [Google Scholar] [CrossRef]
- Li, G.Q.; Deng, C.; Wu, J.; Chen, Z.Y.; Xu, X.B. Rolling Bearing Fault Diagnosis Based on Wavelet Packet Transform and Convolutional Neural Network. Appl. Sci. 2020, 10, 770. [Google Scholar] [CrossRef] [Green Version]
- Pham, M.T.; Kim, J.M.; Kim, C.H. Accurate Bearing Fault Diagnosis under Variable Shaft Speed using Convolutional Neural Networks and Vibration Spectrogram. Appl. Sci. 2020, 10, 6385. [Google Scholar] [CrossRef]
- Sabour, S.; Frosst, N.; Hinton, G.E. Dynamic Routing Between Capsules. In NIPS’17: Proceedings of the 31st International Conference on Neural Information Processing, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 3859–3869. [Google Scholar]
- Yang, C.L.; Chen, Z.X.; Yang, C.Y. Sensor Classification Using Convolutional Neural Network by Encoding Multivariate Time Series as Two-Dimensional Colored Images. Sensors 2020, 20, 168. [Google Scholar] [CrossRef] [Green Version]
- Mitiche, I.; Morison, G.; Nesbitt, A.; Hughes-Narborough, M.; Stewart, B.G.; Boreha, P. Imaging Time Series for the Classification of EMI Discharge Sources. Sensors 2018, 18, 3098. [Google Scholar] [CrossRef] [Green Version]
- Bugueno, M.; Molina, G.; Mena, F.; Olivares, P.; Araya, M. Harnessing the power of CNNs for unevenly-sampled light-curves using Markov Transition Field. Astron. Comput. 2021, 35, 100461. [Google Scholar] [CrossRef]
- Oates, Z.W.T. Imaging Time-Series to Improve Classification and Imputation. In Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence, Las Vegas, NV, USA, 25–31 July 2015; pp. 3939–3945. [Google Scholar]
- Oates, Z.W.T. Encoding Time Series as Images for Visual Inspection and Classification Using Tiled Convolutional Neural Networks. In Proceedings of the Workshops at the Twenty-Ninth AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 25–30 January 2015; pp. 40–46. [Google Scholar]
- Loparo, K. Bearing vibration Data Set; Case Western Reserve University: Cleveland, OH, USA, 2003. [Google Scholar]
- Wan, L.J.; Gong, K.; Zhang, G.; Yuan, X.P.; Li, C.Y.; Deng, X.J. An Efficient Rolling Bearing Fault Diagnosis Method Based on Spark and Improved Random Forest Algorithm. IEEE Access 2021, 9, 37866–37882. [Google Scholar] [CrossRef]
- Wan, L.J.; Chen, Y.W.; Li, H.Y.; Li, C.Y. Rolling-Element Bearing Fault Diagnosis Using Improved LeNet-5 Network. Sensors 2020, 20, 1693. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.J.; Ding, X.X.; Zeng, Q.; Wang, L.M.; Shao, Y.M. Intelligent Rolling Bearing Fault Diagnosis via Vision ConvNet. IEEE Sens. J. 2021, 21, 6600–6609. [Google Scholar] [CrossRef]



| Fault Location | None | Inner | Roller | Outer | Load | |
|---|---|---|---|---|---|---|
| Label | 1 | 2 | 3 | 4 | ||
| A | train | 2304 | 2304 | 2304 | 2304 | 1 |
| test | 576 | 576 | 576 | 576 | ||
| B | train | 2304 | 2304 | 2304 | 2304 | 2 |
| test | 576 | 576 | 576 | 576 | ||
| C | train | 2304 | 2304 | 2304 | 2304 | 3 |
| test | 576 | 576 | 576 | 576 | ||
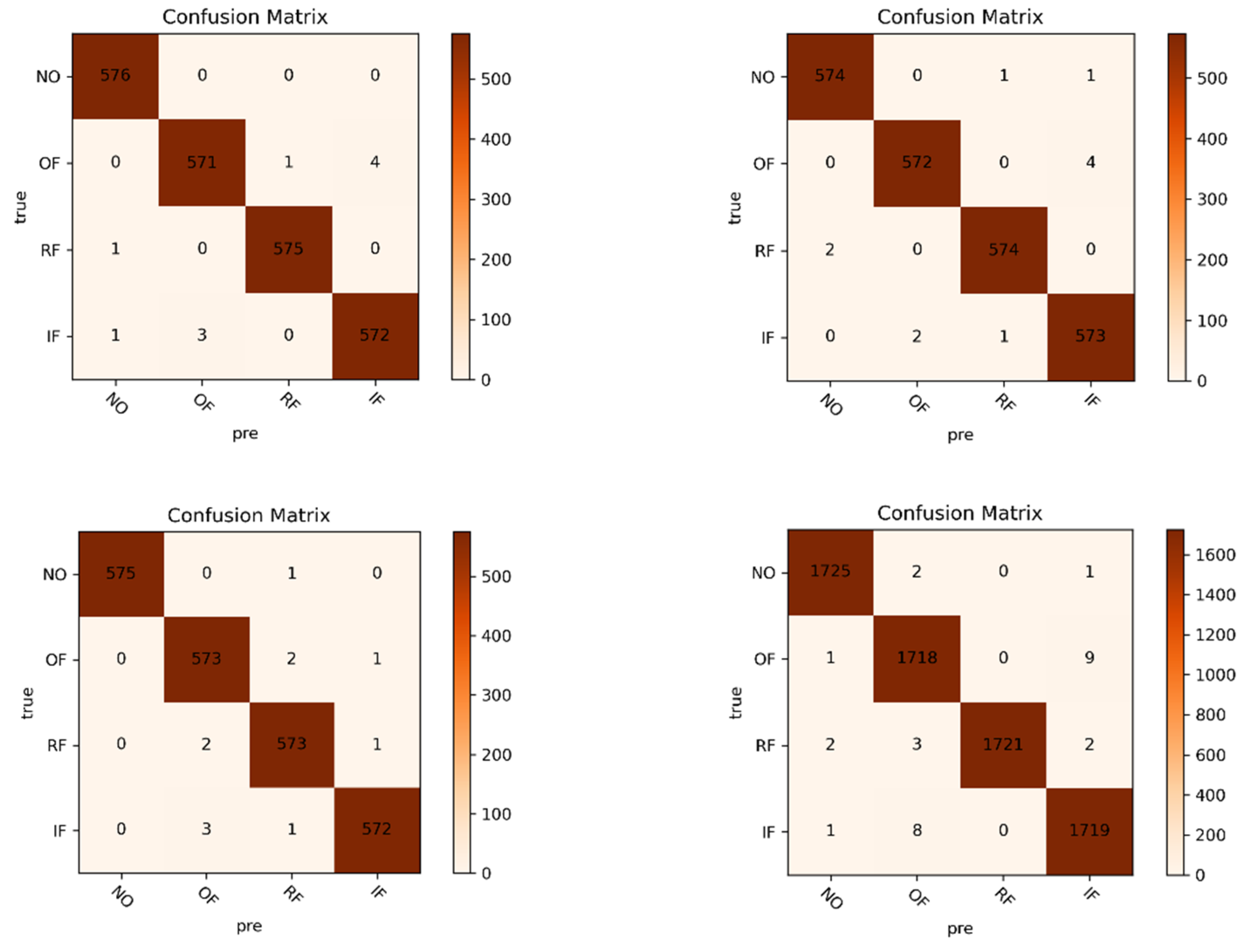
| D | train | 6912 | 6912 | 6912 | 6912 | 1,2,3 |
| test | 1728 | 1728 | 1728 | 1728 | ||
| Fault Location | None | Inner | Roller | Outer | Load | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Label | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| Diameter | 0 | 0.1778 | 0.3556 | 0.5334 | 0.1778 | 0.3556 | 0.5334 | 0.1778 | 0.3556 | 0.5334 | ||
| E | train | 768 | 768 | 768 | 768 | 768 | 768 | 768 | 768 | 768 | 768 | 1 |
| test | 192 | 192 | 192 | 192 | 192 | 192 | 192 | 192 | 192 | 192 | ||
| F | train | 768 | 768 | 768 | 768 | 768 | 768 | 768 | 768 | 768 | 768 | 2 |
| test | 192 | 192 | 192 | 192 | 192 | 192 | 192 | 192 | 192 | 192 | ||
| G | train | 768 | 768 | 768 | 768 | 768 | 768 | 768 | 768 | 768 | 768 | 3 |
| test | 192 | 192 | 192 | 192 | 192 | 192 | 192 | 192 | 192 | 192 | ||
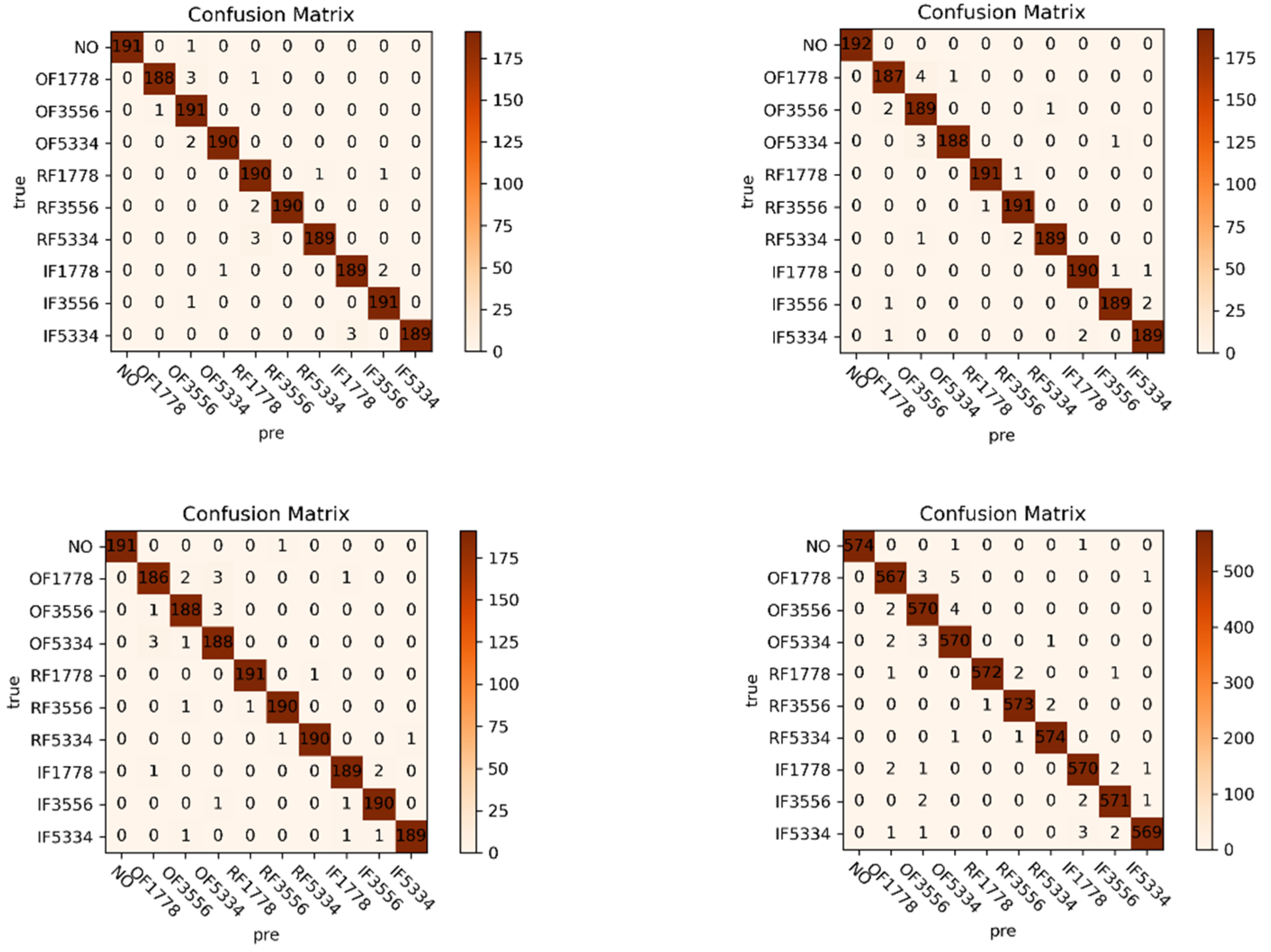
| H | train | 2304 | 2304 | 2304 | 2304 | 2304 | 2304 | 2304 | 2304 | 2304 | 2304 | 1,2,3 |
| test | 576 | 576 | 576 | 576 | 576 | 576 | 576 | 576 | 576 | 576 | ||
| Layer Type | Kernel Size /Caps Dimension | Kernel Channel /Caps Number | Padding | Output |
|---|---|---|---|---|
| Input | 128 × 128 × 2 | |||
| Convolution 1 | 3 × 3 | 64 | Yes | 128 × 128 × 128 |
| Convolution 2 | 3 × 3 | 128 | Yes | 128 × 128 × 128 |
| Pooling | 2 × 2 | 128 | No | 64 × 64 × 128 |
| Convolution 3 | 9 × 9 | 256 | Yes | 64 × 64 × 256 |
| PrimaryCaps | 16 | 64 | 32 × 32 × 16 × 64 | |
| DigitCaps | 16 | 10 | 16 × 10 | |
| Output | 10 |
| Layer Type | Kernel Size /Caps Dimension | Kernel Channel /Caps Number | Padding | Output |
|---|---|---|---|---|
| Input | 128 × 128 × 2 | |||
| Convolution 1 | 3 × 3 | 64 | Yes | 128 × 128 × 128 |
| Convolution 2 | 3 × 3 | 128 | Yes | 128 × 128 × 128 |
| Pooling | 2 × 2 | 128 | No | 64 × 64 × 128 |
| Convolution 3 | 9 × 9 | 256 | Yes | 64 × 64 × 256 |
| PrimaryCaps | 16 | 64 | 32 × 32 × 16 × 64 | |
| DigitCaps | 16 | 4 | 16 × 4 | |
| Output | 4 |
| Datasets | 6:4 | 7:3 | 8:2 | 9:1 |
|---|---|---|---|---|
| D (4-category) | 96.54% | 98.77% | 99.81% | 99.82% |
| H (10-category) | 92.39% | 97.21% | 99.45% | 99.43% |
| Methods | Researchers | Categories | Accuracy |
|---|---|---|---|
| GAFMTF-CapsNet | 4 | 99.81% | |
| 10 | 99.51% | ||
| Spark-IRFA | Wan, L. J. [36] | 4 | 98.12% |
| VI-CNN | Hoang, D. T. [26] | 4 | 100% |
| STFT-CNN | Pham, M. T. [28] | 4 | 99.4% |
| WPT-CNN | Li, G. Q. [27] | 6 | 99.44% |
| Improved 2D LeNet-5 network | Wan, L. J. [37] | 10 | 99.25% |
| Improved 1D LeNet-5 network | Wan, L. J. [37] | 10 | 99.66% |
| VCN | Wang, Y. J. [38] | 10 | 99.53 |
| DFCNN | Zhang, J. Q. [25] | 10 | 100% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, B.; Zhang, H.; Sun, M.; Wu, F. A New Bearing Fault Diagnosis Method Based on Capsule Network and Markov Transition Field/Gramian Angular Field. Sensors 2021, 21, 7762. https://doi.org/10.3390/s21227762
Han B, Zhang H, Sun M, Wu F. A New Bearing Fault Diagnosis Method Based on Capsule Network and Markov Transition Field/Gramian Angular Field. Sensors. 2021; 21(22):7762. https://doi.org/10.3390/s21227762
Chicago/Turabian StyleHan, Bin, Hui Zhang, Ming Sun, and Fengtong Wu. 2021. "A New Bearing Fault Diagnosis Method Based on Capsule Network and Markov Transition Field/Gramian Angular Field" Sensors 21, no. 22: 7762. https://doi.org/10.3390/s21227762
APA StyleHan, B., Zhang, H., Sun, M., & Wu, F. (2021). A New Bearing Fault Diagnosis Method Based on Capsule Network and Markov Transition Field/Gramian Angular Field. Sensors, 21(22), 7762. https://doi.org/10.3390/s21227762






