Blind Watermarking of Color Medical Images Using Hadamard Transform and Fractional-Order Moments
Abstract
:1. Introduction
2. Related Work
- Our method contributes to this evidence by using MFrLFMs. It is known for its stability and invariance to many geometric attacks, which keep robust capability over many attacks such as scaling, rotation, translation, etc.
- In addition, MFrLFMs are not restricted to integer-order values, which give them a high ability to represent the finest details in the image rather than their rival’s orthogonal polynomials of integer order.
- The use of Walsh–Hadamard transform comes under generalized Fourier transforms, known as low-computations compilations. Hadamard transform is a perpendicular function, which is composed of (−1 and +1) values only. Therefore, there is no data redundancy, which makes it widely used in many image processing analyses. FWHT is elastic to low-quality compression compared with other transformations such as traditional DCT and DWT, making it robust to most common image processing attacks.
- The proposed method introduced a new combination method of these multi-channel fractional Legendre–Fourier moments (MFrLFMs) and Hadamard transformation in a holistic way to achieve the main target of the proposed method, which represents robustness to both geometric and image processing attacks.
- The evaluation of our proposed method has been assessed for many common types of attacks and visual imperceptibility measurements.
3. Preliminaries
3.1. Fast Walsh–Hadamard Transformation Technique
3.2. MFrLFM Representation for RGB Color Image
3.3. Geometrical Invariances of MFrLFMs
3.3.1. Rotational Invariance
3.3.2. Scale Invariance
3.3.3. Translation Invariance
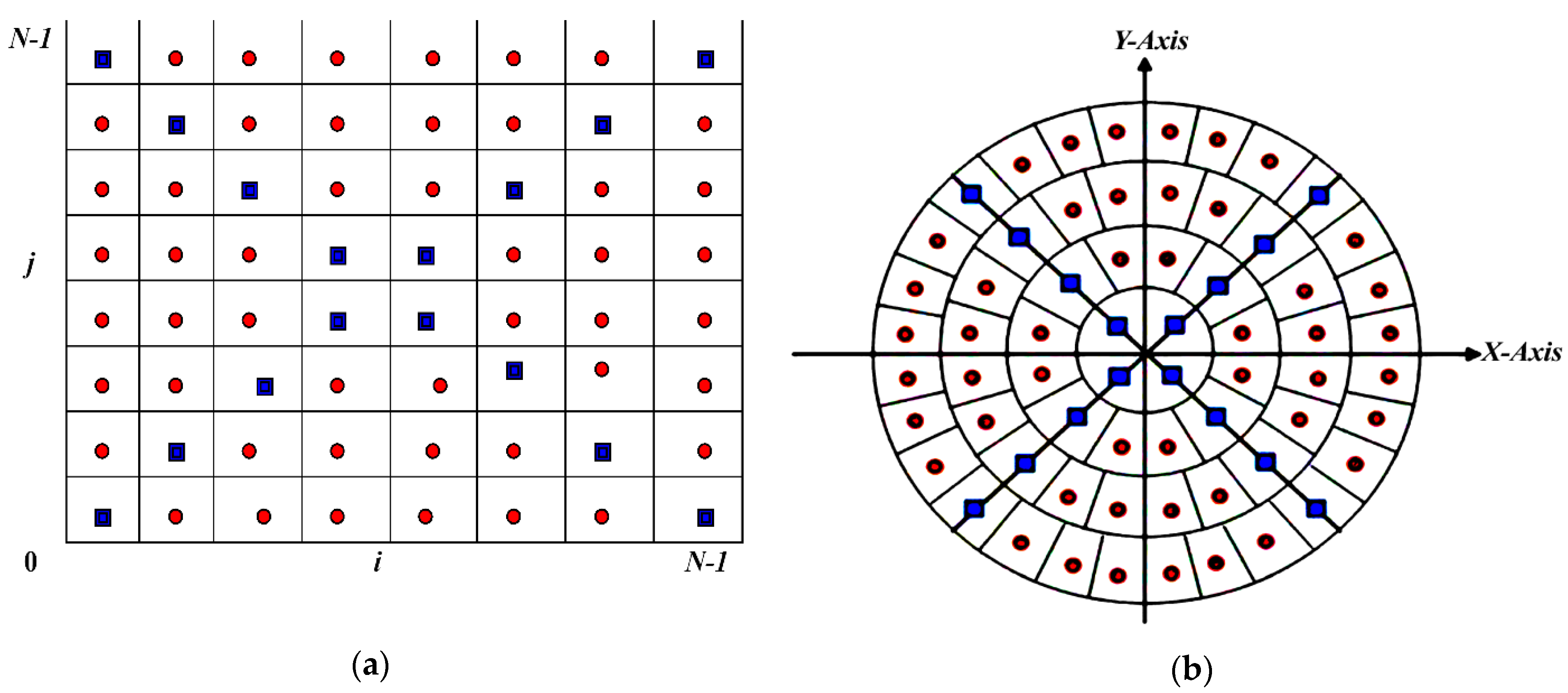
3.4. Accurate MFrLFM Computation
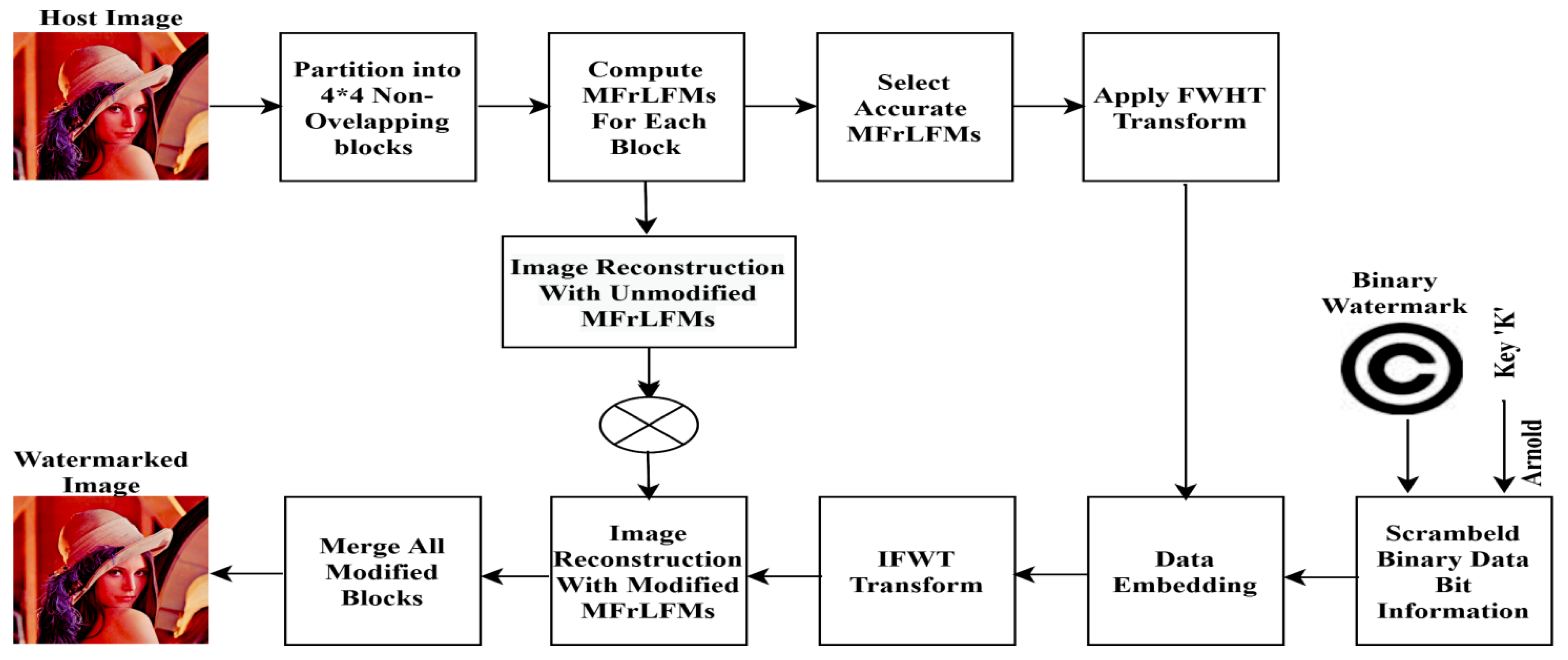
4. Proposed Blind Watermarking
4.1. Watermarking Embedding Process
4.2. Blind Watermarking Extraction
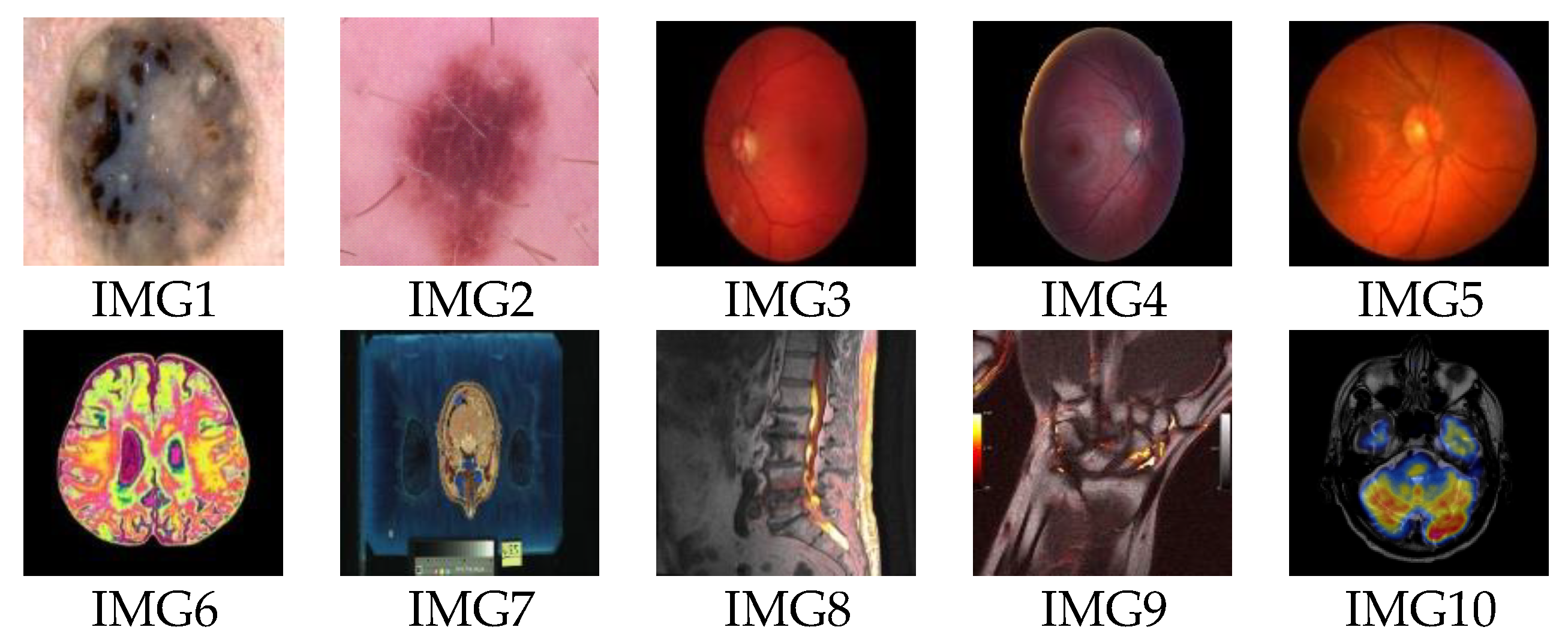
5. Experimental Results
5.1. Visual Imperceptibility
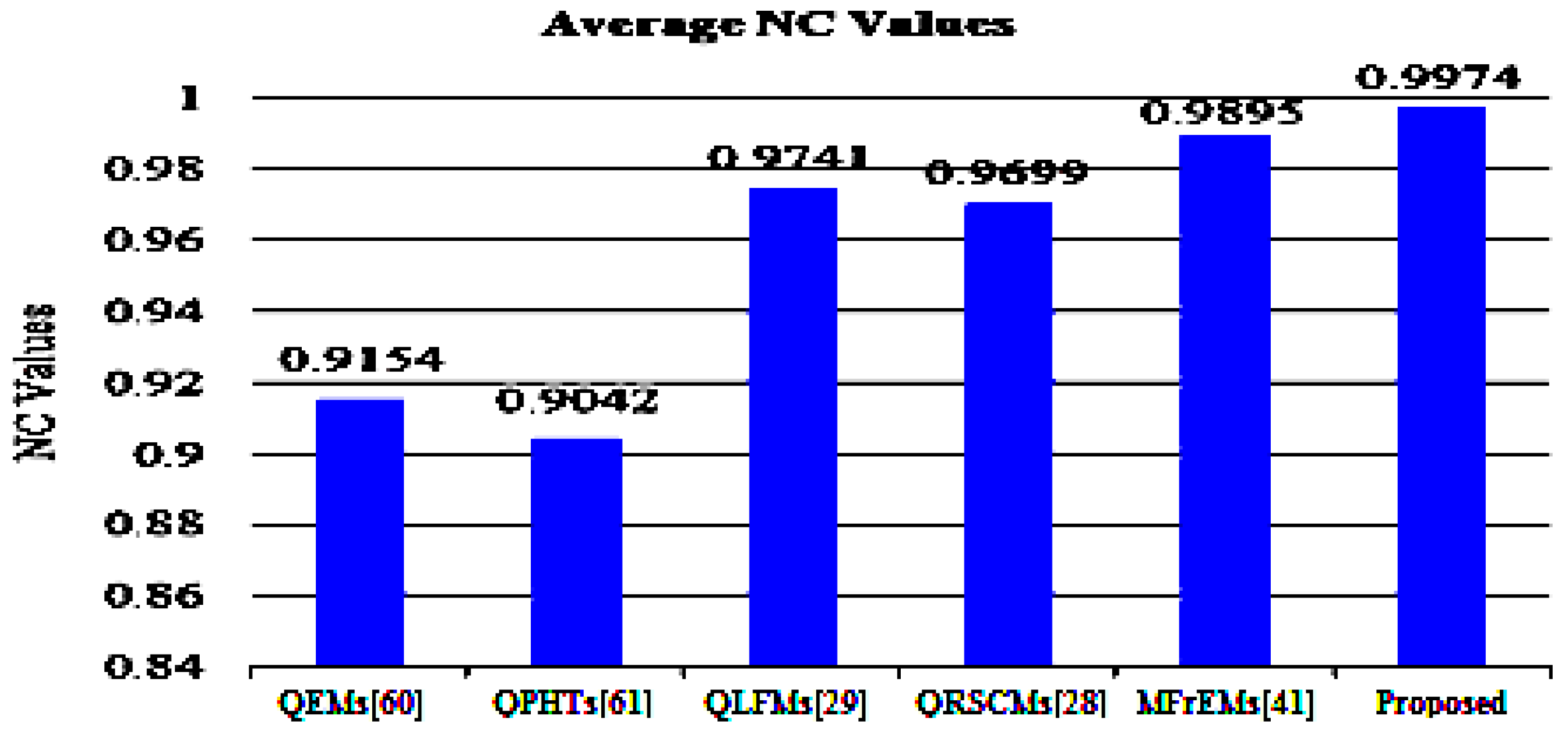
5.2. Robustness Evaluation
5.3. Capacity Evaluation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Qi, X.; Qi, J. A robust content-based digital image watermarking scheme. Signal Process. 2007, 87, 1264–1280. [Google Scholar] [CrossRef]
- Roy, S.S.; Basu, A.; Chattopadhyay, A. On the implementation of a copyright protection scheme using digital image watermarking. Multimed. Tools Appl. 2020, 79, 13125–13138. [Google Scholar] [CrossRef]
- Al-khafaji, A.; Nur, N.; Sjarif, N.N.A.; Mahdi, M.; Shafry, M.; Rahim, M. A review and open issues of diverse text watermarking techniques in spatial domain. J. Theor. Appl. Inf. Technol. 2018, 96, 5819–5840. [Google Scholar]
- Jibrin, B.; Tekanyi, A.; Sani, S. Image Watermarking Algorithm in Frequency Domain: A Review of Technical Literature. ATBU J. Sci. Technol. Educ. 2019, 7, 257–263. [Google Scholar]
- Agarwal, N.; Singh, A.K.; Singh, P.K. Survey of robust and imperceptible watermarking. Multimed. Tools Appl. 2019, 78, 8603–8633. [Google Scholar] [CrossRef]
- Prabha, K.; Sam, I.S. An effective robust and imperceptible blind color image watermarking using WHT. J. King Saud Univ. Comput. Inf. Sci. 2020, in press. [Google Scholar] [CrossRef]
- Naidu, S.; Upadhyay, G. A Review on Blind Watermarking Technique for Copyright Protection of Image-based on DCT, DWT, and SVD Domain. Int. Res. J. Eng. Technol. 2020, 7, 364–366. [Google Scholar]
- Anbarjafari, G.; Ozcinar, C. Imperceptible non-blind watermarking and robustness against tone mapping operation attacks for high dynamic range images. Multimed. Tools Appl. 2018, 77, 24521–24535. [Google Scholar] [CrossRef]
- Izhar, M.N. A Semi Blind Watermarking Technique for Copyright Protection of Image-Based on DCT and SVD Domain. Glob. J. Res. Eng. 2017, 16, 364–366. [Google Scholar]
- Valandar, M.Y.; Barani, M.J.; Ayubi, P. A blind and robust color images watermarking method based on block transform and secured by modified 3-dimensional Hénon map. Soft Comput. 2020, 24, 771–794. [Google Scholar] [CrossRef]
- Feng, B.; Li, X.; Jie, Y.; Guo, C.; Fu, H. A Novel Semi-fragile Digital Watermarking Scheme for Scrambled Image Authentication and Restoration. Mob. Netw. Appl. 2020, 25, 82–94. [Google Scholar] [CrossRef]
- Molina-Garcia, J.; Garcia-Salgado, B.P.; Ponomaryov, V.; Reyes-Reyes, R.; Sadovnychiy, S.; Cruz-Ramos, C. An effective fragile watermarking scheme for color image tampering detection and self-recovery. Signal Process. Image Commun. 2020, 81, 115725. [Google Scholar] [CrossRef]
- Varma, P.R.K.; Kumari, V.V.; Kumar, S.S. Spatial Domain Blind Watermarking for Digital Images. In Progress in Computing, Analytics and Networking; Springer: Singapore, 2018; Volume 710. [Google Scholar] [CrossRef]
- Su, Q.; Chen, B. Robust color image watermarking technique in the spatial domain. Soft Comput. 2018, 22, 91–106. [Google Scholar] [CrossRef]
- Yuan, Z.; Liu, D.; Zhang, X.; Su, Q. New image blind watermarking method based on two-dimensional discrete cosine transform. Optik 2020, 204, 164152. [Google Scholar] [CrossRef]
- Fares, K.; Amine, K.; Salah, E. A robust blind color image watermarking based on Fourier transform domain. Optik 2020, 208, 164562. [Google Scholar] [CrossRef]
- Shukla, M. A Comparative Study of Wavelet and Curvelet Transform for Image Denoising. IOSR J. Electron. Commun. Eng. 2013, 7, 63–68. [Google Scholar] [CrossRef]
- Yuan, Z.; Su, Q.; Liu, D.; Zhang, X. A blind image watermarking scheme combining spatial domain and frequency domain. Vis. Comput. 2020, 37, 1867–1881. [Google Scholar] [CrossRef]
- Ma, B.; Chang, L.; Wang, C.; Li, J.; Wang, X.; Shi, Y.Q. Robust image watermarking using invariant accurate polar harmonic Fourier moments and chaotic mapping. Signal Process. 2020, 172, 107544. [Google Scholar] [CrossRef]
- Yamni, M.; Daoui, A.; El Ogri, O.; Karmouni, H.; Sayyouri, M.; Qjidaa, H.; Flusser, J. Fractional Charlier moments for image reconstruction and image watermarking. Signal Process. 2020, 171, 107509. [Google Scholar] [CrossRef]
- Wang, C.; Wang, X.; Xia, Z.; Zhang, C. Ternary radial harmonic Fourier moments based robust stereo image zero-watermarking algorithm. Inf. Sci. 2019, 470, 109–120. [Google Scholar] [CrossRef]
- Ernawan, F. Tchebichef image watermarking along the edge using YCoCg-R color space for copyright protection. Int. J. Electr. Comput. Eng. 2019, 9, 1850–1860. [Google Scholar] [CrossRef]
- Singh, M.K.; Kumar, S.; Ali, M.; Saini, D. Application of a novel image moment computation in X-ray and M.R.I. image watermarking. IET Image Process. 2021, 15, 666–682. [Google Scholar] [CrossRef]
- Yamni, M.; Karmouni, H.; Daoui, A.; el ogri, O.; Sayyouri, M.; Qjidaa, H. Blind Image Zero-Watermarking Algorithm Based on Radial Krawtchouk Moments and Chaotic System. In Proceedings of the 2020 International Conference on Intelligent Systems and Computer Vision (ISCV), Fez, Morocco, 9–11 June 2020; pp. 1–7. [Google Scholar] [CrossRef]
- Ernawan, F.; Kabir, M.N. An Improved Watermarking Technique for Copyright Protection Based on Tchebichef Moments. IEEE Access 2019, 7, 151985–152003. [Google Scholar] [CrossRef]
- Chen, B.; Shu, H.; Coatrieux, G.; Chen, G.; Sun, X.; Coatrieux, J. Color Image Analysis by Quaternion-Type Moments. J. Math. Imaging Vis. 2014, 51, 124–144. [Google Scholar] [CrossRef]
- Darwish, M.; Hosny, K.; Kamal, S. Improved Color Image Watermarking Using Logistic Maps and Quaternion Legendre-Fourier Moments. In Multimedia Security Using Chaotic Maps: Principles and Methodologies; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar] [CrossRef]
- Hosny, K.; Darwish, M. Resilient Color Image Watermarking Using Accurate Quaternion Radial Substituted Chebyshev Moments. ACM Trans. Multimed. Comput. Commun. Appl. 2019, 15, 46. [Google Scholar] [CrossRef]
- Hosny, K.M.; Darwish, M.M. Robust color image watermarking using invariant quaternion Legendre-Fourier moments. Multimed. Tools Appl. 2018, 77, 24727–24750. [Google Scholar] [CrossRef]
- Li, J.; Yu, C.; Gupta, B.B.; Ren, X. Color image watermarking scheme based on quaternion Hadamard transform and Schur decomposition. Multimed. Tools Appl. 2018, 77, 4545–4561. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, S.; Yang, J. Color image watermark decoder by modeling quaternion polar harmonic transform with B.K.F. distribution. Signal Process. Image Commun. 2020, 88, 115946. [Google Scholar] [CrossRef]
- Xia, Z.; Wang, X.; Li, X.; Wang, C.; Unar, S.; Wang, M.; Zhao, T. Efficient copyright protection for three C.T. images based on quaternion polar harmonic Fourier moments. Signal Process. 2019, 164, 368–379. [Google Scholar] [CrossRef]
- Huynh-The, T.; Hua, C.H.; Tu, N.A.; Hur, T.; Bang, J.; Kim, D.; Amin, M.B.; Kang, B.H.; Seung, H.; Lee, S. Selective bit embedding scheme for robust blind color image watermarking. Inf. Sci. 2018, 426, 1–18. [Google Scholar] [CrossRef]
- Xia, Z.; Wang, X.; Wang, C.; Ma, B.; Wang, M.; Shi, Y. Local quaternion polar harmonic Fourier moments-based multiple zero-watermarking scheme for color medical images. Knowl.-Based Syst. 2021, 216, 106568. [Google Scholar] [CrossRef]
- Xia, Z.; Wang, X.; Wang, M.; Unar, S.; Wang, C.; Liu, Y.; Li, X. Geometrically Invariant Color Medical Image Null-Watermarking Based on Precise Quaternion Polar Harmonic Fourier Moments. IEEE Access 2019, 7, 122544–122560. [Google Scholar] [CrossRef]
- Yamni, M.; Karmouni, H.; Sayyouri, M.; Qjidaa, H. Image watermarking using separable fractional moments of Charlier–Meixner. J. Frankl. Inst. 2021, 358, 2535–2560. [Google Scholar] [CrossRef]
- Liu, X.; Han, G.; Wu, J.; Shao, Z.; Coatrieux, G.; Shu, H. Fractional Krawtchouk Transform with an Application to Image Watermarking. IEEE Trans. Signal Process. 2017, 65, 1894–1908. [Google Scholar] [CrossRef]
- Yang, H.; Qi, S.; Tian, J.; Niu, P.; Wang, X. Robust and discriminative image representation: Fractional-order Jacobi-Fourier moments. Pattern Recognit. 2021, 115, 107898. [Google Scholar] [CrossRef]
- Xiao, B.; Luo, J.; Bi, X.; Li, W.; Chen, B. Fractional discrete Tchebyshev moments and their applications in image encryption and watermarking. Inf. Sci. 2020, 516, 545–559. [Google Scholar] [CrossRef]
- Hosny, K.M.; Darwish, M.M.; Fouda, M.M. New Color Image Zero-Watermarking Using Orthogonal Multi-Channel Fractional-Order Legendre-Fourier Moments. IEEE Access 2021, 9, 91209–91219. [Google Scholar] [CrossRef]
- Hosny, K.M.; Darwish, M.M.; Fouda, M.M. Robust Color Images Watermarking Using New Fractional-Order Exponent Moments. IEEE Access 2021, 9, 47425–47435. [Google Scholar] [CrossRef]
- Vaidya, P.; Pvssr, C.M. A robust semi-blind watermarking for color images based on multiple decompositions. Multimed. Tools Appl. 2017, 76, 25623–25656. [Google Scholar] [CrossRef]
- Elbaşı, E. M-SVD based Quality Measurement in Hybrid non-blind Watermarked Medical Images. In Proceedings of the 2020 43rd International Conference on Telecommunications and Signal Processing (TSP), Milan, Italy, 7–9 July 2020. [Google Scholar] [CrossRef]
- Huh, J.-H.; Kim, T.-J. A location-based mobile health care facility search system for senior citizens. J. Supercomput. 2019, 75, 1831–1848. [Google Scholar] [CrossRef]
- Hosny, K.M.; Darwish, M.M. New geometrically invariant multiple zero-watermarking algorithm for color medical images. Biomed. Signal Process. Control. 2021, 70, 103007. [Google Scholar] [CrossRef]
- Soualmi, A.; Alti, A.; Laouamer, L. Multiple Blind Watermarking Framework for Security and Integrity of Medical Images in E-Health Applications. Int. J. Comput. Vis. Image Process. 2021, 11, 1–16. [Google Scholar] [CrossRef]
- Sun, X.; Bo, S. A blind digital watermarking for color medical images based on P.C.A. In Proceedings of the 2010 IEEE International Conference on Wireless Communications, Networking and Information Security, Beijing, China, 25–27 June 2010; pp. 421–427. [Google Scholar] [CrossRef]
- Meenakshi, K.; Rao, C.S.; Prasad, K.S. A Robust Watermarking Scheme Based Walsh-Hadamard Transform and S.V.D. Using ZIG ZAG Scanning. In Proceedings of the 2014 International Conference on Information Technology, Bhubaneswar, India, 22–24 December 2014; pp. 167–172. [Google Scholar] [CrossRef]
- Erfani, S.; Babolian, E.; Javadi, S.; Shamsi, M. Stable evaluations of fractional derivative of the Müntz–Legendre polynomials and application to fractional differential equations. J. Comput. Appl. Math. 2019, 348, 70–88. [Google Scholar] [CrossRef]
- Hosny, K.M.; Darwish, M.M.; Aboelenen, T. New fractional-order Legendre-Fourier moments for pattern recognition applications. Pattern Recognit. 2020, 103, 107324. [Google Scholar] [CrossRef]
- Suk, T.; Flusser, J. Affine Moment Invariants of Color Images. In Computer Analysis of Images and Patterns; Jiang, X., Petkov, N., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5702. [Google Scholar] [CrossRef]
- Hosny, K.M.; Darwish, M.M. A kernel-based method for fast and accurate computation of PHT in polar coordinates. J. Real-Time Image Process. 2019, 16, 1235–1247. [Google Scholar] [CrossRef]
- Hosny, K.M.; Darwish, M.M. Highly accurate and numerically stable higher order QPCET moments for color image representation. Pattern Recognit. Lett. 2017, 97, 29–36. [Google Scholar] [CrossRef]
- Upneja, R.; Pawlak, M.; Sahan, A.M. An accurate approach for the computation of polar harmonic transforms. Optik 2018, 158, 623–633. [Google Scholar] [CrossRef]
- Yang, H.-Y.; Wang, X.-Y.; Wang, P.; Niu, P.-P. Geometrically resilient digital watermarking scheme based on radial harmonic Fourier moments magnitude. AEU Int. J. Electron. Commun. 2015, 69, 389–399. [Google Scholar] [CrossRef]
- Xin, Y.; Liao, S.; Pawlak, M. Circularly orthogonal moments for geometrically robust image watermarking. Pattern Recognit. 2007, 40, 3740–3752. [Google Scholar] [CrossRef]
- Color Melanoma Images. Available online: https://www.isic-archive.com (accessed on 1 May 2021).
- Color Retinal Images. Available online: https://www5.cs.fau.de (accessed on 1 May 2021).
- Color Anatomical Images. Available online: https://www.nlm.nih.gov (accessed on 1 May 2021).
- Wang, X.Y.; Yang, H.Y.; Niu, P.P.; Wang, C.P. Quaternion exponent moments based robust color image watermarking. J. Comput. Res. Dev. 2016, 53, 651–665. [Google Scholar]
- Xu, H.; Kang, X.; Chen, Y.; Wang, Y. Rotation and scale invariant image watermarking based on polar harmonic transforms. Optik 2019, 183, 401–414. [Google Scholar] [CrossRef]



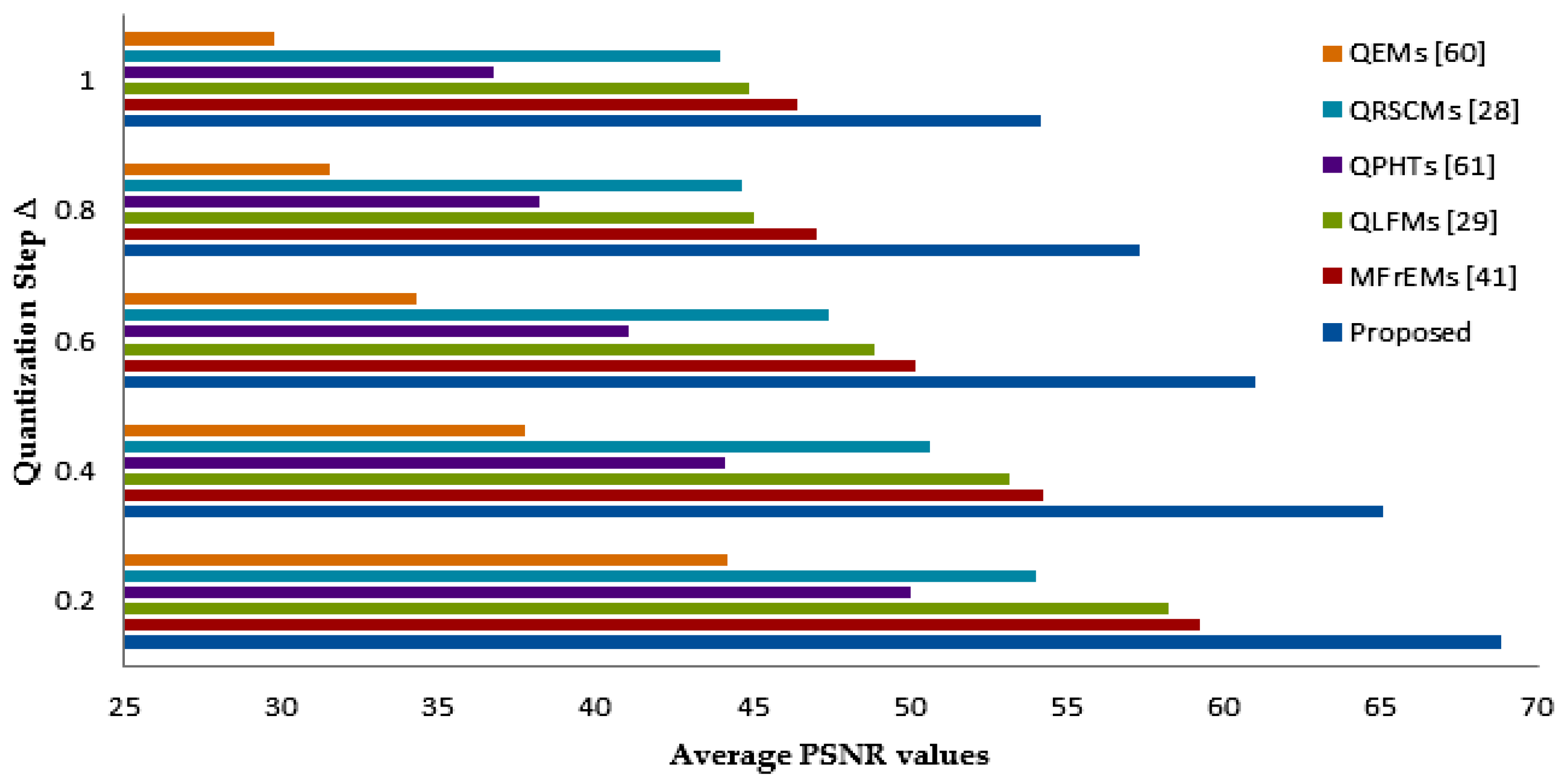

| Quantization Step ∆ | QEMs [60] | QPHTs [61] | QRSCMs [28] | QLFMs [29] | MfrEMs [41] | Proposed Method |
|---|---|---|---|---|---|---|
| 0.2 | 44.20 | 50.03 | 54.03 | 58.25 | 59.27 | 68.84 |
| 0.4 | 37.78 | 44.12 | 50.67 | 53.21 | 54.24 | 66.42 |
| 0.6 | 34.31 | 41.08 | 47.46 | 48.86 | 50.21 | 61.03 |
| 0.8 | 31.51 | 38.25 | 44.67 | 45.05 | 47.05 | 57.32 |
| 1.0 | 29.81 | 36.78 | 43.97 | 44.91 | 46.41 | 54.21 |
| Attacks | BER | NC | Extracted Watermark | |
|---|---|---|---|---|
| No Attack | 0 | 1 |  | |
| Rotation Attack | 5° | 0 | 1 |  |
| 15° | 0 | 1 |  | |
| 25° | 0 | 1 |  | |
| 65° | 0 | 1 |  | |
| Scaling Attack | 0.5 | 0.0023 | 0.9962 |  |
| 0.75 | 0 | 1 |  | |
| 1.25 | 0 | 1 |  | |
| 1.5 | 0 | 1 |  | |
| 2 | 0 | 1 |  | |
| Translation Attack | (15,2) | 0 | 1 |  |
| (20,20) | 0 | 1 |  | |
| (2,15) | 0 | 1 |  | |
| (0,50) | 0.0001 | 0.9998 |  | |
| (50,0) | 0.0001 | 0.9998 |  | |
| Shearing Attack | (0–1%) | 0.0075 | 0.9932 |  |
| Magnification | (1.75) | 0 | 1 |  |
| Cropping, Right | (25%) | 0.0146 | 0.9820 |  |
| Cropping, Top | (25%) | 0.0068 | 0.9916 |  |
| Cropping, Middle | (25%) | 0 | 1 |  |
| Attacks | BER | NC | Extracted Watermark | |
|---|---|---|---|---|
| JPEG Compression | 30 | 0 | 1 |  |
| 40 | 0 | 1 |  | |
| 50 | 0 | 1 |  | |
| 60 | 0 | 1 |  | |
| 70 | 0 | 1 |  | |
| 90 | 0 | 1 |  | |
| Motion Blur | (3,3) | 0 | 1 |  |
| (4,8) | 0 | 1 |  | |
| Lossy Compression (80) | 0 | 1 |  | |
| Salt and Pepper (0.03) | 0 | 1 |  | |
| Gaussian (0.03) | 0 | 1 |  | |
| Gaussian Low-Pass (3,3) | 0 | 1 |  | |
| Poisson Noise | 0 | 1 |  | |
| Speckle Noise Attack | 0 | 1 |  | |
| Median Filter Attack | 0.0002 | 0.9972 |  | |
| Average Filter Attack (3,3) | 0.0003 | 0.9961 |  | |
| Sharpen Attack | 0.0001 | 0.9998 |  | |
| Histogram Equalization | 0 | 1 |  | |
| Attacks | QEMs [60] | QPHTs [61] | QLFMs [29] | QRSCMs [28] | MFrEMs [41] | Proposed Method | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rotation Angle |  | Ber = 0.0703 Nc = 0.9143 |  | Ber = 0.1582 Nc = 0.7850 |  | Ber = 0.0479 Nc = 0.9409 |  | Ber = 0.0479 Nc = 0.9408 |  | Ber = 0.0195 Nc = 0.9759 |  | Ber = 0.0022 Nc = 0.9989 | |
 | Ber = 0.0557 Nc = 0.9316 |  | Ber = 0.1533 Nc = 0.7941 |  | Ber = 0.0361 Nc = 0.9551 |  | Ber = 0.0449 Nc = 0.9445 |  | Ber = 0.0176 Nc = 0.9782 |  | Ber = 0.0050 Nc = 0.9953 | ||
 | Ber = 0.0547 Nc = 0.9322 |  | Ber = 0.1514 Nc = 0.7945 |  | Ber = 0.0459 Nc = 0.9439 |  | Ber = 0.0459 Nc = 0.9434 |  | Ber = 0.0195 Nc = 0.9758 |  | Ber = 0.0025 Nc = 0.9984 | ||
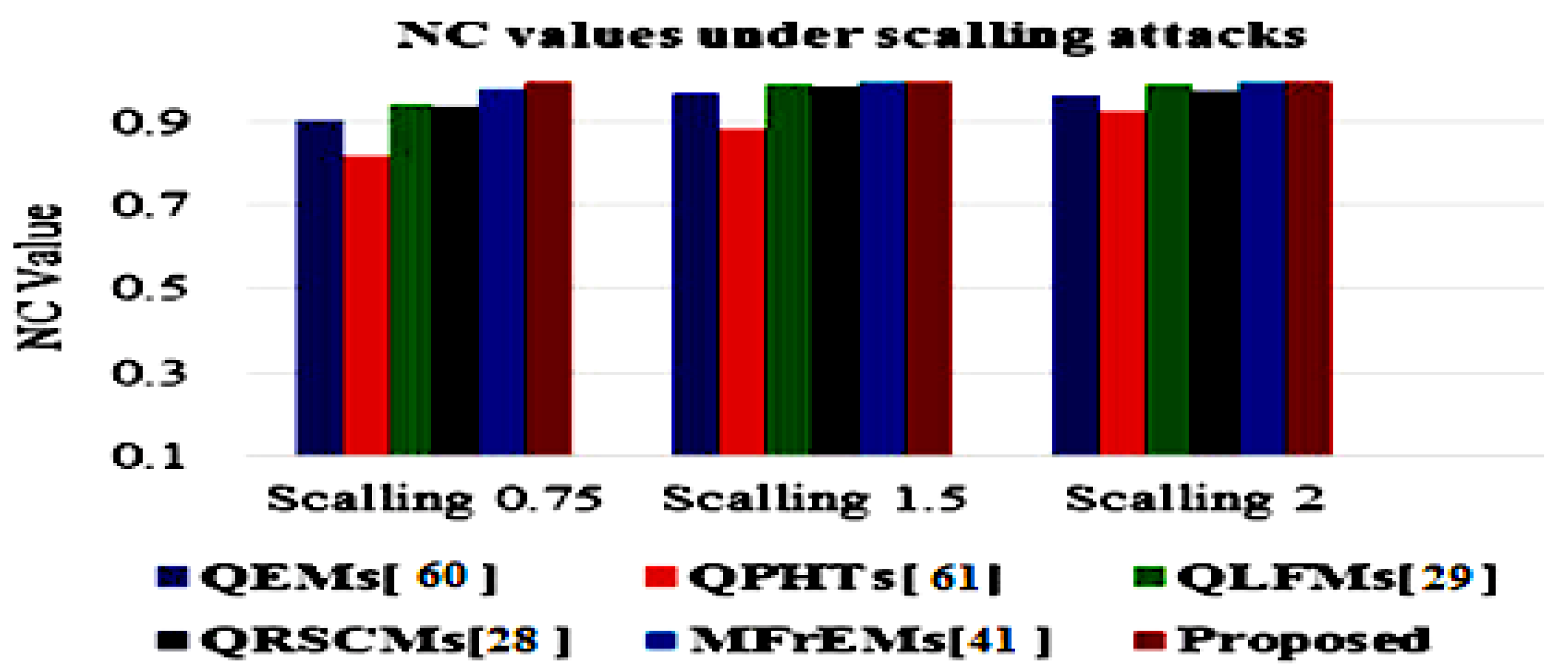
| Scaling Factor | 0.75 |  | Ber = 0.0781 Nc = 0.9048 |  | Ber = 0.1377 Nc = 0.8146 |  | Ber = 0.0469 Nc = 0.9424 |  | Ber = 0.0518 Nc = 0.9374 |  | Ber = 0.0166 Nc = 0.9794 |  | Ber = 0.0084 Nc = 0.9922 |
| 1.5 |  | Ber = 0.0283 Nc = 0.9652 |  | Ber = 0.0898 Nc = 0.8825 |  | Ber = 0.0098 Nc = 0.9880 |  | Ber = 0.0127 Nc = 0.9843 |  | Ber = 0.0049 Nc = 0.9940 |  | Ber = 0.0035 Nc = 0.9954 | |
| 2 |  | Ber = 0.0322 Nc = 0.9605 |  | Ber = 0.0586 Nc = 0.9251 |  | Ber = 0.0078 Nc = 0.9904 |  | Ber = 0.0205 Nc = 0.9745 |  | Ber = 0.0039 Nc = 0.9952 |  | Ber = 0.0023 Nc = 0.9968 | |
| Translation | (H3,V3) |  | Ber = 0.0186 Nc = 0.9770 |  | Ber = 0.0625 Nc = 0.9237 |  | Ber = 0.0205 Nc = 0.9745 |  | Ber = 0.0107 Nc = 0.9867 |  | Ber = 0.0039 Nc = 0.9952 |  | Ber = 0.0012 Nc = 0.9974 |
| (H6,V6) |  | Ber = 0.0479 Nc = 0.9412 |  | Ber = 0.0635 Nc = 0.9226 |  | Ber = 0.0215 Nc = 0.9736 |  | Ber = 0.0205 Nc = 0.9747 |  | Ber = 0.0049 Nc = 0.9940 |  | Ber = 0.0014 Nc = 0.9979 | |
| Compression | JPEG(80) |  | Ber = 0.0205 Nc = 0.9745 |  | Ber = 0.0859 Nc = 0.8839 |  | Ber = 0.0127 Nc = 0.9843 |  | Ber = 0.0186 Nc = 0.9769 |  | Ber = 0.0059 Nc = 0.9928 |  | Ber = 0.0025 Nc = 0.9986 |
| JPEG(90) |  | Ber = 0.0107 Nc = 0.9867 |  | Ber = 0.0693 Nc = 0.9107 |  | Ber = 0.0029 Nc = 0.9964 |  | Ber = 0.0049 Nc = 0.9940 |  | Ber = 0.0039 Nc = 0.9952 |  | Ber = 0.0005 Nc = 0.9998 | |
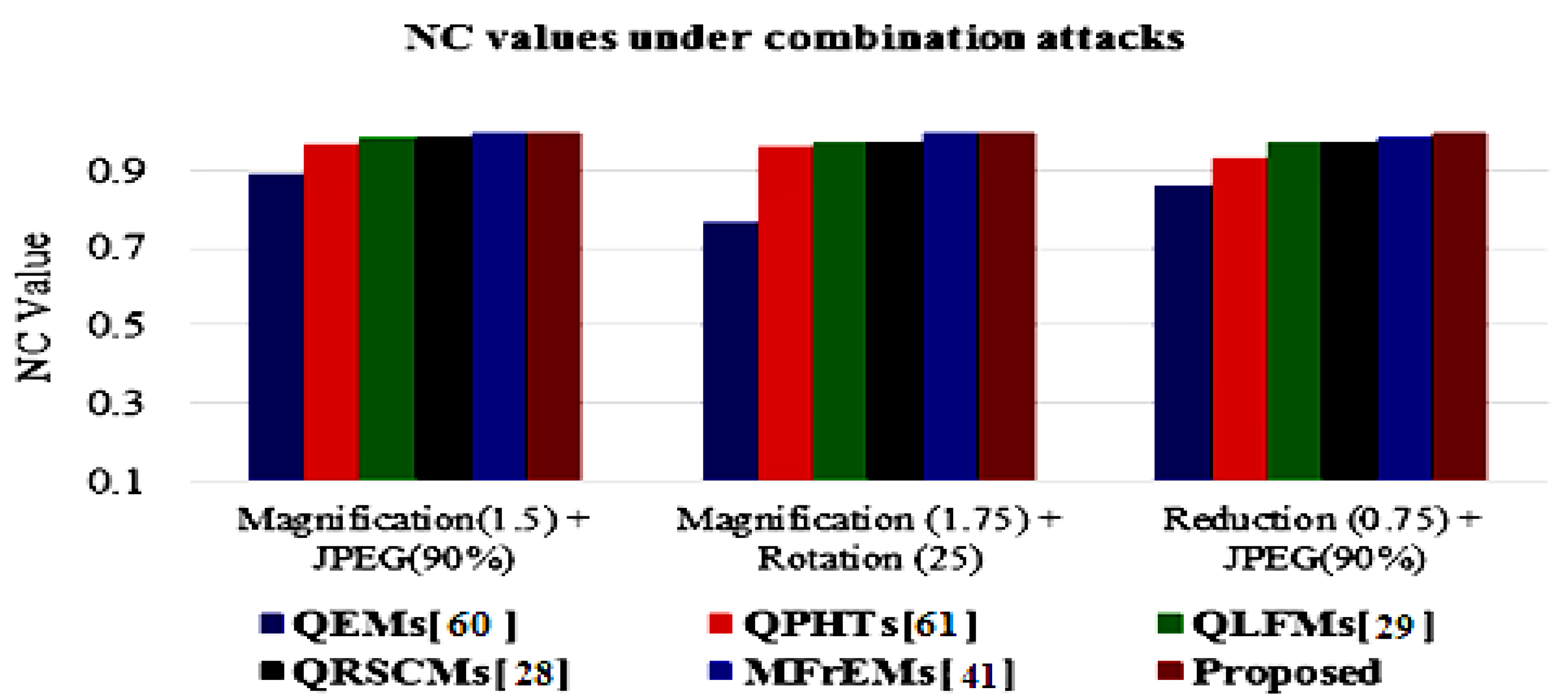
| Magnification (1.5) + (JPEG, 90%) |  | Ber = 0.0889 Nc = 0.8880 |  | Ber = 0.0293 Nc = 0.9643 |  | Ber = 0.0107 Nc = 0.9867 |  | Ber = 0.0127 Nc = 0.9843 |  | Ber = 0.0049 Nc = 0.9940 |  | Ber = 0.0025 Nc = 0.9984 | |
| Magnification(1.75) + Rotation (25o) |  | Ber = 0.1699 Nc = 0.7677 |  | Ber = 0.0342 Nc = 0.9582 |  | Ber = 0.0215 Nc = 0.9737 |  | Ber = 0.0244 Nc = 0.9697 |  | Ber = 0.0049 Nc = 0.9940 |  | Ber = 0.0028 Nc = 0.9956 | |
| Reduction(0.75) + JPEG (90%) |  | Ber = 0.1064 Nc = 0.8591 |  | Ber = 0.0557 Nc = 0.9319 |  | Ber = 0.0205 Nc = 0.9745 |  | Ber = 0.0215 Nc = 0.9736 |  | Ber = 0.0107 Nc = 0.9867 |  | Ber = 0.0072 Nc = 0.9972 | |
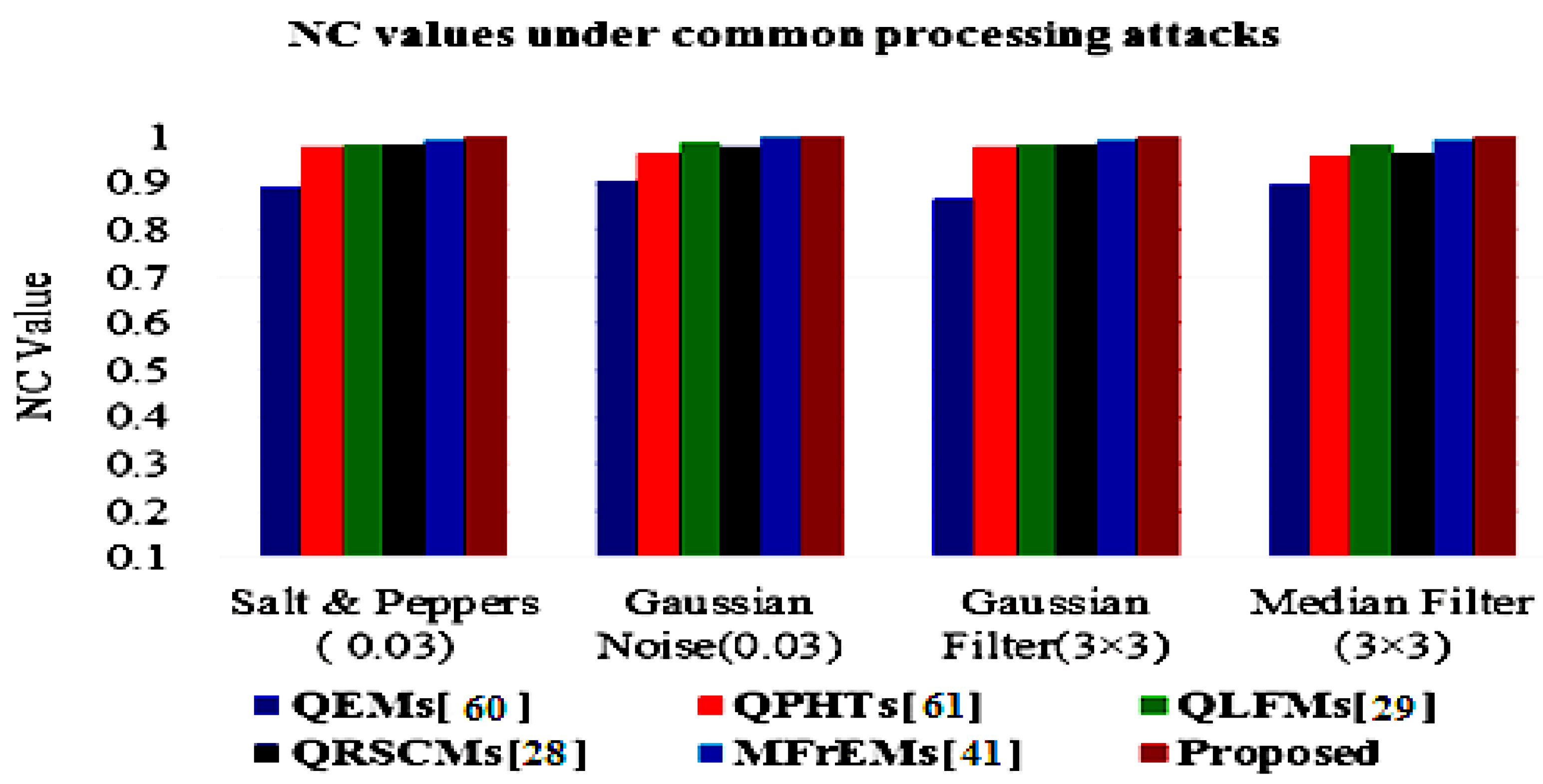
| Noise Salt and Pepper (0.03) |  | Ber = 0.084 Nc = 0.8907 |  | Ber = 0.0166 Nc = 0.9794 |  | Ber = 0.0146 Nc = 0.9820 |  | Ber = 0.0156 Nc = 0.9806 |  | Ber = 0.0068 Nc = 0.9916 |  | Ber = 0.0036 Nc = 0.9989 | |
| Gaussian Noise (0.03) |  | Ber = 0.0723 Nc = 0.9067 |  | Ber = 0.0293 Nc = 0.9643 |  | Ber = 0.0107 Nc = 0.9867 |  | Ber = 0.0186 Nc = 0.9769 |  | Ber = 0.0039 Nc = 0.9952 |  | Ber = 0.0036 Nc = 0.9989 | |
| Gaussian Filter (3 × 3) |  | Ber = 0.1006 Nc = 0.8674 |  | Ber = 0.0166 Nc = 0.9794 |  | Ber = 0.0127 Nc = 0.9843 |  | Ber = 0.0146 Nc = 0.9820 |  | Ber = 0.0049 Nc = 0.9940 |  | Ber = 0.0027 Nc = 0.9992 | |
| Median Filter (3 × 3) |  | Ber = 0.0859 Nc = 0.8953 |  | Ber = 0.0342 Nc = 0.9582 |  | Ber = 0.0137 Nc = 0.9831 |  | Ber = 0.0283 Nc = 0.9650 |  | Ber = 0.0068 Nc = 0.9916 |  | Ber = 0.0039 Nc = 0.9984 | |
| Method | Prabha and Sam [6] | Rahman et al. [9] | Fares et al. [16] | Yuan et al. [18] | Huynh-The et al. [33] | Proposed Method |
|---|---|---|---|---|---|---|
| Max PSNR (dB) | 64.3830 | 35.0406 | 42.42 | 44.4994 | 50.175 | 68.84 |
| Rotation attack | 0.8560 | 0.3567 | 0.9873 | --- | 0.8534 | 0.9984 |
| Scaling attack | 0.9014 | 0.1928 | 0.96131 | --- | 0.999 | 0.9968 |
| JPEG 2000 attack | 0.8577 | 0.9509 | 0.97639 | 0.9944 | 0.852 | 1 |
| JPEG compression | --- | 0.9976 | 0.9998 | 0.9943 | --- | 0.9998 |
| Salt and peppers | 0.9971 | 0.2569 | 0.8739 | 0.9849 | 0.996 | 0.9989 |
| Gaussian | --- | 0.2186 | 0.94325 | --- | 0.915 | 0.9989 |
| Median filter | 0.8370 | 0.9233 | 0.9011 | 0.9460 | 0.924 | 0.9984 |
| Average filtering | --- | 0.8428 | --- | --- | 0.938 | 0.9961 |
| Gaussian low-pass | 0.9075 | --- | --- | --- | --- | 1 |
| Gaussian filtering | --- | 0.9845 | 0.92237 | --- | 0.997 | 0.9992 |
| Blurring attack | 0.9965 | 0.98814 | --- | 0.965 | 1 | |
| Histogram Equalization | --- | 0.9449 | 0.96082 | --- | 0.755 | 1 |
| Zooming attack | --- | 0.9640 | --- | 0.9995 | --- | 1 |
| Sharpen attack | 0.9123 | 0.9179 | 0.98521 | --- | --- | 0.9998 |
| Poisson noise | --- | 0.7168 | --- | --- | --- | 1 |
| Method | Watermark Image (Bits) | Cover Image (Pixels) | Bits/Pixels |
|---|---|---|---|
| Method [8] | 32 × 32 | 512 × 512 × 3 | 0.00130208 |
| Method [24] | 64 × 64 | 512 × 512 × 3 | 0.00520833 |
| Method [25] | 64 × 64 | 512 × 512 × 3 | 0.00520833 |
| QEMs [60] | 16 × 16 | 256 × 256 × 3 | 0.00130208 |
| QPHTs [61] | 32 × 32 | 512 × 512 × 3 | 0.00130208 |
| Proposed | 32 × 32 | 256 × 256 × 3 | 0.00520833 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdel-Aziz, M.M.; Hosny, K.M.; Lashin, N.A.; Fouda, M.M. Blind Watermarking of Color Medical Images Using Hadamard Transform and Fractional-Order Moments. Sensors 2021, 21, 7845. https://doi.org/10.3390/s21237845
Abdel-Aziz MM, Hosny KM, Lashin NA, Fouda MM. Blind Watermarking of Color Medical Images Using Hadamard Transform and Fractional-Order Moments. Sensors. 2021; 21(23):7845. https://doi.org/10.3390/s21237845
Chicago/Turabian StyleAbdel-Aziz, Mostafa M., Khalid M. Hosny, Nabil A. Lashin, and Mostafa M. Fouda. 2021. "Blind Watermarking of Color Medical Images Using Hadamard Transform and Fractional-Order Moments" Sensors 21, no. 23: 7845. https://doi.org/10.3390/s21237845
APA StyleAbdel-Aziz, M. M., Hosny, K. M., Lashin, N. A., & Fouda, M. M. (2021). Blind Watermarking of Color Medical Images Using Hadamard Transform and Fractional-Order Moments. Sensors, 21(23), 7845. https://doi.org/10.3390/s21237845