Energy-Efficient Optimal Power Allocation for SWIPT Based IoT-Enabled Smart Meter
Abstract
:1. Introduction
- (1)
- This research deals with multiple IoT-enabled smart meters, where the non-convex EE maximization problem is transformed into a subtractive form and the solution is based on proportional fairness.
- (2)
- This paper takes a new look at the EE objective function and considers three constraints, i.e., EH constraint, PS ratio at the energy harvester, and DAS transmit power.
- (3)
- An optimal power allocation algorithm is proposed for the non-convex EE maximization problem by adopting nonlinear fractional programming and the Lagrangian method.
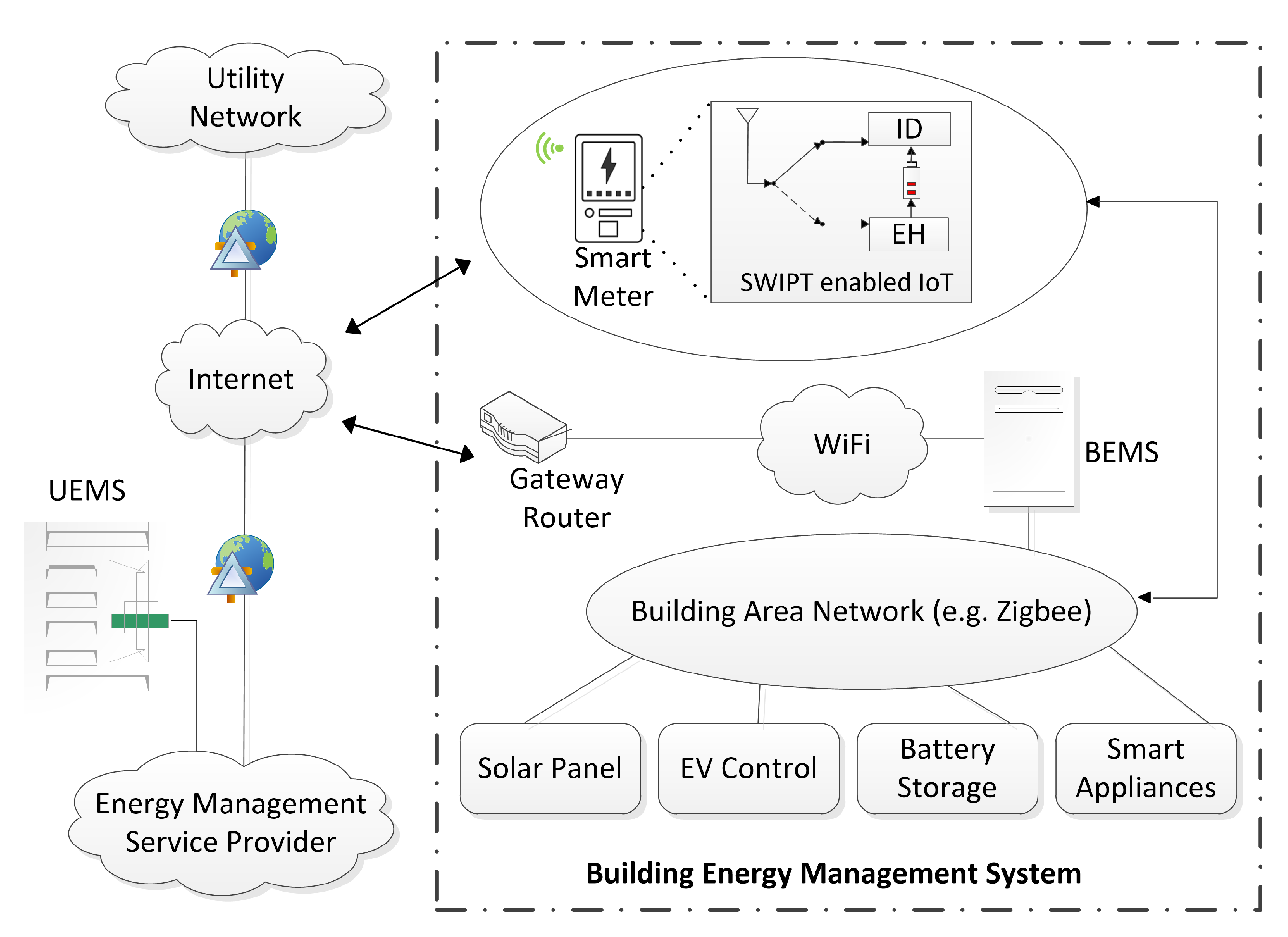
2. System Model
3. Problem Formulation
| Algorithm 1: Optimal transmit power for EE. |
1: Initialization: , , , 2: Set channel gain , 3: for n = 1 : N do 4: while 5: for k = 1 : K do 6: for m = 1 : M do 7: if then, 8: Solve , obtain solution (29), 9: else 10: Solve , obtain solution (30). 11: end for 12: end for 14: end while 15: Compute PS ratio and 16: By using , , and , calculate optimal value of objective function 17: end for |
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Morello, R.; Mukhopadhyay, S.C.; Liu, Z.; Slomovitz, D.; Samantaray, S.R. Advances on sensing technologies for smart cities and power grids: A review. IEEE Sens. J. 2017, 17, 7596–7610. [Google Scholar] [CrossRef]
- Ye, F.; Qian, Y.; Hu, R.Q.; Das, S.K. Reliable energy-efficient uplink transmission for neighborhood area networks in smart grid. IEEE Trans. Smart Grid 2015, 6, 2179–2188. [Google Scholar] [CrossRef]
- Mohamed, N.; Al-Jaroodi, J.; Jawhar, I.; Lazarova-Molnar, S.; Mahmoud, S. SmartCityWare: A service-oriented middleware for cloud and fog enabled smart city services. IEEE Access 2017, 5, 17576–17588. [Google Scholar] [CrossRef]
- Wen, G.; Yu, X.; Liu, Z.W.; Yu, W. Adaptive consensus-based robust strategy for economic dispatch of smart grids subject to communication uncertainties. IEEE Trans. Ind. Inform. 2017, 14, 2484–2496. [Google Scholar] [CrossRef]
- Li, B.; Kisacikoglu, M.C.; Liu, C.; Singh, N.; Erol-Kantarci, M. Big data analytics for electric vehicle integration in green smart cities. IEEE Commun. Mag. 2017, 55, 19–25. [Google Scholar] [CrossRef]
- Hussain, S.S.; Tak, A.; Ustun, T.S.; Ali, I. Communication modeling of solar home system and smart meter in smart grids. IEEE Access 2018, 6, 16985–16996. [Google Scholar] [CrossRef]
- Worighi, I.; Maach, A.; Hafid, A.; Hegazy, O.; Van Mierlo, J. Integrating renewable energy in smart grid system: Architecture, virtualization and analysis. Sustain. Energy Grids Netw. 2019, 18, 100226. [Google Scholar] [CrossRef]
- Sun, Q.; Li, H.; Ma, Z.; Wang, C.; Campillo, J.; Zhang, Q.; Wallin, F.; Guo, J. A comprehensive review of smart energy meters in intelligent energy networks. IEEE Internet Things J. 2015, 3, 464–479. [Google Scholar] [CrossRef]
- Siryani, J.; Tanju, B.; Eveleigh, T.J. A machine learning decision-support system improves the internet of things smart meter operations. IEEE Internet Things J. 2017, 4, 1056–1066. [Google Scholar] [CrossRef]
- Aalamifar, F.; Lampe, L. Optimized WiMAX profile configuration for smart grid communications. IEEE Trans. Smart Grid 2016, 8, 2723–2732. [Google Scholar] [CrossRef]
- Rabie, K.M.; Adebisi, B.; Gacanin, H.; Yarkan, S. Energy-per-bit performance analysis of relay-assisted power line communication systems. IEEE Trans. Green Commun. Netw. 2018, 2, 360–368. [Google Scholar] [CrossRef] [Green Version]
- Sharma, D.; Dubey, A.; Mishra, S.; Mallik, R.K. A frequency control strategy using power line communication in a smart microgrid. IEEE Access 2019, 7, 21712–21721. [Google Scholar] [CrossRef]
- Papadopoulos, T.A.; Kaloudas, C.G.; Chrysochos, A.I.; Papagiannis, G.K. Application of narrowband power-line communication in medium-voltage smart distribution grids. IEEE Trans. Power Del. 2013, 28, 981–988. [Google Scholar] [CrossRef]
- Ke, C.H.; Hsieh, S.Y.; Lin, T.C.; Ho, T.H. Efficiency network construction of advanced metering infrastructure using Zigbee. IEEE Trans. Mobile Comput. 2018, 18, 801–813. [Google Scholar] [CrossRef]
- Bedi, G.; Venayagamoorthy, G.K.; Singh, R.; Brooks, R.R.; Wang, K.C. Review of Internet of Things (IoT) in electric power and energy systems. IEEE Internet Things J. 2018, 5, 847–870. [Google Scholar] [CrossRef]
- Andrawes, A.; Nordin, R.; Abdullah, N.F. Energy-efficient downlink for non-orthogonal multiple access with SWIPT under constrained throughput. Energies 2020, 13, 107. [Google Scholar] [CrossRef] [Green Version]
- Zafari, F.; Papapanagiotou, I.; Christidis, K. Microlocation for internet-of-things-equipped smart buildings. IEEE Internet Things J. 2015, 3, 96–112. [Google Scholar] [CrossRef] [Green Version]
- Barbierato, L.; Estebsari, A.; Pons, E.; Pau, M.; Salassa, F.; Ghirardi, M.; Patti, E. A distributed IoT infrastructure to test and deploy real-time demand response in smart grids. IEEE Internet Things J. 2018, 6, 1136–1146. [Google Scholar] [CrossRef]
- Montori, F.; Bedogni, L.; Bononi, L. A collaborative internet of things architecture for smart cities and environmental monitoring. IEEE Internet Things J. 2017, 5, 592–605. [Google Scholar] [CrossRef]
- Lee, C.; Fumagalli, A. Internet of things security-multilayered method for end to end data communications over cellular networks. In Proceedings of the 2019 IEEE 5th World Forum on Internet of Things (WF-IoT), Limerick, Ireland, 15–18 April 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 24–28. [Google Scholar]
- Morello, R.; De Capua, C.; Fulco, G.; Mukhopadhyay, S.C. A smart power meter to monitor energy flow in smart grids: The role of advanced sensing and IoT in the electric grid of the future. IEEE Sens. J. 2017, 17, 7828–7837. [Google Scholar] [CrossRef]
- Clerckx, B.; Bayguzina, E. Low-complexity adaptive multisine waveform design for wireless power transfer. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 2207–2210. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.; Lee, K.; Cho, D.H. Stability improvement of transmission efficiency based on a relay resonator in a wireless power transfer system. IEEE Trans. Power Electron. 2017, 32, 3297–3300. [Google Scholar] [CrossRef]
- Zhou, W.; Sandeep, S.; Wu, P.; Yang, P.; Yu, W.; Huang, S.Y. A wideband strongly coupled magnetic resonance wireless power transfer system and its circuit analysis. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 1152–1154. [Google Scholar] [CrossRef]
- Hu, S.; Chen, X.; Ni, W.; Wang, X.; Hossain, E. Modeling and analysis of energy harvesting and smart grid-powered wireless communication networks: A contemporary survey. IEEE Trans. Green Commun. Netw. 2020, 4, 461–496. [Google Scholar] [CrossRef]
- Perera, T.D.P.; Jayakody, D.N.K.; Sharma, S.K.; Chatzinotas, S.; Li, J. Simultaneous wireless information and power transfer (SWIPT): Recent advances and future challenges. IEEE Commun. Surv. Tuts. 2017, 20, 264–302. [Google Scholar] [CrossRef] [Green Version]
- Shi, L.; Ye, Y.; Hu, R.Q.; Zhang, H. Energy efficiency maximization for SWIPT enabled two-way DF relaying. IEEE Signal Process. Lett. 2019, 26, 755–759. [Google Scholar] [CrossRef]
- Jalali, J.; Khalili, A. Optimal resource allocation for MC-NOMA in SWIPT-enabled networks. IEEE Commun. Lett. 2020, 24, 2250–2254. [Google Scholar] [CrossRef]
- Rajaram, A.; Khan, R.; Tharranetharan, S.; Jayakody, D.N.K.; Dinis, R.; Panic, S. Novel SWIPT schemes for 5G wireless networks. Sensors 2019, 19, 1169. [Google Scholar] [CrossRef] [Green Version]
- Chae, S.H.; Jeong, C.; Lim, S.H. Simultaneous wireless information and power transfer for Internet of Things sensor networks. IEEE Internet Things J. 2018, 5, 2829–2843. [Google Scholar] [CrossRef]
- Zhu, Z.; Huang, S.; Chu, Z.; Zhou, F.; Zhang, D.; Lee, I. Robust designs of beamforming and power splitting for distributed antenna systems with wireless energy harvesting. IEEE Syst. J. 2018, 13, 30–41. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Xiong, K.; Cao, J.; Yang, X.; Liu, T. Energy efficiency in RF energy harvesting-powered distributed antenna systems for the internet of things. Sensors 2020, 20, 4631. [Google Scholar] [CrossRef]
- Zhu, Z.; Chu, Z.; Zhou, F.; Niu, H.; Wang, Z.; Lee, I. Secure beamforming designs for secrecy MIMO SWIPT systems. IEEE Wirel. Commun. Lett. 2017, 7, 424–427. [Google Scholar] [CrossRef]
- Yuan, F.; Jin, S.; Wong, K.K.; Zhao, J.; Zhu, H. Wireless information and power transfer design for energy cooperation distributed antenna systems. IEEE Access 2017, 5, 8094–8105. [Google Scholar] [CrossRef]
- Xu, D.; Zhu, H. Secure Transmission for SWIPT IoT Systems With Full-Duplex IoT Devices. IEEE Internet Things J. 2019, 6, 10915–10933. [Google Scholar] [CrossRef]
- Yu, X.; Chu, J.; Yu, K.; Teng, T.; Li, N. Energy-Efficiency Optimization for IoT-Distributed Antenna Systems With SWIPT Over Composite Fading Channels. IEEE Internet Things J. 2019, 7, 197–207. [Google Scholar] [CrossRef]
- Ariffin, W.N.S.F.W.; Zhang, X.; Nakhai, M.R. Sparse beamforming for real-time resource management and energy trading in green C-RAN. IEEE Trans. Smart Grid 2016, 8, 2022–2031. [Google Scholar] [CrossRef]
- Xu, D.; Zhu, H. Outage minimized resource allocation for multiuser OFDM systems with SWIPT. IEEE Access 2019, 7, 79714–79725. [Google Scholar] [CrossRef]
- Masood, Z.; Park, H.; Jang, H.S.; Yoo, S.; Jung, S.P.; Choi, Y. Optimal Power Allocation for Maximizing Energy Efficiency in DAS-Based IoT Network. IEEE Syst. J. 2021, 15, 2342–2348. [Google Scholar] [CrossRef]
- Nugraha, G.D.; Musa, A.; Cho, J.; Park, K.; Choi, D. Lambda-based data processing architecture for two-level load forecasting in residential buildings. Energies 2018, 11, 772. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Li, G.; Yang, Y.; Liu, M.; Gui, G. Robust resource allocation and power splitting in SWIPT enabled heterogeneous networks: A robust minimax approach. IEEE Internet Things J. 2019, 6, 10799–10811. [Google Scholar] [CrossRef]
- Tham, M.L.; Chien, S.F.; Holtby, D.W.; Alimov, S. Energy-efficient power allocation for distributed antenna systems with proportional fairness. IEEE Trans. Green Commun. Netw. 2017, 1, 145–157. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, R. Energy beamforming with one-bit feedback. IEEE Trans. Signal Process. 2014, 62, 5370–5381. [Google Scholar] [CrossRef] [Green Version]
- Ye, Y.; Shi, L.; Chu, X.; Lu, G. Throughput fairness guarantee in wireless powered backscatter communications with HTT. IEEE Wirel. Commun. Lett. 2020, 10, 449–453. [Google Scholar] [CrossRef]
- Tang, J.; Luo, J.; Liu, M.; So, D.K.; Alsusa, E.; Chen, G.; Wong, K.K.; Chambers, J.A. Energy efficiency optimization for NOMA with SWIPT. IEEE J. Sel. Topics Signal Process. 2019, 13, 452–466. [Google Scholar] [CrossRef] [Green Version]
- Di, X.; Xiong, K.; Fan, P.; Yang, H.C. Simultaneous wireless information and power transfer in cooperative relay networks with rateless codes. IEEE Trans. Veh. Technol. 2016, 66, 2981–2996. [Google Scholar] [CrossRef]
- Yu, H.; Guo, S.; Yang, Y.; Ji, L.; Yang, Y. Secrecy energy efficiency optimization for downlink two-user OFDMA networks with SWIPT. IEEE Syst. J. 2017, 13, 324–335. [Google Scholar] [CrossRef]
- He, C.; Sheng, B.; Zhu, P.; You, X.; Li, G.Y. Energy-and spectral-efficiency tradeoff for distributed antenna systems with proportional fairness. IEEE J. Sel. Areas Commun. 2013, 31, 894–902. [Google Scholar] [CrossRef]
- Dinkelbach, W. On nonlinear fractional programming. Manage. Sci. 1967, 13, 492–498. [Google Scholar] [CrossRef]
- Wang, S.; Shi, W.; Wang, C. Energy-efficient resource management in OFDM-based cognitive radio networks under channel uncertainty. IEEE Trans. Commun. 2015, 63, 3092–3102. [Google Scholar] [CrossRef]
- Xu, W.; Yu, X.; Leung, S.H.; Chu, J. Energy-Efficient Power Allocation Scheme for Distributed MISO System With OFDM Over Frequency-Selective Fading Channels. IEEE Access 2018, 6, 51217–51226. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, R.; Ho, C.K. Wireless information and power transfer in multiuser OFDM systems. IEEE Trans. Wirel. Commun. 2014, 13, 2282–2294. [Google Scholar] [CrossRef] [Green Version]
- Yu, X.; Xu, W.; Leung, S.H.; Dang, X.; Teng, T. Power allocation schemes for DAS with OFDM under per-antenna power constraint. IEEE Trans. Veh. Technol. 2018, 67, 10102–10106. [Google Scholar] [CrossRef]



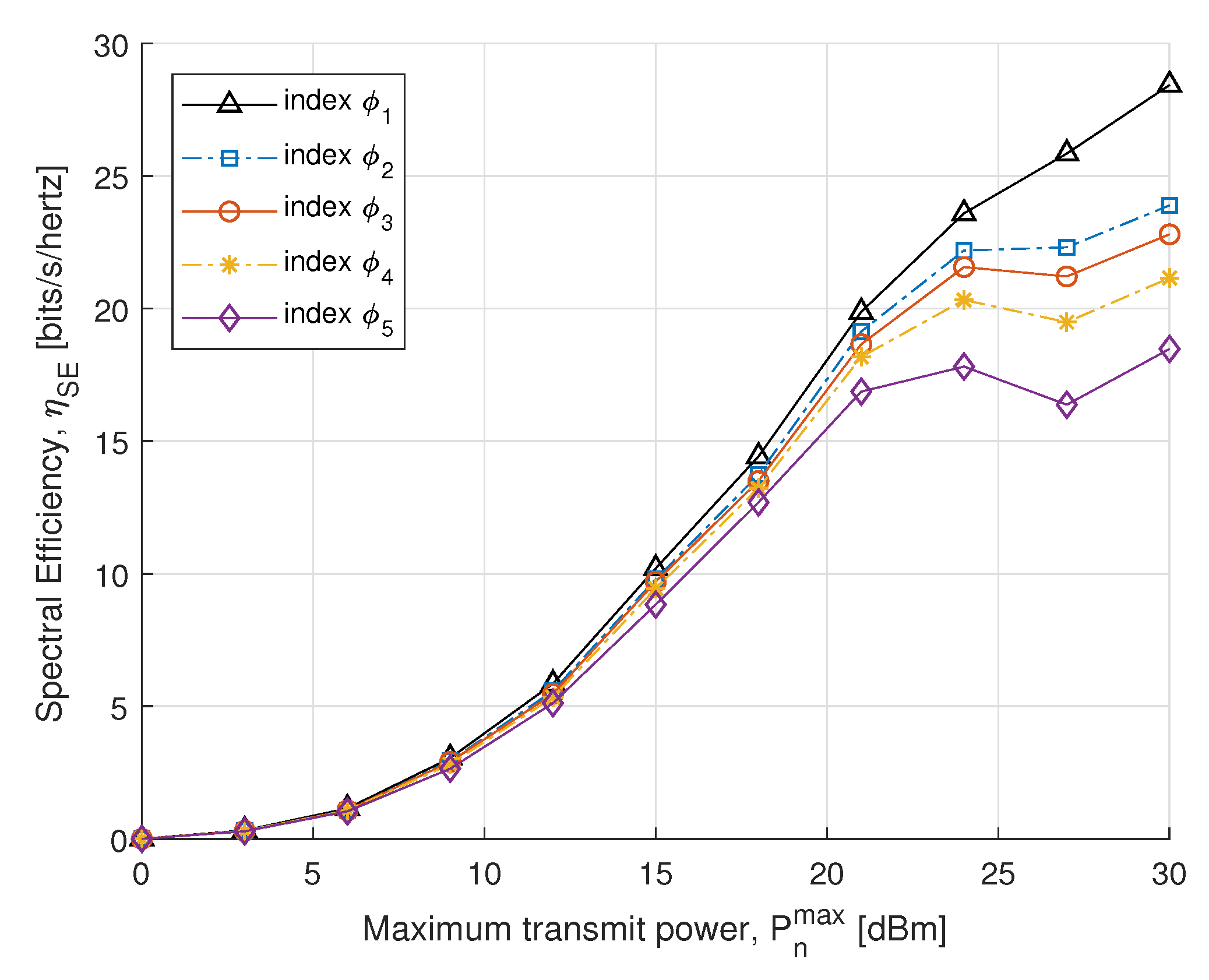

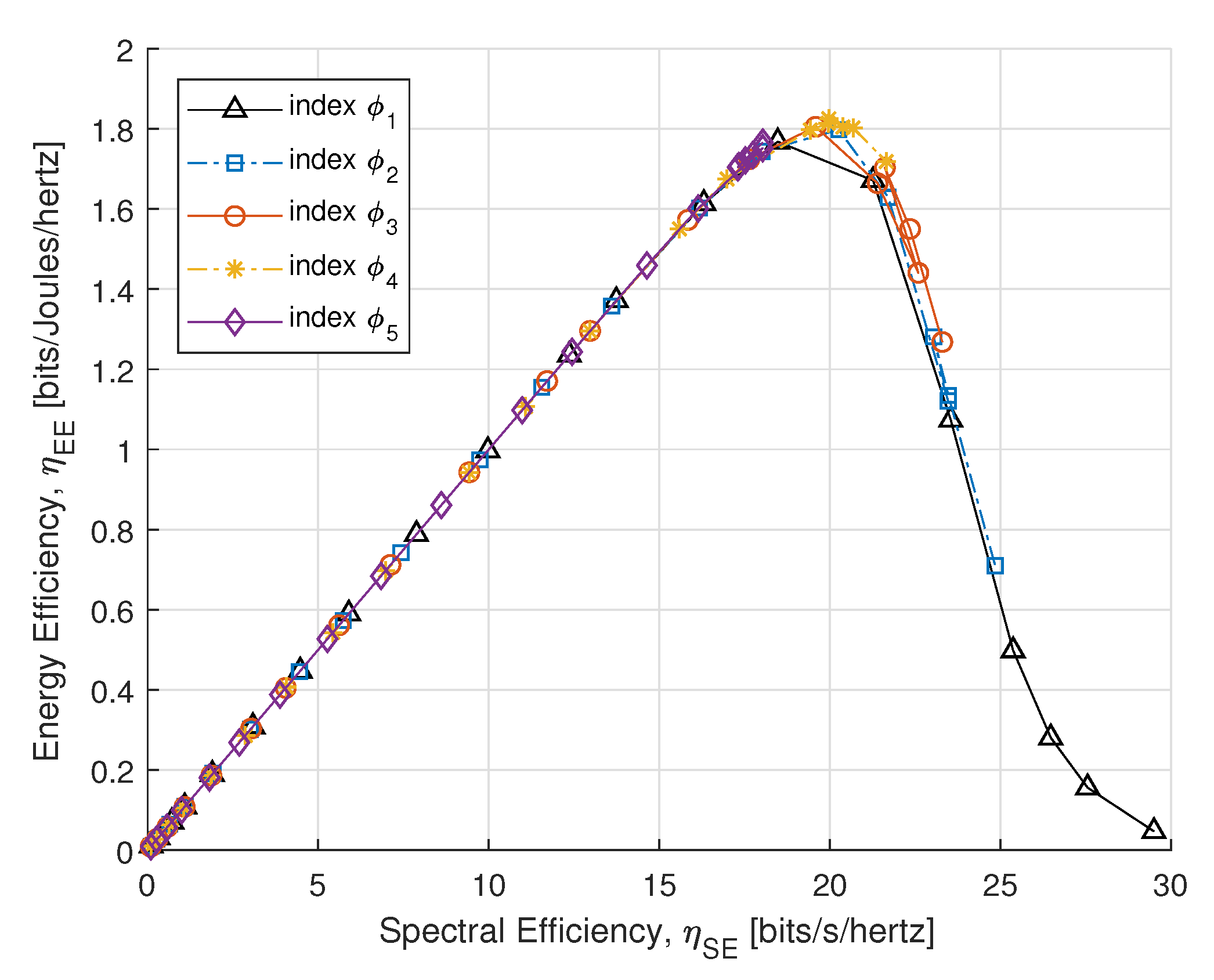


| Fairness index k | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| = = = = | |||||
| = = … = | 1 | 1 | 1 | 1 | 1 |
| Parameter | Value |
|---|---|
| Number of DA ports | 5 |
| Number of IoT enabled smart meter devices | 15 |
| Number of subcarriers (M) | 64 |
| Noise power | dBm |
| Path loss exponent | |
| Circuit power consumption | 5 W |
| Shadow fading standard deviation | 8 dB |
| Radius of the cell | 1000 m |
| Maximum transmit power | 30 dBm |
| Number of channel realization |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Masood, Z.; Ardiansyah; Choi, Y. Energy-Efficient Optimal Power Allocation for SWIPT Based IoT-Enabled Smart Meter. Sensors 2021, 21, 7857. https://doi.org/10.3390/s21237857
Masood Z, Ardiansyah, Choi Y. Energy-Efficient Optimal Power Allocation for SWIPT Based IoT-Enabled Smart Meter. Sensors. 2021; 21(23):7857. https://doi.org/10.3390/s21237857
Chicago/Turabian StyleMasood, Zaki, Ardiansyah, and Yonghoon Choi. 2021. "Energy-Efficient Optimal Power Allocation for SWIPT Based IoT-Enabled Smart Meter" Sensors 21, no. 23: 7857. https://doi.org/10.3390/s21237857
APA StyleMasood, Z., Ardiansyah, & Choi, Y. (2021). Energy-Efficient Optimal Power Allocation for SWIPT Based IoT-Enabled Smart Meter. Sensors, 21(23), 7857. https://doi.org/10.3390/s21237857






