Vulnerability of Satellite Quantum Key Distribution to Disruption from Ground-Based Lasers
Abstract
:1. Introduction
2. Methods
2.1. Satellite Architecture
2.2. Satellite Optical Scattering Model
2.3. Orbital Dynamics
2.4. Free-Space Link Loss
2.5. Impact on Quantum Bit Error Rate
3. Results
3.1. Satellite Optical Scattering Profile
3.2. Orbital Dynamics and Visibility
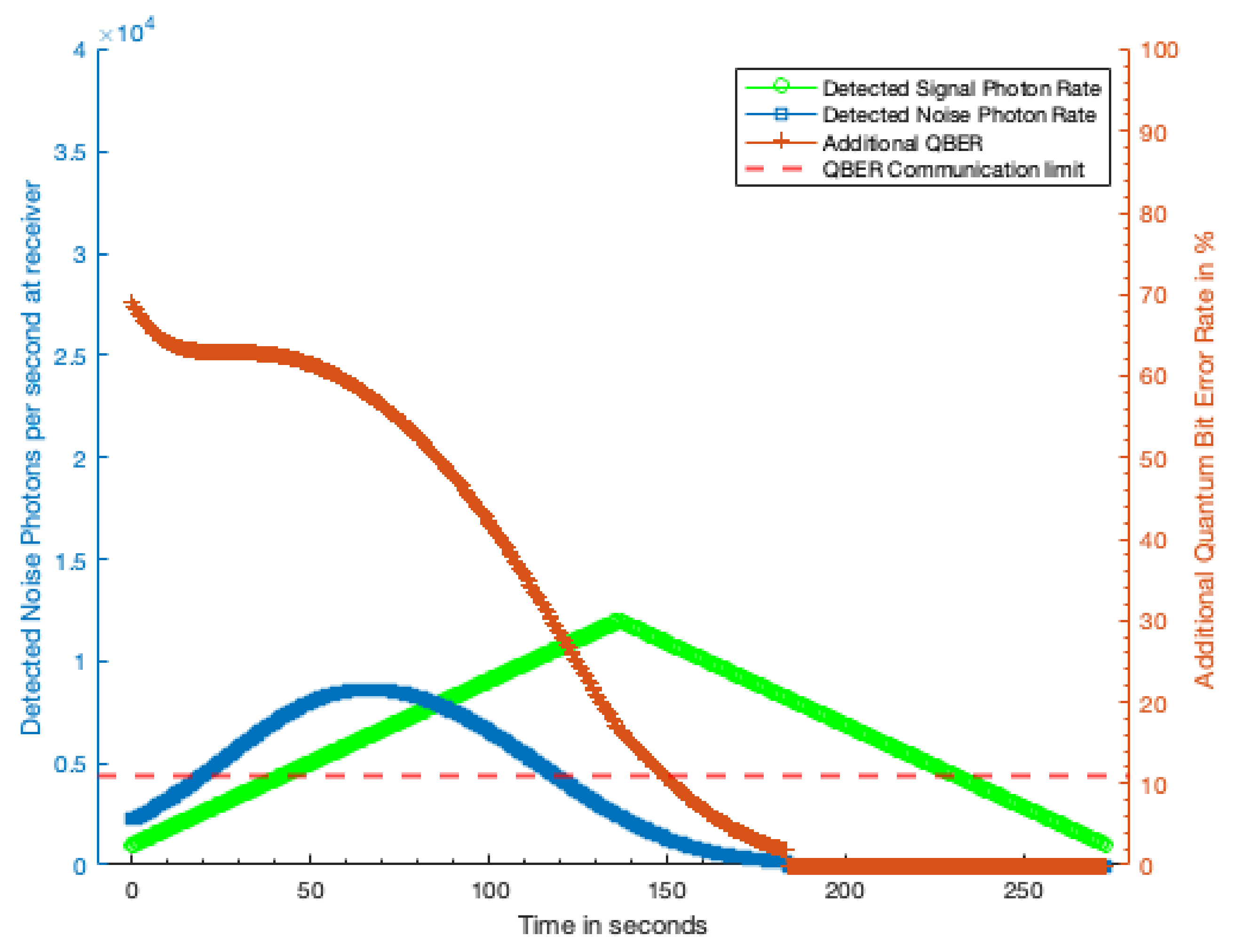
3.3. Excess Photon Rate
3.4. Quantum Bit Error Rate Due to Excess Photons
4. Discussion
4.1. Challenges Facing the Laser Terminal
4.2. Countermeasures
4.2.1. Receiver Gating
4.2.2. Spectral Filtering
4.2.3. Improved Sensitivity
4.2.4. Satellite Architecture
4.2.5. Higher Orbits
4.2.6. QKD Protocols
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SPD | single photon detector |
| QBER | quantum bit error rate |
| QKD | quantum key distribution |
References
- Bennet, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. In Proceedings of the International Conference on Computers, Systems and Signal Processing, Bangalore, India, 9–12 December 1984; pp. 175–179. [Google Scholar]
- Diamanti, E.; Lo, H.K.; Qi, B.; Yuan, Z. Practical challenges in quantum key distribution. NPJ Quant. Inf. 2016, 2, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Yin, H.-L.; Chen, T.-Y.; Yu, Z.-W.; Liu, H.; You, L.-X.; Zhou, Y.-H.; Chen, S.-J.; Mao, Y.; Huang, W.-Q.; Zhang, W.-J.; et al. Measurement-device-independent quantum key distribution over a 404 km optical fiber. Phys. Rev. Lett. 2016, 117, 190501. [Google Scholar] [CrossRef] [PubMed]
- Pittaluga, M.; Minder, M.; Lucamarini, M.; Sanzaro, M.; Woodward, R.I.; Li, M.J.; Yuan, Z.; Shields, A.J. 600-km repeater-like quantum communications with dual-band stabilization. Nat. Phot. 2021, 15, 1–6. [Google Scholar] [CrossRef]
- Brassard, G.; Lutkenhaus, N.; Mor, T.; Sanders, B.C. Limitations on practical quantum cryptography. Phys. Rev. Lett. 2000, 85, 1330–1333. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zukowski, M.; Zeilinger, A.; Horne, M.A.; Ekert, A.K. Event-ready-detectors: Bell experiment via entanglement swapping. Phys. Rev. Lett. 1993, 71, 4287–4290. [Google Scholar] [CrossRef] [PubMed]
- Liao, S.K.; Cai, W.Q.; Liu, W.Y.; Zhang, L.; Li, Y.; Ren, J.; Pan, J.W.; Yin, J.; Shen, Q.; Cao, Y.; et al. Satellite-to-ground quantum key distribution. Nature 2017, 549, 43–47. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bedington, R.; Arrazola, J.M.; Ling, A. Progress in satellite quantum key distribution. Quant. Inf. 2017, 3, 1–3. [Google Scholar] [CrossRef]
- Lo, H.-K.; Ma, X.; Chen, K. Decoy state quantum key distribution. Phys. Rev. Lett. 2005, 94, 230504. [Google Scholar] [CrossRef] [Green Version]
- Degnan, J.J. Millimeter accuracy satellite laser ranging: A review. In Contributions of Space Geodesy to Geodynamics: Technology; Smith, D.E., Turcotte, D.L., Eds.; American Geophysical Union: Washington, DC, USA, 1993; pp. 133–162. [Google Scholar]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation through Random Media, 2nd ed.; SPIE: Bellingham, WA, USA, 2005; pp. 481–492. [Google Scholar]
- Shor, P.W.; Preskill, J. Simple proof of security of the BB84 quantum key distribution protocol. Phys. Rev. Lett. 2000, 85, 441. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Biham, E.; Boyer, M.; Boykin, P.O.; Mor, T.; Roychowdhury, V. A proof of the security of quantum key distribution. J. Cryptol. 2006, 19, 381. [Google Scholar] [CrossRef] [Green Version]
- Mayers, D. Unconditional security in quantum cryptography. J. ACM 2001, 48, 351–406. [Google Scholar] [CrossRef]
- Collins, R.J.; Clarke, P.J.; Fernandez, V.; Gordon, K.J.; Makhonin, M.N.; Timpson, J.A.; Tahraoui, A.; Hopkinson, M.; Fox, A.M.; Skolnick, M.S.; et al. Quantum key distribution system in standard telecommunications fiber using a short wavelength single photon source. J. App. Phys. 2010, 107, 073102. [Google Scholar] [CrossRef] [Green Version]
- Mailloux, L.O.; Engle, R.D.; Grimaila, M.R.; Hodson, D.D.; Colombi, J.M.; McLaughlin, C.V. Modeling decoy state Quantum Key Distribution systems. J. Def. Model. Sim. 2015, 12, 489–506. [Google Scholar] [CrossRef]
- Er-long, M.; Zheng-fu, H.; Shun-sheng, G.; Tao, Z.; Da-Sheng, D.; Guang-Can, G. Background noise of satellite-to-ground quantum key distribution. New J. Phys. 2005, 7, 215. [Google Scholar] [CrossRef]
- Steindorfer, M.A.; Kirchner, G.; Koidl, F.; Wang, P.; Jilete, B.; Flohrer, T. Daylight space debris laser ranging. Nat. Comm. 2020, 11, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grosshans, F.; Grangier, P. CV quantum cryptography using coherent states. Phys. Rev. Lett. 2002, 88, 057902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Braunstein, S.L.; Van Loock, P. Quantum information with continuous variables. J. Rev. Mod. Phys. 2005, 77, 513. [Google Scholar] [CrossRef] [Green Version]
- Dequal, D.; Vidarte, L.T.; Rodriguez, V.R.; Vallone, G.; Villoresi, P.; Leverrier, A.; Diamanti, E. Feasibility of satellite-to-ground continuous-variable quantum key distribution. NPJ Quant. Inf. 2021, 7, 1–10. [Google Scholar] [CrossRef]
- Kirchner, G.; Koidl, F.; Ploner, M.; Lauber, P.; Utzinger, J.; Schreiber, U.; Eckl, J.; Wilkinson, M.; Sherwood, R.; Giessen, A.; et al. Multistatic laser ranging to space debris. In Proceedings of the 18th International Workshop on Laser Ranging, Fujiyoshida, Japan, 11–15 November 2013; pp. 1–9. [Google Scholar]







| Parameter | Satellite Design |
|---|---|
| Orbit | Sun-synchronous circular orbit at 500 km altitude, 7.6 km/s. Satellite visible to ground station from elevations of approximately 15° to 10°. |
| Satellite bus | Approximately 2 m × 2 m, coated in metallized polymer thermal shielding with an albedo of approximately 0.3. |
| Satellite attitude | Coarse pointing — satellite is bodily oriented towards ground station with 0.5° precision. |
| Satellite QKD transmitter optic | 300 mm aperture Cassegrain telescope. 10 rad divergence, 22 dB diffraction loss at 1200 km. |
| Ground station QKD receiver optic | 1 m aperture Ritchey-Chretien telescope. Approximately 16% optical efficiency from aperture to QKD receiver system. |
| QKD wavelength | 848.6 nm |
| QKD protocol | Decoy-state BB84 [9] with three intensity levels. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gozzard, D.R.; Walsh, S.; Weinhold, T. Vulnerability of Satellite Quantum Key Distribution to Disruption from Ground-Based Lasers. Sensors 2021, 21, 7904. https://doi.org/10.3390/s21237904
Gozzard DR, Walsh S, Weinhold T. Vulnerability of Satellite Quantum Key Distribution to Disruption from Ground-Based Lasers. Sensors. 2021; 21(23):7904. https://doi.org/10.3390/s21237904
Chicago/Turabian StyleGozzard, David R., Shane Walsh, and Till Weinhold. 2021. "Vulnerability of Satellite Quantum Key Distribution to Disruption from Ground-Based Lasers" Sensors 21, no. 23: 7904. https://doi.org/10.3390/s21237904
APA StyleGozzard, D. R., Walsh, S., & Weinhold, T. (2021). Vulnerability of Satellite Quantum Key Distribution to Disruption from Ground-Based Lasers. Sensors, 21(23), 7904. https://doi.org/10.3390/s21237904






