Freestanding Flexible Sensor Based on 3ω Technique for Anisotropic Thermal Conductivity Measurement of Potassium Dihydrogen Phosphate Crystal
Abstract
:1. Introduction
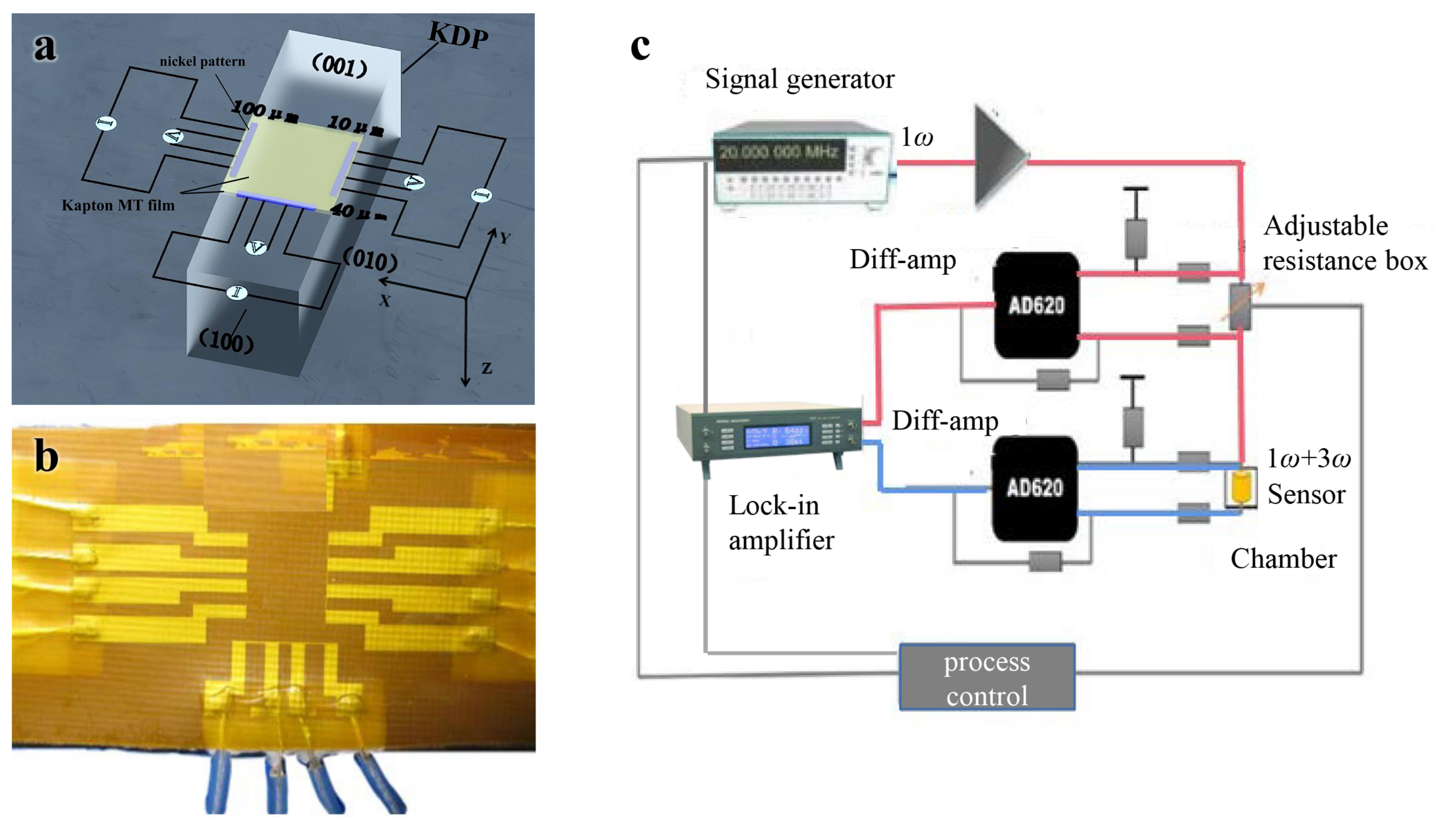
2. Freestanding Sensor Fabrication
3. Experimental Methods
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sivakumar, A.; Suresh, S.; Balachandar, S.; Thirupathy, J.; Martin Britto Dhas, S.A. Effect of shock waves on thermophysical properties of ADP and KDP crystals. Opt. Laser Technol. 2019, 111, 284–289. [Google Scholar] [CrossRef]
- Shen, C.; Wang, D.; Zhang, J.; Zhang, H.; Wang, J.; Boughton, R.I. The growth and investigations of electromechanical properties of Fresnoite Ba2Si2TiO8 crystal as a function of orientation—ScienceDirect. J. Cryst. Growth 2018, 487, 17–22. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.M.; Tao, W.Q. Theoretical accuracy of anisotropic thermal conductivity determined by transient plane source method. Int. J. Heat Mass Transf. 2017, 108, 1634–1644. [Google Scholar] [CrossRef]
- Lee, S.; Kim, D. The evaluation of cross-plane/in-plane thermal diffusivity using laser flash apparatus. Thermochim. Acta 2017, 653, 126–132. [Google Scholar] [CrossRef]
- Ju, Y.S.; Kurabayashi, K.; Goodson, K.E. Thermal characterization of anisotropic thin dielectric films using harmonic Joule heating. Thin Solid Films 1999, 339, 160–164. [Google Scholar] [CrossRef]
- Fan, J.A.; Yeo, W.H.; Su, Y.; Hattori, Y.; Lee, W.; Jung, S.Y.; Zhang, Y.; Liu, Z.; Cheng, H.; Falgout, L. Fractal design concepts for stretchable electronics. Nat. Commun. 2014, 5, 3266. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Petropoulos, A.; Pagonis, D.N.; Kaltsas, G. Flexible PCB-MEMS Flow Sensor. Process Eng. 2012, 47, 236–239. [Google Scholar] [CrossRef] [Green Version]
- Qiu, L.; Zheng, X.H.; Yue, P.; Zhu, J.; Tang, D.W.; Dong, Y.J.; Peng, Y.L. Adaptable thermal conductivity characterization of microporous membranes based on freestanding sensor-based 3ω technique. Int. J. Therm. Sci. 2015, 89, 185–192. [Google Scholar] [CrossRef]
- Lubner, S.D.; Choi, J.; Wehmeyer, G.; Waag, B.; Mishra, V.; Natesan, H.; Bischof, J.C.; Dames, C. Reusable bi-directional 3ω sensor to measure thermal conductivity of 100-µm thick biological tissues. Rev. Sci. Instrum. 2015, 86, 014905. [Google Scholar] [CrossRef] [PubMed]
- Tian, L.; Li, Y.; Webb, R.C.; Krishnan, S.; Bian, Z.; Song, J.; Ning, X.; Crawford, K.; Kurniawan, J.; Bonifas, A.; et al. Flexible and Stretchable 3ω Sensors for Thermal Characterization of Human Skin. Adv. Funct. Mater. 2017, 27, 1701282.1–1701282.9. [Google Scholar] [CrossRef]
- Zhang, J.; Nagao, Y.; Kuwano, S.; Ito, Y. Microstructure and Temperature Coefficient of Resistance of Platinum Films. Jpn. J. Appl. Phys. 1997, 36, 834. [Google Scholar] [CrossRef]
- Han, J.W.; Meyyappan, M. A built-in temperature sensor in an integrated microheater. IEEE Sens. J. 2016, 16, 5543–5547. [Google Scholar] [CrossRef]
- Cahill, D.G. Erratum: Thermal conductivity measurement from 30 to 750 K: The 3ω method. Rev. Sci. Instrum. 1990, 61, 802, Rev. Sci. Instrum.2002, 73, 3701. [Google Scholar]
- Borca-Tasciuc, T.; Kumar, A.R.; Chen, G. Data reduction in 3ω method for thin-film thermal conductivity determination. Rev. Sci. Instrum. 2001, 72, 2139–2147. [Google Scholar] [CrossRef]
- Qiu, L.; Ouyang, Y.; Feng, Y.; Zhang, X.; Wu, J. Thermal barrier effect from internal pore channels on thickened aluminum nanofilm. Int. J. Therm. Sci. 2021, 162, 106781. [Google Scholar] [CrossRef]
- Mishra, V.; Hardin, C.L.; Garay, J.E.; Dames, C. A 3 omega method to measure an arbitrary anisotropic thermal conductivity tensor. Rev. Sci. Instrum. 2015, 86, 201. [Google Scholar] [CrossRef]
- Qiu, L.; Zhang, X.; Guo, Z.; Li, Q. Interfacial heat transport in nano-carbon assemblies. Carbon 2021, 178, 391–412. [Google Scholar] [CrossRef]
- Olson, B.W.; Graham, S.; Chen, K. A practical extension of the 3ω method to multilayer structures. Rev. Sci. Instrum. 2005, 76, 802–811. [Google Scholar] [CrossRef]
- Wang, D.; Shen, C.; Lan, J.; Huang, P.; Cui, Z.; Kang, T.; Niu, Y.; Wang, S.; Wang, J.; Boughton, R.I. Exploration of the correlation between weak absorption and thermal-stress for KDP and 70%-DKDP crystals. J. Alloys Compd. 2019, 790, 212–220. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, L.; Ma, Y.; Ouyang, Y.; Feng, Y.; Zhang, X. Freestanding Flexible Sensor Based on 3ω Technique for Anisotropic Thermal Conductivity Measurement of Potassium Dihydrogen Phosphate Crystal. Sensors 2021, 21, 7968. https://doi.org/10.3390/s21237968
Qiu L, Ma Y, Ouyang Y, Feng Y, Zhang X. Freestanding Flexible Sensor Based on 3ω Technique for Anisotropic Thermal Conductivity Measurement of Potassium Dihydrogen Phosphate Crystal. Sensors. 2021; 21(23):7968. https://doi.org/10.3390/s21237968
Chicago/Turabian StyleQiu, Lin, Yuhao Ma, Yuxin Ouyang, Yanhui Feng, and Xinxin Zhang. 2021. "Freestanding Flexible Sensor Based on 3ω Technique for Anisotropic Thermal Conductivity Measurement of Potassium Dihydrogen Phosphate Crystal" Sensors 21, no. 23: 7968. https://doi.org/10.3390/s21237968
APA StyleQiu, L., Ma, Y., Ouyang, Y., Feng, Y., & Zhang, X. (2021). Freestanding Flexible Sensor Based on 3ω Technique for Anisotropic Thermal Conductivity Measurement of Potassium Dihydrogen Phosphate Crystal. Sensors, 21(23), 7968. https://doi.org/10.3390/s21237968







