A Positioning Method Based on Place Cells and Head-Direction Cells for Inertial/Visual Brain-Inspired Navigation System
Abstract
:1. Introduction
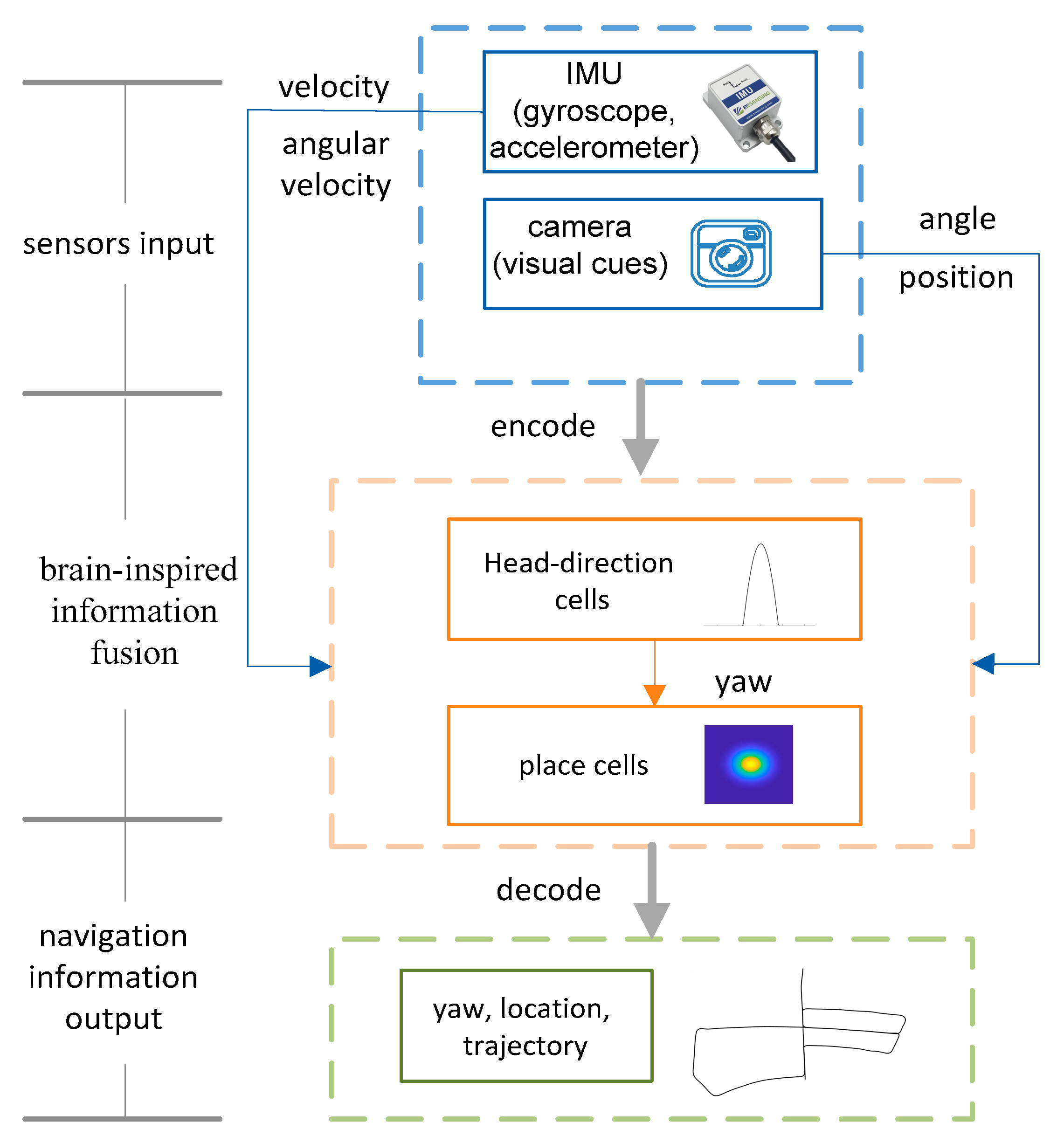
2. Brain-Inspired Navigation Model
2.1. Brain-Inspired Navigation Model Composition
2.2. Vision-Based Motion Estimation
3. Spatial Representation Cells’ Encoding
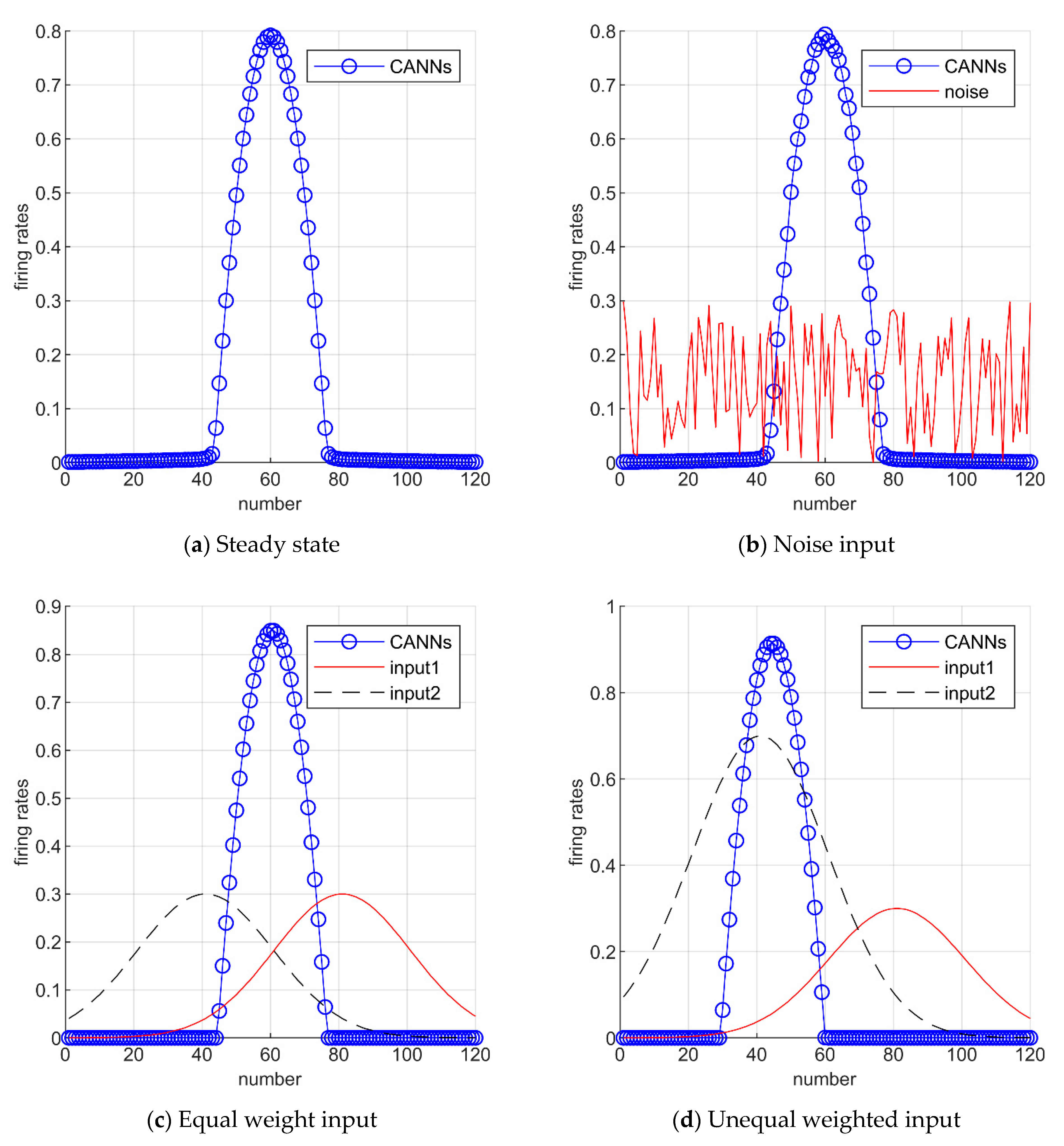
3.1. Continuous Attractor Neural Networks (CANNs)
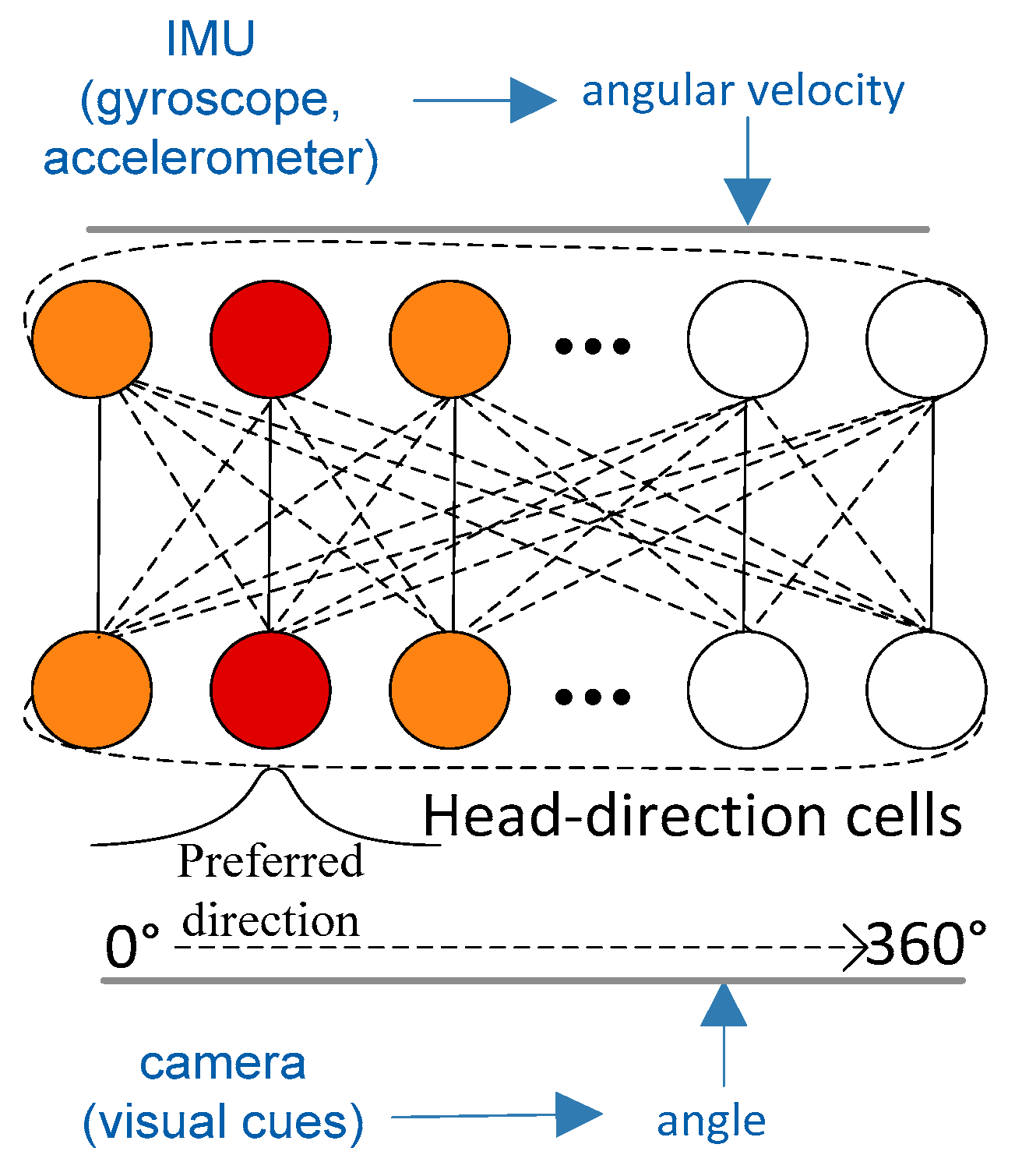
3.2. Head-Direction Cells’ Encoding
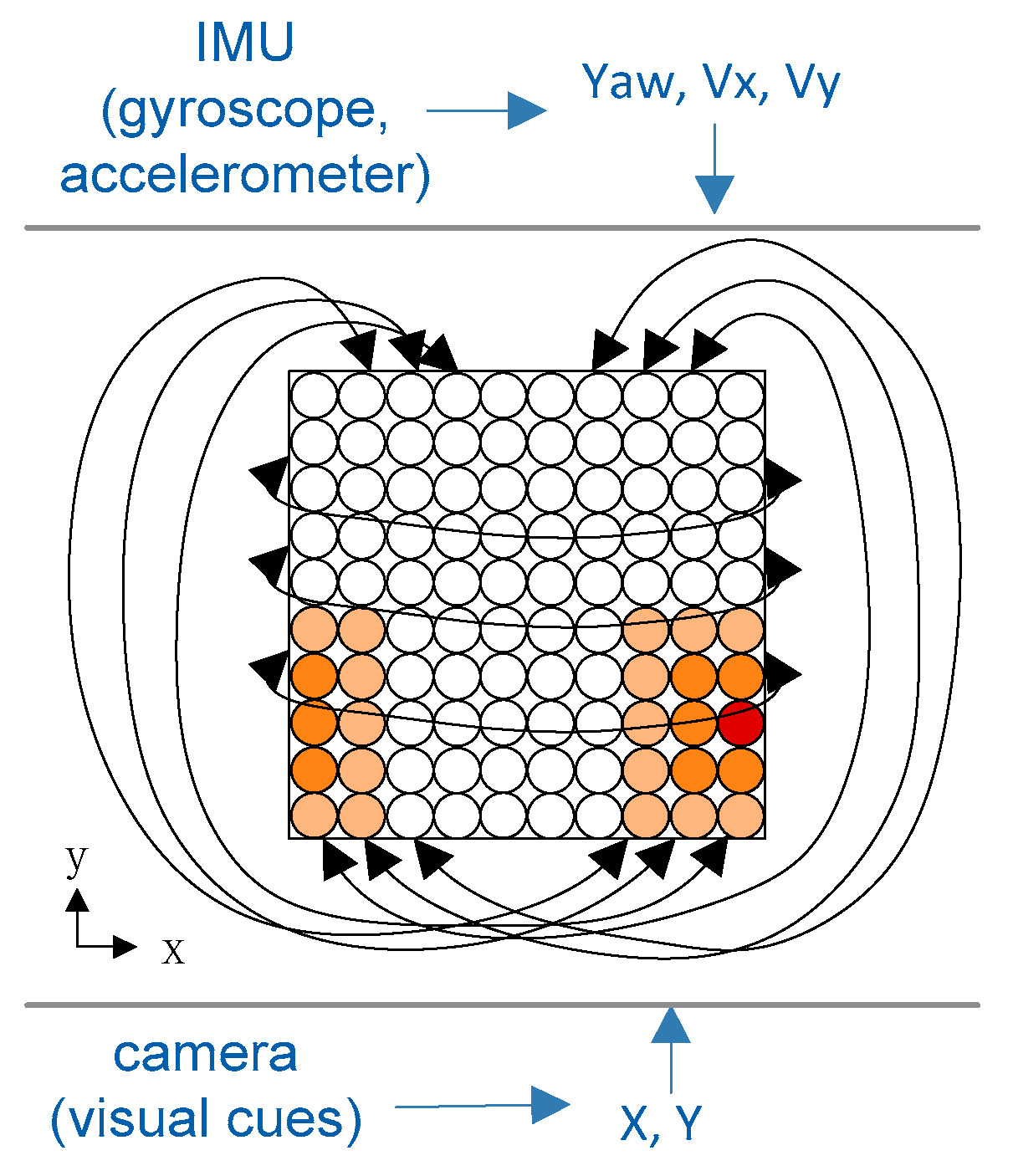
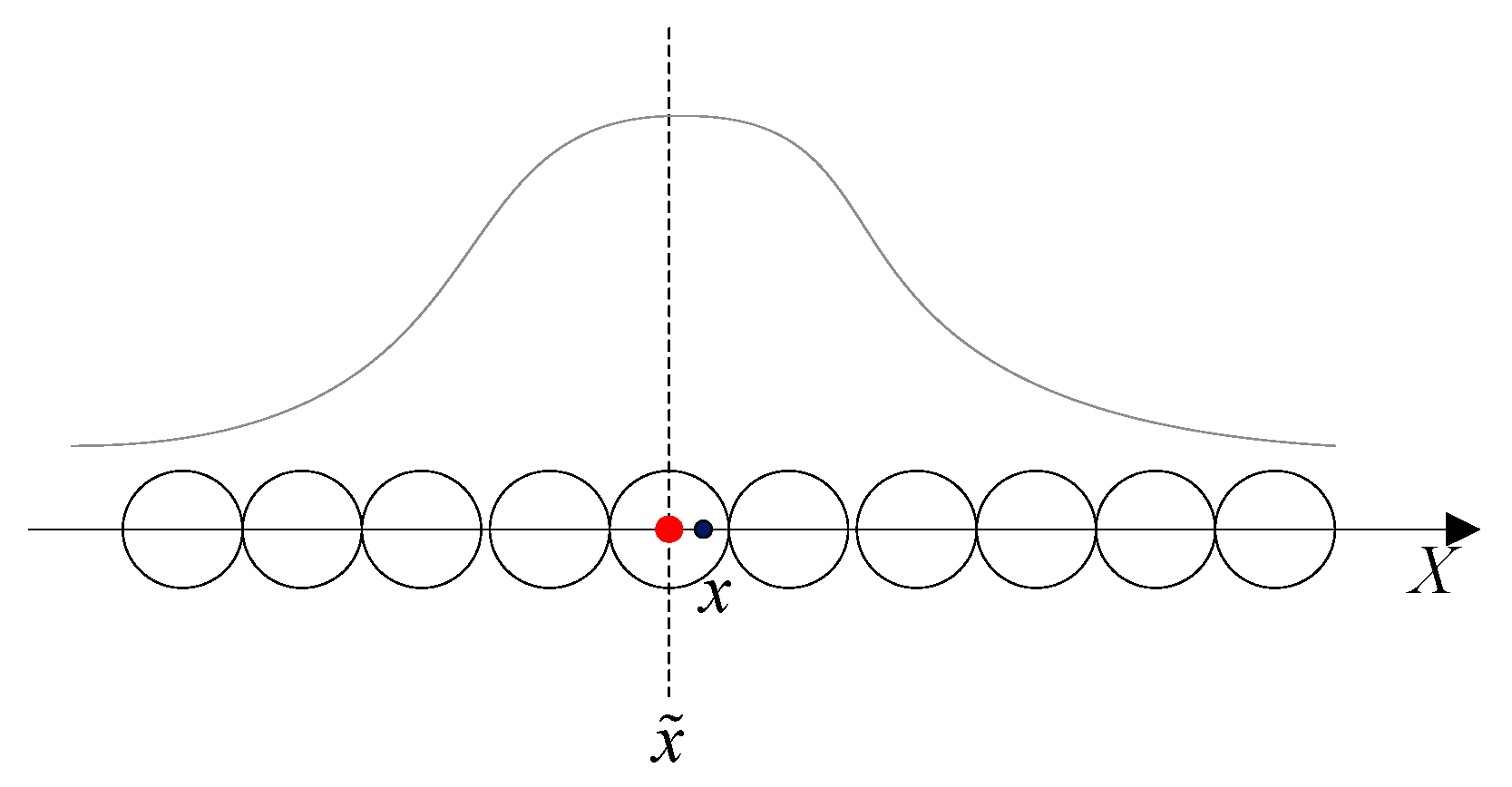
3.3. Place Cells’ Encoding
4. Population Spatial Representation Cells’ Decoding
4.1. Population Neuron Decoding
4.2. Decoding Direction
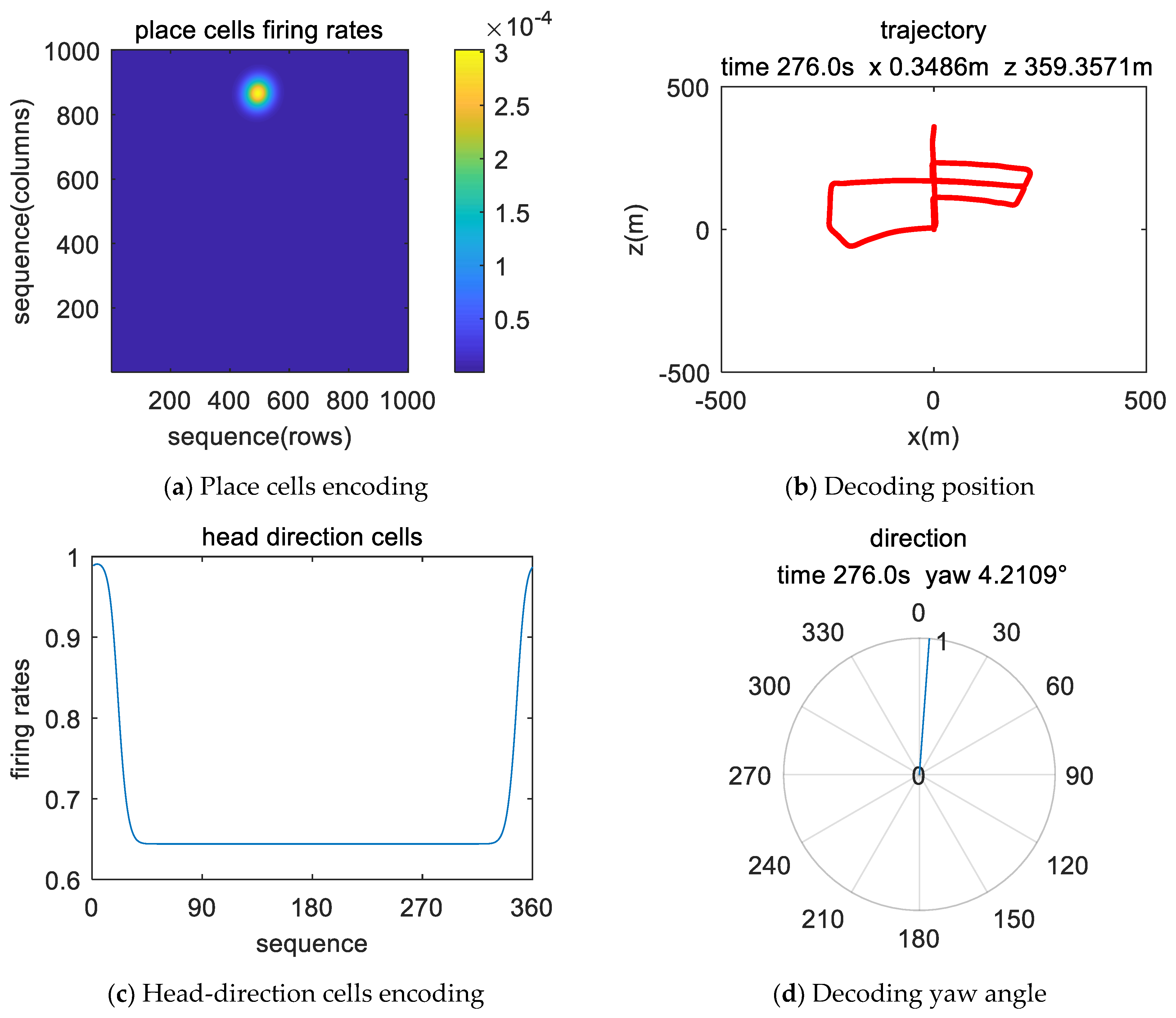
4.3. Decoding Position
5. Experiment and Results
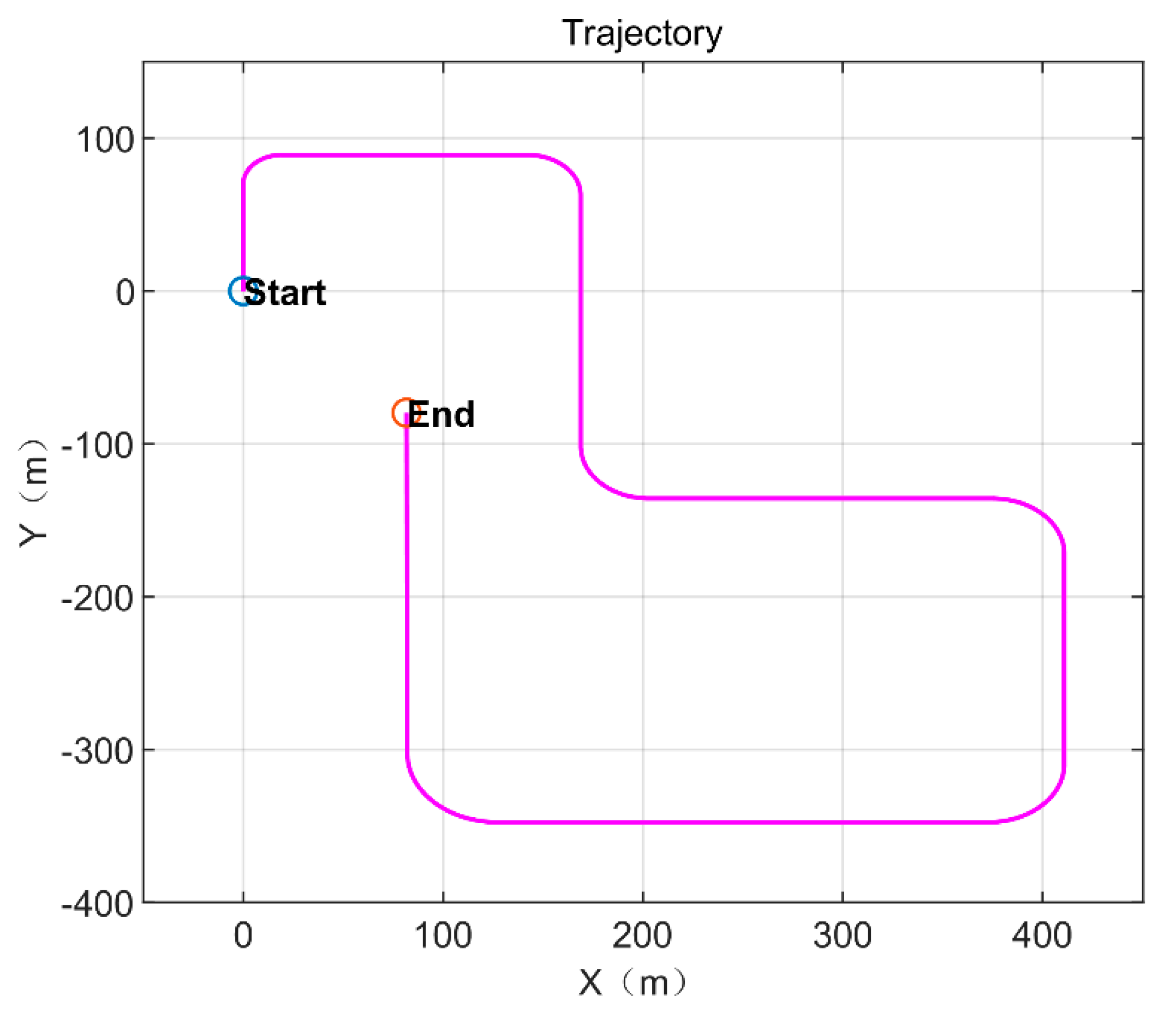
5.1. Simulation Description
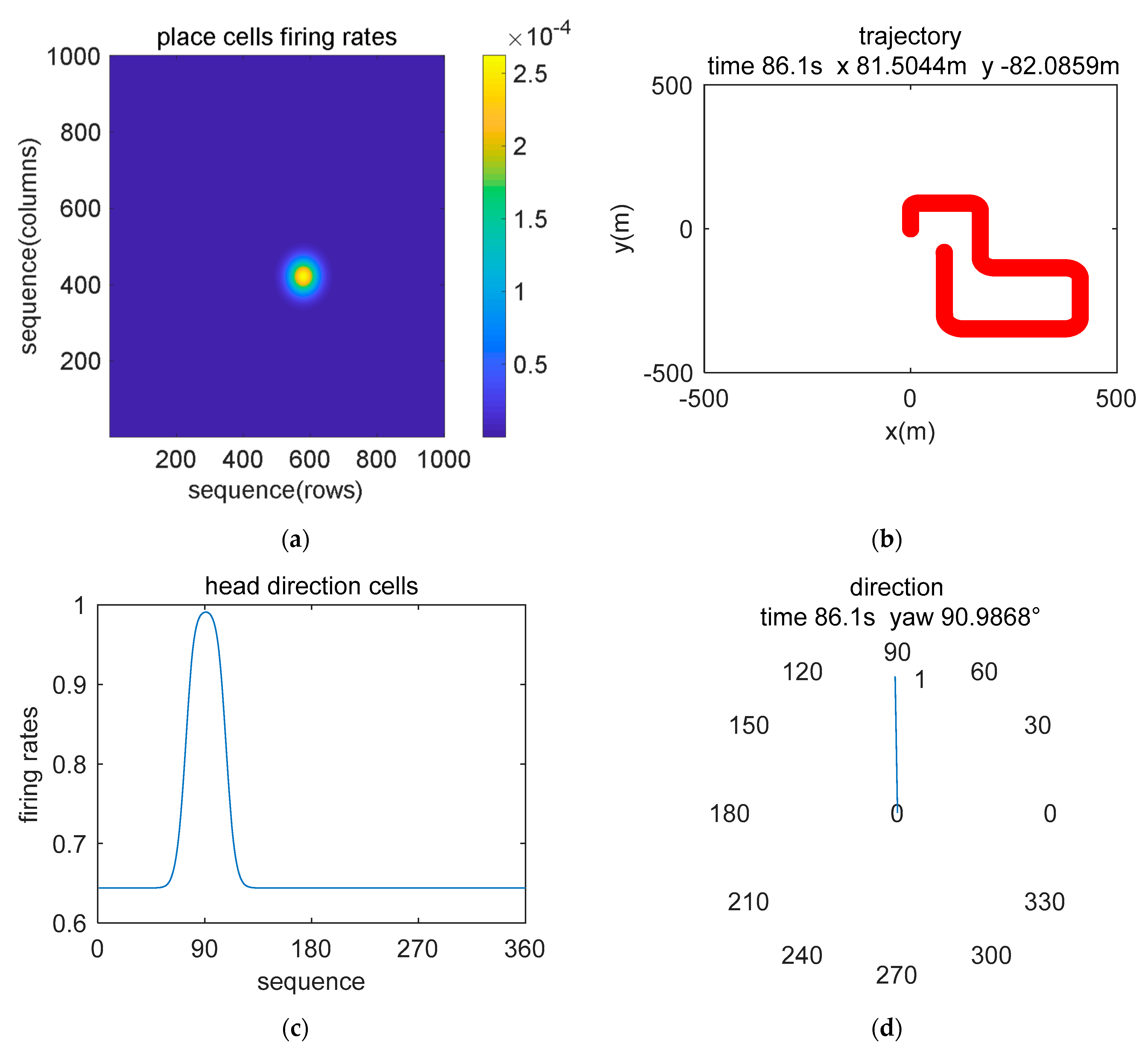
5.2. Simulation Data Experiment
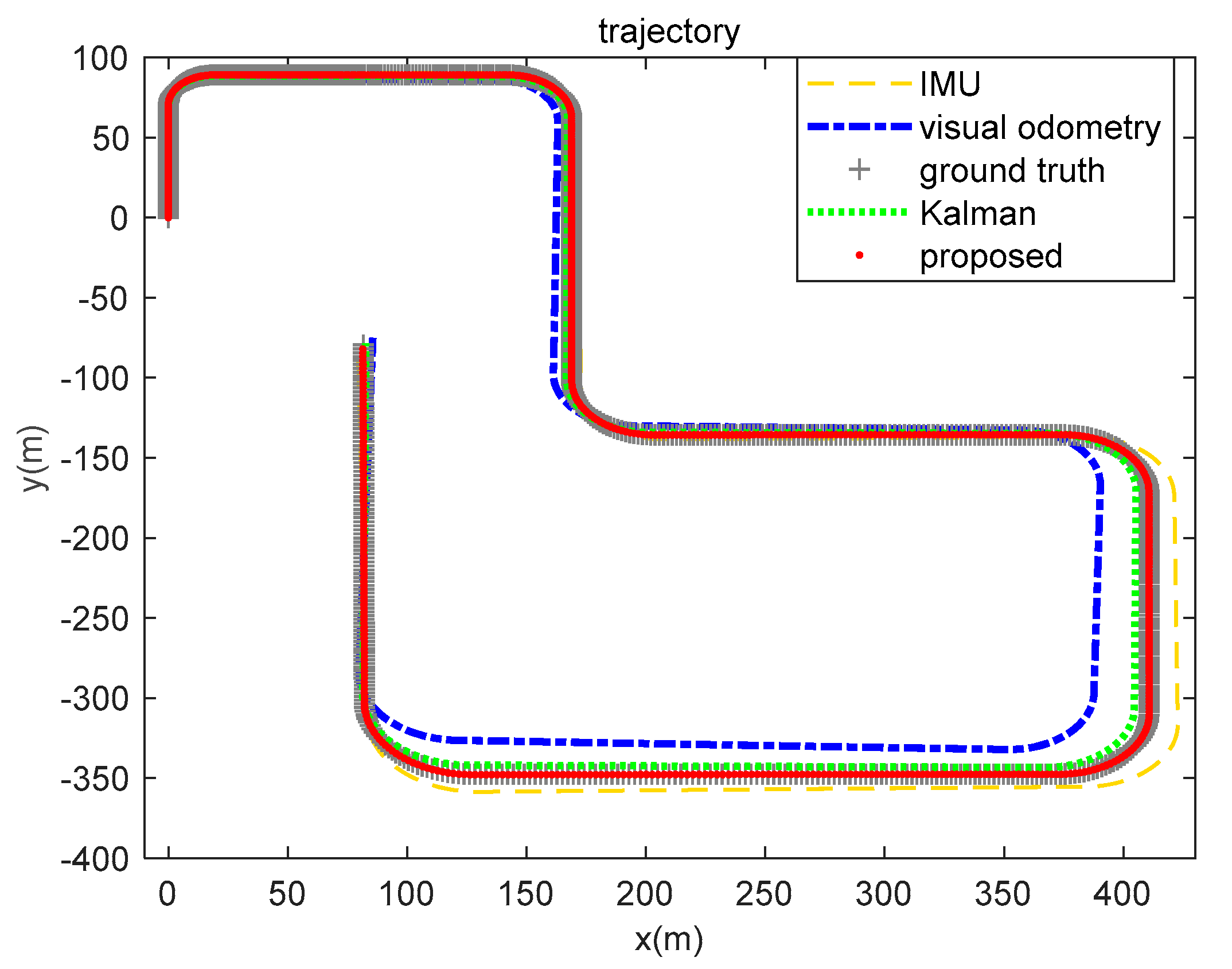
5.3. Real-World Data Experiment
- (1)
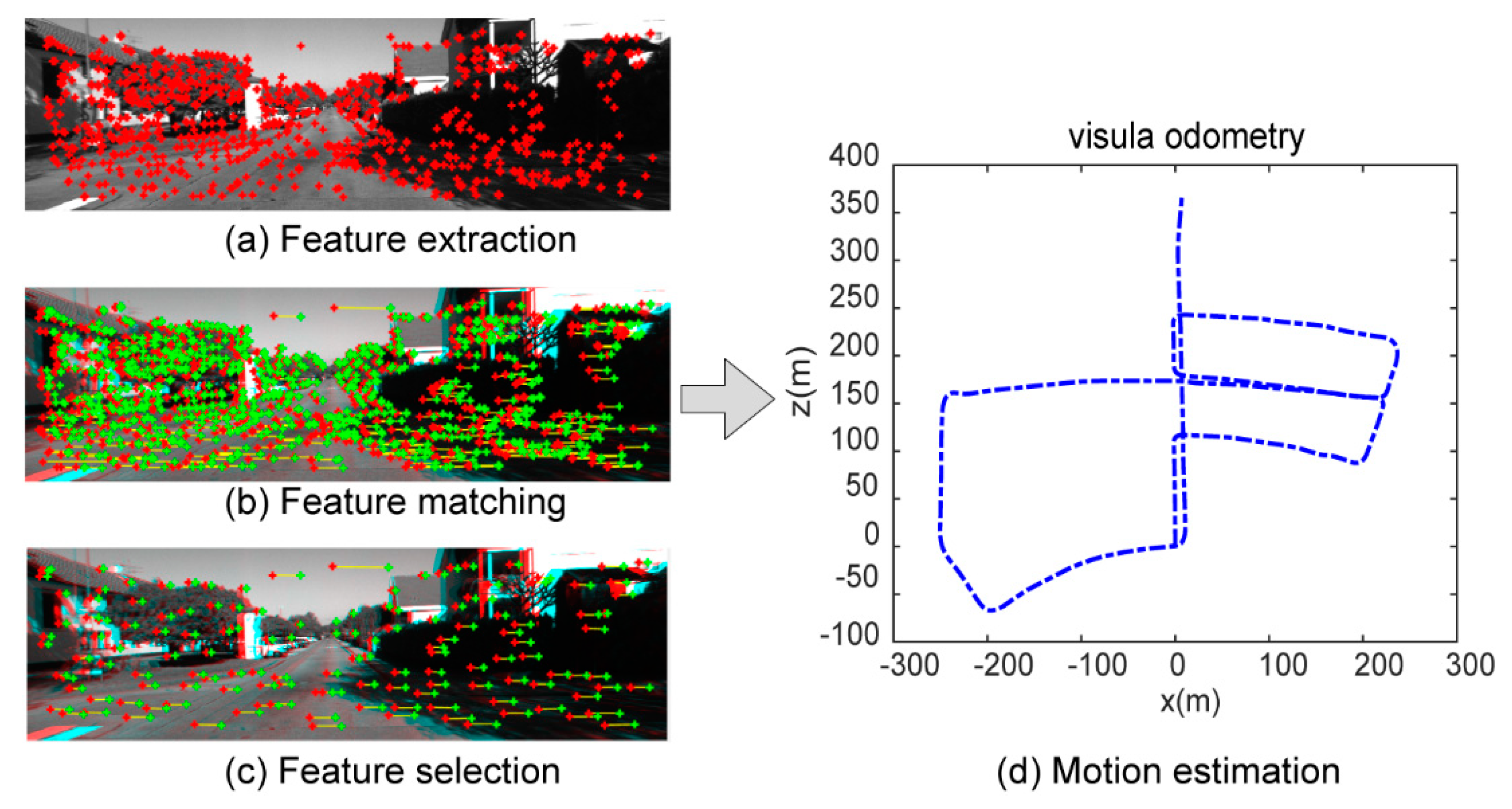
- Feature extraction: each image is extracted with corner and blob features, as shown in Figure 12a.
- (2)
- Feature matching: Starting from all the feature points in the left image at time t, the best matching point is found in the left image at time t-1, and then the feature points are still found in the right image at time t-1 and the right image at time t. The best match is found in four images acquired at consecutive moments, as shown in Figure 12b.
- (3)
- Feature selection: in order to ensure that the features are evenly distributed in the entire image, the entire image is divided into buckets with a size of 50 × 50 pixels, and feature selection is performed to select only the strongest features present in each bucket, as shown in Figure 12c.
- (4)
6. Discussion
6.1. Model Parameter Adjustment
6.2. Other Dataset Experiments
7. Conclusions
- (1)
- A brain-inspired research framework based on visual and inertial information was provided for the intelligent autonomous navigation system in complex environments.
- (2)
- A brain-inspired visual-inertial information encoding method and navigation parameter methods were proposed to explore brain-inspired research ideas from neuroscience to application.
- (3)
- The brain-inspired navigation model promotes the development of more intelligent navigation systems and provides the possibility for the wide application of brain-inspired intelligent robots and aircraft in the future.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, Y.J.; Zhao, J.; Guo, Y.; He, W.H.; Yuan, K. PL-VIO: Tightly-coupled monocular visual-inertial odometry using point and line features. Sensors 2018, 18, 25. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ma, S.J.; Bai, X.H.; Wang, Y.L.; Fang, R. Robust stereo visual-inertial odometry using nonlinear optimization. Sensors 2019, 19, 15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- He, S.; Cha, J.; Park, C.G. EKF-based visual inertial navigation using sliding window nonlinear optimization. IEEE Trans. Intell. Transp. Syst. 2019, 20, 2470–2479. [Google Scholar] [CrossRef]
- Li, D.; Liu, J.Y.; Qiao, L.; Xiong, Z. Fault tolerant navigation method for satellite based on information fusion and unscented Kalman filter. J. Syst. Eng. Electron. 2010, 21, 682–687. [Google Scholar] [CrossRef]
- Pei, L.; Liu, D.H.; Zou, D.P.; Choy, R.L.F.; Chen, Y.W.; He, Z. Optimal heading estimation based multidimensional particle filter for pedestrian indoor positioning. IEEE Access 2018, 6, 49705–49720. [Google Scholar] [CrossRef]
- McNaughton, B.L.; Chen, L.L.; Markus, E.J. “Dead reckoning”, landmark learning, and the sense of direction: A neurophysiological and computational hypothesis. J. Cogn. Neurosci. 1991, 3, 190–202. [Google Scholar] [CrossRef]
- Whishaw, I.Q.; Hines, D.J.; Wallace, D.G. Dead reckoning (path integration) requires the hippocampal formation: Evidence from spontaneous exploration and spatial learning tasks in light (allothetic) and dark (idiothetic) tests. Behav. Brain Res. 2001, 127, 49–69. [Google Scholar] [CrossRef]
- O’Keefe, J. Place units in the hippocampus of the freely moving rat. Exp. Neurol. 1976, 51, 78–109. [Google Scholar] [CrossRef]
- Jayakumar, R.P.; Madhav, M.S.; Savelli, F.; Blair, H.T.; Cowan, N.J.; Knierim, J.J. Recalibration of path integration in hippocampal place cells. Nature 2019, 566, 533–537. [Google Scholar] [CrossRef]
- Taube, J.S. Head direction cells recorded in the anterior thalamic nuclei of freely moving rats. J. Neurosci. 1995, 15, 70–86. [Google Scholar] [CrossRef]
- Hafting, T.; Fyhn, M.; Molden, S.; Moser, M.B.; Moser, E.I. Microstructure of a spatial map in the entorhinal cortex. Nature 2005, 436, 801–806. [Google Scholar] [CrossRef] [PubMed]
- Krupic, J.; Burgess, N.; O’Keefe, J. Neural representations of location composed of spatially periodic bands. Science 2012, 337, 853–857. [Google Scholar] [CrossRef] [Green Version]
- Lever, C.; Burton, S.; Jeewajee, A.; O’Keefe, J.; Burgess, N. Boundary vector cells in the subiculum of the hippocampal formation. J. Neurosci. 2009, 29, 9771–9777. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Milford, M.J.; Wyeth, G.F. Mapping a suburb with a single camera using a biologically inspired SLAM system. IEEE Trans. Robot. 2008, 24, 1038–1053. [Google Scholar] [CrossRef] [Green Version]
- Ball, D.; Heath, S.; Wiles, J.; Wyeth, G.; Corke, P.; Milford, M. OpenRatSLAM: An open source brain-based SLAM system. Auton. Robot. 2013, 34, 149–176. [Google Scholar] [CrossRef]
- Steckel, J.; Peremans, H. BatSLAM: Simultaneous localization and mapping using biomimetic sonar. PLoS ONE 2013, 8, 11. [Google Scholar] [CrossRef]
- Yu, F.W.; Shang, J.G.; Hu, Y.J.; Milford, M. NeuroSLAM: A brain-inspired SLAM system for 3D environments. Biol. Cybern. 2019, 113, 515–545. [Google Scholar] [CrossRef]
- Zou, Q.; Cong, M.; Liu, D.; Du, Y.; Lyu, Z. Robotic episodic cognitive learning inspired by hippocampal spatial cells. IEEE Robot. Autom. Lett. 2020, 5, 5573–5580. [Google Scholar] [CrossRef]
- Yuan, M.L.; Tian, B.; Shim, V.A.; Tang, H.J.; Li, H.Z. An Entorhinal-Hippocampal Model for Simultaneous Cognitive Map Building. In Proceedings of the 29th Association-for-the-Advancement-of-Artificial-Intelligence (AAAI) Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; pp. 586–592. [Google Scholar]
- Nister, D. An efficient solution to the five-point relative pose problem. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Madison, WI, USA, 18–20 June 2003; pp. 195–202. [Google Scholar]
- Knierim, J.J.; Zhang, K. Attractor dynamics of spatially correlated neural activity in the limbic system. Annu. Rev. Neurosci. 2012, 35, 267–285. [Google Scholar] [CrossRef] [Green Version]
- Cai, K.; Shen, J. Continuous attractor neural network model of multisensory integration. In Proceedings of the 2011 International Conference on System Science, Engineering Design and Manufacturing Informatization, Guiyang, China, 22–23 October 2011; pp. 352–355. [Google Scholar]
- Wu, S.; Wong, K.Y.M.; Fung, C.C.A.; Mi, Y.; Zhang, W. Continuous attractor neural networks: Candidate of a canonical model for neural information representation. F1000Research 2016, 5, 1–9. [Google Scholar] [CrossRef]
- Laurens, J.; Angelaki, D.E. The brain compass: A perspective on how self-motion updates the head direction cell attractor. Neuron 2018, 97, 275–289. [Google Scholar] [CrossRef] [Green Version]
- Angelaki, D.E.; Laurens, J. The head direction cell network: Attractor dynamics, integration within the navigation system, and three-dimensional properties. Curr. Opin. Neurobiol. 2020, 60, 136–144. [Google Scholar] [CrossRef]
- Stringer, S.M.; Trappenberg, T.P.; Rolls, E.T.; de Araujo, I.E.T. Self-organizing continuous attractor networks and path integration: One-dimensional models of head direction cells. Netw. Comput. Neural Syst. 2002, 13, 217–242. [Google Scholar] [CrossRef]
- Xie, X.; Hahnloser, R.H.R.; Seung, H.S. Double-ring network model of the head-direction system. Phys. Rev. E 2002, 66, 041902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Go, M.A.; Rogers, J.; Gava, G.P.; Davey, C.E.; Prado, S.; Liu, Y.; Schultz, S.R. Place cells in head-fixed mice navigating a floating real-world environment. Front. Cell. Neurosci. 2021, 15, 16. [Google Scholar] [CrossRef] [PubMed]
- O’Keefe, J.; Dostrovsky, J. The hippocampus as a spatial map. Preliminary evidence from unit activity in the freely-moving rat. Brain Res. 1971, 34, 171–175. [Google Scholar] [CrossRef]
- Stringer, S.M.; Rolls, E.T.; Trappenberg, T.P.; de Araujo, I.E.T. Self-organizing continuous attractor networks and path integration: Two-dimensional models of place cells. Netw. Comput. Neural Syst. 2002, 13, 429–446. [Google Scholar] [CrossRef]
- Graf, A.B.A.; Kohn, A.; Jazayeri, M.; Movshon, J.A. Decoding the activity of neuronal populations in macaque primary visual cortex. Nat. Neurosci. 2011, 14, 239–332. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Yuan, M.; Tang, H. Continuous Attractors and Population Decoding Multiple-peaked Activity. In Proceedings of the 6th IEEE Conference on Cybernetics and Intelligent Systems (CIS), Manila, Philippines, 12–15 November 2013; pp. 128–133. [Google Scholar]
- Georgopoulos, A.P.; Schwartz, A.B.; Kettner, R.E. Neuronal population coding of movement direction. Science 1986, 233, 1416–1419. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Page, H.J.I.; Walters, D.; Stringer, S.M. A speed-accurate self-sustaining head direction cell path integration model without recurrent excitation. Netw. Comput. Neural Syst. 2018, 29, 37–69. [Google Scholar] [CrossRef]
- Barbieri, R.; Frank, L.M.; Nguyen, D.P.; Quirk, M.C.; Solo, V.; Wilson, M.A.; Brown, E.N. A Bayesian decoding algorithm for analysis of information encoding in neural ensembles. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Francisco, CA, USA, 1–5 Septempber 2004; pp. 4483–4486. [Google Scholar]
- Geiger, A.; Lenz, P.; Stiller, C.; Urtasun, R. Vision meets robotics: The KITTI dataset. Int. J. Robot. Res. 2013, 32, 1231–1237. [Google Scholar] [CrossRef] [Green Version]
- Geiger, A.; Ziegler, J.; Stiller, C. StereoScan: Dense 3d Reconstruction in Real-time. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Baden-Baden, Germany, 5–9 Junuary 2011; pp. 963–968. [Google Scholar]





| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 360 | 1440 | ||
| 1001 | 4004 | ||
| , | 1, 1, 1 | , | 500, 500 |
| IMU | Visual Odometry | Kalman (Inertial-Visual) | Proposed (Inertial-Visual) | |
|---|---|---|---|---|
| x(m) | 5.8858 | 11.2778 | 2.9994 | 1.2889 |
| y(m) | 5.0015 | 9.6306 | 2.5736 | 1.3516 |
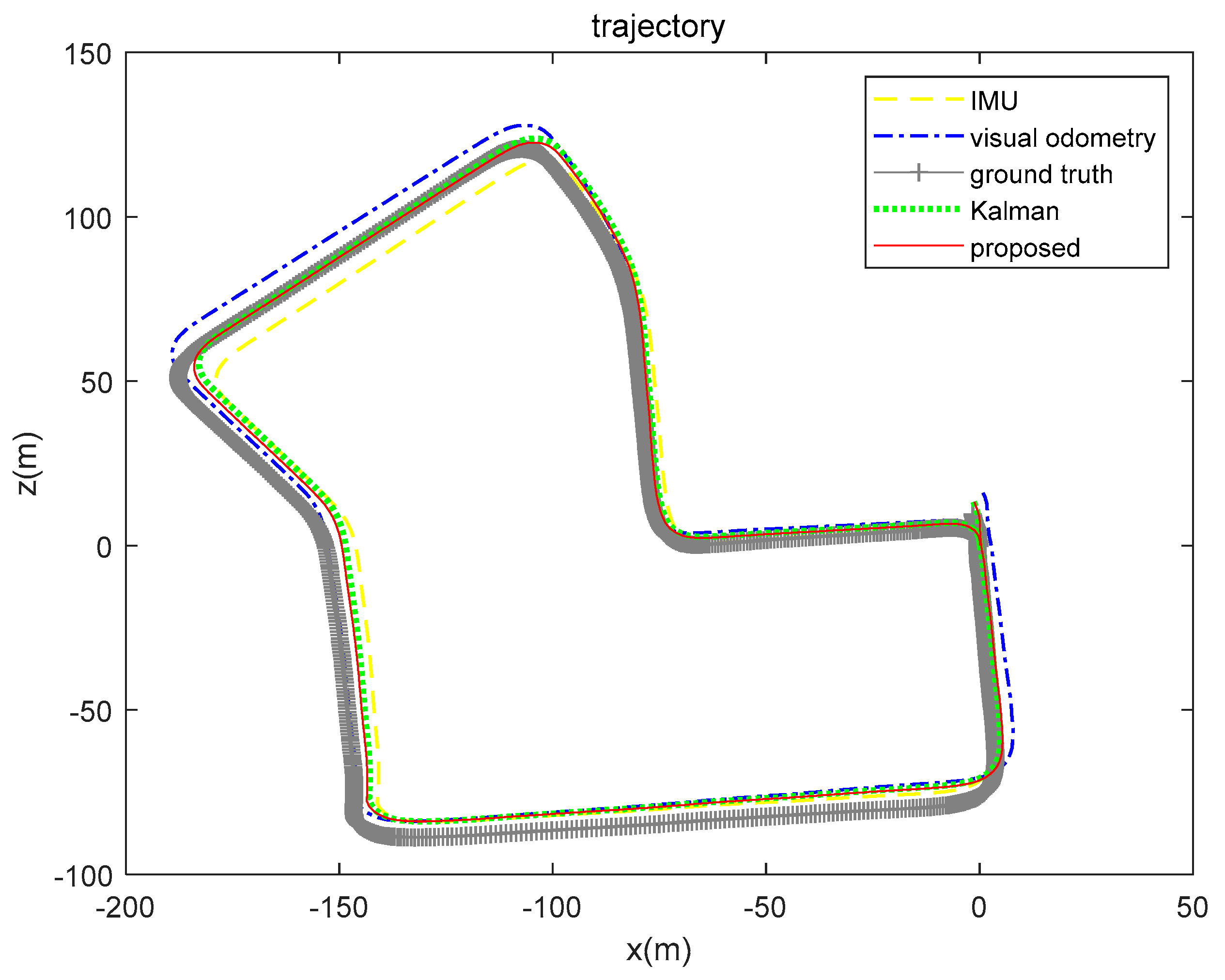
| IMU | Visual Odometry | Kalman (Inertial-Visual) | Proposed (Inertial-Visual) | |
|---|---|---|---|---|
| x(m) | 5.2123 | 7.1180 | 5.5708 | 3.8551 |
| z(m) | 6.3941 | 5.6666 | 4.3949 | 3.9532 |
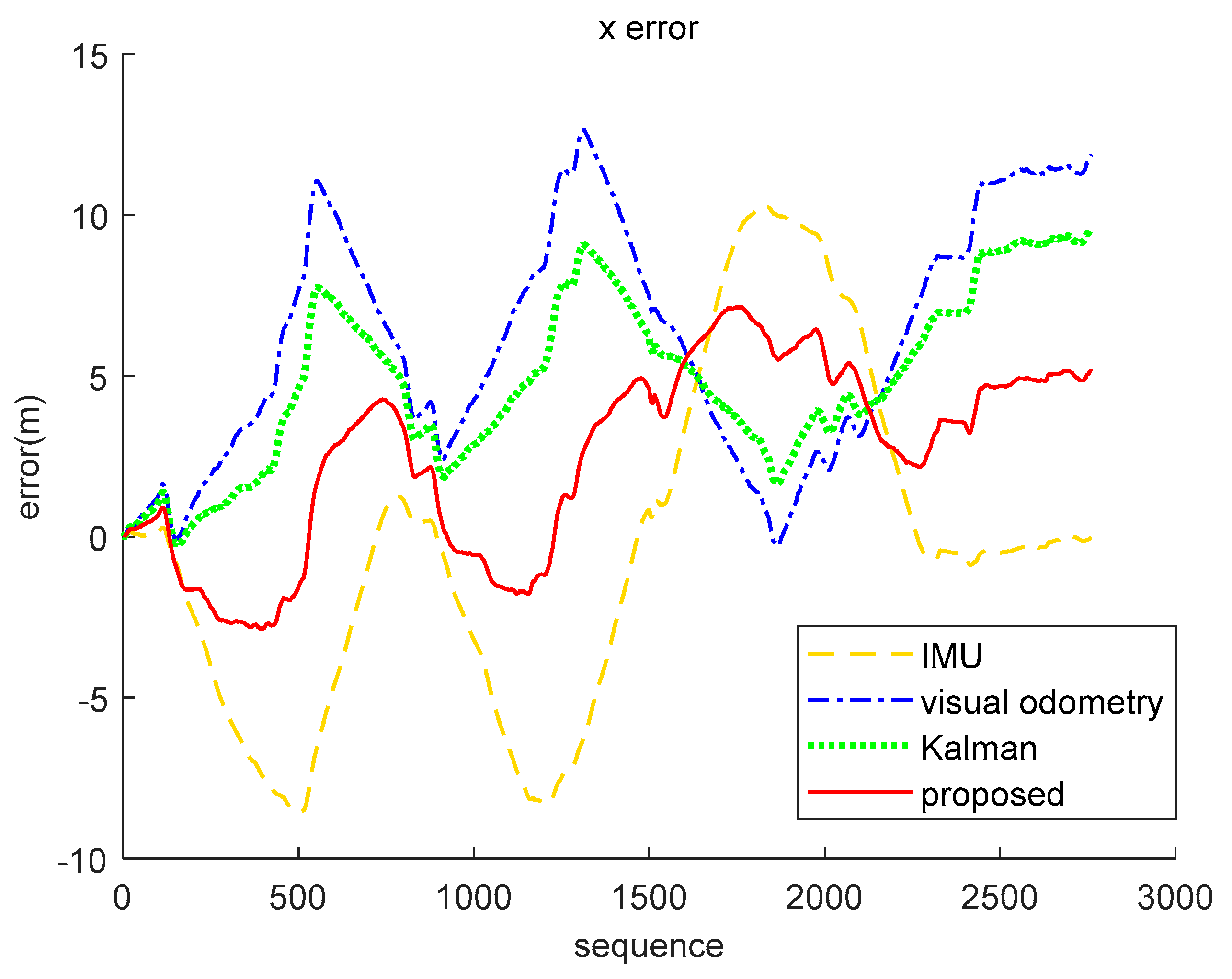
| IMU | Visual Odometry | Kalman (Inertial-Visual) | Proposed (Inertial-Visual) | |
|---|---|---|---|---|
| x(m) | 8.7314 | 26.7076 | 22.0495 | 13.8206 |
| z(m) | 24.0802 | 22.7763 | 20.4295 | 19.6386 |
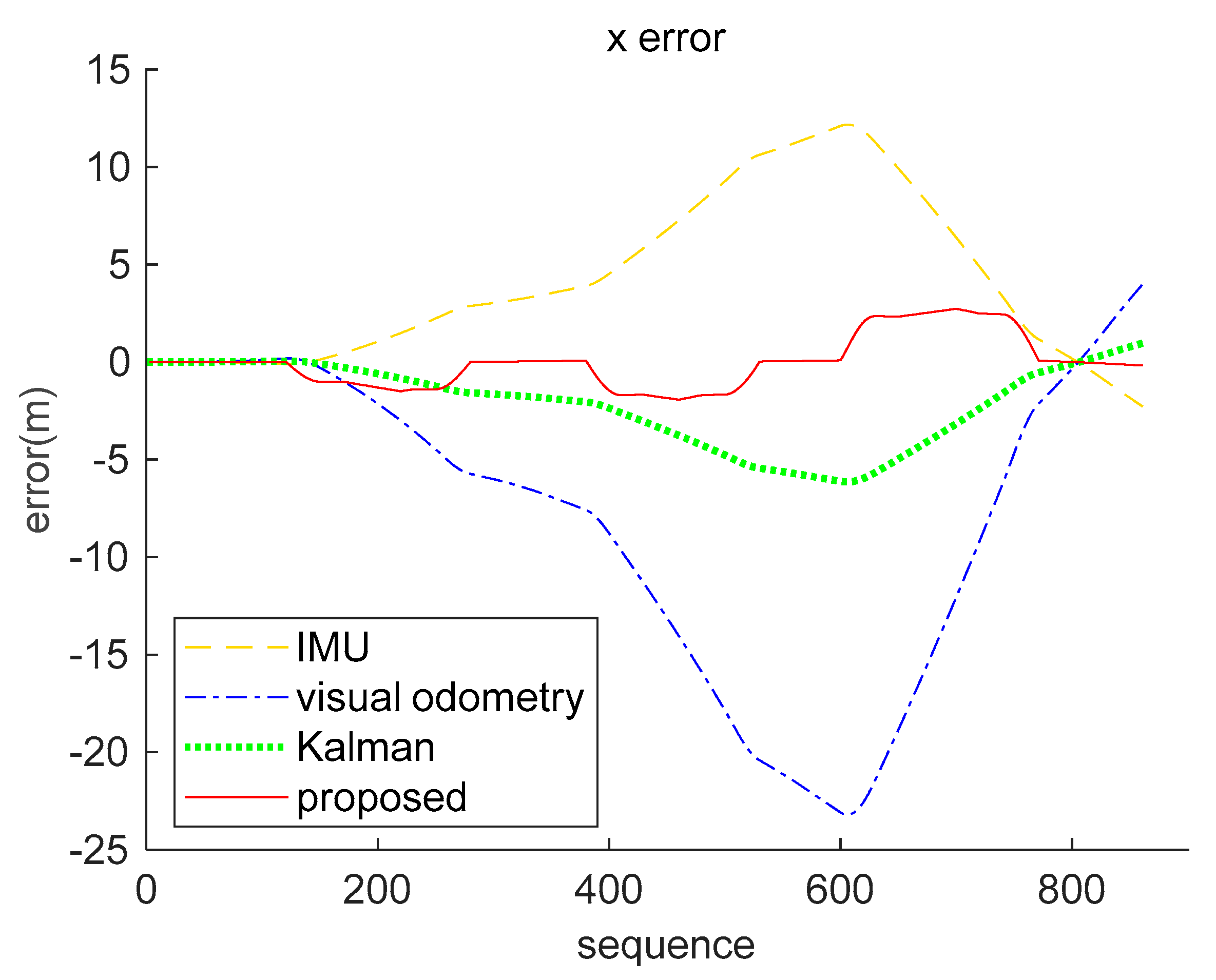
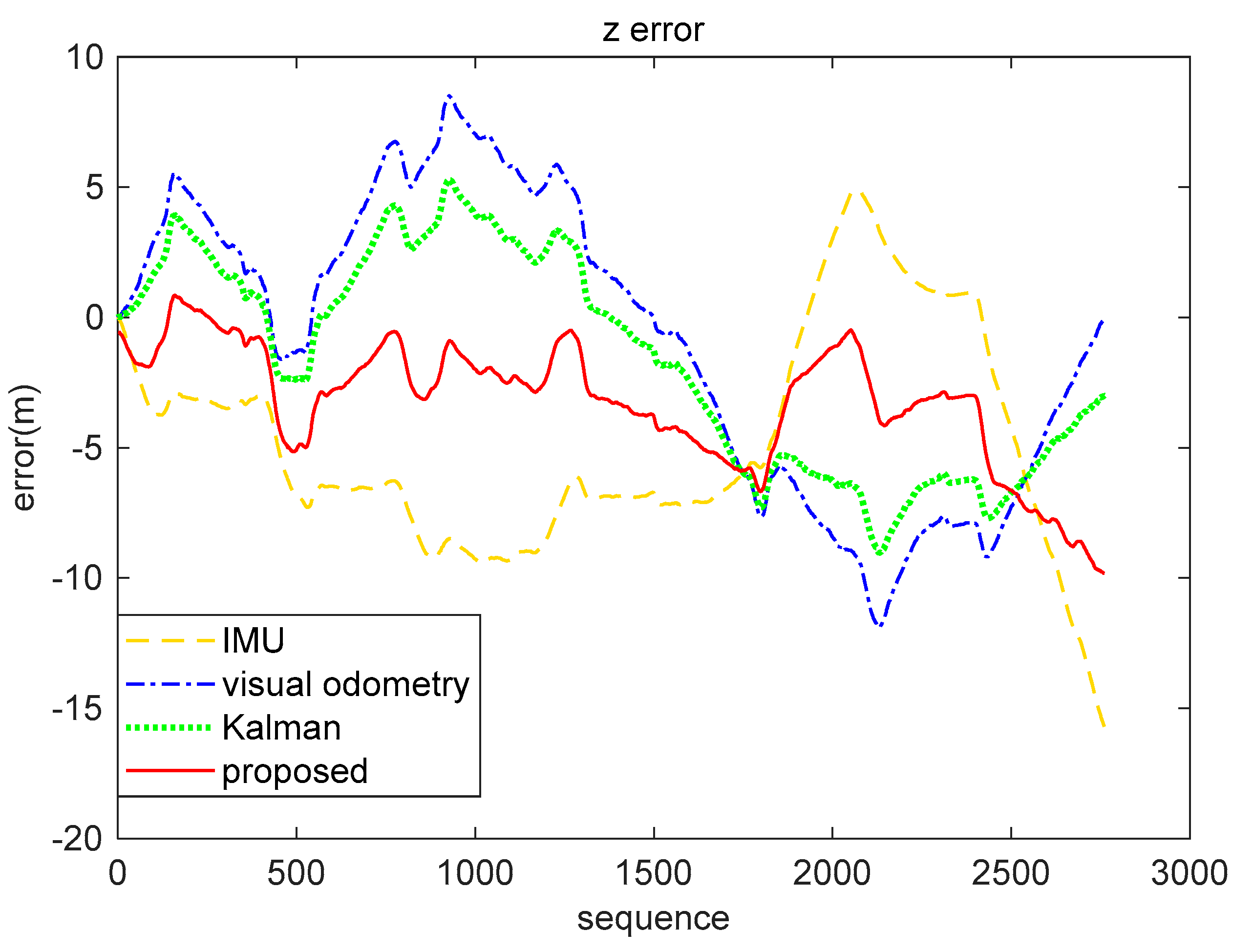
| IMU | Visual Odometry | Kalman (Inertial-Visual) | Proposed (Inertial-Visual) | |
|---|---|---|---|---|
| x(m) | 4.8461 | 1.8431 | 3.0742 | 2.8290 |
| z(m) | 2.8955 | 6.3704 | 4.5074 | 3.1663 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Xiong, Z.; Liu, J.; Yang, C.; Chao, L.; Peng, Y. A Positioning Method Based on Place Cells and Head-Direction Cells for Inertial/Visual Brain-Inspired Navigation System. Sensors 2021, 21, 7988. https://doi.org/10.3390/s21237988
Chen Y, Xiong Z, Liu J, Yang C, Chao L, Peng Y. A Positioning Method Based on Place Cells and Head-Direction Cells for Inertial/Visual Brain-Inspired Navigation System. Sensors. 2021; 21(23):7988. https://doi.org/10.3390/s21237988
Chicago/Turabian StyleChen, Yudi, Zhi Xiong, Jianye Liu, Chuang Yang, Lijun Chao, and Yang Peng. 2021. "A Positioning Method Based on Place Cells and Head-Direction Cells for Inertial/Visual Brain-Inspired Navigation System" Sensors 21, no. 23: 7988. https://doi.org/10.3390/s21237988
APA StyleChen, Y., Xiong, Z., Liu, J., Yang, C., Chao, L., & Peng, Y. (2021). A Positioning Method Based on Place Cells and Head-Direction Cells for Inertial/Visual Brain-Inspired Navigation System. Sensors, 21(23), 7988. https://doi.org/10.3390/s21237988





