Time-Optimal Velocity Tracking Control for Consensus Formation of Multiple Nonholonomic Mobile Robots
Abstract
:1. Introduction
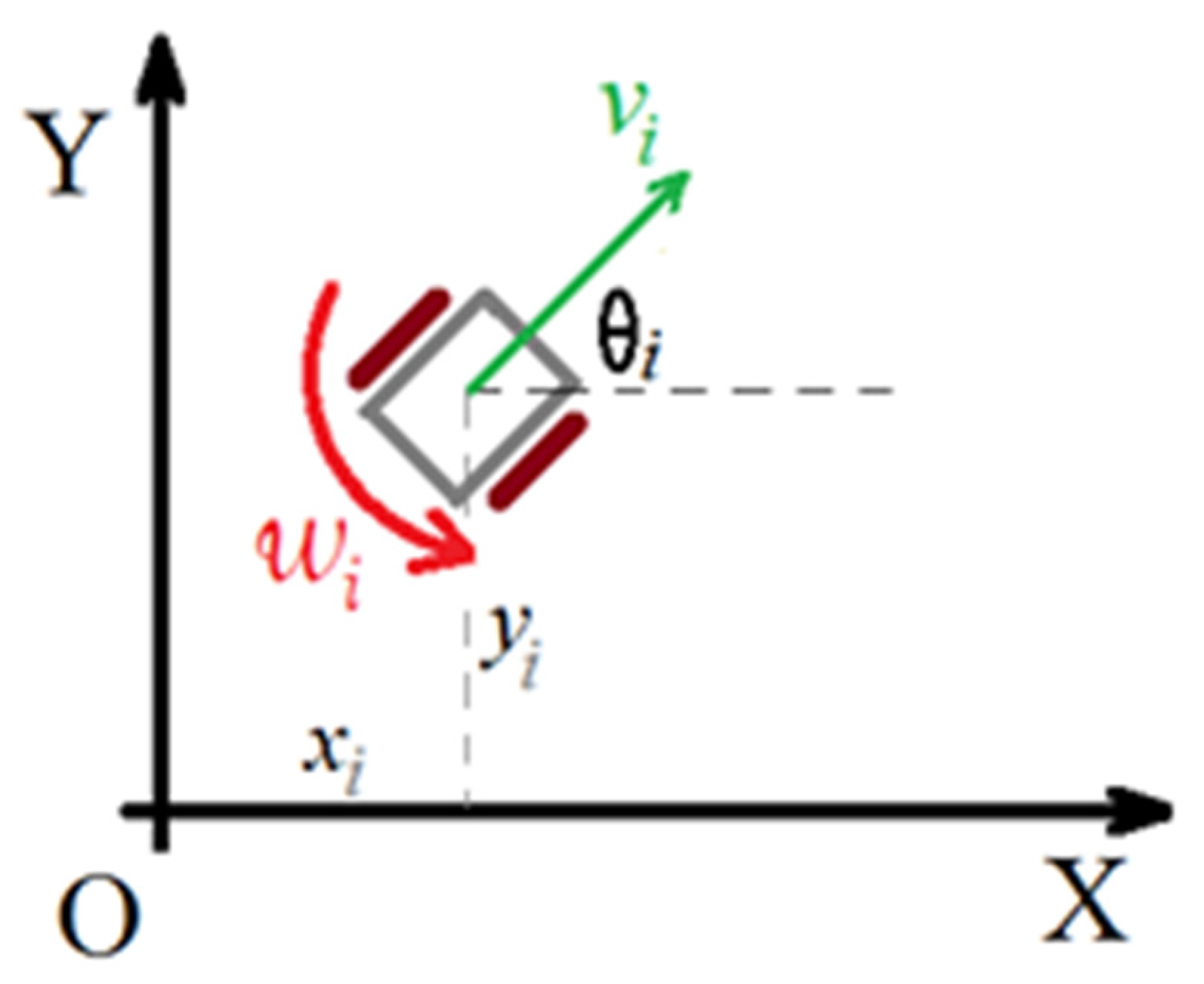
2. Dynamics of Wheeled Mobile Robots
3. Time-Optimal Control of WMRs
4. Time-Optimal Consensus Algorithm Strategies
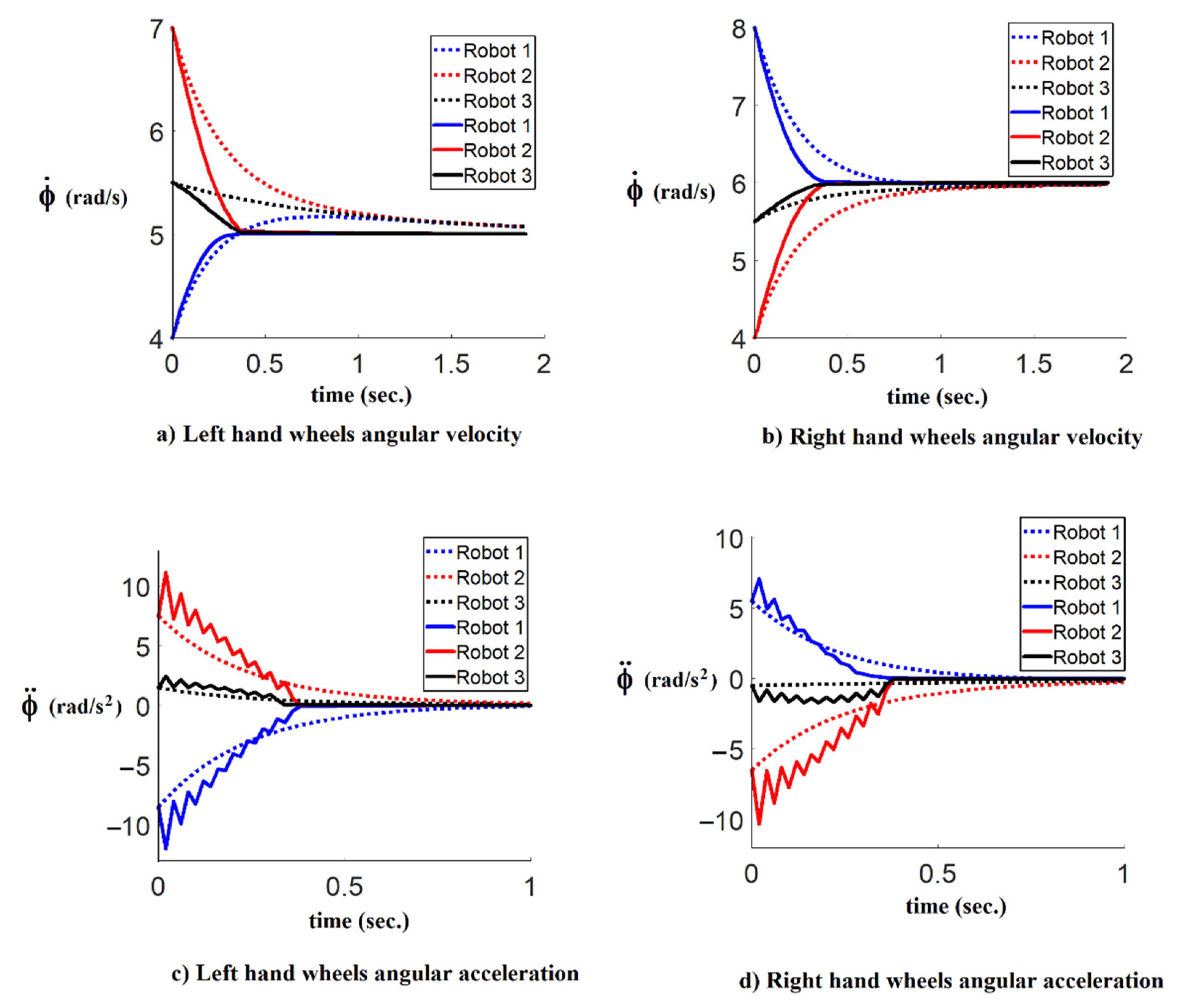
5. Simulations
5.1. Comparison of the Performance of Velocity Tracking Consensus Formation with and without a Time-Optimal Strategy
5.2. The Effect of Network Topology and the Number of Agents on the Convergence Time
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Acevedo, J.J.; Arrue, B.C.; Maza, I.; Ollero, A. A decentralised algorithm for area surveillance missions using a team of aerial robots with different sensing capabilities. In Proceedings of the IEEE International Conference on Robotics and Automation, Hong Kong, China, 31 May–7 June 2014; pp. 4735–4740. [Google Scholar]
- Casbeer, D.W.; Kingston, D.B.; Beard, R.W.; McLain, T.W. Cooperative forest fire surveillance using a team of small unmanned air vehicles. Int. J. Syst. Sci. 2006, 37, 351–360. [Google Scholar] [CrossRef]
- Zhou, J.; Hu, Q.; Friswell, M.I. Decentralised finite time attitude synchronisation control of satellite formation flying. J. Guid. Control. Dyn. 2012, 36, 185–195. [Google Scholar] [CrossRef] [Green Version]
- Ren, W.; Beard, R.W. Formation feedback control for multiple spacecraft via virtual structures. IEEE Proc. Control. Theory Appl. 2004, 151, 357–368. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.K.C.; Hadaegh, F.Y. Coordination and control of multiple microspacecraft moving in formation. J. Astronaut. Sci. 1996, 44, 315–355. [Google Scholar]
- Ren, W.; Beard, R.W. Decentralised scheme for spacecraft formation flying via the virtual structure approach. AIAA J. Guid. Contr. Dyn. 2004, 27, 73–82. [Google Scholar] [CrossRef]
- Consolini, L.; Morbidi, F.; Prattichizzo, D.; Tosques, M. Leader–follower formation control of nonholonomic mobile robots with input constraints. Automatica 2008, 44, 1343–1349. [Google Scholar] [CrossRef]
- Poonawala, H.A.; Satici, A.C.; Spong, M.W. Leader-follower formation control of nonholonomic wheeled mobile robots using only position measurements. In Proceedings of the IEEE 9th Asian Control Conference, Istanbul, Turkey, 23–26 June 2013; pp. 1–6. [Google Scholar]
- Sira-Ramírez, H.; Castro-Linares, R.; Puriel-Gil, G. An active disturbance rejection approach to leader-follower controlled formation. Asian J. Control. 2014, 16, 382–395. [Google Scholar] [CrossRef]
- Lewis, M.A.; Tan, K.-H. High precision formation control of mobile robots using virtual structures. Auton. Robot. 1997, 4, 387–403. [Google Scholar] [CrossRef]
- Egerstedt, M.; Hu, X.; Stotsky, A. Control of mobile platforms using a virtual vehicle approach. IEEE Trans. Automat. Contr. 2001, 46, 1777–1782. [Google Scholar] [CrossRef]
- Kan, Z.; Dani, A.P.; Shea, J.M.; Dixon, W.E. Network Connectivity Preserving Formation Stabilization and Obstacle Avoidance via a Decentralised Controller. IEEE Trans. Autom. Control. 2012, 57, 1827–1832. [Google Scholar] [CrossRef]
- Yu, H.; Dai, K.; Li, H.; Zou, Y.; Ma, X.; Ma, S.; Zhang, H. Distributed cooperative guidance law for multiple missiles with input delay and topology switching. J. Frankl. Inst. 2021, 358, 9061–9085. [Google Scholar] [CrossRef]
- Das, B.; Subudhi, B.; Pati, B.B. Cooperative formation control of autonomous underwater vehicles: An overview. Int. J. Autom. Comput. 2016, 13, 199–225. [Google Scholar] [CrossRef]
- Cao, Y.; Yu, W.; Ren, W.; Chen, G. An Overview of Recent Progress in the Study of Distributed Multi-agent Coordination. IEEE Trans. Ind. Inform. 2013, 9, 427–438. [Google Scholar] [CrossRef] [Green Version]
- Ren, W.; Beard, R.W.; Atkins, E.M. Information consensus in multivehicle cooperative control: Collective group behavior through local interaction. IEEE Control Syst. Mag. 2007, 27, 71–82. [Google Scholar]
- Ren, W. On Consensus Algorithms for Double-integrator Dynamics. IEEE Trans. Autom. Control. 2008, 53, 1503–1509. [Google Scholar] [CrossRef]
- Poonawala, H.A.; Spong, M.W. From Nonholonomy to Holonomy: Time-Optimal Velocity Control of Differential Drive Robots. In Proceedings of the 10th International Workshop on Robot Motion and Control, Poznan University of Technology, Poznan, Poland, 6–8 July 2015. [Google Scholar]
- Zhang, Y.; Tang, S.; Guo, J. Two-stage cooperative guidance strategy using a prescribed-time optimal consensus method. Aerosp. Sci. Technol. 2020, 100, 105641. [Google Scholar] [CrossRef]
- Semsar-Kazerooni, E.; Khorasani, K. Optimal consensus algorithms for cooperative team of agents subject to partial information. Automatica 2008, 44, 2766–2777. [Google Scholar] [CrossRef]
- Li, R.; Shi, Y. Finite-time optimal consensus control for second-order multi-agent systems. J. Ind. Manag. Optim. 2014, 10, 929–943. [Google Scholar] [CrossRef]
- Das, P.K.; Behera, H.S.; Jena, P.K.; Panigrahi, B.K. An intelligent multi-robot path planning in a dynamic environment using improved gravitational search algorithm. Int. J. Autom. Comput. 2016, 3, 295–313. [Google Scholar] [CrossRef]
- Yang, A.; Naeem, W.; Fei, M.; Liu, L.; Tu, X. Multiple robots formation manoeuvring and collision avoidance strategy. Int. J. Autom. Comput. 2017, 14, 696–705. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S. Adaptive near-optimal consensus of high-order non-linear multi-agent systems with heterogeneity. Automatica 2017, 85, 426–432. [Google Scholar] [CrossRef]
- Zhang, H.; Jiang, H.; Luo, Y.; Xiao, G. Data-Driven Optimal Consensus Control for Discrete-Time Multi-Agent Systems with Unknown Dynamics Using Reinforcement Learning Method. IEEE Trans. Ind. Electron. 2017, 64, 4091–4100. [Google Scholar] [CrossRef]
- Wei, M.; Chen, G.; Guo, Z. A fixed-time optimal consensus algorithm over undirected networks. In Proceedings of the Chinese Control And Decision Conference (CCDC), Shenyang, China, 9–11 June 2018. [Google Scholar] [CrossRef]
- Zhang, T. Unmanned Aerial Vehicle Formation Inspired by Bird Flocking and Foraging behavior. Int. J. Autom. Comput. 2018, 15, 402–416. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, P.; Du, G.; Li, F. A distributed method for dynamic multi-robot task allocation problems with critical time constraints. Robot. Auton. Syst. 2019, 118, 31–46. [Google Scholar] [CrossRef]
- Alonso-Mora, J.; Montijano, E.; Nägeli, T.; Hilliges, O.; Schwager, M.; Rus, D. Distributed multi-robot formation control in dynamic environments. Auton. Robot. 2019, 43, 1079–1100. [Google Scholar] [CrossRef] [Green Version]
- Mateo, D.; Horsevad, N.; Hassani, V.; Chamanbaz, M.; Bouffanais, R. Optimal network topology for responsive collective behavior. Sci. Adv. 2019, 5, eaau0999. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shabbir, M.; Li, J.; Abbas, W.; Koutsoukos, X. Resilient vector consensus in multi-agent networks using centerpoints. In Proceedings of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; pp. 4387–4392. [Google Scholar]
- López-González, A.; Campaña, J.M.; Martínez, E.H.; Contro, P.P. Multi robot distance based formation using Parallel Genetic Algorithm. Appl. Soft Comput. 2020, 86, 105929. [Google Scholar] [CrossRef]
- Fahham, H.R.; Farid, M. Minimum-time trajectory planning of spatial cable-suspended robots along a specified path considering both tension and velocity constraints. Eng. Optim. 2010, 42, 387–402. [Google Scholar] [CrossRef]
- Fahham, H.R.; Farid, M.; Khooran, M. Time optimal trajectory tracking of redundant planar cable-suspended robots considering both tension and velocity constraints. J. Dyn. Syst. Meas. Control 2011, 133, 011004. [Google Scholar] [CrossRef] [Green Version]
- Lin, Z.; Francis, B.; Maggiore, M. Necessary and sufficient graphical conditions for formation control of unicycles. IEEE Trans. Automat. Contr. 2005, 50, 121–127. [Google Scholar]
- Caughman, J.S.; Lafferriere, G.; Veerman, J.J.P.; Williams, A. Decentralised control of vehicle formations. Syst. Control Lett. 2005, 54, 899–910. [Google Scholar]










| Ref. | Date | Proposed Method | Objectives |
|---|---|---|---|
| [21] | 2014 | A gradient-based optimisation algorithm, using the constraint transcription and a time scaling transform method. | An optimal parameter selection problem with continuous state inequality constraints and free terminal time. |
| [22] | 2016 | An improved gravitational search algorithm is used to optimise the trajectory of the path for multiple robots. | A multi-robot path planning problem in a dynamic environment. |
| [23] | 2017 | The direction priority sequential selection algorithm and extension-decomposition aggregation scheme are applied to solve the formation control problem and achieve collision avoidance during the formation manoeuvre. | A collision avoidance strategy based on the formation control model. |
| [24] | 2017 | Based on sliding-mode auxiliary systems, an adaptive near-optimal protocol is presented to control multi-agent systems. | A normal near-optimal protocol was designed by making an approximation of the performance index. |
| [25] | 2017 | A data-based adaptive dynamic programming method is presented using the current/past system data. | Used a discounted performance index and formulated the optimal consensus problem via the Bellman optimality principle. |
| [26] | 2018 | The fixed-time consensus theory and continuous-time zero-gradient algorithms are used | Addressed the problem of the global cost function being the sum of strictly convex local cost functions. |
| [28] | 2019 | A dynamic allocation method is proposed to increase exploration capabilities, extending them in both the inclusion phase and consensus phase of the tasks. | They solved the problems of allocation approaches that tended to trap in a local optimal and cannot obtain high-quality solutions. |
| [29] | 2019 | A constrained non-linear optimisation is combined with consensus to compute the parameters of the multi-robot formation. | A distributed method was used to solve the consensus formation of a team of aerial or mobile robots navigating with static and dynamic obstacles, when each robot has a finite communication and visibility radius. |
| [30] | 2019 | An archetypal model of distributed decision-making is used to study the capacity of the system to follow a driving signal for varying topologies and system sizes | Navigating with static and dynamic obstacles when each robot has a finite communication and visibility radius. |
| [31] | 2020 | Using the idea of CenterPoint, which is an extension of the median in higher dimensions, instead of a Tverberg partition, provides a better characterisation of the necessary and sufficient conditions guaranteeing resilient vector consensus of a multi-agent system. | Resilience guarantees improvement of the existing consensus algorithms in multi-agent networks. |
| [32] | 2020 | An alternative method to achieve a distance-based formation that used genetic algorithms to find a solution based on the distance and angle, and a constant velocity while avoiding collisions. | A parallel scheme was extended to improve the performance and find the best ways to converge to the desired distances while avoiding collisions. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fahham, H.; Zaraki, A.; Tucker, G.; Spong, M.W. Time-Optimal Velocity Tracking Control for Consensus Formation of Multiple Nonholonomic Mobile Robots. Sensors 2021, 21, 7997. https://doi.org/10.3390/s21237997
Fahham H, Zaraki A, Tucker G, Spong MW. Time-Optimal Velocity Tracking Control for Consensus Formation of Multiple Nonholonomic Mobile Robots. Sensors. 2021; 21(23):7997. https://doi.org/10.3390/s21237997
Chicago/Turabian StyleFahham, Hamidreza, Abolfazl Zaraki, Gareth Tucker, and Mark W. Spong. 2021. "Time-Optimal Velocity Tracking Control for Consensus Formation of Multiple Nonholonomic Mobile Robots" Sensors 21, no. 23: 7997. https://doi.org/10.3390/s21237997
APA StyleFahham, H., Zaraki, A., Tucker, G., & Spong, M. W. (2021). Time-Optimal Velocity Tracking Control for Consensus Formation of Multiple Nonholonomic Mobile Robots. Sensors, 21(23), 7997. https://doi.org/10.3390/s21237997






