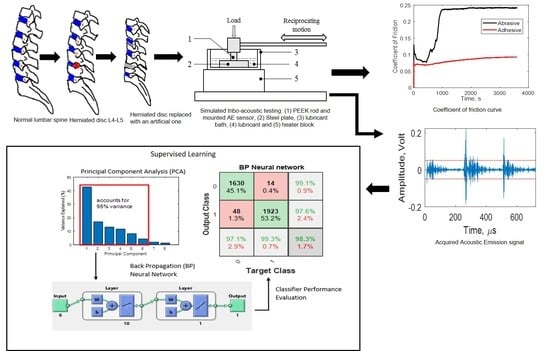
Towards a Diagnostic Tool for Diagnosing Joint Pathologies: Supervised Learning of Acoustic Emission Signals
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Parameters
2.1.1. Test Parameters
2.1.2. AE Signal Acquisition and Post-Processing
2.2. Pattern Recognition Techniques
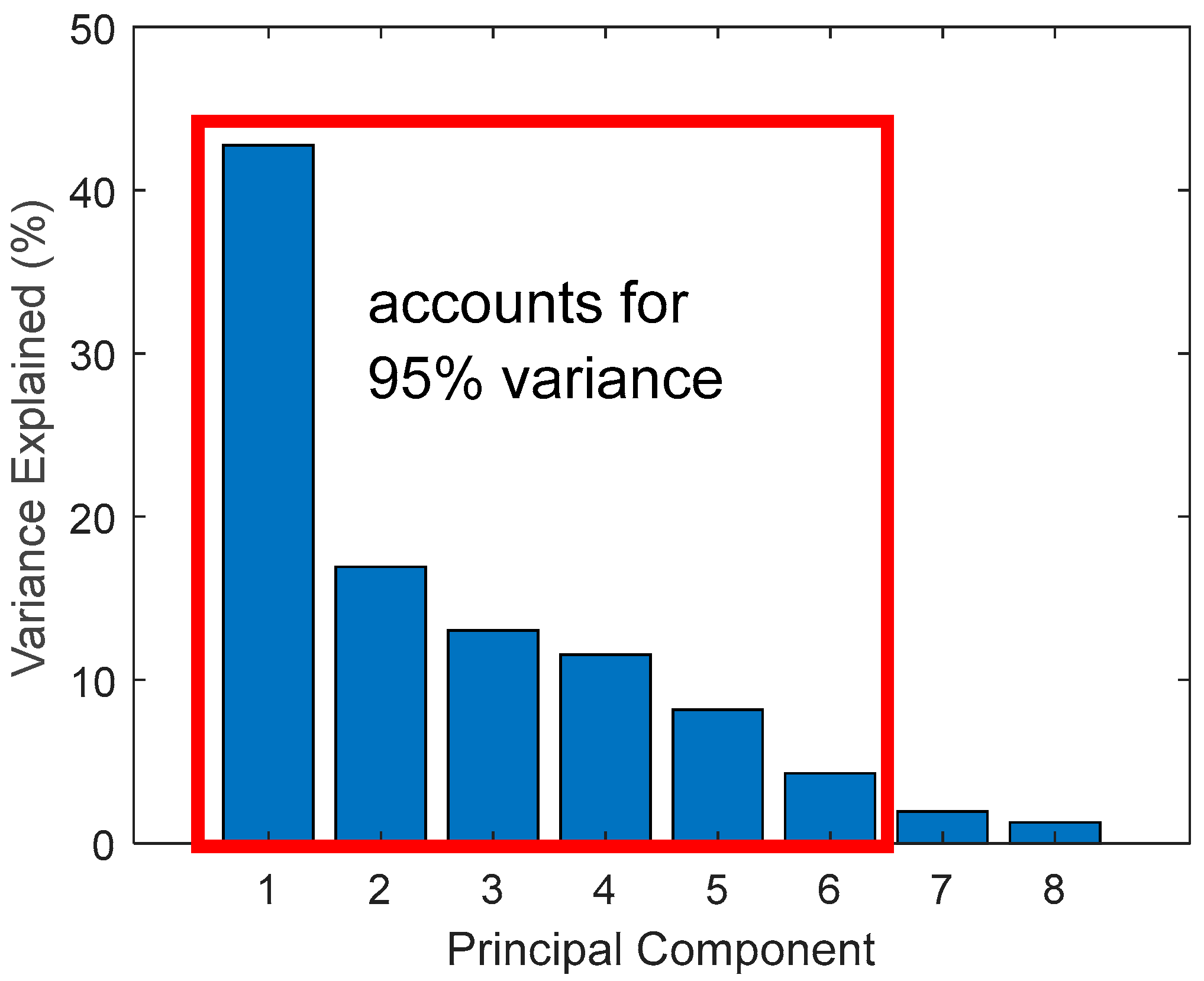
2.2.1. Feature Selection and Extraction
2.2.2. k-Means Clustering (Unsupervised Learning)
- 1.
- Sample data sets were defined as , where X denotes the categories of clusters and represents the initial cluster centre. The clusters satisfy:
- a.
- ;
- b.
- c.
- .
- 2.
- samples were randomly selected, and was defined as the initial clustering centre.
- 3.
- Using the squared Euclidean distance, each sample in the data sets was assigned to the cluster centres .
- 4.
- The centre of new cluster , i.e., , where is the cluster domain containing the number of samples, could then be calculated; if , then step (3) was repeated. Otherwise, the algorithm converged, and the analysis ended. Finally, the Silhouette Index () was used to find the optimal cluster number [31]. As a result, the optimal cluster number had the highest value.
2.2.3. Supervised Classification of AE Signals
Logistic Regression Classifier
K-Nearest Neighbours (KNN) Classifier
Neural Network Classifier
3. Results and Discussion
3.1. AE Hits and Wear Mechanisms
- Running-in (initial collision of surface asperities and a slight decrease in CoF).
- A second increase in CoF during prolonged sliding.
- Steady-state.
3.2. k-Means Clustering
3.2.1. Adhesive Wear
3.2.2. Abrasive Wear
3.3. Supervised AE Data Classification
- Increase the number of neurons in the hidden layer for the BP neural network [44].
- Increase features used for classification [45] by choosing more features or deriving new features through the mathematical combination of original features. More features can help improve the model by recognising more patterns between features and improving the classification accuracy.
- Increase the number of training examples. Having more examples would help the model learn better, thereby improving classification accuracy.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Abu-Amer, Y.; Darwech, I.; Clohisy, J.C. Aseptic loosening of total joint replacements: Mechanisms underlying osteolysis and potential therapies. Arthritis Res. Ther. 2007, 9, 1–7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, K.T.; Lee, S.; Ko, D.O.; Seo, B.S.; Jung, W.S.; Chang, B.K. Causes of Failure after Total Knee Arthroplasty in Osteoarthritis Patients 55 Years of Age or Younger. Knee Surg. Relat. Res. 2014, 26, 13–19. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McKellop, H.A. The lexicon of polyethylene wear in artificial joints. Biomaterials 2007, 28, 5049–5057. [Google Scholar] [CrossRef]
- Williams, J.A. Engineering Tribology; Oxford University Press: New York, NY, USA, 1994. [Google Scholar]
- Bhushan, B. Introduction to Tribology; John Wiley & Sons, Incorporated: New York, NY, USA, 2002. [Google Scholar]
- Karl, K. Tribology and Total Hip Arthroplasty Implants. Orthopedics 2013, 36, 854–855. [Google Scholar] [CrossRef] [Green Version]
- Devin, C.J.; Myers, T.G.; Kang, J.D. Chronic failure of a lumbar total disc replacement with osteolysis: Report of a case with nineteen-year follow-up. J. Bone Jt. Surg.-Ser. A 2008, 90, 2230–2234. [Google Scholar] [CrossRef]
- Hellier, C.J. Chapter 10: Acoustic Emission Testing. In Handbook of Nondestructive Evaluation; The McGraw-Hill Companies, Inc.: Boston, MA, USA, 2003; pp. 10.1–10.39. [Google Scholar]
- Olorunlambe, K.A.; Shepherd, D.E.T.; Dearn, K.D. A review of acoustic emission as a biotribological diagnostic tool. Tribol.-Mater. Surf. Interfaces 2019, 13, 161–171. [Google Scholar] [CrossRef]
- Schwalbe, H.J.; Bamfaste, G.; Franke, R.P. Non-destructive and non-invasive observation of friction and wear of human joints and of fracture initiation by acoustic emission. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 1999, 213, 41–48. [Google Scholar] [CrossRef]
- Franke, R.P.; Dorner, P.; Schwalbe, H.J.; Ziegler, B. Acoustic Emission Measurement System for the Orthopedical Diagnostics of the Human Femur and Knee Joint. J. Acoust. Emiss. 2004, 22, 236–242. [Google Scholar]
- Shark, L.K.; Chen, H.; Goodacre, J. Knee acoustic emission: A potential biomarker for quantitative assessment of joint ageing and degeneration. Med. Eng. Phys. 2011, 33, 534–545. [Google Scholar] [CrossRef]
- Sawaryn, B.; Piaseczna, N.; Siecinski, S.; Doniec, R.; Duraj, K.; Komorowski, D.; Tkacz, E. The Assessment of the Condition of Knee Joint Surfaces with Acoustic Emission Analysis. Sensors 2021, 21, 6495. [Google Scholar] [CrossRef]
- Rodgers, G.W.; Young, J.L.; Fields, A.V.; Shearer, R.Z.; Woodfield, T.B.F.; Hooper, G.J.; Chase, J.G. Acoustic Emission Monitoring of Total Hip Arthroplasty Implants. IFAC Proc. Vol. 2014, 47, 4796–4800. [Google Scholar] [CrossRef]
- Khan-Edmundson, A.; Rodgers, G.W.; Woodfield, T.B.F.; Hooper, G.J.; Chase, J.G. Tissue attenuation characteristics of Acoustic Emission signals for wear and degradation of total hip arthroplasty implants. IFAC Proc. Vol. 2012, 45, 355–360. [Google Scholar] [CrossRef] [Green Version]
- FitzPatrick, A.J.; Rodgers, G.W.; Hooper, G.J.; Woodfield, T.B.F. Development and validation of an acoustic emission device to measure wear in total hip replacements in-vitro and in-vivo. Biomed. Signal Process. Control 2017, 33, 281–288. [Google Scholar] [CrossRef]
- Gutkin, R.; Green, C.J.; Vangrattanachai, S.; Pinho, S.T.; Robinson, P.; Curtis, P.T. On acoustic emission for failure investigation in CFRP: Pattern recognition and peak frequency analyses. Mech. Syst. Signal Process. 2011, 25, 1393–1407. [Google Scholar] [CrossRef]
- Qiao, X.; Weng, W.; Li, Q. Acoustic emission monitoring and failure behavior discrimination of 8YSZ thermal barrier coatings under Vickers indentation testing. Surf. Coat. Technol. 2019, 358, 913–922. [Google Scholar] [CrossRef]
- Yao, Y.; Li, X.; Yuan, Z. Tool wear detection with fuzzy classification and wavelet fuzzy neural network. Int. J. Mach. Tools Manuf. 1999, 39, 1525–1538. [Google Scholar] [CrossRef] [Green Version]
- Shark, L.-K.; Chen, H.; Goodacre, J. Discovering differences in acoustic emission between healthy and osteoarthritic knees using a four-phase model of sit-stand-sit movements. Open Med. Inform. J. 2010, 4, 116–125. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Clohisy, J.C.; Calvert, G.; Tull, F.; McDonald, D.; Maloney, W.J. Reasons for revision hip surgery: A retrospective review. Clin. Orthop. Relat. Res. 2004, 429, 188–192. [Google Scholar] [CrossRef]
- Dalury, D.F.; Pomeroy, D.L.; Gorab, R.S.; Adams, M.J. Why are total knee arthroplasties being revised? J. Arthroplasty 2013, 28, 120–121. [Google Scholar] [CrossRef]
- Reeks, J.; Liang, H. Materials and Their Failure Mechanisms in Total Disc Replacement. Lubricants 2015, 3, 346–364. [Google Scholar] [CrossRef] [Green Version]
- Capón-García, D.; López-Pardo, A.; Alves-Pérez, M.T. Causes for revision surgery in total hip replacement. A retrospective epidemiological analysis. Rev. Española Cirugía Ortopédica Traumatol. 2016, 60, 160–166. [Google Scholar] [CrossRef]
- ASTM International. F732-17(2017) Standard Test Method for Wear Testing of Polymeric Materials Used in Total Joint Prostheses; ASTM International: West Conshohocken, PA, USA, 2017. [Google Scholar]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1985; ISBN 0-521-25576-7. [Google Scholar]
- Moghadas, P.; Mahomed, A.; Shepherd, D.E.T.; Hukins, D.W.L. Wear of the Charité® lumbar intervertebral disc replacement investigated using an electro-mechanical spine simulator. Proc. Inst. Mech. Eng. H. 2015, 229, 264–268. [Google Scholar] [CrossRef] [Green Version]
- British Standards Institution. BS ISO 18192-1 BSI Standards Publication Implants for Surgery—Wear of Total Intervertebral Spinal Disc Prostheses Part 1: Loading and Displacement Parameters for Wear Testing and Corresponding Environmental Conditions for Test, 2nd ed.; British Standards Institution: London, UK, 2011. [Google Scholar]
- Momon, S.; Godin, N.; Reynaud, P.; R’Mili, M.; Fantozzi, G. Unsupervised and supervised classification of AE data collected during fatigue test on CMC at high temperature. Compos. Part A Appl. Sci. Manuf. 2012, 43, 254–260. [Google Scholar] [CrossRef]
- Ech-Choudany, Y.; Assarar, M.; Scida, D.; Morain-Nicolier, F.; Bellach, B. Unsupervised clustering for building a learning database of acoustic emission signals to identify damage mechanisms in unidirectional laminates. Appl. Acoust. 2017, 123, 123–132. [Google Scholar] [CrossRef]
- Rousseeuw, P. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef] [Green Version]
- Forte, G.; Alberini, F.; Simmons, M.; Stitt, H.E. Use of acoustic emission in combination with machine learning: Monitoring of gas–liquid mixing in stirred tanks. J. Intell. Manuf. 2020, 32, 633–647. [Google Scholar] [CrossRef]
- Kleinbaum, D.G.; Klein, M. Logistic Regression: A Self-Learning Text, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2002; ISBN 0-387-95397-3. [Google Scholar]
- Curry, B.; Rumelhart, D. MSnet: A Neural Network which Classifies Mass Spectra. Tetrahedron Comput. Methodol. 1990, 3, 213–237. [Google Scholar] [CrossRef]
- Foresee, F.D.; Hagan, M.T. Gauss-Newton approximation to bayesian learning. In Proceedings of the International Conference on Neural Networks (ICNN’97), Houston, TX, USA, 9–12 June 1997; pp. 1930–1935. [Google Scholar]
- Hase, A.; Mishina, H.; Wada, M. Correlation between features of acoustic emission signals and mechanical wear mechanisms. Wear 2012, 292–293, 144–150. [Google Scholar] [CrossRef]
- Mishina, H.; Hase, A. Wear equation for adhesive wear established through elementary process of wear. Wear 2013, 308, 186–192. [Google Scholar] [CrossRef]
- Mishina, H.; Hase, A. Effect of the adhesion force on the equation of adhesive wear and the generation process of wear elements in adhesive wear of metals. Wear 2019, 432, 202936. [Google Scholar] [CrossRef]
- Yang, G.; Garrison, W. A comparison of microstructural effects on two-body and three-body abrasive wear. Wear 1989, 129, 93–103. [Google Scholar] [CrossRef]
- Boness, R.J.; McBride, S.L. Adhesive and abrasive wear studies using acoustic emission techniques. Wear 1991, 149, 41–53. [Google Scholar] [CrossRef]
- Belyi, V.A.; Kholodilov, O.V.; Sviridyonok, A.I. Acoustic spectrometry as used for the evaluation of tribological systems. Wear 1981, 69, 309–319. [Google Scholar] [CrossRef]
- Asamene, K.; Sundaresan, M. Analysis of experimentally generated friction related acoustic emission signals. Wear 2012, 296, 607–618. [Google Scholar] [CrossRef]
- McCrory, J.P.; Al-Jumaili, S.K.; Crivelli, D.; Pearson, M.R.; Eaton, M.J.; Featherston, C.A.; Guagliano, M.; Holford, K.M.; Pullin, R. Damage classification in carbon fibre composites using acoustic emission: A comparison of three techniques. Compos. Part B Eng. 2015, 68, 424–430. [Google Scholar] [CrossRef] [Green Version]
- Yu, H.; Samuels, D.C.; Zhao, Y.Y.; Guo, Y. Architectures and accuracy of artificial neural network for disease classification from omics data. BMC Genom. 2019, 20, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Ray, S. 8 Proven Ways for Boosting the “Accuracy” of a Machine Learning Model. Available online: https://www.analyticsvidhya.com/blog/2015/12/improve-machine-learning-results/ (accessed on 28 November 2021).
- Lorena, A.C.; Jacintho, L.F.O.; Siqueira, M.F.; De Giovanni, R.; Lohmann, L.G.; De Carvalho, A.C.P.L.F.; Yamamoto, M. Comparing machine learning classifiers in potential distribution modelling. Expert Syst. Appl. 2011, 38, 5268–5275. [Google Scholar] [CrossRef]
- Crivelli, D.; Guagliano, M.; Monici, A. Development of an artificial neural network processing technique for the analysis of damage evolution in pultruded composites with acoustic emission. Compos. Part B 2014, 56, 948–959. [Google Scholar] [CrossRef] [Green Version]











| Parameters | Value | |
|---|---|---|
| TE77 TEST PARAMETERS | Load | 150 N |
| Frequency | 2 Hz | |
| Stroke | 12.5 mm | |
| Test Duration | 1 h | |
| Lubricant | Dry (to induce adhesive wear) and Ringer’s Solution (to induce abrasive wear) | |
| AE ACQUISITION PARAMETERS | Threshold | 40 dB |
| Pre-amplifier gain | 60 dB | |
| Band Pass filter | 100–600 kHz | |
| Sampling rate | 2 MHz. |
| No. | AE Features | Definition |
|---|---|---|
| 1 | Amplitude | Maximum amplitude of the signal. |
| 2 | Duration | The time from first threshold crossing to the last threshold crossing. |
| 3 | Counts to Peak | Number of crossings from first crossing to the point where maximum amplitude is reached. |
| 4 | RA Value | Time per amplitude needed for signal to reach its peak value. Expressed as ratio of risetime to amplitude. |
| 5 | Average Frequency | Signal counts over signal duration. |
| 6 | Peak Frequency | Frequency corresponding to the peak value of the power spectrum of the FFT transform. |
| 7 | AE Root Mean Square | Root mean square of voltage curve. |
| 8 | Absolute Energy | The true energy of the signal on a 10 kohm resistor. |
| AE Features | Cluster 1 | Cluster 2 | ||
|---|---|---|---|---|
| Range | Mean (std) | Range | Mean (std) | |
| Amplitude, dB | 40–71.43 | 43.81 (4.30) | 40.27–79.99 | 56.70 (14.67) |
| Duration, µs | 0.5–1308 | 85.71 (133.16) | 226.5–1998.5 | 1048.60 (347.05) |
| RA Value, µs/dB | 0–12.47 | 0.57 (1.27) | 0.01–35.25 | 10.08 (7.84) |
| Average Frequency, kHz | 0–1000 | 333.73 (378.23) | 1.46–194.26 | 60.36 (54.67) |
| Absolute Energy, attoJ | 0.26–28,610 | 96.48 (648.62) | 41.29–687,510 | 59,834 (1.20 × 109) |
| AE Features | Cluster 1 | Cluster 2 | ||
|---|---|---|---|---|
| Range | Mean (std) | Range | Mean (std) | |
| Amplitude, dB | 40.01–55.42 | 43.76 (2.80) | 40.14–75.36 | 46.22 (3.28) |
| Duration, µs | 0.5–1200 | 116.84 (157.93) | 45.5–2010 | 1060 (422.05) |
| RA Value, µs/dB | 0.01–14.42 | 0.87 (1.75) | 0.01–42.55 | 13.54 (9.40) |
| Average Frequency, kHz | 0–2000 | 212.22 (298.36) | 1.57–193.80 | 27.72 (23.44) |
| Absolute Energy, attoJ | 0.57–567.11 | 45.99 (58.10) | 11.73–30,200 | 326.96 (472.03) |
| CLASSIFIER | Average Training Accuracy (±std) | Average Test Accuracy (±std) | Average F-Score (±std) | |
|---|---|---|---|---|
| Adhesive is positive | Abrasive is positive | |||
| Logistic Regression | 0.73 (±0.0025) | 0.72 (±0.0048) | 0.66 (±0.0096) | 0.77 (±0.0036) |
| Weighted k-Nearest Neighbours | 0.96 (±0.0007) | 0.97 (±0.0026) | 0.96 (±0.0029) | 0.97 (±0.0025) |
| Back Propagation Neural Network | 0.98 (±0.0014) | 0.98 (±0.0024) | 0.98 (±0.0024) | 0.98 (±0.0023) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olorunlambe, K.A.; Hua, Z.; Shepherd, D.E.T.; Dearn, K.D. Towards a Diagnostic Tool for Diagnosing Joint Pathologies: Supervised Learning of Acoustic Emission Signals. Sensors 2021, 21, 8091. https://doi.org/10.3390/s21238091
Olorunlambe KA, Hua Z, Shepherd DET, Dearn KD. Towards a Diagnostic Tool for Diagnosing Joint Pathologies: Supervised Learning of Acoustic Emission Signals. Sensors. 2021; 21(23):8091. https://doi.org/10.3390/s21238091
Chicago/Turabian StyleOlorunlambe, Khadijat A., Zhe Hua, Duncan E. T. Shepherd, and Karl D. Dearn. 2021. "Towards a Diagnostic Tool for Diagnosing Joint Pathologies: Supervised Learning of Acoustic Emission Signals" Sensors 21, no. 23: 8091. https://doi.org/10.3390/s21238091
APA StyleOlorunlambe, K. A., Hua, Z., Shepherd, D. E. T., & Dearn, K. D. (2021). Towards a Diagnostic Tool for Diagnosing Joint Pathologies: Supervised Learning of Acoustic Emission Signals. Sensors, 21(23), 8091. https://doi.org/10.3390/s21238091