The Computational Fluid Dynamics (CFD) Analysis of the Pressure Sensor Used in Pulse-Operated Low-Pressure Gas-Phase Solenoid Valve Measurements
Abstract
:1. Introduction
2. Materials and Methods
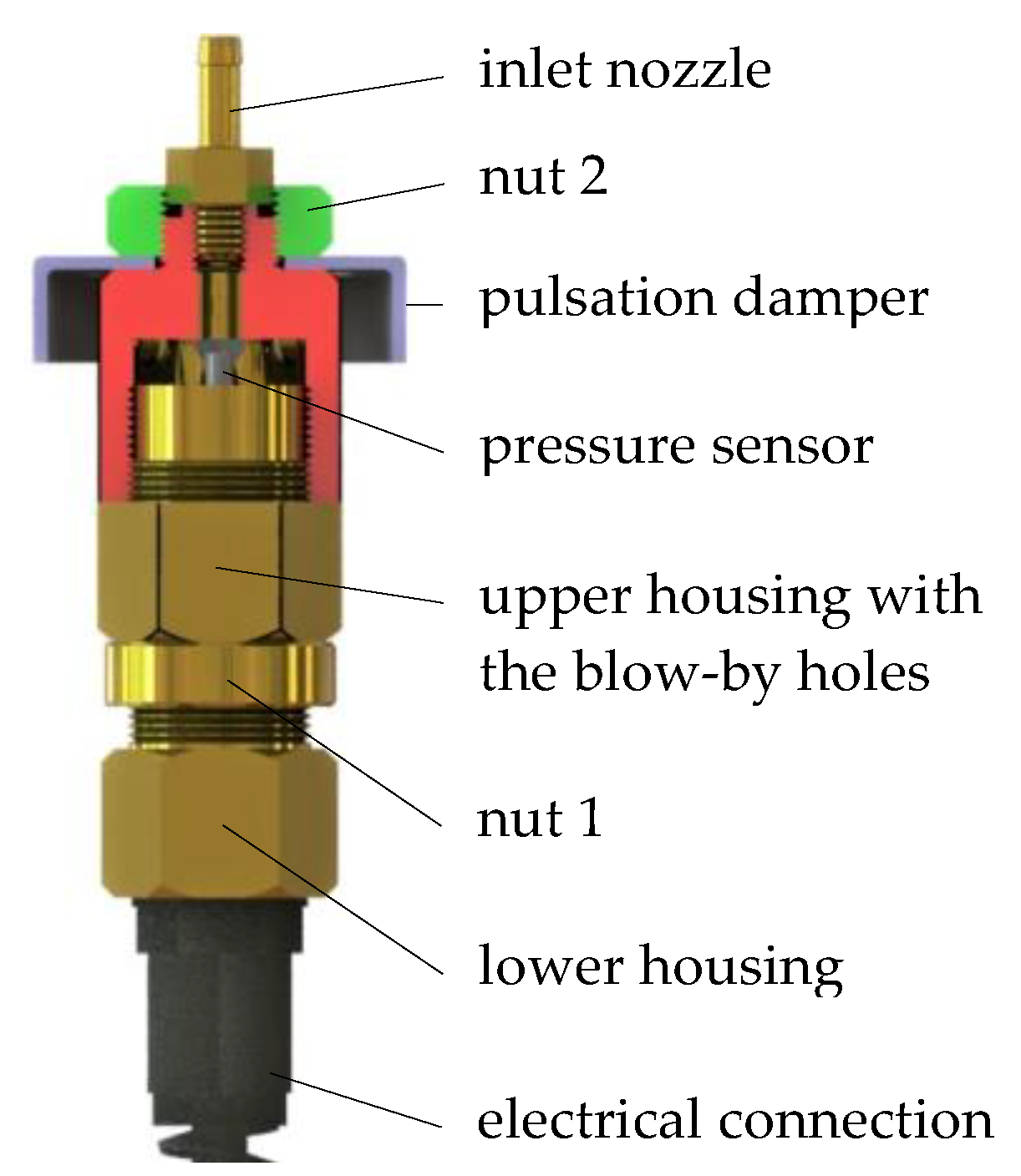
2.1. The Analysed Sensor
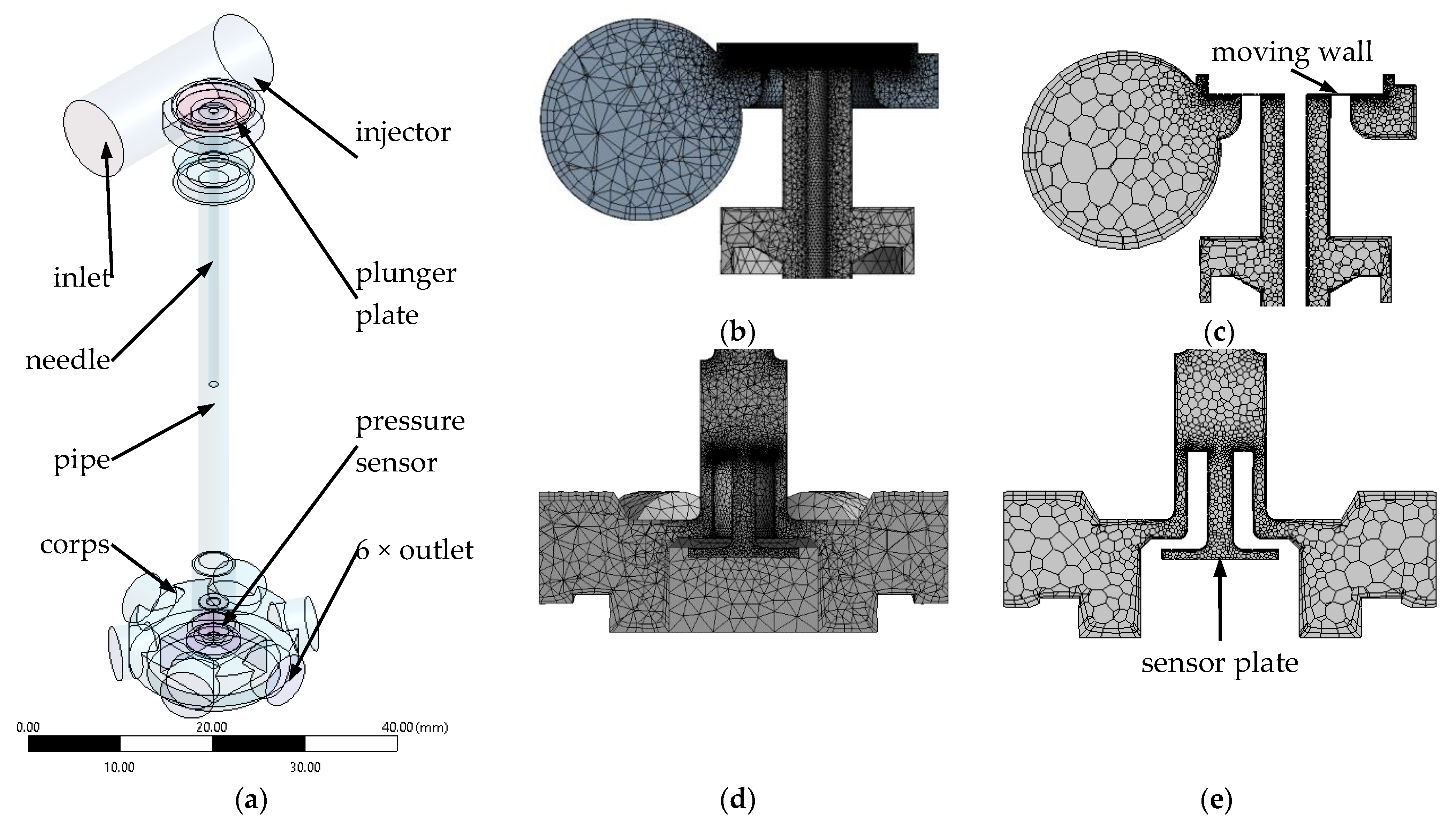
2.2. The Tested Low-Pressure Gas-Phase Solenoid Valve
2.3. The Flow Analysis
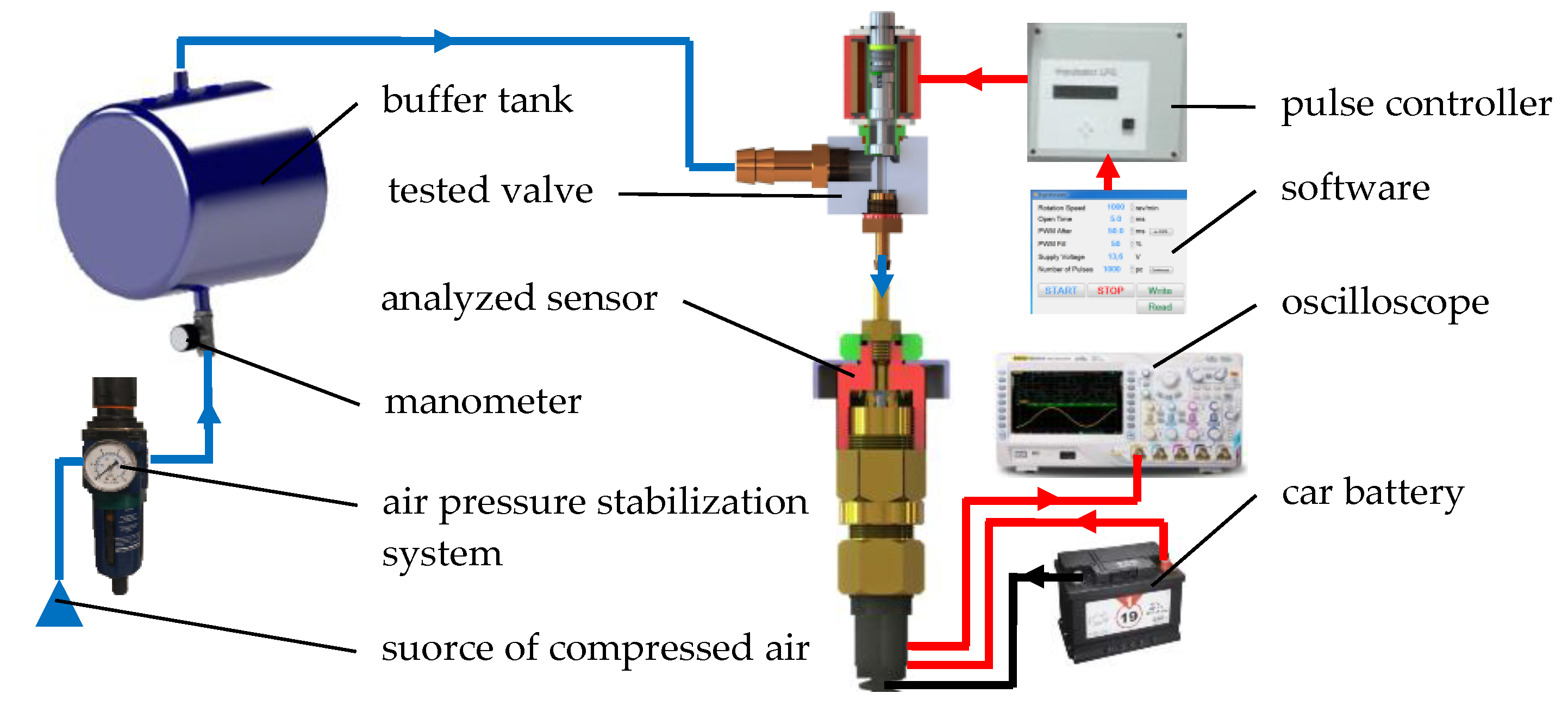
2.4. The Experimental Test Stand
3. Results and Discussion
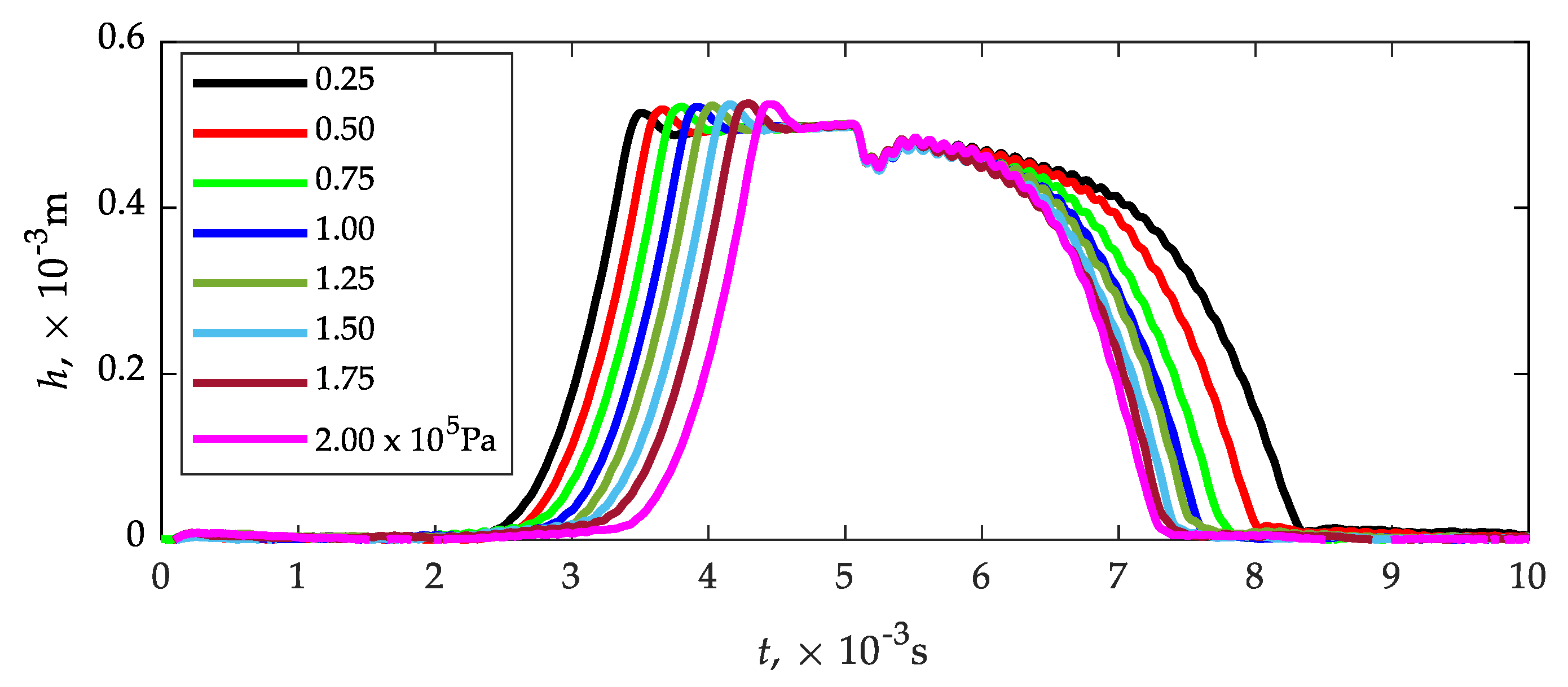
3.1. Plunger Lift
3.2. CFD Analysis
3.3. Validation of the CFD Calculation Results
4. Conclusions
- The proposed simplified solid fluid model allowed to reflect the flow capabilities of the investigated gas injector—pressure sensor system.
- The analyzed mesh densities in a global view together with local user definitions showed differences in the runs. In all mesh cases, the mean quality parameters, skewness (0.22), and orthogonal quality (0.86) were of good quality. Each of the presented mesh densities gave the possibility to identify the times until full opening and closing of the injector, so it was decided to use the system-proposed mesh with local user definitions. Due to time-consuming calculations, the final models used a polyhedral mesh built systemically with cell optimization.
- Experimental studies using a plunger displacement sensor showed a 15% increase in time until full opening and 21% increase in time until full closing. This was due to the use of a needle in the injector operating system. The results were necessary to initiate a dynamic mesh in Ansys Fluent. The needle was left in CFD calculations and validation on the experimental bench.
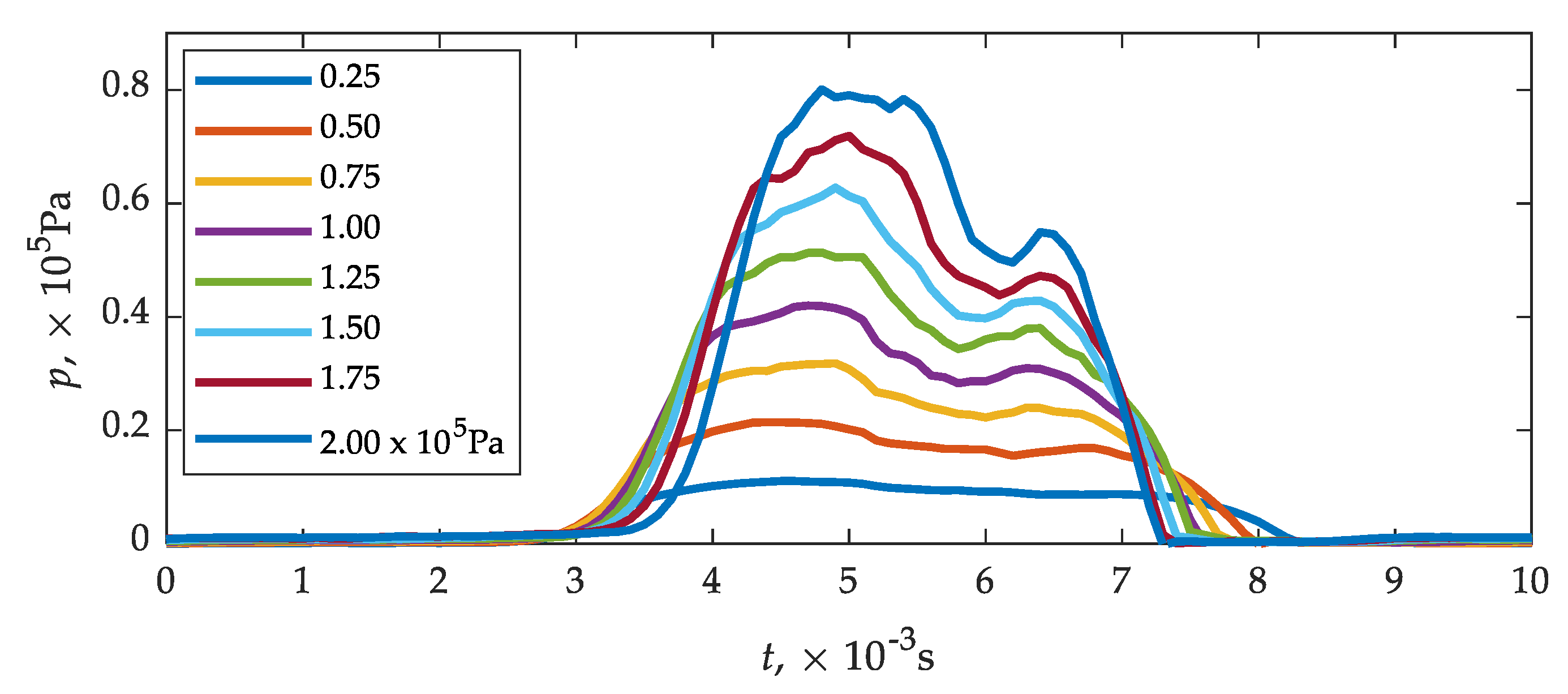
- The indirect method of evaluating times until full opening based on the pressure waveform on the pressure sensor plate had a positive effect. The drop in the pressure rise gradient coincided with the maximum lift determined using the plunger displacement sensor.
- The indirect method of evaluating times until full injector closing, when pressure at the pressure sensor plate drops to 0 Pa, is also able to represent the end of the injector closing process.
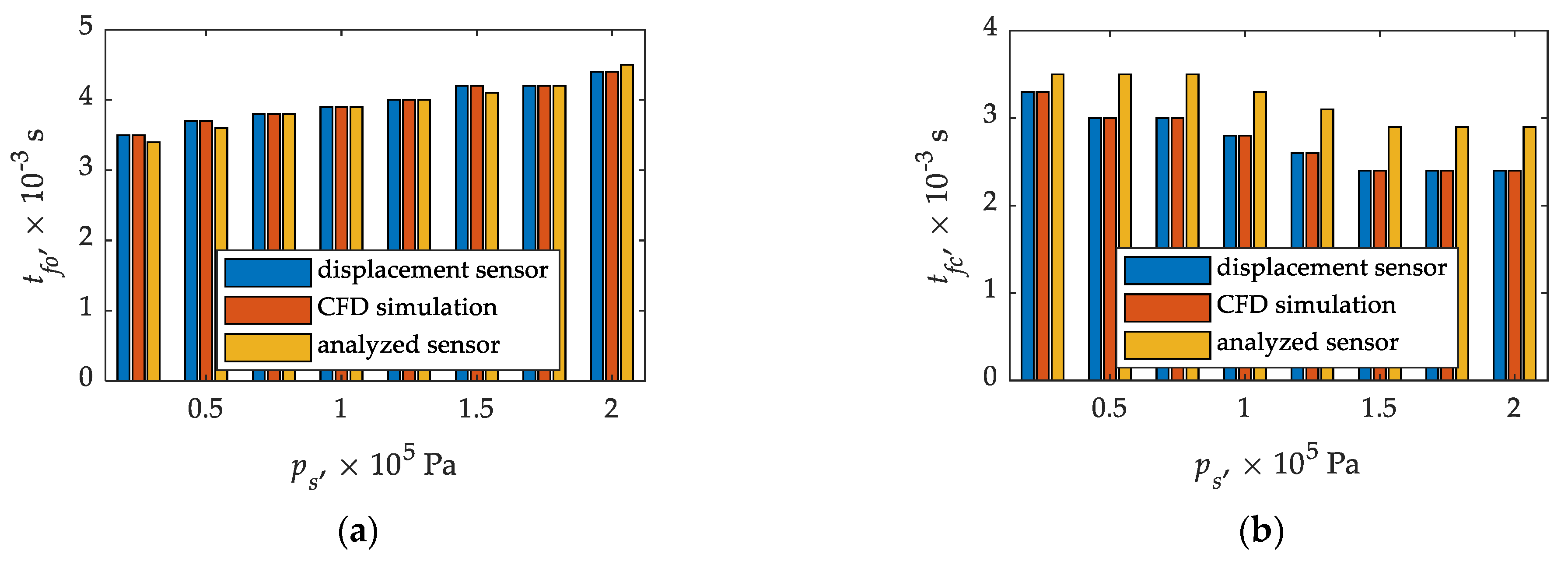
- The times until full opening of the injector determined using plunger displacement sensor, CFD simulation, and pressure plate sensor give similar results. No differences were found at inlet–outlet pressure differences (0.75; 1.00; 1.25, and 1.75) × 105 Pa by relating the pressure waveforms to the displacement sensor. In the remaining cases (0.25, 0.50, 1.50, and 2.00) × 105 Pa, the differences did not exceed 3%;
- In the case of times until full closing of the injector in the relation CFD calculations—experimental studies, only for the pressure difference of 0.25 × 105 Pa the relative error is below 10%, in the remaining cases it reached 21%. The simplification of the solid model of the fluid on the one hand, and the reaction time of the real object on the other, may be responsible for such a significant difference;
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Raslavičius, L.; Keršys, A.; Makaras, R. Management of hybrid powertrain dynamics and energy consumption for 2WD, 4WD, and HMMWV vehicles. Renew. Sustain. Energy Rev. 2017, 68, 380–396. [Google Scholar] [CrossRef]
- Brejaud, P.; Higelin, P.; Charlet, A.; Colin, G.; Chamaillard, Y. Échange de chaleur convectif dans un moteur hybride pneumatique. Oil Gas Sci. Technol. 2011, 66, 1035–1051. [Google Scholar] [CrossRef]
- Raslavičius, L.; Azzopardi, B.; Keršys, A.; Starevičius, M.; Bazaras, Ž.; Makaras, R. Electric vehicles challenges and opportunities: Lithuanian review. Renew. Sustain. Energy Rev. 2015, 42, 786–800. [Google Scholar] [CrossRef]
- Fang, Y.; Lu, Y.; Yu, X.; Roskilly, A.P. Experimental study of a pneumatic engine with heat supply to improve the overall performance. Appl. Therm. Eng. 2018, 134, 78–85. [Google Scholar] [CrossRef] [Green Version]
- Korbut, M.; Szpica, D. A Review of Compressed Air Engine in The Vehicle Propulsion System. Acta Mech. Autom. 2021, 15, 215–226. [Google Scholar] [CrossRef]
- Dimitrova, Z.; Maréchal, F. Gasoline hybrid pneumatic engine for efficient vehicle powertrain hybridization. Appl. Energy 2015, 151, 168–177. [Google Scholar] [CrossRef]
- Myung, C.-L.; Lee, H.; Choi, K.; Lee, Y.J.; Park, S. Effects of gasoline, diesel, LPG, and low-carbon fuels and various certification modes on nanoparticle emission characteristics in light-duty vehicles. Int. J. Automot. Technol. 2009, 10, 537–544. [Google Scholar] [CrossRef]
- Jemni, M.A.; Kassem, S.H.; Driss, Z.; Abid, M.S. Effects of hydrogen enrichment and injection location on in-cylinder flow characteristics, performance and emissions of gaseous LPG engine. Energy 2018, 150, 92–108. [Google Scholar] [CrossRef]
- Bielaczyc, P.; Woodburn, J. Trends in Automotive Emission Legislation: Impact on LD Engine Development, Fuels, Lubricants and Test Methods: A Global View, with a Focus on WLTP and RDE Regulations. Emiss. Control Sci. Technol. 2019, 5, 86–98. [Google Scholar] [CrossRef] [Green Version]
- Clairotte, M.; Suarez-Bertoa, R.; Zardini, A.A.; Giechaskiel, B.; Pavlovic, J.; Valverde, V.; Ciuffo, B.; Astorga, C. Exhaust emission factors of greenhouse gases (GHGs) from European road vehicles. Environ. Sci. Eur. 2020, 32, 125. [Google Scholar] [CrossRef]
- Jeuland, N.; Montagne, X.; Duret, P. New HCCI/CAI combustion process development: Methodology for determination of relevant fuel parameters. Oil Gas Sci. Technol. 2004, 59, 571–579. [Google Scholar] [CrossRef]
- Haraldsson, G. Closed-Loop Combustion Control of a Multi Cylinder HCCI Engine using Variable Compression Ratio and Fast Thermal Management; Division of Combustion Engines, Lund Institute of Technology: Lund, Sweden, 2005. [Google Scholar]
- Mikulski, M.; Balakrishnan, P.R.; Doosje, E.; Bekdemir, C. Variable Valve Actuation Strategies for Better Efficiency Load Range and Thermal Management in an RCCI Engine. SAE Tech. Pap. 2018, 1, 254. [Google Scholar]
- Pielecha, I.; Sidorowicz, M. Effects of mixture formation strategies on combustion in dual-fuel engines—A review. Combust. Engines 2021, 184, 30–40. [Google Scholar] [CrossRef]
- Ziegler, M. The Road to Euro 7. MTZ Worldw. 2020, 81, 14–15. [Google Scholar] [CrossRef]
- Ball, D.; Meng, X.; Weiwei, G. Vehicle Emission Solutions for China 6b and Euro 7. SAE Tech. Pap. 2020, 1, 654. [Google Scholar]
- Council of the European Union. Council Directive 2014/94/EU of 22 October 2014 on the Deployment of Alternative Fuels Infrastructure; Council of the European Union: Strasbourg, France, 2014.
- Mitukiewicz, G.; Dychto, R.; Leyko, J. Relationship between LPG fuel and gasoline injection duration for gasoline direct injection engines. Fuel 2015, 153, 526–534. [Google Scholar] [CrossRef]
- Dziewiątkowski, M.; Szpica, D.; Borawski, A. Evaluation of impact of combustion engine controller adaptation process on level of exhaust gas emissions in gasoline and compressed natural gas supply process. In Proceedings of the Engineering for Rural Development; 2020; Volume 19, pp. 541–548, ERD 2020, Jelgava. [Google Scholar]
- Warguła, Ł.; Kukla, M.; Lijewski, P.; Dobrzyński, M.; Markiewicz, F. Influence of the use of Liquefied Petroleum Gas (LPG) systems in woodchippers powered by small engines on exhaust emissions and operating costs. Energies 2020, 13, 5773. [Google Scholar] [CrossRef]
- Warguła, Ł.; Kukla, M.; Lijewski, P.; Dobrzyński, M.; Markiewicz, F. Impact of Compressed Natural Gas (CNG) fuel systems in small engine wood chippers on exhaust emissions and fuel consumption. Energies 2020, 13, 6709. [Google Scholar]
- Jin, J.; Feng, M. Research and development of marine LPG engines. In Proceedings of the Energy and the Environment—Proceedings of the International Conference on Energy and the Environment; 2003; Volume 1. [Google Scholar]
- Machacon, H.T.C.; Yamagata, T.; Sekita, H.; Uchiyama, K.; Shiga, S.; Karasawa, T.; Nakamura, H. CNG operation of a two-stroke, two-cylinder marine S.I. Engine and its characteristics of self-ignition combustion. JSAE Rev. 2000, 21, 1–10. [Google Scholar] [CrossRef]
- Wendeker, M.; Jakliński, P.; Czarnigowski, J.; Boulet, P.; Breaban, F. Operational parameters of LPG fueled si engine—Comparison of simultaneous and sequential port injection. SAE Tech. Pap. 2007, 2007-01–2051. [Google Scholar]
- Raslavičius, L.; Keršys, A.; Mockus, S.; Keršiene, N.; Starevičius, M. Liquefied petroleum gas (LPG) as a medium-term option in the transition to sustainable fuels and transport. Renew. Sustain. Energy Rev. 2014, 32, 513–525. [Google Scholar] [CrossRef]
- Korzeniewski, M. Development of a hybrid gas and electrical installation for direct-injected engine vehicles. Prz. Elektrotechniczny 2020, 97, 121–124. [Google Scholar] [CrossRef]
- Czarnigowski, J. Teoretyczno-Empiryczne Studium Modelowania Impulsowego Wtryskiwacza Gazu; Wydawnictwo Politechniki Lubelskiej: Lublin, Poland, 2012. [Google Scholar]
- Szpica, D. The influence of selected adjustment parameters on the operation of LPG vapor phase pulse injectors. J. Nat. Gas Sci. Eng. 2016, 34, 1127–1136. [Google Scholar] [CrossRef]
- Szpica, D.; Czaban, J. Operational assessment of selected gasoline and LPG vapour injector dosage regularity. Mechanika 2014, 20, 480–488. [Google Scholar] [CrossRef] [Green Version]
- Majerczyk, A.; Radzimirski, S. Effect of LPG gas fuel injectors on the properties of flow emission vehicles. J. KONES Powertrain Transp. 2012, 19, 401–410. [Google Scholar] [CrossRef]
- Sim, H.; Lee, K.; Chung, N.; Sunwoo, M. A study on the injection characteristics of a liquid-phase liquefied petroleum gas injector for air-fuel ratio control. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2005, 219, 1037–1046. [Google Scholar] [CrossRef]
- Myung, C.-L.; Ko, A.; Lim, Y.; Kim, S.; Lee, J.; Choi, K.; Park, S. Mobile source air toxic emissions from direct injection spark ignition gasoline and LPG passenger car under various in-use vehicle driving modes in Korea. Fuel Process. Technol. 2014, 119, 19–31. [Google Scholar] [CrossRef]
- Masi, M. Experimental analysis on a spark ignition petrol engine fuelled with LPG (liquefied petroleum gas). Energy 2012, 41, 252–260. [Google Scholar] [CrossRef]
- Szpica, D. New Leiderman–Khlystov Coefficients for Estimating Engine Full Load Characteristics and Performance. Chinese J. Mech. Eng. 2019, 32. [Google Scholar] [CrossRef] [Green Version]
- Duk, M.; Czarnigowski, J. The method for indirect identification gas injector opening delay time. Prz. Elektrotechniczny 2012, 88, 59–63. [Google Scholar]
- Szpica, D. Validation of indirect methods used in the operational assessment of LPG vapor phase pulse injectors. Meas. J. Int. Meas. Confed. 2018, 118, 253–261. [Google Scholar] [CrossRef]
- Więcławski, K.; Mączak, J.; Szczurowski, K. Electric current waveform of the injector as a source of diagnostic information. Sensors 2020, 20, 4151. [Google Scholar] [CrossRef]
- Czarnigowski, J. The impact of supply pressure on gas injector expenditure characteristics. Silniki Spalinowe 2010, 49, 18–26. [Google Scholar] [CrossRef]
- Szpica, D. The determination of the flow characteristics of a low-pressure vapor-phase injector with a dynamic method. Flow Meas. Instrum. 2018, 62, 44–55. [Google Scholar] [CrossRef]
- Szpica, D. Investigating fuel dosage non-repeatability of low-pressure gas-phase injectors. Flow Meas. Instrum. 2018, 59, 147–156. [Google Scholar] [CrossRef]
- Ambrozik, A.; Kurczyński, D. Analysis of fast-changing quantities in the AD3.152 UR engine running of mineral fuel, plant fuel and their blends. Motrol 2008, 10, 11–22. [Google Scholar]
- Borawski, A. Simulation studies of LPG injector used in 4th generation installations. Combust. Engines 2015, 160, 49–55. [Google Scholar] [CrossRef]
- Dongiovanni, C.; Dongiovanni, C.; Coppo, M. Accurate Modelling of an Injector for Common Rail Systems. In Fuel Injection; Daniela, S., Ed.; IntechOpen: London, UK, 2010. [Google Scholar]
- Amirante, R.; Coratella, C.; Distaso, E.; Rossini, G.; Tamburrano, P. Optical device for measuring the injectors opening in common rail systems. Int. J. Automot. Technol. 2017, 18, 729–742. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Y.; Yuan, X.Y. Noncontact measurement of needle displacement in electronic controlled fuel injector. In Proceedings of the 2010 International Conference on Measuring Technology and Mechatronics Automation, ICMTMA 2010, Changsha, China, 13–14 March 2010; Volume 2, pp. 777–780. [Google Scholar]
- AC STAG Autogas Section. Available online: https://www.ac.com.pl/en (accessed on 10 May 2020).
- Aleiferis, P.G.; Serras-Pereira, J.; Augoye, A.; Davies, T.J.; Cracknell, R.F.; Richardson, D. Effect of fuel temperature on in-nozzle cavitation and spray formation of liquid hydrocarbons and alcohols from a real-size optical injector for direct-injection spark-ignition engines. Int. J. Heat Mass Transf. 2010, 53, 4588–4606. [Google Scholar] [CrossRef] [Green Version]
- Jang, C.; Kim, S.; Choi, S. An experimental and analytical study of the spray characteristics of an intermittent air-assisted fuel injector. At. Sprays 2000, 10, 199–217. [Google Scholar] [CrossRef]
- Panão, M.R.O.; Moreira, A.L.N. Flow characteristics of spray impingement in PFI injection systems. Exp. Fluids 2005, 39, 364–374. [Google Scholar] [CrossRef] [Green Version]
- Borawski, A. Modification of a fourth generation LPG installation improving the power supply to a spark ignition engine. Eksploat. Niezawodn. 2015, 17, 1–6. [Google Scholar] [CrossRef]
- Aleiferis, P.G.; Van Romunde, Z.R. An analysis of spray development with iso-octane, n-pentane, gasoline, ethanol and n-butanol from a multi-hole injector under hot fuel conditions. Fuel 2013, 105, 143–168. [Google Scholar] [CrossRef] [Green Version]
- Leach, B.; Zhao, H.; Li, Y.; Ma, T. Two-phase fuel distribution measurements in a gasoline direct injection engine with an air-assisted injector using advanced optical diagnostics. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2007, 221, 663–673. [Google Scholar] [CrossRef]
- Serras-Pereira, J.; Aleiferis, P.G.; Walmsley, H.L.; Davies, T.J.; Cracknell, R.F. Heat flux characteristics of spray wall impingement with ethanol, butanol, iso-octane, gasoline and E10 fuels. Int. J. Heat Fluid Flow 2013, 44, 662–683. [Google Scholar] [CrossRef] [Green Version]
- Walaszyk, A.; Busz, W. Application of optical method for the analysis delay between control injector coil and beginning of the fuel injection. Combust. Engines 2013, 154, 1038–1041. [Google Scholar]
- Bor, M.; Borowczyk, T.; Karpiuk, W.; Smolec, R. Determination of the response time of new generation electromagnetic injectors as a function of fuel pressure using the internal photoelectric effect. In Proceedings of the 2018 International Interdisciplinary PhD Workshop, IIPhDW, Świnoujście, Poland, 9–12 May 2018; pp. 335–339. [Google Scholar]
- Kakuhou, A.; Urushihara, T.; Itoh, T.; Takagi, Y. Characteristics of mixture formation in a direct injection SI engine with optimized in-cylinder swirl air motion. J. Engines 1999, 108, 550–558. [Google Scholar]
- Robart, D.; Breuer, S.; Reckers, W.; Kneer, R. Assessment of pulsed gasoline fuel sprays by means of qualitative and quantitative laser-based diagnostic methods. Part. Part. Syst. Charact. 2001, 18, 179–189. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, F.; Zhang, Z.; Wang, E.; Liu, B. Experimental investigation on the spray characteristic of air-assisted hollow-cone gasoline injector. Appl. Therm. Eng. 2019, 151, 354–363. [Google Scholar] [CrossRef]
- Spencer, A.; Brend, M.; Butcher, D.; Dunham, D.; Cheng, L.; Hollis, D. Tomographic PIV in the near field of a swirl-stabilised fuel injector. In Proceedings of the ASME Turbo Expo, Oslo, Norway, 11–15 June 2018; Volume 4A-2018. [Google Scholar]
- Westerweel, J.; Scarano, F. Universal outlier detection for PIV data. Exp. Fluids 2005, 39, 1096–1100. [Google Scholar] [CrossRef]
- Duncan, J.; Dabiri, D.; Hove, J.; Gharib, M. Universal outlier detection for particle image velocimetry (PIV) and particle tracking velocimetry (PTV) data. Meas. Sci. Technol. 2010, 21, 057002. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Li, T.; Zhang, D. A monolithic piezoresistive pressure-flow sensor with integrated signal-conditioning circuit. IEEE Sens. J. 2011, 11, 2122–2128. [Google Scholar] [CrossRef]
- Nawi, M.N.M.; Azeman, N.S.S.; Ab Razak, M.R. The effect of sensor structure and coplanar electrode for capacitive based flow sensor. Int. J. Recent Technol. Eng. 2019, 8, 4795–4799. [Google Scholar]
- Chávez, A.; De Santiago, O. Determining a pressure response function of the hose and sensor arrangement for measurements of dynamic pressure in a dry gas seal film. Tribol. Int. 2020, 143, 106007. [Google Scholar] [CrossRef]
- Bin Amari, M.D.; Shukor, M.S.B.A.; Abdullah, S.C. Optimization of velocity flap structures in high sensitivity macrofluidic airflow sensor. Int. J. Eng. Technol. 2018, 7, 11–15. [Google Scholar] [CrossRef] [Green Version]
- Bochio, G.; Cely, M.M.H.; Teixeira, A.F.A.; Rodriguez, O.M.H. Experimental and numerical study of stratified viscous oil–water flow. AIChE J. 2021, 67, e17239. [Google Scholar] [CrossRef]
- Guru Prasad, A.S.; Sharath, U.; Nagarjun, V.; Hegde, G.M.; Asokan, S. Measurement of temperature and pressure on the surface of a blunt cone using FBG sensor in hypersonic wind tunnel. Meas. Sci. Technol. 2013, 24, 095302. [Google Scholar] [CrossRef]
- Schreiner, F.; Paepenmöller, S.; Skoda, R. 3D flow simulations and pressure measurements for the evaluation of cavitation dynamics and flow aggressiveness in ultrasonic erosion devices with varying gap widths. Ultrason. Sonochem. 2020, 67, 105091. [Google Scholar] [CrossRef]
- Berberig, O.; Nottmeyer, K.; Mizuno, J.; Kanai, Y.; Kobayashi, T. The Prandtl micro flow sensor (PMFS): A novel silicon diaphragm capacitive sensor for flow-velocity measurement. Sensors Actuators A Phys. 1998, 66, 155–158. [Google Scholar] [CrossRef]
- Corti, E.; Forte, C.; Cazzoli, G.; Moro, D.; Falfari, S.; Ravaglioli, V. Comparison of Knock Indexes Based on CFD Analysis. Energy Procedia 2016, 101, 917–924. [Google Scholar] [CrossRef]
- Park, W.; Lee, J.; Min, K.; Yu, J.; Park, S.; Cho, S. Prediction of real-time NO based on the in-cylinder pressure in Diesel engines. Proc. Combust. Inst. 2013, 34, 3075–3082. [Google Scholar] [CrossRef]
- Aravind, S.; Ragupathi, P.; Kumar, D.S.; Vignesh, G. A Numerical Investigation of Automotive Lambda Sensor to Improve the Life Span of the Sensor using CFD. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Chennai, India, 20–21 February 2020; Volume 923, p. 012003. [Google Scholar]
- Hurault, J.; Kouidri, S.; Bakir, F. Experimental investigations on the wall pressure measurement on the blade of axial flow fans. Exp. Therm. Fluid Sci. 2012, 40, 29–37. [Google Scholar] [CrossRef]
- Mojarab, A.; Kamali, R. Design, optimization and numerical simulation of a MicroFlow sensor in the realistic model of human aorta. Flow Meas. Instrum. 2020, 74, 101791. [Google Scholar] [CrossRef]
- Integrated Pressure Sensor MPXH6400A—Technical Data. Available online: https://www.nxp.com/docs/en/data-sheet/MPXH6400A (accessed on 2 February 2020).
- Valtek Type 30—Technical Data. Available online: https://www.valtek.it (accessed on 2 February 2020).
- Yang, Z.; Cheng, X.; Zheng, X.; Chen, H. Reynolds-Averaged Navier-Stokes Equations Describing Turbulent Flow and Heat Transfer Behavior for Supercritical Fluid. J. Therm. Sci. 2021, 30, 191–200. [Google Scholar] [CrossRef]
- Matyushenko, A.A.; Garbaruk, A.V. Adjustment of the k-ω SST turbulence model for prediction of airfoil characteristics near stall. J.Phys. Conf.Ser. 2016, 769, 012082. [Google Scholar] [CrossRef] [Green Version]
- Spiegel, M.; Redel, T.; Zhang, J.J.; Struffert, T.; Hornegger, J.; Grossman, R.G.; Doerfler, A.; Karmonik, C. Tetrahedral vs. polyhedral mesh size evaluation on flow velocity and wall shear stress for cerebral hemodynamic simulation. Comput. Methods Biomech. Biomed. Engin. 2011, 14, 9–22. [Google Scholar] [CrossRef]
- Michalcová, V.; Kotrasová, K. The numerical diffusion effect on the cfd simulation accuracy of velocity and temperature field for the application of sustainable architecture methodology. Sustainability 2020, 12, 10173. [Google Scholar] [CrossRef]
- Zhang, H.; Tang, S.; Yue, H.; Wu, K.; Zhu, Y.; Liu, C.; Liang, B.; Li, C. Comparison of computational fluid dynamic simulation of a stirred tank with polyhedral and tetrahedral meshes. Iran. J. Chem. Chem. Eng. 2020, 39, 311–319. [Google Scholar]
- Muigg, P.; Hadwiger, M.; Doleisch, H.; Gröller, E. Interactive volume visualization of general polyhedral grids. IEEE Trans. Vis. Comput. Graph. 2011, 17, 2115–2124. [Google Scholar] [CrossRef] [Green Version]
- ANSYS Fluent Tutorial Guide 18. Available online: http://ansys.fem.ir/ansys_fluent_tutorial.pdf (accessed on 2 February 2020).
- Szpica, D.; Borawski, A.; Mieczkowski, G.; Kusznier, M.; Awad, M.M.; Sadik, A.M.; Sallah, M. Evaluation of the influence of the supply pressure on functional parameters of the impulse low-pressure gas-phase injector. Acta Mech. Autom. 2020, 14, 180–185. [Google Scholar] [CrossRef]





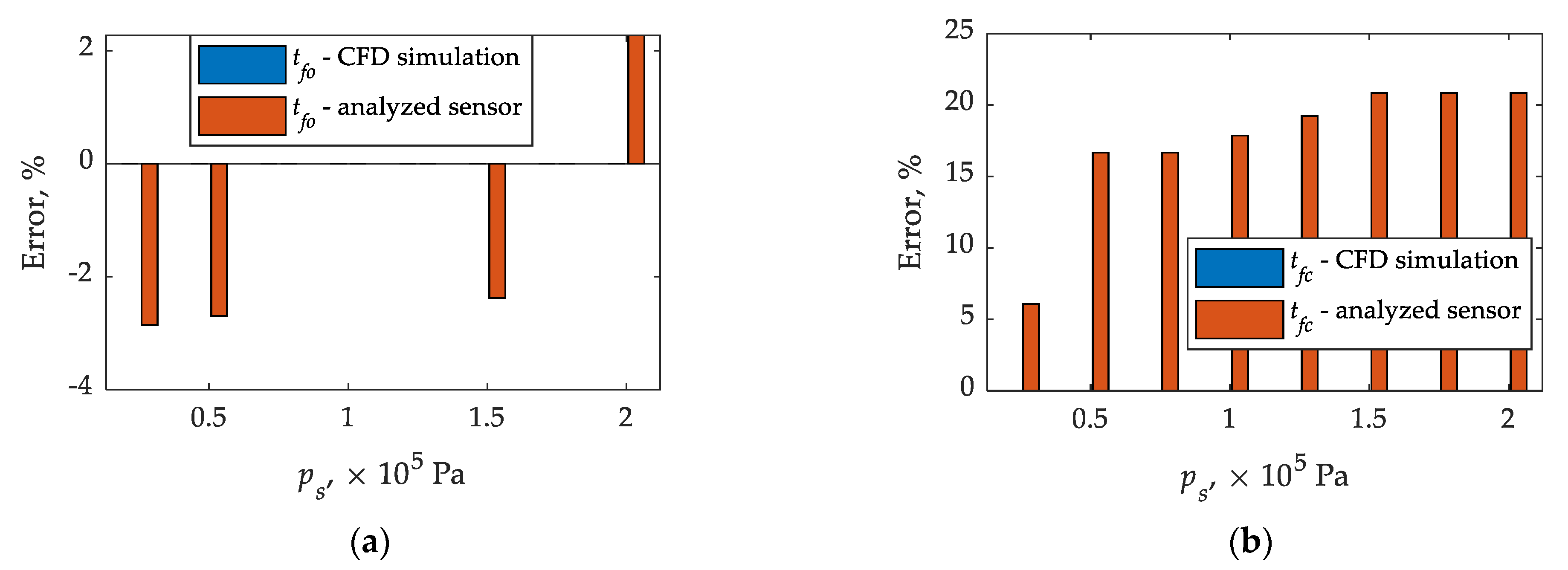
| Parameter | Value |
|---|---|
| Nozzle size | 4 × 10−3 m |
| Pressure range | (20...400) × 103 Pa |
| Max. pressure | 1600 × 103 Pa |
| Storage temperature | (−40…+125) + 273.15 K |
| Supply voltage | (4.64…5.36) V |
| Supply current | 3 × 10−3 A |
| Accuracy (0…85 °C) | ±1.5% |
| Sensitivity | 12.1 (10−3 V / 103 Pa) |
| Response time | <1.0 × 10−3 s |
| Warm-up time | 20 × 10−3 s |
| Offset stability | ±0.25% V |
| Parameter | Value |
|---|---|
| Nozzle size | 4 × 10−3 m |
| Piston stroke | 0.4 × 10−3 m |
| Coil resistance | 3 Ω |
| Time until full opening | 3.4 × 10−3 s |
| Time until full closing | 2.2 × 10−3 s |
| Max. working pressure | 4.5 × 103 Pa |
| Operating temperature | (−20…+120) + 273.15 K |
| Variant | Min Size, mm | Max Face Size, mm | Max Face Size, mm | Curvature Normal Angle, deg | Growth Rate | Elements | Skewness | Orthogonal Quality |
|---|---|---|---|---|---|---|---|---|
| mesh 1 * | 0.01 | 1.22 | 2.45 | 18 | 1.2 | 2,353,288 | 0.2264 | 0.8675 |
| mesh 2 | 0.01 | 1.00 | 2.00 | 18 | 1.2 | 2,357,922 | 0.2265 | 0.8647 |
| mesh 3 | 0.01 | 0.25 | 0.50 | 18 | 1.2 | 3,282,392 | 0.2249 | 0.8679 |
| mesh 4 | 0.01 | 0.10 | 0.20 | 18 | 1.2 | 13,064,272 | 0.2151 | 0.8708 |
| Method | Time, × 10−3 s | ps × 105 Pa | |||||||
| 0.25 | 0.50 | 0.75 | 1.00 | 1.25 | 1.50 | 1.75 | 2.00 | ||
| displacement sensor | ttfo | 3.50 | 3.70 | 3.80 | 3.90 | 4.00 | 4.20 | 4.20 | 4.40 |
| ttfc | 3.30 | 3.00 | 3.00 | 2.80 | 2.60 | 2.40 | 2.40 | 2.40 | |
| CFD simulation | ttfo | 3.50 | 3.70 | 3.80 | 3.90 | 4.00 | 4.20 | 4.20 | 4.40 |
| ttfc | 3.30 | 3.00 | 3.00 | 2.80 | 2.60 | 2.40 | 2.40 | 2.40 | |
| experimentally | ttfo | 3.40 | 3.60 | 3.80 | 3.90 | 4.00 | 4.10 | 4.20 | 4.50 |
| ttfc | 3.50 | 3.50 | 3.50 | 3.30 | 3.10 | 2.90 | 2.90 | 2.90 | |
| Method | Relative Difference, % | ps × 105 Pa | |||||||
| 0.25 | 0.50 | 0.75 | 1.00 | 1.25 | 1.50 | 1.75 | 2.00 | ||
| CFD simulation | Δttfo | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Δttfc | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| experimentally | Δttfo | −2.86 | −2.70 | 0.00 | 0.00 | 0.00 | −2.38 | 0.00 | 2.27 |
| Δttfc | 6.06 | 16.67 | 16.67 | 17.86 | 19.23 | 20.83 | 20.83 | 20.83 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szpica, D.; Mieczkowski, G.; Borawski, A.; Leisis, V.; Diliunas, S.; Pilkaite, T. The Computational Fluid Dynamics (CFD) Analysis of the Pressure Sensor Used in Pulse-Operated Low-Pressure Gas-Phase Solenoid Valve Measurements. Sensors 2021, 21, 8287. https://doi.org/10.3390/s21248287
Szpica D, Mieczkowski G, Borawski A, Leisis V, Diliunas S, Pilkaite T. The Computational Fluid Dynamics (CFD) Analysis of the Pressure Sensor Used in Pulse-Operated Low-Pressure Gas-Phase Solenoid Valve Measurements. Sensors. 2021; 21(24):8287. https://doi.org/10.3390/s21248287
Chicago/Turabian StyleSzpica, Dariusz, Grzegorz Mieczkowski, Andrzej Borawski, Vitalis Leisis, Saulius Diliunas, and Tilmute Pilkaite. 2021. "The Computational Fluid Dynamics (CFD) Analysis of the Pressure Sensor Used in Pulse-Operated Low-Pressure Gas-Phase Solenoid Valve Measurements" Sensors 21, no. 24: 8287. https://doi.org/10.3390/s21248287
APA StyleSzpica, D., Mieczkowski, G., Borawski, A., Leisis, V., Diliunas, S., & Pilkaite, T. (2021). The Computational Fluid Dynamics (CFD) Analysis of the Pressure Sensor Used in Pulse-Operated Low-Pressure Gas-Phase Solenoid Valve Measurements. Sensors, 21(24), 8287. https://doi.org/10.3390/s21248287









