Temperature Sensor Based on Periodically Tapered Optical Fibers
Abstract
:1. Introduction
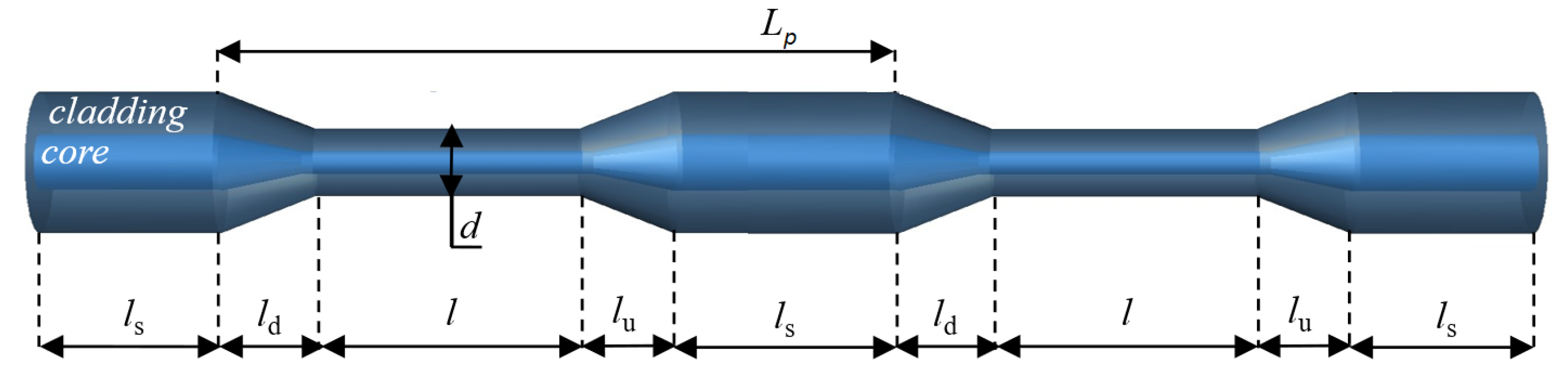
2. Principle of Operation
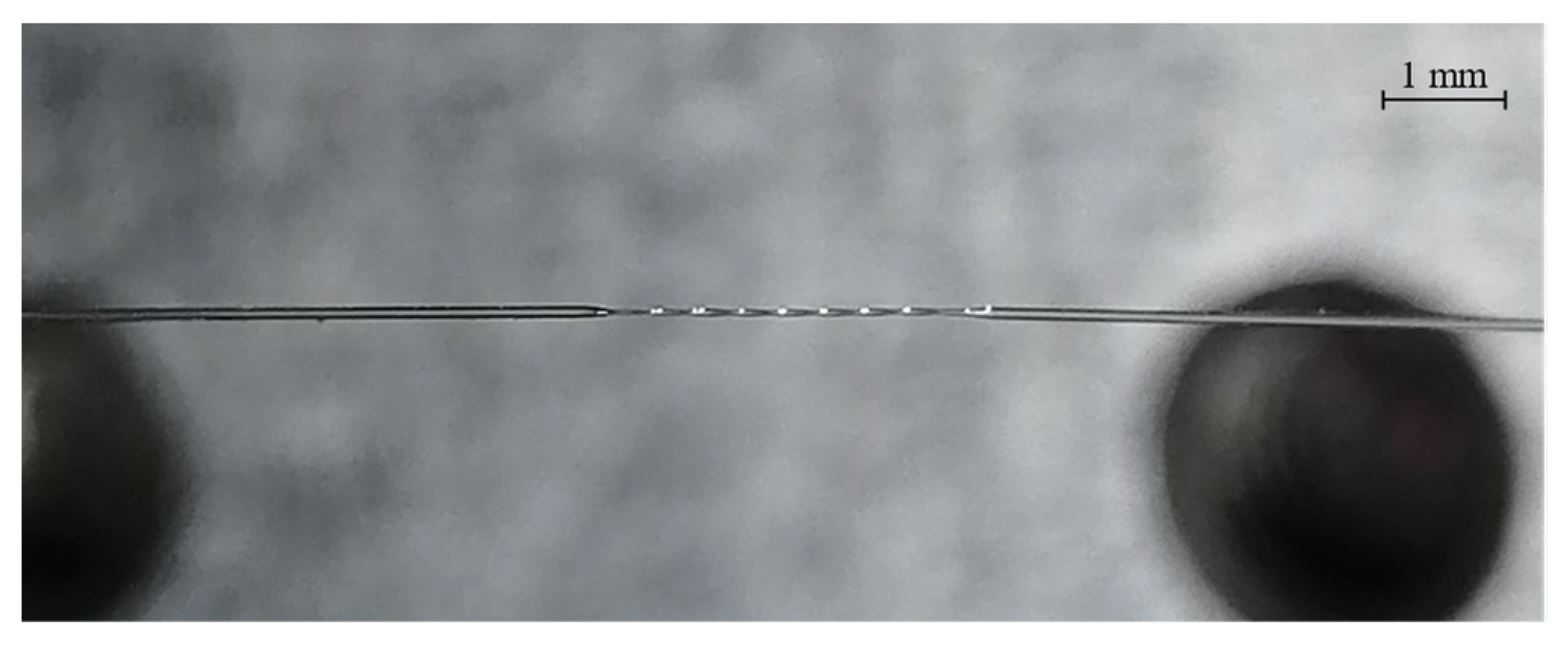
3. Fabrication Process
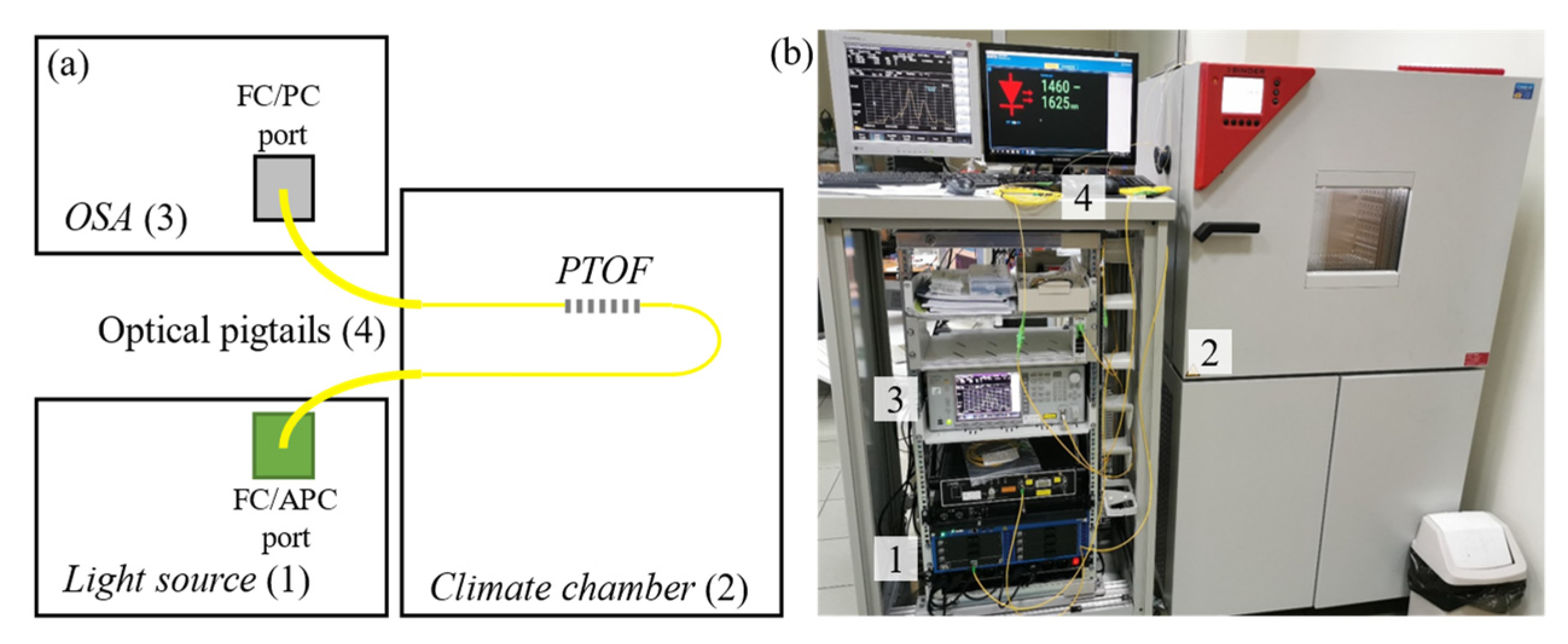
4. Measurement Setup and Procedure
5. Results and Discussion
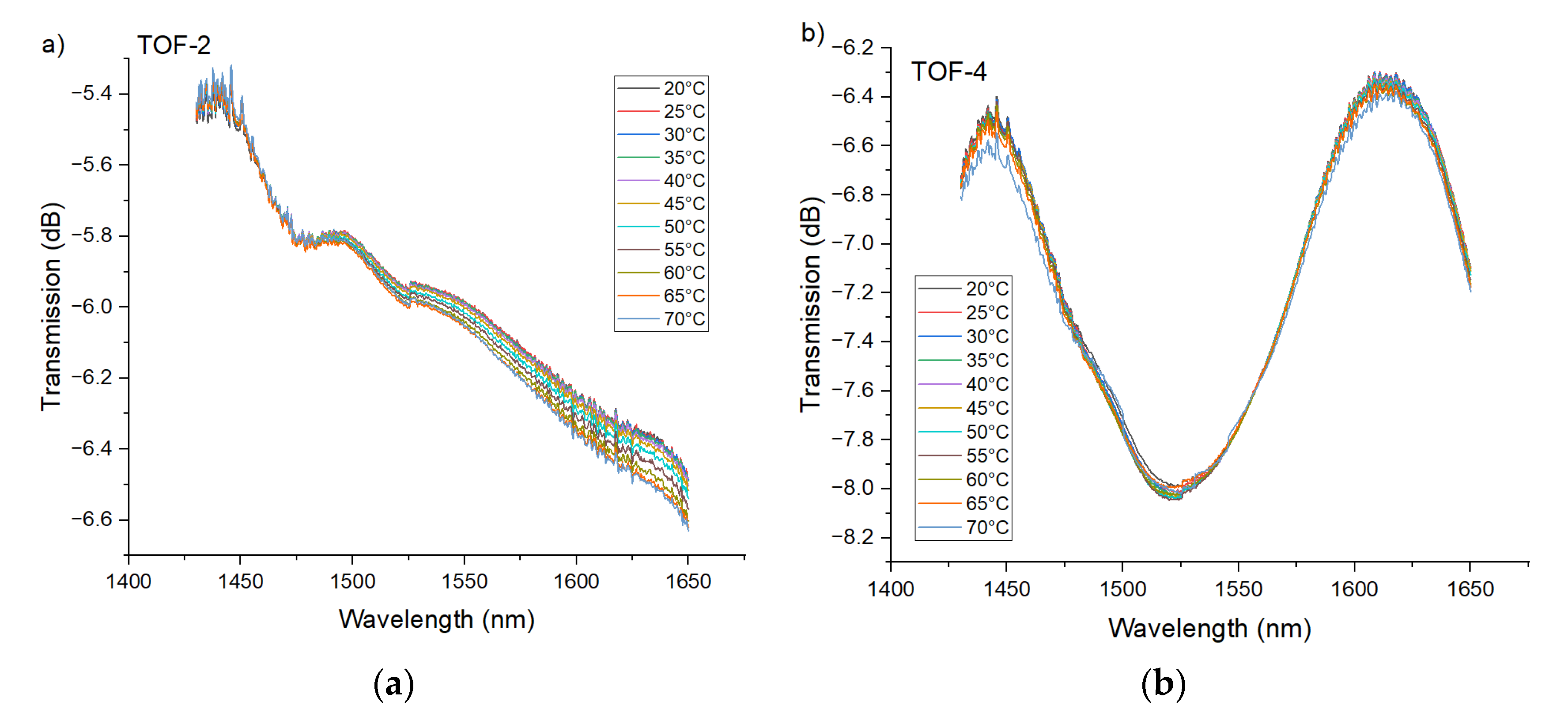
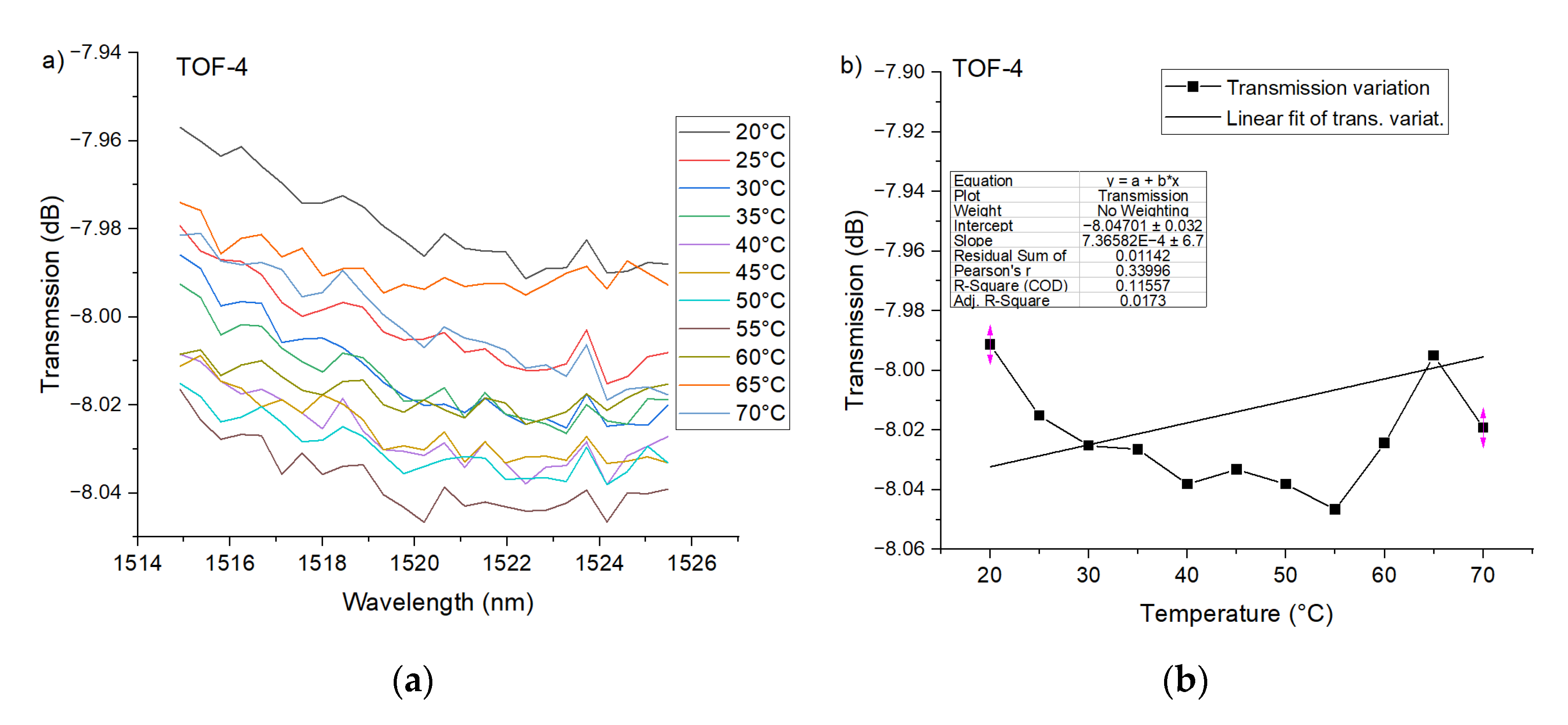
5.1. PTOF with Two and Four Waists
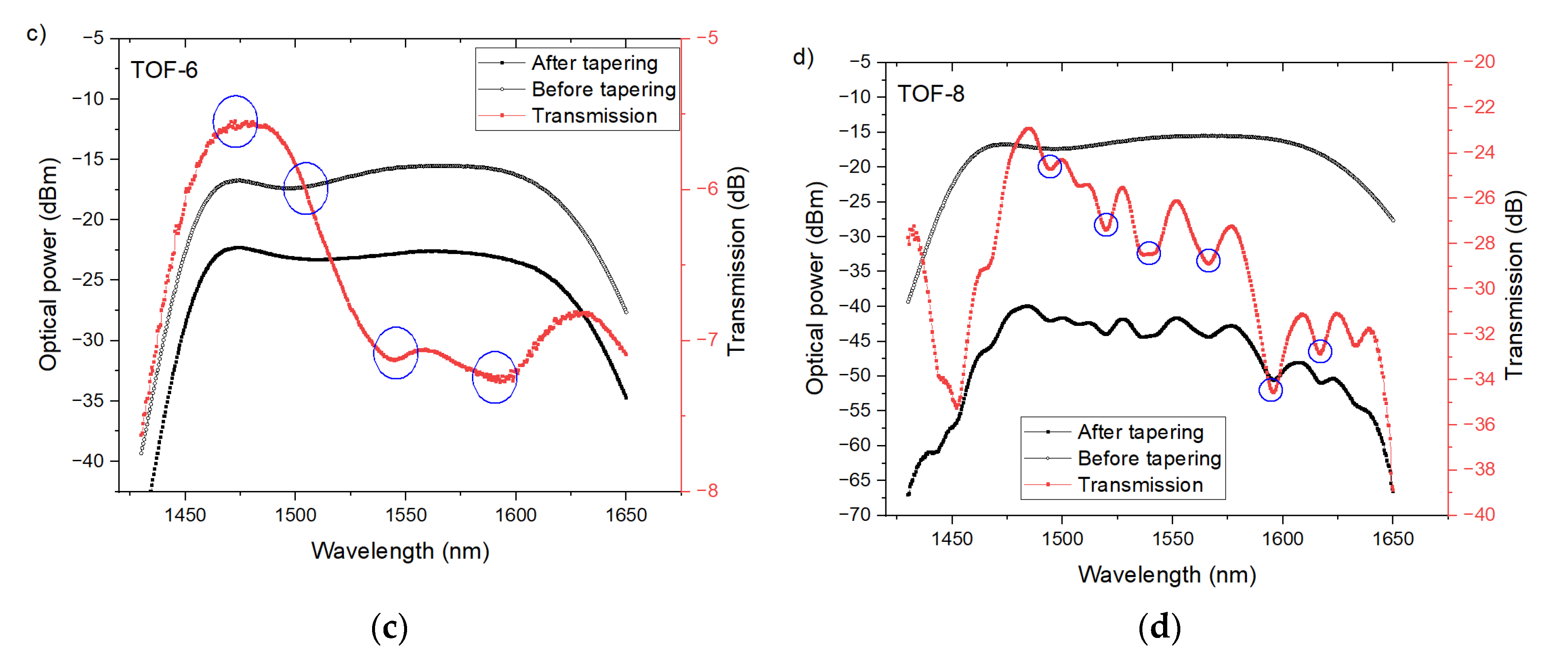
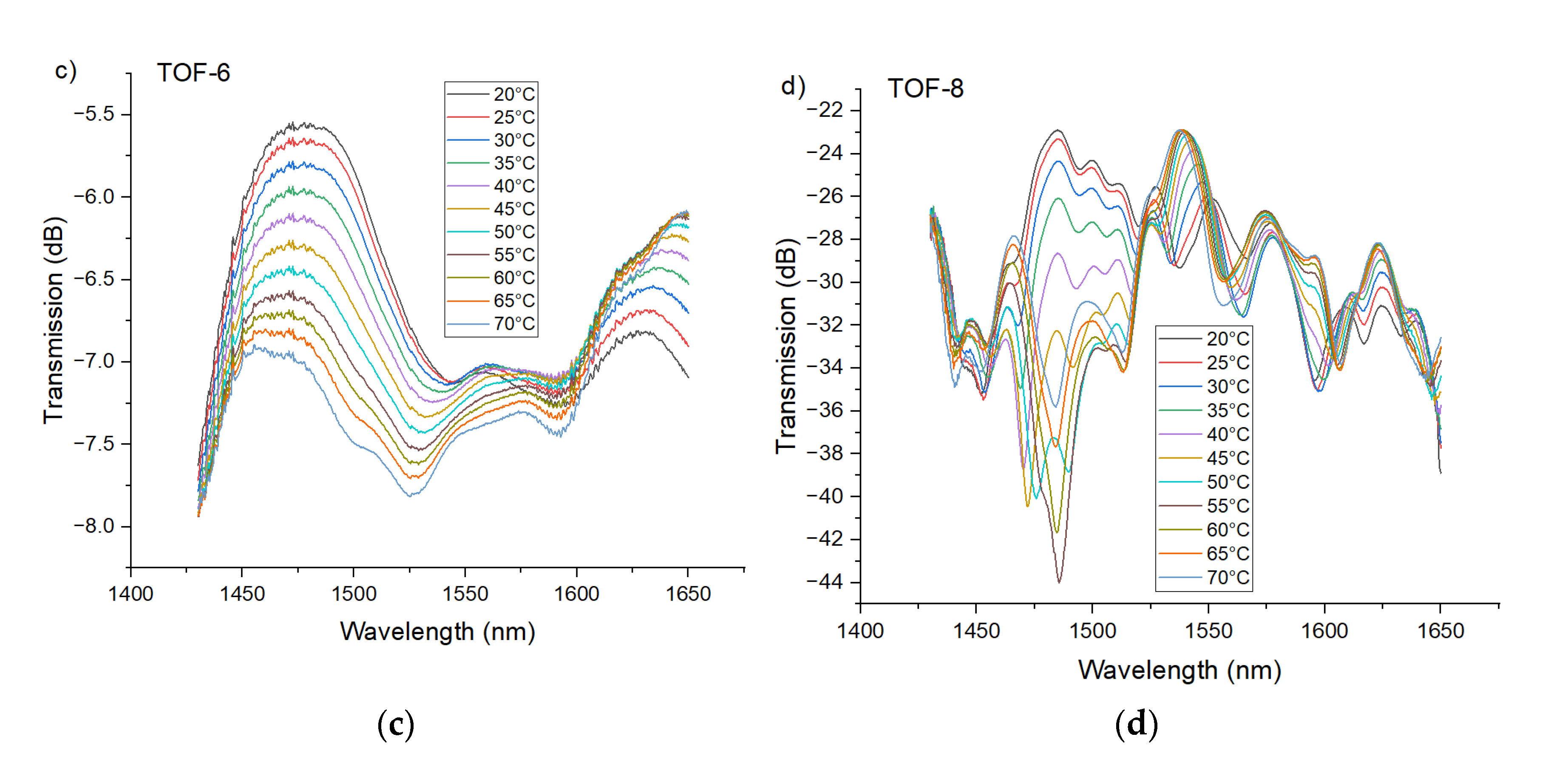
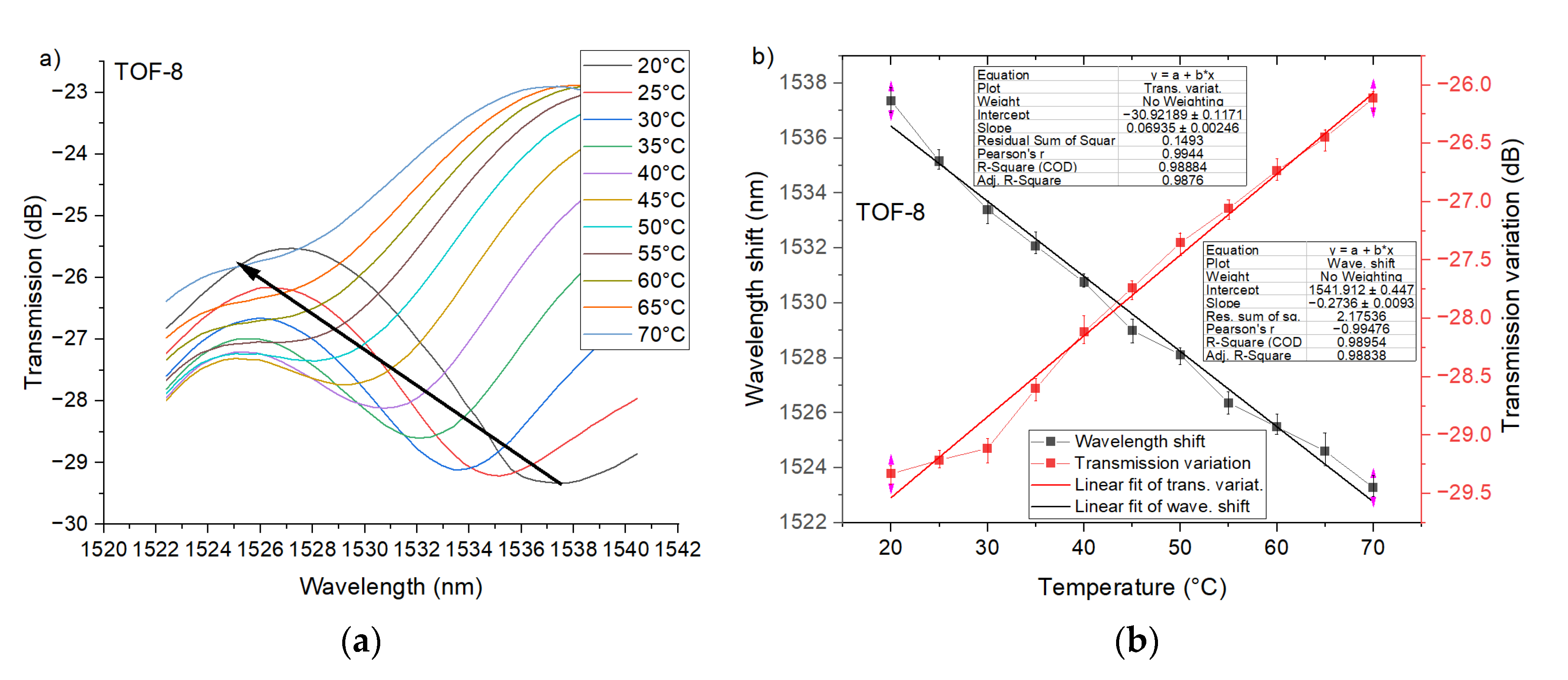
5.2. PTOF with Six and Eight Waists
5.3. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mrooz, O.; Kovalski, A.; Pogorzelska, J.; Shpotyuk, O.; Vakiv, M.; Butkiewicz, B.; Maciak, J. Thermoelectrical degradation processes in NTC thermistors for in-rush current protection of electronic circuits. Microelectron. Reliab. 2001, 41, 773–777. [Google Scholar] [CrossRef]
- Mulla, R.; Dunnill, C.W. Single material thermocouples from graphite traces: Fabricating extremely simple and low cost thermal sensors. Carbon Trends 2021, 4, 100077. [Google Scholar] [CrossRef]
- Kumar, V.; Verma, J.; Maan, A.S.; Akhtar, J. Epitaxial 4H–SiC based Schottky diode temperature sensors in ultra-low current range. Vacuum 2020, 182, 109590. [Google Scholar] [CrossRef]
- Kumar, V.; Maan, A.S.; Akhtar, J. Barrier height inhomogeneities induced anomaly in thermal sensitivity of Ni/4H-SiC Schottky diode temperature sensor. J. Vac. Sci. Technol. 2014, 32, 041203. [Google Scholar] [CrossRef]
- Aime, L.F.J.; Kissinger, T.; James, S.W.; Chehura, E.; Verzeletti, A.; Tatam, R.P. High sensitivity pressure measurement using optical fibre sensors mounted on a composite diaphragm. Opt. Express 2021, 29, 4105–4123. [Google Scholar] [CrossRef]
- Datta, P.; Matias, I.; Aramburu, C.; Bakas, A.; López-Amo, M.; Otón, J.M. Tapered optical-fiber temperature sensor. Microw. Opt. Technol. Lett. 1996, 11, 93–95. [Google Scholar] [CrossRef]
- Allsop, T.; Floreani, F.; Jedrzejewski, K.P.; Marques, P.V.S.; Romero, R.; Webb, D.J.; Bennion, I. Spectral Characteristics of Tapered LPG Device as a Sensing Element for Refractive Index and Temperature. J. Lightwave Technol. 2006, 24, 870–878. [Google Scholar] [CrossRef] [Green Version]
- Hu, D.J.J.; Lim, J.L.; Jiang, M.; Wang, Y.X.; Luan, F.; Shum, P.P.; Wei, H.F.; Tong, W.J. Long period grating cascaded to photonic crystal fiber modal interferometer for simultaneous measurement of temperature and refractive index. Opt. Lett. 2012, 37, 2283–2285. [Google Scholar]
- Guzowski, B.; Lakomski, M.; Cywinski, M. Proximity sensors based on ball-lensed optical fibers. IOP Conf. Ser. Mater. Sci. Eng. 2016, 104, 0120311. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Tian, D.; Chen, K.; Zhou, X.; Gong, Z.; Yu, Q. A Fiber-Optic Displacement Sensor Using the Spectral Demodulation Method. J. Lightwave Technol. 2018, 36, 3666–3671. [Google Scholar] [CrossRef]
- Wu, J.; Miao, Y.; Song, B.; Lin, W.; Zhang, K.; Zhang, H.; Liu, B.; Yao, J. Simultaneous measurement of displacement and temperature based on thin-core fiber modal interferometer. Opt. Commun. 2015, 340, 136–140. [Google Scholar] [CrossRef]
- Guzowski, B.; Lakomski, M. Realization of fiber optic displacement sensors. Opt. Fiber Technol. 2018, 41, 34–39. [Google Scholar] [CrossRef]
- Hou, M.; Wang, Y.; Liu, S.; Guo, J.; Li, Z.; Lu, P. Sensitivity-Enhanced Pressure Sensor with Hollow-Core Photonic Crystal Fiber. J. Lightwave Technol. 2014, 32, 4035–4039. [Google Scholar]
- Kissinger, T.; Correia, R.; Charrett, T.O.H.; James, S.W.; Tatam, R.P. Fiber Segment Interferometry for Dynamic Strain Measurements. J. Light. Technol. 2016, 34, 4620–4626. [Google Scholar] [CrossRef] [Green Version]
- Kolli, V.R.; Basavaprasad; Bahaddur, I.; Talabattula, S. A high sensitive photonic crystal Mach-Zehnder-Interferometer based pressure-sensor. Res. Opt. 2021, 5, 100118. [Google Scholar] [CrossRef]
- Bock, W.J.; Chen, J.; Mikulic, P.; Eftimov, T. A Novel Fiber-Optic Tapered Long-Period Grating Sensor for Pressure Monitoring. IEEE Trans. Instrum. Meas. 2007, 56, 1176–1180. [Google Scholar] [CrossRef]
- Zawisza, R.; Jaroszewicz, L.R.; Mikulic, P.; Bock, W.J. An interferometric structure with a dual-resonance long period grating for strain sensing. Opto-Electron. Rev. 2018, 26, 325–328. [Google Scholar] [CrossRef]
- Eftimov, T.; Janik, M.; Koba, M.; Śmietana, M.; Mikulic, P.; Bock, W.J. Long-period gratings and microcavity in-line Mach Zehnder interferometers as highly sensitive optical fiber platforms for bacteria sensing. Sensors 2020, 20, 3772. [Google Scholar] [CrossRef] [PubMed]
- Latifi, H.; Zibaii, M.I.; Hosseini, S.M.; Jorge, P. Nonadiabatic tapered optical fiber for biosensor applications. Photonic Sens. 2012, 2, 340–356. [Google Scholar] [CrossRef]
- Zhang, W.; Ni, X.; Wang, J.; Ai, F.; Luo, Y.; Yan, Z.; Liu, D.; Su, Q. Microstructured Optical Fiber Based Distributed Sensor for In Vivo Pressure Detection. J. Lightwave Technol. 2019, 37, 1865–1872. [Google Scholar] [CrossRef]
- Ahmed, F.; Jun, M.B.G. Filament-based fabrication and performance analysis of fiber Bragg grating sensors using ultrashort pulse laser. J. Micro. Nano-Manuf. 2014, 2, 021007-1–021007-6. [Google Scholar] [CrossRef]
- Ju, S.; Watekar, P.R.; Han, W.-T. Enhanced Sensitivity of the FBG Temperature Sensor Based on the PbO-GeO2-SiO2 Glass Optical Fiber. J. Lightwave Technol. 2010, 28, 2697–2700. [Google Scholar] [CrossRef]
- Zhu, S.; Pang, F.; Wang, T. Single-mode tapered optical fiber for temperature sensor based on multimode interference. Opt. Sens. Biophotonics 2011, 8311, 83112B. [Google Scholar]
- Bilsel, M.; Navruz, I. Tapered Optical Fiber Sensor for Discrimination of Strain and Temperature. Adv. Electr. Electron. Eng. 2020, 18, 50–56. [Google Scholar] [CrossRef]
- Zhou, G.; Zhang, C.; Xie, X.; Wan, Y.; Yao, C.; Liu, J.; Niu, L.; Miao, X.; Zhou, H.; Jiang, X.; et al. A Low-Cost High-Temperature Sensor Based on Long-Period Fiber/Microfiber Gratings by Local Fictive Temperature Modification. J. Chem. 2020, 2020, 1–6. [Google Scholar] [CrossRef]
- Chen, L.; Chan, C.C.; Sun, J. High resolution long-period grating temperature sensor. J. Optoelectron. Adv. M 2008, 10, 190–193. [Google Scholar]
- Lee, C.E.; Taylor, H.F. Fiber-optic Fabry-Perot Temperature Sensor Using a Low-Coherence Light Source. J. Light. Technol. 1991, 9, 129–134. [Google Scholar] [CrossRef]
- Chen, Z.; Xiong, S.; Gao, S.; Zhang, H.; Wan, L.; Huang, X.; Huang, B.; Feng, Y.; Liu, W.; Li, Z. High-Temperature Sensor Based on Fabry-Perot Interferometer in Microfiber Tip. Sensors 2018, 18, 202. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, M.-q.; Zhao, Y.; Xia, F.; Peng, Y.; Tong, R.-j. High sensitivity temperature sensor based on fiber Air-Microbubble Fabry-Perot interferometer with PDMS-filled hollow-core fiber. Sens. Actuators A 2018, 275, 60–66. [Google Scholar] [CrossRef]
- Cárdenas-Sevilla, G.A.; Monzón-Hernández, D.; Torres-Gómez, I.; Martínez-Ríos, A. Mechanically induced long-period fiber gratings on tapered fibers. Opt. Commun. 2009, 282, 2823–2826. [Google Scholar] [CrossRef]
- Chunxia, Y.; Hui, D.; Wei, D.; Chaowei, X. Weakly-coupled multicore optical fiber taper-based high-temperature sensor. Sens. Actuators A 2018, 280, 139–144. [Google Scholar] [CrossRef]
- Yang, S.; Feng, Z.; Jia, X.; Pickrell, G.; Ng, W.; Wang, A.; Zhu, Y. All-Sapphire Miniature Optical Fiber Tip Sensor for High Temperature Measurement. J. Light. Technol. 2019, 38, 1988–1997. [Google Scholar] [CrossRef]
- Grobnic, D.; Mihailov, S.J.; Smelser, C.W.; Ding, H. Sapphire Fiber Bragg Grating Sensor Made Using Femtosecond Laser Radiation for Ultrahigh Temperature Applications. IEEE Photon. Technol. Lett. 2018, 16, 2505–2507. [Google Scholar] [CrossRef]
- Yang, S.; Hu, D.; Wang, A. Point-by-point fabrication and characterization of sapphire fiber Bragg gratings. Opt. Lett. 2017, 42, 4219–4222. [Google Scholar] [CrossRef]
- Habisreuther, T.; Elsmann, T.; Pan, Z.; Graf, A.; Willsch, R.; Schmidt, M.A. Sapphire fiber Bragg gratings for high temperature and dynamic temperature diagnostics. Appl. Therm. Eng. 2015, 91, 860–865. [Google Scholar] [CrossRef]
- Mihalov, S.J.; Grobnic, D.; Smelser, C.W. High-temperature multiparameter sensor based on sapphire fiber Bragg gratings. Opt. Lett. 2010, 35, 2810–2812. [Google Scholar] [CrossRef]
- Leal-Junior, A.; Frizera-Neto, A.; Marques, C.; Pontes, M.J. A polymer optical fiber temperature sensor based on material features. Sensors 2018, 18, 301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fu, X.; Zhang, Y.; Wang, Y.; Fu, G.; Jin, W.; Bi, W. A temperature sensor based on tapered few mode fiber long-period grating induced by CO2 laser and fusion tapering. Opt. Laser Technol. 2020, 121, 105825. [Google Scholar] [CrossRef]
- Wei, T.; Lan, X.; Xiao, H. Fiber Inline Core–Cladding-Mode Mach–Zehnder Interferometer Fabricated by Two-Point CO2 Laser Irradiations. IEEE Photon. Technol. Lett. 2009, 21, 669–671. [Google Scholar]
- Liu, W.; Wu, X.; Zhang, G.; Li, S.; Zuo, C.; Fang, S.; Yu, B. Refractive index and temperature sensor based on Mach-Zehnder interferometer with thin fibers. Opt. Fiber Technol. 2020, 54, 102101. [Google Scholar] [CrossRef]
- Kowal, D.; Urbanczyk, W.; Mergo, P. Twin-Core Fiber-Based Mach Zehnder Interferometer for Simultaneous Measurement of Strain and Temperature. Sensors 2018, 18, 95. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Gao, S.; Luo, Y.; Chen, Z.; Xiong, S.; Wan, L.; Huang, X.; Huang, B.; Feng, Y.; He, M.; et al. Ultrasensitive Mach-Zehnder Interferometric Temperature Sensor Based on Liquid-Filled D-Shaped Fiber Cavity. Sensors 2018, 18, 1239. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, N.; Lin, Q.; Jiang, Z.; Yao, K.; Tian, B.; Fang, X.; Shi, P.; Zhang, Z. High Temperature High Sensitivity Multipoint Sensing System Based on Three Cascade Mach–Zehnder Interferometers. Sensors 2018, 18, 2688. [Google Scholar] [CrossRef] [Green Version]
- Marrujo-García, S.; Hernández-Romano, I.; May-Arrioja, D.A.; Minkovich, V.P.; Torres-Cisneros, M. In-Line Mach–Zehnder Interferometers Based on a Capillary Hollow-Core Fiber Using Vernier Effect for a Highly Sensitive Temperature Sensor. Sensors 2021, 21, 5471. [Google Scholar] [CrossRef] [PubMed]
- Su, H.; Zhao, C.; Song, X.; Kong, F.; Zhang, Z.; Liu, C. High-sensitivity optical fiber temperature sensor with cascaded configuration of MZI and FPI based on Vernier effect. Opt. Fiber Technol. 2021, 67, 102751. [Google Scholar] [CrossRef]
- Zhao, C.; Qiu, H.; Chen, H.; Hu, X.; Yu, A.; Lian, Z.; Li, J.; Qu, H. In-fiber Mach-Zehnder temperature sensor using silicone-oil-filled dual core fiber. Sens. Actuators A 2021, 323, 112644. [Google Scholar] [CrossRef]
- Ahsani, V.; Ahmed, F.; Jun, M.B.G.; Bradley, C. Tapered Fiber-Optic Mach-Zehnder Interferometer for Ultra-High Sensitivity Measurement of Refractive Index. Sensors 2019, 19, 1652. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Wang, B.-T.; Kong, L.-X.; Zhao, T. Comparative Analyses of Bi-Tapered Fiber Mach–Zehnder Interferometer for Refractive Index Sensing. IEEE Trans. Instrum. Meas. 2017, 66, 2483–2489. [Google Scholar] [CrossRef]
- Lu, P.; Men, L.; Sooley, K.; Chen, Q. Tapered fiber Mach–Zehnder interferometer for simultaneous measurement of refractive index and temperature. Appl. Phys. Lett. 2009, 94, 131110. [Google Scholar] [CrossRef] [Green Version]
- Tian, Z.; Yam, S.S.-H. In-Line Abrupt Taper Optical Fiber Mach–Zehnder Interferometric Strain Sensor. IEEE Photon. Technol. Lett. 2009, 21, 161–163. [Google Scholar] [CrossRef]
- Yue, X.; Chen, H.; Qu, H.; Min, R.; Woyessa, G.; Bang, O.; Hu, X. Polycarbonate mPOF-Based Mach–Zehnder Interferometer for Temperature and Strain Measurement. Sensors 2020, 20, 6643. [Google Scholar] [CrossRef] [PubMed]
- Lakomski, M.; Guzowski, B.; Wozniak, A. Fabrication of ultra-long tapered optical fibers. Microelectron. Eng. 2020, 221, 111193. [Google Scholar] [CrossRef]
- Yadav, T.K.; Narayanaswamy, R.; Bakar, M.H.A.; Kamil, Y.M.; Mahdi, M.A. Single mode tapered fiber-optic interferometer based refractive index sensor and its application to protein sensing. Opt. Express 2014, 22, 22802–22807. [Google Scholar] [CrossRef] [PubMed]
- Xiong, M.; Gong, H.; Wang, Z.; Zhao, C.; Dong, X. Simultaneous Refractive index and Temperature Measurement based on Mach-Zehnder Interferometer Concatenating Two Bi-tapers and A Long-Period Grating. IEEE Sens. J. 2016, 16, 4295–4299. [Google Scholar] [CrossRef]
- Miao, Y.; He, Y.; Ma, X.; Zhang, H.; Song, B.; Yang, X.; Xue, L.; Liu, B.; Yao, J. Low-Temperature Cross-Sensitivity Refractive Index Sensor Based on Single-Mode Fiber with Periodically Modulated Taper. IEEE Sens. J. 2016, 16, 2442–2446. [Google Scholar] [CrossRef]
- Tian, Z.; Yam, S.S.-H.; Barnes, J.; Bock, W.J.; Greig, P.; Fraser, J.M.; Loock, H.P.; Oleschuk, R.D. Refractive Index Sensing with Mach–Zehnder Interferometer Based on Concatenating Two Single-Mode Fiber Tapers. IEEE Photon. Technol. Lett. 2008, 20, 626–628. [Google Scholar] [CrossRef]
- Nguyen, L.V.; Hwang, D.; Moon, S.; Moon, D.S.; Chung, Y. High temperature fiber sensor with high sensitivity based on core diameter mismatch. Opt. Express 2008, 16, 11369–11375. [Google Scholar] [CrossRef]
- Kim, Y.-J.; Paek, U.-C.; Lee, B.H. Measurement of refractive-index variation with temperature by use of long-period fiber gratings. Opt. Lett. 2002, 27, 1297–1299. [Google Scholar] [CrossRef] [PubMed]
- Raji, Y.M.; Lin, H.S.; Ibrahim, S.A.; Mokhtar, M.R.; Yusoff, Z. Intensity-modulated abrupt tapered Fiber Mach-Zehnder Interferometer for the simultaneous sensing of temperature and curvature. Opt. Laser Technol. 2016, 86, 8–13. [Google Scholar] [CrossRef] [Green Version]
- Yang, N.; Qiu, Q.; Su, J.; Shi, S.-j. Research on the temperature characteristics of optical fiber refractive index. Optik 2014, 125, 5813–5815. [Google Scholar] [CrossRef]
- Gu, B.; Yin, M.; Zhang, A.P.; Qian, J.; He, S. Low-cost high-performance fiber-optic pH sensor based on thin-core fiber modal interferometer. Opt. Exp. 2009, 17, 22296–22302. [Google Scholar] [CrossRef] [PubMed]
- Yoon, M.; Park, S.; Han, Y. Simultaneous Measurement of Strain and Temperature by Using a Micro-Tapered Fiber Grating. J. Lightwave Technol. 2012, 30, 1156–1160. [Google Scholar] [CrossRef]
- Guzowski, B.; Gozdur, R.; Lakomski, M. WDM power supply for identification system of fibre optic connectors. Metrol. Meas. Syst. 2018, 25, 235–244. [Google Scholar]
- Guzowski, B.; Gozdur, R.; Lakomski, M.; Bernacki, L. RFID monitoring system of fiber optic connectors. Circuit World 2017, 43, 32–37. [Google Scholar] [CrossRef]
- Pigłowska, M.; Kurc, B.; Galiński, M.; Fuć, P.; Kamińska, M.; Szymlet, N.; Daszkiewicz, P. Challenges for Safe Electrolytes Applied in Lithium-Ion Cells—A Review. Materials 2021, 14, 6783. [Google Scholar] [CrossRef] [PubMed]
- Gozdur, R.; Guzowski, B.; Dimitrova, Z.; Noury, A.; Mitukiewicz, G.; Batory, D. An energy balance evaluation in lithium-ion battery module under high temperature operation. Energy Convers. Manag. 2021, 227, 113565. [Google Scholar] [CrossRef]
- Jasim, A.A.; Harun, S.W.; Arof, H.; Ahmad, H. Inline Microfiber Mach–Zehnder Interferometer for High Temperature Sensing. IEEE Sens. J. 2013, 13, 626–628. [Google Scholar] [CrossRef]





| Electric Arc Power P (mW) | Arc Duration t (s) | Holder Travel s (µm) | Speed of Holders v (µm/s) |
|---|---|---|---|
| 20 | 1.5 | 500 | 122 |
| Name | Waist No. | Avg. Waist Diameter d (µm) | Min/Max Waist Diameter d (µm) | Avg. Waist Period (µm) |
|---|---|---|---|---|
| PTOF-2 | 2 | 44.3 | 41.4/47.3 | 620 |
| PTOF-4 | 4 | 48.9 | 46.4/51.6 | 605 |
| PTOF-6 | 6 | 49.7 | 45.3/53.0 | 533 |
| PTOF-8 | 8 | 51.1 | 49.0/53.0 | 581 |
| Name | ∆neff | L (mm) | λdip (nm) | Theoretical FSR (nm) | Experimental FSR (nm) |
|---|---|---|---|---|---|
| PTOF-2 | 0.02 | 1.2 | 1475 | 87 | 85 |
| PTOF-4 | 2.4 | 1475 | 45 | 49 | |
| PTOF-6 | 3.2 | 1545 | 38 | 44 | |
| PTOF-8 | 4.6 | 1524 | 24 | 22 |
| Type | Temperature Range | Sensitivity | Ref. |
|---|---|---|---|
| FBG on microfiber | 22.5–95 °C | 31.32 pm/°C | [21] |
| Tapered LPG | 0–60 °C | 87 pm/°C | [7] |
| Weakly coupled multicore fiber taper | 0–1000 °C | 36.8 pm/°C | [31] |
| Tapered few modes fiber with LPG | 30–90 °C | 39.3 pm/°C | [38] |
| Tapered microfiber | 50–800 °C | 13.4 pm/°C | [67] |
| Abrupt tapered single-mode fiber | 15–50 °C | 0.0829 dBm/°C | [59] |
| PTOF SMF | 20–70 °C | 390 pm/°C and 270 pm/°C | This study |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guzowski, B.; Łakomski, M. Temperature Sensor Based on Periodically Tapered Optical Fibers. Sensors 2021, 21, 8358. https://doi.org/10.3390/s21248358
Guzowski B, Łakomski M. Temperature Sensor Based on Periodically Tapered Optical Fibers. Sensors. 2021; 21(24):8358. https://doi.org/10.3390/s21248358
Chicago/Turabian StyleGuzowski, Bartlomiej, and Mateusz Łakomski. 2021. "Temperature Sensor Based on Periodically Tapered Optical Fibers" Sensors 21, no. 24: 8358. https://doi.org/10.3390/s21248358
APA StyleGuzowski, B., & Łakomski, M. (2021). Temperature Sensor Based on Periodically Tapered Optical Fibers. Sensors, 21(24), 8358. https://doi.org/10.3390/s21248358







