Uncertainty Propagation for Inertial Navigation with Coning, Sculling, and Scrolling Corrections
Abstract
:1. Introduction
2. Inertial Navigation
2.1. Attitude Integration (Coning) Algorithm
2.2. Velocity Integration (Sculling) Algorithm
2.3. Position Integration (Scrolling) Algorithm
2.4. Discrete Dead-Reckoning Dynamics
2.5. Strapdown IMU Model
3. Error Propagation Development
3.1. Method for Error Analysis
3.2. Parametric Estimation Errors
3.3. Coning Error Propagation
3.4. Sculling Error Propagation
3.5. Scrolling Error Propagation
3.6. State Estimation Error Dynamics
3.7. Covariance Propagation
4. Simulation
4.1. Nominal Simulation
4.2. Coning, Sculling, and Scrolling Simulation
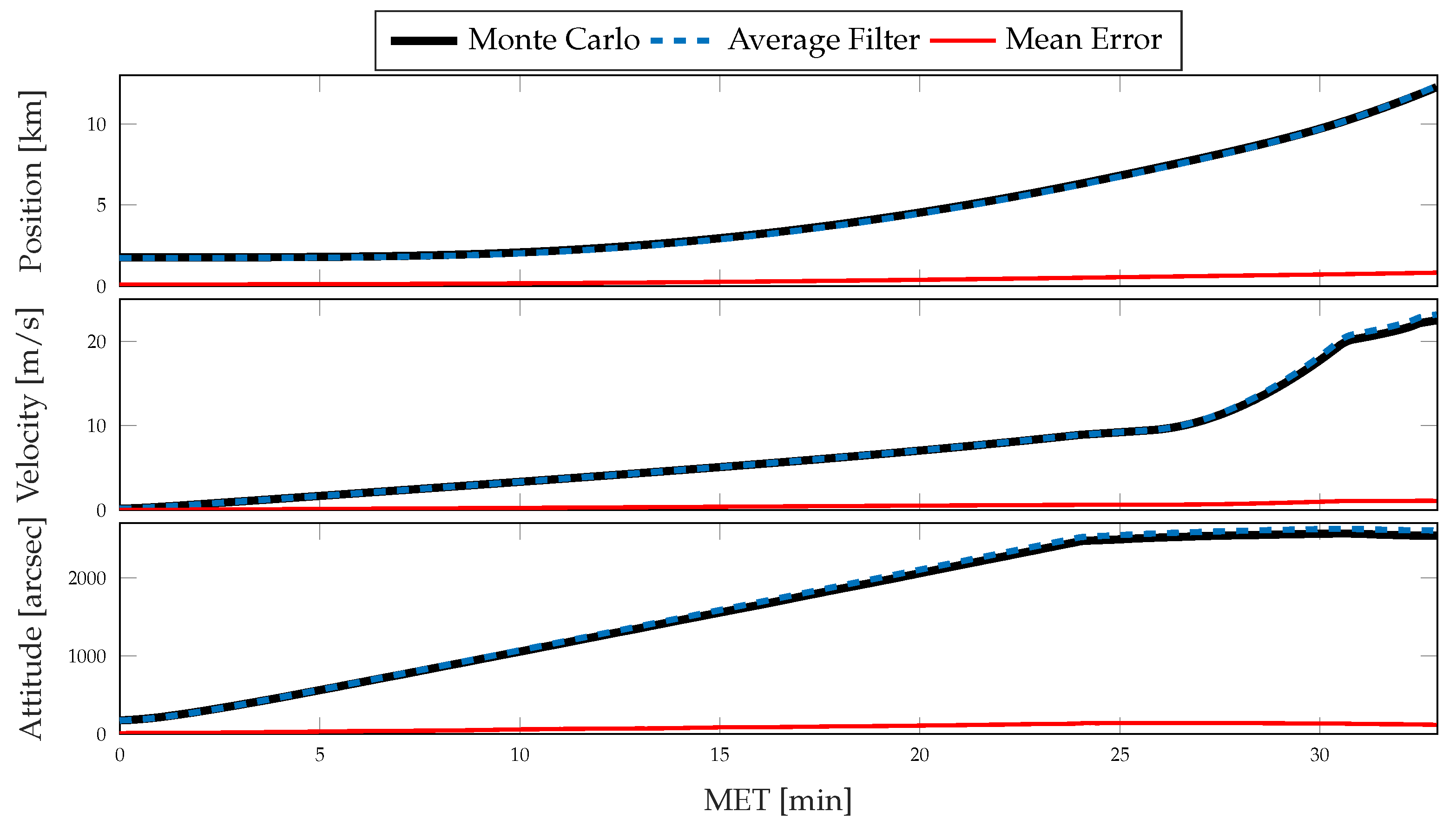
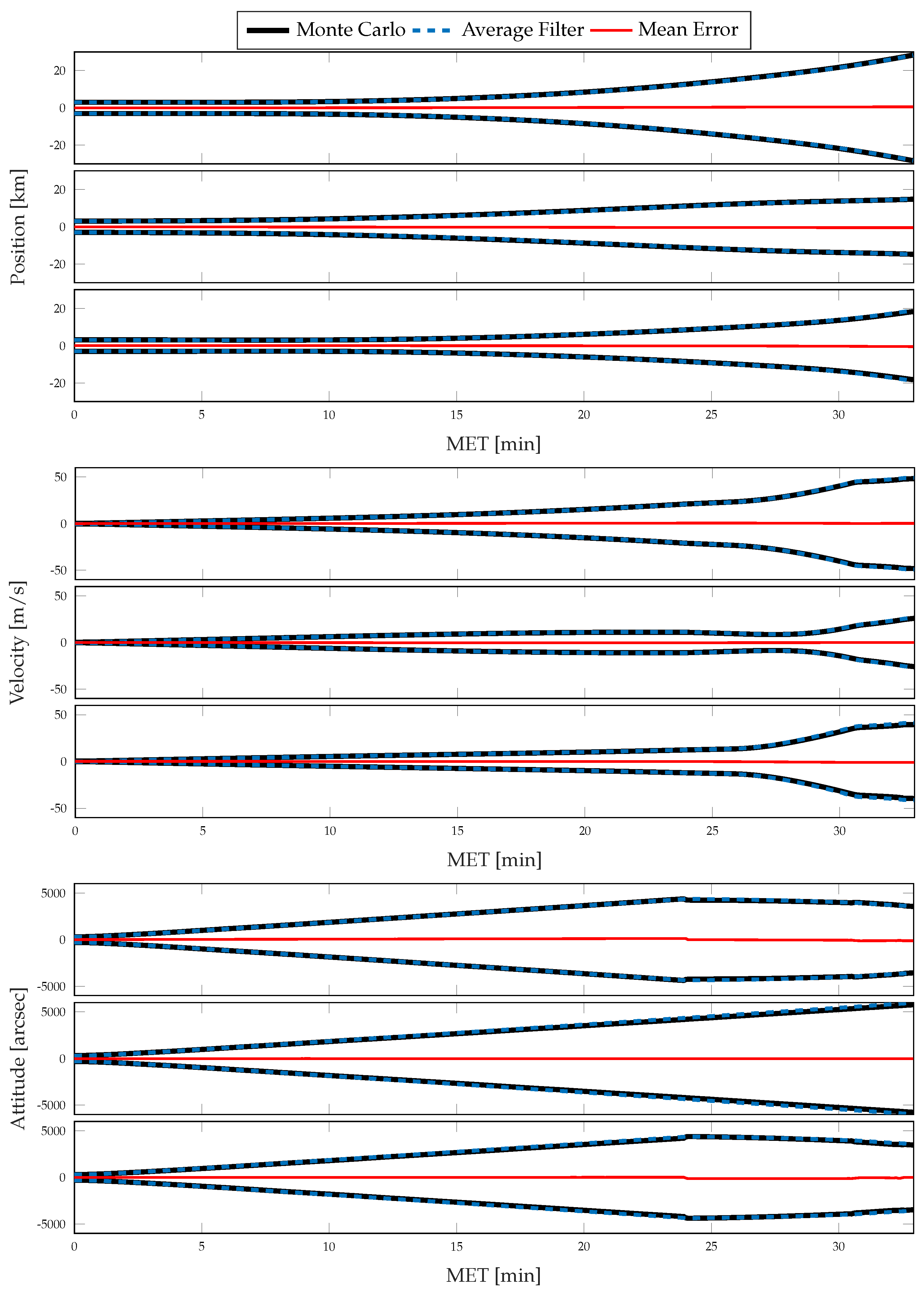
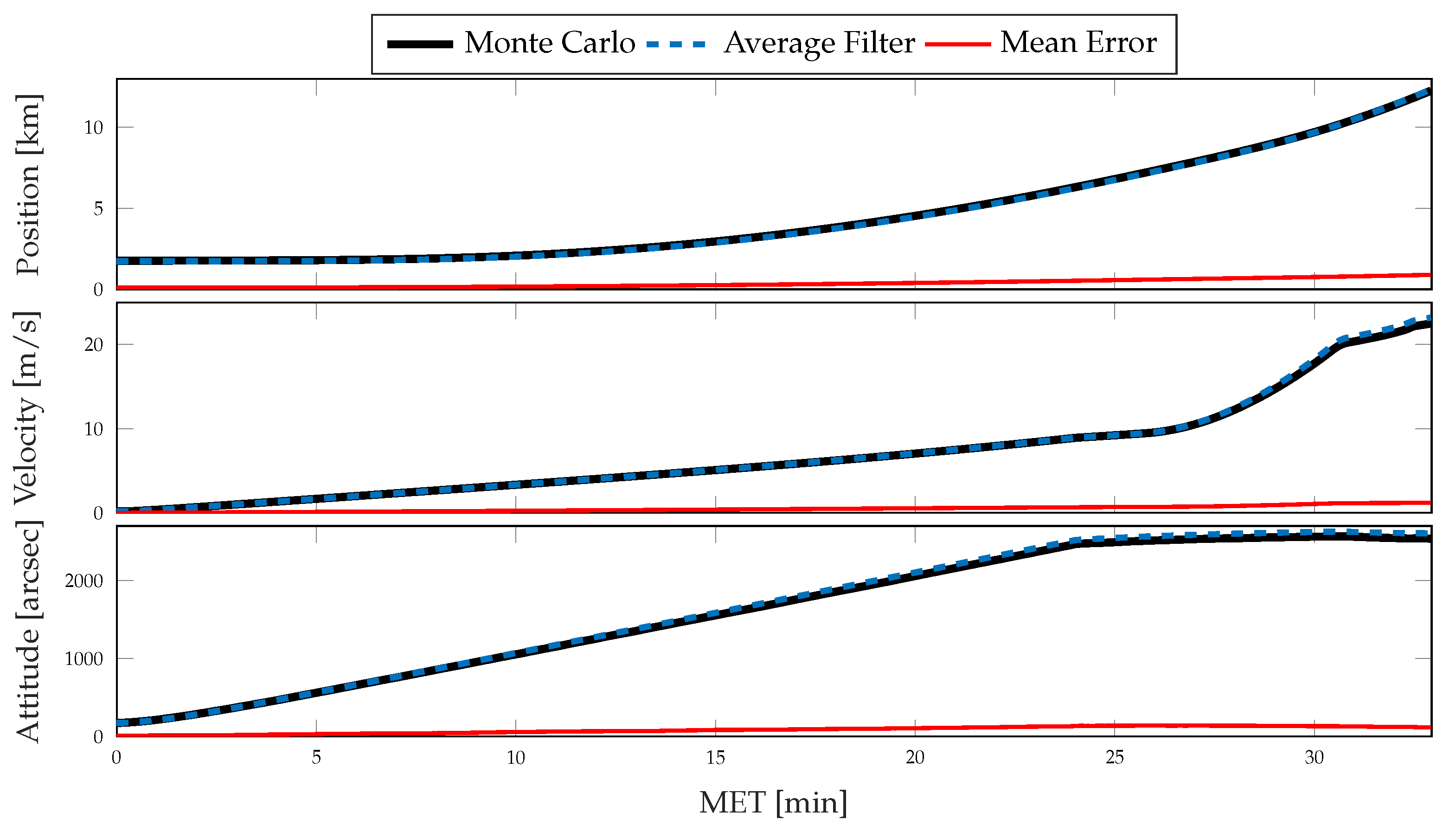
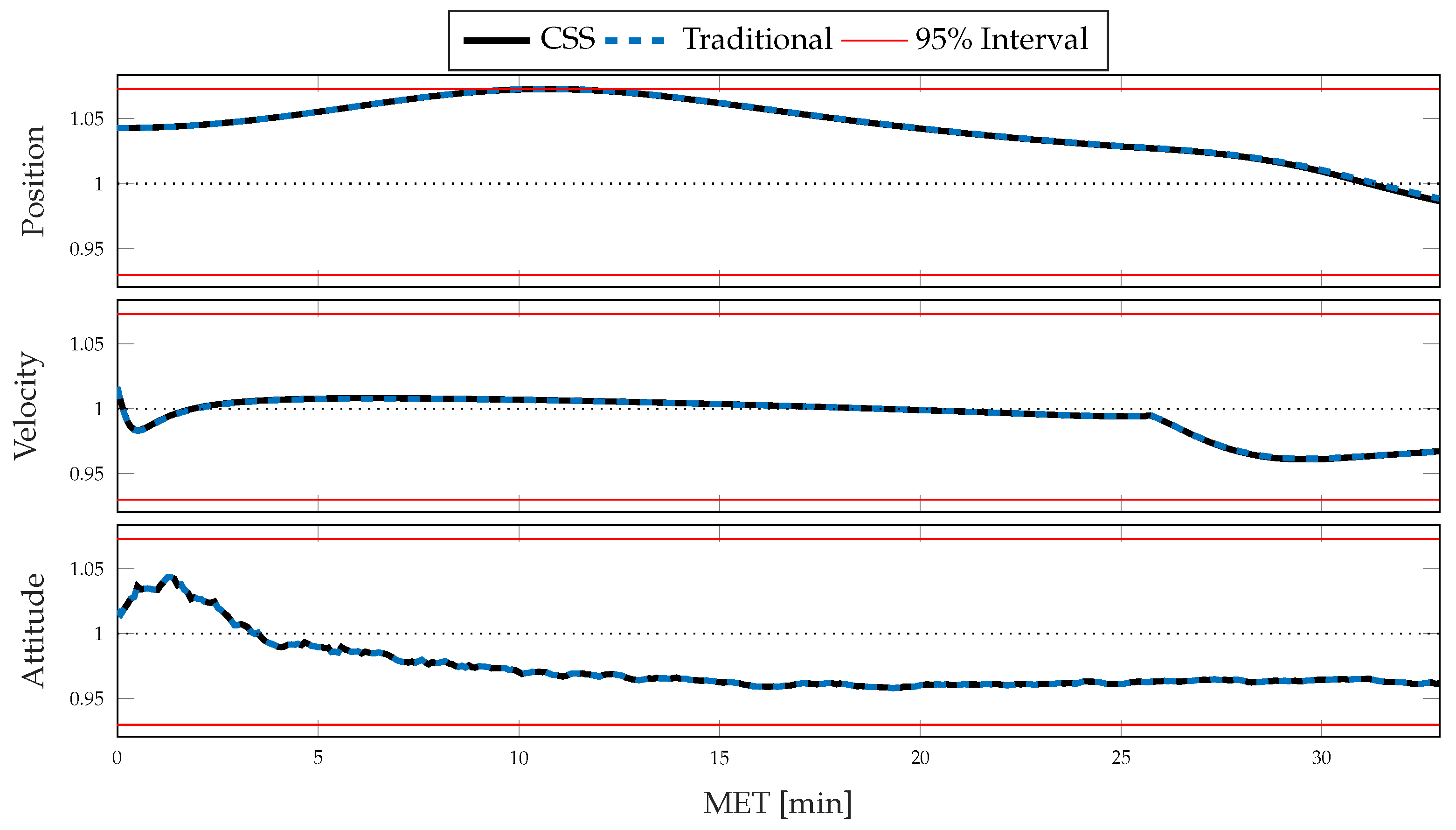
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Incorporating the Strapdown Sensor Model
Appendix A.1. Attitude
Appendix A.2. Velocity
Appendix A.3. Position
References
- Kalman, R.E.; Bucy, R.S. New Results in Linear Filtering and Prediction Theory. J. Basic Eng. 1961, 83, 95–108. [Google Scholar] [CrossRef]
- Holley, M.D. Apollo Experience Report–Guidance and Control Systems: Primary Guidance, Navigation, and Control System Development; Technical Report TN-D-8227; NASA: Washington, DC, USA, 1976. [Google Scholar]
- Wang, H.G.; Williams, T.C. Strategic Inertial Navigation Systems: High-Accuracy Inertially Stabilized Platforms for Hostile Environments. IEEE Control Syst. Mag. 2008, 28, 65–85. [Google Scholar] [CrossRef]
- Savage, P.G. Strapdown Analytics, Parts 1 and 2; Strapdown Associates, Inc.: Maple Plain, MN, USA, 2000. [Google Scholar]
- Edwards, A., Jr. The State of Strapdown Inertial Guidance and Navigation. Navigation 1971, 18, 386–401. [Google Scholar] [CrossRef]
- United Aircraft Corporation. A Study of the Critical Computational Problems Associated with Strapdown Inertial Navigation Systems; Technical Report CR-968; NASA: Washington, DC, USA, 1968. [Google Scholar]
- Platus, D.H. Missile and Spacecraft Coning Instabilities. J. Guid. Control Dyn. 1994, 17, 1011–1018. [Google Scholar] [CrossRef]
- Savage, P.G. A New Second-Order Solution for Strapped-Down Attitude Computation. In Proceedings of the AIAA/JACC Guidance and Control Conference, Seattle, WA, USA, 15–17 August 1966; pp. 60–71. [Google Scholar] [CrossRef]
- McKern, R.A. A Study of Transformation Algorithms for Use in a Digital Computer. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1968. [Google Scholar]
- Jordan, J.W. An Accurate Strapdown Direction Cosine Algorithm; Technical Report TN-D-5384; NASA: Washington, DC, USA, September 1969. [Google Scholar]
- Bortz, J.E. A New Mathematical Formulation for Strapdown Inertial Navigation. IEEE Trans. Aerosp. Electron. Syst. 1971, 7, 61–66. [Google Scholar] [CrossRef]
- Miller, R.B. A New Strapdown Attitude Algorithm. J. Guid. Control Dyn. 1983, 6, 287–291. [Google Scholar] [CrossRef]
- Savage, P.G. Strapdown Inertial Navigation Integration Algorithm Design Part 1: Attitude Algorithms. J. Guid. Control Dyn. 1998, 21, 19–28. [Google Scholar] [CrossRef]
- Savage, P.G. Strapdown Inertial Navigation Integration Algorithm Design Part 2: Velocity and Position Algorithms. J. Guid. Control Dyn. 1998, 21, 208–221. [Google Scholar] [CrossRef]
- Ignagni, M.B. Efficient Class of Optimized Coning Compensation Algorithms. J. Guid. Control Dyn. 1996, 19, 424–429. [Google Scholar] [CrossRef]
- Ignagni, M. Optimal Sculling and Coning Algorithms for Analog-sensor Systems. J.Guid. Control Dyn. 2012, 35, 851–860. [Google Scholar] [CrossRef]
- Park, C.G.; Kim, K.J.; Lee, J.G.; Chung, D. Formalized approach to obtaining optimal coefficients for coning algorithms. J. Guid. Control Dyn. 1999, 22, 165–168. [Google Scholar] [CrossRef]
- Ignani, M.B. Duality of Optimal Strapdown Sculling and Coning Compensation Algorithms. Navigation 1998, 45, 85–96. [Google Scholar] [CrossRef]
- Roscoe, K.M. Equivalency Between Strapdown Inertial Navigation Coning and Sculling Integrals/Algorithms. J. Guid. Control Dyn. 2001, 24, 201–205. [Google Scholar] [CrossRef]
- Zanetti, R.; D’Souza, C.N. Observability Analysis and Filter Design for the Orion Earth–Moon Attitude Filter. J. Guid. Control Dyn. 2016, 39, 201–213. [Google Scholar] [CrossRef] [Green Version]
- Zanetti, R.; Holt, G.; Gay, R.; D’Souza, C.; Sud, J.; Mamich, H.; Gillis, R. Design and Flight Performance of the Orion Prelaunch Navigation System. J. Guid. Control Dyn. 2017, 40, 2289–2300. [Google Scholar] [CrossRef]
- Ward, K.C.; Fritsch, G.S.; Helmuth, J.C.; DeMars, K.J. Design and Analysis of Descent-to-Landing Navigation Incorporating Terrain Effects. J. Spacecr. Rocket. 2020, 57, 261–277. [Google Scholar] [CrossRef]
- Zanetti, R.; Holt, G.; Gay, R.; D’Souza, C.; Sud, J.; Mamich, H.; Clark, F.D. Absolute Navigation Performance of the Orion Exploration Flight Test 1. J. Guid. Control Dyn. 2017, 40, 1106–1116. [Google Scholar] [CrossRef]
- Savage, P.G. Coning Algorithm Design by Explicit Frequency Shaping. J. Guid. Control Dyn. 2010, 33, 1123–1132. [Google Scholar] [CrossRef]
- Ignagni, M.B. Optimal Strapdown Attitude Integration Algorithms. J. Guid. Control Dyn. 1990, 13, 363–369. [Google Scholar] [CrossRef]
- Zanetti, R. Advanced Navigation Algorithms for Precision Landing. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2007. [Google Scholar]
- Golub, G.H.; Van Loan, C.F. Matrix Computations, 3rd ed.; The Johns Hopkins University Press: Baltimore, MD, USA, 1996. [Google Scholar]
- Schmidt, S.F. Application of State-Space Methods to Navigation Problems. In Advances in Control Systems; Elsevier: Amsterdam, The Netherlands, 1966; Volume 3, pp. 293–340. [Google Scholar]
- Zanetti, R.; Bishop, R.H. Kalman Filters with Uncompensated Biases. J. Guid. Control Dyn. 2012, 35, 327–330. [Google Scholar] [CrossRef]
- DeMars, K.J.; Ward, K.C. Modular framework for implementation and analysis of recursive filters with considered and neglected parameters. Navigation 2020, 67, 843–863. [Google Scholar] [CrossRef]
- Woodbury, D.; Junkins, J. On the consider Kalman filter. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Toronto, ON, Canada, 2–5 August 2010; p. 7752. [Google Scholar]
- Holt, G.; D’Souza, C. Orion Absolute Navigation System Progress and Challenges. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Minneapolis, MN, USA, 13–16 August 2012; p. 4995. [Google Scholar]
- Holt, G.N.; Zanetti, R.; D’Souza, C.N. Tuning and Robustness Analysis for the Orion Absolute Navigation System. In Proceedings of the AIAA Guidance, Navigation, and Control (GNC) Conference, Boston, MA, USA, 19–22 August 2013; p. 4876. [Google Scholar]
- Brouk, J.D.; DeMars, K.J. Uncertainty Analysis of a Generalized Coning Algorithm for Inertial Navigation. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Portland, ME, USA, 11–15 August 2019. [Google Scholar]
- Brouk, J.D. Propagation of Uncertainty Through Coning, Sculling, and Scrolling Corrections for Inertial Navigation. Master’s Thesis, Missouri University of Science and Technology, Rolla, MO, USA, 2019. [Google Scholar]
- Crassidis, J.L.; Junkins, J.L. Optimal Estimation of Dynamic Systems; Chapman and Hall/CRC: Boca Raton, FL, USA, 2004. [Google Scholar]
- Ward, K.C.; Helmuth, J.C.; Fritsch, G.S.; DeMars, K.J. Fusion of Multiple Terrain-Based Sensors for Descent-to-Landing Navigation. In Proceedings of the AIAA SciTech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar] [CrossRef]
- LN-200S Inertial Measurement Unit Datasheet. Available online: https://www.northropgrumman.com/wp-content/uploads/LN-200S-Inertial-Measurement-Unit-IMU-datasheet.pdf (accessed on 13 December 2021).
- Bar-Shalom, Y.; Birmiwal, K. Consistency and robustness of PDAF for Target Tracking in Cluttered Environments. Automatica 1983, 19, 431–437. [Google Scholar] [CrossRef]
- Li, X.R.; Zhao, Z.; Li, X.B. Evaluation of Estimation Algorithms–Credibility Tests. IEEE Trans. Aerosp. Electron. Syst. 2012, 42, 147–163. [Google Scholar] [CrossRef]
- Li, X.R.; Zhao, Z.; Jilkov, V.P. Practical Measures and Test for Credibility of an Estimator. In Proceedings of the Workshop on Estimation, Tracking, and Fusion—A Tribute to Yaakov Bar-Shalom, Monterey, CA, USA, 12–17 May 2001; pp. 481–495. [Google Scholar]



| Uncertainty (1) | |
|---|---|
| Position | 1000 m |
| Velocity | 0.1 |
| Attitude | 100 arcsec |
| Gyroscope | Accelerometer | |
|---|---|---|
| Frequency | 400 Hz | 400 Hz |
| Noise | 0.07 | 35 |
| Bias | 1 | 300 |
| Scale factor | 300 ppm | 100 ppm |
| Misalignment | 0.1 mrad | 0.1 mrad |
| Nonorthogonality | 0.1 mrad | 0.1 mrad |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brouk, J.D.; DeMars, K.J. Uncertainty Propagation for Inertial Navigation with Coning, Sculling, and Scrolling Corrections. Sensors 2021, 21, 8457. https://doi.org/10.3390/s21248457
Brouk JD, DeMars KJ. Uncertainty Propagation for Inertial Navigation with Coning, Sculling, and Scrolling Corrections. Sensors. 2021; 21(24):8457. https://doi.org/10.3390/s21248457
Chicago/Turabian StyleBrouk, James D., and Kyle J. DeMars. 2021. "Uncertainty Propagation for Inertial Navigation with Coning, Sculling, and Scrolling Corrections" Sensors 21, no. 24: 8457. https://doi.org/10.3390/s21248457
APA StyleBrouk, J. D., & DeMars, K. J. (2021). Uncertainty Propagation for Inertial Navigation with Coning, Sculling, and Scrolling Corrections. Sensors, 21(24), 8457. https://doi.org/10.3390/s21248457






