An Enhanced Indoor Positioning Technique Based on a Novel Received Signal Strength Indicator Distance Prediction and Correction Model
Abstract
:1. Introduction
- A new distance prediction and correction formula is introduced. The correction factors are based on RSSI log-distance distribution model. A large number of RSSI samples are collected and each RSSI sample is converted into its equivalent distance based on the logarithmic relationship between received signal strength and distance. The correction factors are driven from the RSSI-distances samples rather than the RSSI samples themselves. We proved that this approach has more measurement stability, which leads to higher positioning stability results with improved accuracy.
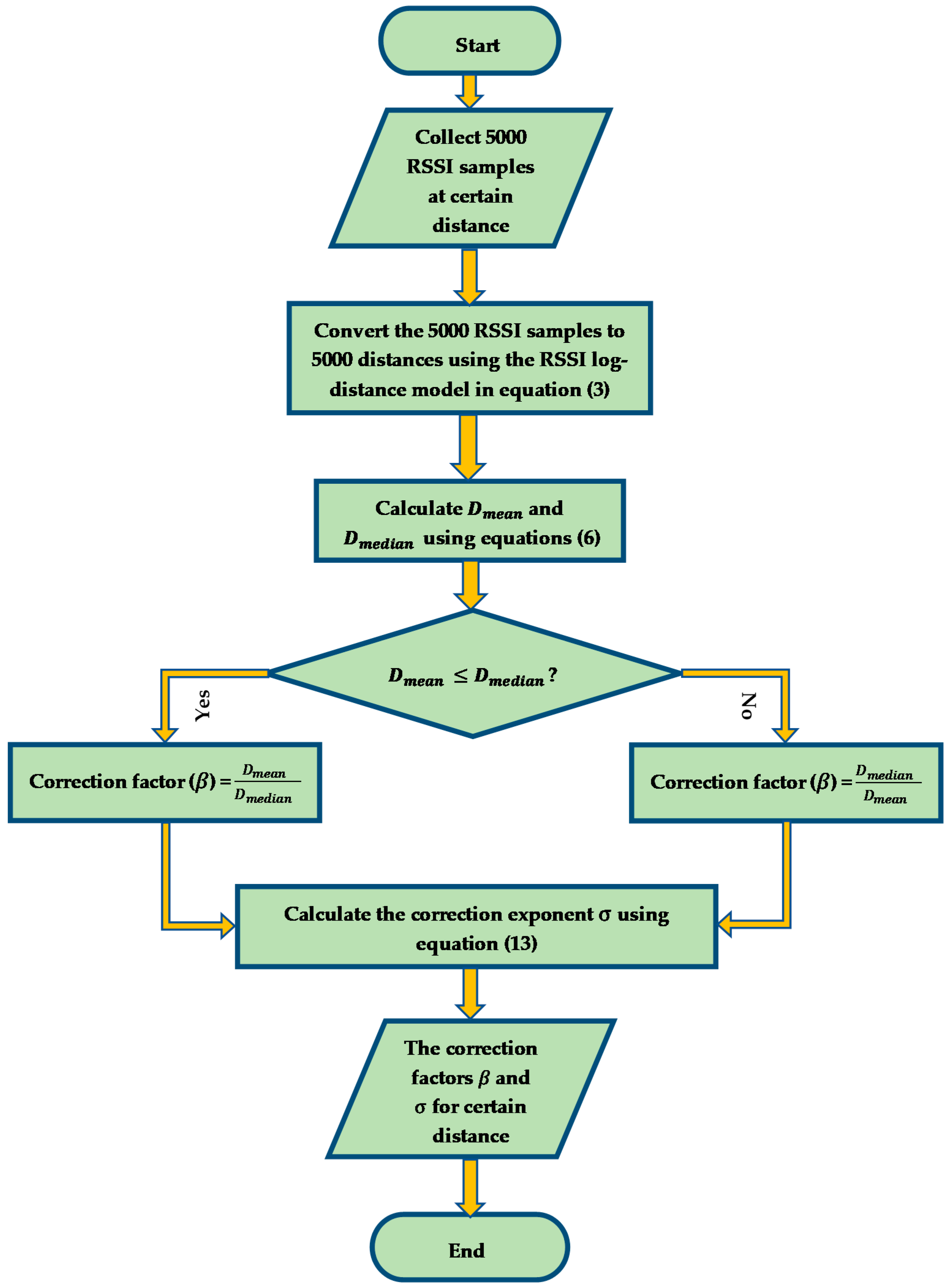
- A correction factor and a correction exponent for different distances are driven from the correction formula at each beacon. First, the correction factor for a certain distance is determined by calculating the mean and the median of RSSI samples equivalent distances. Then, the correction exponent is driven for each distance from the correction formula. Each beacon has its correction factors for certain distances according to the indoor environment area.
- At the unknown terminal, the calculated correction factors for each beacon are stored in a lookup table. By utilizing those factors on the unknown node, an enhanced centroid positioning algorithm is applied by correcting the estimated distance from the real-time RSSI samples and finally calculate the real coordinates of the unknown node. The algorithm does not consume much time to find the position of the unknown terminal. Thus, complexity is relatively lower. The experimental results of our method show improvement in both positioning accuracy and stability compared to other existed algorithms.
2. Methods
2.1. RSSI Distance Model
2.2. RSSI Distance Prediction and Correction Model
2.3. The Triangle Centroid Positioning Algorithm
2.4. The Weighted Centroid Positioning Algorithm
2.5. The Iterative Centroid Positioning Algorithm
- After receiving RSSI samples from the beacons, The blind (unknown node) chooses the highest three RSSI values and calculate their distances from log-distance model using Equation (3), recall them ; where is the calculated distance between the unknown node and one of the closest beacons to it using the log-distance distribution model.
- The distances between the three beacons and the unknown node are used in the triangle centroid positioning algorithm to calculate the initial coordinates of the unknown node. Then the calculated coordinates of the unknown node are used to find the distance between it and the three beacon nodes, recall them where is the calculated distance between the unknown node and one of the closest beacons to it using the triangle centroid positioning algorithm.
- To measure the deviation between the RSSI log-distance model calculated distances and the triangle centroid localization algorithm calculated distances, a distance deviation coefficient is introduced using Equation (18);
- The distance deviation coefficients are sorted to find the median value of them, recall it where is the median distance deviation coefficient, which is used to correct the log-distance model calculated distances.
- The corrected distances can be obtained by using Equation (19):
- The corrected distances are inserted into the triangle centroid localization algorithm iteratively starting from step 2 until a termination condition is satisfied. Since the iteration error no longer varies after 10 iterations, we set the number of iterations to be 10 in our comparative analysis.
2.6. The Proposed Enhanced Centroid Positioning Algorithm
3. Experiments
3.1. Device and Software
3.2. Experimental Sites
4. Results and Discussion
4.1. The Correction Factors of the Proposed RSSI Distance Prediction and Correction Model
4.2. Predicted Distances Accuracy
4.3. Localization Accuracy
4.4. Positioning Stability
4.5. The Effect of Different RSSI Samples’ Number on the Localization Accuracy
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, T.; Xia, H.; Liu, S.; Qiao, Y. Probability-based indoor positioning algorithm using ibeacons. Sensors 2019, 19, 5226. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Paul, A.K.; Sato, T. Localization in wireless sensor networks: A survey on algorithms, measurement techniques, applications and challenges. J. Sens. Actuator Netw. 2017, 6, 24. [Google Scholar] [CrossRef] [Green Version]
- Ren, A.; Zhou, F.; Rahman, A.; Wang, X.; Zhao, N.; Yang, X. A study of indoor positioning based on UWB base-station configurations. In Proceedings of the 2017 IEEE 2nd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 25–26 March 2017; pp. 1939–1943. [Google Scholar]
- Davidson, P.; Piché, R. A survey of selected indoor positioning methods for smartphones. IEEE Commun. Surv. Tutor. 2017, 19, 1347–1370. [Google Scholar] [CrossRef]
- Tian, Y.; Shigaki, D.; Wang, W.; Ahn, C.J. A weighted least-squares method using received signal strength measurements for WLAN indoor positioning system. In Proceedings of the 2017 20th International Symposium on Wireless Personal Multimedia Communications (WPMC), Bali, Indonesia, 17–20 December 2017; pp. 310–314. [Google Scholar]
- Saab, S.S.; Nakad, Z.S. A standalone RFID indoor positioning system using passive tags. IEEE Trans. Ind. Electron. 2011, 58, 1961–1970. [Google Scholar] [CrossRef]
- Wu, C.; Mu, Q.; Zhang, Z.; Jin, Y.; Wang, Z.; Shi, G. Indoor positioning system based on inertial MEMS sensors: Design and realization. In Proceedings of the 2016 IEEE International Conference on Cyber Technology in Automation, Control, and Intelligent Systems (CYBER), Chengdu, China, 19–22 June 2016; pp. 370–375. [Google Scholar]
- Pasku, V.; Angelis, A.D.; Dionigi, M.; Angelis, G.D.; Moschitta, A.; Carbone, P. A positioning system based on low-frequency magnetic fields. IEEE Trans. Ind. Electron. 2016, 63, 2457–2468. [Google Scholar] [CrossRef]
- Qi, J.; Liu, G.P. A robust high-accuracy ultrasound indoor positioning system based on a wireless sensor network. Sensors 2017, 17, 2554. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Jun, H. Vision-based location positioning using augmented reality for indoor navigation. IEEE Trans. Consum. Electron. 2008, 54, 954–962. [Google Scholar] [CrossRef]
- Raharijaona, T.; Mawonou, R.; Nguyen, T.V.; Colonnier, F.; Boyron, M.; Diperi, J.; Viollet, S. Local positioning system using flickering infrared LEDs. Sensors 2017, 17, 2518. [Google Scholar] [CrossRef] [Green Version]
- Newman, N. Apple ibeacon technology briefing. J. Direct Data Digit. Mark. Pract. 2014, 15, 222–225. [Google Scholar] [CrossRef] [Green Version]
- Sahu, P.K.; Wu, E.H.-K.; Sahoo, J. DuRT: Dual RSSI trend based localization for wireless sensor networks. IEEE Sens. J. 2013, 13, 3115–3123. [Google Scholar] [CrossRef]
- Han, D.; Yu, Y.; Li, K.-C.; de Mello, R.F. Enhancing the sensor node localization algorithm based on improved DV-hop and DE algorithms in wireless sensor networks. Sensors 2020, 20, 343. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hou, Y.; Yang, X.; Abbasi, Q.H. Efficient AoA-based wireless indoor localization for hospital outpatients using mobile devices. Sensors 2018, 18, 3698. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Y.; Deng, Z.; Gao, Y. Angle of arrival passive location algorithm based on proximal policy optimization. Electronics 2019, 8, 1558. [Google Scholar] [CrossRef] [Green Version]
- Shin, D.-H.; Sung, T.-K. Comparisons of error characteristics between TOA and TDOA positioning. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 307–311. [Google Scholar]
- Gioia, C.; Sermi, F.; Tarchi, D. Multi-network asynchronous TDOA algorithm test in a simulated maritime scenario. Sensors 2020, 20, 1842. [Google Scholar] [CrossRef] [Green Version]
- Yaghoubi, F.; Abbasfar, A.A.; Maham, B. Energy-efficient RSSI-based localization for wireless sensor networks. IEEE Commun. Lett. 2014, 18, 973–976. [Google Scholar] [CrossRef]
- Li, J.Z.; Ren, P.; Shi, L.L.; Zhang, S.X. Optimisation of moving target’s low-power and high-precision monitoring with RSSI based on static and dynamic clustering. Int. J. Embed. Syst. 2015, 7, 334–344. [Google Scholar]
- Tomic, S.; Beko, M.; Dinis, R. RSS-based localization in wireless sensor networks using convex relaxation: Noncooperative and cooperative schemes. IEEE Trans. Veh. Technol. 2015, 64, 2037–2050. [Google Scholar] [CrossRef] [Green Version]
- Shi, Y.; Shi, W.; Liu, X.; Xiao, X. An RSSI classification and tracing algorithm to improve trilateration-based positioning. Sensors 2020, 20, 4244. [Google Scholar] [CrossRef]
- Bullmann, M.; Fetzer, T.; Ebner, F.; Ebner, M.; Deinzer, F.; Grzegorzek, M. Comparison of 2.4 GHz WiFi FTM- and RSSI-based indoor positioning methods in realistic scenarios. Sensors 2020, 20, 4515. [Google Scholar] [CrossRef]
- Zhang, D.; Yin, H. Study on centroid localization algorithm based on the cellular distribution of anchor nodes. In Proceedings of the 2013 Joint International Conference on Pervasive Computing and the Networked World (ICPCA/SWS), Vina del Mar, Chile, 5–7 December 2013; pp. 783–789. [Google Scholar]
- Zhang, C.W.; Zhao, X. The wireless sensor network (WSN) triangle centroid localization algorithm based on RSSI. MATEC Web Conf. 2016, 63, 05008. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Chen, D. An improved RSSI-based centroid localization algorithm in wireless sensor networks. In Proceedings of the 2011 IEEE International Conference on Computer Science and Service System (CSSS), Nanjing, China, 27–29 June 2011; pp. 3008–3011. [Google Scholar]
- Bai, Y.; Li, C.M.; Xue, Y. A centroid localization algorithm for wireless sensor networks based on RSSI. Appl. Mech. Mater. 2013, 303–306, 197–200. [Google Scholar] [CrossRef]
- Xie, S.; Hu, Y.; Wang, Y. Weighted centroid localization for wireless sensor networks. In Proceedings of the 2014 IEEE International Conference on Consumer Electronics, Shenzhen, China, 9–13 April 2014; pp. 1–4. [Google Scholar]
- Liu, Q.; Xu, X.; Zhang, T. Positioning method of weighted centroid aided inertial measurement. Preprints 2018, 2018030124. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.-M.; Zheng, Y. The study of the weighted centroid localization algorithm based on RSSI. In Proceedings of the 2014 IEEE International Conference on Wireless Communication and Sensor Network, Wuhan, China, 13–14 December 2014; pp. 276–279. [Google Scholar]
- Sharma, N.; Chawla, G.; Khurana, M. Weighted centroid range free localization algorithm based on IOT. Int. J. Comput. Appl. 2013, 83, 27–30. [Google Scholar] [CrossRef]
- Lee, S.; Kim, J.; Moon, N. Random forest and WiFi fingerprint-based indoor location recognition system using smart watch. Hum. Centric Comput. Inform. Sci. 2019, 9, 6. [Google Scholar] [CrossRef]
- Orujov, F.; Maskeliūnas, R.; Damaševičius, R.; Wei, W.; Li, Y. Smartphone based intelligent indoor positioning using fuzzy logic. Future Gener. Comput. Syst. 2018, 89, 335–348. [Google Scholar] [CrossRef]
- AL-Madani, B.; Orujov, F.; Maskeliūnas, R.; Damaševičius, R.; Venčkauskas, A. Fuzzy logic type-2 based wireless indoor localization system for navigation of visually impaired people in buildings. Sensors 2019, 19, 2114. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Trogh, J.; Plets, D.; Tanghe, E.; Hoebeke, J.; Poorter, E.D.; Joseph, W. CRLB-based positioning performance of indoor hybrid AoA/RSS/ToF localization. In Proceedings of the 2019 IEEE International Conference on Indoor Positioning and Indoor Navigation (IPIN), Pisa, Italy, 30 September–3 October 2019; pp. 1–6. [Google Scholar]
- Gang, H.-S.; Pyun, J.-Y. A smartphone indoor positioning system using hybrid localization technology. Energies 2019, 12, 3702. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Wang, S.; Ouyang, M.; Xuan, Y.; Li, K.-C. Iterative positioning algorithm for indoor node based on distance correction in WSNs. Sensors 2019, 19, 4871. [Google Scholar] [CrossRef] [Green Version]
- Yoshida, S. Propagation measurements and models for wireless communications channels. IEEE Commun. Mag. 1995, 33, 42–49. [Google Scholar]
- Canton Paterna, V.; Calveras Auge, A.; Paradells Aspas, J.; Perez Bullones, M.A. A bluetooth low energy indoor positioning system with channel diversity, weighted trilateration and kalman filtering. Sensors 2017, 17, 2927. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jung, S.; Lee, C.-O.; Han, D. Wi-Fi fingerprint-based approaches following log-distance path loss model for indoor positioning. In Proceedings of the 2011 IEEE MTT-S International Microwave Workshop Series on Intelligent Radio for Future Personal Terminals, Daejeon, Korea, 24–25 August 2011; pp. 1–2. [Google Scholar]
- Google Play. Available online: https://play.google.com/store/apps/details?id=net.alea.beaconsimulator (accessed on 27 August 2020).
- Liu, G.-Y.; Chang, T.-Y.; Chiang, Y.-C.; Lin, P.-C.; Mar, J. Path loss measurements of indoor LTE system for the internet of things. Appl. Sci. 2017, 7, 537. [Google Scholar] [CrossRef] [Green Version]
- Google Play. Available online: https://play.google.com/store/apps/details?id=com.bridou_n.beaconscanner (accessed on 15 January 2021).
- Android Beacon Library. Available online: https://altbeacon.github.io/android-beacon-library/ (accessed on 28 August 2020).
- ISO. Information Technology–Real Time Locating Systems–Test. and Evaluation of Localization and Tracking Systems (ISO/IEC 18305:2016); International Organization for Standardization: Geneva, Switzerland, 2016; pp. 1–76.












| Real Distance (m) | Standard Deviation | |
|---|---|---|
| RSSI Samples (dBm) | Distance Samples (m) | |
| 1 | 3.32 | 0.547 |
| 2 | 2.642 | 0.792 |
| 3 | 2.658 | 1.258 |
| 4 | 2.571 | 1.171 |
| 5 | 2.576 | 1.802 |
| 6 | 3.017 | 2.281 |
| Real Distance (m) | Correction Exponent (σ) | Correction Factor (β) | Mean Distance in Meters (Dmean) |
|---|---|---|---|
| 1 | 7.114 | 0.917 | 2.014 |
| 2 | 21.993 | 0.97 | 3.863 |
| 3 | 19.561 | 0.964 | 6.085 |
| 4 | 15.285 | 0.993 | 5.519 |
| 5 | 11.109 | 0.959 | 8.281 |
| 6 | 130.354 | 0.996 | 10.039 |
| Real Distance (m) | Correction Exponent (σ) | Correction Factor (β) | Mean Distance in Meters (Dmean) |
|---|---|---|---|
| 1 | 6.568 | 0.91 | 1.847 |
| 2 | 26.654 | 0.975 | 3.883 |
| 3 | 28.65 | 0.979 | 5.411 |
| 4 | 11.913 | 0.993 | 0.965 |
| 5 | 12.282 | 0.963 | 7.943 |
| 6 | 78.746 | 0.993 | 9.999 |
| Experimental Site | Localization Accuracy Percentage Range | |||
|---|---|---|---|---|
| Centroid | Weighted Centroid | Iterative Centroid | Proposed Enhanced Centroid | |
| Office Room | 77.46–81.36% | 81.042–83.74% | 87.86–89.14% | 94.19–95.707% |
| Corridor | 82.7–87.15% | 85.95–92.44% | 90.36–93.78% | 94.57–95.776% |
| Test Point Number | Sample Standard Deviation (SSD) in Meters | |||
|---|---|---|---|---|
| Centroid | Weighted Centroid | Iterative Centroid | Proposed Enhanced Centroid | |
| 1 | 0.12 | 0.088 | 0.058 | 0.031 |
| 2 | 0.176 | 0.046 | 0.042 | 0.05 |
| 3 | 0.157 | 0.229 | 0.181 | 0.153 |
| 4 | 0.137 | 0.143 | 0.066 | 0.044 |
| 5 | 0.113 | 0.115 | 0.066 | 0.041 |
| Average SSD | 0.141 | 0.178 | 0.184 | 0.086 |
| Test Point Number | Sample Standard Deviation (SSD) in Meters | |||
|---|---|---|---|---|
| Centroid | Weighted Centroid | Iterative Centroid | Proposed Enhanced Centroid | |
| 1 | 0.117 | 0.088 | 0.058 | 0.032 |
| 2 | 0.043 | 0.046 | 0.042 | 0.05 |
| 3 | 0.365 | 0.229 | 0.181 | 0.153 |
| 4 | 0.147 | 0.143 | 0.066 | 0.044 |
| 5 | 0.064 | 0.115 | 0.066 | 0.041 |
| Average SSD | 0.147 | 0.124 | 0.083 | 0.064 |
| RSSI Samples’ Number | Localization Error (m) | |||||
|---|---|---|---|---|---|---|
| Test-Point 1 | Test-Point 2 | Test-Point 3 | Test-Point 4 | Test-Point 5 | Overall ALE | |
| 100 RSSI | 0.311 | 0.286 | 0.223 | 0.432 | 0.312 | 0.313 |
| 90 RSSI | 0.331 | 0.29 | 0.203 | 0.425 | 0.322 | 0.314 |
| 80 RSSI | 0.305 | 0.303 | 0.217 | 0.434 | 0.326 | 0.317 |
| 70 RSSI | 0.312 | 0.307 | 0.22 | 0.438 | 0.316 | 0.319 |
| 60 RSSI | 0.329 | 0.32 | 0.235 | 0.422 | 0.33 | 0.327 |
| 50 RSSI | 0.352 | 0.32 | 0.233 | 0.442 | 0.341 | 0.337 |
| RSSI Samples’ Number | Localization Error (m) | |||||
|---|---|---|---|---|---|---|
| Test-Point 1 | Test-Point 2 | Test-Point 3 | Test-Point 4 | Test-Point 5 | Overall ALE | |
| 100 RSSI | 0.411 | 0.445 | 0.144 | 0.354 | 0.278 | 0.326 |
| 90 RSSI | 0.411 | 0.455 | 0.156 | 0.361 | 0.286 | 0.334 |
| 80 RSSI | 0.417 | 0.455 | 0.159 | 0.368 | 0.291 | 0.338 |
| 70 RSSI | 0.418 | 0.467 | 0.165 | 0.381 | 0.288 | 0.344 |
| 60 RSSI | 0.415 | 0.465 | 0.176 | 0.382 | 0.293 | 0.346 |
| 50 RSSI | 0.423 | 0.468 | 0.193 | 0.386 | 0.3 | 0.354 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nagah Amr, M.; ELAttar, H.M.; Abd El Azeem, M.H.; El Badawy, H. An Enhanced Indoor Positioning Technique Based on a Novel Received Signal Strength Indicator Distance Prediction and Correction Model. Sensors 2021, 21, 719. https://doi.org/10.3390/s21030719
Nagah Amr M, ELAttar HM, Abd El Azeem MH, El Badawy H. An Enhanced Indoor Positioning Technique Based on a Novel Received Signal Strength Indicator Distance Prediction and Correction Model. Sensors. 2021; 21(3):719. https://doi.org/10.3390/s21030719
Chicago/Turabian StyleNagah Amr, Mohammed, Hussein M. ELAttar, Mohamed H. Abd El Azeem, and Hesham El Badawy. 2021. "An Enhanced Indoor Positioning Technique Based on a Novel Received Signal Strength Indicator Distance Prediction and Correction Model" Sensors 21, no. 3: 719. https://doi.org/10.3390/s21030719
APA StyleNagah Amr, M., ELAttar, H. M., Abd El Azeem, M. H., & El Badawy, H. (2021). An Enhanced Indoor Positioning Technique Based on a Novel Received Signal Strength Indicator Distance Prediction and Correction Model. Sensors, 21(3), 719. https://doi.org/10.3390/s21030719








