Train-Induced Vibration Monitoring of Track Slab under Long-Term Temperature Load Using Fiber-Optic Accelerometers
Abstract
:1. Introduction
2. Methods
2.1. Train-Induced Vibration Signal Acquisition System
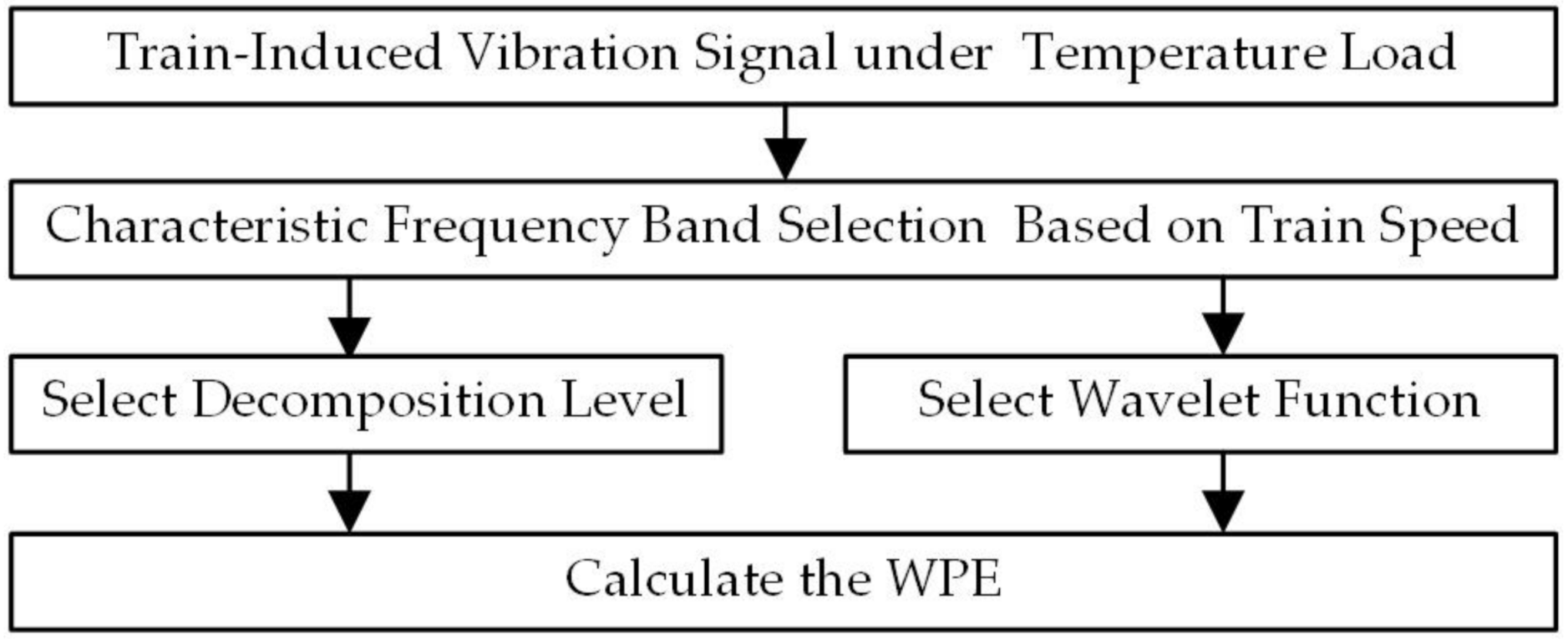
2.2. Vibration Response Analysis Based on WPE
3. Field Test
4. Results and Discussion
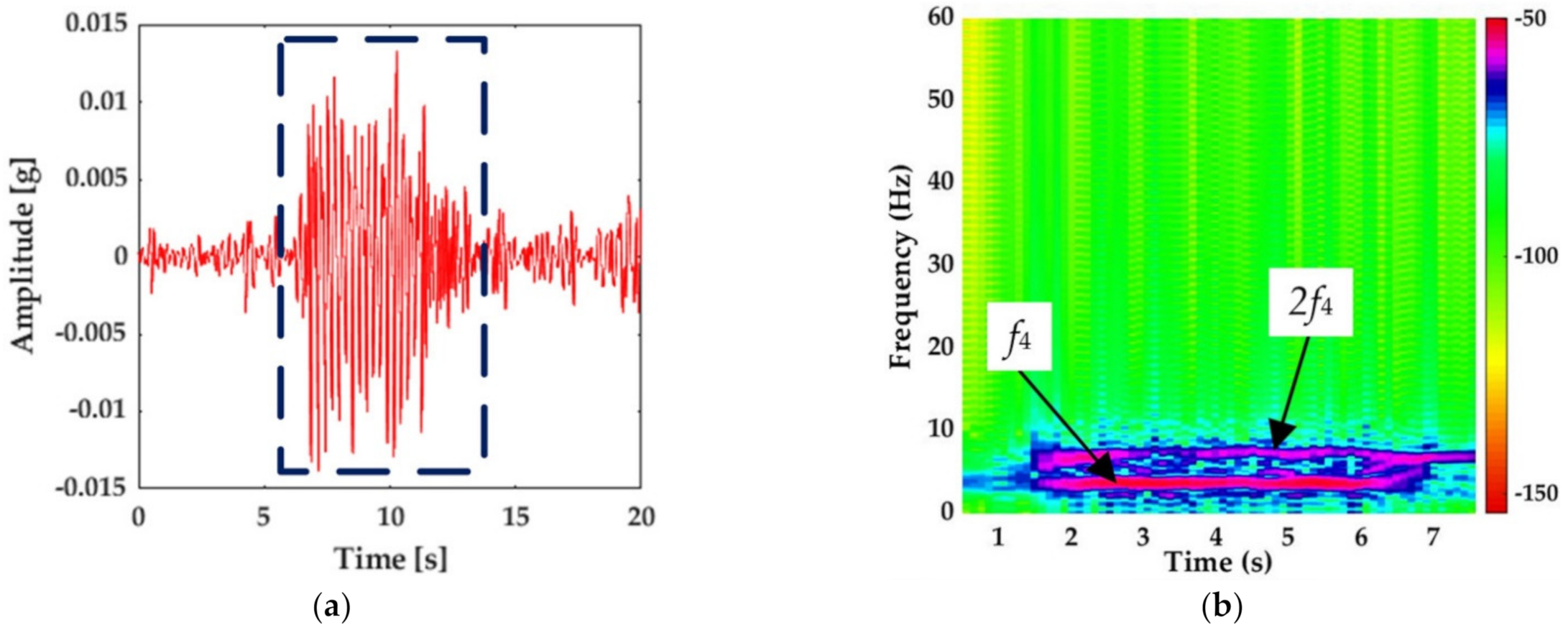
4.1. Selection of Feature Frequency Band
- The significant frequency components in the spectra were spaced evenly, about 3.44 Hz, close to the integral multiple of the characteristic frequency (f4 = v/L4) induced by the center distance of two neighboring cars (25 m) of the CRH380AL train at the speed of 285 km/h;
- The characteristic frequency f2 caused by the center distance of the adjacent bogies between the forward car and the backward L2 (7.5 m) was about 10.3 Hz, consistent with the dominant frequency of three-fold of f4;
- The first dominant frequency was about 34.5 Hz, consistent with the characteristic frequency f1 caused by the wheelbase (2.5 m) and 10-fold of f4;
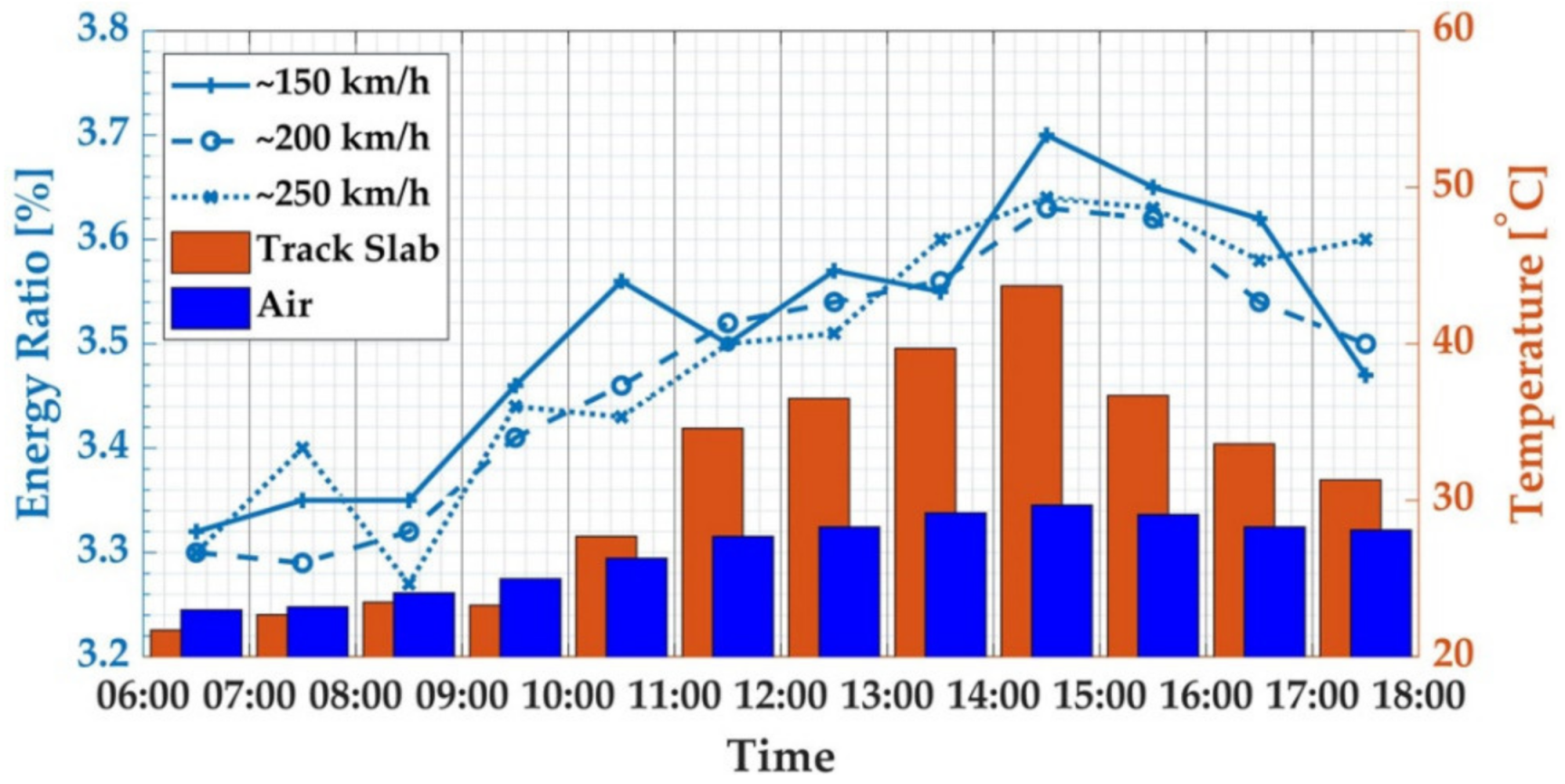
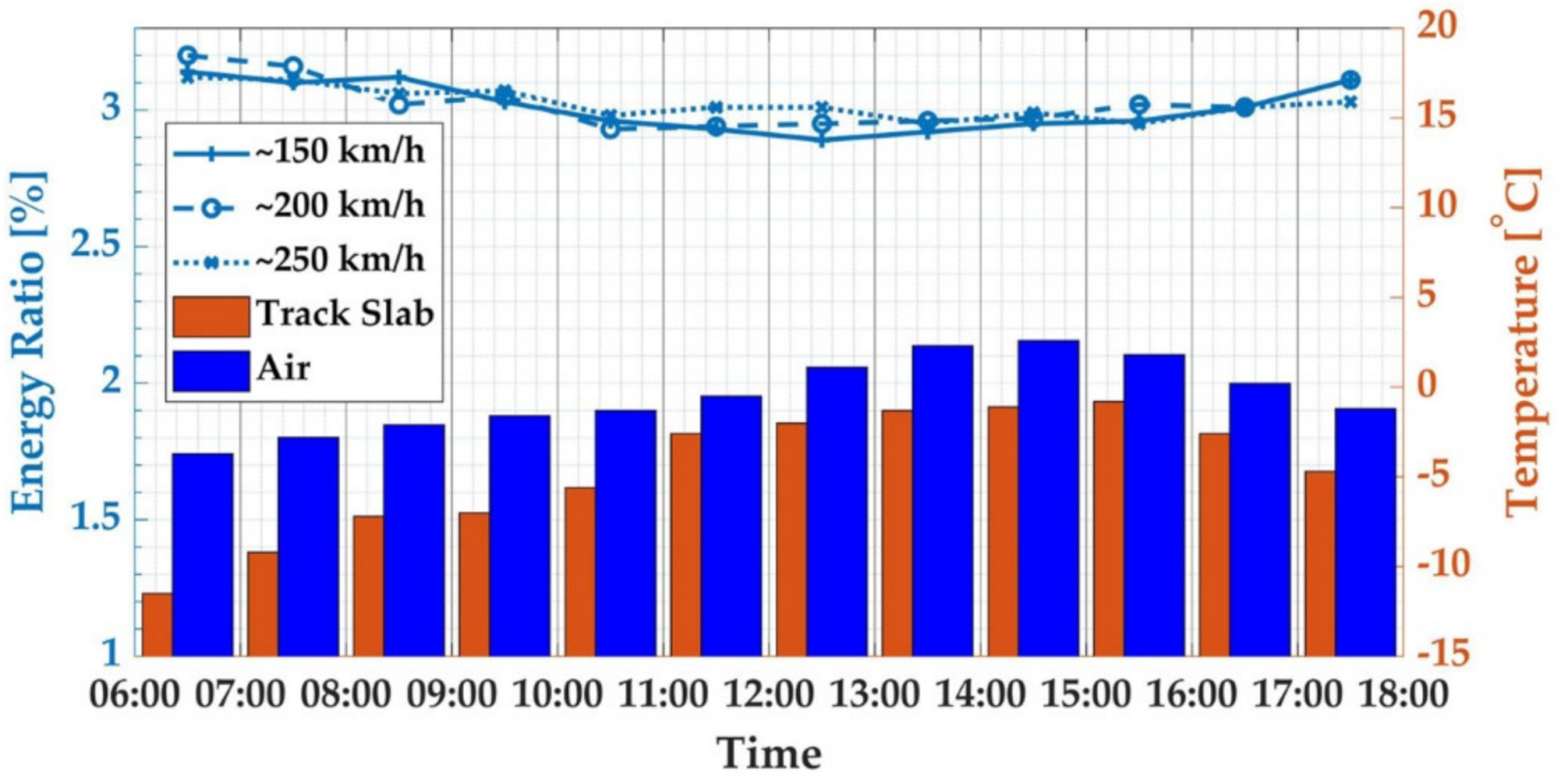
4.2. WPT Energy of Vibration Response with Temperature-Induced Deformation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, J.; Ping, W.; An, B.; Ma, X.; Chen, R. Damage detection of ballastless railway tracks by the impact-echo method. Proc. Inst. Civ. Eng. Transp. 2017, 171, 1–9. [Google Scholar] [CrossRef]
- Xu, Q.; Fan, H.; Li, B. Influence of temperature gradient load of slab on dynamic characteristic of train-slab track on subgrade system. J. Railw. Sci. Eng. 2013, 10, 1–6. [Google Scholar]
- Ling, X.Z.; Chen, S.J.; Zhu, Z.Y.; Zhang, F.; Wang, L.N.; Zou, Z.Y. Field monitoring on the train-induced vibration response of track structure in the Beiluhe permafrost region along Qinghai–Tibet railway in China. Cold Reg. Sci. Technol. 2010, 60, 75–83. [Google Scholar] [CrossRef]
- Xi, S.L.; Xiong, Y.L.; Shan, A.; Zhou, J.Z. Analysis of Ballastless Track Plate Vertical Deformation Characteristics under Thermal Stress. Urban Mass Transit 2020, 23, 54–57. [Google Scholar]
- Guo, C.; Lu, Z.R.; Lv, F.; Min, S.X. Research on the Temperature Features of CRTSⅡ Ballastless Track Slab in Severe Cold Region. J. Railw. Eng. Soc. 2016, 33, 29–34. [Google Scholar]
- Xu, Y.D.; Yan, D.B.; Zhu, W.J.; Zhou, Y. Study on the mechanical performance and interface damage of CRTS II slab track with debonding repairment. Constr. Build. Mater. 2020, 257, 1–16. [Google Scholar] [CrossRef]
- Shi, H.; Yu, Z.J.; Shi, H.M.; Zhu, L.Q. Recognition algorithm for the disengagement of cement asphalt mortar based on dynamic responses of vehicles. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2019, 233, 270–282. [Google Scholar] [CrossRef]
- Shi, H.; Zhu, L.Q.; Shi, H.M.; Yu, Z.J. Estimation of Cement Asphalt Mortar Disengagement Degree Using Vehicle Dynamic Response. Shock Vib. 2019, 2019, 1–11. [Google Scholar] [CrossRef]
- Liu, H.; Lu, H.; He, Y.; Li, Z. Iop Neural Network Based Temperature Field Mapping Model for CRTS II Type Ballastless Track. In Proceedings of the 2018 2nd International Conference on Artificial Intelligence Applications and Technologies, Shanghai, China, 8–10 August 2018; Volume 435. [Google Scholar]
- Song, X.; Zhao, C.; Zhu, X. Temperature-induced deformation of CRTS Ⅱ slab track and its effect on track dynamical properties. Sci. China Technol. Sci. 2014, 57, 1917–1924. [Google Scholar] [CrossRef]
- Shao, P.; Li, H.; Wu, S.; Wang, T.; Liu, Z.; Li, H. Measurement and Research on Temperature Warping of CRTS I Track Slab and Crack between Track Slab and Cement Asphalt Mortar Cushion. China Railw. Sci. 2013, 2, 18–22. [Google Scholar]
- Zhao, J.; Xie, K.Z.; Zhao, W.G.Z.; Zhang, X.D. Identification of void in mortar layer of CRTS II slab ballastless track based on strain mode. J. Beijing Jiaotong Univ. 2020, 44, 57–64. [Google Scholar]
- Zhang, X.; Liang, Q. A study on crack and motor-void identification of ballastless track slab using strain modal. J. Vib. Shock 2020, 39, 179–184. [Google Scholar]
- Chen, J.; Zhou, Y.; Zhou, G.; Fu, B. Experimental Vibration Investigation on High-Speed Railway Ballastless Track-Subgrade Structure. Int. J. Struct. Stab. Dyn. 2020, 20, 1–25. [Google Scholar] [CrossRef]
- Wang, P.; Xu, H.; Chen, R. Effect of Cement Asphalt Mortar Debonding on Dynamic Properties of CRTS II Slab Ballastless Track. Adv. Mater. Sci. Eng. 2014, 2014, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Rao, P.S.; Mahendra, N.V.D. Vibration Based Damage Identification Method for Cantilever Beam Using Artificial Neural Network; Springer: Cham, Switzerland, 2017; pp. 85–93. [Google Scholar]
- Peeters, B.; Maeck, J.; Roeck, G.D. Vibration-based damage detection in civil engineering: Excitation sources and temperature effects. Smart Mater. Struct. 2001, 10, 518–527. [Google Scholar] [CrossRef]
- Wang, J. Study on the spectrum characteristics of CRTS II type ballastless track on subgrade under High-Speed condition. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2017. [Google Scholar]
- Zhu, S.; Cai, C. Interface damage and its effect on vibrations of slab track under temperature and vehicle dynamic loads. Int. J. Non Linear Mech. 2014, 58, 222–232. [Google Scholar] [CrossRef]
- Yüksel, K.; Kinet, D.; Moeyaert, V.; Kouroussis, G.; Caucheteur, C. Railway monitoring system using optical fiber grating accelerometers. Smart Mater. Struct. 2018, 27, 1–9. [Google Scholar] [CrossRef]
- Jiang, D.S.; Zhang, W.T.; Li, F. All-Metal Optical Fiber Accelerometer With Low Transverse Sensitivity for Seismic Monitoring. IEEE Sens. J. 2013, 13, 4556–4560. [Google Scholar] [CrossRef]
- Bian, X.; Jiang, H.; Chang, C.; Hu, J.; Chen, Y. Track and ground vibrations generated by high-speed train running on ballastless railway with excitation of vertical track irregularities. Soil Dyn. Earthq. Eng. 2015, 76, 29–43. [Google Scholar] [CrossRef]
- Zhu, S.; Cai, C. Analysis on Vertical Vibration Characteristics of Double-block Ballastless Roadbed with Cracks. J. China Railw. Soc. 2012, 34, 82–86. [Google Scholar]
- Huang, W.; Zhang, W.; Huang, J.; Li, F. Demonstration of multi-channel fiber optic interrogator based on time-division locking technique in subway intrusion detection. Opt. Express 2020, 28, 11472–11481. [Google Scholar] [CrossRef] [PubMed]
- Zhai, W.; Wei, K.; Song, X.; Shao, M. Experimental investigation into ground vibrations induced by very high speed trains on a non-ballasted track. Soil Dyn. Earthq. Eng. 2015, 72, 24–36. [Google Scholar] [CrossRef] [Green Version]
- JinChen, Y. Research on Crack Generation Mechanism and Repair Scheme of II-type Plate Ballastless Track Structure. J. Shijiangzhuang Tiedao Univ. 2012, 25, 54–58. [Google Scholar]
- Yen, G.G.; Lin, K. Wavelet packet feature extraction for vibration monitoring. IEEE Trans. Ind. Electron. 2000, 47, 650–667. [Google Scholar] [CrossRef] [Green Version]
- Daubechies, I. Ten Lectures on Wavelets. Comput. Phys. 1998, 6, 1671. [Google Scholar]
- Gómez, M.J.; Castejón, C.; Corral, E.; García-Prada, J.C. Railway Axle Condition Monitoring Technique Based on Wavelet Packet Transform Features and Support Vector Machines. Sensors 2020, 20, 3575. [Google Scholar] [CrossRef]
- Goswami, J.; Chan, A. Fundamentals of Wavelets: Theory, Algorithms, and Applications, 2nd ed.; Wiley Publishing: Hoboken, NJ, USA, 2011; p. 240. [Google Scholar]
- Ju, S.H.; Lin, H.T.; Huang, J.Y. Dominant frequencies of train-induced vibrations. J. Sound Vibr. 2009, 319, 247–259. [Google Scholar] [CrossRef]
- Auersch, L. Ground vibration due to railway traffic—The calculation of the effects of moving static loads and their experimental verification. J. Sound Vibr. 2006, 293, 599–610. [Google Scholar] [CrossRef]
- Kouroussis, G.; Connolly, D.P.; Verlinden, O. Railway-induced ground vibrations—A review of vehicle effects. Int. J. Rail Transp. 2014, 2, 69–110. [Google Scholar] [CrossRef] [Green Version]
- Gómez, M.J.; Castejón, C.; García-Prada, J.C. Crack detection in rotating shafts based on 3× energy: Analytical and experimental analyses. Mech. Mach. Theory 2016, 96, 94–106. [Google Scholar] [CrossRef]
- Gómez, M.J.; Castejón, C.; García-Prada, J.C. New stopping criteria for crack detection during fatigue tests of railway axles. Eng. Fail. Anal. 2015, 56, 530–537. [Google Scholar] [CrossRef]
- Wang, J.; You, R.; Wang, M.; Jiang, C. Research on the Slab Temperature Warping of the Unit Slab Track System. China Railw. Sci. 2010, 31, 9–14. [Google Scholar]
- Zhu, X. Analysis of the Temperature Effect of CRTS II Track Slab and Its Influence on Train Operation Safety. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2012. [Google Scholar]




| Parameter | Value |
|---|---|
| Wavelet function | Daubechies 6 |
| Sampling frequency (Hz) | 1000 |
| Decomposition level l | 6 |
| Number of packets 2l | 64 |
| Frequency resolution of each packet (Hz) | 7.82 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Huang, W.; Zhang, W.; Li, F.; Du, Y. Train-Induced Vibration Monitoring of Track Slab under Long-Term Temperature Load Using Fiber-Optic Accelerometers. Sensors 2021, 21, 787. https://doi.org/10.3390/s21030787
Zhang J, Huang W, Zhang W, Li F, Du Y. Train-Induced Vibration Monitoring of Track Slab under Long-Term Temperature Load Using Fiber-Optic Accelerometers. Sensors. 2021; 21(3):787. https://doi.org/10.3390/s21030787
Chicago/Turabian StyleZhang, Jianxiang, Wenzhu Huang, Wentao Zhang, Fang Li, and Yanliang Du. 2021. "Train-Induced Vibration Monitoring of Track Slab under Long-Term Temperature Load Using Fiber-Optic Accelerometers" Sensors 21, no. 3: 787. https://doi.org/10.3390/s21030787
APA StyleZhang, J., Huang, W., Zhang, W., Li, F., & Du, Y. (2021). Train-Induced Vibration Monitoring of Track Slab under Long-Term Temperature Load Using Fiber-Optic Accelerometers. Sensors, 21(3), 787. https://doi.org/10.3390/s21030787








