3D Multiple-Antenna Channel Modeling and Propagation Characteristics Analysis for Mobile Internet of Things
Abstract
:1. Introduction
2. Proposed 3D Channel Model
2.1. Description of Theoretical Model
2.1.1. Line-of-Sight Component
2.1.2. Single-Bounced Component
2.1.3. Double-Bounced Component
2.2. Distribution of Effective Scatterers
3. Channel Statistical Properties and Simulation Model
3.1. Sparial–Temporal Correlation Function
3.1.1. Line-of-Sight Component
3.1.2. Single-Bounced Component
3.1.3. Double-Bounced Component
3.2. Simulation Model
4. Numerical Results and Analysis
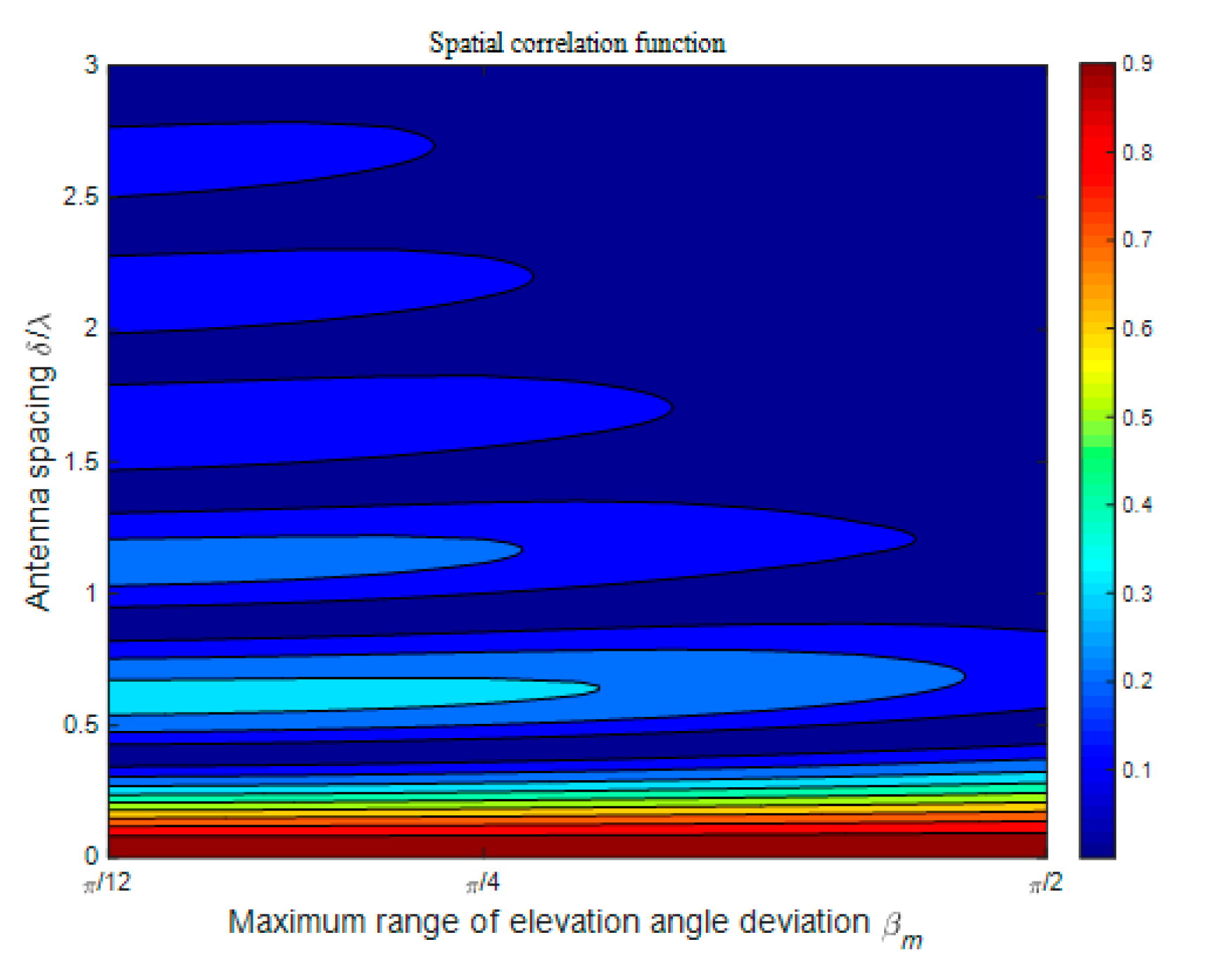
4.1. Spatial Correlation
4.1.1. Isotropic Scattering Scenarios
4.1.2. Non-Isotropic Scattering Scenarios
4.2. Spatial–Temporal Correlation
4.3. Simulation Model
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Al-Fuqaha, A.; Guizani, M.; Mohammadi, M.; Aledhari, M.; Ayyash, M. Internet of Things: A survey on enabling technologies, protocols, and applications. IEEE Commun. Surv. Tutor. 2015, 17, 2347–2376. [Google Scholar] [CrossRef]
- Da Xu, L.; He, W.; Li, S. Internet of Things in industries: A survey. IEEE Trans. Ind. Inform. 2014, 10, 2233–2243. [Google Scholar]
- Guerrero-Ibanez, J.A.; Zeadally, S.; Contreras-Castillo, J. Integration challenges of intelligent transportation systems with connected vehicle, cloud computing, and Internet of Things technologies. IEEE Wirel. Commun. 2015, 22, 122–128. [Google Scholar]
- Islam, S.M.R.; Kwak, D.; Humaun Kabir, M.; Hossain, M.-S.; Kwak, K. The Internet of Things for health care: A comprehensive survey. IEEE Access 2015, 3, 678–708. [Google Scholar] [CrossRef]
- Zanella, A.; Bui, N.; Castellani, A.; Vangelista, L.; Zorzi, M. Internet of Things for smart cities. IEEE Internet Things J. 2014, 1, 22–32. [Google Scholar] [CrossRef]
- Saleem, Y.; Crespi, N.; Rehmani, M.H.; Copeland, R. Inter-net of things-aided smart grid: Technologies, architectures, applications, prototypes, and future research directions. IEEE Access 2019, 7, 62962–63003. [Google Scholar] [CrossRef]
- Kabir, M.H.; Thappa, K.; Yang, J.Y.; Yang, S.H. State-Space based Linear Modeling for Human Activity Recognition in Smart Space. Intell. Autom. Soft Comput. 2019, 25, 673–681. [Google Scholar] [CrossRef]
- Ma, Z.; Xiao, M.; Xiao, Y.; Pang, Z.; Poor, H.V.; Vucetic, B. High-reliability and low-latency wireless communication for Internet of Things: Challenges, fundamentals, and enabling technologies. IEEE Internet Things J. 2019, 6, 7946–7970. [Google Scholar] [CrossRef]
- Okhovvat, M.; Kangavari, M.R. A mathematical task dispatching model in wireless sensor actor networks. Int. J. Comput. Syst. Sci. Eng. 2019, 34, 5–12. [Google Scholar]
- Zhang, J.; Zhong, S.; Wang, T.; Chao, H.; Wang, J. Blockchain-based Systems and Applications: A Survey. J. Internet Technol. 2020, 21, 1–14. [Google Scholar]
- Wang, J.; Yang, Y.; Wang, T.; Sherratt, R.S.; Zhang, J. Big Data Service Architecture: A Survey. J. Internet Technol. 2020, 21, 393–405. [Google Scholar]
- Palattella, M.R. Internet of Things in the 5G era: Enablers, architecture, and business models. IEEE J. Sel. Areas Commun. 2016, 34, 510–527. [Google Scholar] [CrossRef] [Green Version]
- Lee, B.M.; Yang, H. Massive MIMO with Massive Connectivity for Industrial Internet of Things. IEEE Trans. Ind. Electron. 2020, 67, 5187–5196. [Google Scholar] [CrossRef]
- Li, X.; Qiu, L.; Dong, Y. Asymptotic equivalent performance of mul-ticell massive MIMO with spatial-temporal correlation. IEEE Commun. Lett. 2016, 20, 518–521. [Google Scholar] [CrossRef]
- Wang, W.; Capitaneanu, S.L.; Marinca, D.; Lohan, E.-S. Comparative analysis of channel models for industrial IoT wireless communication. IEEE Access 2019, 7, 91627–91640. [Google Scholar] [CrossRef]
- Kermoal, J.-P.; Schumacher, L.; Pedersen, K.I.; Mogensen, P.E.; Frederiksen, F. A stochastic MIMO radio channel model with experimental validation. IEEE J. Sel. Areas Commun. 2002, 20, 1211–1226. [Google Scholar] [CrossRef] [Green Version]
- Yun, Z.; Iskander, M.F. Ray tracing for radio propagation modeling: Principles and applications. IEEE Access 2015, 3, 1089–1100. [Google Scholar] [CrossRef]
- Cheng, X.; Wang, C.-X.; Laurenson, D.I.; Salous, S.; Vasilakos, A.V. An adaptive geometry-based stochastic model for non-isotropic MIMO mobile-to-mobile channels. IEEE Trans. Wirel. Commun. 2009, 8, 4824–4835. [Google Scholar]
- Zhou, T.; Tao, C.; Salous, S.; Liu, L. Geometry-based multilink channel modeling for high-speed train communication networks. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1229–1238. [Google Scholar] [CrossRef]
- Cheng, X.; Li, Y. A 3D geometry-based stochastic model for UAV-MIMO wideband non-stationary channels. IEEE Internet Things J. 2019, 6, 1654–1662. [Google Scholar] [CrossRef]
- Zajic, A.G.; Stuber, G.L. Space-time correlated mobile-to-mobile channels: Modelling and simulation. IEEE Trans. Veh. Technol. 2008, 57, 715–726. [Google Scholar] [CrossRef]
- Wu, S.; Wang, C.X.; Haas, H.; Aggoune, E.H.M.; Alwakeel, M.M.; Ai, B. A non-stationary wideband channel model for massive MIMO communication systems. IEEE Trans. Wirel. Commun. 2015, 14, 1434–1446. [Google Scholar] [CrossRef]
- Chelli, A.; Pätzold, M. A non-stationary MIMO vehicle-to-vehicle channel model based on the geometrical T-junction model. In Proceedings of the 2009 International Conference on Wireless Communications & Signal Processing, Nanjing, China, 13–15 November 2009; pp. 1–5. [Google Scholar]
- Akki, A.S.; Haber, F. A statistical model of mobile-to-mobile land communication channel. IEEE Trans. Veh. Technol. 1986, 35, 2–7. [Google Scholar] [CrossRef]
- Pätzold, M.; Hogstad, B.O.; Youssef, N. Modeling, analysis, and simulation of MIMO mobile-to-mobile fading channels. IEEE Trans. Wirel. Commun. 2008, 7, 510–520. [Google Scholar] [CrossRef]
- Zhang, G.C.; Peng, X.H.; Gu, X.Y. Impact of Scatterer Density on the Performances of Double-Scattering MIMO Channels. In Proceedings of the 10th IEEE International Conference on Computer and Information Technology (CIT 2010), Bradford, UK, 29 June–1 July 2010. [Google Scholar]
- Oestges, C.; Erceg, V.; Paulraj, A.J. A physical scattering model for MIMO macrocellular broadband wireless channels. IEEE J. Sel. Areas Commun. 2003, 21, 721–729. [Google Scholar] [CrossRef] [Green Version]
- Yu, Y. 3D vs. 2D channel models: Spatial correlation and channel capacity comparison and analysis. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–7. [Google Scholar]
- Almesaeed, R.N.; Ameen, A.S.; Mellios, E.; Doufexi, A.; Nix, A. 3D channel models: Principles, characteristics, and system implications. IEEE Commun. Mag. 2017, 55, 152–159. [Google Scholar] [CrossRef] [Green Version]
- Zajić, A.G.; Stüber, G.L. Three-dimensional modeling, simulation, and capacity analysis of space-time correlated mobile-to-mobile channels. IEEE Trans. Veh. Technol. 2008, 57, 2042–2054. [Google Scholar] [CrossRef]
- Kafle, P.L.; Intarapanich, A.; Sesay, A.B.; Mcrory, J.; Davies, R.J. Spatial correlation and capacity measurements for wideband MIMO channels in indoor office environment. IEEE Trans. Wirel. Commun. 2008, 7, 1560–1571. [Google Scholar] [CrossRef]










| Notations or Parameter | Definition |
|---|---|
| MT (MR) | The number of antenna of MT (MR) |
| Tq (Rq) | The p-th (q-th) antenna of MT (MR) |
| OT (OR) | The antenna center of MT and MR |
| M1 (M2) | The single-sphere around MT (MR) |
| M3 | The ellipsoid model |
| Ni | The number of effective scatterers on the model Mi |
| The ni-th scatterer on the model Mi | |
| RT (RR) | radius of M1 (M2) |
| a, D | semi-major axis and focal length of M3 |
| δT (δR) | antenna element spacing at MT (MR) |
| θT (θR) | antenna array orientation of MT (MR) |
| ψT (ψR) | antenna array elevation angle of MT (MR) |
| vT (vR) | mobile velocities of MT (MR) |
| γT (γR) | mobile directions of MT (MR) |
| αLoS | AAoA of LoS path |
| , | AAoD and AAoA impinged on the effective , |
| , | EAoD and EAoA impinged on the effective |
| ξpq, ξp-ni, ξni-q, ξn1-n2, ξT-ni, ξni-R | distance of (Tp − Rq), (Tp − ), ( − Rq), ( − ), (OT − ), ( − OR) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, W.; He, Y.; Li, B.; Wang, S. 3D Multiple-Antenna Channel Modeling and Propagation Characteristics Analysis for Mobile Internet of Things. Sensors 2021, 21, 989. https://doi.org/10.3390/s21030989
Zeng W, He Y, Li B, Wang S. 3D Multiple-Antenna Channel Modeling and Propagation Characteristics Analysis for Mobile Internet of Things. Sensors. 2021; 21(3):989. https://doi.org/10.3390/s21030989
Chicago/Turabian StyleZeng, Wenbo, Yigang He, Bing Li, and Shudong Wang. 2021. "3D Multiple-Antenna Channel Modeling and Propagation Characteristics Analysis for Mobile Internet of Things" Sensors 21, no. 3: 989. https://doi.org/10.3390/s21030989
APA StyleZeng, W., He, Y., Li, B., & Wang, S. (2021). 3D Multiple-Antenna Channel Modeling and Propagation Characteristics Analysis for Mobile Internet of Things. Sensors, 21(3), 989. https://doi.org/10.3390/s21030989





