Synergy-Based Sensor Reduction for Recording the Whole Hand Kinematics
Abstract
:1. Introduction
2. Materials and Methods
- (1)
- Hand kinematic synergies extraction: For each subject in the KIN-MUS UJI database [3], subject-specific kinematic synergies were extracted by applying a PCA to the kinematic data recorded during the performance of the 26 ADL in the database.
- (2)
- Synergy clustering and selection of candidate DoF for each synergy: Hierarchical Clustering was used to group extracted synergies that are similar among subjects, and one or more representative joint angles were chosen for each resulting synergy as candidate DoF.
- (3)
- Selection of the best combination of angles: The joint angles that were not selected as representative were estimated from different combinations of those that were selected. Root mean square errors (RMSE) of the estimated joint angles were computed and the best combination of representative joint angles was selected.
- (4)
- Goodness of the method: Using the joint angles selected in the previous step, the joint angles recorded in another kinematic database (33 complex ADL from 20 subjects of KINE-ADL BE-UJI database) were estimated, and RMSE were computed.
2.1. Hand Kinematic Synergies Extraction
2.1.1. Experiment A
2.1.2. Kinematics Acquisition
2.1.3. Synergies Extraction
2.2. Synergy Clustering and Selection of Representative DoF for Each Synergy
- If the averaged PC represents the predominant motion of only one DoF (CC > 0.8 for only one DoF, and CC < 0.3 for all other DoF), that independent DoF was selected as representative.
- Otherwise, the averaged PC represents a coordinated motion of different DoF, and all DoF with CC > 0.4 were considered as candidates to be representative.
2.3. Selection of the Best Combination of Angles
2.4. Evaluation of the Goodness of the Method
2.4.1. Experiment B
2.4.2. Evaluation of the Goodness
- Global RMSE errors (across all frames and subjects, thus one RMSE value per joint)
- RMSE per ADL (across subjects and frames)
3. Results
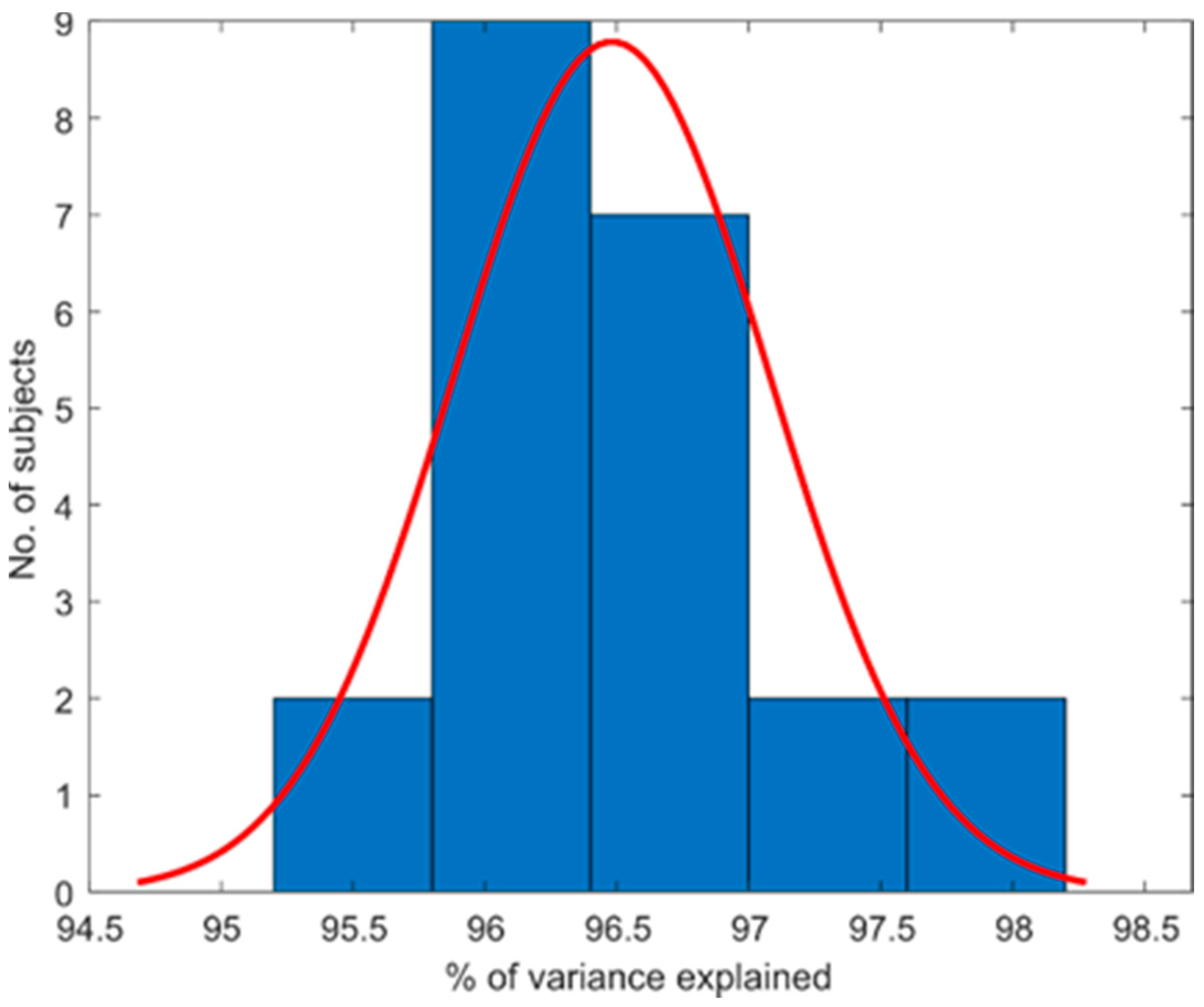
3.1. Hand Kinematic Synergies Extraction
3.2. Synergy Clustering and Selection of Representative DoF for Each Synergy
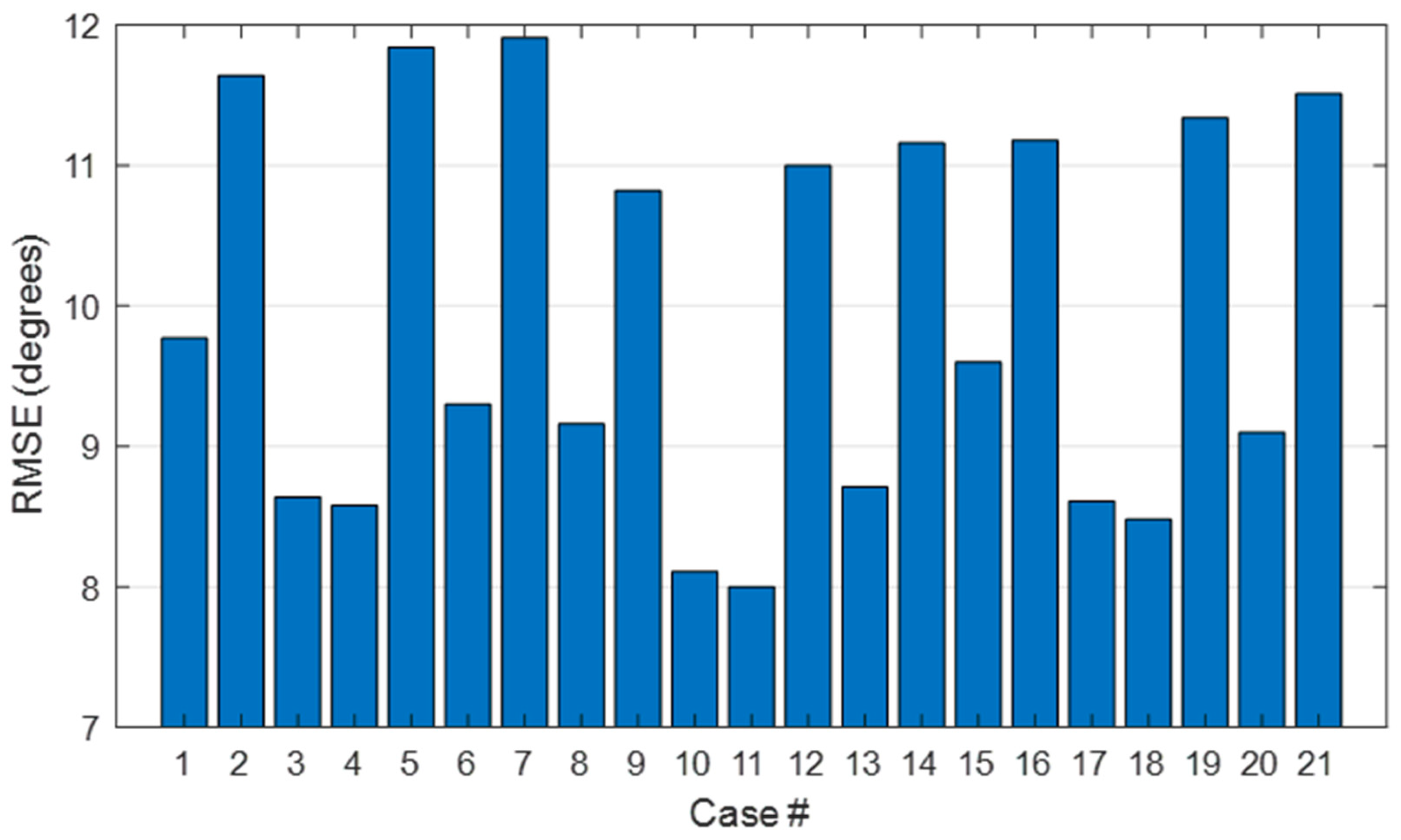
3.3. Selection of the Best Combination of Angles
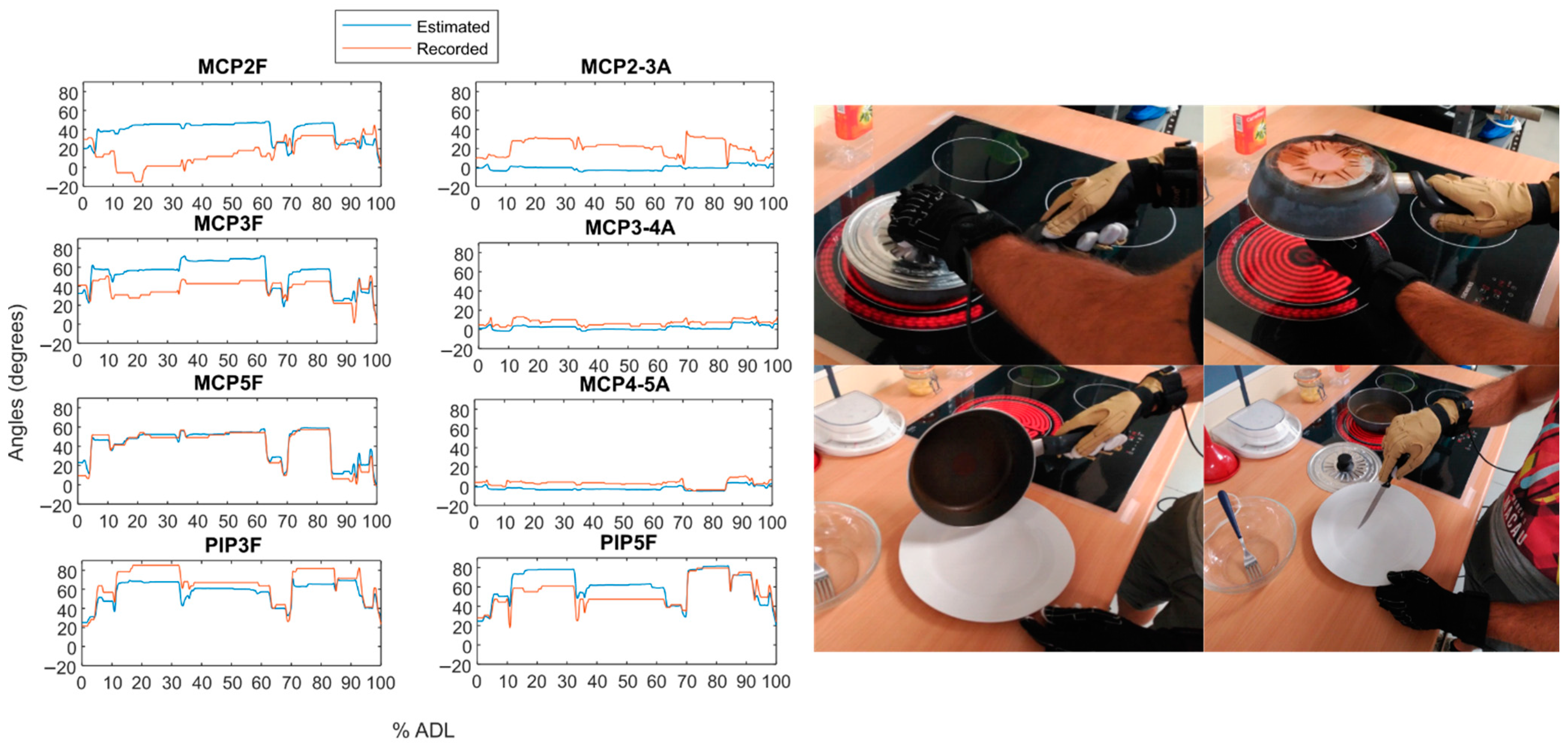
3.4. Evaluation of the Goodness of the Method
4. Discussion
4.1. Hand Kinematic Synergies
4.2. Estimation of Physiological Angles
- Abduction/Adduction between index and middle fingers obtained the lowest errors when using MCP flexion/extension movement of the index finger as representative.
- Abduction/Adduction between middle and ring fingers obtained the lowest errors when using Abduction/Adduction between index and middle fingers as representative.
- Abduction/Adduction between ring and little fingers obtained the lowest errors when using MCP flexion/extension movement of the little finger as representative.
- MCP flexion/extension movement of the index and middle fingers are mainly estimated from flexion/extension of the MCP joints and CMC thumb joint. This means that MCP movements of these fingers are highly related to thumb position and MCP movement of the other fingers.
- In general, PIP joints are mainly related to the PIP joint of the adjacent finger. In particular, PIP of the middle finger presents a mainly high relation to PIP of the ring finger, with some influence from PIP of the index finger and CMC thumb flexion. PIP of the little finger mainly presents a relation with PIP of the ring finger with some influence from MCP of the ring finger.
- MCP abduction/adduction movement between index, middle and ring fingers are more related to thumb CMC flexion/extension and MCP flexion/extension of ring finger. This means that abduction/adduction movement is also related to the thumb position (in this case only with CMC flexion movement) and MCP flexion/extension movements. MCP abduction/adduction between the ring and little fingers are only related to MCP flexion/extension movement.
4.3. Evaluation of the Goodness of the Method
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| A | Abduction/adduction |
| ADL | Activities of daily living |
| DOF | Degrees of freedom |
| CMC | Carpometacarpal joint |
| F | Flexion/extension |
| IP | Interphalangeal joint |
| MCP | Metacarpophalangeal joint |
| ROM | Range of motion |
| PalmArch | Palmar arch |
| PCA | Principal component analysis |
| PCs | Principal components |
| PIP | Proximal interphalangeal joint |
| RMSE | Root mean square error |
References
- Faisal, A.I.; Majumder, S.; Mondal, T.; Cowan, D.; Naseh, S.; Deen, M.J. Monitoring methods of human body joints: State-of-the-art and research challenges. Sensors 2019, 19, 2629. [Google Scholar] [CrossRef] [Green Version]
- Bashardoust Tajali, S.; MacDermid, J.C.; Grewal, R.; Young, C. Reliability and Validity of Electro-Goniometric Range of Motion Measurements in Patients with Hand and Wrist Limitations. Open Orthop. J. 2016, 10, 190–205. [Google Scholar] [CrossRef] [Green Version]
- Jarque-Bou, N.J.; Vergara, M.; Sancho-Bru, J.L.; Gracia-Ibáñez, V.; Roda-Sales, A. A calibrated database of kinematics and EMG of the forearm and hand during activities of daily living. Sci. Data 2019, 6, 270. [Google Scholar] [CrossRef]
- Roda-Sales, A.; Vergara, M.; Sancho-Bru, J.L.; Gracia-Ibáñez, V.; Jarque-Bou, N.J. Human hand kinematic data during feeding and cooking tasks. Sci. Data 2019, 6, 167. [Google Scholar] [CrossRef]
- Lemos, J.D.; Hernandez, A.M.; Soto-Romero, G. An instrumented glove to assess manual dexterity in simulation-based neurosurgical education. Sensors 2017, 17, 988. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Jung, K.; Park, J.; You, H. Development of a 25-DOF Hand Forward Kinematic Model Using Motion Data. In Proceedings of the 2010 Fall Conference of Ergonomics Society of Korea, Suwon, Korea, September 2010; pp. 136–139. [Google Scholar]
- Windolf, M.; Götzen, N.; Morlock, M. Systematic accuracy and precision analysis of video motion capturing systems--exemplified on the Vicon-460 system. J. Biomech. 2008, 41, 2776–2780. [Google Scholar] [CrossRef]
- Sancho-Bru, J.L.; Jarque-Bou, N.J.; Vergara, M.; Pérez-González, A. Validity of a simple videogrammetric method to measure the movement of all hand segments for clinical purposes. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2014, 228, 182–189. [Google Scholar] [CrossRef] [Green Version]
- Menolotto, M.; Komaris, D.S.; Tedesco, S.; O’flynn, B.; Walsh, M. Motion capture technology in industrial applications: A systematic review. Sensors 2020, 20, 5687. [Google Scholar] [CrossRef] [PubMed]
- Kortier, H.G.; Sluiter, V.I.; Roetenberg, D.; Veltink, P.H. Assessment of hand kinematics using inertial and magnetic sensors. J. Neuroeng. Rehabil. 2014, 11, 70. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gómez Echeverry, L.L.; Jaramillo Henao, A.M.; Ruiz Molina, M.A.; Velásquez Restrepo, S.M.; Páramo Velásquez, C.A.; Silva Bolívar, G.J.; Gómez Echeverry, L.L.; Jaramillo Henao, A.M.; Ruiz Molina, M.A.; Velásquez Restrepo, S.M.; et al. Human motion capture and analysis systems: A systematic review/Sistemas de captura y análisis de movimiento cinemático humano: Una revisión sistemática. Prospectiva 2018, 16, 24–34. [Google Scholar] [CrossRef] [Green Version]
- Rigoni, M.; Gill, S.; Babazadeh, S.; Elsewaisy, O.; Gillies, H.; Nguyen, N.; Pathirana, P.N.; Page, R. Assessment of shoulder range of motion using a wireless inertial motion capture device—A validation study. Sensors 2019, 19, 1781. [Google Scholar] [CrossRef] [Green Version]
- Sabatini, A.M. Estimating three-dimensional orientation of human body parts by inertial/magnetic sensing. Sensors 2011, 11, 1489–1525. [Google Scholar] [CrossRef] [Green Version]
- Norkin, C.; White, D. Measurement of Joint Motion: A Guide to Goniometry, 5th ed.; F.A. Davis Company: Philadelphia, PA, USA, 2016; ISBN 9780803645660. [Google Scholar]
- Reissner, L.; Fischer, G.; List, R.; Giovanoli, P.; Calcagni, M. Assessment of hand function during activities of daily living using motion tracking cameras: A systematic review. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2019, 233, 764–783. [Google Scholar] [CrossRef] [PubMed]
- van der Kruk, E.; Reijne, M.M. Accuracy of human motion capture systems for sport applications; state-of-the-art review. Eur. J. Sport Sci. 2018, 18, 806–819. [Google Scholar] [CrossRef]
- Fischer, G.; Jermann, D.; List, R.; Reissner, L.; Calcagni, M. Development and application of a motion analysis protocol for the kinematic evaluation of basic and functional hand and finger movements using motion capture in a clinical setting-A repeatability study. Appl. Sci. 2020, 10, 6436. [Google Scholar] [CrossRef]
- Leardini, A.; Biagi, F.; Belvedere, C.; Benedetti, M.G. Quantitative comparison of current models for trunk motion in human movement analysis. Clin. Biomech. 2009, 24, 542–550. [Google Scholar] [CrossRef] [PubMed]
- Metcalf, C.D.; Notley, S.V.; Chappell, P.H.; Burridge, J.H.; Yule, V.T. Validation and application of a computational model for wrist and hand movements using surface markers. IEEE Trans. Biomed. Eng. 2008, 55, 1199–1210. [Google Scholar] [CrossRef]
- Lee, K.S.; Jung, M.C. Quantitative comparison of marker attachment methods for hand motion analysis. Int. J. Occup. Saf. Ergon. 2015, 21, 30–38. [Google Scholar] [CrossRef]
- Garcia-Rosas, R.; Oetomo, D.; Manzie, C.; Tan, Y.; Choong, P. Task-space Synergies for Reaching using Upper-limb Prostheses. IEEE Trans. Neural Syst. Rehabil. Eng. 2020. [Google Scholar] [CrossRef]
- Barbour, N.; Schmidt, G. Inertial sensor technology trends. IEEE Sens. J. 2001, 1, 332–339. [Google Scholar] [CrossRef]
- Roda-Sales, A.; Sancho-Bru, J.L.; Vergara, M.; Gracia-Ibáñez, V.; Jarque-Bou, N.J. Effect on manual skills of wearing instrumented gloves during manipulation. J. Biomech. 2020, 98, 109512. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.Z.J.; Malric, F.; Shirmohammadi, S. A new hand-measurement method to simplify calibration in cyberglove-based virtual rehabilitation. IEEE Trans. Instrum. Meas. 2010, 59, 2496–2504. [Google Scholar] [CrossRef]
- Gracia-Ibáñez, V.; Vergara, M.; Buffi, J.H.; Murray, W.M.; Sancho-Bru, J.L. Across-subject calibration of an instrumented glove to measure hand movement for clinical purposes. Comput. Methods Biomech. Biomed. Eng. 2017, 20, 587–597. [Google Scholar] [CrossRef] [PubMed]
- Bernshteĭn, N.A. The Co-Ordination and Regulation of Movements; Pergamon Press: Oxford, UK, 1967. [Google Scholar]
- Santello, M.; Baud-Bovy, G.; Jörntell, H. Neural bases of hand synergies. Front. Comput. Neurosci. 2013, 7, 23. [Google Scholar] [CrossRef] [Green Version]
- Lang, C.E.; Schieber, M.H. Human finger independence: Limitations due to passive mechanical coupling versus active neuromuscular control. J. Neurophysiol. 2004, 92, 2802–2810. [Google Scholar] [CrossRef] [Green Version]
- d’Avella, A.; Saltiel, P.; Bizzi, E. Combinations of muscle synergies in the construction of a natural motor behavior. Nat. Neurosci. 2003, 6, 300–308. [Google Scholar] [CrossRef]
- Smeets, J.B.J.; Brenner, E. Synergies in Grasping. In Advances in Experimental Medicine and Biology; Springer: Cham, Switzerland, 2016; Volume 957, pp. 21–34. [Google Scholar]
- Jarque-Bou, N.J.; Vergara, M.; Sancho-Bru, J.L.; Gracia-Ibanez, V.; Roda-Sales, A. Hand Kinematics Characterization while Performing Activities of Daily Living through Kinematics Reduction. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 1556–1565. [Google Scholar] [CrossRef]
- Jarrassé, N.; Ribeiro, A.T.; Sahbani, A.; Bachta, W.; Roby-Brami, A. Analysis of hand synergies in healthy subjects during bimanual manipulation of various objects. J. Neuroeng. Rehabil. 2014, 11, 113. [Google Scholar] [CrossRef]
- Lambert-Shirzad, N.; Machiel Van Der Loos, H.F. On identifying kinematic and muscle synergies: A comparison of matrix factorization methods using experimental data from the healthy population. J. Neurophysiol. 2017, 117, 290–302. [Google Scholar] [CrossRef]
- Li, S.; Chen, X.; Sheng, X.; Zhu, X. Preliminary study on proportional and simultaneous estimation of hand posture using surface EMG based on synergy concept. In Proceedings of the 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Osaka, Japan, 3–7 July 2013; pp. 6199–6202. [Google Scholar] [CrossRef]
- Santello, M.; Flanders, M.; Soechting, J.F. Patterns of hand motion during grasping and the influence of sensory guidance. J. Neurosci. 2002, 22, 1426–1435. [Google Scholar] [CrossRef] [Green Version]
- Santello, M.; Flanders, M.; Soechting, J.F. Postural hand synergies for tool use. J. Neurosci. 1998, 18, 10105–10115. [Google Scholar] [CrossRef]
- Della Santina, C.; Bianchi, M.; Averta, G.; Ciotti, S.; Arapi, V.; Fani, S.; Battaglia, E.; Catalano, M.G.; Santello, M.; Bicchi, A. Postural hand synergies during environmental constraint exploitation. Front. Neurorobot. 2017, 11, 41. [Google Scholar] [CrossRef]
- Prevete, R.; Donnarumma, F.; d’Avella, A.; Pezzulo, G. Evidence for sparse synergies in grasping actions. Sci. Rep. 2018, 8, 616. [Google Scholar] [CrossRef]
- Soechting, J.F.; Flanders, M. Flexibility and repeatability of finger movements during typing: Analysis of multiple degrees of freedom. J. Comput. Neurosci. 1997, 4, 29–46. [Google Scholar] [CrossRef] [PubMed]
- Bianchi, M.; Salaris, P.; Bicchi, A. Synergy-based hand pose sensing: Optimal glove design. Int. J. Rob. Res. 2013, 32, 407–424. [Google Scholar] [CrossRef] [Green Version]
- Ciotti, S.; Battaglia, E.; Carbonaro, N.; Bicchi, A.; Tognetti, A.; Bianchi, M. A synergy-based optimally designed sensing glove for functional grasp recognition. Sensors 2016, 16, 811. [Google Scholar] [CrossRef] [Green Version]
- Vergara, M.; Sancho-Bru, J.L.; Gracia-Ibáñez, V.; Pérez-González, A. An introductory study of common grasps used by adults during performance of activities of daily living. J. Hand Ther. 2014, 27, 225–233. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jarque-Bou, N.J.; Scano, A.; Atxori, M.; Müller, H. Kinematic synergies of hand grasps: A comprehensive study on a large publicly available dataset. J. Neuroeng. Rehabil. 2019, 16, 63. [Google Scholar] [CrossRef]
- Gracia-Ibáñez, V.; Sancho-Bru, J.L.; Vergara, M.; Jarque-Bou, N.J.; Roda-Sales, A. Sharing of hand kinematic synergies across subjects in daily living activities. Sci. Rep. 2020, 10, 6116. [Google Scholar] [CrossRef] [PubMed]
- Jarque-Bou, N.; Gracia-Ibáñez, V.; Sancho-Bru, J.-L.; Vergara, M.; Pérez-González, A.; Andrés, F.J. Using kinematic reduction for studying grasping postures. An application to power and precision grasp of cylinders. Appl. Ergon. 2016, 56, 52–61. [Google Scholar] [CrossRef]
- Hair, J.F.; Black, W.C., Jr.; Barry, J.B.; Anderson, E.R. Multivariate Data Analysis, 7th ed.; Prentice Hall, Ed.; Prentice Hall: Upper New Jersey River, NJ, USA, 2009; ISBN 9780138132637. [Google Scholar]
- Schober, P.; Schwarte, L.A. Correlation coefficients: Appropriate use and interpretation. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef] [PubMed]
- Mason, C.R.; Gomez, J.E.; Ebner, T.J. Hand Synergies during Reach-to-Grasp. J. Neurophysiol. 2001, 86, 2896–2910. [Google Scholar] [CrossRef] [PubMed]
- Ha, C.; Schieber, M.H.; Häger-Ross, C.; Schieber, M.H. Quantifying the Independence of Human Finger Movements: Comparisons of Digits, Hands, and Movement Frequencies. J. Neurosci. 2000, 20, 8542–8550. [Google Scholar] [CrossRef] [Green Version]
- Ingram, J.N.; Körding, K.P.; Howard, I.S.; Wolpert, D.M.; Kording, K.P.; Howard, I.S.; Wolpert, D.M. The statistics of natural hand movements. Exp. Brain Res. 2008, 188, 223–236. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gracia-Ibáñez, V.; Sancho-Bru, J.L.; Vergara, M. Relevance of grasp types to assess functionality for personal autonomy. J. Hand Ther. 2018, 1, 102–110. [Google Scholar] [CrossRef] [Green Version]


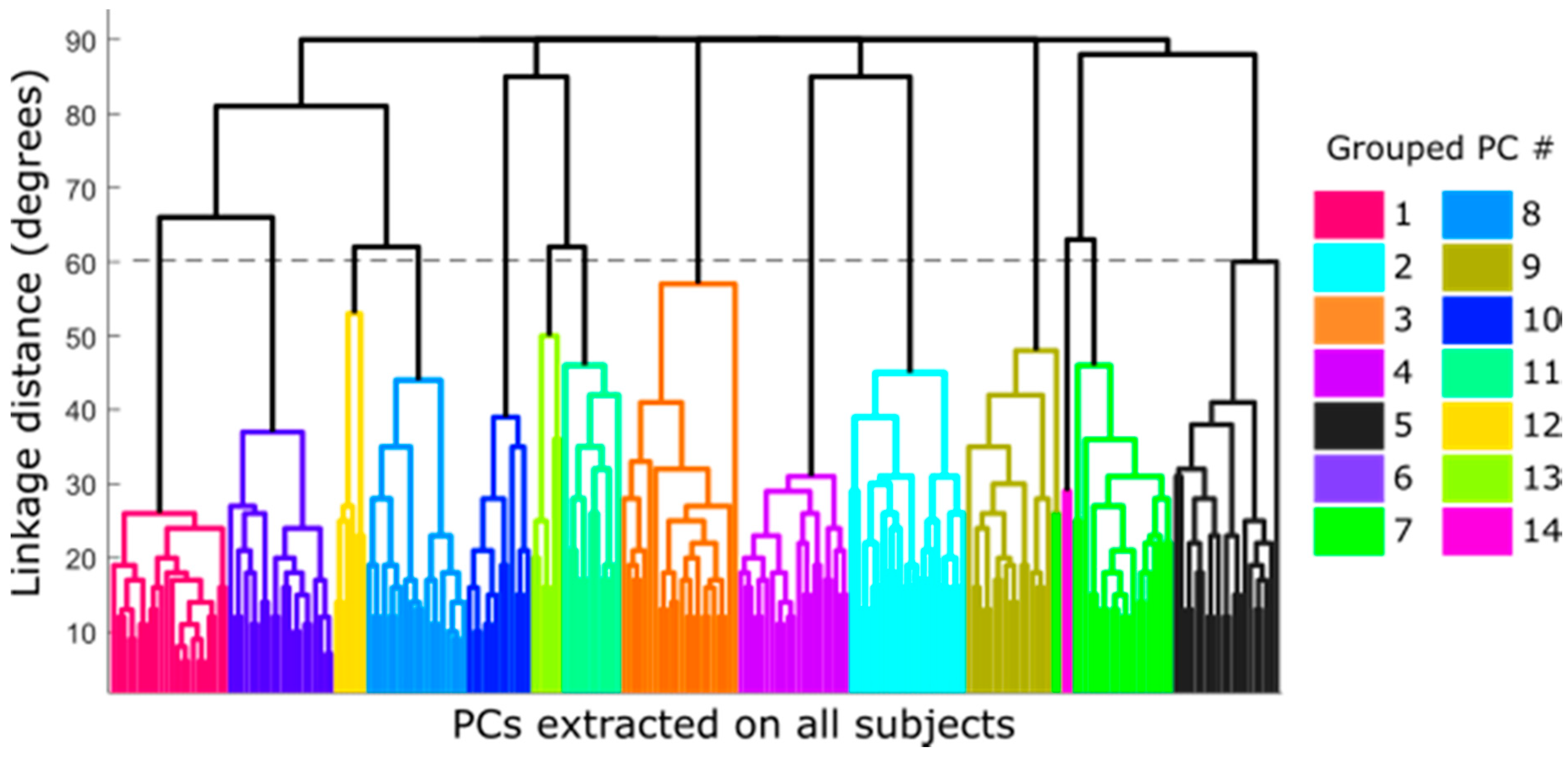




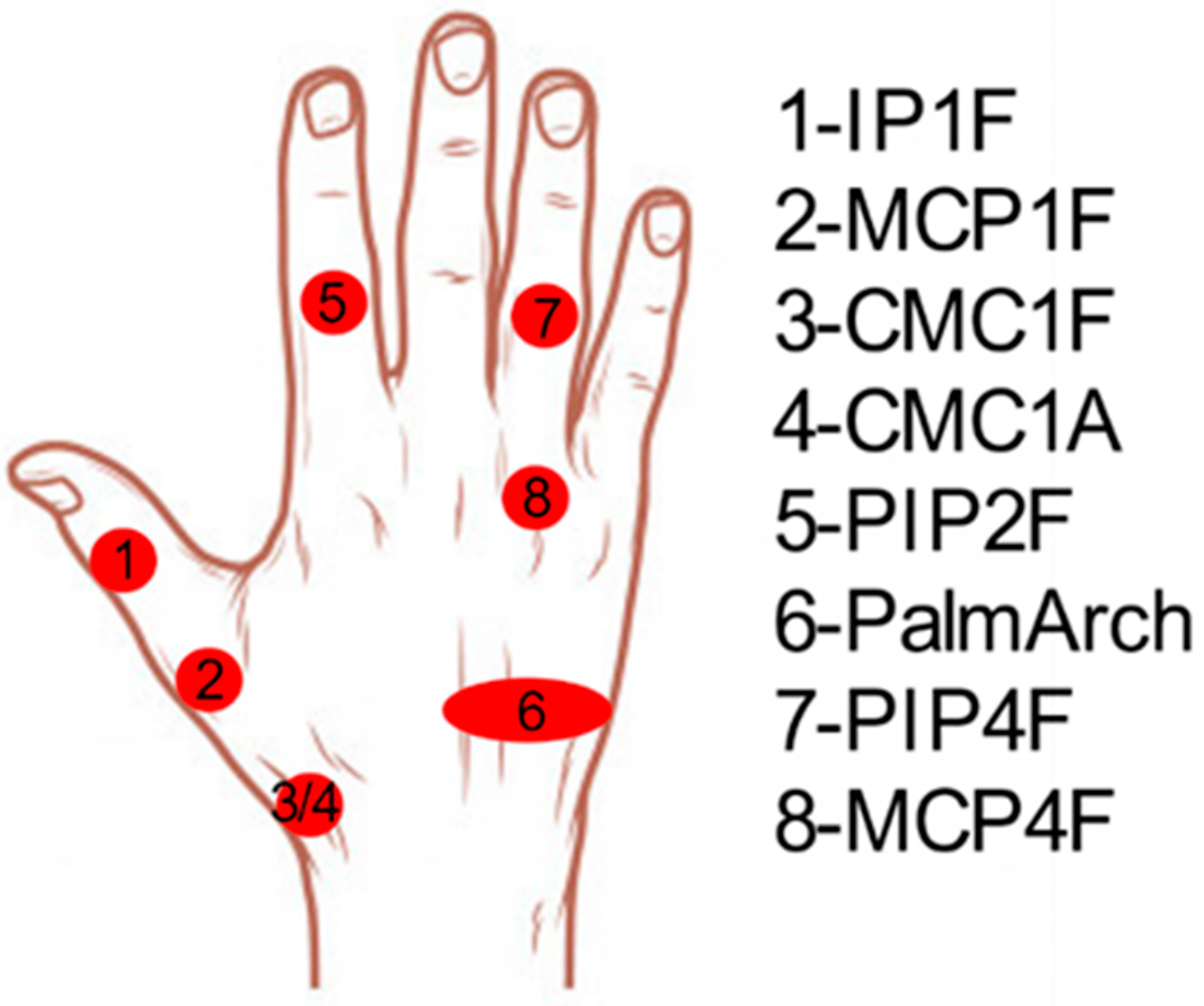
| Groups | Subjects (%) | Predominant DoF | Description |
|---|---|---|---|
| 1 | 100 | PIP4F, PIP5F PIP3F PIP2F | Fingers 2–5 PIPF coordination |
| 2 | 100 | CMC1A | Thumb CMCA movement |
| 3 | 100 | MCP1F | Thumb MCPF movement |
| 4 | 95.5 | IP1F | Thumb IPF movement |
| 5 | 90.9 | CMC1F | Thumb CMCF movement |
| 6 | 90.9 | MCP4–5A, MCP4F, MCP5F | Fingers 2–5 MCP coordination (more weight from Fingers 4 and 5) |
| 7 | 86.4 | PIP2F | Index PIPF movement |
| 8 | 86.4 | MCP3F, MCP2F, MCP4F | Fingers 2–5 MCP coordination (more weight from Fingers 2–4) |
| 9 | 81.8 | PalmArch | Palmar arch movement |
| 10 | 54.5 | MCP2–3A | MCP2–3A movement |
| 11 | 50.5 | MCP3–4A | MCP3–4A movement |
| 12 | 27.2 | MCP2F, MCPF2–3A, MCP3F, MCP4F, MCP3–4A | Fingers 2–5 MCP coordination (with any DoF predominance) |
| 13 | 27.2 | MCP3–4A, MCP2–3A | MCP2–3A and MCP3–4A coordination |
| 14 | 9.0 | PalmArch, PIP2F | PalmArch, and PIP2F coordination |
| Independent DoF | DoF Candidate of PIP Coordination (from Group 1) | DoF Candidate of MCP Coordination (from Groups 6, 8 and 12) |
|---|---|---|
| CMC1A | PIP3F | MCP2F |
| CMC1F | PIP4F | MCP2–3A |
| MCP1F | PIP5F | MCP3F |
| IPF1 | MCP4F | |
| PIP2F | MCP3–4A | |
| PalmArch | MCP5F | |
| MCP4–5A |
| Candidate DoF | RMSE (Degrees) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Case | 1 | 2 | MCP2F | MCP2–3A | MCP3F | PIP3F | MCP4F | MCP3–4A | PIP4F | MCP5F | MCP4–5A | PIP5F |
| 1 | PIP3F | MCP2F | 5.7 | 10.5 | 13.7 | 4.8 | 9.2 | 16.0 | 4.3 | 13.9 | ||
| 2 | PIP3F | MCP2–3A | 12.0 | 15.4 | 15.9 | 4.5 | 9.4 | 17.3 | 4.4 | 14.1 | ||
| 3 | PIP3F | MCP3F | 9.0 | 6.3 | 9.1 | 4.6 | 9.1 | 13.3 | 4.2 | 13.6 | ||
| 4 | PIP3F | MCP4F | 12.2 | 6.7 | 9.4 | 4.6 | 9.3 | 8.7 | 3.9 | 13.8 | ||
| 5 | PIP3F | MCP3–4A | 13.6 | 6.1 | 15.2 | 14.6 | 9.5 | 17.2 | 4.3 | 14.2 | ||
| 6 | PIP3F | MCP5F | 13.8 | 7.1 | 13.3 | 8.4 | 5.2 | 9.3 | 3.2 | 14.0 | ||
| 7 | PIP3F | MCP4–5A | 14.8 | 7.2 | 16.8 | 14.9 | 5.3 | 9.5 | 12.6 | 14.2 | ||
| 8 | PIP4F | MCP2F | 5.8 | 10.5 | 7.6 | 13.7 | 4.9 | 16.0 | 4.3 | 10.4 | ||
| 9 | PIP4F | MCP2–3A | 11.8 | 15.0 | 7.5 | 15.7 | 4.6 | 17.1 | 4.4 | 10.4 | ||
| 10 | PIP4F | MCP3F | 9.0 | 6.3 | 7.5 | 9.3 | 4.6 | 13.6 | 4.2 | 10.3 | ||
| 11 | PIP4F | MCP4F | 12.1 | 6.8 | 9.7 | 7.7 | 4.7 | 8.8 | 3.9 | 10.3 | ||
| 12 | PIP4F | MCP3–4A | 13.3 | 6.1 | 14.8 | 7.6 | 14.4 | 16.9 | 4.3 | 10.5 | ||
| 13 | PIP4F | MCP5F | 13.7 | 7.2 | 13.6 | 7.7 | 8.5 | 5.3 | 3.2 | 10.4 | ||
| 14 | PIP4F | MCP4–5A | 14.6 | 7.2 | 16.7 | 7.7 | 14.8 | 5.3 | 12.5 | 10.5 | ||
| 15 | PIP5F | MCP2F | 5.9 | 10.5 | 11.2 | 13.6 | 4.9 | 10.2 | 16.2 | 4.3 | ||
| 16 | PIP5F | MCP2–3A | 11.8 | 14.8 | 10.9 | 15.5 | 4.6 | 10.1 | 17.3 | 4.4 | ||
| 17 | PIP5F | MCP3F | 9.0 | 6.3 | 11.1 | 9.3 | 4.6 | 10.2 | 13.9 | 4.2 | ||
| 18 | PIP5F | MCP4F | 12.1 | 6.9 | 9.7 | 11.3 | 4.7 | 10.2 | 9.1 | 3.9 | ||
| 19 | PIP5F | MCP3–4A | 13.2 | 6.1 | 14.5 | 11.1 | 14.2 | 10.1 | 17.1 | 4.4 | ||
| 20 | PIP5F | MCP5F | 13.6 | 7.2 | 13.6 | 11.1 | 8.5 | 5.3 | 10.1 | 3.2 | ||
| 21 | PIP5F | MCP4–5A | 14.5 | 7.3 | 16.5 | 11.2 | 14.6 | 5.4 | 10.3 | 12.6 | ||
| Statistics across cases | Minimum | 9.0 | 5.7 | 9.43 | 7.5 | 8.4 | 4.5 | 9.1 | 8.7 | 3.2 | 10.3 | |
| Maximum | 14.8 | 7.3 | 16.8 | 11.3 | 15.9 | 5.4 | 10.2 | 17.3 | 4.4 | 14.2 | ||
| Average | 12.5 | 6.6 | 13.4 | 9.4 | 12.7 | 4.9 | 9.7 | 14.2 | 4.1 | 12.2 | ||
| Coefficients x(k) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Estimated Angles | Intercept | CMC1F | CMC1A | MCP1F | IP1F | PIP2F | PIP4F | MCP4F | P_Arch |
| MCP2F | 8.66 | - | −0.24 | 0.32 | −0.01 | −0.04 | 0.06 | 0.52 | 0.01 |
| MCP2–3A | 3.53 | −0.05 | −0.19 | −0.04 | 0.01 | −0.03 | 0.06 | −0.16 | 0.02 |
| MCP3F | 8.91 | - | −0.21 | 0.19 | −0.07 | 0.08 | −0.04 | 0.87 | 0.08 |
| PIP3F | −0.05 | −0.05 | −0.07 | −0.03 | −0.02 | 0.19 | 0.69 | −0.02 | 0.02 |
| MCP3–4A | 3.67 | −0.07 | −0.15 | −0.01 | 0.01 | −0.01 | 0.06 | −0.17 | 0.05 |
| MCP5F | −5.78 | −0.14 | −0.01 | −0.07 | 0.05 | −0.03 | 0.15 | 0.89 | −0.04 |
| MCP4–5A | 5.49 | 0.00 | −0.04 | 0.05 | −0.03 | 0.00 | −0.03 | −0.13 | −0.01 |
| PIP5F | 1.89 | 0.07 | −0.04 | 0.06 | 0.05 | −0.06 | 0.82 | 0.13 | 0.01 |
| RMSE (Degrees) | |||||||
|---|---|---|---|---|---|---|---|
| MCP2F | MCP2–3A | MCP3F | PIP3F | MCP3–4A | MCP5F | MCP4–5A | PIP5F |
| 14.35 | 7.63 | 10.68 | 8.92 | 4.18 | 10.25 | 4.25 | 10.54 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jarque-Bou, N.J.; Sancho-Bru, J.L.; Vergara, M. Synergy-Based Sensor Reduction for Recording the Whole Hand Kinematics. Sensors 2021, 21, 1049. https://doi.org/10.3390/s21041049
Jarque-Bou NJ, Sancho-Bru JL, Vergara M. Synergy-Based Sensor Reduction for Recording the Whole Hand Kinematics. Sensors. 2021; 21(4):1049. https://doi.org/10.3390/s21041049
Chicago/Turabian StyleJarque-Bou, Néstor J., Joaquín L. Sancho-Bru, and Margarita Vergara. 2021. "Synergy-Based Sensor Reduction for Recording the Whole Hand Kinematics" Sensors 21, no. 4: 1049. https://doi.org/10.3390/s21041049
APA StyleJarque-Bou, N. J., Sancho-Bru, J. L., & Vergara, M. (2021). Synergy-Based Sensor Reduction for Recording the Whole Hand Kinematics. Sensors, 21(4), 1049. https://doi.org/10.3390/s21041049







