Influence of Precise Products on the Day-Boundary Discontinuities in GNSS Carrier Phase Time Transfer
Abstract
:1. Introduction
2. Principle and Methods
2.1. The PPP Principle
2.2. GPS and Galileo Precise Products and the Discontinuities Problem in Clock Products
2.3. Network Processing Solution to Eliminate Day-Boundary Discontinuities in PPP
3. Experimental Design and Data Processing
4. Results and Analysis
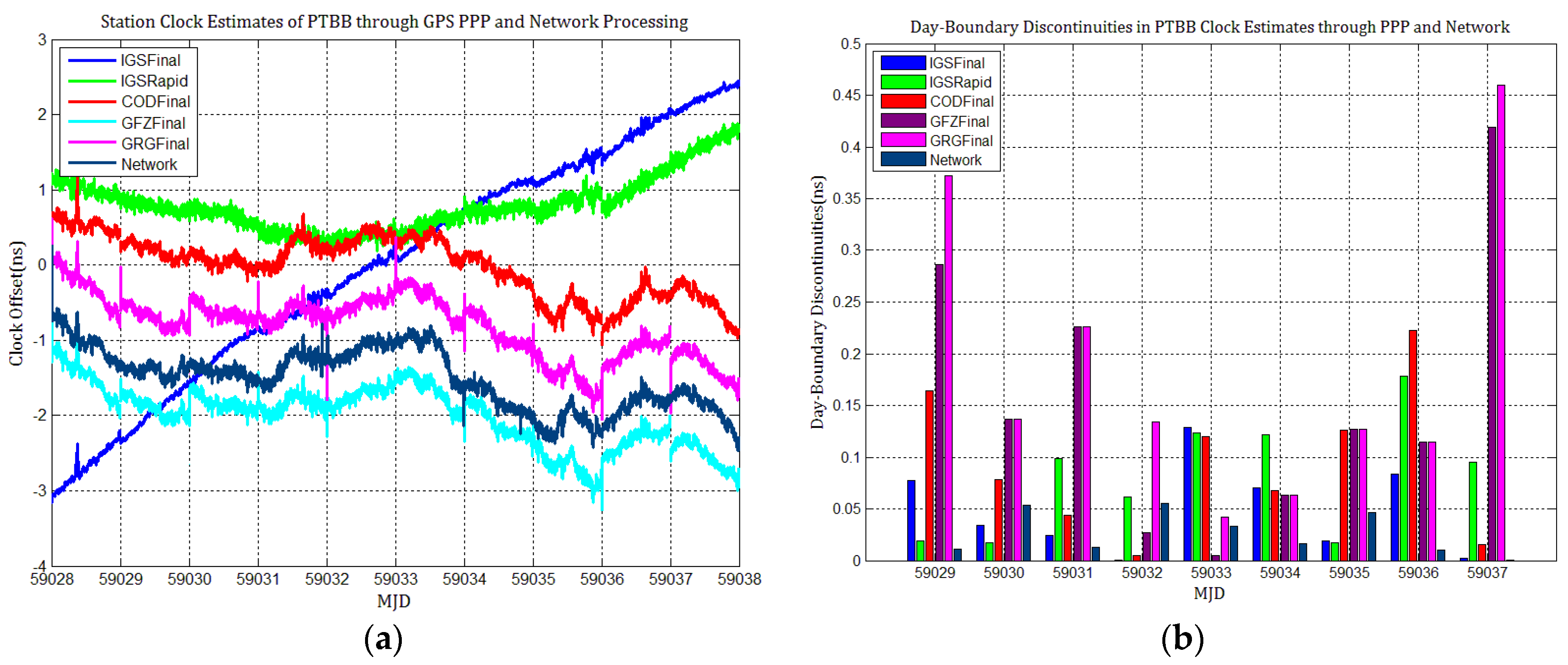
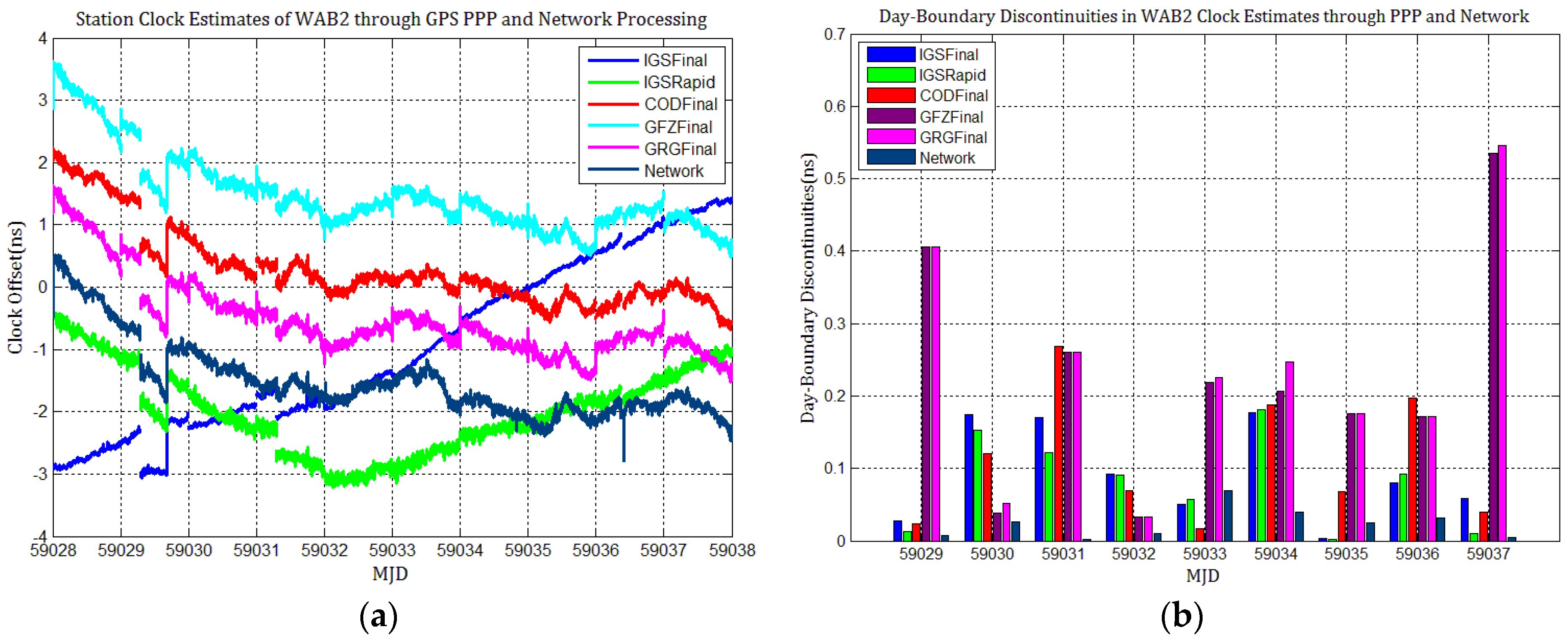
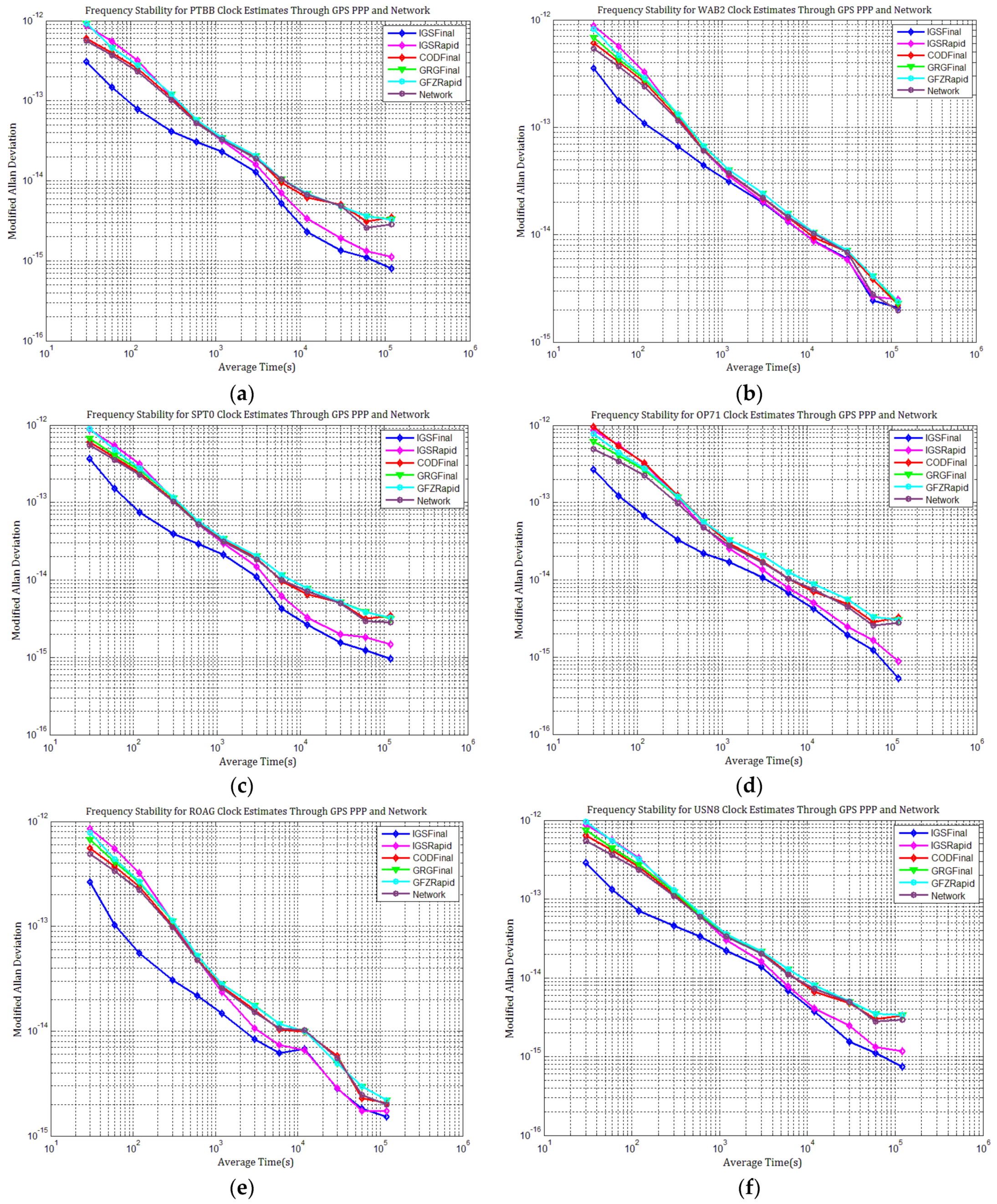
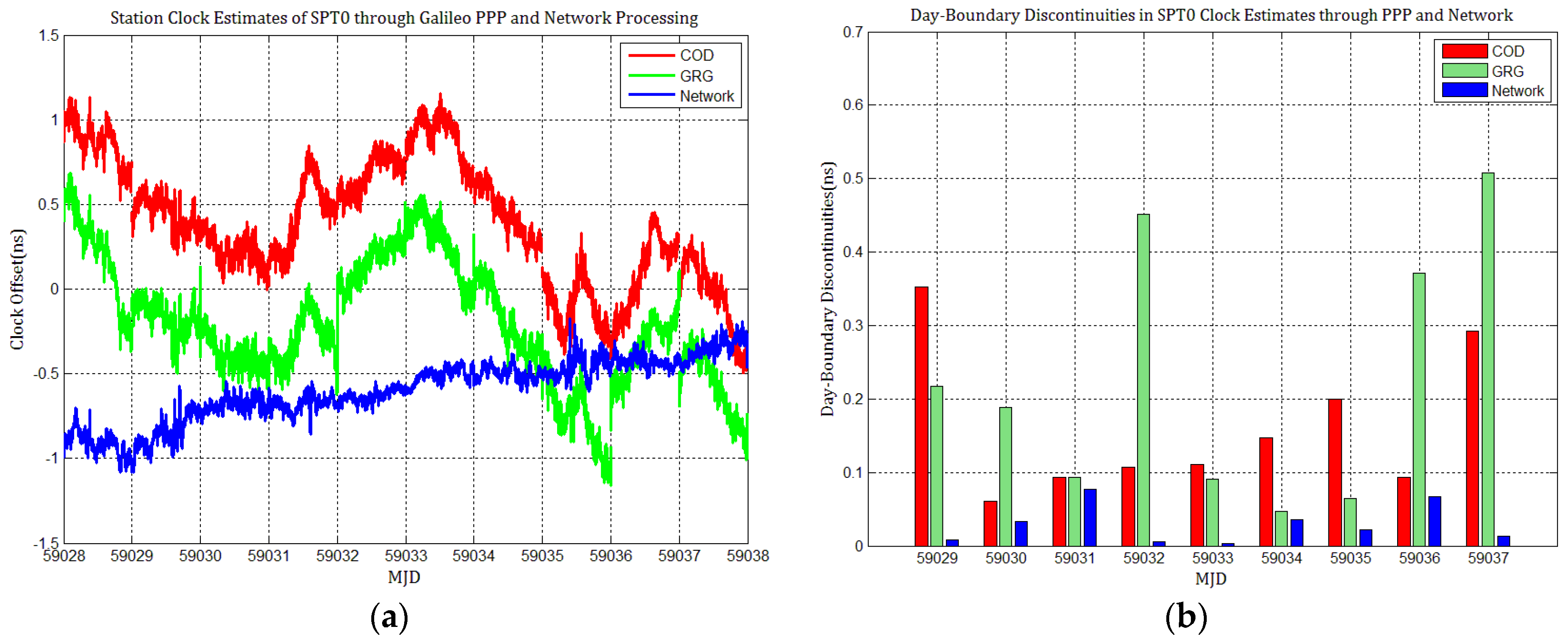
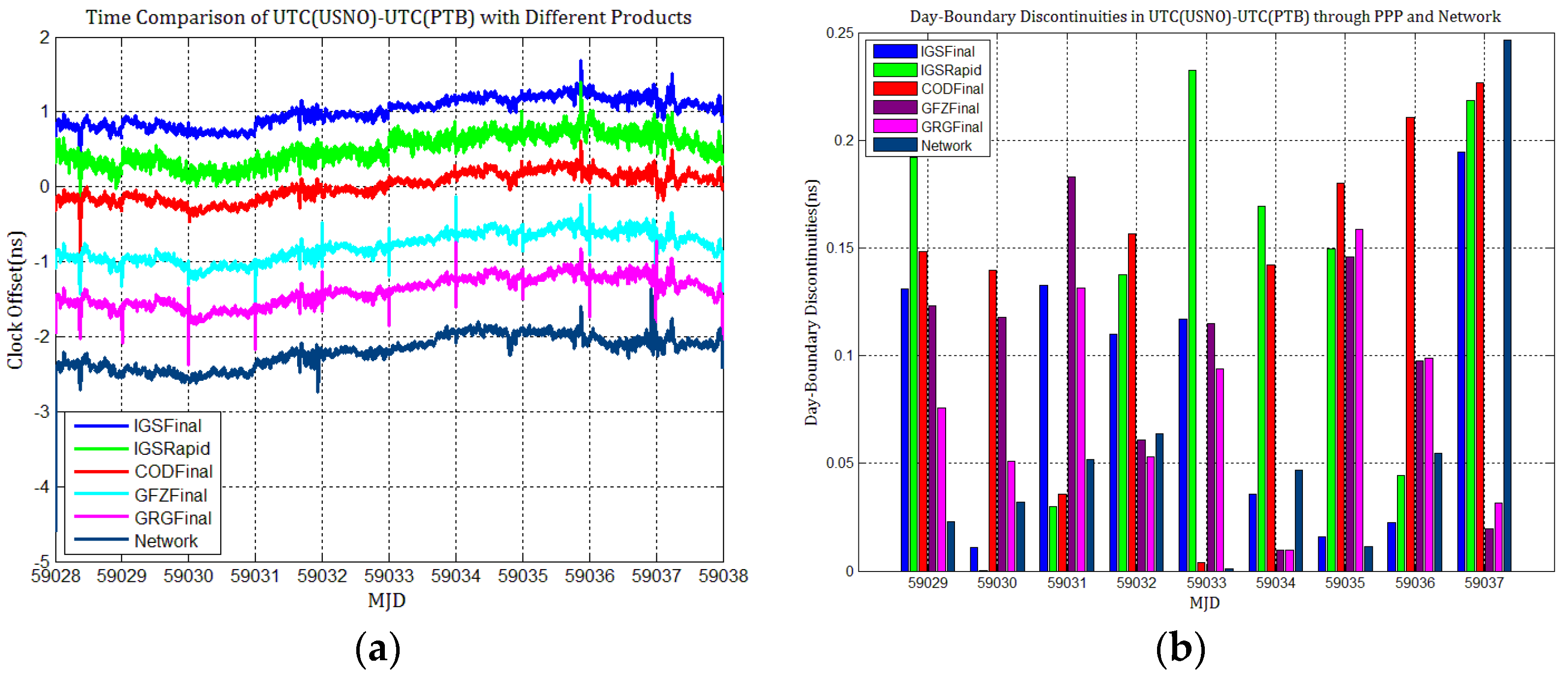
4.1. Influence of Discontinuities in Different GPS Products on PPP Station Clock Estimates
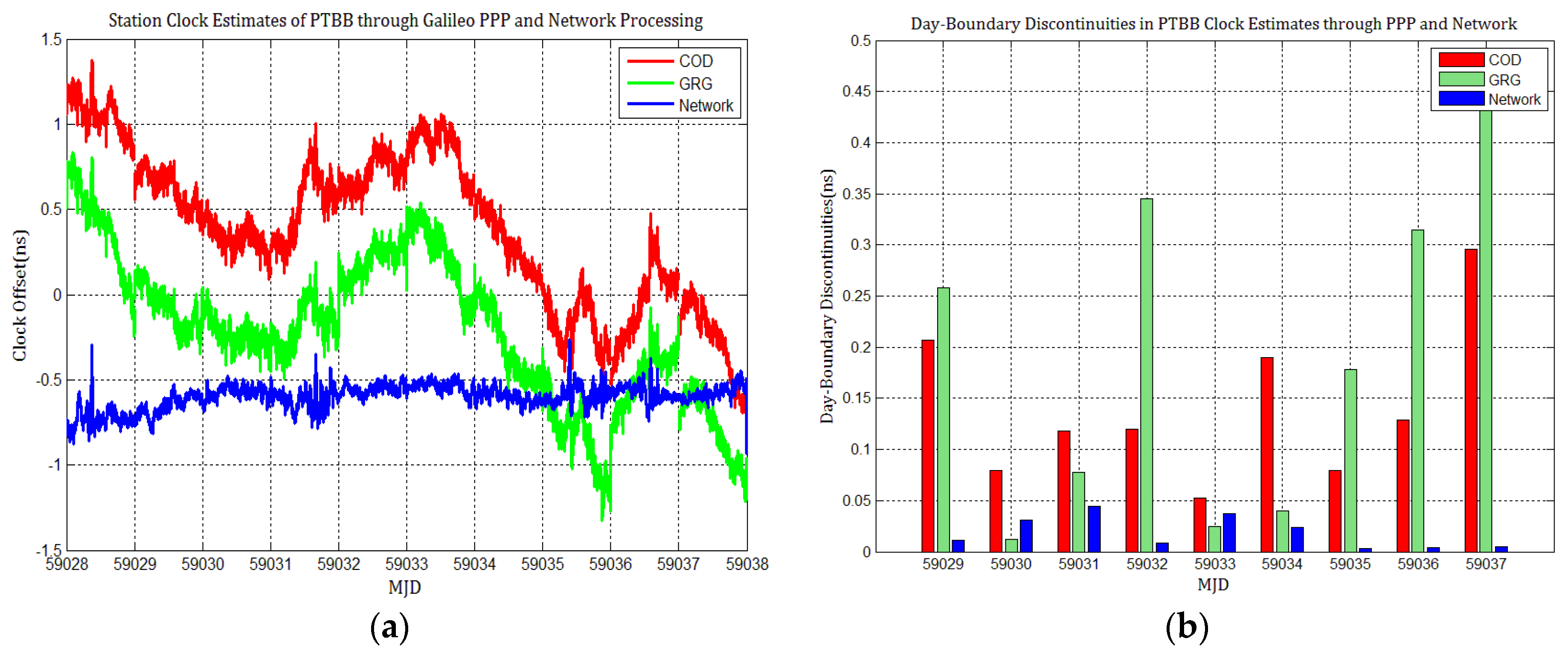
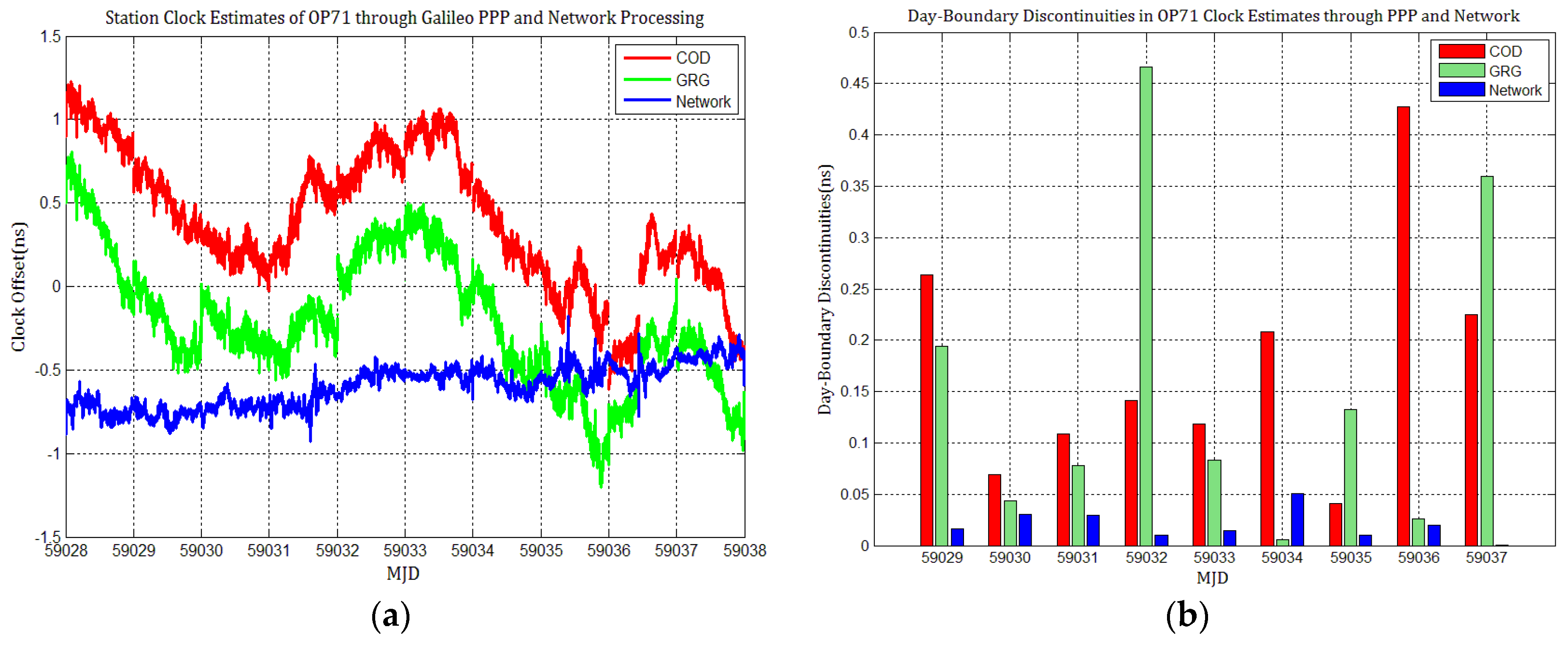
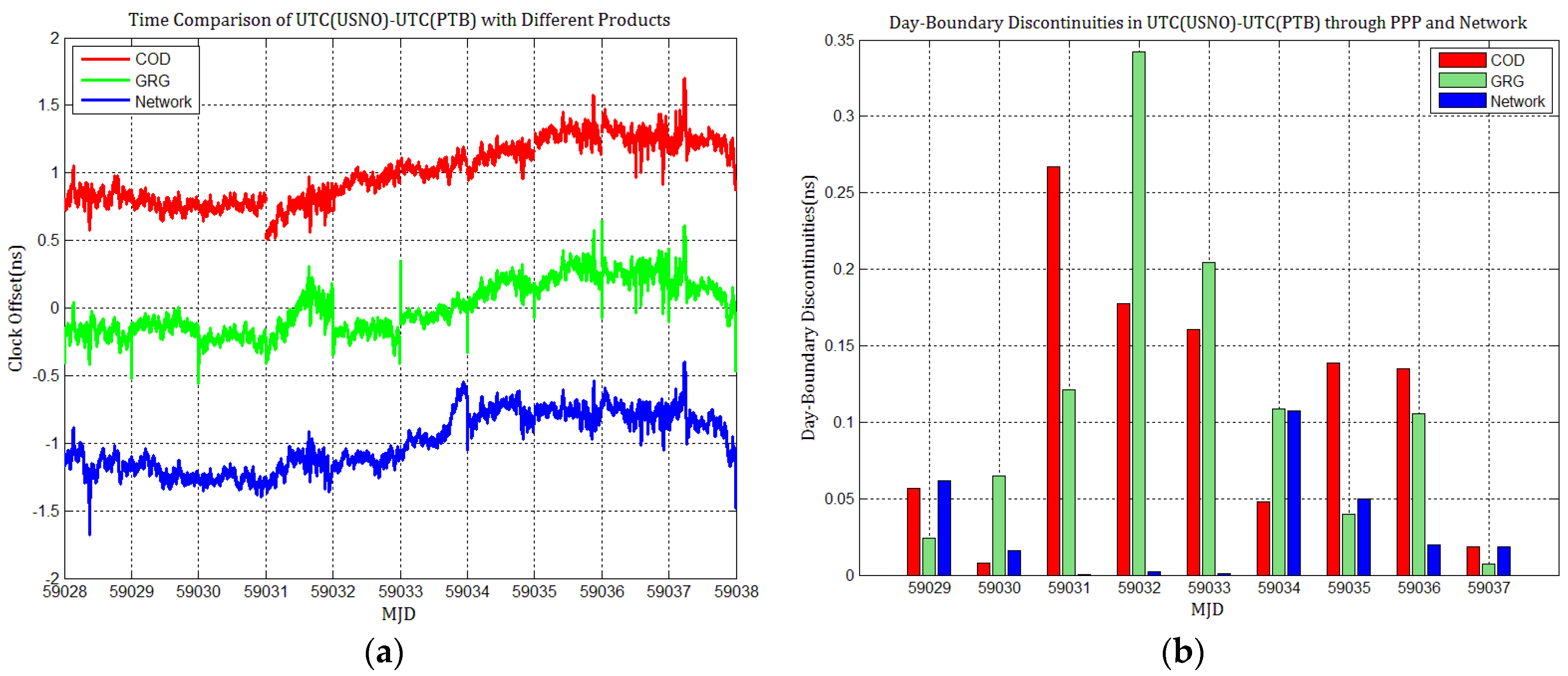
4.2. The Influence of Discontinuities in Different Galileo Products on PPP Station Clock Estimates
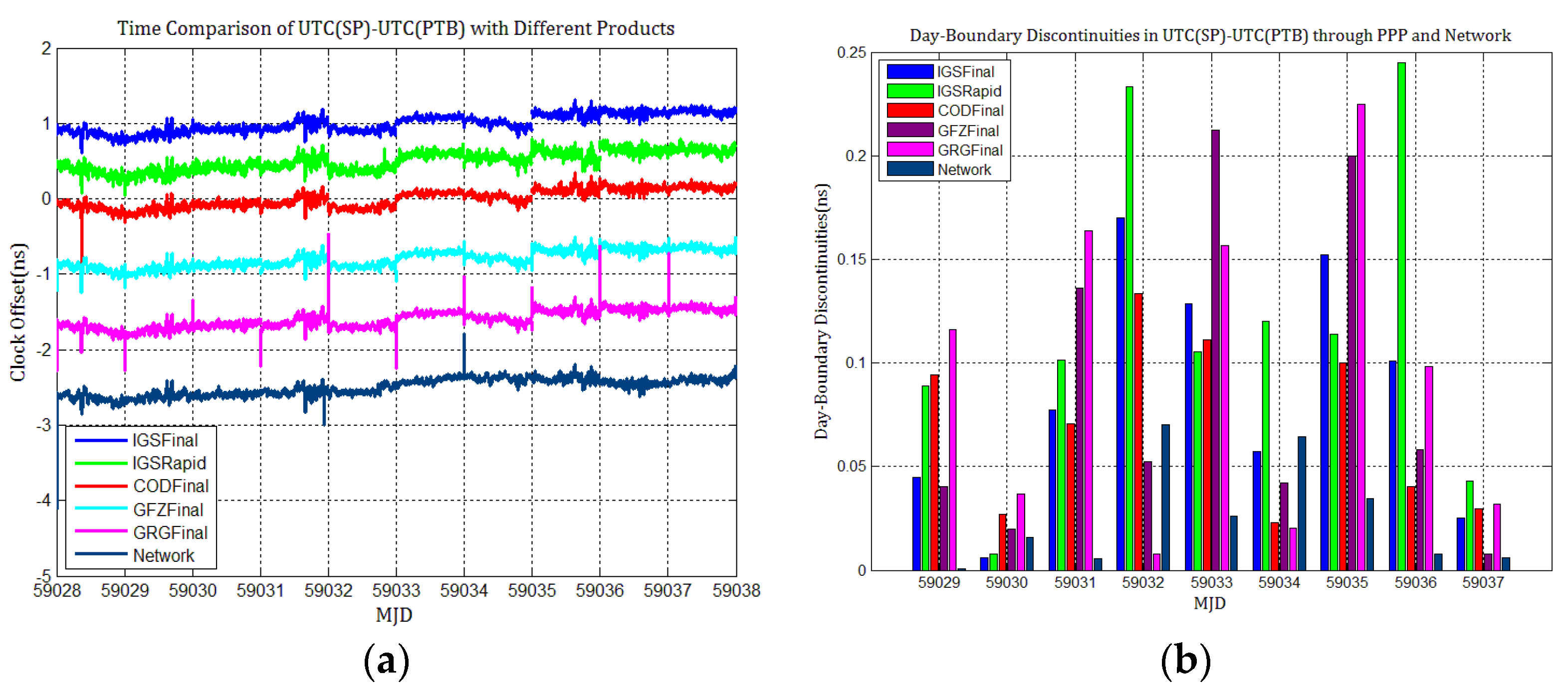
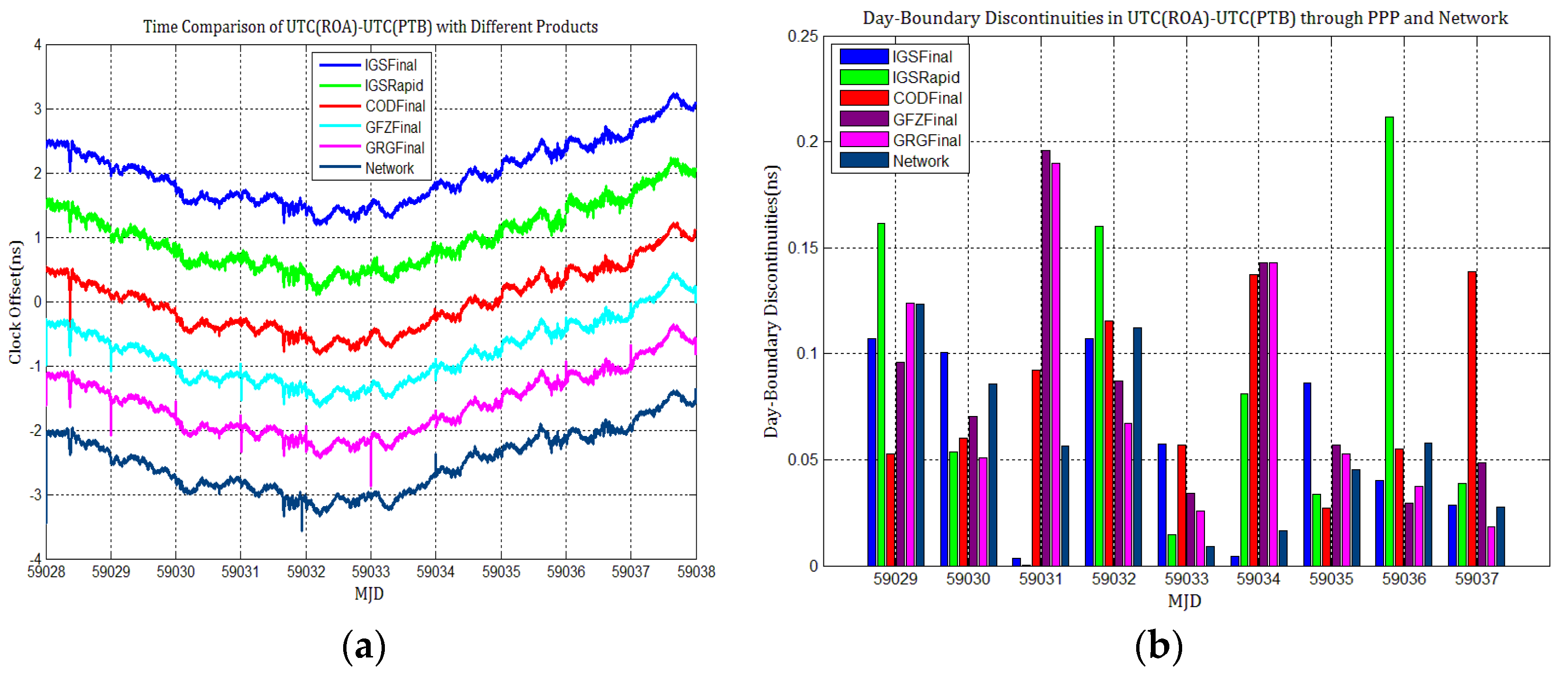
4.3. The Influence of Discontinuities in Products on PPP Time Transfer
5. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schildknecht, T.; Beutler, G.; Gurtner, W.; Rothacher, M. Towards Subnanosecond GPS Time Transfer using Geodetic Processing Techniques. In Proceedings of the 4th European Frequency and Time Forum (EFTF), Neuchâtel, Switzerland, 13−15 March 1990; pp. 335–346. [Google Scholar]
- Larson, K.M.; Levine, J. Time transfer using the phase of the GPS carrier. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1998, 45, 539–540. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ray, J.; Petit, G. IGS/BIPM pilot project to study time and frequency comparisons using GPS phase and code measurements. In Proceedings of the 14th Meeting of the Consultative Committee for Time and Frequency, BIPM, Sèvres, France, 14 October 1999. [Google Scholar]
- Ray, J.; Senior, K. IGS/BIPM pilot project: GPS carrier phase for time/frequency transfer and timescale formation. Metrologia 2003, 40, 270–288. [Google Scholar] [CrossRef]
- Ray, J.; Senior, K. Geodetic Techniques for Time and Frequency Comparisons Using GPS Phase and Code Measurements. Metrologia 2005, 42, 215–232. [Google Scholar] [CrossRef] [Green Version]
- Petit, G.; Jiang, Z. Precise point positioning for TAI computation. Int. J. Navig. Obs. 2008, 1–8. [Google Scholar] [CrossRef]
- Kouba, J.; Heroux, P. Precise point positioning using IGS orbit and clock products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
- Dach, R.; Beutler, G.; Hugentobler, U.; Schaer, S.; Schildknecht, T.; Springer, T.; Dudle, G.; Prost, L. Time transfer using GPS carrier phase: Error propagation and results. J. Geod. 2003, 77, 1–14. [Google Scholar] [CrossRef]
- Hackman, C.; Levine, J.; Parker, T. A New Technique for Estimating Frequency from GPS Carrier-Phase Time Transfer Data. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2004, 53, 1570–1583. [Google Scholar] [CrossRef]
- Hackman, C.; Levine, J.; Parker, T.E.; Piester, D.; Becker, J. A straight forward frequency estimation technique for GPS carrier-phase time transfer. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2006, 53, 1570–1583. [Google Scholar] [CrossRef]
- Senior, K.; Powers, E.; Matsakis, D. Attenuating Day-Boundary Discontinuities in GPS Carrier–Phase Time Transfer. In Proceedings of the 31st Precise Time and Time Interval Systems and Application(PTTI) Meeting, Dana Point, CA, USA, 7–9 December 1999; pp. 481–490. [Google Scholar]
- Dach, R.; Hugentobler, U.; Schildknecht, T.; Bernier, L.-G.; Dudle, G. Precise Continuous Time and Frequency transfer using GPS carrier phase. In Proceedings of the 2005 IEEE International Frequency Control Symposium and Exposition, Vancouver, BC, Canada, 29–31 August 2005; pp. 329–336. [Google Scholar]
- Defraigne, P.; Bruyninx, C. On the link between GPS pseudorange noise and day-boundary dis continuities in geodetic time transfer solutions. GPS Solut. 2007, 11, 239–249. [Google Scholar] [CrossRef]
- Bruyninx, C.; Defraigne, P. Frequency transfer using GPS code and phases: Short- and long-term stability. In Proceedings of the 31st Annual Precise Time and Time Interval (PTTI) Meeting, Dana Point, CA, USA, 7–9 December 1999; pp. 471–479. [Google Scholar]
- Dach, R.; Schildknecht, T.; Springer, T.; Dudle, G.; Prost, L. Continuous time transfer using GPS carrier phase. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2002, 49, 1480–1490. [Google Scholar] [CrossRef]
- Dach, R.; Schildknecht, T.; Hugentobler, U.; Bernier, L.-G.; Dudle, G. Continuous geodetic time transfer analysis methods. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2006, 53, 1250–1259. [Google Scholar] [CrossRef]
- Orgiazzi, D.; Tavella, P.; Lahaye, F. Further Characterization of the Time Transfer Capabilities of Precise Point Positioning (PPP): The Sliding Batch Procedure. In Proceedings of the 2005 Joint IEEE Int. Frequency Control Symp and Precise Time and Time Interval (PTTI) Systems and Applications Meeting, Vancouver, BC, Canada, 29–31 August 2005. [Google Scholar]
- Defraigne, P.; Bruyninx, C.; Guyennon, N. PPP and phase-only GPS time and frequency transfer. In Proceedings of the IEEE International Frequency Control Symposium Jointly with the 21st European Frequency and Time Forum, 30 May–2 June 2007; pp. 904–908. [Google Scholar]
- Yao, J.; Levine, J. A new algorithm to eliminate GPS carrier-phase time transfer boundary discontinuity. In Proceedings of the Proceedings of 2013 Precise Time and Time Interval (PTTI) Meeting, Bellevue, WA, USA, 2–5 December 2013. [Google Scholar]
- Laurichesse, D.; Mercier, F. Integer Ambiguity Resolution Undifferenced GPS Phase Measurements and its Application to PPP. In Proceedings of the 20th International Technical Meeting of the Satellite Divisionof The Institute of Navigation, Fort Worth, TX, USA, 25–28 September 2007. [Google Scholar]
- Delporte, J.; Mercier, F.; Laurichesse, D.; Galy, O. GPS Carrier-Phase Time Transfer Using Single-Difference Integer Ambiguity Resolution. Int. J. Navig. Observ. 2008, 2008, 273785. [Google Scholar] [CrossRef] [Green Version]
- Petit, G.; Kanj, A.; Loyer, S.; Delporte, J.; Mercier, F.; Perosanz, F. 1 × 10−16 frequency transfer by GPS PPP with integer ambiguity resolution. Metrologia 2015, 52, 301–309. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, H.; Shu, B. Research on time transfer: Based on BDS precise point positioning and accuracy comparison. Geod. Geodyn. 2017, 37, 1070–1073. [Google Scholar]
- Ge, Y.; Zhou, F.; Dai, P.; Qin, W.; Wang, S.; Yang, X. Precise point positioning time transfer with multi-GNSS single-frequency observations. Measurement 2019, 146, 628–642. [Google Scholar] [CrossRef]
- Zhang, X.; Guo, J.; Hu, Y.; Zhao, D.; He, Z. Research of Eliminating the Day-Boundary Discontinuities in GNSS Carrier Phase Time Transfer through Network Processing. Sensors 2020, 20, 2622. [Google Scholar] [CrossRef] [PubMed]
- Zhou, F.; Dong, D.; Li, P.; Li, X.; Schuh, H. Influence of stochastic modeling for inter-system biases on multi-GNSS undifferenced and uncombined precise point positioning. GPS Solut. 2019, 59, 23. [Google Scholar] [CrossRef]
- Kouba, J.; Springer, T. New IGS station and satellite clock combination. GPS Solut. 2001, 4, 31–36. [Google Scholar] [CrossRef]
- Kouba, J. A Guide to Using International GNSS Service (IGS) Products; Technical Report; International GNSS: Pasadena, CA, USA, 2009. [Google Scholar]
- Available online: ftp://igs.org/pub/center/analysis/code.acn (accessed on 10 November 2020).
- Arnold, D.; Meindl, M.; Beutler, G.; Dach, R.; Schaer, S.; Lutz, S.; Prange, L.; Sosnica, K.; Mervart, L.; Jäggi, A. CODE’s new solar radiation pressure model for GNSS orbit determination. GPS Solut. 2015, 89, 775–791. [Google Scholar] [CrossRef] [Green Version]
- Prange, L.; Orliac, E.; Dach, R.; Arnold, D.; Beutler, G.; Schaer, S.; Jäggi, A. CODE’s five-system orbit and clock solution—The challenges of multi-GNSS data analysis. J. Geod. 2017, 91, 345–360. [Google Scholar] [CrossRef] [Green Version]
- Dach, R.; Schaer, S.; Arnold, D.; Lutz, S.; Bock, H.; Orliac, E.; Prange, L.; Bertone, S.; Jean, Y.; Meyer, U.; et al. Activities at the CODE Analysis Center. In Proceedings of the IGS Workshop 2018, Wuhan, China, 29 October–2 November 2018. [Google Scholar]
- Prange, L.; Villiger, A.; Sidorov, D.; Schaer, S.; Beutler, G.; Dach, R.; Jäggi, A. Overview of CODE’s MGEX solution with the focus on Galileo. Adv. Space Res. 2020, 66, 2786–2798. [Google Scholar] [CrossRef]
- Steigenberger, P.; Hugentobler, U.; Loyer, S.; Perosanz, F.; Prange, L.; Dach, R.; Uhlemann, M.; Gendt, G.; Montenbruck, O. Galileo orbit and clock quality of the IGS Multi-GNSS Experiment. Adv. Space Res. 2015, 55, 269–281. [Google Scholar] [CrossRef]
- Guo, F.; Li, X.; Zhang, X.; Wang, J. Assessment of precise orbit and clock products for Galileo, BeiDou, and QZSS from IGS multi-GNSS experiment (MGEX). GPS Solut. 2017, 21, 279–290. [Google Scholar] [CrossRef]
- Steigenberger, P.; Montenbruck, O. Consistency of MGEX Orbit and Clock Products. Engineering 2020, 6, 898–903. [Google Scholar] [CrossRef]
- Loyer, S.; Mercier, F.; Capdeville, H.; Mezerette, A.; Perosanz, F. GR2 reprocessing from CNES/CLS IGS Analysis Center: Specificities and results. In Proceedings of the IGS Workshop 2014, Pasadena, CA, USA, 23–27 June 2014. [Google Scholar]
- Steigenberger, P.; Fritsche, M.; Dach, R.; Schmid, R.; Montenbruck, O.; Uhlemann, M.; Prange, L. Estimation of satellite antenna phase center offsets for Galileo. J. Geod. 2016, 90, 773–785. [Google Scholar] [CrossRef]
- Wang, B.; Chen, J.; Wang, B.H. Analysis of Galileo Clock Products of MGEX-ACs. In Proceedings of the The International Conference of 2019 European Navigation Conference (ENC), Warsaw, Poland, 9–12 April 2019. [Google Scholar]
- Loyer, S.; Perosanz, F.; Versini, L.; Katsigianni, G.; Mercier, F.; Mezerette, A. CNES/CLS IGS Analysis Center: Specificities and results. In Proceedings of the IGS Workshop of 2018, Wuhan, China, 29 October–2 November 2018. [Google Scholar]
- Ge, M.; Gendt, G.; Dick, G.; Zhang, F.P. Improving carrier-phase ambiguity resolution in global GPS network solutions. J. Geod. 2005, 79, 103–110. [Google Scholar] [CrossRef]
- Griffiths, J.; Jim, R. Sub-daily alias and draconitic errors in the IGS orbits. GPS Solut. 2013, 17, 413–422. [Google Scholar] [CrossRef]















| Station | Receiver | Country | Antenna | External Reference |
|---|---|---|---|---|
| PTBB | SEPT POLARX5TR | Germany | LEIAR25.R4 | UTC(PTB) |
| SPT0 | SEPT POLARX5TR | Sweden | LEIAR25.R4 | UTC(SP) |
| WAB2 | SEPT POLARX5TR | Switzerland | SEPCHOKE_B3E6 | UTC(CH) |
| OP71 | SEPT POLARX4TR | France | LEIAR25.R4 | UTC(OP) |
| ROAG | SEPT POLARX5TR | Spain | LEIAR25.R4 | UTC(ROA) |
| USN8 | SEPT POLARX5TR | USA | TPSCR.G5 | UTC(USNO) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Guo, J.; Hu, Y.; Sun, B.; Wu, J.; Zhao, D.; He, Z. Influence of Precise Products on the Day-Boundary Discontinuities in GNSS Carrier Phase Time Transfer. Sensors 2021, 21, 1156. https://doi.org/10.3390/s21041156
Zhang X, Guo J, Hu Y, Sun B, Wu J, Zhao D, He Z. Influence of Precise Products on the Day-Boundary Discontinuities in GNSS Carrier Phase Time Transfer. Sensors. 2021; 21(4):1156. https://doi.org/10.3390/s21041156
Chicago/Turabian StyleZhang, Xiangbo, Ji Guo, Yonghui Hu, Baoqi Sun, Jianfeng Wu, Dangli Zhao, and Zaimin He. 2021. "Influence of Precise Products on the Day-Boundary Discontinuities in GNSS Carrier Phase Time Transfer" Sensors 21, no. 4: 1156. https://doi.org/10.3390/s21041156







