High Sensitivity Plasmonic Sensor Based on Fano Resonance with Inverted U-Shaped Resonator
Abstract
:1. Introduction
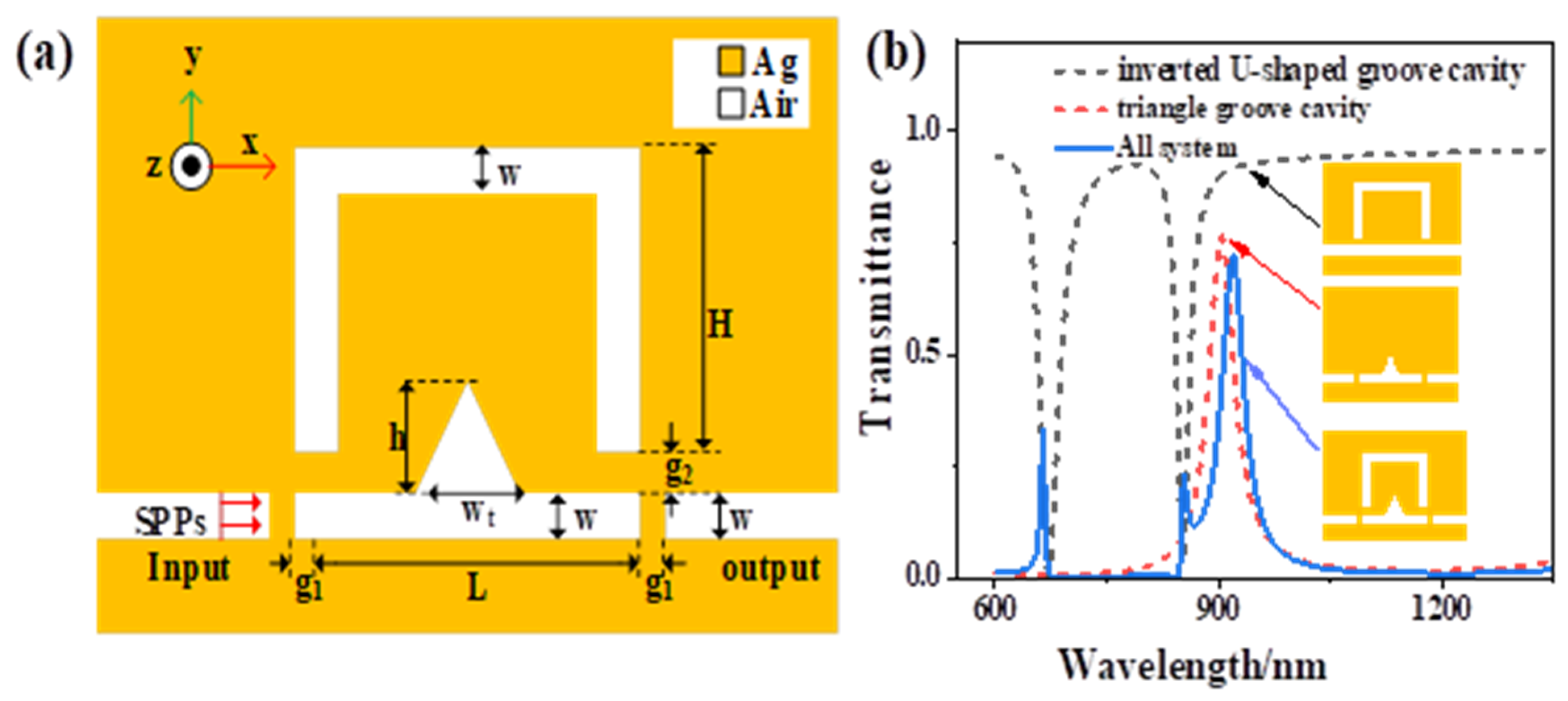
2. Model and Theoretical Analysis
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Homola, J.; Yee, S.S.; Gauglitz, G. Surface plasmon resonance sensors. Sens. Actuators B Chem. 1999, 54, 3–15. [Google Scholar] [CrossRef]
- Anker, J.N.; Hall, W.P.; Lyandres, O.; Shah, N.C.; Zhao, J.; Van Duyne, R.P. Biosensing with plasmonic nanosensors. Nanosci. Technol. 2010, 308–319. [Google Scholar] [CrossRef]
- Xu, Y.; Bai, P.; Zhou, X.; Akimov, Y.; Png, C.E.; Ang, L.; Knoll, W.; Wu, L. Optical Refractive Index Sensors with Plasmonic and Photonic Structures: Promising and Inconvenient Truth. Adv. Opt. Mater. 2019, 7, 7. [Google Scholar] [CrossRef]
- Sekkat, Z.; Hayashi, S.; Nesterenko, D.V.; Rahmouni, A.; Refki, S.; Ishitobi, H.; Inouye, Y.; Kawata, S. Plasmonic coupled modes in metal-dielectric multilayer structures: Fano resonance and giant field enhancement. Opt. Express 2016, 24, 20080–20088. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Liu, X.; Li, L.; He, J.; Fan, C.; Tian, Y.; Ding, P.; Chen, D.; Xue, Q.; Liang, E. Huge electric field enhancement and highly sensitive sensing based on the Fano resonance effect in an asymmetric nanorod pair. J. Opt. 2013, 15, 105003. [Google Scholar] [CrossRef]
- Hayashi, S.; Nesterenko, D.V.; Sekkat, Z. Waveguide-coupled surface plasmon resonance sensor structures: Fano lineshape engineering for ultrahigh-resolution sensing. J. Phys. D Appl. Phys. 2015, 48, 325303. [Google Scholar] [CrossRef]
- Limonov, M.F.; Rybin, M.V.; Poddubny, A.N.; Kivshar, Y.S. Fano resonances in photonics. Nat. Photonics 2017, 11, 543–554. [Google Scholar] [CrossRef]
- Luk’Yanchuk, B.; Zheludev, N.I.; Maier, S.A.; Halas, N.J.; Nordlander, P.; Giessen, H.; Chong, C.T. The Fano resonance in plasmonic nanostructures and metamaterials. Nat. Mater. 2010, 9, 707–715. [Google Scholar] [CrossRef] [PubMed]
- Zheng, C.; Jia, T.; Zhao, H.; Xia, Y.; Zhang, S.; Feng, D.; Sun, Z.-R. Theoretical study on narrow Fano resonance of nanocrescent for the label-free detection of single molecules and single nanoparticles. RSC Adv. 2018, 8, 3381–3391. [Google Scholar] [CrossRef] [Green Version]
- Shuai, Y.; Zhao, D.; Chadha, A.S.; Seo, J.-H.; Yang, H.; Fan, S.; Ma, Z.; Zhou, W. Coupled double-layer Fano resonance photonic crystal filters with lattice-displacement. Appl. Phys. Lett. 2013, 103, 241106. [Google Scholar] [CrossRef]
- Mao, J.; Zhai, X.; Wang, L.; Li, H. Numerical analysis of near-infrared plasmonic filter with high Figof merit based on Fano resonance. Appl. Phys. Express 2017, 10, 082201. [Google Scholar] [CrossRef]
- Yan, S.; Zhang, M.; Zhao, X.; Zhang, Y.; Wang, J.; Jin, W. Refractive Index Sensor Based on a Metal–Insulator–Metal Waveguide Coupled with a Symmetric Structure. Sensors 2017, 17, 2879. [Google Scholar] [CrossRef] [Green Version]
- Yu, S.; Zhao, T.; Yu, J.; Pan, D. Tuning Multiple Fano Resonances for On-Chip Sensors in a Plasmonic System. Sensors 2019, 19, 1559. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, B.; Meng, H.; Wang, Q.; Wang, H.; Zhang, X.; Yu, W.; Tan, C.; Huang, X.; Wang, F. Plasmonic-Induced Transparency and Slow-Light Effect Based on Stub Waveguide with Nanodisk Resonator. Plasmon 2016, 11, 543–550. [Google Scholar] [CrossRef]
- Li, D.; Du, K.; Liang, S.; Zhang, W.; Mei, T. Wide band dispersionless slow light in hetero-MIM plasmonic waveguide. Opt. Express 2016, 24, 22432. [Google Scholar] [CrossRef] [PubMed]
- Nozaki, K.; Shinya, A.; Matsuo, S.; Sato, T.; Kuramochi, E.; Notomi, M. Ultralow-energy and high-contrast all-optical switch involving Fano resonance based on coupled photonic crystal nanocavities. Opt. Express 2013, 21, 11877–11888. [Google Scholar] [CrossRef] [PubMed]
- Zayats, A.V.; Smolyaninov, I.I.; Maradudin, A.A. Nano-optics of surface plasmon polaritons. Phys. Rep. 2005, 408, 131–314. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Zhang, Y.; Mølmer, K. Surface Plasmon Launching by Polariton Superradiance. ACS Photonics 2019, 6, 871–877. [Google Scholar] [CrossRef] [Green Version]
- Lin, X.-S.; Huang, X. Tooth-shaped plasmonic waveguide filters with nanometeric sizes. Opt. Lett. 2008, 33, 2874–2876. [Google Scholar] [CrossRef]
- Gramotnev, D.K.; Bozhevolnyi, S.I. Plasmonics beyond the diffraction limit. Nat. Photonics 2010, 4, 83–91. [Google Scholar] [CrossRef]
- Zhang, Z.; Luo, L.; Xue, C.; Zhang, W.; Yan, S. Fano Resonance Based on Metal-Insulator-Metal Waveguide-Coupled Double Rectangular Cavities for Plasmonic Nanosensors. Sensors 2016, 16, 642. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, X.; Zhang, Z.; Yan, S. Tunable Fano Resonance in Asymmetric MIM Waveguide Structure. Sensors 2017, 17, 1494. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, X.; Hua, E.; Wang, M.; Wang, Y.; Wen, F.; Yan, S. Fano Resonance in a MIM Waveguide with Two Triangle Stubs Coupled with a Split-Ring Nanocavity for Sensing Application. Sensors 2019, 19, 4972. [Google Scholar] [CrossRef] [Green Version]
- Kabashin, A.V.; Evans, P.; Pastkovsky, S.; Hendren, W.; Wurtz, G.A.; Atkinson, R.; Pollard, R.; Podolskiy, V.A.; Zayats, A.V. Plasmonc nanorod metamaterials for biosensing. Nat. Mater. 2009, 8, 867–871. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Zhou, J.; Liu, T.; Tao, Y.; Jiang, R.; Liu, M.; Xiao, G.; Zhu, J.; Zhou, Z.-K.; Wang, X.; et al. Plasmonic gold mushroom arrays with refractive index sensing figures of merit approaching the theoretical limit. Nat. Commun. 2013, 4, 2381. [Google Scholar] [CrossRef] [PubMed]
- Kravets, V.G.; Schedin, F.; Jalil, R.; Britnell, L.; Gorbachev, R.V.; Ansell, D.; Thackray, B.; Novoselov, K.S.; Geim, A.K.; Kabashin, A.V.; et al. Singular phase nano-optics in plasmonic metamaterials for label-free single-molecule detection. Nat. Mater. 2013, 12, 304–309. [Google Scholar] [CrossRef] [PubMed]
- Sreekanth, K.V.; Alapan, Y.; ElKabbash, M.; Ilker, E.; Hinczewski, M.; Gurkan, U.A.; De Luca, A.; Strangi, G. Extreme sensitivity biosensing platform based on hyperbolic metamaterials. Nat. Mater. 2016, 15, 621–627. [Google Scholar] [CrossRef] [Green Version]
- Garoli, D.; Calandrini, E.; Giovannini, G.; Hubarevich, A.; Caligiuri, V.; De Angelis, F. Nanoporous gold metamaterials for high sensitivity plasmonic sensing. Nanoscale Horiz. 2019, 4, 1153–1157. [Google Scholar] [CrossRef]
- Li, Z.; Wen, K.; Chen, L.; Lei, L.; Zhou, J.; Zhou, D.; Fang, Y.; Wu, B. Refractive index sensor based on multiple Fano resonances in a plasmonic MIM structure. Appl. Opt. 2019, 58, 4878–4883. [Google Scholar] [CrossRef]
- Li, S.; Wang, Y.; Jiao, R.; Wang, L.; Duan, G.; Yu, L. Fano resonances based on multimode and degenerate mode interference in plasmonic resonator system. Opt. Express 2017, 25, 3525–3533. [Google Scholar] [CrossRef]
- Qi, J.; Chen, Z.; Chen, J.; Li, Y.; Qiang, W.; Xu, J.; Qian, S. Independently tunable double Fano resonances in asymmetric MIM waveguide structure. Opt. Express 2014, 22, 14688–14695. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Zhang, Y.; Song, X.; Wang, Y.; Yu, L. Tunable triple Fano resonances based on multimode interference in coupled plasmonic resonator system. Opt. Express 2016, 24, 15351–15361. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Chen, H.; Zhang, Z.; Tang, J.; Cui, J.; Xue, C.; Yan, S. Transmission and refractive index sensing based on Fano resonance in MIM waveguide-coupled trapezoid cavity. Aip Adv. 2017, 7, 015020. [Google Scholar] [CrossRef] [Green Version]
- Alipour, A.; Farmani, A.; Mir, A. High Sensitivity and Tunable Nanoscale Sensor Based on Plasmon-Induced Transparency in Plasmonic Metasurface. IEEE Sens. J. 2018, 18, 7047–7054. [Google Scholar] [CrossRef]
- Wang, L.; Zeng, Y.P.; Wang, Z.Y.; Xia, X.P.; Liang, Q.Q. A refractive index sensor based on an analogy T shaped metal–insulator–metal waveguide. Optik 2018, 172, 1199–1204. [Google Scholar] [CrossRef]
- Rifat, A.A.; Rahmani, M.; Xu, L.; Miroshnichenko, A.E. Hybrid metasurface based tunable near-perfect absorber and plasmonic sensor. Materials 2018, 11, 1091. [Google Scholar] [CrossRef] [Green Version]
- Qiao, L.; Zhang, G.; Wang, Z.; Fan, G.; Yan, Y. Study on the Fano resonance of coupling M-type cavity based on surface plasmon polaritons. Opt. Commun. 2019, 433, 144–149. [Google Scholar] [CrossRef]
- El Haffar, R.; Farkhsi, A.; Mahboub, O. Optical properties of MIM plasmonic waveguide with an elliptical cavity resonator. Appl. Phys. A 2020, 126, 1–10. [Google Scholar] [CrossRef]
- Chen, F.; Zhang, H.; Sun, L.; Li, J.; Yu, C. Temperature tunable Fano resonance based on ring resonator side coupled with a MIM waveguide. Opt. Laser Technol. 2019, 116, 293–299. [Google Scholar] [CrossRef]






| Reference | Year | S (nm/RIU) | FOM | Structure |
|---|---|---|---|---|
| [21] | 2016 | 596 | 7.5 | Double rectangular cavity |
| [22] | 2017 | 718 | 4354 | Asymmetric ring cavity |
| [31] | 2014 | 600 | 650 | Rectangular cavity |
| [32] | 2016 | 600 | 3803 | Two rectangular cavity |
| [33] | 2017 | 750 | 68.3 | Trapezoid cavity |
| [34] | 2018 | 497.8 | 480 | Plasmonic metasurface |
| [35] | 2018 | 680 | 8.68 | T shaped cavity |
| [36] | 2018 | 350 | 15 | Hybrid Metasurface |
| [37] | 2019 | 780 | 1.56 × 105 | M-type resonant cavity |
| [38] | 2020 | 540 | 101.3 | Elliptical cavity |
| This work | 2020 | 840 | 3.9 × 105 | Inverted U cavity |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, G.; Xu, Y.; Yang, H.; Ou, Z.; Chen, J.; Li, H.; Liu, X.; Zeng, L.; Li, J. High Sensitivity Plasmonic Sensor Based on Fano Resonance with Inverted U-Shaped Resonator. Sensors 2021, 21, 1164. https://doi.org/10.3390/s21041164
Xiao G, Xu Y, Yang H, Ou Z, Chen J, Li H, Liu X, Zeng L, Li J. High Sensitivity Plasmonic Sensor Based on Fano Resonance with Inverted U-Shaped Resonator. Sensors. 2021; 21(4):1164. https://doi.org/10.3390/s21041164
Chicago/Turabian StyleXiao, Gongli, Yanping Xu, Hongyan Yang, Zetao Ou, Jianyun Chen, Haiou Li, Xingpeng Liu, Lizhen Zeng, and Jianqing Li. 2021. "High Sensitivity Plasmonic Sensor Based on Fano Resonance with Inverted U-Shaped Resonator" Sensors 21, no. 4: 1164. https://doi.org/10.3390/s21041164
APA StyleXiao, G., Xu, Y., Yang, H., Ou, Z., Chen, J., Li, H., Liu, X., Zeng, L., & Li, J. (2021). High Sensitivity Plasmonic Sensor Based on Fano Resonance with Inverted U-Shaped Resonator. Sensors, 21(4), 1164. https://doi.org/10.3390/s21041164








