Research on a Measurement Method for Downhole Drill String Eccentricity Based on a Multi-Sensor Layout
Abstract
:1. Introduction
2. The Composition and Operation Characteristics of the Downhole Drill String
2.1. Composition of the Bottom Drill String
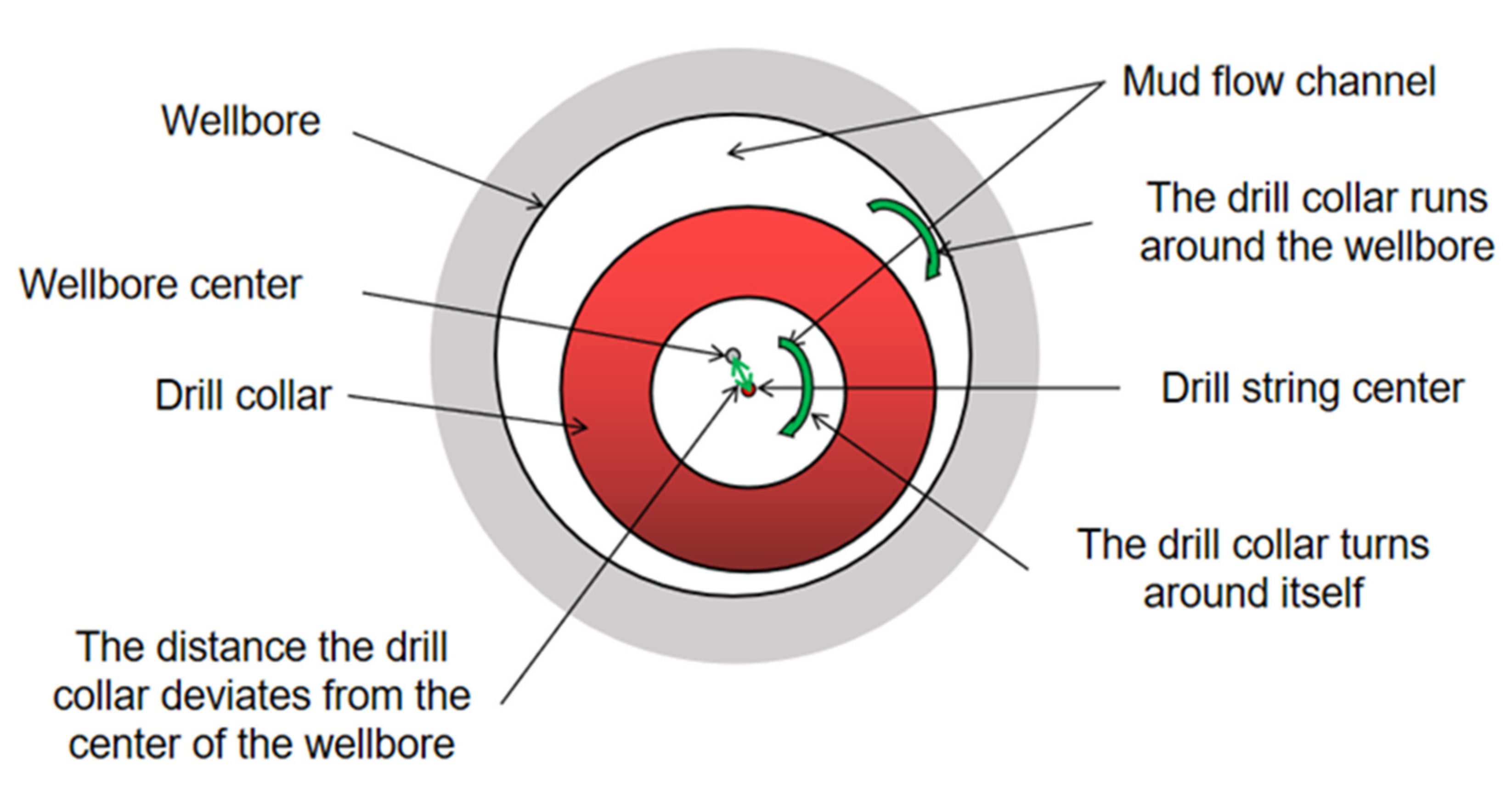
2.2. Causes of Drill String Eccentricity
2.3. Operational Characteristics of the Drill String
2.4. Influence of Eccentric Factors on Measurement
3. Borehole Eccentricity Multi-Sensor Measurement Principle and Measurement Method
3.1. Composition of Sensors for Measuring Drill String Eccentricity
3.2. Acquisition of Multi-Directional Diameter and Drill Collar Attitude
3.2.1. Obtain Borehole Inclination, Azimuth, and Tool Face
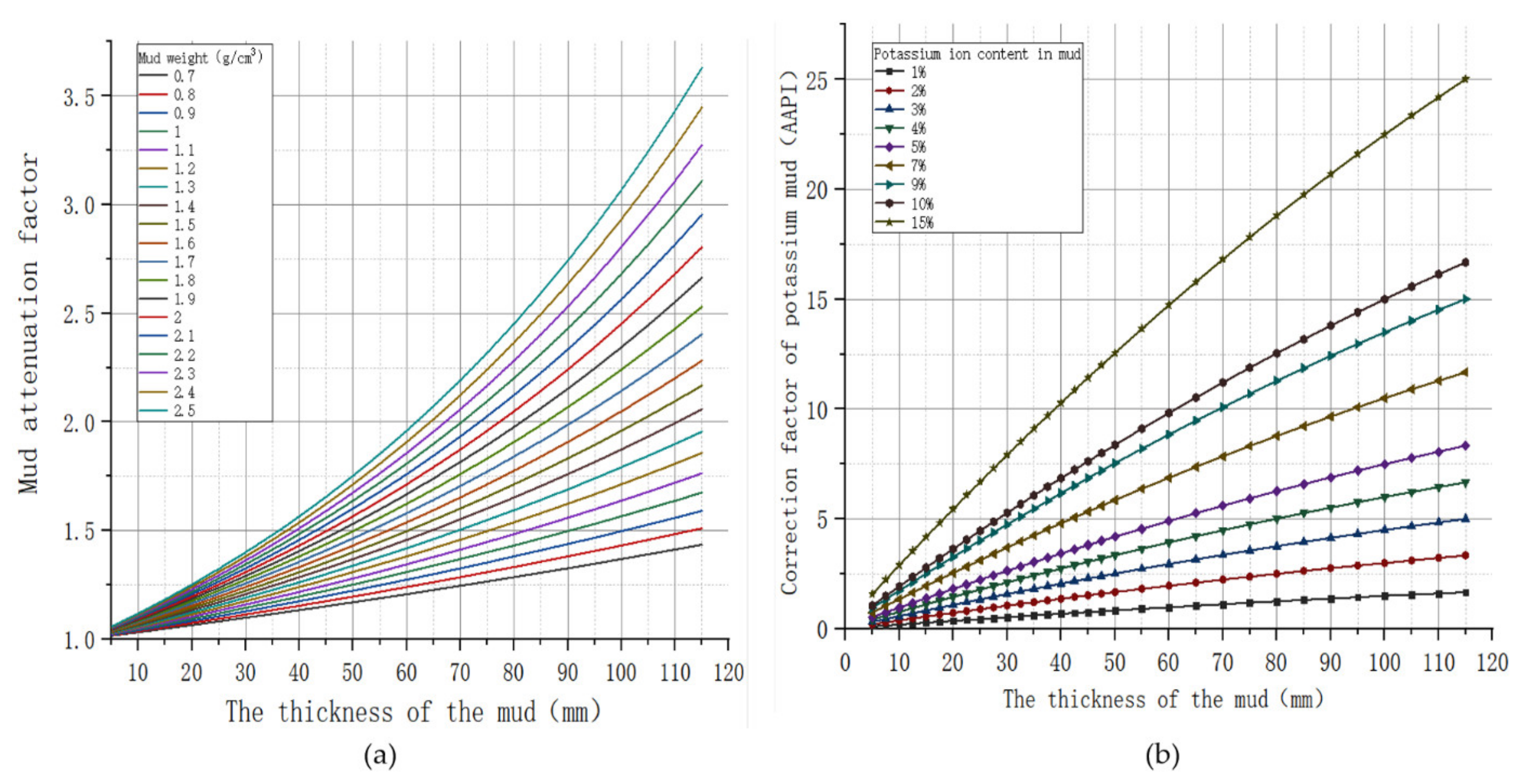
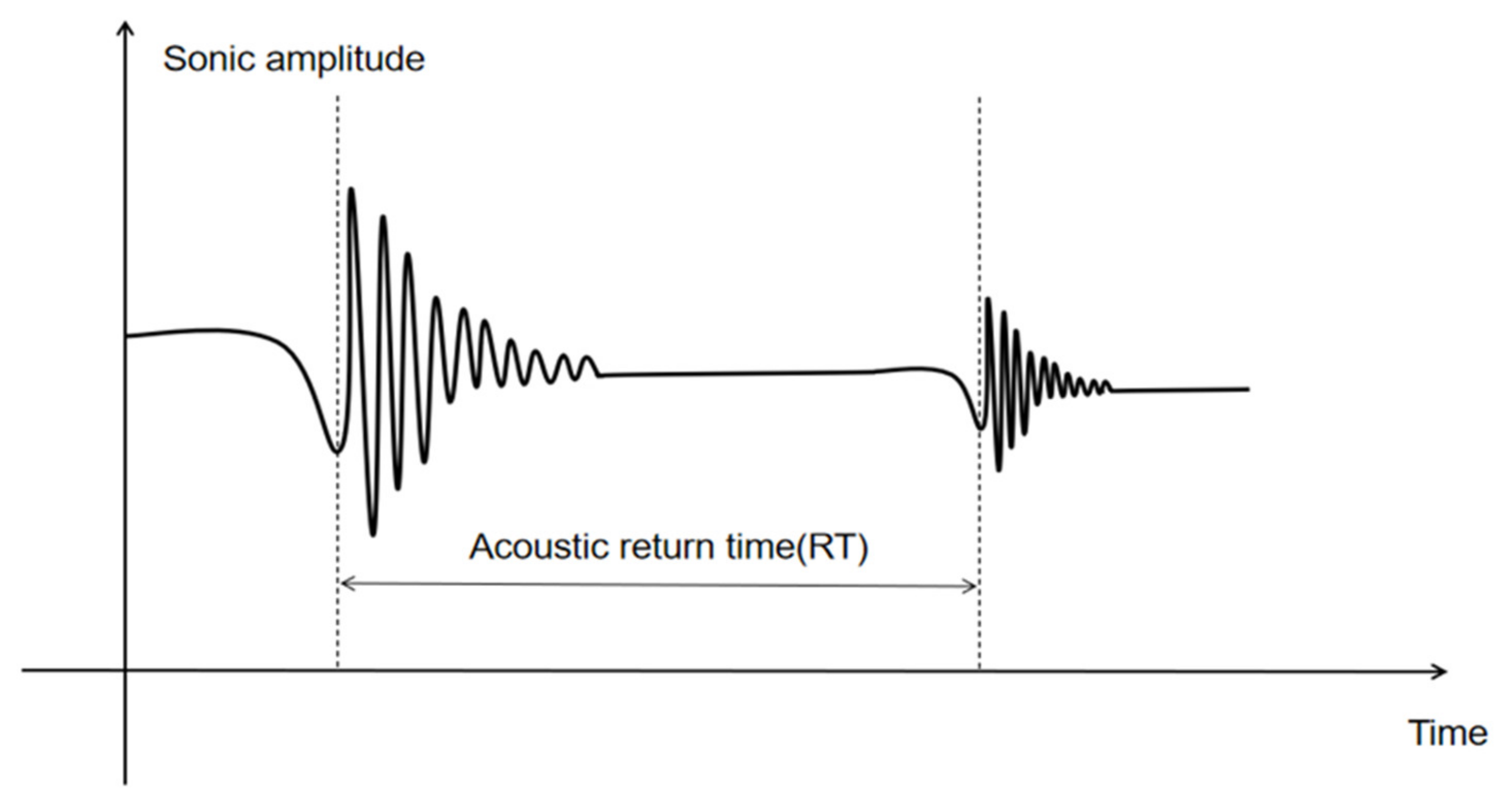
3.2.2. Calipers Sensor
3.3. Methods and Equations for Determining the Eccentricity of Two Groups of Sensors
3.4. Representation of Eccentricity Matrix at a Measuring Point Along the Drill Collar
4. Simulation Analysis and Field Test of Drill String Eccentricity State
4.1. Analysis of Eccentricity Characteristics in Case of No Bending of Drill String and Zero Included Angle
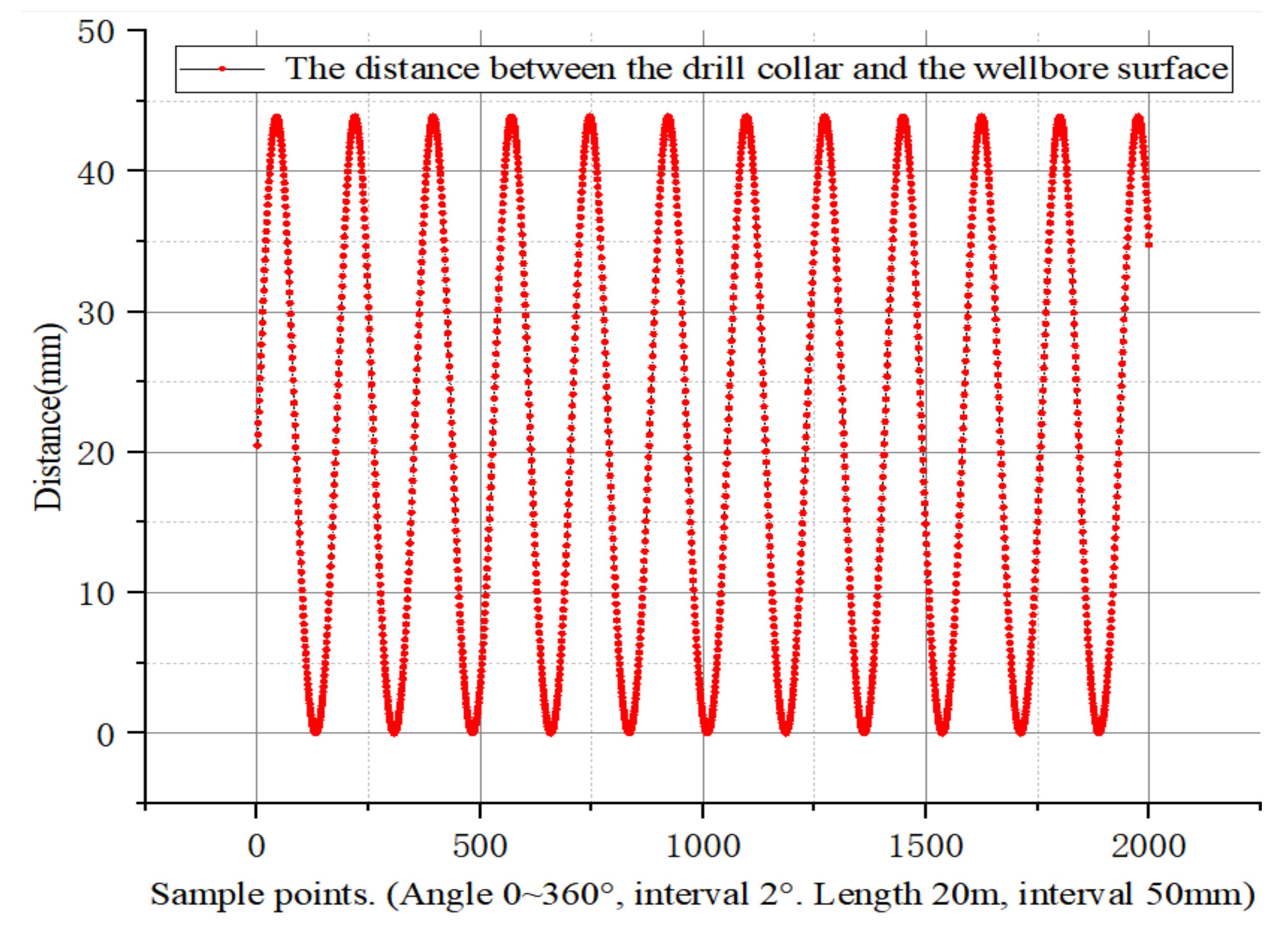
4.1.1. Center Rotation
4.1.2. Eccentric Rotation
4.2. Analysis of Eccentricity Characteristics in the Case of No Bending of Drill String and Included Angle Greater Than Zero
4.2.1. Tilting Rotation
4.2.2. Tilting Rotation 60 RPM and Revolution
4.3. Analysis of Eccentric Characteristics of the Drill String with Bending
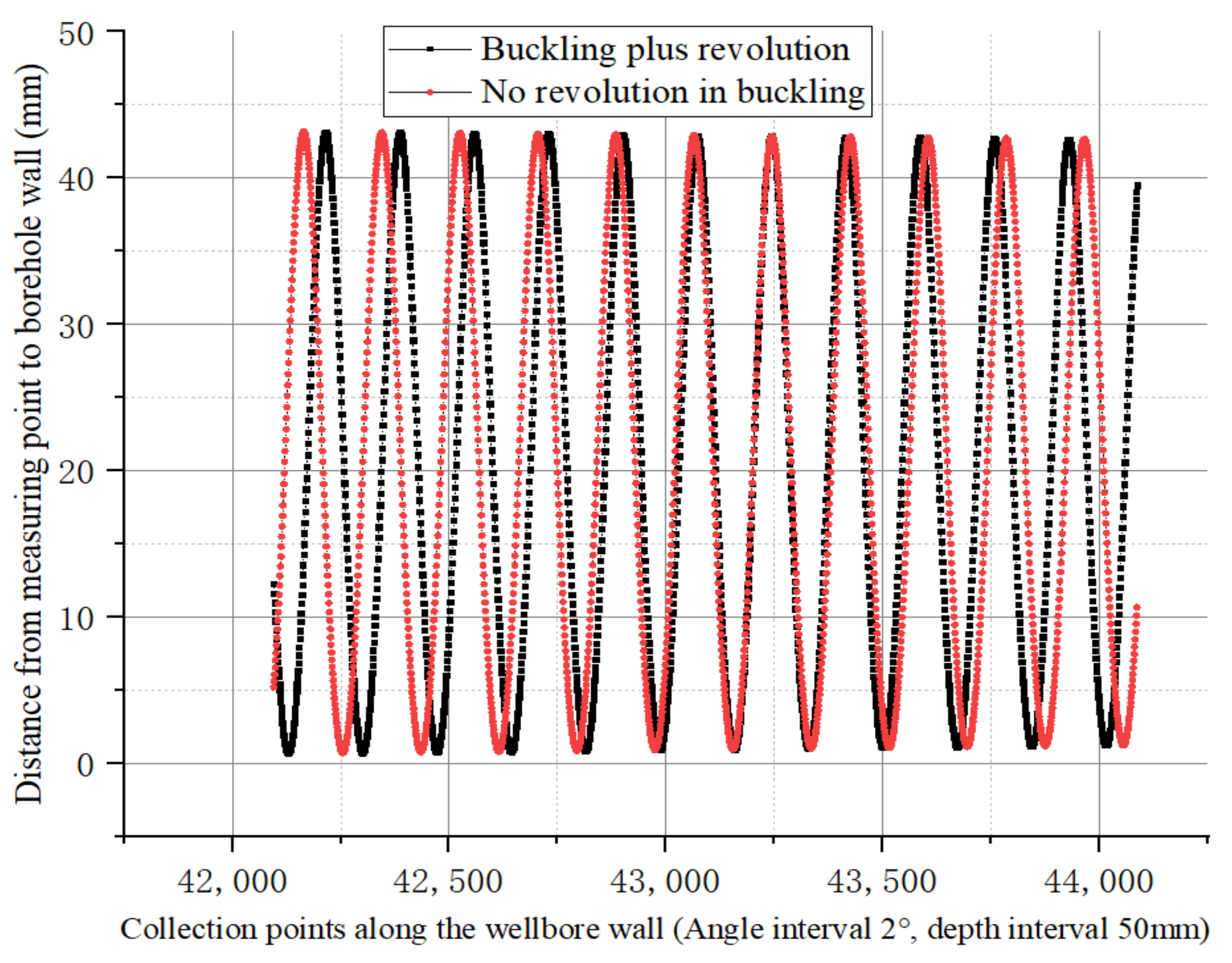
4.3.1. Buckling Rotation without Revolution
4.3.2. There Is Revolution in Buckling
4.4. Analysis and Discussion of Drill String Eccentricity Characteristics
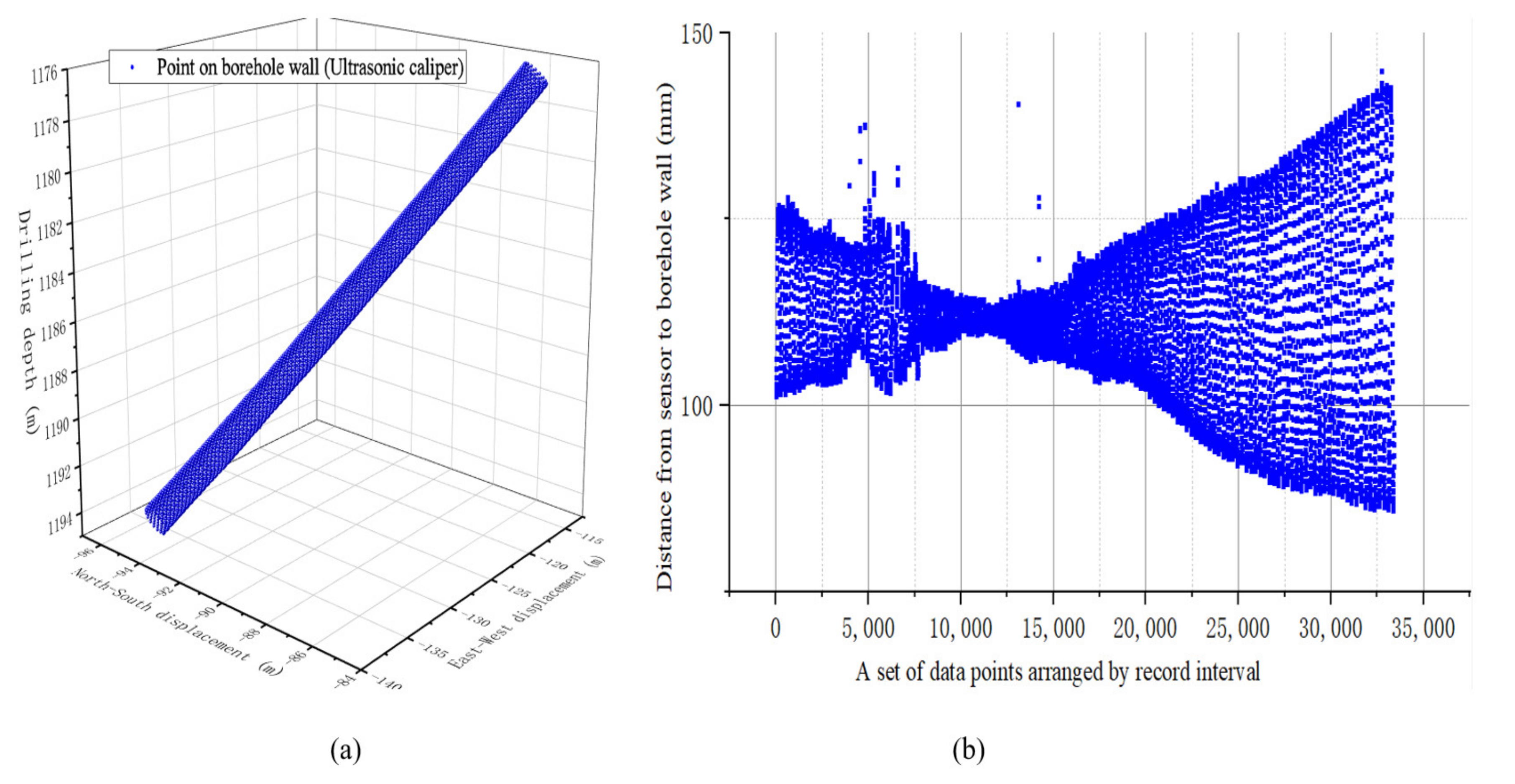
4.5. Field Test
5. Discussion and Conclusions
5.1. Discussion
5.2. Conclusions
- (1)
- The multi-sensor layout scheme proposed in this paper can separate the rotation and revolution velocities of drill collars in the wellbore and analyze the eccentric characteristics of drill collars in the wellbore.
- (2)
- The inclination, parallel eccentricity, buckling, and revolution of the drill string are all related to the distance between the measuring point and the borehole wall.
- (3)
- Under the conditions of a relatively regular wellbore and a relatively regular downhole movement of drill collars, the matrix of distance between each measuring tool face and wellbore wall distributed along the axis of drill collars at each measurement point was obtained.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yan, C.; Li, Y.; Yan, X.; Cheng, Y.; Han, Z.; Tian, W.; Ren, X. Wellbore shrinkage during drilling in methane hydrate reservoirs. Energy Sci. Eng. 2019, 7, 930–942. [Google Scholar] [CrossRef] [Green Version]
- Zeynali, M.E. Mechanical and physico-chemical aspects of wellbore stability during drilling operations. J. Pet. Sci. Eng. 2012, 82, 120–124. [Google Scholar] [CrossRef]
- Erge, O.; Ozbayoglu, E.M.; Miska, S.; Yu, M.; Takach, N.; Saasen, A.; May, R. The effects of drill string-eccentricity,-rotation, and-buckling configurations on annular frictional pressure losses while circulating yield-power-law fluids. SPE Drill. Completion 2015, 30, 257–271. [Google Scholar] [CrossRef]
- Dokhani, V.; Ma, Y.; Li, Z.; Geng, T.; Yu, M. Effects of drill string eccentricity on frictional pressure losses in annuli. J. Pet. Sci. Eng. 2020, 187, 106853. [Google Scholar] [CrossRef]
- Heydari, O.; Sahraei, E.; Skalle, P. Investigating the impact of drillpipe’s rotation and eccentricity on cuttings transport phenomenon in various horizontal annuluses using computational fluid dynamics (CFD). J. Pet. Sci. Eng. 2017, 156, 801–813. [Google Scholar] [CrossRef]
- Erge, O.; van Oort, E. Modeling Cuttings Transport and Annular Pack-Off Using Local Fluid Velocities with the Effects of Drill string Rotation and Eccentricitz. In IADC/SPE International Drilling Conference and Exhibition; Society of Petroleum Engineers: Richardson, TX, USA, 2020. [Google Scholar]
- Butlin, T.; Langley, R.S. An efficient model of drill string dynamics. J. Sound Vib. 2015, 35, 100–123. [Google Scholar] [CrossRef] [Green Version]
- Ambrus, A.; Skadsem, H.J.; Mihai, R.G. Similarity analysis for downscaling a full size drill string to a laboratory scale test drilling rig. In Proceedings of the ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering, Madrid, Spain, 17–22 June 2018. [Google Scholar]
- Westermann, H.; Gorelik, I.; Rudat, J.; Moritz, C.; Neubauer, M.; Wallaschek, J.; Hohn, O. A new test rig for experimental studies of drill string vibrations. SPE Drill. Completion 2015, 30, 119–128. [Google Scholar] [CrossRef]
- Gulyayev, V.I.; Shevchuk, L.V. Drill string bit whirl simulation with the use of frictional and nonholonomic models. J. Vib. Acoust. 2016, 138, 011021. [Google Scholar] [CrossRef]
- Feng, T.; Vadali, M.; Chen, D. Modeling and Analysis of Directional Drilling Dynamics. In Proceedings of the ASME 2017 Dynamic Systems and Control Conference, Tysons, VA, USA, 11–13 October 2017. [Google Scholar]
- Grydzhuk, J.; Chudyk, I.; Velychkovych, A.; Andrusyak, A. Analytical estimation of inertial properties of the curved rotating section in a drill string. East. Eur. J. Enterp. Technol. 2019, 1, 6–14. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Tao, G.; Fehler, M.C. Investigation of the high-frequency wavefield of an off-center monopole acoustic logging-while-drilling tool. Geophysics 2015, 80, D329–D341. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Wang, H. Investigation of eccentricity effects and depth of investigation of azimuthal resistivity LWD tools using 3D finite difference method. J. Pet. Sci. Eng. 2016, 143, 211–225. [Google Scholar] [CrossRef]
- Xue, Q. Signal Processing in Logging While Drilling. In Data Analytics for Drilling Engineering; Springer: Cham, Switzerland, 2020; pp. 247–278. [Google Scholar]
- Liu, J.; Wu, H.; Zhang, F.; Liu, S.; Liu, Z.; Yan, H. Improvement in the method for borehole caliper measurement based on azimuthal gamma-gamma density well logging. Appl. Radiat. Isot. 2019, 145, 68–72. [Google Scholar] [CrossRef] [PubMed]
- Solberg, L.; Titjen, J.; Morris, S. Borehole stability applications using high-resolution LWD acoustic caliper images[C]//Third EAGE Borehole Geology Workshop. Eur. Assoc. Geosci. Eng. 2019, 2019, 1–5. [Google Scholar]
- Al-Ameri, A.; Bandyopadhyay, I.; Balbaheeth, A.H.; Bittar, M.; Aki, A.L.; Essam, R. Improved Formation Evaluation with Inversion Techniques using Logging While Drilling Azimuthal Deep Resistivity Sensor—A Case Study. In Proceedings of the SPWLA 56th Annual Logging Symposium, Long Beach, CA, USA, 18–22 July 2015. [Google Scholar]
- Zhen, Y.; Jinzhou, Y.; Laiju, H. A real-time borehole correction of electromagnetic wave resistivity logging while drilling. Pet. Explor. Dev. 2013, 40, 671–675. [Google Scholar]
- Lubinski, A.; Woods, H.B. Factors affecting the angle of inclination and dog-legging in rotary bore holes. In Drilling and Production Practice; American Petroleum Institute: Washington, DC, USA, 1953. [Google Scholar]
- Dellinger, T.B.; Gravley, W.; Walraven, J.E. Preventing Buckling in Drill String. U.S. Patent 4,384,483A, 24 May 1983. [Google Scholar]
- Dawson, R. Drill pipe buckling in inclined holes. J. Pet. Technol. 1984, 36, 1734–1738. [Google Scholar] [CrossRef]
- Tao, H.; Yongming, L.; Shisheng, W.; Zhiyong, H. Test of drilling string stability. Pet. Drill. Tech. 1999, 10, 10–15. [Google Scholar]
- Wang, L.; Zhang, C.; Lin, T.; Li, X.; Wang, T. Characterization of a fiber optic gyroscope in a measurement while drilling system with the dynamic Allan variance. Measurement 2015, 75, 263–272. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.; Deng, Y.; Noureldin, A.; Li, P. Drilling trajectory survey technology based on 3D RISS with a single fiber optic gyroscope. Optik 2020, 203, 163971. [Google Scholar] [CrossRef]
- Song, R.; Chen, X.; Huang, H. Nonstationary dynamic stochastic error analysis of fiber optic gyroscope based on optimized Allan variance. Sens. Actuators A Phys. 2018, 276, 26–33. [Google Scholar] [CrossRef]
- Xue, Q.; Wang, R.; Liu, B.; Huang, L. Dynamic measurement of spatial attitude at bottom rotating drill string: Simulation, experimental, and field test. J. Energy Resour. Technol. 2016, 138, 022903. [Google Scholar] [CrossRef]
- Yao, Y.; Ju, X.; Lu, J.; Men, B. Acoustic emission and echo signal compensation techniques applied to an ultrasonic logging-while-drilling caliper. Sensors 2017, 17, 1351. [Google Scholar]
- Elahifar, B.; Esmaeili, A.; Fruhwirth, R.K.; Thonhauser, G. Real time measurement of borehole shape and calipers by using ultrasonic caliper in different drilling fluid and wellbore conditions for detecting instabilities. In Proceedings of the SPE Canadian Unconventional Resources Conference, Calgary, AB, Canada, 30 October–1 November 2012. [Google Scholar]






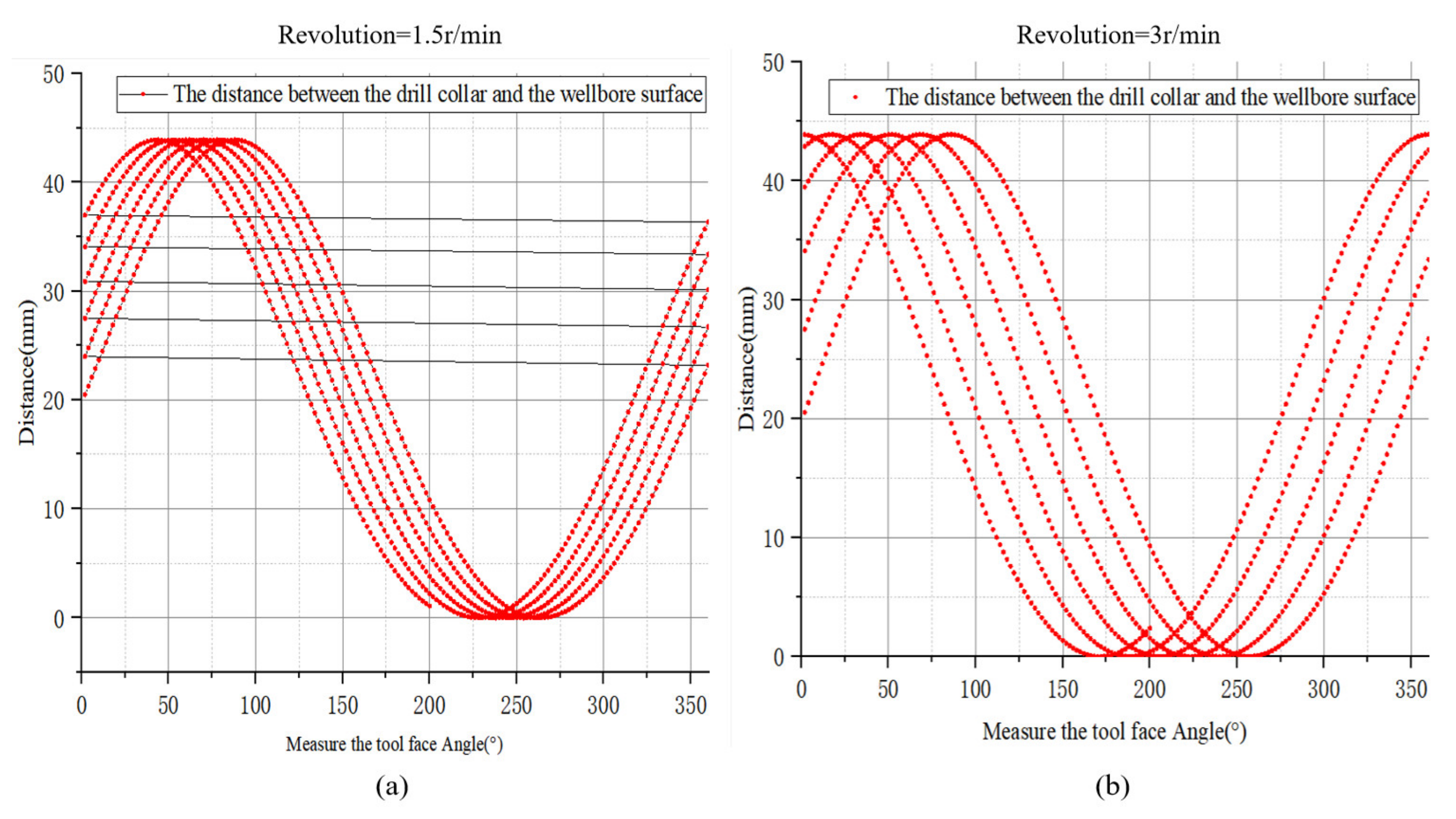

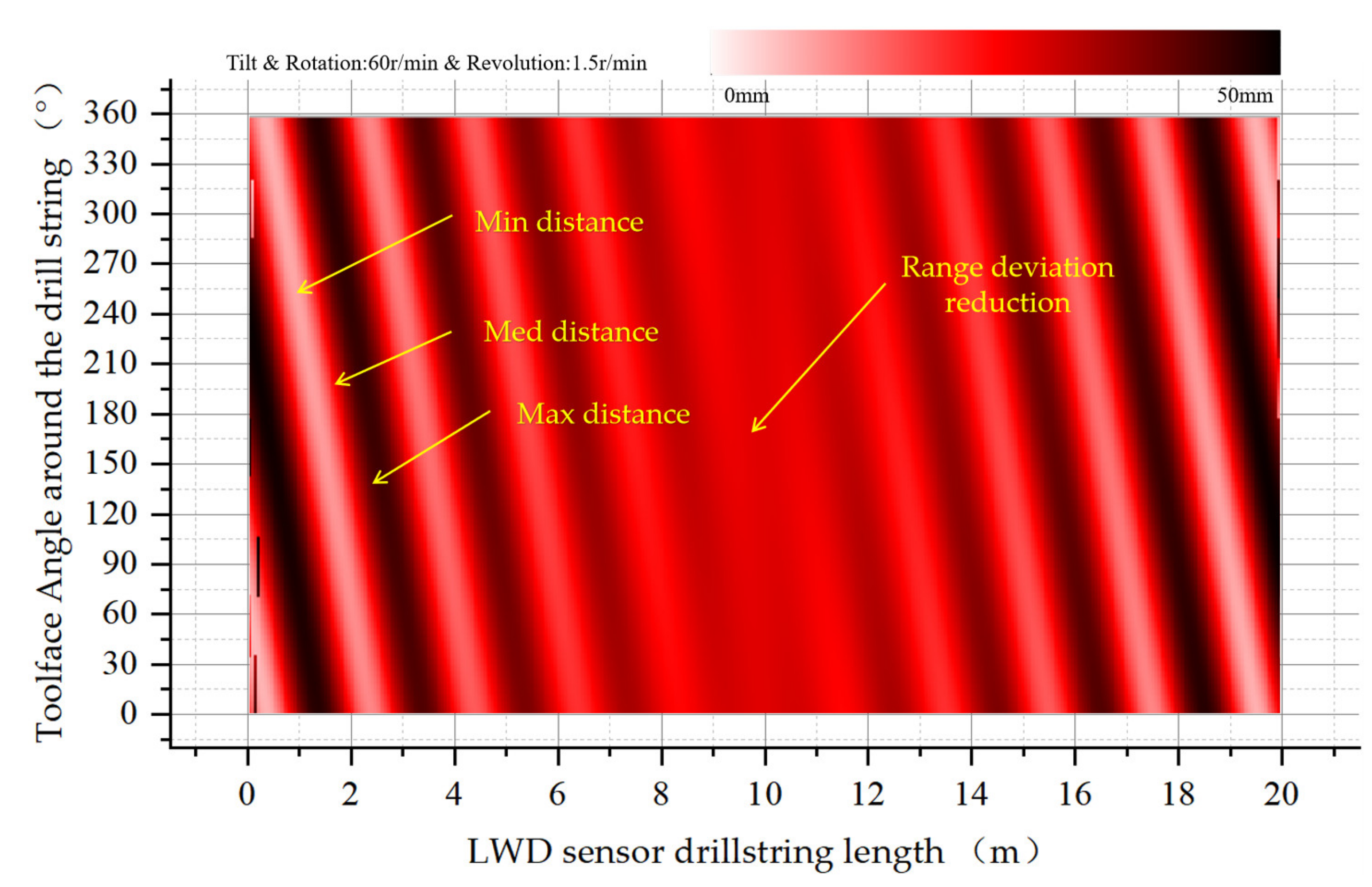
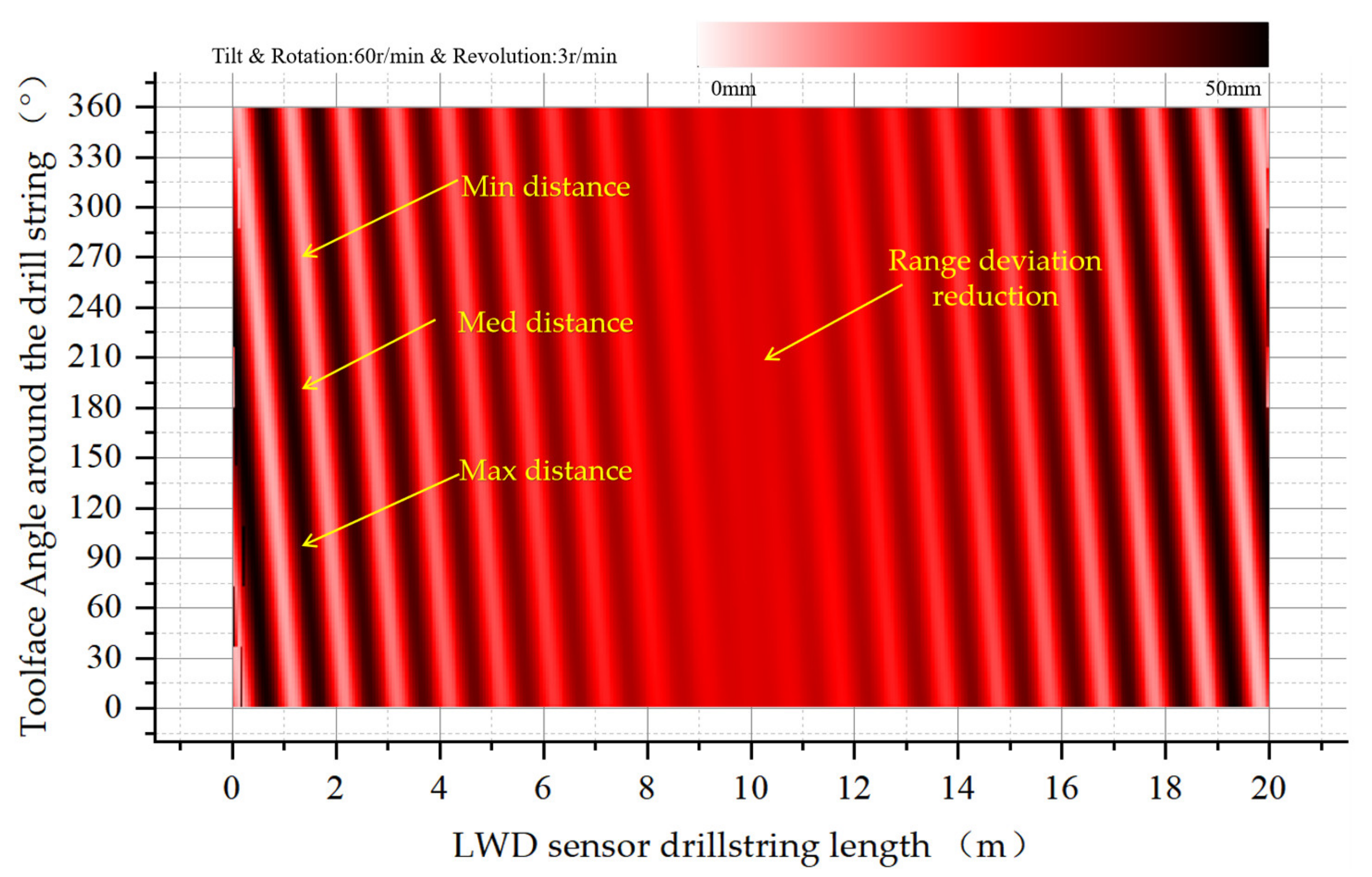
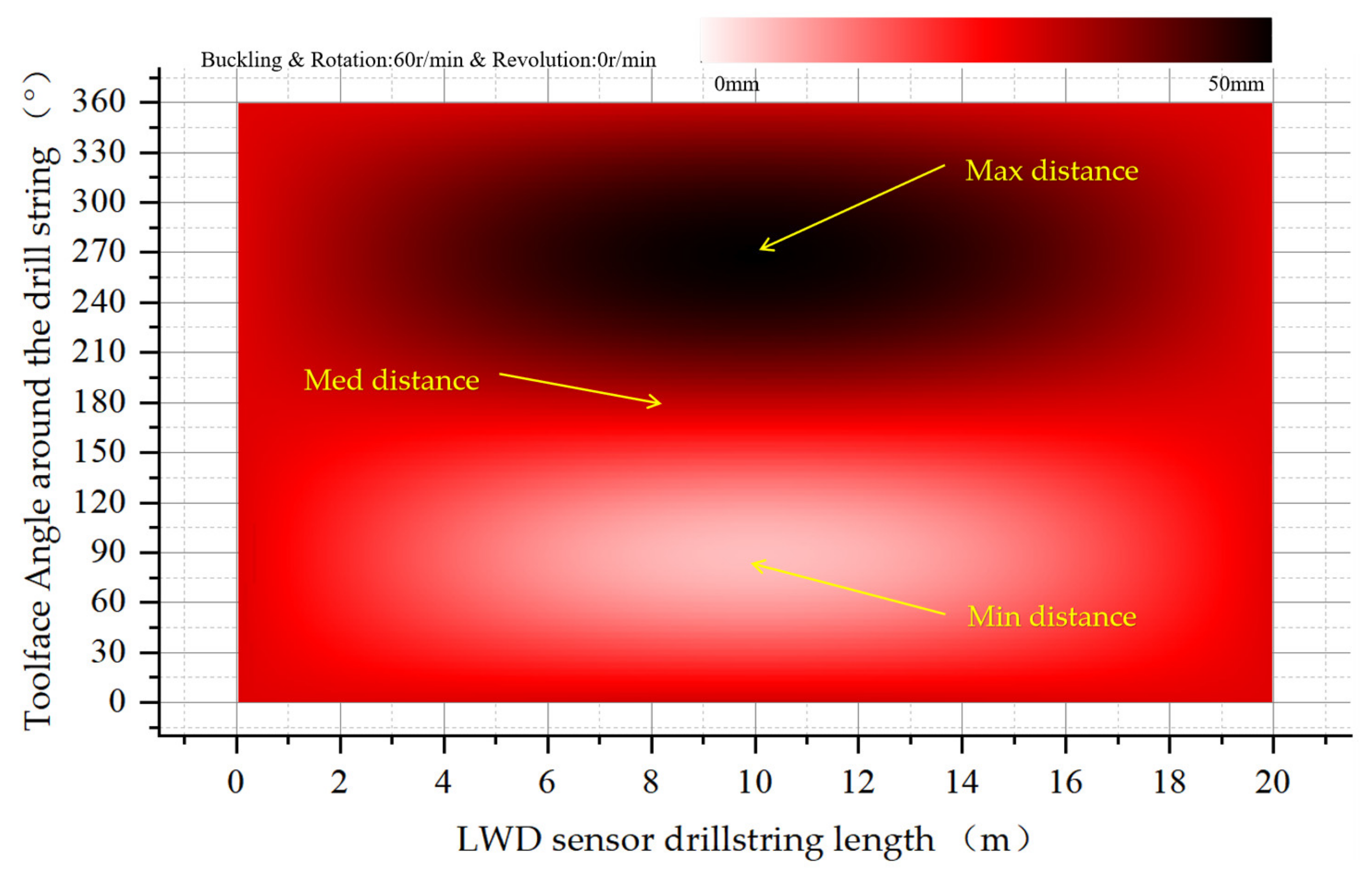




| No. | Bit Size (mm) | Downhole Motor (DM) Type (mm) | Downhole Motor (DM) Angle (°) | Drill Collar of the Instrument While Drilling (DCWD)(mm) | DCWD Length (m) | Magnification of the Hole (MH), | Range of Distance from the Sensor to the Wellbore Wall (RDSW) (mm) | Buckling |
|---|---|---|---|---|---|---|---|---|
| 1 | ϕ149.2 | ϕ120 | 1,1.25,1.5,1.75 | ϕ120 | 10~30 | 0.05~0.15 | 0~29.2 ± 15 | Easy |
| 2 | ϕ152.4 | ϕ120 | 1,1.25,1.5,1.75 | ϕ120 | 10~30 | 0.05~0.15 | 0~32.4 ± 15 | Easy |
| 3 | ϕ215.9 | ϕ172 | 1,1.25,1.5,1.75 | ϕ172 | 10~30 | 0.05~0.15 | 0~43.9 ± 20 | Medium |
| 4 | ϕ241.3 | ϕ203.2 | 1,1.25,1.5,1.75 | ϕ203.2 | 10~30 | 0.05~0.15 | 0~38.1 ± 24 | Difficult |
| 5 | ϕ311.1 | ϕ203.2 | 1,1.25,1.5,1.75 | ϕ203.2 | 10~30 | 0.05~0.15 | 107.9 ± 31 | Difficult |
| 6 | ϕ346.1 | ϕ203.2 | 1,1.25,1.5,1.75 | ϕ203.2 | 10~30 | 0.05~0.15 | 142.9 ± 34 | Difficult |
| No. | Drill String Eccentric Type | Whether to Rotate Around Itself (30 r/m~75 r/m) | Additional Rotation Around the WellBore |
|---|---|---|---|
| 1 | Centering | Yes | Yes/No |
| 2 | Eccentricity | Yes | Yes/No |
| 3 | Tilt | Yes | Yes/No |
| 4 | Buckling | Yes | Yes/No |
| No. | Center | Center and Revolution | Eccentric Tool Face (Tf) | Eccentric = and Revolution | Tilt | Tilt and Revolution | Buckling | Buckling and Revolution | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Max distance | Same | Same | Specific Tf | Change | Both ends of DC | Both ends of DC | Central DC | Central DC |
| 2 | Min distance | Same | Same | Specific Tf | Change | Both ends of DC | Both ends of DC | Central DC | Central DC |
| 3 | Med distance | Same | Same | Specific Tf | Change | Central DC | Central DC | Both ends of DC | Both ends of DC |
| 4 | Drill collar length correlation | No | No | No | NO | Yes | Yes | Yes | Yes |
| 5 | Change over time | No | No | No | Yes | No | Yes | No | Yes |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Wang, R. Research on a Measurement Method for Downhole Drill String Eccentricity Based on a Multi-Sensor Layout. Sensors 2021, 21, 1258. https://doi.org/10.3390/s21041258
Li H, Wang R. Research on a Measurement Method for Downhole Drill String Eccentricity Based on a Multi-Sensor Layout. Sensors. 2021; 21(4):1258. https://doi.org/10.3390/s21041258
Chicago/Turabian StyleLi, Hongqiang, and Ruihe Wang. 2021. "Research on a Measurement Method for Downhole Drill String Eccentricity Based on a Multi-Sensor Layout" Sensors 21, no. 4: 1258. https://doi.org/10.3390/s21041258
APA StyleLi, H., & Wang, R. (2021). Research on a Measurement Method for Downhole Drill String Eccentricity Based on a Multi-Sensor Layout. Sensors, 21(4), 1258. https://doi.org/10.3390/s21041258





