Low Complexity Robust Data Demodulation for GNSS
Abstract
:1. Introduction
- We derive a closed-form LLR expression under AWGN channels, which could be directly applied in the following cases: (i) The codeword data are demodulated over an open sky scenario with variations of the signal-to-noise ratio (SNR). (ii) The codeword data are demodulated over an interference scenario where an additive Gaussian noise is added to the entire codeword. To this end, we reformulate the problem of obtaining the LLR values by first computing the joint pdf of symbols and estimated variance, which is then marginalized in order to compute the desired LLRs used at the decoder. To implement such marginalization in practice, we propose to impose a conjugate prior distribution that allows for an analytic closed-form approximation that enables a reduced complexity implementation when compared to the ML solution. Then, assuming statistical knowledge of the estimation error of the noise power per symbol, a closed-from LLR approximation is derived. In our approach, we consider that the noise variance is not perfectly known, but instead, symbol-wise independent estimations of this noise variance per symbol are available. We further assume a statistical distribution of such estimated variance. In this work, we model the variance of the n-th symbol as a random variable, which is characterized by an inverse log-normal distribution (with the aim of taking advantage of the conjugate prior distribution) whose mean and variance are estimated at the decoder.
- We derive a closed-form LLR expression that can be directly applied over a pulsed jamming scenario characterized by a small percentage of codeword symbols disrupted with extra Gaussian noise. Since the Gaussian distribution is known to not fit well the heavy tails caused by pulsed jamming [33], we propose to represent the received symbol distribution with a Laplacian distribution. Then, we compute the marginalized joint pdf of symbols and estimated variance in order to compute the desired LLRs used at the decoder. Again, we propose to compute the marginalization by imposing a conjugate prior distribution that allows for an analytic closed-form expression.
2. System Models and Assumptions
2.1. Open Sky Communications
LLR Expression
2.2. Communications under Gaussian Jamming
LLR Expression
2.3. Communications under Pulsed Jamming
LLR Expression
3. Closed-Form LLR Expression with Uncertain Noise Variance
3.1. Closed-Form LLR Expression with Statistical CSI on the Noise Variance
3.2. Closed-Form LLR Approximation with First and Second Order Moments of the SNR
4. Closed-Form LLR Expression for Pulsed Jamming Scenarios
4.1. Closed-Form LLR Expression under the Likelihood Laplacian Assumption with Statistical CSI on the Noise Variance
4.2. Closed-Form LLR Approximation with First and Second Order Moments of the SNR
5. Summary of the State-of-the-Art and Proposed LLR Estimates
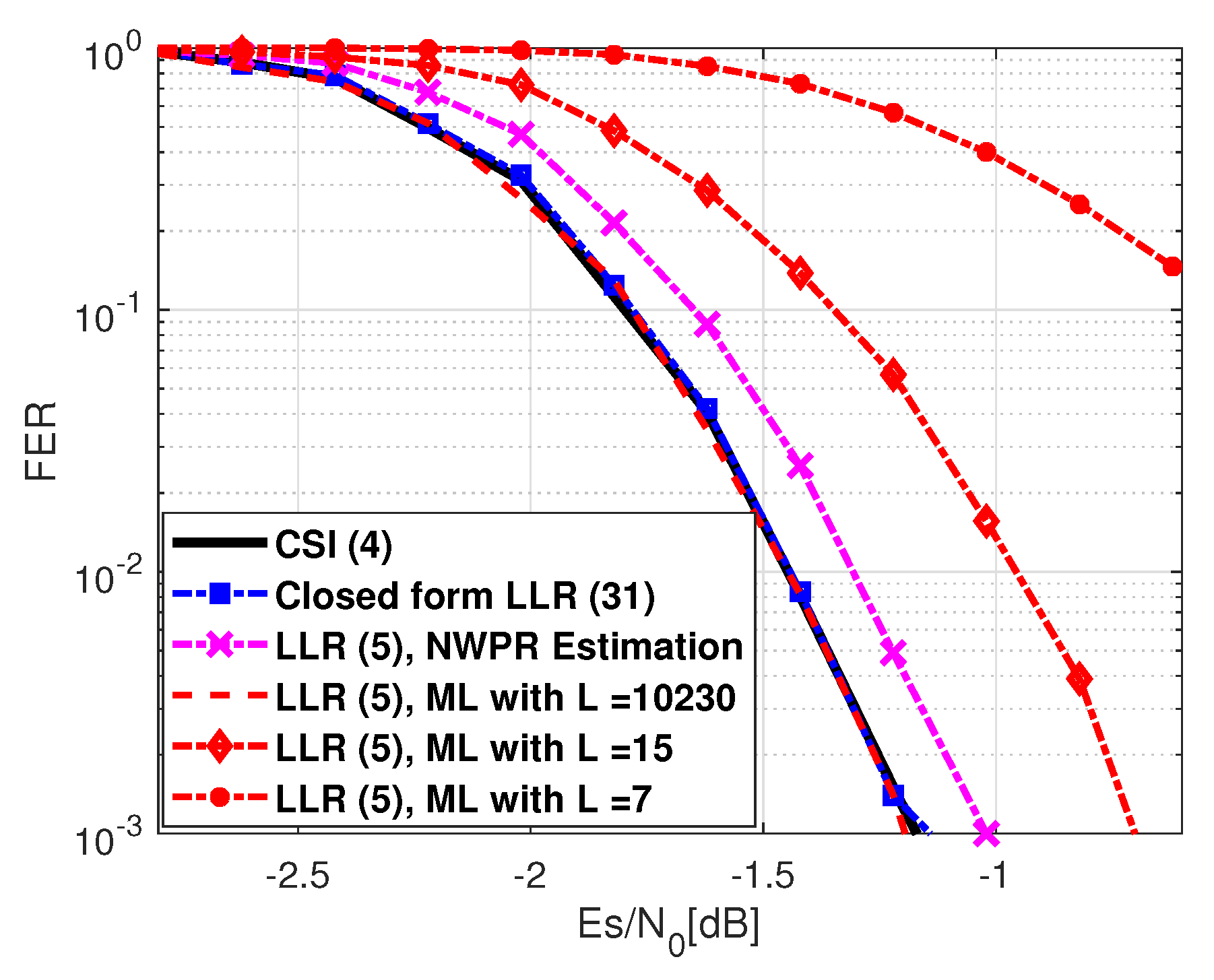
6. Results
7. Conclusions
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
Appendix A. Derivation of the LLR Expression with Variance Uncertainty under Conjugacy
Appendix B. Log-Normal Modeling of the Detail Estimate Considering a Gaussian Distribution
Appendix C. Calculation of the LLR Values under Gamma Conjugacy and the Laplacian Likelihood
Appendix D. Normal Modeling of the Detail Estimate Considering a Laplacian Distribution
References
- Dardari, D.; Falletti, E.; Luise, M. Satellite and Terrestrial Radio Positioning Techniques: A Signal Processing Perspective; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Teunissen, P.J.G.; Montenbruck, O. (Eds.) Handbook of Global Navigation Satellite Systems; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Morton, Y.J.; van Diggelen, F.; Spilker, J.J., Jr.; Parkinson, B.W.; Lo, S.; Gao, G. Position, Navigation, and Timing Technologies in the 21st Century, Volumes 1 and 2: Integrated Satellite Navigation, Sensor Systems, and Civil Applications, Set; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Amin, M.G.; Closas, P.; Broumandan, A.; Volakis, J.L. Vulnerabilities, threats, and authentication in satellite-based navigation systems [scanning the issue]. Proc. IEEE 2016, 104, 1169–1173. [Google Scholar] [CrossRef]
- Landry, R., Jr.; Renard, A. Analysis of potential interference sources and assessment of present solutions for GPS/GNSS receivers. In Proceedings of the 4th Saint Petersburg International Conference on Integrated Navigation Systems, Saint Petersburg, Russia, 26–28 May 1997. [Google Scholar]
- Mitch, R.H.; Dougherty, R.C.; Psiaki, M.L.; Powell, S.P.; O’Hanlon, B.W.; Bhatti, J.A.; Humphreys, T.E. Signal characteristics of civil GPS jammers. In Proceedings of the 24th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2011), Portland, OR, USA, 20–23 September 2011; pp. 1907–1919. [Google Scholar]
- Kuusniemi, H.; Airos, E.; Zahidul, M.; Bhuiyan, H.; Kroger, T. Effect of GNSS jammers on consumer grade satellite navigation receivers. In Proceedings of the European Navigation Conference, Gdansk, Poland, 25–27 April 2012; p. 14. [Google Scholar]
- Betz, J.W. Effect of narrowband interference on GPS code tracking accuracy. In Proceedings of the National Technical Meeting of The Institute of Navigation, Anaheim, CA, USA, 26–28 January 2000; pp. 16–27. [Google Scholar]
- Betz, J.W. Effect of Partial-Band Interference on Receiver Estimation of C/N0: Theory; Technical Report; MITRE CORP: Bedford, MA, USA, 2001. [Google Scholar]
- Motella, B.; Savasta, S.; Margaria, D.; Dovis, F. Method for assessing the interference impact on GNSS receivers. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1416–1432. [Google Scholar] [CrossRef]
- Jang, J.; Paonni, M.; Eissfeller, B. CW interference effects on tracking performance of GNSS receivers. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 243–258. [Google Scholar] [CrossRef]
- Curran, J.T.; Bavaro, M.; Closas, P.; Navarro, M. On the threat of systematic jamming of GNSS. In Proceedings of the ION GNSS, Portland, OR, USA, 12–16 September 2016; pp. 313–321. [Google Scholar]
- Fante, R.L.; Vaccaro, J.J. Wideband cancellation of interference in a GPS receive array. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 549–564. [Google Scholar] [CrossRef]
- Seco-Granados, G.; Fernández-Rubio, J.A.; Fernández-Prades, C. ML estimator and hybrid beamformer for multipath and interference mitigation in GNSS receivers. IEEE Trans. Signal Process. 2005, 53, 1194–1208. [Google Scholar] [CrossRef]
- Amin, M.G.; Sun, W. A novel interference suppression scheme for global navigation satellite systems using antenna array. IEEE J. Sel. Areas Commun. 2005, 23, 999–1012. [Google Scholar] [CrossRef]
- Closas, P.; Fernández-Prades, C. A statistical multipath detector for antenna array based GNSS receivers. IEEE Trans. Wirel. Commun. 2011, 10, 916–929. [Google Scholar] [CrossRef]
- Arribas, J.; Fernandez-Prades, C.; Closas, P. Antenna array based GNSS signal acquisition for interference mitigation. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 223–243. [Google Scholar] [CrossRef]
- Arribas, J.; Closas, P.; Fernández-Prades, C.; Cuntz, M.; Meurer, M.; Konovaltsev, A. Advances in the theory and implementation of GNSS antenna array receivers. In Microwave and Millimeter Wave Circuits and Systems: Emerging Design, Technologies, and Applications; Wiley: Hoboken, NJ, USA, 2012; pp. 227–273. [Google Scholar]
- Curran, J.T.; Bavaro, M.; Fortuny, J. Analog and digital nulling techniques for multi-element antennas in gnss receivers. In Proceedings of the 28th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+ 2015), Tampa, FL, USA, 14–18 September 2015; pp. 3249–3261. [Google Scholar]
- Abdizadeh, M.; Curran, J.T.; Lachapelle, G. Quantization effects in GNSS receivers in the presence of interference. In Proceedings of the ION International Technical Meeting, Nashville, TN, USA, 17–21 September 2012; Volume 29. [Google Scholar]
- Pany, T. Navigation Signal Processing for GNSS Software Receivers; Artech House: London, UK, 2010. [Google Scholar]
- Chien, Y.R. Design of GPS anti-jamming systems using adaptive notch filters. IEEE Syst. J. 2013, 9, 451–460. [Google Scholar] [CrossRef]
- Borio, D. Swept GNSS jamming mitigation through pulse blanking. In Proceedings of the IEEE European Navigation Conference (ENC), Helsinki, Finland, 30 May–2 June 2016; pp. 1–8. [Google Scholar]
- Borio, D. Robust signal processing for GNSS. In Proceedings of the IEEE European Navigation Conference (ENC), Lausanne, Switzerland, 9–12 May 2017; pp. 150–158. [Google Scholar]
- Borio, D.; Closas, P. A fresh look at GNSS anti-jamming. Inside GNSS 2017, 12, 54–61. [Google Scholar]
- Borio, D.; Closas, P. Complex Signum Non-Linearity for Robust GNSS Signal Mitigation. IET Radar Sonar Navig. 2018, 1–10. [Google Scholar] [CrossRef]
- Borio, D.; Li, H.; Closas, P. Huber’s Non-Linearity for GNSS Interference Mitigation. Sensors 2018, 18, 2217. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Borio, D.; Closas, P. Robust Transform Domain Signal Processing for GNSS. Navigation 2019. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Borio, D.; Closas, P. Dual-Domain Robust GNSS Interference Mitigation. In Proceedings of the International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+ 2019), Miami, FL, USA, 16–20 September 2019. [Google Scholar]
- Medina, D.; Li, H.; Vilà-Valls, J.; Closas, P. Robust statistics for GNSS positioning under harsh conditions: A useful tool? Sensors 2019, 19, 5402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, H.; Medina, D.; Vilà-Valls, J.; Closas, P. Robust Variational-Based Kalman Filter for Outlier Rejection With Correlated Measurements. IEEE Trans. Signal Process. 2021, 69, 357–369. [Google Scholar] [CrossRef]
- Curran, J.; Navarro, M.; Anghileri, M.; Closas, P.; Pfletschinger, S. Coding aspects of secure GNSS receivers. Proc. IEEE 2016, 104, 1271–1287. [Google Scholar] [CrossRef]
- Ortega, L.; Closas, P.; Poulliat, C.; Boucheret, M.; Aubault, M.; Al-Bitar, H. Data Decoding Analysis of Next Generation GNSS Signals. In Proceedings of the ION GNSS+, Miami, FL, USA, 16–20 September 2019. [Google Scholar]
- Ortega, L.; Poulliat, C.; Boucheret, M.; Aubault-Roudier, M.; Al-Bitar, H. Optimal Channel Coding Structures for Fast Acquisition Signals in Harsh Environment Conditions. In Proceedings of the ION GNSS+, Miami, FL, USA, 16–20 September 2019. [Google Scholar]
- Ortega, L.; Vilà-Valls, J.; Poulliat, C.; Closas, P. GNSS data demodulation over fading environments: Antipodal and M-ary CSK modulations. IET Radar Sonar Navig. 2021. [Google Scholar] [CrossRef]
- Ryan, W.; Lin, S. Channel Codes: Classical and Modern; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Ortega, L.; Aubault-Roudier, M.; Poulliat, C.; Boucheret, M.L.; Al-Bitar, H.; Closas, P. LLR Approximation for Fading Channels using a Bayesian Approach. IEEE Commun. Lett. 2020, 24, 1244–1248. [Google Scholar]
- Saeedi, H.; Banihashemi, A.H. Performance of Belief Propagation for Decoding LDPC Codes in the Presence of Channel Estimation Error. IEEE Trans. Commun. 2007, 55, 83–89. [Google Scholar] [CrossRef]
- Saeedi, H.; Banihashemi, A.H. Design of irregular LDPC codes for BIAWGN channels with SNR mismatch. IEEE Trans. Commun. 2009, 57, 6–11. [Google Scholar] [CrossRef]
- Falletti, E.; Pini, M.; Presti, L.L. Low Complexity Carrier-to-Noise Ratio Estimators for GNSS Digital Receivers. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 420–437. [Google Scholar] [CrossRef]
- Borio, D.; Cano, E. Evaluation of GNSS pulsed interference mitigation techniques accounting for signal conditioning. In Proceedings of the European Navigation Conference (ENC), Gdanks, Poland, 25–27 April 2012; pp. 1–10. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning (Information Science and Statistics); Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Senst, M.; Ascheid, G. A message passing approach to iterative Bayesian SNR estimation. In Proceedings of the International Symposium on Signals, Systems, and Electronics (ISSSE), Potsdam, Germany, 3–5 October 2012; pp. 1–6. [Google Scholar]
- Yuan, Z.; Zhang, C.; Wang, Z.; Guo, Q.; Xi, J. Joint spare channel estimation and decoding for orthogonal frequency division multiplexing using combined message passing. IET Commun. 2018, 12, 2022–2029. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Statist. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Aydin, N.S. Financial Modelling with Forward-Looking Information: An Intuitive Approach to Asset Pricing; Springer: Berlin, Germany, 2017. [Google Scholar]
- Interface Specification IS-GPS-800 NavStar GPS Space Segment/UserSegment L1C Interface. Technical Report. Available online: https://www.gps.gov/technical/icwg/IS-GPS-800A.pdf (accessed on 12 February 2021).
- Johnson, S. Iterative Error Correction: Turbo, Low-Density Parity-Check and Repeat-Accumulate Codes; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]





| Scenarios | |||
|---|---|---|---|
| Type of CSI Used | Open Sky Scenario | Gaussian Jamming Scenario | Pulsed Jamming Scenario |
| Perfect CSI | Equation (4) | Equation (9) | Equation (9) Approx (14) Approx. (16) |
| Mismatched CSI using NWPR estimates | Equation (5) with estimated with NWPR | Equation (10) with estimated with NWPR | Equation (10) with estimated with NWPR |
| Mismatched CSI using ML estimates | Equation (5) with estimated with ML | Equation (10) with estimated with ML | Not evaluated |
| Statistical CSI using proposed approx. and related parameter estimates | Closed-Form (41) | Closed-Form (31) | Closed-Form (31) Closed-Form (31) |
| CSI (4) | Closed-Form LLR (31) | LLR (5) with NWPR Estimation | LLR (5) ML and L = 10,230 | LLR (5) ML and L = 15 | LLR (5) ML and L = 7 | |
|---|---|---|---|---|---|---|
| −1.45 dB | −1.44 dB | −1.30 dB | −1.44 dB | −0.96 dB | 0 dB |
| CSI (4) | Closed-Form LLR (31) | LLR (5) with NWPR Estimation | LLR (5) ML and L = 10,230 | LLR (5) ML and L = 15 | LLR (5) ML and L = 7 | |
|---|---|---|---|---|---|---|
| −1.45 dB | −1.44 dB | −1.26 dB | −1.44 dB | −0.94 dB | 0.2 dB |
| CSI (4) | Closed-Form LLR (31) | LLR (5) with NWPR Estimation | |
|---|---|---|---|
| with dB | −0.44 dB | −0.43 dB | −0.20 dB |
| with dB | 0.56 dB | 0.57 dB | 0.80 dB |
| with dB | 1.56 dB | 1.57 dB | 1.80 dB |
| with dB | 3.56 dB | 3.57 dB | 3.80 dB |
| CSI (4) | CSI (14) Gaussian Approx. | CSI (16) Laplacian Approx. | Closed-Form LLR (31) | Closed-Form LLR (41) | LLR (5) NWPR Estimation | |
|---|---|---|---|---|---|---|
| −1.36 dB | −1.28 dB | −1.17 dB | −1.28 dB | −1.15 dB | 1.15 dB | |
| −1 dB | −0.6 dB | −0.65 dB | −0.68 dB | −0.62 dB | −0.4 dB |
| CSI (4) | CSI (14) Gaussian Approx. | CSI (16) Laplacian Approx. | Closed-Form LLR (31) | Closed-Form LLR (41) | LLR (5) NWPR Estimation | |
|---|---|---|---|---|---|---|
| −1.32 dB | −0.5 dB | −1 dB | −1 dB | −1 dB | −0.3 dB | |
| −0.8 dB | 1.95 dB | 0.23 dB | 0.63 dB | −0.21 dB | 2.5 dB | |
| 8 dB | 8.17 dB | 8.3 dB | 8.17 dB | 8.33 dB | 8.45 dB | |
| 8.56 dB | 8.56 dB | 8.72 dB | 8.57 dB | 8.73 dB | 8.77 dB |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ortega, L.; Poulliat, C.; Boucheret, M.L.; Aubault Roudier, M.; Al-Bitar, H.; Closas, P. Low Complexity Robust Data Demodulation for GNSS. Sensors 2021, 21, 1341. https://doi.org/10.3390/s21041341
Ortega L, Poulliat C, Boucheret ML, Aubault Roudier M, Al-Bitar H, Closas P. Low Complexity Robust Data Demodulation for GNSS. Sensors. 2021; 21(4):1341. https://doi.org/10.3390/s21041341
Chicago/Turabian StyleOrtega, Lorenzo, Charly Poulliat, Marie Laure Boucheret, Marion Aubault Roudier, Hanaa Al-Bitar, and Pau Closas. 2021. "Low Complexity Robust Data Demodulation for GNSS" Sensors 21, no. 4: 1341. https://doi.org/10.3390/s21041341
APA StyleOrtega, L., Poulliat, C., Boucheret, M. L., Aubault Roudier, M., Al-Bitar, H., & Closas, P. (2021). Low Complexity Robust Data Demodulation for GNSS. Sensors, 21(4), 1341. https://doi.org/10.3390/s21041341







