A Classification Method for the Cellular Images Based on Active Learning and Cross-Modal Transfer Learning
Abstract
:1. Introduction
2. Proposed Method
2.1. Parallel Deep Residual Networks
2.2. Active Learning Using the Pretrained Parallel Residual Networks
3. Results
3.1. Datasets, Experimental Setup and Initial Learning Results
3.2. Results without Cross-Modal Transfer Learning
3.3. Results with Cross-Modal Transfer Learning
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rigon, A.; Soda, P.; Zennaro, D.; Iannello, G.; Afeltra, A. Indirect immunofluorescence in autoimmune diseases: Assessment of digital images for diagnostic purpose. Cytom. B Clin. Cytom. 2007, 72, 472–477. [Google Scholar] [CrossRef] [PubMed]
- Foggia, P.; Percannella, G.; Soda, P.; Vento, M. Benchmarking HEp-2 cells classification methods. IEEE Trans. Med. Imaging 2013, 32, 1878–1889. [Google Scholar] [CrossRef] [PubMed]
- Foggia, P.; Percannella, G.; Saggese, A.; Vento, M. Pattern recognition in stained HEp-2 cells: Where are we now? Pattern Recognit. 2014, 47, 2305–2314. [Google Scholar] [CrossRef]
- Cataldo, S.D.; Bottino, A.; Ficarra, E.; Macii, E. Applying textural features to the classification of HEp-2 cell patterns in IIF images. In Proceedings of the 21st International Conference on Pattern Recognition (ICPR2012), Tsukuba, Japan, 11–15 November 2012; pp. 689–694. [Google Scholar]
- Wiliem, A.; Wong, Y.; Sanderson, C.; Hobson, P.; Chen, S.; Lovell, B.C. Classification of human epithelial type 2 cell indirect immunofluorescence images via codebook based descriptors. In Proceedings of the 2013 IEEE Workshop on Applications of Computer Vision (WACV), Tampa, FL, USA, 15–17 January 2013; pp. 95–102. [Google Scholar] [CrossRef] [Green Version]
- Stoklasa, R.; Majtner, T.; Svoboda, D. Efficient k-NN based HEp-2 cells classifier. Pattern Recognit. 2014, 47, 249–2418. [Google Scholar] [CrossRef]
- Nosaka, R.; Fukui, K. HEp-2 cell classification using rotation invariant co-occurrence among local binary patterns. Pattern Recognit. 2014, 47, 2428–2436. [Google Scholar] [CrossRef]
- Cataldo, S.D.; Bottino, A.; Islam, I.U.; Vieira, T.F.; Ficarra, E. Subclass discriminant analysis of morphological and textural features for HEp-2 staining pattern classification. Pattern Recognit. 2014, 47, 2389–2399. [Google Scholar] [CrossRef] [Green Version]
- Theodorakopoulos, I.; Kastaniotis, D.; Economou, G.; Fotopoulos, S. HEp-2cells classification via sparse representation of textural features fused into dissimilarity space. Pattern Recognit. 2014, 47, 2367–2378. [Google Scholar] [CrossRef]
- Huang, Y.C.; Hsieh, T.Y.; Chang, C.Y.; Cheng, W.T.; Lin, Y.C.; Huang, Y.L. HEp-2 cell images classification based on textural and statistic features using self-organizing map. In Proceedings of the 4th Asian Conference on Intelligent Information and Database Systems, Part II, Kaohsiung, Taiwan, 19–21 March 2012; pp. 529–538. [Google Scholar]
- Thibault, G.; Angulo, J.; Meyer, F. Advanced statistical matrices for texture characterization: Application to cell classification. IEEE Trans. Biomed. Eng. 2014, 61, 630–637. [Google Scholar] [CrossRef] [PubMed]
- Wiliem, A.; Sanderson, C.; Wong, Y.; Hobson, P.; Minchin, R.F.; Lovell, B.C. Automatic classification of human epithelial type 2 cell indirect immunofluorescence images using cell pyramid matching. Pattern Recognit. 2014, 47, 2315–2324. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.; Lin, F.; Ng, C.; Leong, K.P. Automated classification for HEp-2 cells based on linear local distance coding framework. J. Image Video Proc. 2015, 2015, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Ponomarev, G.V.; Arlazarov, V.L.; Gelfand, M.S.; Kazanov, M.D. ANA HEp-2 cells image classification using number, size, shape and localization of targeted cell regions. Pattern Recognit. 2014, 47, 2360–2366. [Google Scholar] [CrossRef] [Green Version]
- Shen, L.; Lin, J.; Wu, S.; Yu, S. HEp-2 image classification using intensity order pooling based features and bag of words. Pattern Recognit. 2014, 47, 2419–2427. [Google Scholar] [CrossRef]
- Gao, Z.; Wang, L.; Zhou, L.; Zhang, J. HEp-2 cell image classification with deep convolutional neural networks. IEEE J. Biomed. Health Inf. 2017, 21, 416–428. [Google Scholar] [CrossRef] [Green Version]
- Bayramoglu, N.; Kannala, J.; Heikkilä, J. Human epithelial type 2 cell classification with convolutional neural networks. In Proceedings of the IEEE 15th Intrenational Conference on Bioinformatics and Bioengineering (BIBE), Belgrade, Serbia, 2–4 November 2015; pp. 1–6. [Google Scholar]
- Jia, Y.; Shelhamer, E.; Donahue, J.; Karayev, S.; Long, J.; Girshick, R.; Guadarrama, S.; Darrell, T. Caffe: Convolutional architecture for fast feature embedding. In Proceedings of the 22nd ACM International Conference on Multimedia, Orlando, FL, USA, 3–7 November 2014; pp. 675–678. [Google Scholar] [CrossRef]
- Liu, J.; Xu, B.; Shen, L.; Garibaldi, J.; Qiu, G. HEp-2 cell classification based on a deep autoencoding-classification convolutional neural network. In Proceedings of the 14th IEEE International Symposium on Biomedical Imaging (ISBI 2017), Melbourne, Australia, 18–21 April 2017; pp. 1019–1023. [Google Scholar] [CrossRef]
- Rodrigues, L.F.; Naldi, M.C.; Mari, J.F. Comparing convolutional neural networks and preprocessing techniques for HEp-2 cell classification in immunofluorescence images. Comput. Biol. Med. 2020, 116, 103542. [Google Scholar] [CrossRef]
- Xi, J.; Linlin, S.; Xiande, Z.; Shiqi, Y. Deep convolutional neural network based HEp-2 cell classification. In Proceedings of the 2016 23rd International Conference on Pattern Recognition (ICPR), Cancun, Mexico, 4–8 December 2016; pp. 77–80. [Google Scholar] [CrossRef]
- Li, Y.; Shen, L. A deep residual inception network for HEp-2 cell classification. In Proceedings of the3rd International Workshop, DLMIA 2017, and 7th International Workshop, ML-CDS 2017, Québec City, QC, Canada, 14 September 2017. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P. Going deeper with convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Shen, L.; Jia, X.; Li, Y. Deep cross residual network for HEp-2 cell staining pattern classification. Pattern Recognit. 2018, 82, 68–78. [Google Scholar] [CrossRef]
- Majtner, T.; Bajic, B.; Lindblad, J.; Sladoje, N.; Blanes-Vidal, V.; Nadimi, E.S. On the effectiveness of generative adversarial networks as HEp-2 image augmentation tool. In Proceedings of the Scandinavian Conference on Image Analysis (SCIA 2019), Norrkoping, Sweden, 11–13 June 2019; pp. 439–451. Available online: https://link.springer.com/chapter/10.1007%2F978-3-030-20205-7_36 (accessed on 16 January 2021).
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the 27th International Conference on Neural Information Processing Systems (NIPS 2014), Montréal, QC, Canada, 8–13 December 2014; pp. 2672–2680. Available online: https://arxiv.org/pdf/1406.2661.pdf (accessed on 16 January 2021).
- Radford, A.; Metz, L.; Chintala, S. Unsupervised representation learning with deep convolutional generative adversarial networks. In Proceedings of the 4th International Conference on Learning Representations (ICLR 2016), San Juan, Puerto Rico, 2–4 May 2016; Available online: https://arxiv.org/pdf/1511.06434.pdf (accessed on 16 January 2021).
- Li, Y.; Shen, L. HEp-Net: A smaller and better deep-learning network for HEp-2 cell classification. Comput. Methods Biomech. Biomed. Eng. 2019, 7, 266–272. [Google Scholar] [CrossRef]
- Vununu, C.; Lee, S.-K.; Kwon, K.-R. A Deep feature extraction method for HEp-2 image classification. Electronics 2018, 8, 20. [Google Scholar] [CrossRef] [Green Version]
- Vununu, C.; Lee, S.-K.; Kwon, K.-R. A strictly unsupervised deep learning method for HEp-2 cell image classification. Sensors 2020, 20, 2717. [Google Scholar] [CrossRef]
- Phan, H.T.H.; Kumar, A.; Kim, J.; Feng, D. Transfer learning of a convolutional neural network for HEp-2 cell image classification. In Proceedings of the 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI), Prague, Czech Republic, 16 June 2016; pp. 1208–1211. [Google Scholar]
- Simonyan, K.; Zisserman, A. A very deep convolutional networks for large-scale image recognition. In Proceedings of the 2015 International Conference on Learning Representation (ICLR15), San Diego, CA, USA, 7–9 May 2015; Available online: https://arxiv.org/pdf/1409.1556.pdf (accessed on 16 January 2021).
- Lu, M.; Gao, L.; Guo, X.; Liu, Q.; Yin, J. HEp-2 cell image classification method based on very deep convolutional networks with small datasets. In Proceedings of the 9th International Conference on Digital Image Processing (ICDIP 2017), Hong Kong, China, 19–22 May 2017. [Google Scholar] [CrossRef]
- Nguyen, L.D.; Gao, R.; Lin, D.; Lin, Z. Biomedical image classification based on a feature concatenation and ensemble of deep CNNs. J. Ambient Intell. Hum. Comput. 2019. [Google Scholar] [CrossRef]
- Cascio, D.; Taormina, V.; Raso, G. Deep CNN for IIF images classification in autoimmune diagnostics. Appl. Sci. 2019, 9, 1618. [Google Scholar] [CrossRef] [Green Version]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. In Proceedings of the 25th International Conference on Neural Information Processing Systems (NIPS’12), Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Lei, H.; Han, T.; Zhou, F.; Yu, Z.; Qin, J.; Elazab, A.; Lei, B. A deeply supervised residual network for HEp-2 cell classification via cross-modal transfer learning. Pattern Recognit. 2018, 79, 290–302. [Google Scholar] [CrossRef]
- Lovell, B.C.; Percannella, G.; Saggese, A.; Vento, M.; Wiliem, A. International contest on pattern recognition techniques for indirect immunofluorescence images analysis. In Proceedings of the 2016 23rd International Conference on Pattern Recognition (ICPR), Cancun, Mexico, 4–8 December 2016; pp. 74–76. [Google Scholar]
- Lewis, D.D.; Catlett, J. Heterogeneous uncertainty sampling for supervised learning. In Proceedings of the Eleventh International Conference on Machine Learning, New Brunswick, NJ, USA, 10–13 July 1994; pp. 148–156. [Google Scholar] [CrossRef] [Green Version]
- Seung, H.S.; Opper, M.; Sompolinsky, H. Query by committee. In Proceedings of the Fifth Annual Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July 1992; pp. 287–294. [Google Scholar] [CrossRef]
- Shi, F.; Wang, Z.; Hu, M.; Zhai, G. Active learning plus deep learning can establish cost-effective and robust model for multichannel image: A case of hyperspectral image classification. Sensors 2020, 20, 4975. [Google Scholar] [CrossRef]
- Wang, D.; Shang, Y. A new active labeling method for deep learning. In Proceedings of the 2014 International Joint Conference on Neural Networks (IJCNN), Beijing, China, 6–11 July 2014; pp. 112–119. [Google Scholar] [CrossRef]
- Zhou, Z.; Shin, J.; Zhang, L.; Gurudu, S.; Gotway, M.; Liang, J. Fine-tuning convolutional neural networks for biomedical image analysis: Actively and incrementally. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 7340–7351. [Google Scholar] [CrossRef]
- Sener, O.; Savarese, S. Active learning for convolutional neural networks: A core-set approach. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018; Available online: https://arxiv.org/pdf/1708.00489.pdf (accessed on 16 January 2021).
- Tkachenko, R.; Izonin, I. Model and principals for the implementation of neural-like structures based on geometric data transformations. Adv. Intell. Syst. Comput. 2019, 754, 578–587. [Google Scholar] [CrossRef]
- Cascio, D.; Taormina, V.; Raso, G. Deep convolutional neural network for HEp-2 fluorescence intensity classification. Appl. Sci. 2019, 9, 408. [Google Scholar] [CrossRef] [Green Version]
- Merone, M.; Sansone, C.; Soda, P. A computer-aided diagnosis system for HEp-2 fluorescence intensity classification. Artif. Intell. Med. 2019, 97, 71–78. [Google Scholar] [CrossRef]
- Nigam, I.; Agrawal, S.; Singh, R.; Vatsa, M. Revisiting HEp-2 cell classification. IEEE Access 2015, 3, 3102–3113. [Google Scholar] [CrossRef]
- Vununu, C.; Lee, S.-K.; Kwon, O.-J.; Kwon, K.-R. A dynamic learning method for the classification of the HEp-2 cell images. Electronics 2019, 8, 850. [Google Scholar] [CrossRef] [Green Version]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 7–9 July 2015; pp. 448–456. [Google Scholar]
- Bengio, Y. Learning deep architecture for AI. Foundat. Trends Mach. Learn. 2009, 2, 1–127. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. ACM Sigmob. Mob. Comput. Commun. Rev. 2001, 5, 3–55. [Google Scholar] [CrossRef]
- Lewis, D.D.; Gale, W.A. A sequential algorithm for training text classifiers. In Proceedings of the 17th ACM International Conference on Research and Development in Information Retrieval, Dublin, Ireland, 3–6 July 1994; pp. 3–12. [Google Scholar] [CrossRef]
- Scheffer, T.; Decomain, C.; Wrobel, S. Active hidden markov models for information extraction. In International Symposium on Intelligent Data Analysis; Springer: Berlin/Heidelberg, Germany, 2001; pp. 309–318. [Google Scholar] [CrossRef]
- Tong, S.; Koller, D. Support vector machine active learning with applications to text classification. J. Mach. Learn. Res. 2001, 2, 45–66. [Google Scholar] [CrossRef]
- Abe, N.; Mamitsuka, H. Query learning strategies using boosting and bagging. In Proceedings of the Fifteenth International Conference on Machine Learning (ICML 1998), Madison, WI, USA, 24–27 July 1998; pp. 1–8. [Google Scholar]
- Huo, L.Z.; Tang, P. A batch-mode active learning algorithm using region-partitioning diversity for SVM classifier. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1036–1046. [Google Scholar] [CrossRef]
- Qi, X.; Zhao, G.; Chen, J.; Pietikainen, M. Exploring illumination robust descriptors for human epithelial type 2 cell classification. Pattern Recognit. 2016, 60, 420–429. [Google Scholar] [CrossRef]

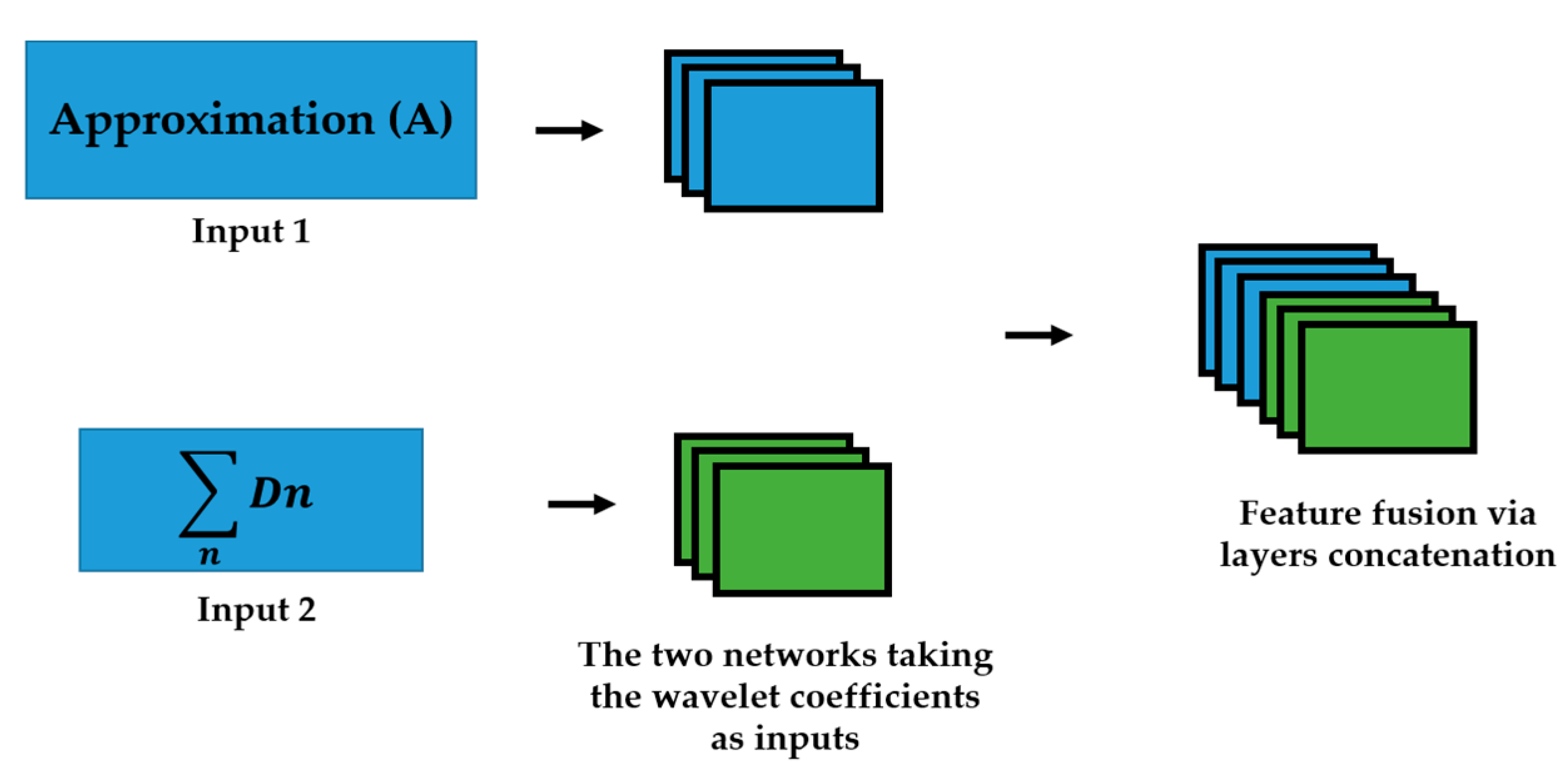













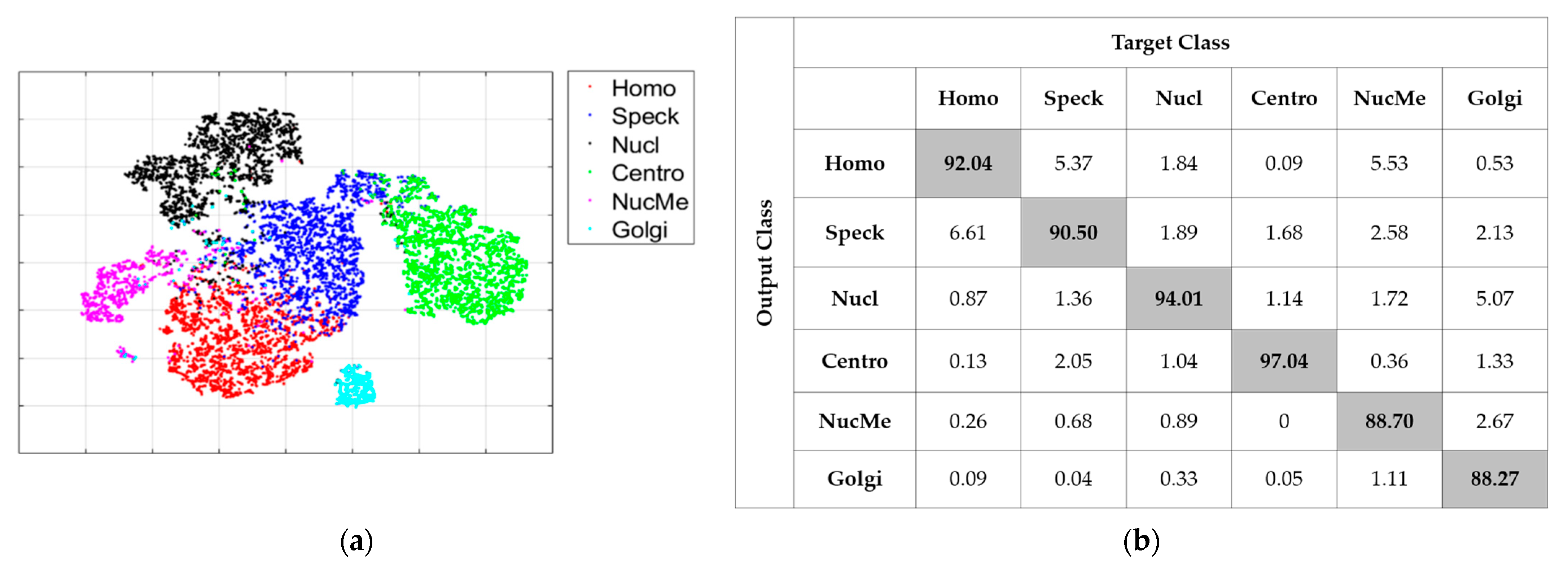



| Step No. | Actions | Comments |
|---|---|---|
| 1 | We train our networks using the small dataset. | The small dataset used here is the SNPHEp-2 dataset, which contains around 1000 images for training. |
| 2 | Using the targeted dataset, we select randomly and label k samples. We fine-tune the networks by using these k samples as the training data. As described in Section 2.1, the early layers remain fixed and we only update the late layers. | Note that by choosing the number k, we select randomly (as opposed to select by using active learning) the data to label. In fact, we want this number k to be as small as possible, in order to not complicate the labeling process. This is made possible by the pretraining made in step 1 using the small dataset. |
| 3 | We use the fine-tuned networks over all the remaining data in order to get their probability scores. We compute the confidence (entropy) using Equation (3) for each data. | Equations (4) and (5) can also be used to estimate the confidence. |
| 4 | We rank the data according to their confidence, from the lowest to the highest. | Note that in Figure 7, we show the data with the lowest confidence (highest entropy) in the bottom for the illustration purpose. |
| 5 | We select the first m data in the ranking in step 4 and annotate them. These are the data for which the networks are the most uncertain about. | The number m is chosen according to the limitations that we have in terms of manual labeling. |
| 6 | The newly annotated data in step 5 are mixed with the k data that were previously labeled in step 2 in order to create the newly annotated set. | The newly annotated dataset contains now data. |
| 7 | We fine-tune again the networks using this newly annotated dataset | After this step, we get back to step 3 (use the newly fine-tuned networks to compute the scores and the confidence). |
| Case Name | Comments |
|---|---|
| RS (random sampling) | No initial learning, and selection using random sampling. |
| AL (active learning) | No initial learning, and selection using active learning. |
| IN-RS (random sampling with cross-modal transfer learning) | Initial learning involved, and selection using random sampling. |
| IN-AL (active learning with cross-modal transfer learning) | Initial learning involved, and selection using active learning. |
| Methods | Accuracy (ACA) |
|---|---|
| Handcrafted features-based approach [60] | 86.61% |
| LeNet-5-like CNN without transfer learning [16] | 88.75% |
| VGG-16-like network without transfer learning [21] | 90.23% |
| Transfer learning using the pretrained VGG-19 | 91.57% |
| Transfer learning using the pretrained AlexNet | 92.41% |
| Transfer learning using the pretrained VGG-16 [32] | 92.89% |
| DCR-Net [25] | 94.15% |
| Transfer learning using the pretrained ResNet-50 | 94.36% |
| Our proposed deep parallel residual nets without cross-modal transfer learning | 94.79% |
| Cross-modal transfer learning using ResNet-50 [38] | 95.94% |
| Our proposed deep parallel residual nets with cross-modal transfer learning | 96.33% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vununu, C.; Lee, S.-H.; Kwon, K.-R. A Classification Method for the Cellular Images Based on Active Learning and Cross-Modal Transfer Learning. Sensors 2021, 21, 1469. https://doi.org/10.3390/s21041469
Vununu C, Lee S-H, Kwon K-R. A Classification Method for the Cellular Images Based on Active Learning and Cross-Modal Transfer Learning. Sensors. 2021; 21(4):1469. https://doi.org/10.3390/s21041469
Chicago/Turabian StyleVununu, Caleb, Suk-Hwan Lee, and Ki-Ryong Kwon. 2021. "A Classification Method for the Cellular Images Based on Active Learning and Cross-Modal Transfer Learning" Sensors 21, no. 4: 1469. https://doi.org/10.3390/s21041469
APA StyleVununu, C., Lee, S. -H., & Kwon, K. -R. (2021). A Classification Method for the Cellular Images Based on Active Learning and Cross-Modal Transfer Learning. Sensors, 21(4), 1469. https://doi.org/10.3390/s21041469






