Wavelet-Prototypical Network Based on Fusion of Time and Frequency Domain for Fault Diagnosis
Abstract
1. Introduction
2. Related Background and Terminology
2.1. Meta Learning
2.2. Few-Shot Learning
3. The Proposed WPNF
3.1. The Architecture of the Proposed Model
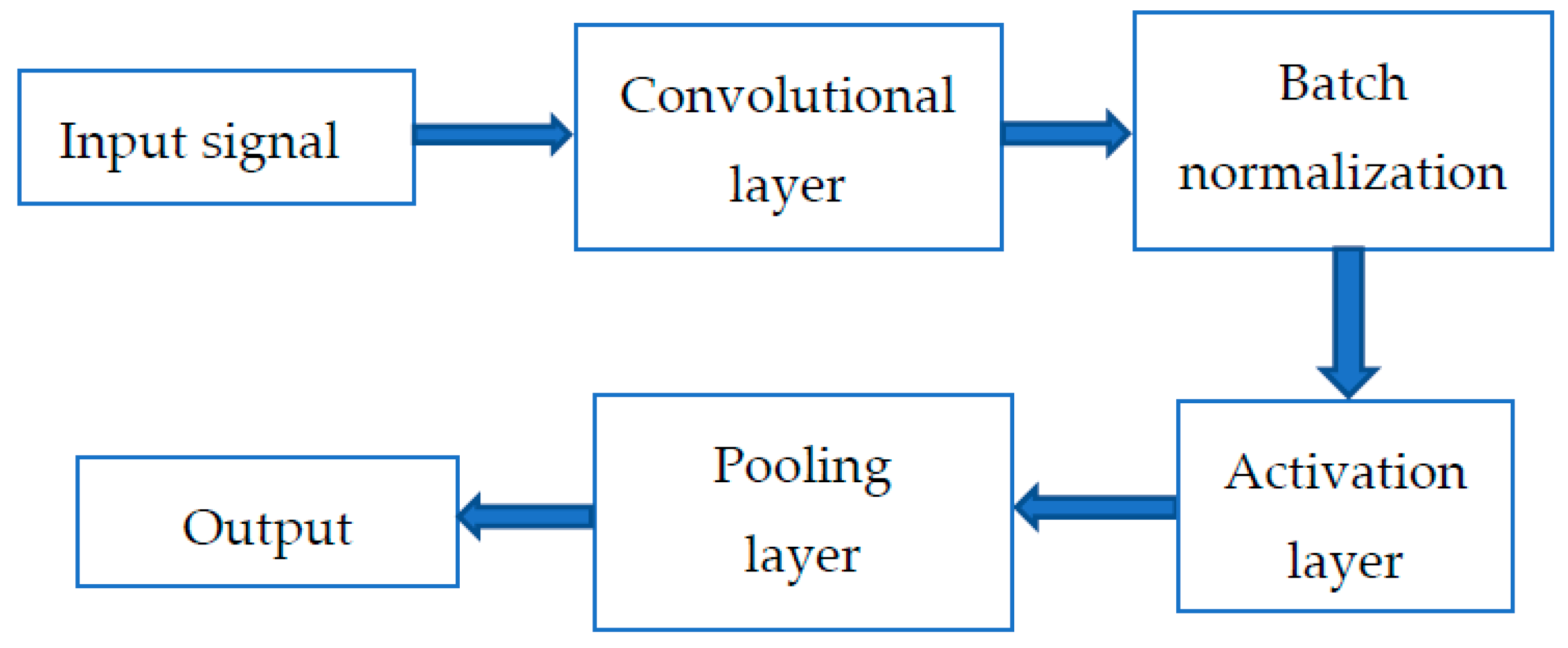
3.2. Convolutional Block
3.3. Wavelet Layer
3.3.1. Wavelet Transform
3.3.2. Wavelet Layer Design
3.4. Prototypical Layer
3.5. Training of the Model
| Algorithm 1 Update the trainable parameter of WPNF via the stochastic gradient descent method of momentum |
| Require: learning rate , Momentum parameter , Initial parameters , Initial speed |
| For epoch to set value, do: |
| For episode to set value, do: |
| Randomly take samples from the query set, and their true labels are |
| Compute gradient of the samples: |
| Compute speed update: |
| Update parameters: |
| End For |
| End For |
4. Experiments
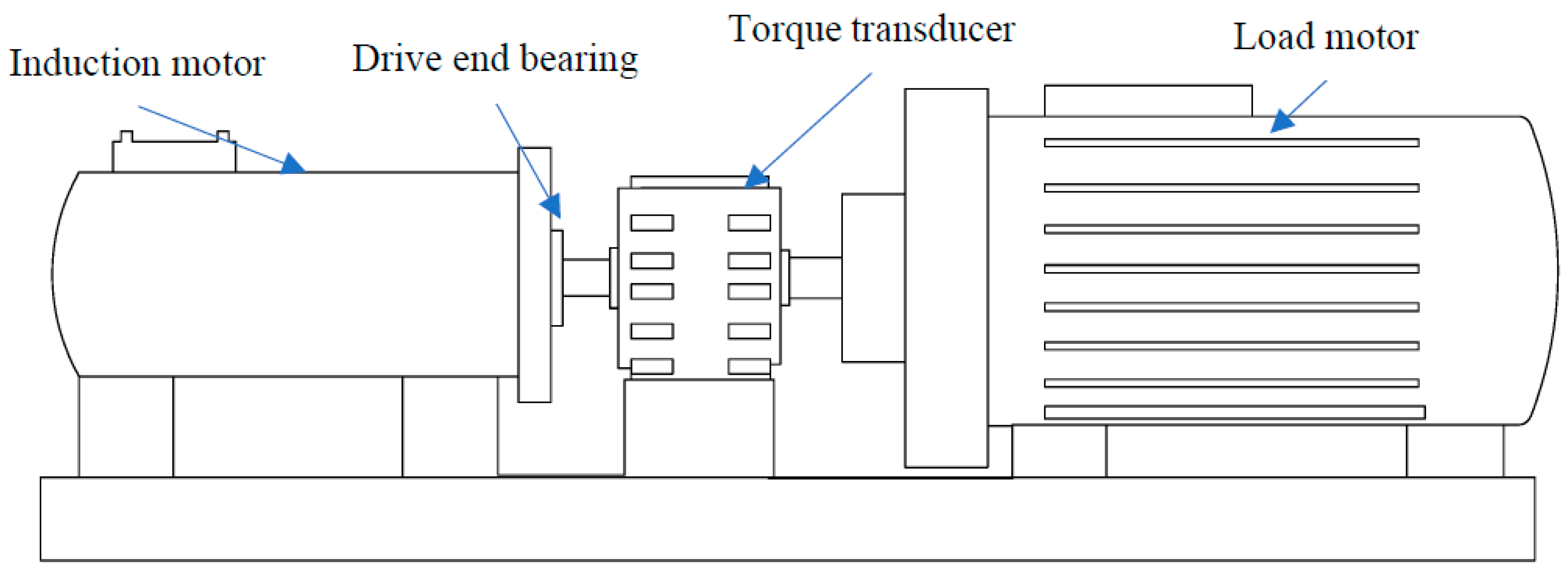
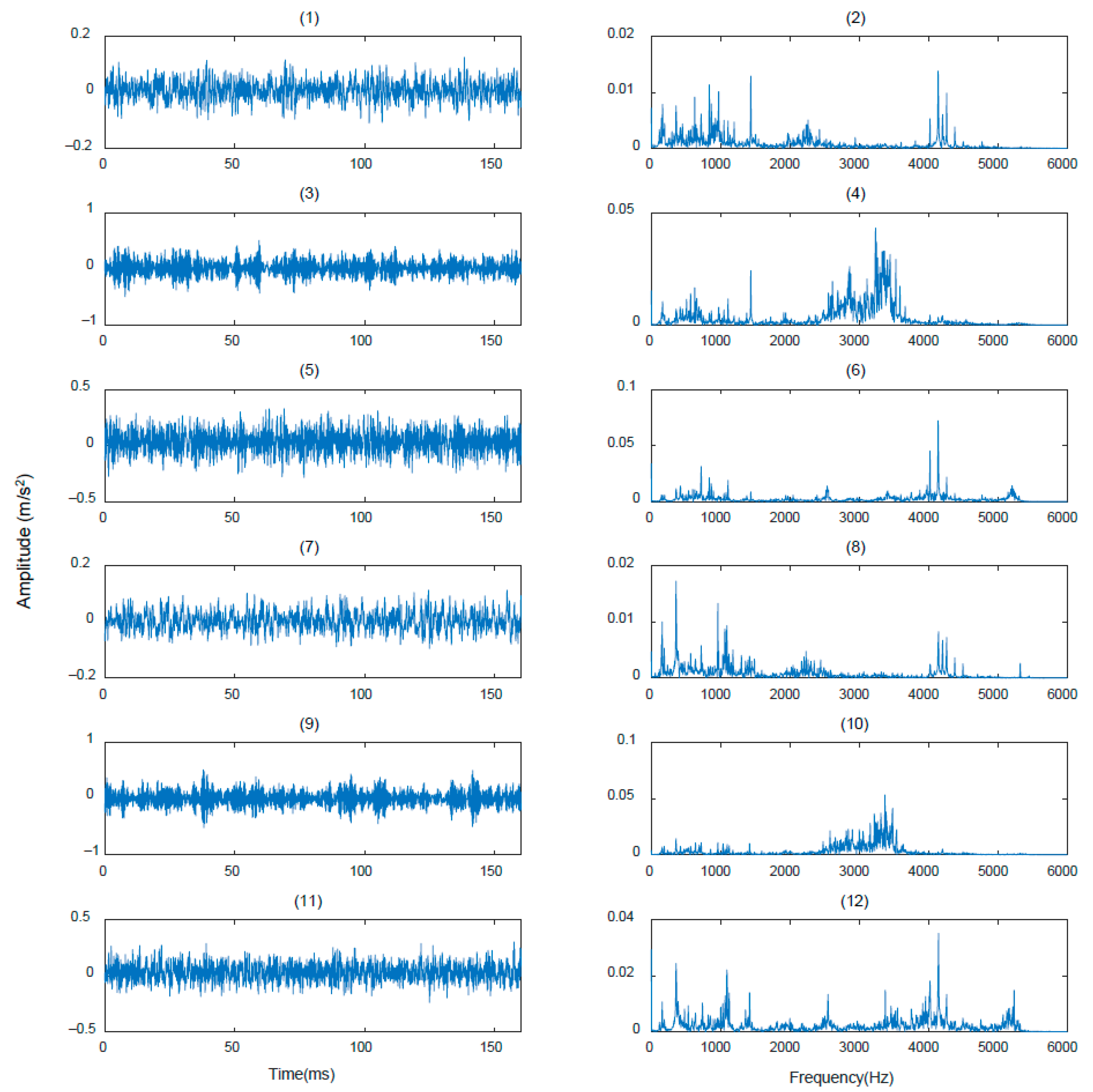
4.1. Description of Experimental Data
4.2. Hyperparameters Setting of WPNF
4.3. Several Models for Comparison
4.4. Comparison of Experimental Results
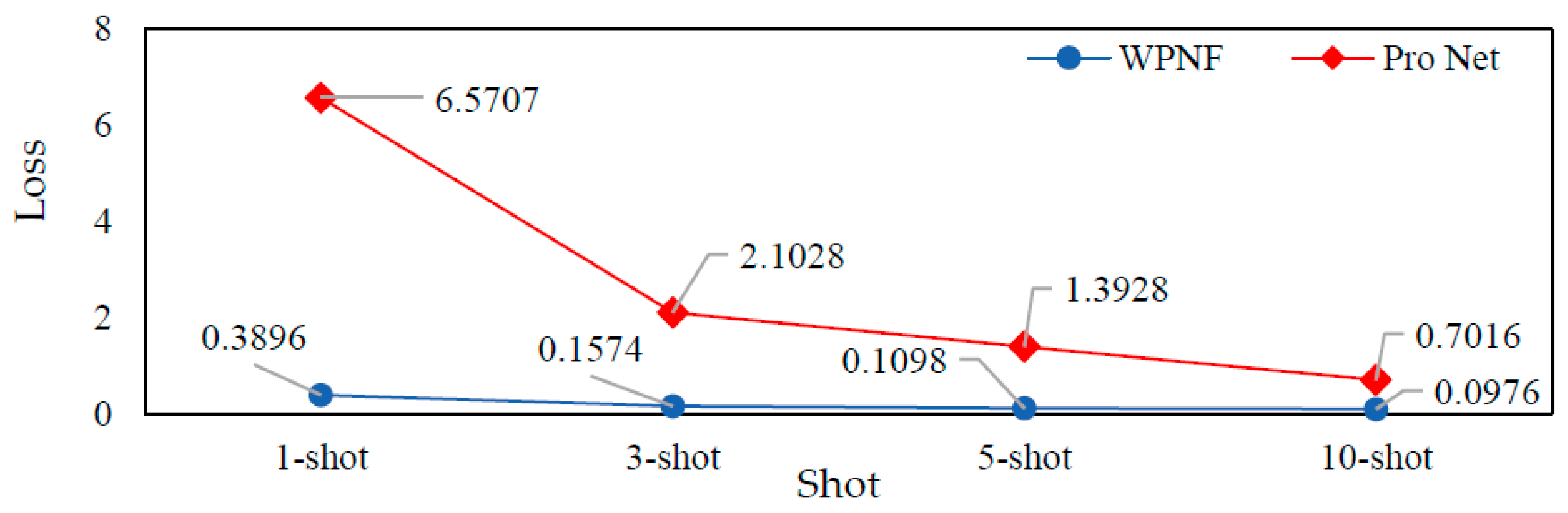
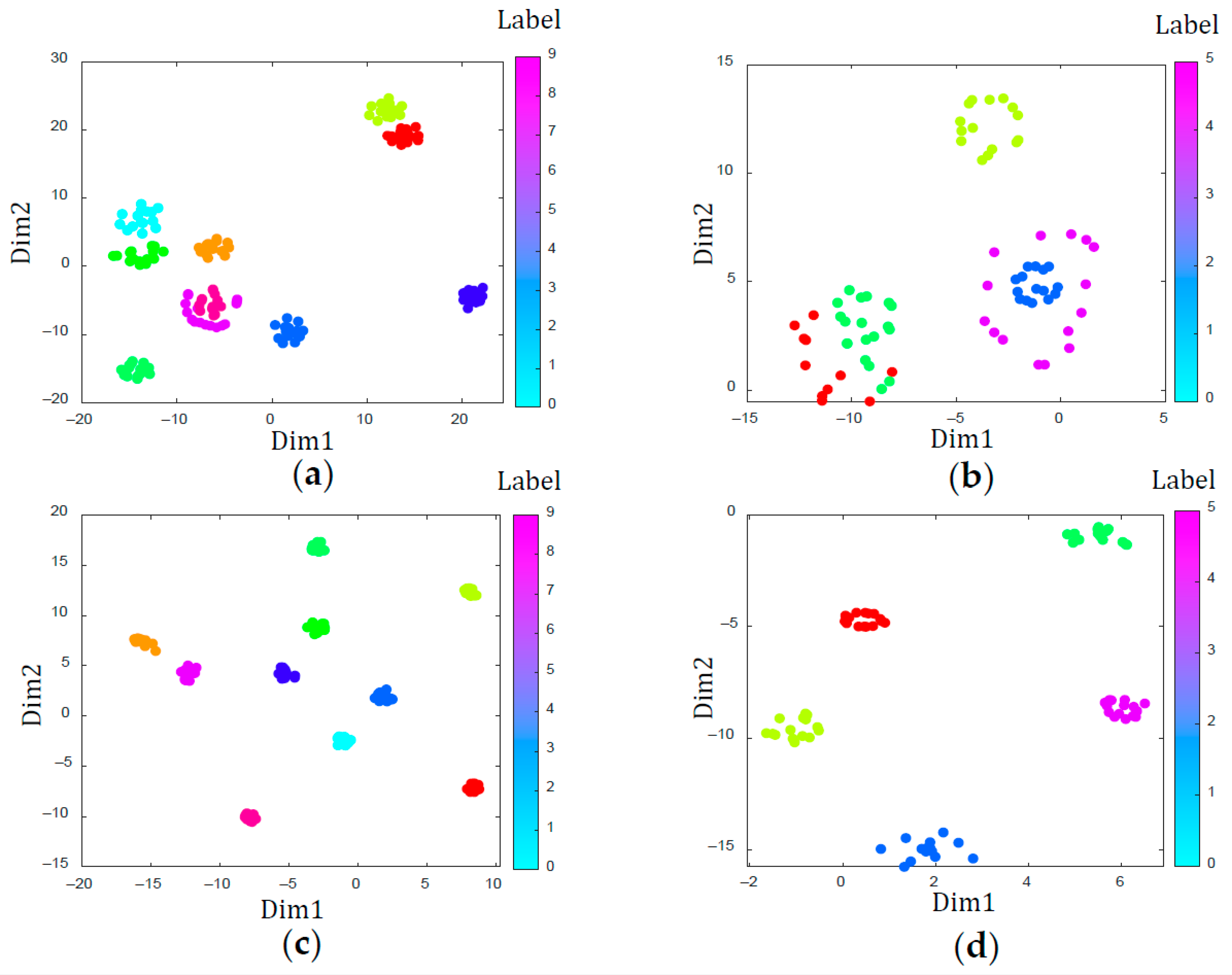
4.4.1. Visualization of the Performance of WPNF and Pro Net
4.4.2. Comparison of WPNF and Several Other Models
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Furse, C.M.; Kafal, M.; Razzaghi, R.; Shin, Y.J. Fault diagnosis for electrical systems and power networks: A review. IEEE Sens. J. 2020, 21, 888–906. [Google Scholar] [CrossRef]
- Bachschmid, N.; Pennacchi, P. Crack effects in rotordynamics. Mech. Syst. Signal Process. 2008, 22, 761–762. [Google Scholar] [CrossRef]
- Chen, P.; Toyota, T.; He, Z. Automated function generation of symptom parameters and application to fault diagnosis of machinery under variable operating conditions. Inf. Med Equip. 2005, 31, 775–781. [Google Scholar]
- McDonald, G.L.; Zhao, Q. Multipoint Optimal Minimum Entropy Deconvolution and Convolution Fix: Application to vibration fault detection. Mech. Syst. Signal Process. 2017, 82, 461–477. [Google Scholar] [CrossRef]
- Pan, H.; Yang, Y.; Li, X.; Zheng, J.; Cheng, J. Symplectic geometry mode decomposition and its application to rotating machinery compound fault diagnosis. Mech. Syst. Signal Process. 2019, 114, 189–211. [Google Scholar] [CrossRef]
- Chen, Z.; Mauricio, A.; Li, W.; Gryllias, K. A deep learning method for bearing fault diagnosis based on cyclic spectral coherence and convolutional neural networks. Mech. Syst. Signal Process. 2020, 140, 106683. [Google Scholar] [CrossRef]
- Lei, Y.; Yang, B.; Jiang, X.; Jia, F.; Li, N.; Nandi, A.K. Applications of machine learning to machine fault diagnosis: A review and roadmap. Mech. Syst. Signal Process. 2020, 138, 106587. [Google Scholar] [CrossRef]
- Tao, X.; Ren, C.; Wu, Y.; Li, Q.; Guo, W.; Liu, R.; He, Q.; Zou, J. Bearings fault detection using wavelet transform and generalized Gaussian density modeling. Measurement 2020, 155, 107557. [Google Scholar] [CrossRef]
- Uddin, P.; Mamun, A.; Hossain, A. PCA-based feature reduction for hyperspectral remote sensing image classification. IETE Tech. Rev. 2020, 1–21. [Google Scholar] [CrossRef]
- He, W.; Zi, Y.; Chen, B.; Wu, F.; He, Z. Automatic fault feature extraction of mechanical anomaly on induction motor bearing using ensemble super-wavelet transform. Mech. Syst. Signal Process. 2015, 54, 457–480. [Google Scholar] [CrossRef]
- Su, Z.Q.; Tang, B.P.; Yao, J.B. Fault diagnosis method based on sensitive feature selection and manifold learning dimension reduction. J. Vib. Shock 2014, 33, 70–75. [Google Scholar]
- Xue, Y.; Dou, D.; Yang, J. Multi-fault diagnosis of rotating machinery based on deep convolution neural network and support vector machine. Measurement 2020, 156, 107571. [Google Scholar] [CrossRef]
- Xu, X.; Cao, D.; Zhou, Y.; Gao, J. Application of neural network algorithm in fault diagnosis of mechanical intelligence. Mech. Syst. Signal Process. 2020, 141, 106625. [Google Scholar] [CrossRef]
- Miao, D.; Di, M. Research on fault diagnosis of high-voltage circuit breaker based on support vector machine. Int. J. Pattern Recognit. Artif. Intell. 2019, 33, 1959019. [Google Scholar] [CrossRef]
- Zhang, W.; Peng, G.; Li, C.; Chen, Y.; Zhang, Z. A New Deep Learning Model for Fault Diagnosis with Good Anti-Noise and Domain Adaptation Ability on Raw Vibration Signals. Sensors 2017, 17, 425. [Google Scholar] [CrossRef]
- Yao, Y.; Zhang, S.; Yang, S.; Gui, G. Learning attention representation with a multi-scale CNN for gear fault diagnosis under different working conditions. Sensors 2020, 20, 1233. [Google Scholar] [CrossRef]
- Jia, Z.; Liu, Z.; Vong, C.-M.; Pecht, M. A rotating machinery fault diagnosis method based on feature learning of thermal images. IEEE Access 2019, 7, 12348–12359. [Google Scholar] [CrossRef]
- Glowacz, A. Fault diagnosis of electric impact drills using thermal imaging. Measurement 2021, 171, 108815. [Google Scholar] [CrossRef]
- Zhang, A.; Li, S.; Cui, Y.; Yang, W.; Dong, R.; Hu, J. Limited data rolling bearing fault diagnosis with few-shot learning. IEEE Access 2019, 2019.7, 110895–110904. [Google Scholar] [CrossRef]
- Li, Q.; Tang, B.; Deng, L.; Wu, Y.; Wang, Y. Deep balanced domain adaptation neural networks for fault diagnosis of planetary gearboxes with limited labeled data. Measurement 2020, 156, 107570. [Google Scholar] [CrossRef]
- Sun, C.S.; Liu, J.; Qin, Y.; Zhang, Y. Intelligent Detection Method for Rail Flaw Based on Deep Learning. China Railw. Sci. 2018, 39, 52–57. [Google Scholar]
- Wang, Y.; Yao, Q.; Kwok, J.T.; Ni, L.M. Generalizing from a few examples: A survey on few-shot learning. ACM Comput. Surv. (CSUR) 2020, 53, 1–34. [Google Scholar] [CrossRef]
- Tuyet-Doan, V.N.; Tran-Thi, N.D.; Youn, Y.W.; Kim, Y.H. One-Shot Learning for Partial Discharge Diagnosis Using Ultra-High-Frequency Sensor in Gas-Insulated Switchgear. Sensors 2020, 20, 5562. [Google Scholar] [CrossRef] [PubMed]
- Han, T.; Liu, C.; Yang, W.; Jiang, D. Deep transfer network with joint distribution adaptation: A new intelligent fault diagnosis framework for industry application. ISA Trans. 2020, 97, 269–281. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A comprehensive survey on transfer learning. Proc. IEEE 2020, 109, 43–76. [Google Scholar] [CrossRef]
- Wen, L.; Gao, L.; Li, X. A new deep transfer learning based on sparse auto-encoder for fault diagnosis. IEEE Trans. Syst. Man Cybern. Syst. 2017, 49, 136–144. [Google Scholar] [CrossRef]
- Wang, J.; Chen, Y.; Feng, W.; Yu, H.; Huang, M.; Yang, Q. Transfer learning with dynamic distribution adaptation. ACM Trans. Intell. Syst. Technol. (TIST) 2020, 11, 1–25. [Google Scholar]
- Chen, W.Y.; Liu, Y.C.; Kira, Z.; Wang, Y.C.F.; Huang, J.B. A closer look at few-shot classification. arXiv 2019, arXiv:1904.04232. [Google Scholar]
- Antoniou, A.; Edwards, H.; Storkey, A. How to train your MAML. arXiv 2018, arXiv:1810.09502. [Google Scholar]
- Chelsea, F.; Abbeel, P.; Levine, S. Model-agnostic meta-learning for fast adaptation of deep networks. arXiv 2017, arXiv:1703.03400. [Google Scholar]
- Chicco, D. Siamese neural networks: An overview. Artif. Neural Netw. 2021, 2190, 73–94. [Google Scholar]
- Jadon, S.; Srinivasan, A.A. Improving Siamese Networks for One-Shot Learning Using Kernel-Based Activation Functions. In Data Management, Analytics and Innovation; Springer: Singapore, 2020; pp. 353–367. [Google Scholar]
- Hsiao, S.-C.; Kao, D.-Y.; Liu, Z.-Y.; Tso, R. Malware Image Classification Using One-Shot Learning with Siamese Networks. Procedia Comput. Sci. 2019, 159, 1863–1871. [Google Scholar] [CrossRef]
- Zhang, K.; Chen, J.; Zhang, T.; He, S.; Pan, T.; Zhou, Z. Intelligent fault diagnosis of mechanical equipment under varying working condition via iterative matching network augmented with selective Signal reuse strategy. J. Manuf. Syst. 2020, 57, 400–415. [Google Scholar] [CrossRef]
- Xia, T.; Song, Y.; Zheng, Y.; Pan, E.; Xi, L. An ensemble framework based on convolutional bi-directional LSTM with multiple time windows for remaining useful life estimation. Comput. Ind. 2020, 115, 103182. [Google Scholar] [CrossRef]
- Li, B.; Tang, B.; Deng, L.; Yu, X. Multiscale dynamic fusion prototypical cluster network for fault diagnosis of planetary gearbox under few labeled samples. Comput. Ind. 2020, 123, 103331. [Google Scholar] [CrossRef]
- Wang, H.; Bai, X.; Tan, J.; Yang, J. Deep prototypical networks based domain adaptation for fault diagnosis. J. Intell. Manuf. 2020, 2020, 1–11. [Google Scholar] [CrossRef]
- Zan, T.; Wang, H.; Wang, M.; Liu, Z.; Gao, X. Application of multi-dimension input convolutional neural network in fault diagnosis of rolling bearings. Appl. Sci. 2019, 9, 2690. [Google Scholar] [CrossRef]
- Snell, J.; Swersky, K.; Zemel, R. Prototypical networks for few-shot learning. arXiv 2017, arXiv:1703.05175. [Google Scholar]
- Zhang, Q.; Benveniste, A. Wavelet networks. IEEE Trans. Neural Netw. 1992, 3, 889–898. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, B.; Dong, J. Time-series prediction using a local linear wavelet neural network. Neurocomputing 2006, 69, 449–465. [Google Scholar] [CrossRef]
- Daubechies, I. The wavelet transform, time-frequency localization and signal analysis. IEEE Trans. Inf. Theory 1990, 36, 961–1005. [Google Scholar] [CrossRef]
- Vanschoren, J. Meta-learning. In Automated Machine Learning; Springe: Cham, Switzland, 2019; pp. 35–61. [Google Scholar]
- Chen, J.; Zhan, L.M.; Wu, X.M.; Chung, F.L. Variational metric scaling for metric-based meta-learning. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 3478–3485. [Google Scholar]
- Tian, P.; Wu, Z.; Qi, L.; Wang, L.; Shi, Y.; Gao, Y. Differentiable meta-learning model for few-shot semantic segmentation. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 12087–12094. [Google Scholar]
- Yao, L.; Xiao, Y.; Gong, X.; Hou, J.; Chen, X. A novel intelligent method for fault diagnosis of electric vehicle battery system based on wavelet neural network. J. Power Sources 2020, 453, 227870. [Google Scholar] [CrossRef]
- Case Western Reserve University. Bearing Data Center Web-Site: Bearing Data Center Seeded Fault Test Data. Available online: https://csegroups.case.edu/bearingdatacenter/pages/download-data-file (accessed on 27 November 2007).
- Laurens, V.D.M.; Hinton., G. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]








| Name | Filters | Kernel Size/Stride (Convolution)/Stride (Pooling) | Input Size | Output Size | Activation Function |
|---|---|---|---|---|---|
| convolutional block1 | 64 | 64 × 1/1 × 1/2 × 1 | 1 × 2048 | 64 × 992 | Relu |
| convolutional block2 | 64 | 3 × 1/1 × 1/2 × 1 | 64 × 992 | 64 × 495 | Relu |
| convolutional block3 | 64 | 3 × 1/1 × 1/2 × 1 | 64 × 495 | 64 × 246 | Relu |
| convolutional block4 | 64 | 3 × 1/1 × 1/2 × 1 | 64 × 246 | 64 × 122 | Relu |
| convolutional block5 | 64 | 64 × 1/1 × 1/2 × 1 | 1 × 1024 | 64 × 480 | Relu |
| convolutional block6 | 64 | 3 × 1/1 × 1/2 × 1 | 64 × 480 | 64 × 239 | Relu |
| convolutional block7 | 64 | 3 × 1/1 × 1/2 × 1 | 64 × 239 | 64 × 118 | Relu |
| convolutional block8 | 64 | 3 × 1/1 × 1/2 × 1 | 64 × 118 | 64 × 58 | Relu |
| Wavelet layer | / | / | 11520 | 5120 | Morlet |
| Prototypical layer | / | / | 5120 | 5120 | Softmax |
| SVM | WDCNN | Pro Net | WPNF | |
|---|---|---|---|---|
| 1-shot | 0.6024 | 0.2481 | 0.8031 | 0.8591 |
| 3-shot | 0.7294 | 0.2764 | 0.9135 | 0.9488 |
| 5-shot | 0.7511 | 0.3124 | 0.9367 | 0.9696 |
| 10-shot | 0.8712 | 0.4289 | 0.9642 | 0.9736 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Chen, L.; Liu, Y.; Gao, L. Wavelet-Prototypical Network Based on Fusion of Time and Frequency Domain for Fault Diagnosis. Sensors 2021, 21, 1483. https://doi.org/10.3390/s21041483
Wang Y, Chen L, Liu Y, Gao L. Wavelet-Prototypical Network Based on Fusion of Time and Frequency Domain for Fault Diagnosis. Sensors. 2021; 21(4):1483. https://doi.org/10.3390/s21041483
Chicago/Turabian StyleWang, Yu, Lei Chen, Yang Liu, and Lipeng Gao. 2021. "Wavelet-Prototypical Network Based on Fusion of Time and Frequency Domain for Fault Diagnosis" Sensors 21, no. 4: 1483. https://doi.org/10.3390/s21041483
APA StyleWang, Y., Chen, L., Liu, Y., & Gao, L. (2021). Wavelet-Prototypical Network Based on Fusion of Time and Frequency Domain for Fault Diagnosis. Sensors, 21(4), 1483. https://doi.org/10.3390/s21041483






