Quantitative Evaluation of Burn Injuries Based on Electrical Impedance Spectroscopy of Blood with a Seven-Parameter Equivalent Circuit
Abstract
:1. Introduction
2. Experiment
2.1. Experimental Setup
2.2. Sample Preparation
2.3. Experimental Results
3. Discussion
3.1. Equivalent Circuit
3.2. Modified Hanai Equation
3.3. Calculation Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- François, P.; Rémi, G.; François, M.; Stéphan, T.; Josée, B. Continuous venovenous hemofiltration using customized replacement fluid for acute kidney injury with severe hypernatremia. Clin. Kidney J. 2016, 9, 540–542. [Google Scholar]
- Priya, K.S.; Gnanamani, A.; Radhakrishnan, N.; Babu, M. Healing potential of Datura alba on burn wounds in albino rats. J. Ethnopharmacol. 2002, 83, 193–199. [Google Scholar] [CrossRef]
- Upadhyay, N.; Kumar, K.R.; Mandotra, S.K.; Meena, R.N.; Siddiqui, M.S.; Sawhney, R.C.; Gupta, A. Safety and healing efficacy of Sea buckthorn (Hippophae rhamnoides L.) seed oil on burn wounds in rats. Food Chem. Toxicol. 2009, 47, 1146–1153. [Google Scholar] [CrossRef]
- Monstrey, S.; Hoeksema, H.; Verbelen, J.; Pirayesh, A.; Blondeel, P. Assessment of burn depth and burn wound healing potential. Burns 2008, 34, 761–769. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Heimbach, D.; Engrav, L.; Grube, B.; Marvin, J. Burn Depth: A Review. World J. Surg. 1992, 16, 10–15. [Google Scholar] [CrossRef]
- Godina, M.; Derganc, M.; Brčič, A. The reliability of clinical assessment of the depth of burns. Burns 1977, 4, 92–96. [Google Scholar] [CrossRef]
- Kahn, A.M.; McCrady, V.L.; Rosen, V.J. Burn wound biopsy multiple uses in patient management. Scand. J. Plast. Recons. 1979, 13, 53–56. [Google Scholar] [CrossRef]
- Niazi, Z.B.M.; Essex, T.J.H.; Papini, R.; Scott, D.; McLean, N.R.; Black, M.J.M. New laser doppler scanner, a valuable adjunct in burn depth assessment. Burns 1993, 19, 485–489. [Google Scholar] [CrossRef]
- Brink, J.A.; Sheets, P.W.; Dines, K.A.; Etchison, M.R.; Hanke, C.W.; Sadove, A.M. Quantitative assessment of burn Injury in porcine skin with high-frequency ultrasonic imaging. Invest. Radiol. 1986, 21, 645–651. [Google Scholar] [CrossRef]
- Anand, G.; Lowe, A. Investigating electrical impedance spectroscopy for estimating blood flow-induced variations in human forearm. Sensors 2020, 20, 5333. [Google Scholar] [CrossRef]
- Bruna, G.P.; David, C.M.; Pedro, B.F. Analytical Model for Blood Glucose Detection Using Electrical Impedance Spectroscopy. Sensors 2020, 20, 6928. [Google Scholar]
- Wan, Y.; Su, Y.; Zhu, X.; Liu, G.; Fan, C. Development of electrochemical immunosensors towards point of care diagnostics. Biosens. Bioelectron. 2013, 47, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Xie, X.; Duan, Y.; Wang, L.; Cheng, Z.; Cheng, J. A review of impedance measurements of whole cells. Biosens. Bioelectron. 2016, 77, 824–836. [Google Scholar] [CrossRef]
- Negahdary, M. Aptamers in nanostructure-based electrochemical biosensors for cardiac biomarkers and cancer biomarkers: A review. Biosens. Bioelectron. 2020, 152, 112018. [Google Scholar] [CrossRef] [PubMed]
- Asami, K. Characterization of heterogeneous systems by dielectric spectroscopy. Prog. Polym. Sci. 2002, 27, 1617–1659. [Google Scholar] [CrossRef]
- Li, J.; Sapkota, A.; Kikuchi, D.; Sakota, D.; Maruyama, O.; Takei, M. Red blood cells aggregability measurement of coagulating blood in extracorporeal circulation system with multiple-frequency electrical impedance spectroscopy. Biosens. Bioelectron. 2018, 112, 79–85. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Wan, N.; Wen, J.; Cheng, G.; He, L.; Cheng, L. Quantitative detection and evaluation of thrombus formation based on electrical impedance spectroscopy. Biosens. Bioelectron. 2019, 141, 111437. [Google Scholar] [CrossRef]
- DMishra, S.K.; Kumar, D.; Biradar, A.M.; Rajesh. Electrochemical impedance spectroscopy characterization of mercaptopropionic acid capped ZnS nanocrystal based bioelectrode for the detection of the cardiac biomarker—myoglobin. Bioelectrochemistry 2012, 88, 118–126. [Google Scholar] [CrossRef]
- Nguyen, N.-V.; Jen, C.-P. Impedance detection integrated with dielectrophoresis enrichment platform for lung circulating tumor cells in a microfluidic channe. Biosens. Bioelectron. 2018, 121, 10–18. [Google Scholar] [CrossRef]
- Ngoc, L.; Hien, T.; Kim, J.; Park, J.; Cho, S. A Review of Electrical Impedance Characterization of Cells for Label-Free and Real-Time Assays. Biochip. J. 2019, 13, 295–305. [Google Scholar] [CrossRef]
- Hassan, Q.; Ahmadi, S.; Kerman, K. Recent Advances in Monitoring Cell Behavior Using Cell-Based Impedance Spectroscopy. Micromachines 2020, 11, 590. [Google Scholar] [CrossRef]
- Sen, S.; Hsei, L.; Tran, N.; Romanowski, K.; Palmieri, T.; Greenhalgh, D.; Cho, K. Early clinical complete blood count changes in severe burn injuries. Burns 2018, 45, 97–102. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, J.; Wu, J. Autoimmune hemolytic anemia occurred in burn patient: A case report. Burns 2014, 40, e9–e11. [Google Scholar] [CrossRef]
- Grzelińska, E.; Bartosz, G.; Leyko, W.; Chapman, I.V. Effect of hyperthermia and ionizing radiation on the erythrocyte membrane. Nt. J. Radiat. Biol. 1982, 42, 45–55. [Google Scholar] [CrossRef]
- Zahid, M.F.; Alsammak, M.S. Spurious thrombocytosis in the setting of hemolytic anemia and microcytosis secondary to extensive burn injury. Turk. J. Hematol. 2018, 35, 205–206. [Google Scholar] [CrossRef]
- Shoar Abouzari, M.R.; Berkemeier, F.; Schmitz, G.; Wilmer, D. On the physical interpretation of constant phase elements. Solid. State. Ionics 2009, 180, 922–927. [Google Scholar] [CrossRef]
- Zhbanov, A.; Yang, S. Electrochemical impedance spectroscopy of blood for sensitive detection of blood hematocrit, sedimentation and dielectric properties. Anal. Methods. 2017, 9, 3302–3313. [Google Scholar] [CrossRef]


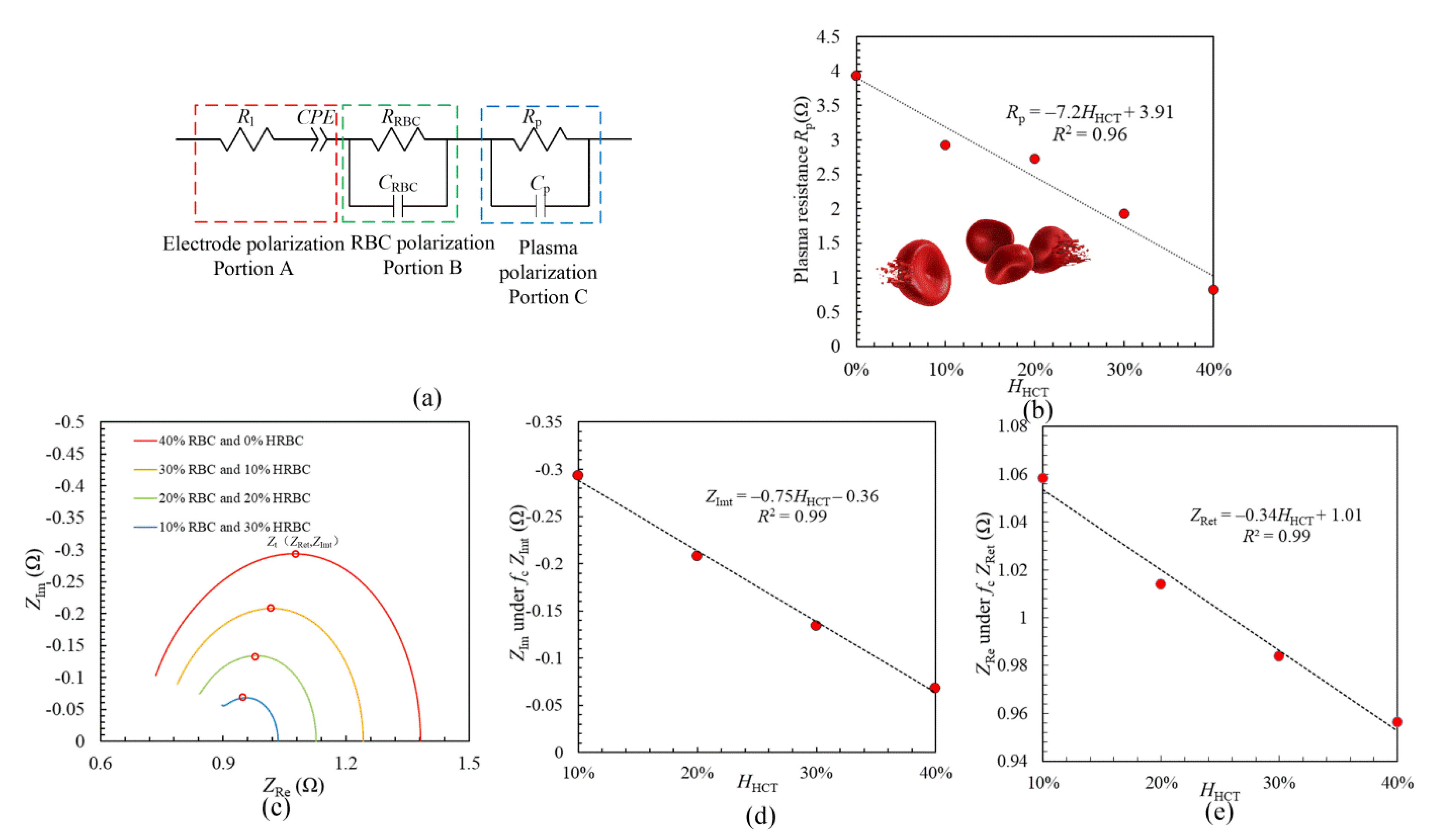
| HHCT (-) | R1 (Ω) | CPE-T (F·sec−0.28) | p-T (-) | RRBC (Ω) | CRBC (F) | RP (Ω) | Cp (F) |
|---|---|---|---|---|---|---|---|
| 40% | 9.2 | 0.55 | 0.72 | 0.9 | 0.02 | 0.83 | 0.01 |
| 30% | 9.2 | 0.55 | 0.72 | 0.8 | 0.01 | 1.93 | 0.02 |
| 20% | 9.2 | 0.55 | 0.72 | 0.85 | 0.01 | 2.73 | 0.018 |
| 10% | 9.2 | 0.55 | 0.72 | 0.75 | 0.01 | 2.93 | 0.02 |
| 0 | 9.2 | 0.55 | 0.72 | 0.5 | 0.005 | 3.93 | 0.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, H.; Li, J.; Wen, J.; Cheng, L.; Hu, Y.; Zhang, Y.; Wan, N.; Takei, M. Quantitative Evaluation of Burn Injuries Based on Electrical Impedance Spectroscopy of Blood with a Seven-Parameter Equivalent Circuit. Sensors 2021, 21, 1496. https://doi.org/10.3390/s21041496
Bao H, Li J, Wen J, Cheng L, Hu Y, Zhang Y, Wan N, Takei M. Quantitative Evaluation of Burn Injuries Based on Electrical Impedance Spectroscopy of Blood with a Seven-Parameter Equivalent Circuit. Sensors. 2021; 21(4):1496. https://doi.org/10.3390/s21041496
Chicago/Turabian StyleBao, Huilu, Jianping Li, Jianming Wen, Li Cheng, Yili Hu, Yu Zhang, Nen Wan, and Masahiro Takei. 2021. "Quantitative Evaluation of Burn Injuries Based on Electrical Impedance Spectroscopy of Blood with a Seven-Parameter Equivalent Circuit" Sensors 21, no. 4: 1496. https://doi.org/10.3390/s21041496
APA StyleBao, H., Li, J., Wen, J., Cheng, L., Hu, Y., Zhang, Y., Wan, N., & Takei, M. (2021). Quantitative Evaluation of Burn Injuries Based on Electrical Impedance Spectroscopy of Blood with a Seven-Parameter Equivalent Circuit. Sensors, 21(4), 1496. https://doi.org/10.3390/s21041496







