A Contact-Mode Triboelectric Nanogenerator for Energy Harvesting from Marine Pipe Vibrations
Abstract
:1. Introduction
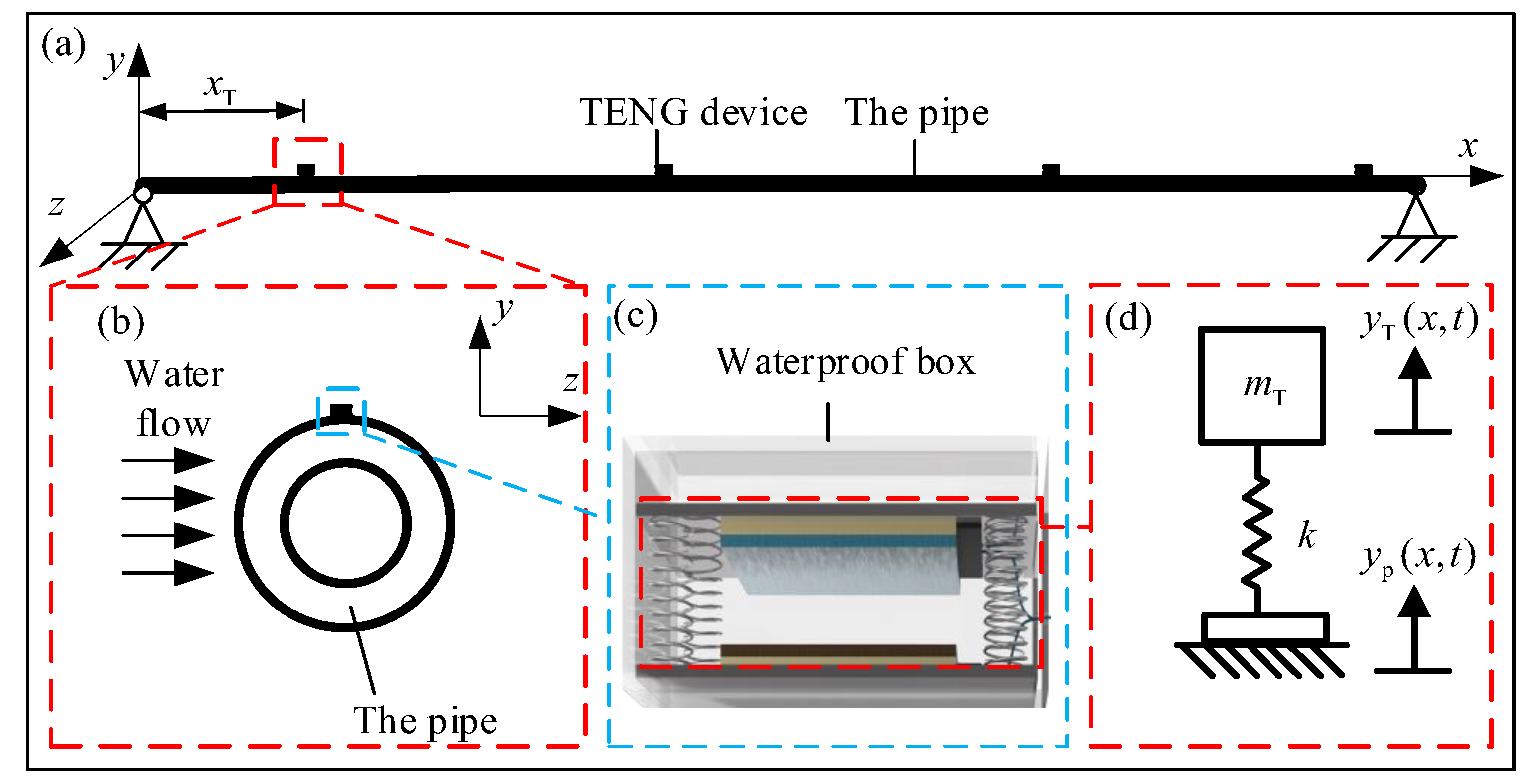
2. Materials and Methods
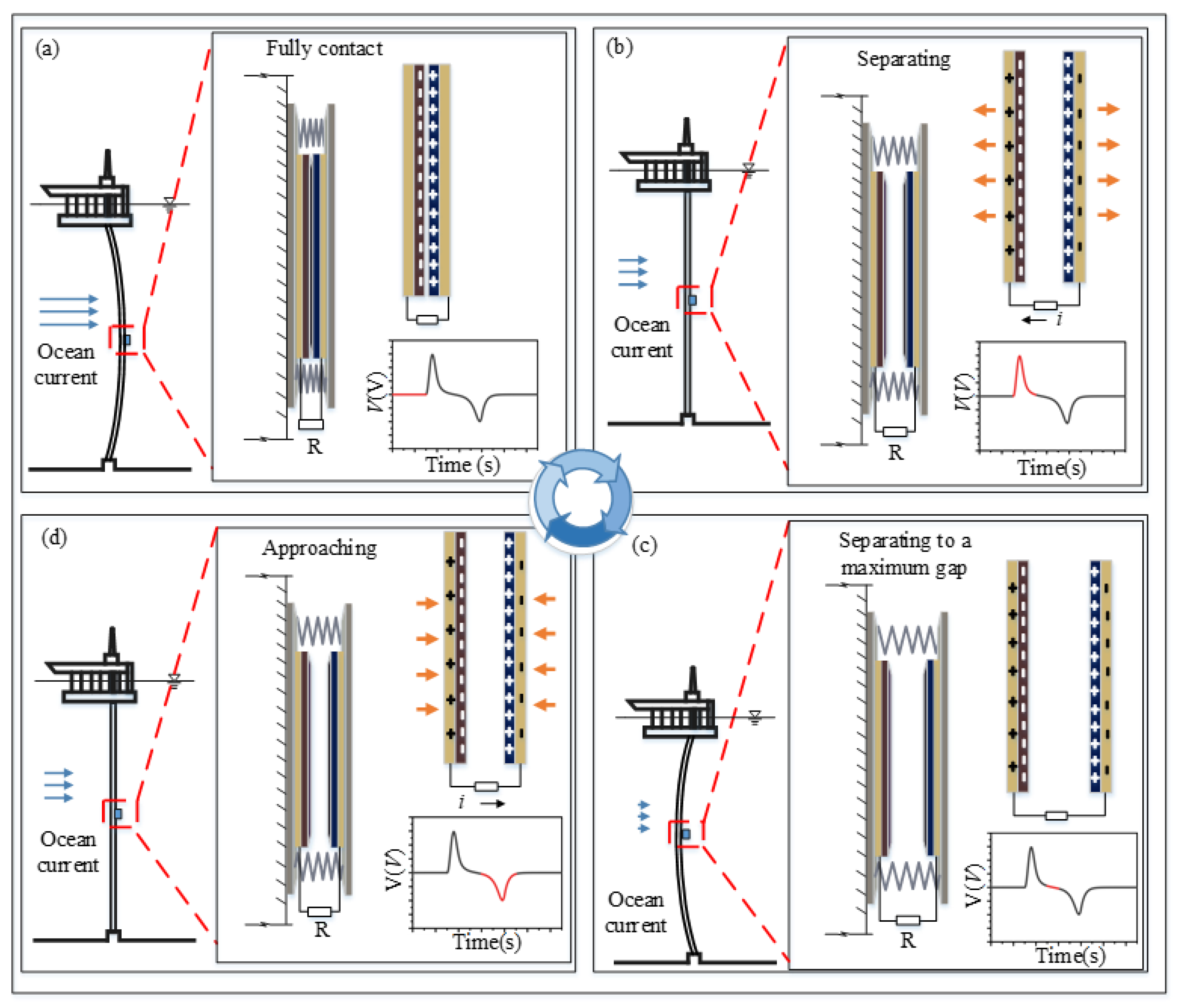
3. Experimental Test
4. Theoretical Modelling
4.1. Dynamic Responses of the Pipe and the Mass-Spring Base
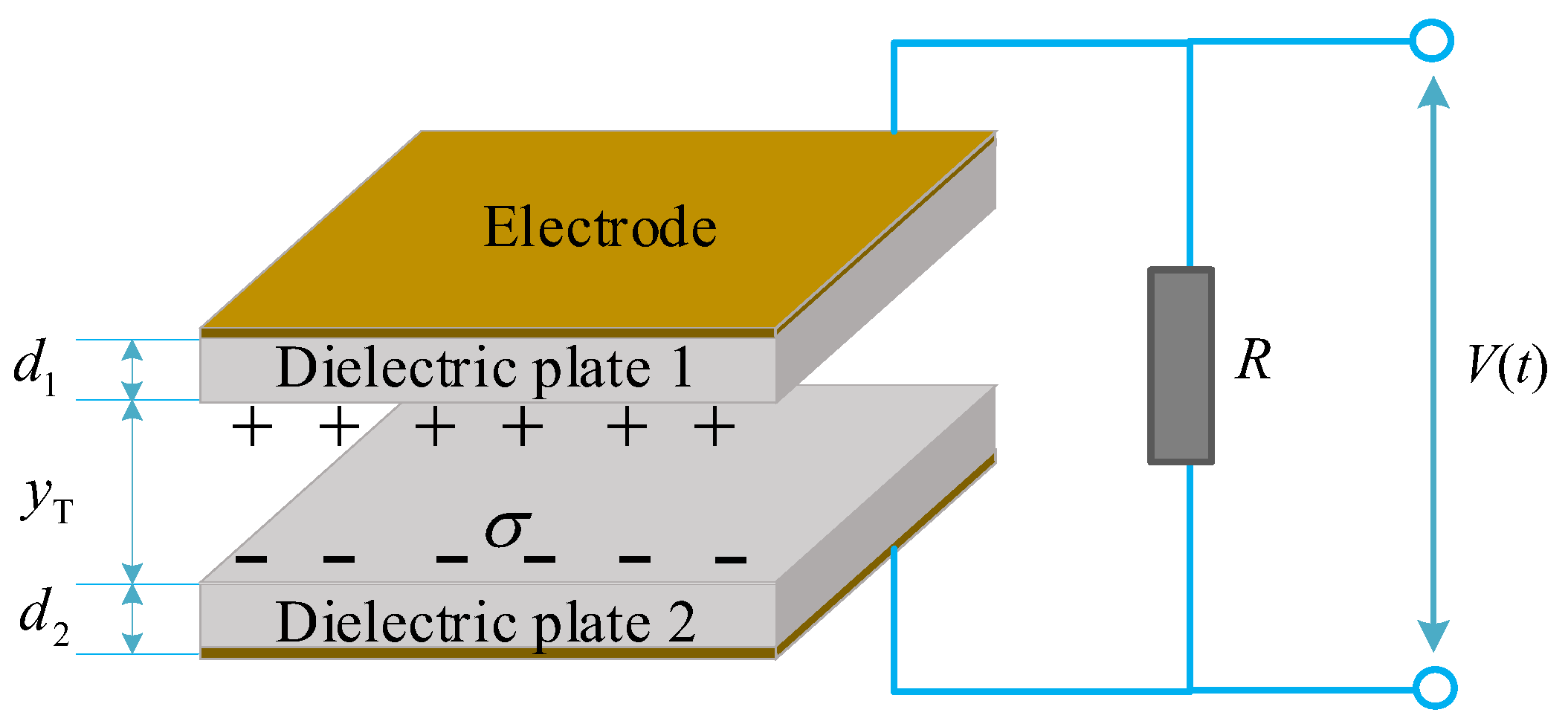
4.2. The Electric Output of TENG Device
4.3. Scaling Laws
5. Theoretical Case Study
5.1. Validation of the Theoretical Model
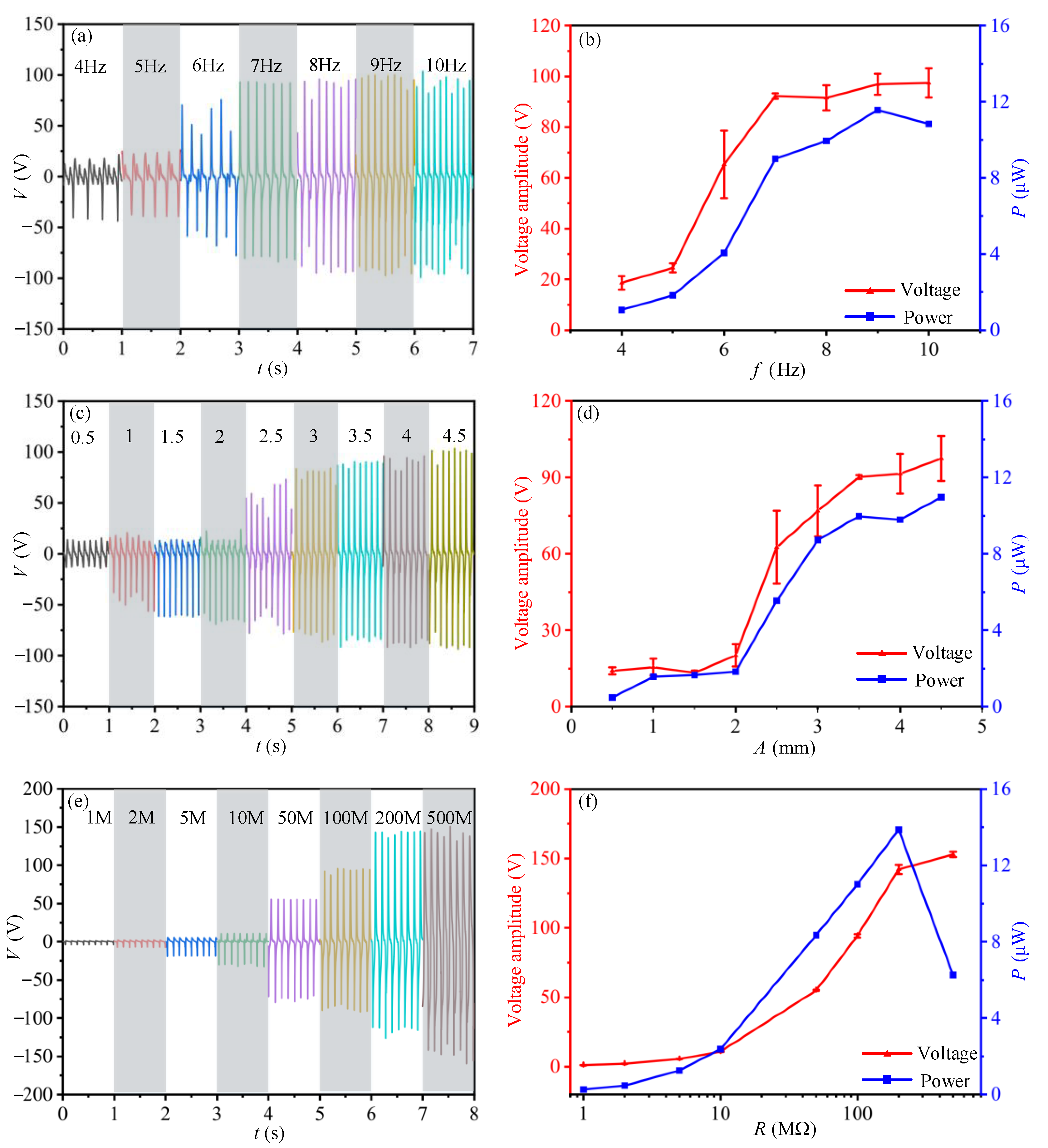
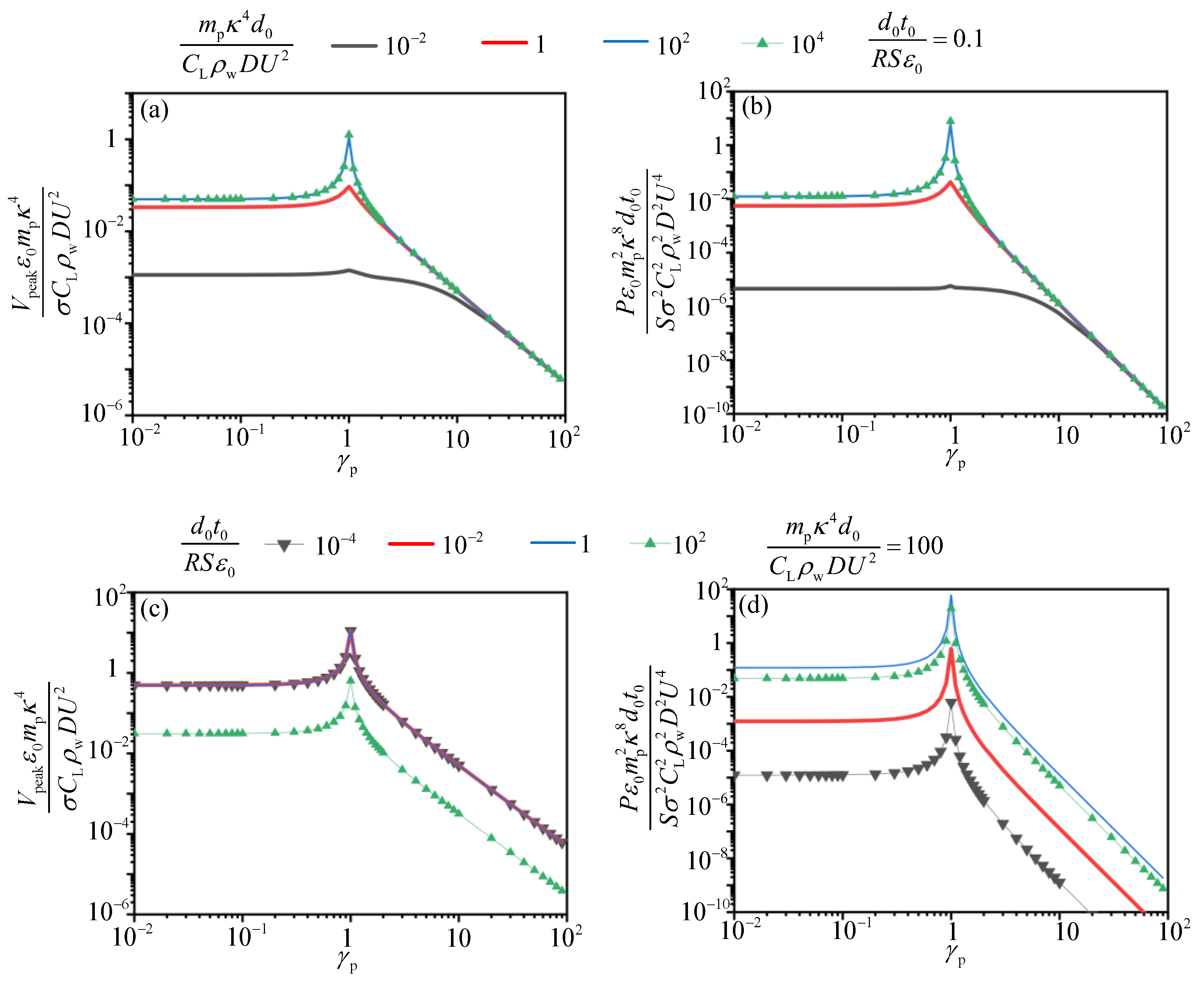
5.2. Individual Parameter Analysis of Output Performance
5.3. Multiple Parameters Analysis of Output Performance
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gabbai, R.D.; Benaroya, H. An overview of modeling and experiments of vortex-induced vibration of circular cylinders. J. Sound Vib. 2005, 282, 575–616. [Google Scholar] [CrossRef]
- Lu, P.; Lalam, N.; Badar, M.; Liu, B.; Ohodnicki, P.R. Distributed optical fiber sensing: Review and perspective. Appl. Phys. Rev. 2019, 6, 041302. [Google Scholar] [CrossRef]
- Nishimoto, T.; Miyahara, T.; Takehana, H.; Tateno, F. Development of 66kV XLPE submarine cable using optical fiber as a mechanical-damage-detection-sensor. IEEE T Power Deliv. 2002, 10, 1711–1717. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, J.; Huang, X.; Zhang, J.; Guo, X. Trend of soil temperature during pipeline leakage of high-pressure natural gas: Experimental and numerical study. Measurement 2020, 153, 107440. [Google Scholar] [CrossRef]
- Ren, L.; Jiang, T.; Jia, Z.G.; Li, D.S.; Yuan, C.L.; Li, H.N. Pipeline corrosion and leakage monitoring based on the distributed optical fiber sensing technology. Measurement 2018, 57–65. [Google Scholar] [CrossRef]
- Xia, H.; Xia, Y.; Ye, Y.; Qian, L.; Shi, G. Simultaneous Wireless Strain Sensing and Energy Harvesting from Multiple Piezo-Patches for Structural Health Monitoring Applications. IEEE T Ind. Electron 2019, 66, 8235–8243. [Google Scholar] [CrossRef]
- Othmani, C.; Zhang, H.; Lü, C. Effects of initial stresses on guided wave propagation in multilayered PZT-4/PZT-5A composites: A polynomial expansion approach. Appl Math Model 2020, 78, 148–168. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, H.; Lü, C.; Chen, Y.; Wang, J. Piezoelectric energy harvesting from roadway deformation under various traffic flow conditions. J. Intel. Mat. Syst. Str. 2020, 31, 1751–1762. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, K.; Zhang, Z.; Xiang, T.; Quan, L. Piezoelectric Energy Harvesting From Roadways Based on Pavement Compatible Package. Journal of Applied Mechanics 2019, 86. [Google Scholar] [CrossRef]
- Zhang, H.; Ye, G.; Zhang, Z. Acoustic Radiation of a Cylindrical Piezoelectric Power Transformer. Journal of Applied Mechanics 2013, 80. [Google Scholar] [CrossRef]
- Zhang, H.; Yao, L.; Quan, L.; Zheng, X. Theories for triboelectric nanogenerators: A comprehensive review. Nanotechnol Rev. 2020, 9, 610–625. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, H.; Zhang, J.; Zhang, Z.; Dong, S. A Novel Rhombic-shaped Paper-based Triboelectric Nanogenerator for Harvesting Energy from Environmental Vibration. Sensors Actuators A Phys. 2019, 302, 111806. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, C.; Yu, Y.; Zhou, Y.; Luo, J. Origami-tessellation-based triboelectric nanogenerator for energy harvesting with application in road pavement. Nano Energy 2020, 78, 105177. [Google Scholar] [CrossRef]
- Okosun, F.; Cahill, P.; Hazra, B.; Pakrashi, V. Vibration-based leak detection and monitoring of water pipes using output-only piezoelectric sensors. Eur. Phys. J. Spec. Top. 2019, 228, 1659–1675. [Google Scholar] [CrossRef]
- Rui, X.; Zeng, Z.; Zhang, Y.; Li, Y.; Xu, T. An intelligent self-powered pipeline inner spherical detector with piezoelectric energy harvesting. IEEE Access. 2019, 7, 104621–104629. [Google Scholar] [CrossRef]
- Cao, D.; Duan, X.; Guo, X.; Lai, S. Design and performance enhancement of a force-amplified piezoelectric stack energy harvester under pressure fluctuations in hydraulic pipeline systems. Sens. Actuators A Phys. 2020, 309, 112031. [Google Scholar] [CrossRef]
- Aramendia, I.; Fernandez-Gamiz, U.; Zulueta Guerrero, E.; Lopez-Guede, J.M.; Sancho, J. Power Control Optimization of an Underwater Piezoelectric Energy Harvester. Appl. Sci. 2018, 8, 389. [Google Scholar] [CrossRef] [Green Version]
- Aphayvong, S.; Yoshimura, T.; Murakami, S.; Kanda, K.; Fujimura, N. Investigation of efficient piezoelectric energy harvesting from impulsive force. Jpn. J. Appl. Phys. 2020, 59, SPPD04. [Google Scholar] [CrossRef]
- Wang, Z.L. Triboelectric Nanogenerators as New Energy Technology for Self-Powered Systems and as Active Mechanical and Chemical Sensors. Acs Nano 2013, 7, 9533–9557. [Google Scholar] [CrossRef]
- Chen, J.; Yang, J.; Li, Z.; Fan, X.; Zi, Y.; Jing, Q.; Guo, H.; Wen, Z.; Pradel, K.C.; Niu, S. Networks of Triboelectric Nanogenerators for Harvesting Water Wave Energy: A Potential Approach toward Blue Energy. ACS Nano 2015, 9, 3324–3331. [Google Scholar] [CrossRef]
- Wen, Z.; Guo, H.; Zi, Y.; Yeh, M.; Wang, X.; Deng, J.; Wang, J.; Li, S.; Hu, C.; Zhu, L.; et al. Harvesting Broad Frequency Band Blue Energy by a Triboelectric–Electromagnetic Hybrid Nanogenerator. Acs Nano 2016, 10, 6526–6534. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.L.; Jiang, T.; Xu, L. Toward the blue energy dream by triboelectric nanogenerator networks. Nano Energy 2017, 39, 9–23. [Google Scholar] [CrossRef]
- Chen, H.; Xing, C.; Li, Y.; Wang, J.; Xu, Y. Triboelectric nanogenerators for a macro-scale blue energy harvesting and self-powered marine environmental monitoring system. Sustain Energ Fuels 2020, 4, 1063–1077. [Google Scholar] [CrossRef]
- Xi, Y.; Guo, H.; Zi, Y.; Li, X.; Wang, J.; Deng, J.; Li, S.; Hu, C.; Cao, X.; Wang, Z.L. Multifunctional TENG for Blue Energy Scavenging and Self-Powered Wind-Speed Sensor. Adv. Energy Mater. 2017, 7, 1602397. [Google Scholar] [CrossRef]
- Saadatnia, Z.; Asadi, E.; Askari, H.; Esmailzadeh, E.; Naguib, H.E. A heaving point absorber-based triboelectric-electromagnetic wave energy harvester: An efficient approach toward blue energy. Int. J. Energy Res. 2018, 42, 2431–2447. [Google Scholar] [CrossRef]
- Shao, H.; Wen, Z.; Cheng, P.; Sun, N.; Shen, Q.; Zhou, C.; Peng, M.; Yang, Y.; Xie, X.; Sun, X. Multifunctional Power Unit by Hybridizing Contact-Separate Triboelectric Nanogenerator, Electromagnetic Generator and Solar Cell for Harvesting Blue Energy. Nano Energy 2017, 39, 608–615. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, X.; Yin, M.; Wang, J.; Gao, Q.; Yu, Y.; Cheng, T.; Wang, Z.L. Gravity triboelectric nanogenerator for the steady harvesting of natural wind energy. Nano Energy 2021, 82, 105740. [Google Scholar] [CrossRef]
- Guo, H.; Wen, Z.; Zi, Y.; Yeh, M.; Wang, J.; Zhu, L.; Hu, C.; Wang, Z.L. A Water-Proof Triboelectric–Electromagnetic Hybrid Generator for Energy Harvesting in Harsh Environments. Adv. Energy Mater. 2016, 6, 1501593. [Google Scholar] [CrossRef]
- Jiang, T.; Zhang, L.M.; Chen, X.; Han, C.B.; Tang, W.; Zhang, C.; Xu, L.; Wang, Z.L. Structural Optimization of Triboelectric Nanogenerator for Harvesting Water Wave Energy. Acs Nano 2015, 9, 12562–12572. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.J.; Zhu, G.; Fan, Y.J.; Li, H.Y.; Wang, Z.L. Triboelectric Charging at the Nanostructured Solid/Liquid Interface for Area-Scalable Wave Energy Conversion and Its Use in Corrosion Protection. ACS Nano 2015, 9, 7671–7677. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Pang, Y.; Zhang, C.; Jiang, T.; Chen, X.; Luo, J.; Tang, W.; Cao, X.; Wang, Z.L. Integrated triboelectric nanogenerator array based on air-driven membrane structures for water wave energy harvesting. Nano Energy 2017, 31, 351–358. [Google Scholar] [CrossRef]
- Wang, Z.L. On Maxwell’s displacement current for energy and sensors: The origin of nanogenerators. Mater. Today 2017, 20, 74–82. [Google Scholar] [CrossRef]
- Totovic, A.R.; Dabos, G.; Passalis, N.; Tefas, A. Femtojoule per MAC Neuromorphic Photonics: An Energy and Technology Roadmap. Ieee J Sel Top Quant 2020, 26, 1–15. [Google Scholar] [CrossRef]
- Paultre, P. Dynamics of Structures; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Farshidianfar, A.; Zanganeh, H. A modified wake oscillator model for vortex-induced vibration of circular cylinders for a wide range of mass-damping ratio. J. Fluids Struct. 2010, 26, 430–441. [Google Scholar] [CrossRef]
- Niu, S.; Wang, S.; Lin, L.; Liu, Y.; Zhou, Y.S.; Hu, Y.; Wang, Z.L. Theoretical study of contact-mode triboelectric nanogenerators as an effective power source. Energy Environ. Sci. 2013, 6, 3576–3583. [Google Scholar] [CrossRef]
- Zhang, H.; Quan, L.; Chen, J.; Xu, C.; Zhang, C.; Dong, S.; Lü, C.; Luo, J. A general optimization approach for contact-separation triboelectric nanogenerator. Nano Energy 2019, 56, 700–707. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, C.; Zhang, J.; Quan, L.; Huang, H.; Jiang, J.; Dong, S.; Luo, J. A theoretical approach for optimizing sliding-mode triboelectric nanogenerator based on multi-parameter analysis. Nano Energy 2019, 61, 442–453. [Google Scholar] [CrossRef]




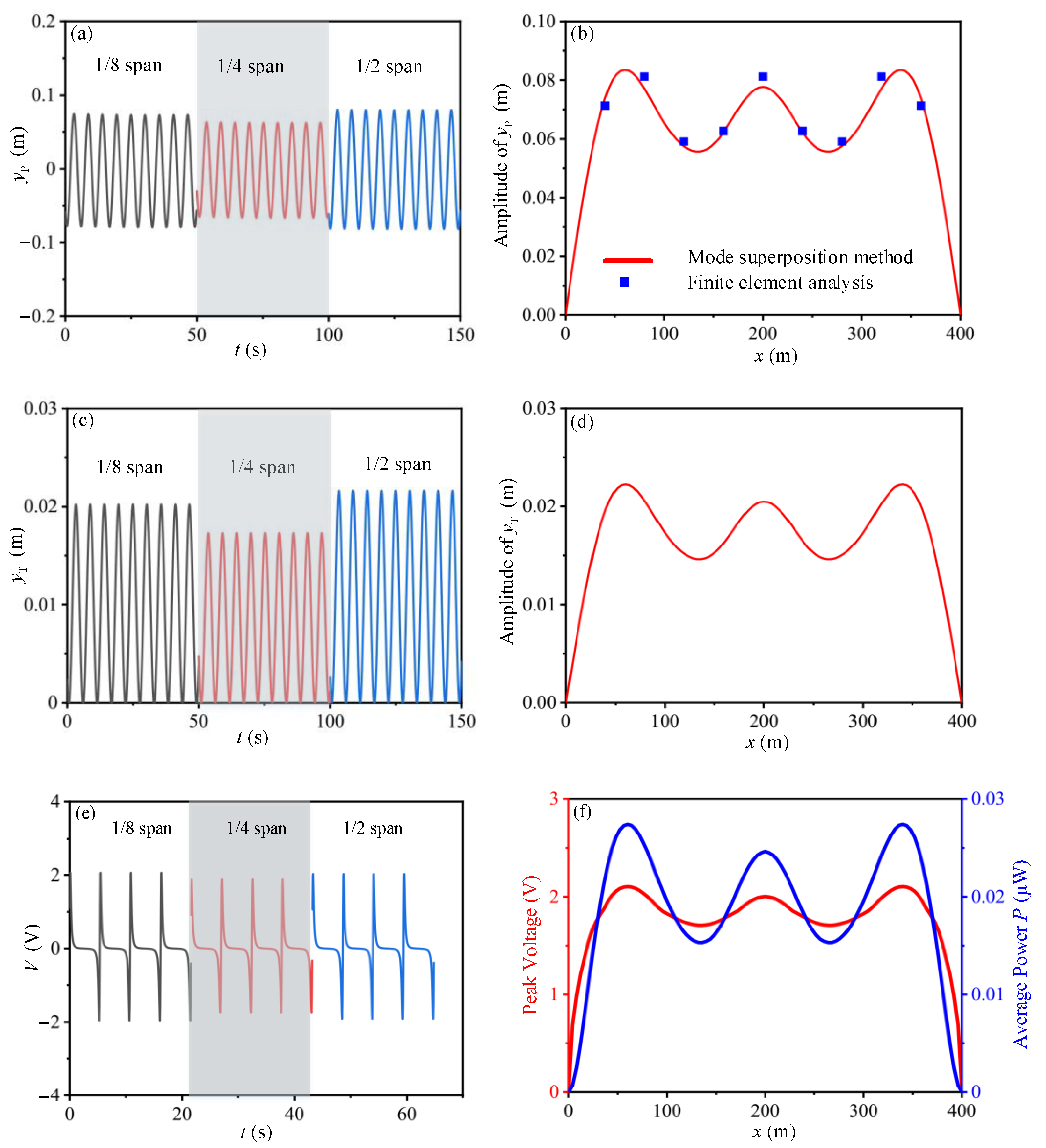
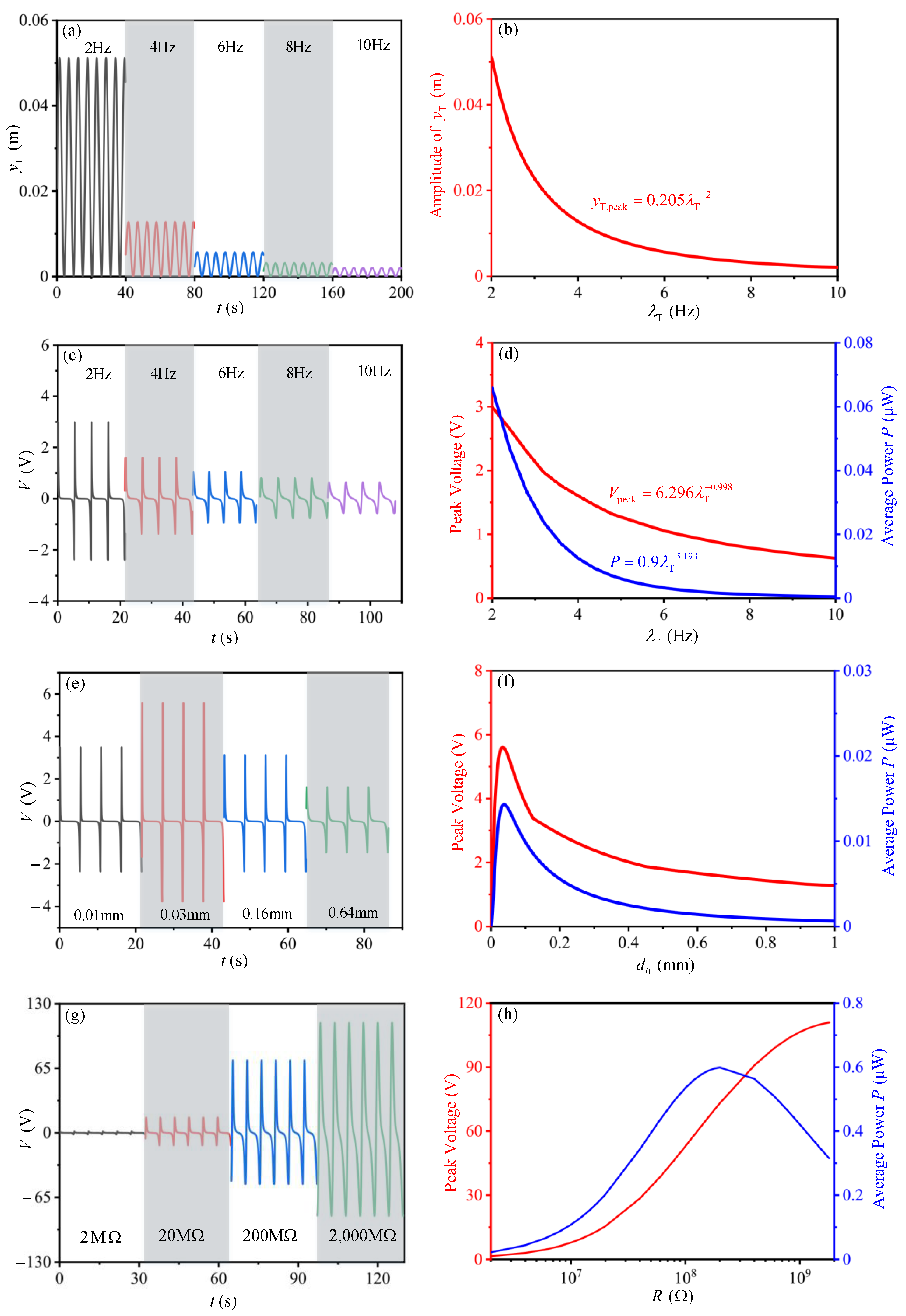
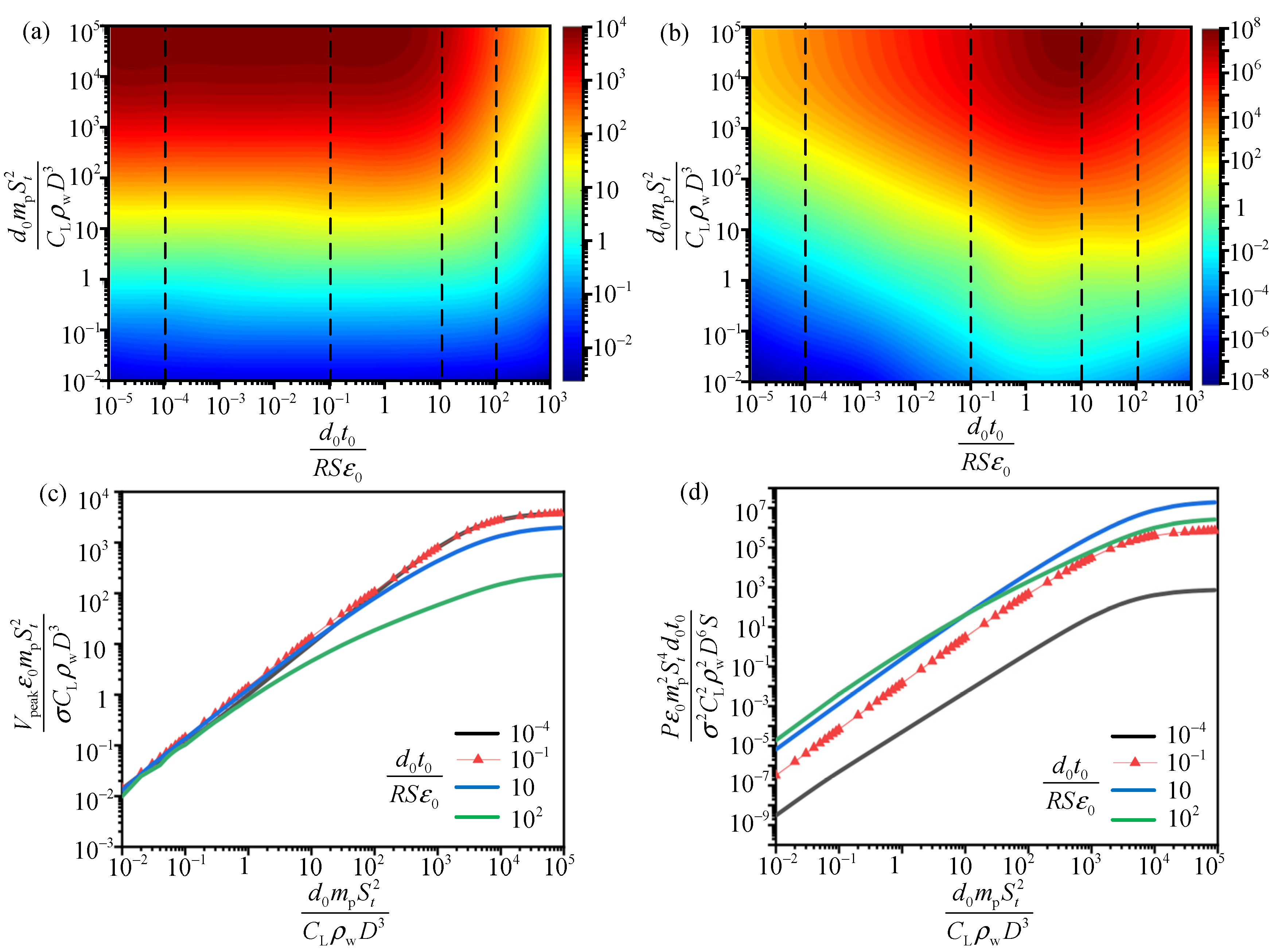
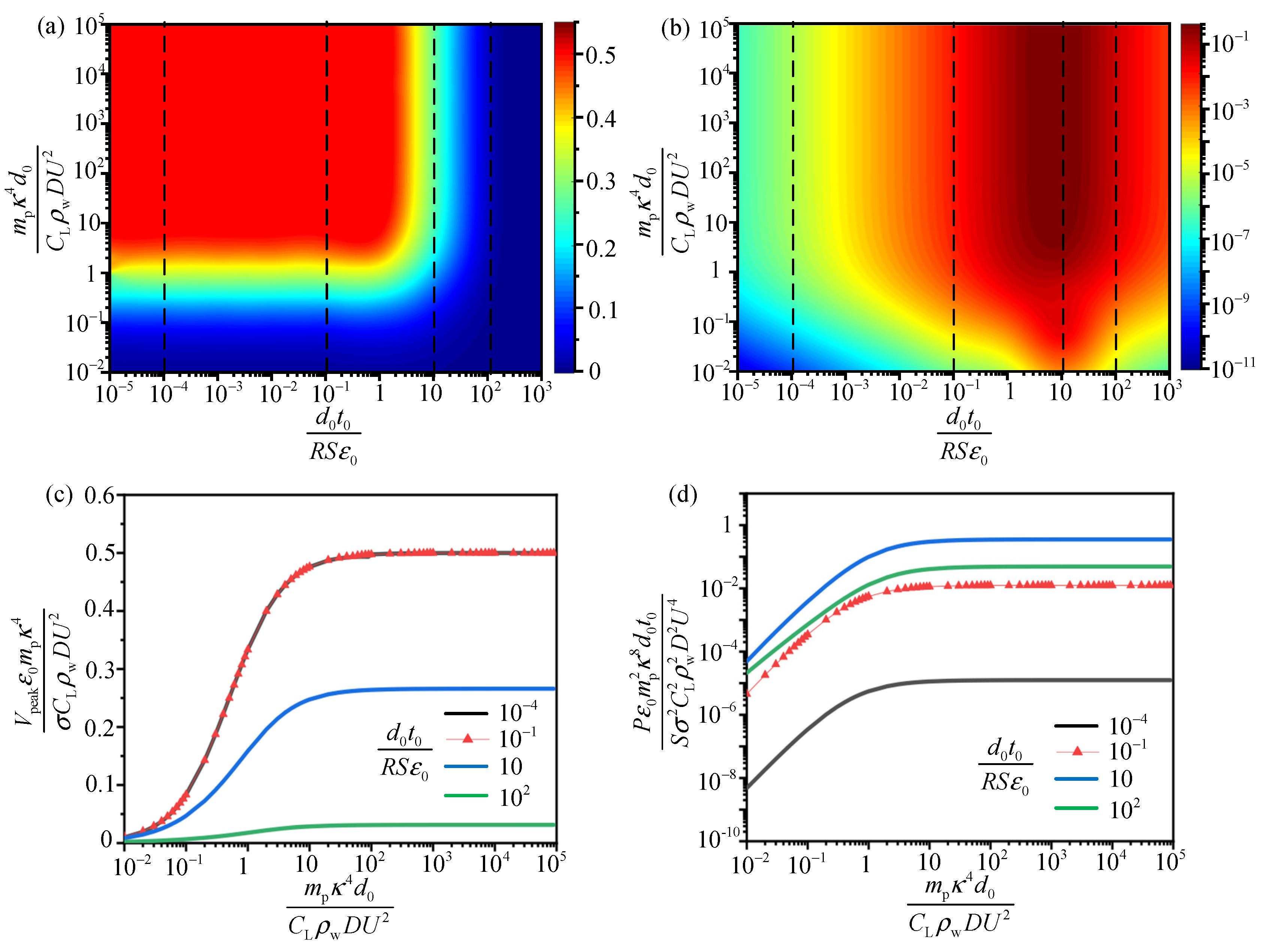

| Parameter | Value |
|---|---|
| Pipe length L | 1.2 m |
| Pipe diameter D | 0.02 m |
| 2.55 | |
| 4.55 | |
| 0.05 mm | |
| 0.05 mm | |
| 4 | |
| 8 | |
| 4 mm | |
| 0.15 mm | |
| 19.46 g | |
| 7.1 Hz | |
| 100 MΩ | |
| 8.854 × 10−12 | |
| 5–20 μC/m2 | |
| Temperature T | 20 °C |
| Humidity | 40% |
| Dimensions of tribo-pair | 5 cm × 5 cm |
| Parameter | Value |
|---|---|
| Pipe length | |
| The external diameter of pipeline | |
| The inner diameter of pipeline | |
| The water current velocity | |
| Lift coefficient of the current |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.; Zhang, H.; Wang, L.; Liu, G. A Contact-Mode Triboelectric Nanogenerator for Energy Harvesting from Marine Pipe Vibrations. Sensors 2021, 21, 1514. https://doi.org/10.3390/s21041514
Li R, Zhang H, Wang L, Liu G. A Contact-Mode Triboelectric Nanogenerator for Energy Harvesting from Marine Pipe Vibrations. Sensors. 2021; 21(4):1514. https://doi.org/10.3390/s21041514
Chicago/Turabian StyleLi, Rui, He Zhang, Li Wang, and Guohua Liu. 2021. "A Contact-Mode Triboelectric Nanogenerator for Energy Harvesting from Marine Pipe Vibrations" Sensors 21, no. 4: 1514. https://doi.org/10.3390/s21041514
APA StyleLi, R., Zhang, H., Wang, L., & Liu, G. (2021). A Contact-Mode Triboelectric Nanogenerator for Energy Harvesting from Marine Pipe Vibrations. Sensors, 21(4), 1514. https://doi.org/10.3390/s21041514







