Using Secure Multi-Party Computation to Protect Privacy on a Permissioned Blockchain
Abstract
:1. Introduction
2. Related Work
3. The Proposed Method
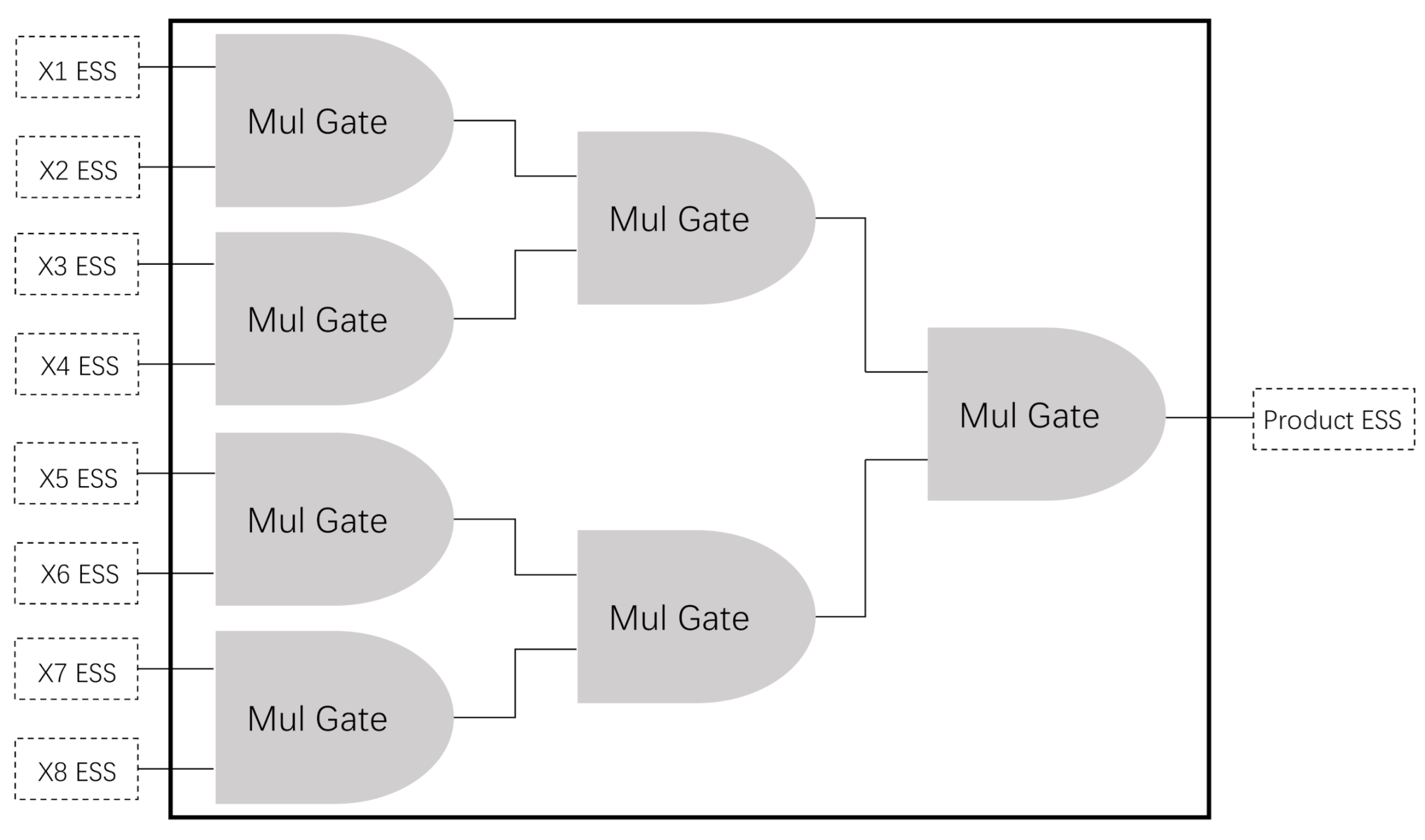
3.1. Overview of Our Framework
- Participant: the data owner.
- Peer: compute node in Hyperledger Fabric, concretely the endorsement node.
- Decryptor: a component in the Peer assisting decrypting during the endorsement phase. (details can be seen in Section 3.4.3).
- Compute function: the computational logic provided by participants.
- On-chain MPC protocol: the auxiliary protocol utilized to perform on-chain, secure, multi-party computation.
- Quadruple generation protocol: the protocol used to generate preprocessing data ( quadruples) for on-chain secure multi-party computation.
- Sacrifice protocol: the protocol used to check whether a quadruple is valid.
- (Off-chain preprocessing phase): All participants use the quadruple generation protocol to obtain a sufficient number of quadruples and check whether the quadruples are valid using the sacrifice protocol. This step is not necessary for every task. A huge number of quadruples can be generated in advance for future tasks.
- (On-chain computation phase): All participants break raw input values to secret shares, encrypt secret shares and quadruple shares, generate commitments and submit all of them to the ledger.
- (On-chain computation phase): Participants store the addresses of decryptors to the ledger.
- (On-chain computation phase): The invoker (one of the participants) invokes the MPC smart contract to execute the computation task.
- (On-chain computation phase): Participants decrypt their outputs, which can also be carried out by decryptors, and reconstruct the final result.
3.2. The Algorithms Used
- (1)
- Additive homomorphism encryption
- KeyGen(): takes the security parameter as the input, and outputs the private key sk and the public key pk.
- Enc(pk, m): takes the message and the public key pk as the inputs, and outputs the ciphertext .
- Dec(sk, c): takes the ciphertext and a private key sk as the inputs, and outputs the decrypted result .
- Add(c1, c2): takes two ciphertexts as the inputs, and outputs the ciphertext , so that
- Sub(c1, c2): takes two ciphertexts as the inputs, and outputs the ciphertext , so that
- cMul(m1, c1): takes the scalar and the ciphertext as the inputs, and outputs the ciphertext , so that
- (2)
- Additive secret sharing
- Secret shares: To share a secret a, the dealer chooses random shares () in GF(p), and computes . The dealer then sends the shares to participant ().
- Secret reconstruction: All participants collaboratively reconstruct the secret: .
- (3)
- Pedersen
- Setup Phase: All participants agree on an elliptic curve E over a field , a generator and .
- Commitment Phase: Participant chooses a random number , and computes the point , which represents the commitment for ’s secret . r is a blinding factor that prevents observers from guessing . sends to the receiver .
- Open Phase: sends (, r) to the receiver and verifies whether equals . refuses the commitment if they are not equal.
3.3. The Secure MPC Protocol
- Privacy confidentiality: All the input values and output values are in encrypted form and no one learns anything except his own input secret and output values.
- Publicly verifiable: Computations can be publicly executed and are controlled by no one. Any step during computation can be publicly verified.
3.3.1. On-Chain Computation Procotol
- Protocol Input
- All participants use the Paillier algorithm to generate their private key and public key .
- Each participant serves as a dealer, who uses additive secret sharing to break his secret to n shares (), and then encrypts the share for using ’s public key:
- chooses n random blinding factor (), and computes the commitments for shares ():
- encrypts the blinding factor:
- generates the commitment of the secret value itself:
- Finally, submits his inputto PTP.
- (2)
- Protocol Addition
- To compute , PTP computes:
- For a public scalar and a secret input , to compute , PTP computes:
- To compute , PTP computes:
- For :
- For :
- For :
- (3)
- Protocol Multiplication
- Obtain the encrypted shares of and :
- Obtain t, s and :
- Obtain the encrypted shares of :
- (4)
- Protocol Output
3.3.2. Off-Chain Preprocessing Protocol
- Each participant generates . Let
- Each participant computes and broadcasts
- All participants set
- All participants compute
- Participants set
- Participants invoke “Sacrifice” to check that indeed :
3.4. On-Chain Secure MPC in Hyperledger Fabric
3.4.1. A Brief Introduction to Hyperledger Fabric
3.4.2. A Crucial Additional Component
3.4.3. Implementation Details
 |
4. Security Analysis
5. Experimental Results and Discussions
5.1. Comparison of Running Time Based on Different Key Sizes
5.2. Comparison of Response Time Based on Different Schemes
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| MPC | Multi-party Computation |
| PTP | Publicly Trusted Processor |
References
- De Montesquieu, C. Montesquieu: The Spirit of the Laws; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. Technical Report. 2019. Available online: https://git.dhimmel.com/bitcoin-whitepaper/ (accessed on 22 February 2021).
- Benhamouda, F.; DeCaro, A.; Halevi, S.; Halevi, T.; Jutla, C.; Manevich, Y.; Zhang, Q. Initial public offering (IPO) on permissioned blockchain using secure multiparty computation. In Proceedings of the 2019 IEEE International Conference on Blockchain (Blockchain), Atlanta, GA, USA, 14–17 July 2019. [Google Scholar]
- Kayes, A.; Kalaria, R.; Sarker, I.H.; Islam, M.; Watters, P.A.; Ng, A.; Hammoudeh, M.; Badsha, S.; Kumara, I. A survey of context-aware access control mechanisms for cloud and fog networks: Taxonomy and open research issues. Sensors 2020, 20, 2464. [Google Scholar] [CrossRef] [PubMed]
- Yao, A.C. Protocols for secure computations. In Proceedings of the 23rd Annual Symposium on Foundations of Computer Science (sfcs 1982), Chicago, IL, USA, 3–5 November 1982; pp. 160–164. [Google Scholar]
- Crépeau, C.; van de Graaf, J.; Tapp, A. Committed oblivious transfer and private multi-party computation. In Annual International Cryptology Conference; Springer: Berlin, Germany, 1995; pp. 110–123. [Google Scholar]
- Ben-Efraim, A.; Lindell, Y.; Omri, E. Efficient scalable constant-round MPC via garbled circuits. In International Conference on the Theory and Application of Cryptology and Information Security; Springer: Berlin, Germany, 2017; pp. 471–498. [Google Scholar]
- Wiki. Available online: https://en.wikipedia.org/wiki/Homomorphic_encryption (accessed on 22 February 2021).
- Shamir, A. How to share a secret. Commun. ACM 1979, 22, 612–613. [Google Scholar] [CrossRef]
- Blakley, G.R. Safeguarding cryptographic keys. In Proceedings of the 1979 International Workshop on Managing Requirements Knowledge (MARK), New York, NY, USA, 4–7 June 1979; pp. 313–318. [Google Scholar]
- Zhong, H.; Sang, Y.; Zhang, Y.; Xi, Z. Secure multi-party computation on blockchain: An overview. In International Symposium on Parallel Architectures, Algorithms and Programming; Springer: Berlin, Germany, 2019; pp. 452–460. [Google Scholar]
- Ghadamyari, M.; Samet, S. Privacy-Preserving Statistical Analysis of Health Data Using Paillier Homomorphic Encryption and Permissioned Blockchain. In Proceedings of the 2019 IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, 9–12 December 2019; pp. 5474–5479. [Google Scholar]
- Zaghloul, E.; Li, T.; Ren, J. Anonymous and Coercion-Resistant Distributed Electronic Voting. In Proceedings of the 2020 International Conference on Computing, Networking and Communications (ICNC), Big Island, HI, USA, 17–20 February 2020; pp. 389–393. [Google Scholar]
- Yan, X.; Wu, Q.; Sun, Y. A Homomorphic Encryption and Privacy Protection Method Based on Blockchain and Edge Computing. Wirel. Commun. Mob. Comput. 2020, 2020, 8832341. [Google Scholar] [CrossRef]
- Hyperledger Fabric. Available online: https://hyperledger-fabric.readthedocs.io/en/latest/whatis.html (accessed on 22 February 2021).
- Pedersen, T.P. Non-interactive and information-theoretic secure verifiable secret sharing. In Annual International Cryptology Conference; Springer: Berlin, Germany, 1991; pp. 129–140. [Google Scholar]
- Beaver, D. Efficient multiparty protocols using circuit randomization. In Annual International Cryptology Conference; Springer: Berlin, Germany, 1991; pp. 420–432. [Google Scholar]
- Damgård, I.; Pastro, V.; Smart, N.; Zakarias, S. Multiparty computation from somewhat homomorphic encryption. In Annual Cryptology Conference; Springer: Berlin, Germany, 2012; pp. 643–662. [Google Scholar]
- Feng, Q.; He, D.; Zeadally, S.; Khan, M.K.; Kumar, N. A survey on privacy protection in blockchain system. J. Netw. Comput. Appl. 2019, 126, 45–58. [Google Scholar] [CrossRef]
- Miers, I.; Garman, C.; Green, M.; Rubin, A.D. Zerocoin: Anonymous distributed e-cash from bitcoin. In Proceedings of the 2013 IEEE Symposium on Security and Privacy, Berkeley, CA, USA, 19–22 May 2013; pp. 397–411. [Google Scholar]
- Bonneau, J.; Narayanan, A.; Miller, A.; Clark, J.; Kroll, J.A.; Felten, E.W. Mixcoin: Anonymity for bitcoin with accountable mixes. In International Conference on Financial Cryptography and Data Security; Springer: Berlin, Germany, 2014; pp. 486–504. [Google Scholar]
- Heilman, E.; Baldimtsi, F.; Goldberg, S. Blindly signed contracts: Anonymous on-blockchain and off-blockchain bitcoin transactions. In International Conference on Financial Cryptography and Data Security; Springer: Berlin, Germany, 2016; pp. 43–60. [Google Scholar]
- Sun, S.F.; Au, M.H.; Liu, J.K.; Yuen, T.H. Ringct 2.0: A compact accumulator-based (linkable ring signature) protocol for blockchain cryptocurrency monero. In European Symposium on Research in Computer Security; Springer: Berlin, Germany, 2017; pp. 456–474. [Google Scholar]
- Andrychowicz, M.; Dziembowski, S.; Malinowski, D.; Mazurek, L. Secure multiparty computations on bitcoin. In Proceedings of the 2014 IEEE Symposium on Security and Privacy, Berkeley, CA, USA, 18–21 May 2014; pp. 443–458. [Google Scholar]
- Bentov, I.; Kumaresan, R. How to use bitcoin to design fair protocols. In Annual Cryptology Conference; Springer: Berlin, Germany, 2014; pp. 421–439. [Google Scholar]
- Kumaresan, R.; Vaikuntanathan, V.; Vasudevan, P.N. Improvements to secure computation with penalties. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; pp. 406–417. [Google Scholar]
- Sánchez, D.C. Raziel: Private and verifiable smart contracts on blockchains. arXiv 2018, arXiv:1807.09484. [Google Scholar]
- Zyskind, G.; Nathan, O.; Pentland, A. Enigma: Decentralized computation platform with guaranteed privacy. arXiv 2015, arXiv:1506.03471. [Google Scholar]
- Kosba, A.; Miller, A.; Shi, E.; Wen, Z.; Papamanthou, C. Hawk: The blockchain model of cryptography and privacy-preserving smart contracts. In Proceedings of the 2016 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 22–26 May 2016; pp. 839–858. [Google Scholar]
- Choudhuri, A.R.; Green, M.; Jain, A.; Kaptchuk, G.; Miers, I. Fairness in an unfair world: Fair multiparty computation from public bulletin boards. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, Dallas, TX, USA, 30 October–3 November 2017; pp. 719–728. [Google Scholar]
- Benhamouda, F.; Halevi, S.; Halevi, T. Supporting private data on hyperledger fabric with secure multiparty computation. IBM J. Res. Dev. 2019, 63, 3:1–3:8. [Google Scholar] [CrossRef]
- Paillier, P. Public-key cryptosystems based on composite degree residuosity classes. In International Conference on the Theory and Applications of Cryptographic Techniques; Springer: Berlin, Germany, 1999; pp. 223–238. [Google Scholar]
- Ghodosi, H.; Pieprzyk, J.; Steinfeld, R. Multi-party computation with conversion of secret sharing. Des. Codes Cryptogr. 2012, 62, 259–272. [Google Scholar] [CrossRef] [Green Version]
- Chatzigiannakis, I.; Pyrgelis, A.; Spirakis, P.G.; Stamatiou, Y.C. Elliptic curve based zero knowledge proofs and their applicability on resource constrained devices. In Proceedings of the 2011 IEEE Eighth International Conference on Mobile Ad-Hoc and Sensor Systems, Valencia, Spain, 17–22 October 2011; pp. 715–720. [Google Scholar]
- Keller, M.; Pastro, V.; Rotaru, D. Overdrive: Making SPDZ great again. In Annual International Conference on the Theory and Applications of Cryptographic Techniques; Springer: Berlin, Germany, 2018; pp. 158–189. [Google Scholar]
- Liang, S. The JAVA Native Interface: Programmer’s Guide and Specification; Addison-Wesley Professional: Boston, MA, USA, 1999. [Google Scholar]
- Scozzafava, P. Uniform distribution and sum modulo m of independent random variables. Stat. Probab. Lett. 1993, 18, 313–314. [Google Scholar] [CrossRef]
- Barker, E.; Burr, W.; Jones, A.; Polk, T.; Rose, S.; Smid, M.; Dang, Q. Recommendation for key management part 3: Application-specific key management guidance. NIST Spec. Publ. 2009, 800, 57. [Google Scholar]
- Fan, J.; Vercauteren, F. Somewhat Practical Fully Homomorphic Encryption. IACR Cryptol. ePrint Arch. 2012, 2012, 144. [Google Scholar]
- Microsoft. Available online: https://github.com/microsoft/SEAL (accessed on 22 February 2021).



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Feng, Y.; Wang, Z.; Guo, D. Using Secure Multi-Party Computation to Protect Privacy on a Permissioned Blockchain. Sensors 2021, 21, 1540. https://doi.org/10.3390/s21041540
Zhou J, Feng Y, Wang Z, Guo D. Using Secure Multi-Party Computation to Protect Privacy on a Permissioned Blockchain. Sensors. 2021; 21(4):1540. https://doi.org/10.3390/s21041540
Chicago/Turabian StyleZhou, Jiapeng, Yuxiang Feng, Zhenyu Wang, and Danyi Guo. 2021. "Using Secure Multi-Party Computation to Protect Privacy on a Permissioned Blockchain" Sensors 21, no. 4: 1540. https://doi.org/10.3390/s21041540
APA StyleZhou, J., Feng, Y., Wang, Z., & Guo, D. (2021). Using Secure Multi-Party Computation to Protect Privacy on a Permissioned Blockchain. Sensors, 21(4), 1540. https://doi.org/10.3390/s21041540





