Planar Phase-Variation Microwave Sensors for Material Characterization: A Review and Comparison of Various Approaches
Abstract
:1. Introduction
2. Towards Sensitivity Optimization in Phase-Variation Microwave Sensors
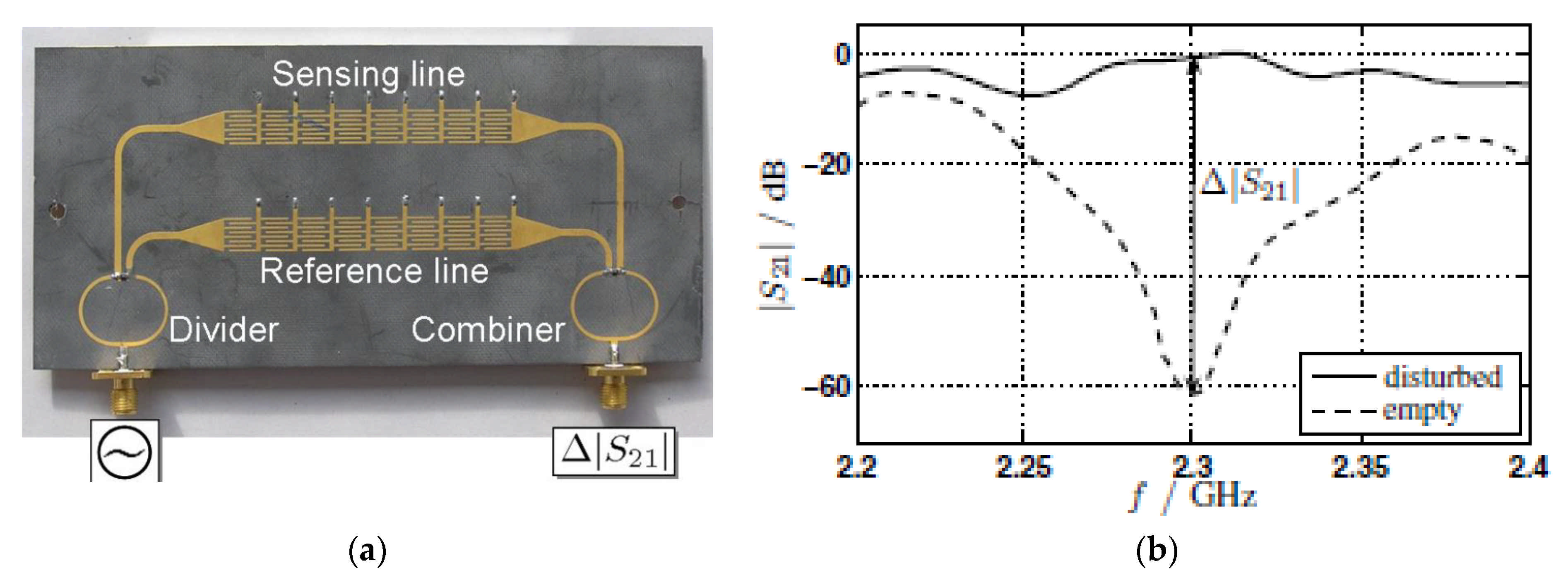
3. Phase-Variation Sensors Based on Meandered Lines
4. Phase-Variation Sensors Based on Slow-Wave Artificial Transmission Lines
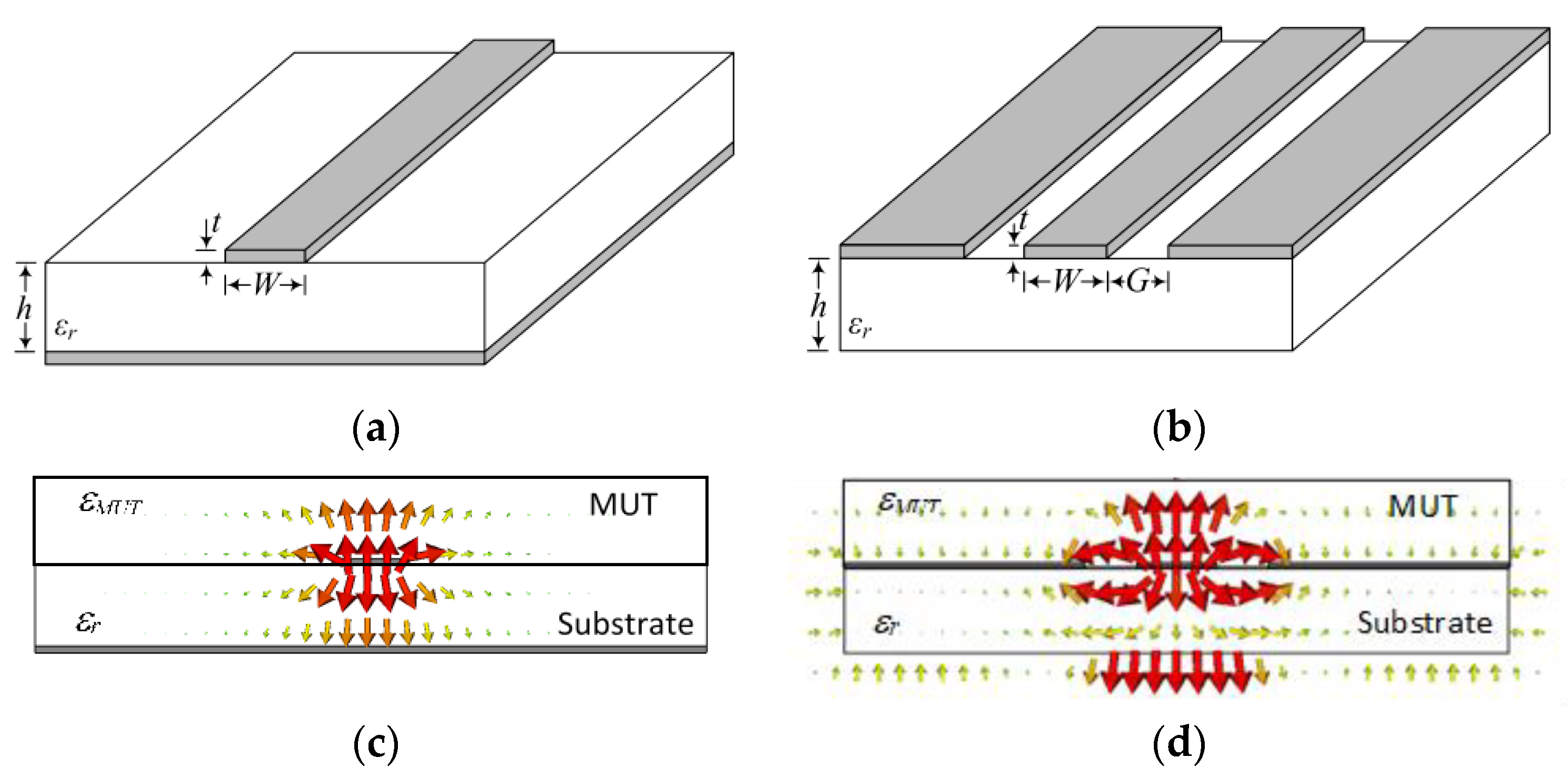
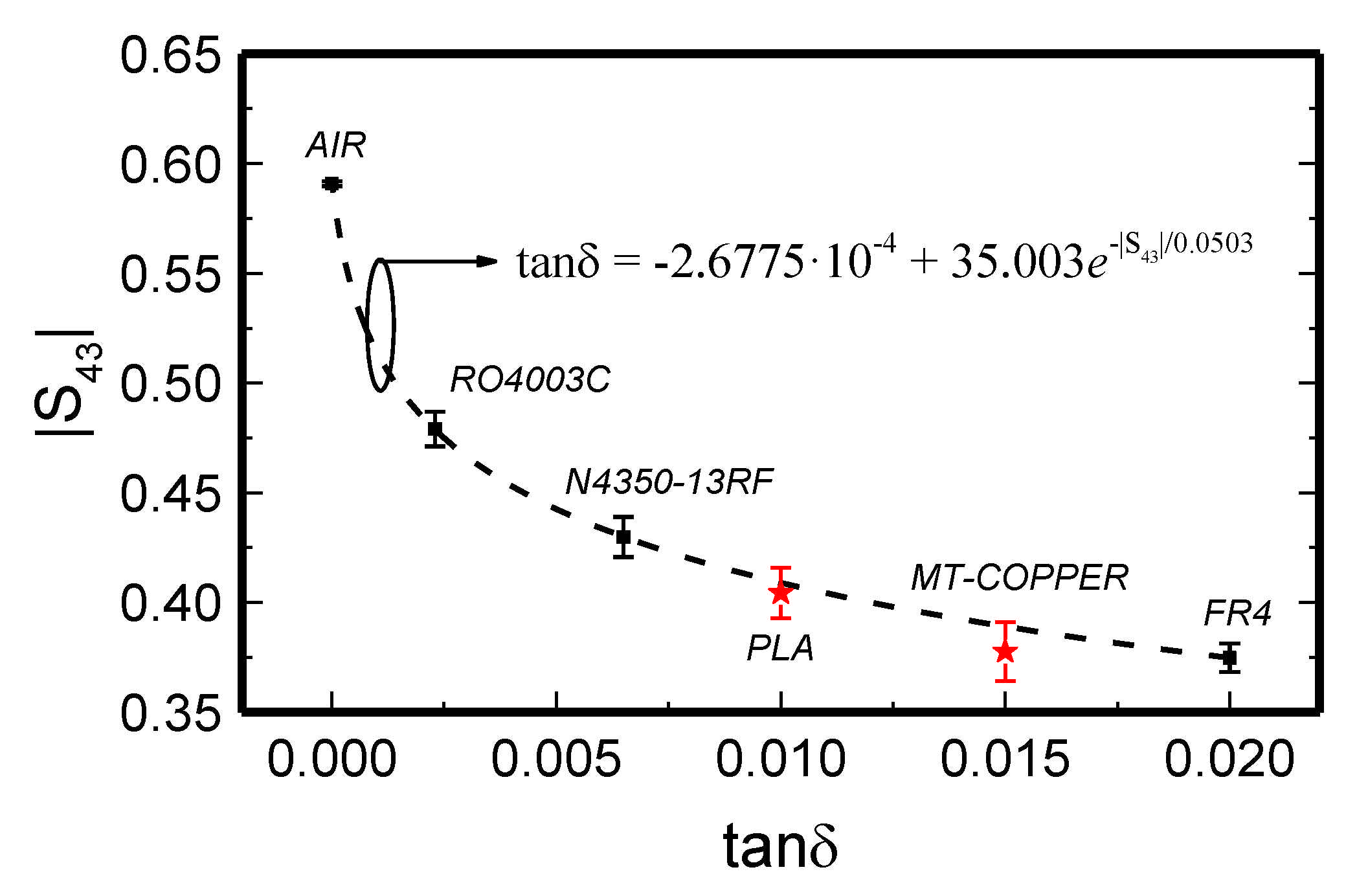
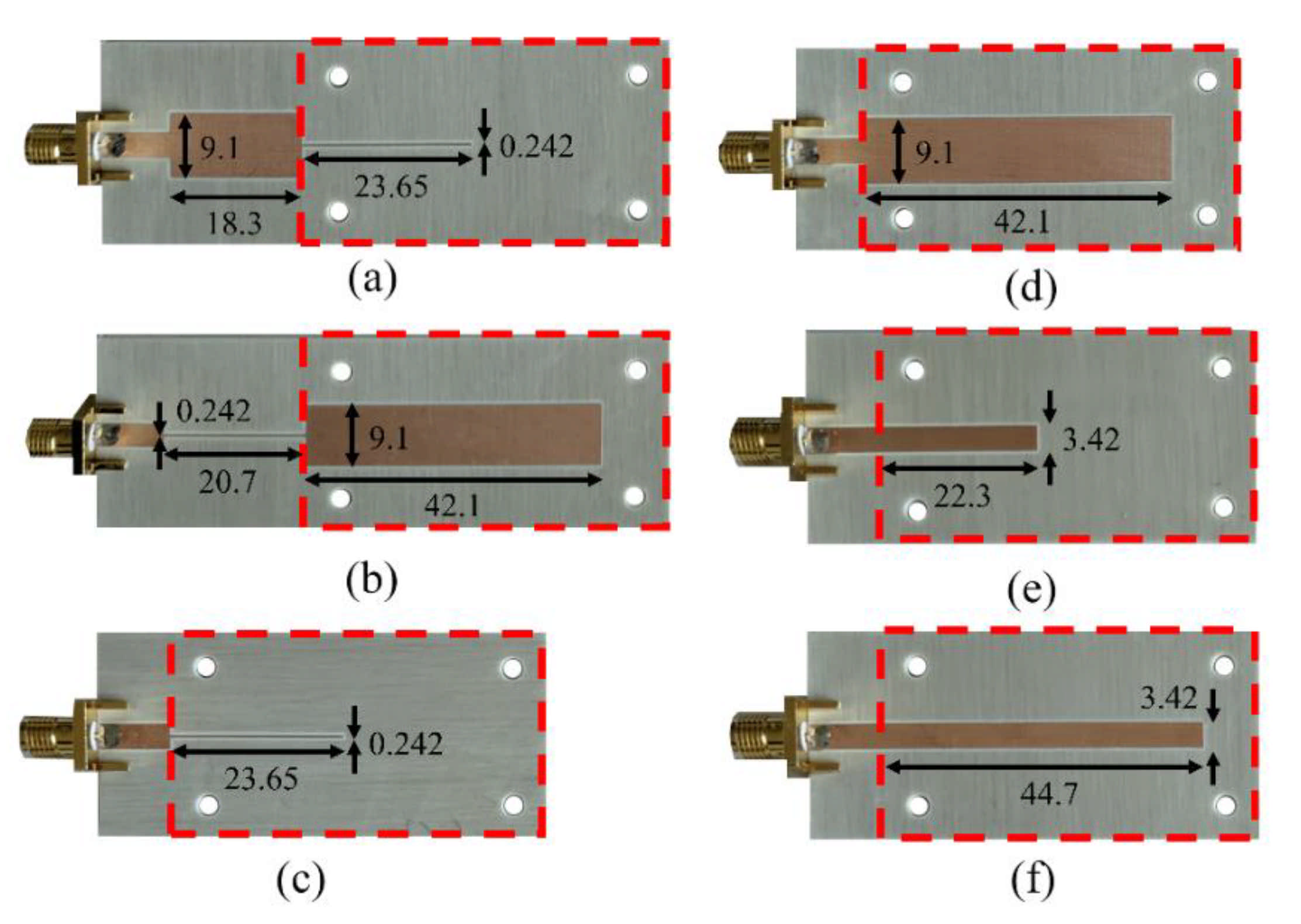
5. Phase-Variation Sensors Based on Step-Impedance Line Sections and Open-Ended Quarter- and Half-Wavelength Sensing Lines
- (i)
- For N odd (cases A and B), the characteristic impedance of a section with odd order (i odd) appears as . By contrast, for an even-order section, the corresponding term in the product appears as the inverse, i.e., . According to this, the requirement of a high or low value of Zi for sensitivity optimization depends on whether the product operator is present either in the numerator or in the denominator in Equations (32). For case A, where the product operator appears in the denominator, the odd-order transmission line sections must exhibit low impedance values, whereas high characteristic impedance sections are required for the even sections. For case B, the opposite conditions apply, since the product operator appears in the numerator of (32b).
- (ii)
- For N even (cases C and D) and i odd, the impedance is negative squared (), whereas it appears as for N even and i even. This means that for case C, with the product operator in the numerator of (32c), the odd sections must exhibit low characteristic impedance, and the line impedance must be high for the even sections. It is obvious that for case D (half-wavelength sensing line), the sections that should exhibit high impedance for sensitivity optimization are those with odd index.
6. Other Phase-Variation Sensors
6.1. Differential Phase-Variation Sensors Based on a Composite Right/Left Handed (CRLH) Line
6.2. Phase-Variation Sensor for Rotation Measurements
7. Comparative Analysis
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mandel, C.; Kubina, B.; Schüßler, M.; Jakoby, R. Passive chipless wireless sensor for two-dimensional displacement measurement. In Proceedings of the 41st European Microwave Conference, Manchester, UK, 10–13 October 2011; pp. 79–82. [Google Scholar]
- Puentes, M. Planar Metamaterial Based Microwave Sensor Arrays for Biomedical Analysis and Treatment; Springer: Berlin/Heidelberg, Germany, 2014; ISBN 978-3319060408. [Google Scholar]
- Ebrahimi, A.; Withayachumnankul, W.; Al-Sarawi, S.; Abbott, D. High-sensitivity metamaterial-inspired sensor for microfluidic dielectric characterization. IEEE Sens. J. 2013, 14, 1345–1351. [Google Scholar] [CrossRef] [Green Version]
- Schüßler, M.; Mandel, C.; Puentes, M.; Jakoby, R. Metamaterial inspired microwave sensors. IEEE Microw. Mag. 2012, 13, 57–68. [Google Scholar] [CrossRef]
- Boybay, M.S.; Ramahi, O.M. Material characterization using complementary split-ring resonators. IEEE Trans. Instrum. Meas. 2012, 61, 3039–3046. [Google Scholar] [CrossRef]
- Lee, C.S.; Yang, C.L. Complementary split-ring resonators for measuring dielectric constants and loss tangents. IEEE Microw. Wirel. Compon. Lett. 2014, 24, 563–565. [Google Scholar] [CrossRef]
- Yang, C.L.; Lee, C.S.; Chen, K.W.; Chen, K.Z. Noncontact measurement of complex permittivity and thickness by using planar resonators. IEEE Trans. Microw. Theory Tech. 2015, 64, 247–257. [Google Scholar] [CrossRef]
- Withayachumnankul, W.; Jaruwongrungsee, K.; Tuantranont, A.; Fumeaux, C.; Abbott, D. Metamaterial-based microfluidic sensor for dielectric characterization. Sens. Actuators A Phys. 2013, 189, 233–237. [Google Scholar] [CrossRef] [Green Version]
- Salim, A.; Lim, S. Complementary split-ring resonator-loaded microfluidic ethanol chemical sensor. Sensors 2016, 16, 1802. [Google Scholar] [CrossRef] [Green Version]
- Su, L.; Mata-Contreras, J.; Vélez, P.; Fernández-Prieto, A.; Martín, F. Analytical method to estimate the complex permittivity of oil samples. Sensors 2018, 18, 984. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abdolrazzaghi, M.; Zarifi, M.H.; Daneshmand, M. Sensitivity enhancement of split ring resonator based liquid sensors. In Proceedings of the 2016 IEEE Sensors, Orlando, FL, USA, 30 October–3 November 2016. [Google Scholar]
- Abdolrazzaghi, M.; Zarifi, M.H.; Pedrycz, W.; Daneshmand, M. Robust ultra-high resolution microwave planar sensor using fuzzy neural network approach. IEEE Sens. J. 2016, 17, 323–332. [Google Scholar] [CrossRef]
- Zarifi, M.H.; Daneshmand, M. Monitoring solid particle deposition in lossy medium using planar resonator sensor. IEEE Sens. J. 2017, 17, 7981–7989. [Google Scholar] [CrossRef]
- Zarifi, M.H.; Deif, S.; Abdolrazzaghi, M.; Chen, B.; Ramsawak, D.; Amyotte, M.; Vahabisani, N.; Hashisho, Z.; Chen, W.; Daneshmand, M. A microwave ring resonator sensor for early detection of breaches in pipeline coatings. IEEE Trans. Ind. Electron. 2017, 65, 1626–1635. [Google Scholar] [CrossRef]
- Abdolrazzaghi, M.; Daneshmand, M.; Iyer, A.K. Strongly enhanced sensitivity in planar microwave sensors based on metamaterial coupling. IEEE Trans. Microw. Theory Tech. 2018, 66, 1843–1855. [Google Scholar] [CrossRef] [Green Version]
- Zarifi, M.H.; Sadabadi, H.; Hejazi, S.H.; Daneshmand, M.; Sanati-Nezhad, A. Noncontact and nonintrusive microwave-microfluidic flow sensor for energy and biomedical engineering. Sci. Rep. 2018, 8, 139. [Google Scholar] [CrossRef] [Green Version]
- Ebrahimi, A.; Scott, J.; Ghorbani, K. Ultrahigh-Sensitivity Microwave Sensor for Microfluidic Complex Permittivity Measurement. IEEE Trans. Microw. Theory Tech. 2019, 67, 4269–4277. [Google Scholar] [CrossRef]
- Xu, K.; Liu, Y.; Chen, S.; Zhao, P.; Peng, L.; Dong, L.; Wang, G. Novel Microwave Sensors Based on Split Ring Resonators for Measuring Permittivity. IEEE Access 2018, 6, 26111–26120. [Google Scholar] [CrossRef]
- Abdolrazzaghi, M.; Daneshmand, M. Exploiting Sensitivity Enhancement in Micro-wave Planar Sensors Using Intermodulation Products with Phase Noise Analysis. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 4382–4395. [Google Scholar] [CrossRef]
- Albishi, A.M.; Badawe, M.K.E.; Nayyeri, V.; Ramahi, O.M. Enhancing the Sensitivity of Dielectric Sensors with Multiple Coupled Complementary Split-Ring Resonators. IEEE Trans. Microw. Theory Tech. 2020, 68, 4340–4347. [Google Scholar] [CrossRef]
- Saadat-Safa, M.; Nayyeri, V.; Khanjarian, M.; Soleimani, M.; Ramahi, O.M. A CSRR-Based Sensor for Full Characterization of Magneto-Dielectric Materials. IEEE Trans. Microw. Theory Tech. 2019, 67, 806–814. [Google Scholar] [CrossRef]
- Mohammadi, S.; Wiltshire, B.; Jain, M.C.; Nadaraja, A.V.; Clements, A.; Golovin, K.; Roberts, D.J.; Johnson, T.; Foulds, I.; Zarifi, M.H. Gold Coplanar Waveguide Resonator Integrated with a Microfluidic Channel for Aqueous Dielectric Detection. IEEE Sens. J. 2020, 20, 9825–9833. [Google Scholar] [CrossRef]
- Amirian, M.; Karimi, G.; Wiltshire, B.D.; Zarifi, M.H. Differential Narrow Bandpass Microstrip Filter Design for Material and Liquid Purity Interrogation. IEEE Sens. J. 2019, 19, 10545–10553. [Google Scholar] [CrossRef]
- Wiltshire, B.D.; Mohammadi, S.; Zarifi, M.H. Integrating 3D Printed Microfluidic Channels with Planar Resonator Sensors for Low Cost and Sensitive Liquid Detection. In Proceedings of the 2018 18th International Symposium on Antenna Technology and Applied Electromagnetics (ANTEM), Waterloo, ON, Canada, 19–22 August 2018; pp. 1–2. [Google Scholar]
- Horestani, A.K.; Naqui, J.; Shaterian, Z.; Abbott, D.; Fumeaux, C.; Martín, F. Two-dimensional alignment and displacement sensor based on movable broadside-coupled split ring resonators. Sens. Actuators A Phys. 2014, 210, 18–24. [Google Scholar] [CrossRef] [Green Version]
- Naqui, J.; Damm, C.; Wiens, A.; Jakoby, R.; Su, L.; Martín, F. Transmission lines loaded with pairs of magnetically coupled stepped impedance resonators (SIRs): Modeling and application to microwave sensors. In Proceedings of the 2014 IEEE MTT-S International Microwave Symposium, Tampa, FL, USA, 1–6 June 2014; pp. 1–4. [Google Scholar]
- Su, L.; Naqui, J.; Mata-Contreras, J.; Martín, F. Modeling metamaterial transmission lines loaded with pairs of coupled split-ring resonators. IEEE Antennas Wirel. Propag. Lett. 2014, 14, 68–71. [Google Scholar] [CrossRef] [Green Version]
- Su, L.; Naqui, J.; Mata, J.; Martín, F. Dual-band epsilon-negative (ENG) transmission line metamaterials based on microstrip lines loaded with pairs of coupled complementary split ring resonators (CSRRs): Modeling, analysis and applications. In Proceedings of the 9th International Congress on Advanced Electromagnetic Materials in Microwaves and Optics, Metamaterials 2015, Oxford, UK, 7–12 September 2015; pp. 298–300. [Google Scholar]
- Su, L.; Naqui, J.; Mata-Contreras, J.; Vélez, P.; Martín, F. Transmission line metamaterials based on pairs of coupled split ring resonators (SRRs) and complementary split ring resonators (CSRR): A comparison to the light of the lumped element equivalent circuits. In Proceedings of the International Conference on Electromagnetics for Advanced Applications, ICEAA 2015, Torino, Italy, 7–11 September 2015; pp. 891–894. [Google Scholar]
- Su, L.; Naqui, J.; Mata-Contreras, J.; Martín, F. Modeling and applications of metamaterial transmission lines loaded with pairs of coupled complementary split-ring resonators (CSRRs). IEEE Antennas Wirel. Propag. Lett. 2015, 15, 154–157. [Google Scholar] [CrossRef] [Green Version]
- Naqui, J.; Damm, C.; Wiens, A.; Jakoby, R.; Su, L.; Mata-Contreras, J.; Martín, F. Transmission lines loaded with pairs of stepped impedance resonators: Modeling and application to differential permittivity measurements. IEEE Trans. Microw. Theory Tech. 2016, 64, 3864–3877. [Google Scholar] [CrossRef] [Green Version]
- Su, L.; Mata-Contreras, J.; Vélez, P.; Martín, F. Splitter/combiner microstrip sections loaded with pairs of complementary split ring resonators (CSRRs): Modeling and optimization for differential sensing applications. IEEE Trans. Microw. Theory Tech. 2016, 64, 4362–4370. [Google Scholar] [CrossRef]
- Vélez, P.; Su, L.; Grenier, K.; Mata-Contreras, J.; Dubuc, D.; Martín, F. Microwave microfluidic sensor based on a microstrip splitter/combiner configuration and split ring resonators (SRRs) for dielectric characterization of liquids. IEEE Sens. J. 2017, 17, 6589–6598. [Google Scholar] [CrossRef] [Green Version]
- Ebrahimi, A.; Scott, J.; Ghorbani, K. Differential sensors using microstrip lines loaded with two split-ring resonators. IEEE Sens. J. 2018, 18, 5786–5793. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Beziuk, G.; Scott, J.; Ghorbani, K. Microwave Differential Frequency Splitting Sensor Using Magnetic-LC Resonators. Sensors 2020, 20, 1066. [Google Scholar] [CrossRef] [Green Version]
- Ferrández-Pastor, F.J.; García-Chamizo, J.M.; Nieto-Hidalgo, M. Electromagnetic differential measuring method: Application in microstrip sensors developing. Sensors 2017, 17, 1650. [Google Scholar] [CrossRef] [Green Version]
- Muñoz-Enano, J.; Vélez, P.; Gil, M.; Martín, F. An analytical method to implement high sensitivity transmission line differential sensors for dielectric constant measurements. IEEE Sens. J. 2020, 20, 178–184. [Google Scholar] [CrossRef]
- Damm, C.; Schüßler, M.; Puentes, M.; Maune, H.; Maasch, M.; Jakoby, R. Artificial transmission lines for high sensitive microwave sensors. In Proceedings of the IEEE Sensors Conference, Christchurch, New Zealand, 25–28 October 2009; pp. 755–758. [Google Scholar]
- Vélez, P.; Mata-Contreras, J.; Su, L.; Dubuc, D.; Grenier, K.; Martín, F. Modeling and Analysis of Pairs of Open Complementary Split Ring Resonators (OCSRRs) for Differential Permittivity Sensing. In Proceedings of the 2017 IEEE MTT-S International Microwave Workshop Series on Advanced Materials and Processes (IMWS-AMP 2017), Pavia, Italy, 20–22 September 2017. [Google Scholar]
- Vélez, P.; Grenier, K.; Mata-Contreras, J.; Dubuc, D.; Martín, F. Highly-Sensitive Microwave Sensors Based on Open Complementary Split Ring Resonators (OCSRRs) for Dielectric Characterization and Solute Concentration Measurement in Liquids. IEEE Access 2018, 6, 48324–48338. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Scott, J.; Ghorbani, K. Transmission Lines Terminated with LC Resonators for Differential Permittivity Sensing. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 1149–1151. [Google Scholar] [CrossRef]
- Vélez, P.; Muñoz-Enano, J.; Grenier, K.; Mata-Contreras, J.; Dubuc, D.; Martín, F. Split ring resonator (SRR) based microwave fluidic sensor for electrolyte concentration measurements. IEEE Sens. J. 2019, 19, 2562–2569. [Google Scholar] [CrossRef]
- Vélez, P.; Muñoz-Enano, J.; Gil, M.; Mata-Contreras, J.; Martín, F. Differential microfluidic sensors based on dumbbell-shaped defect ground structures in microstrip technology: Analysis, optimization, and applications. Sensors 2019, 19, 3189. [Google Scholar] [CrossRef] [Green Version]
- Vélez, P.; Muñoz-Enano, J.; Martín, F. Differential sensing based on quasi-microstrip-mode to slot-mode conversion. IEEE Microw. Wirel. Compon. Lett. 2019, 29, 690–692. [Google Scholar] [CrossRef]
- Gil, M.; Vélez, P.; Aznar-Ballesta, F.; Muñoz-Enano, J.; Martín, F. Differential sensor based on electro-inductive wave (EIW) transmission lines for dielectric constant measurements and defect detection. IEEE Trans. Ant. Propag. 2020, 68, 1876–1886. [Google Scholar] [CrossRef]
- Muñoz-Enano, J.; Vélez, P.; Gil, M.; Mata-Contreras, J.; Martín, F. Differential-mode to common-mode conversion detector based on rat-race couplers: Analysis and application to microwave sensors and comparators. IEEE Trans. Microw. Theory Tech. 2020, 68, 1312–1325. [Google Scholar] [CrossRef]
- Naqui, J.; Durán-Sindreu, M.; Martín, F. Novel sensors based on the symmetry properties of split ring resonators (SRRs). Sensors 2011, 11, 7545–7553. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Naqui, J.; Durán-Sindreu, M.; Martín, F. On the symmetry properties of coplanar waveguides loaded with symmetric resonators: Analysis and potential applications. In Proceedings of the 2012 IEEE/MTT-S International Microwave Symposium Digest, Montreal, QC, Canada, 17–22 June 2012; pp. 1–3. [Google Scholar]
- Naqui, J.; Durán-Sindreu, M.; Martín, F. Alignment and position sensors based on split ring resonators. Sensors 2012, 12, 11790–11797. [Google Scholar] [CrossRef] [Green Version]
- Naqui, J.; Durán-Sindreu, M.; Martín, F. Transmission lines loaded with bisymmetric resonators and applications. In Proceedings of the IEEE MTT-S International Microwave Symposium Digest, Seattle, WA, USA, 2–7 June 2013; pp. 1–3. [Google Scholar]
- Horestani, A.K.; Fumeaux, C.; Al-Sarawi, S.F.; Abbott, D. Displacement sensor based on diamond-shaped tapered split ring resonator. IEEE Sens. J. 2012, 13, 1153–1160. [Google Scholar] [CrossRef]
- Horestani, A.K.; Abbott, D.; Fumeaux, C. Rotation sensor based on horn-shaped split ring resonator. IEEE Sens. J. 2013, 13, 3014–3015. [Google Scholar] [CrossRef]
- Naqui, J.; Martín, F. Transmission lines loaded with bisymmetric resonators and their application to angular displacement and velocity sensors. IEEE Trans. Microw. Theory Tech. 2013, 61, 4700–4713. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Withayachumnankul, W.; Al-Sarawi, S.F.; Abbott, D. Metamaterial-inspired rotation sensor with wide dynamic range. IEEE Sens. J. 2014, 14, 2609–2614. [Google Scholar] [CrossRef] [Green Version]
- Horestani, A.K.; Naqui, J.; Abbott, D.; Fumeaux, C.; Martín, F. Two-dimensional displacement and alignment sensor based on reflection coefficients of open microstrip lines loaded with split ring resonators. Electron. Lett. 2014, 50, 620–622. [Google Scholar] [CrossRef] [Green Version]
- Naqui, J.; Martín, F. Angular displacement and velocity sensors based on electric-LC (ELC) loaded microstrip lines. IEEE Sens. J. 2013, 14, 939–940. [Google Scholar] [CrossRef] [Green Version]
- Naqui, J.; Coromina, J.; Karami-Horestani, A.; Fumeaux, C.; Martín, F. Angular displacement and velocity sensors based on coplanar waveguides (CPWs) loaded with S-shaped split ring resonators (S-SRR). Sensors 2015, 15, 9628–9650. [Google Scholar] [CrossRef] [Green Version]
- Naqui, J.; Martín, F. Application of broadside-coupled split ring resonator (BC-SRR) loaded transmission lines to the design of rotary encoders for space applications. In Proceedings of the IEEE MTT-S International Microwave Symposium, San Francisco, CA, USA, 22–27 May 2016; pp. 1–4. [Google Scholar]
- Mata-Contreras, J.; Herrojo, C.; Martín, F. Application of split ring resonator (SRR) loaded transmission lines to the design of angular displacement and velocity sensors for space applications. IEEE Trans. Microw. Theory Tech. 2017, 65, 4450–4460. [Google Scholar] [CrossRef] [Green Version]
- Mata-Contreras, J.; Herrojo, C.; Martín, F. Detecting the rotation direction in contactless angular velocity sensors implemented with rotors loaded with multiple chains of resonators. IEEE Sens. J. 2018, 18, 7055–7065. [Google Scholar] [CrossRef]
- Coromina, J.; Muñoz-Enano, J.; Vélez, P.; Ebrahimi, A.; Scott, J.; Ghorbani, K.; Martín, F. Capacitively-Loaded Slow-Wave Transmission Lines for Sensitivity Improvement in Phase-Variation Permittivity Sensors. In Proceedings of the 50th European Microwave Conference, Utrecht, The Netherlands, 12–14 January 2021. [Google Scholar]
- Muñoz-Enano, J.; Vélez, P.; Gil, M.; Martín, F. On the sensitivity of reflective-mode phase variation sensors based on open-ended stepped-impedance transmission lines: Theoretical analysis and experimental validation. IEEE Trans. Microw. Theory Tech. 2021, 69, 308–324. [Google Scholar] [CrossRef]
- Su, L.; Muñoz-Enano, J.; Vélez, P.; Casacuberta, P.; Gil, M.; Martín, F. Highly sensitive phase variation sensors based on step-impedance coplanar waveguide (CPW) transmission lines. IEEE Sens. J. 2021, 21, 2864–2872. [Google Scholar]
- Casacuberta, P.; Muñoz-Enano, J.; Vélez, P.; Su, L.; Gil, M.; Martín, F. Highly sensitive reflective-mode detectors and dielectric constant sensors based on open-ended stepped-impedance transmission lines. Sensors 2020, 20, 6236. [Google Scholar] [CrossRef]
- Jha, A.K.; Lamecki, A.; Mrozowski, M.; Bozzi, M. A Highly Sensitive Planar Microwave Sensor for Detecting Direction and Angle of Rotation. IEEE Trans. Microw. Theory Tech. 2020, 68, 1598–1609. [Google Scholar] [CrossRef]
- Karami Horestani, A.; Shaterian, Z.; Martín, F. Rotation Sensor Based on the Cross-Polarized Excitation of Split Ring Resonators (SRRs). IEEE Sens. J. 2020, 20, 9706–9714. [Google Scholar] [CrossRef]
- Muñoz-Enano, J.; Vélez, P.; Su, L.; Gil, M.; Martín, F. A reflective-mode phase-variation displacement sensor. IEEE Access 2020, 8, 189565–189575. [Google Scholar] [CrossRef]
- Pozar, D.M. Microwave Engineering, 4th ed.; John Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Martín, F. Artificial Transmission Lines for RF and Microwave Applications; John Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Caloz, C.; Itoh, T. Electromagnetic Metamaterials: Transmission Line Theory and Microwave Applications; Wiley-IEEE Press: Piscataway, NJ, USA, 2005. [Google Scholar]
- Eleftheriades, G.; Balmain, K.G. Negative Refraction Metamaterials: Fundamental Principles and Applications; Wiley-IEEE Press: Piscataway, NJ, USA, 2005. [Google Scholar]
- Caloz, C.; Itoh, T. Novel microwave devices and structures based on the transmission line approach of metamaterials. In Proceedings of the IEEE MTT-S International Microwave Symposium Digest, Philadelphia, PA, USA, 8–13 June 2003; Volume 1, pp. 195–198. [Google Scholar]
- Beruete, M.; Falcone, F.; Freire, M.J.; Marqués, R.; Baena, J.D. Electroinductive waves in chains of complementary metamaterial elements. Appl. Phys. Lett. 2006, 88, 083503. [Google Scholar] [CrossRef] [Green Version]
- Wu, K. Slow wave structures. In Encyclopedia of Electrical and Electronics Engineering; Webster, J.G., Ed.; Wiley: New York, NY, USA, 1999; Volume 19, pp. 366–381. [Google Scholar]
- Görür, A. A novel coplanar slow-wave structure. IEEE Microw. Guided Wave Lett. 1994, 4, 86–88. [Google Scholar] [CrossRef]
- Orellana, M.; Selga, J.; Vélez, P.; Rodríguez, A.; Boria, V.; Martín, F. Design of capacitively-loaded coupled line bandpass filters with compact size and spurious suppression. IEEE Trans. Microw. Theory. Tech. 2017, 65, 1235–1248. [Google Scholar] [CrossRef]
- Scardelletti, M.C.; Ponchak, G.E.; Weller, T.M. Miniaturized wilkinson power dividers utilizing capacitive loading. IEEE Microw. Wirel. Compon. Lett. 2002, 12, 6–8. [Google Scholar] [CrossRef] [Green Version]
- Eccleston, K.W.; Ong, S.H.M. Compact planar microstripline branch-line and rat-race couplers. IEEE Trans. Microw. Theory Tech. 2003, 51, 2119–2125. [Google Scholar] [CrossRef] [Green Version]
- García-García, J.; Bonache, J.; Martín, F. Application of electromagnetic bandgaps (EBGs) to the design of ultra wide band pass filters (UWBPFs) with good out-of-band performance. IEEE Trans. Microw. Theory Tech. 2006, 54, 4136–4140. [Google Scholar] [CrossRef]
- Shie, C.-I.; Cheng, J.-C.; Chou, S.-C.; Chiang, Y.-C. Transdirectional coupled-line couplers implemented by periodical shunt capacitors. IEEE Trans. Microw. Theory Tech. 2009, 57, 2981–2988. [Google Scholar] [CrossRef]
- Orellana, M.; Selga, J.; Sans, M.; Rodríguez, A.; Boria, V.; Martín, F. Synthesis of slow-wave structures based on capacitive-loaded lines through aggressive space mapping (ASM). Int. J. RF Microw. Comput. Aided Eng. 2015, 25, 629–638. [Google Scholar] [CrossRef] [Green Version]
- Coromina, J.; Selga, J.; Vélez, P.; Bonache, J.; Martín, F. Size reduction and harmonic suppression in branch line couplers implemented by means of capacitively-loaded slow-wave transmission lines. Microw. Opt. Technol. Lett. 2017, 59, 2822–2830. [Google Scholar] [CrossRef]
- Coromina, J.; Vélez, P.; Bonache, J.; Martín, F. Branch line couplers with small size and harmonic suppression based on non-periodic step impedance shunt stub (SISS) loaded lines. IEEE Access 2020, 8, 67310–67320. [Google Scholar] [CrossRef]
- Zhu, L. Guided-wave characteristics of periodic microstrip lines with inductive loading: Slow-wave and bandstop behaviors. Microw. Opt. Technol. Lett. 2004, 41, 77–79. [Google Scholar] [CrossRef]
- Lee, S.; Lee, Y. Generalized miniaturization method for coupled-line bandpass filters by reactive loading. IEEE Trans. Microw. Theory Tech. 2010, 58, 2383–2391. [Google Scholar] [CrossRef]
- Vélez, P.; Selga, J.; Bonache, J.; Martín, F. Slow-wave inductively-loaded electromagnetic bandgap (EBG) coplanar waveguide (CPW) transmission lines and application to compact power dividers. In Proceedings of the 2016 46th European Microwave Conference (EuMC), London, UK, 4–6 October 2016. [Google Scholar]
- Selga, J.; Vélez, P.; Bonache, J.; Martín, F. EBG-based transmission lines with slow-wave characteristics and application to miniaturization of microwave components. Appl. Phys. A 2016, 123, 44. [Google Scholar] [CrossRef]
- Aznar, F.; Selga, J.; Fernández-Prieto, A.; Coromina, J.; Vélez, P.; Bonache, J.; Martín, F. Slow wave coplanar waveguides based on inductive and capacitive loading and application to compact and harmonic suppressed power splitters. Int. J. Microw. Wirel. Technol. 2018, 10, 530–537. [Google Scholar] [CrossRef] [Green Version]
- Selga, J.; Vélez, P.; Coromina, J.; Fernández-Prieto, A.; Bonache, J.; Martín, F. Harmonic suppression in branch-line couplers based on slow wave transmission lines with simultaneous inductive and capacitive loading. Microw. Opt. Tech. Lett. 2018, 60, 2374–2384. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Coromina, J.; Muñoz-Enano, J.; Vélez, P.; Scott, J.; Ghorbani, K.; Martín, F. Highly sensitive phase-variation dielectric constant sensor based on a capacitively-loaded slow-wave transmission line. IEEE Trans. Circuits Syst. 2021. submitted for publication. [Google Scholar]
- Muñoz-Enano, J.; Casacuberta, P.; Su, L.; Vélez, P.; Gil, M.; Martín, F. Open-Ended-Line Reflective-Mode Phase-Variation Sensors for Dielectric Constant Measurements. In Proceedings of the IEEE Sensors 2020, Rotterdam, The Netherlands, 25–28 October 2020. [Google Scholar]













| Ref. | Type | Mode | Size * (λ2) | Max. Sensitivity | FoM (°/λ2) |
|---|---|---|---|---|---|
| [62] | IMPEDANCE CONTRAST | REFLECTIVE | 0.025 | 528.7° | 21148 |
| [63] | IMPEDANCE CONTRAST | REFLECTIVE | 0.1 | 45.5° | 455 |
| [64] | IMPEDANCE CONTRAST | REFLECTIVE | 0.025 | 101.3° | 4052 |
| [38] | ARTIFICIAL LINE (CRLH) | TRANSMISSION | --- | 600 dB | --- |
| [36] | MEANDER LINE | TRANSMISSION | --- | 54.8° | --- |
| [37] | MEANDER LINE | TRANSMISSION | 12.9 | 415.6° | 32.2 |
| [45] | ARTIFICIAL LINE (EIW) | TRANSMISSION | 0.075 | 25.3 dB | --- |
| [46] | MEANDER LINE | TRANSMISSION | 0.02 | 17.6 dB | --- |
| [61] | ARTIFICIAL LINE (SLOW-WAVE) | TRANSMISSION | 0.03 | 7.7° | 257 |
| [90] | ARTIFICIAL LINE (SLOW-WAVE) | TRANSMISSION | 0.04 | 20.0° | 500 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muñoz-Enano, J.; Coromina, J.; Vélez, P.; Su, L.; Gil, M.; Casacuberta, P.; Martín, F. Planar Phase-Variation Microwave Sensors for Material Characterization: A Review and Comparison of Various Approaches. Sensors 2021, 21, 1542. https://doi.org/10.3390/s21041542
Muñoz-Enano J, Coromina J, Vélez P, Su L, Gil M, Casacuberta P, Martín F. Planar Phase-Variation Microwave Sensors for Material Characterization: A Review and Comparison of Various Approaches. Sensors. 2021; 21(4):1542. https://doi.org/10.3390/s21041542
Chicago/Turabian StyleMuñoz-Enano, Jonathan, Jan Coromina, Paris Vélez, Lijuan Su, Marta Gil, Pau Casacuberta, and Ferran Martín. 2021. "Planar Phase-Variation Microwave Sensors for Material Characterization: A Review and Comparison of Various Approaches" Sensors 21, no. 4: 1542. https://doi.org/10.3390/s21041542
APA StyleMuñoz-Enano, J., Coromina, J., Vélez, P., Su, L., Gil, M., Casacuberta, P., & Martín, F. (2021). Planar Phase-Variation Microwave Sensors for Material Characterization: A Review and Comparison of Various Approaches. Sensors, 21(4), 1542. https://doi.org/10.3390/s21041542








