1. Introduction
Fault Diagnosis (FD) is a term that describes the general problem of detecting and isolating faults in physical components or in the instrumentation of a system [
1]. A broad class of FD methods is based on the concept of Analytical Redundancy (AR) [
2]. The essence of AR methods lies in the comparison of the behavior of the system with the response of a mathematical model. Inconsistency between the actual and model response is considered a symptom of a possible failure. An FD scheme elaborates this information in real time to detect and isolate faults.
Mathematical models play a central role in AR-based FD; these are derived from either physical laws governing the dynamics of the system or are inferred directly from experimental data exploiting system identification techniques [
3].
In the last 30 years, FD has been widely investigated, and many techniques have been proposed. Considering model-based approaches, the main research directions can be coarsely categorized as fault detection filters, parity-space schemes, diagnostic observers, and parameter estimation [
1]. Classic methods dealing with model-based approaches can be found in [
4,
5,
6,
7,
8,
9]. More recently, approaches based on optimal criteria [
10,
11] and extensions to nonlinear [
12], hybrid [
13], and distributed systems [
14] have been proposed. A collection of successful applications of model-based FD was presented in [
15].
Data-based approaches are preferable instead in case the system dynamics is not precisely known and/or when the system input-output physical relations are too complex [
16]. Currently, thanks to the advances in ICT technologies in both hardware and software, substantial amounts of data are available for continuous monitoring and FD of engineering systems. This generated a great interest in FD techniques capable of handling large amounts of data. In this context, the most established and widespread techniques are Principal Component Analysis (PCA), Independent Component Analysis (ICA), Partial Least Squares (PLS), Fisher Discriminant Analysis (FDA), the Subspace-Aided approach (SAP), as well as their recent advancements [
17]. Remaining in the data-based domain, FD diagnostic systems based on neural networks [
18], computational intelligence [
19], and machine learning [
20,
21] have attracted substantial interest in very recent years. Specifically, in the aviation and flight control systems community, there is abundant technical literature that clearly shows that the main reason for catastrophic accidents can be attributed, ultimately, to failures and/or malfunction of sensors, control surfaces, or components of the propulsion system, as reported in [
22,
23]. This explains the critical need for on-board FD systems able to promptly detect and identify the faulty components and, next, to enable a predetermined online failure recovery strategy [
24]. Typically, hardware redundancy (featuring multiple sensors or actuators with the same function) and simple majority voting schemes are used to cope with FD. Although these methods are widespread, there is an increasing number of applications where the additional cost, weight, and size of the components are major constraints, such as small and autonomous flying vehicles. For these applications, AR-based FD methods are appealing approaches to increase flight safety. An excellent review on the state-of-the-art of AR-based FD methods in aerospace systems can be found in [
25].
Regardless of the approach, the performance of an FD system is strictly related to the level of modeling uncertainty and measurement noise, whose presence implies that in fault-free conditions, the residual signals might significantly deviate statistically from zero. This entails that residuals must be robust with respect to uncertainties where the robustness of a residual is defined as the degree of sensitivity to faults compared to the sensitivity to uncertainty and noise [
26]. Robustness issues become evident when dealing with experimental flight data [
27,
28,
29,
30,
31]. Indeed, experimental data are affected by several additional sources of uncertainty such as, but not limited to, signal synchronization and quantization errors and imperfect positioning and calibration of the sensors [
32,
33]. Therefore, a fundamental step before the deployment of an FD scheme is its validation with actual flight data. Despite the relevance of these aspects in the mentioned studies, the problem of a detailed performance evaluation and comparison of Fault Isolation (FI) and Fault Estimation (FE) schemes using multi-flight data has been rarely fully addressed.
Building on the last considerations, the present study is entirely devoted to the setup and the quantitative comparison of well-known FI and FE methods using experimental sensor flight data. Specifically, different consolidated data-driven FI and FE schemes are applied to evaluate their performance on a set of 14 primary sensors of a semi-autonomous Tecnam P92 aircraft [
34].
In the effort, experimental linear regression models of the sensors’ response are identified from correlated measurements using multivariate linear regression techniques [
3]. The identified models provide a natural set of primary residuals; however, the faults’ directional properties are often not optimized to be used for sensor FI [
35,
36]. For this reason, enhanced residuals are derived by applying a linear transformation that allows better separation between the fault directions. The approach proposed in [
37] that optimizes fault directions separation taking also into account experimental modeling errors is herein implemented.
Sensor FI is then performed using two different approaches. The first approach associates the fault with the sensor providing the smaller directional distance compared to the sensor fault directions [
35]; the second approach, instead, is based on the reconstruction-based method proposed in [
38].
A comprehensive (offline) analysis based on multi-flight data is performed to derive quantitative Fault Isolation (FI) and Fault Estimation (FE) performance as a function of the fault amplitudes.
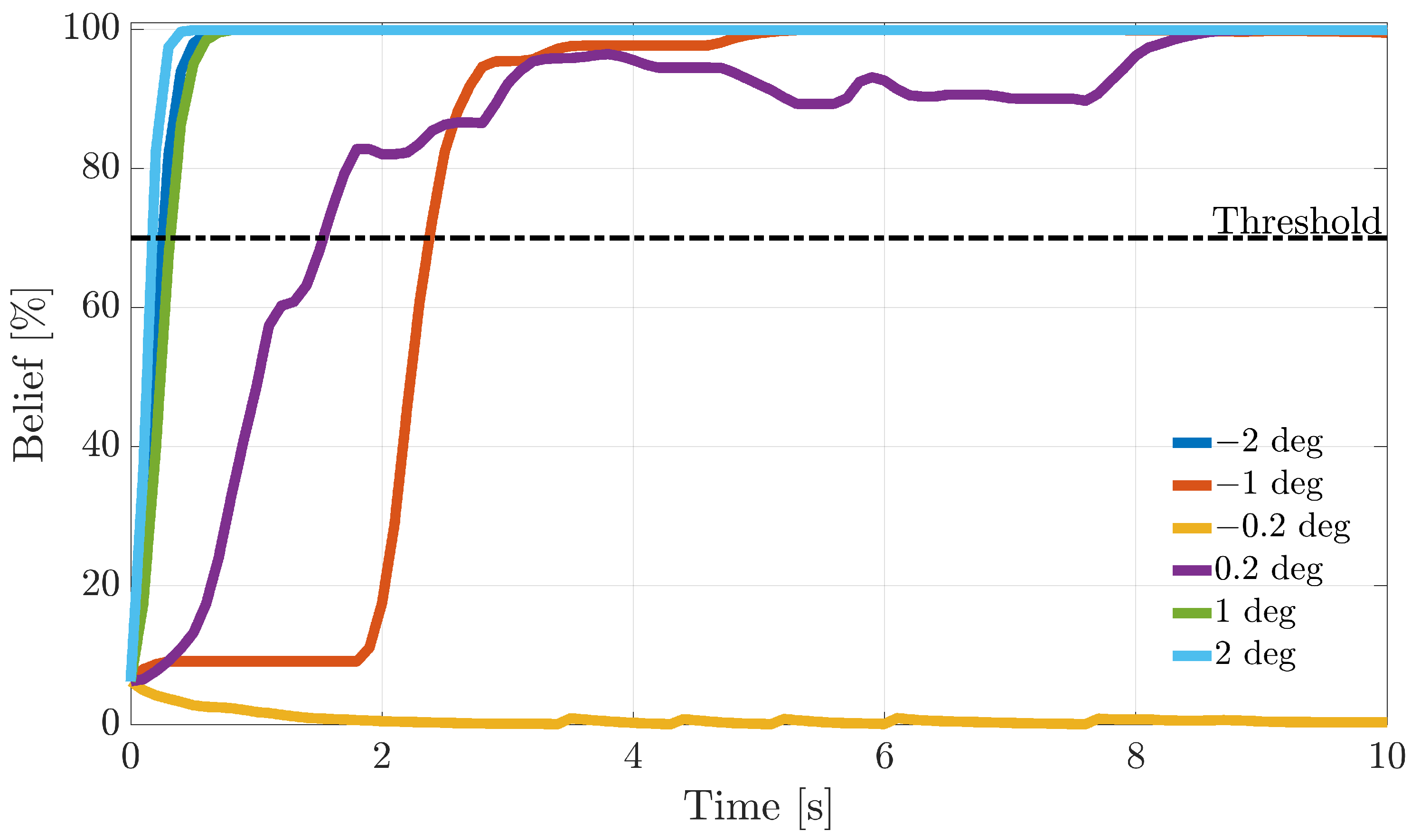
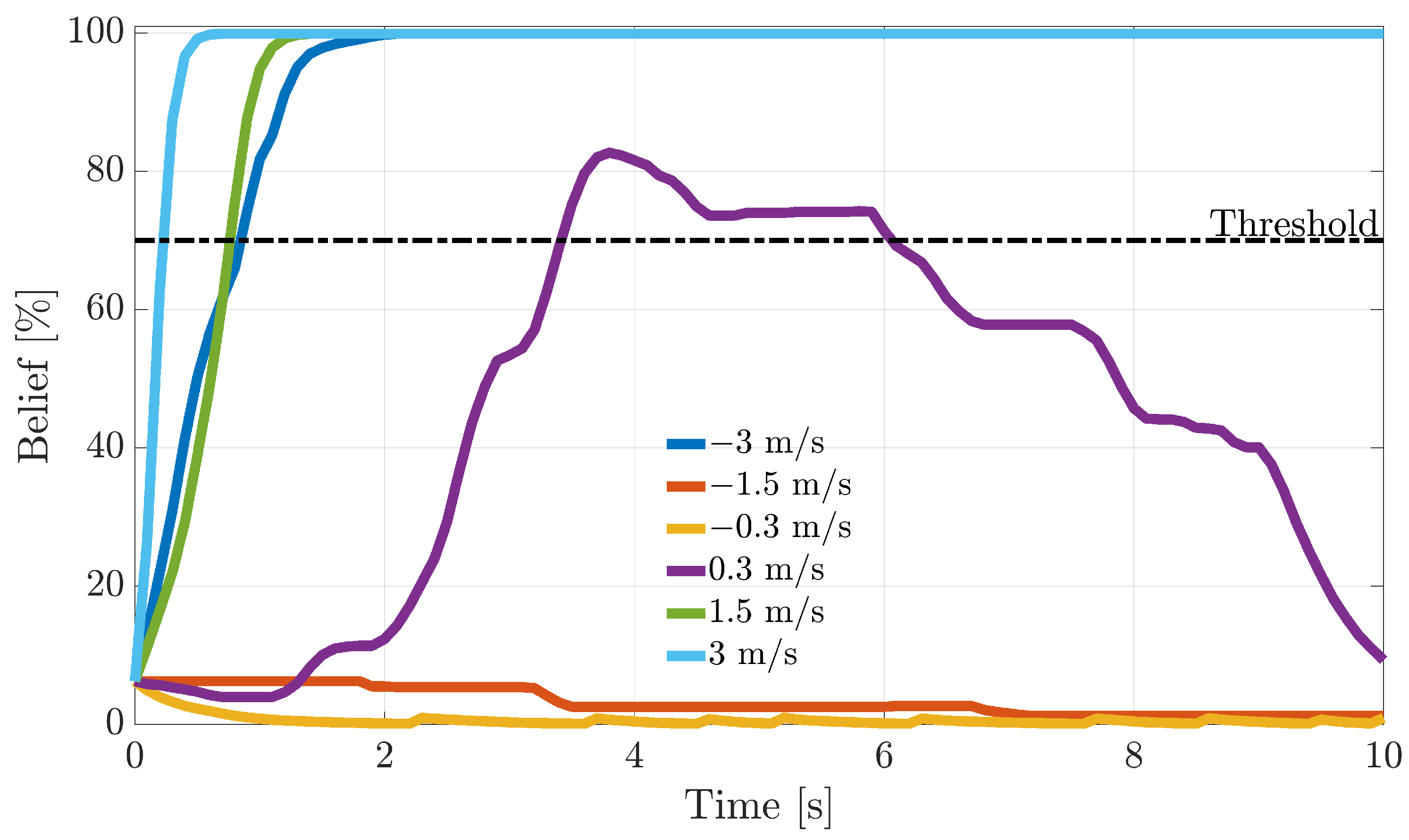
Next, another study is performed to assess online sensor FI performance by monitoring the temporal history of the residuals and, using this information, to increase or decrease the belief in a fault hypothesis over time. For this purpose, a bank of recursive Bayesian filters is designed to infer in-flight sensors’ fault probabilities. During online operation, a fault is declared when a fault probability reaches a defined threshold. This allows the computation of FI delays. The accumulated evidence in the probabilistic filters allows more reliable fault isolation, decreasing the false alarm rate at the expense of a small and acceptable delay in the diagnosis.
A detailed evaluation of offline and online FD performance is presented for failures on the air data sensors, including the True Air Speed (TAS, ), the Angle of Attack (AoA, ), and the Angle of Sideslip (AoS, ).
The present study is application oriented; therefore, the main contribution is not the development of a novel FD technique, but, rather, the design of consolidated data-driven sensor FD schemes and the quantitative evolution of fundamental quantities such as the fault isolation percentage, fault reconstruction accuracy, and in-flight fault isolation delays using multi-flight validation data. Therefore, the study provides a clear picture of the required design effort along with the achievable performance using consolidated FD schemes.
The paper is organized as follows.
Section 2 introduces linear regression models for sensors’ fault diagnosis;
Section 3 introduces the FI and FE methods based on primary residuals, while
Section 4 introduces the FI and FE methods based on transformed residuals.
Section 5 introduces the Bayesian filters for online FI.
Section 6 describes the multi-flight data, while
Section 7 deals with the identification of experimental models. FI and FE results on validation data are discussed in
Section 8 and
Section 9. Concluding and summary remarks are provided in
Section 10.
2. Models for Sensor Fault Diagnosis
In this study, a set of
potentially faulty sensors is considered. The corresponding signals are concatenated in a vector
;
is another vector of
signals functionally correlated with
such as control inputs, set-points, and other sensor measurements (assumed not to be faulty). It is assumed that in fault-free conditions, the sensor measurements
can be expressed in linear regression form as a function of
and
, that is:
where
and
are the coefficients of the linear combination and
characterizes modeling nonlinearity, uncertainty, and measurement noise concerning the
i-th sensor. For simplicity, the linear models in (
1) are rearranged as:
where
and
. Putting the above
equations together, we get the following vector expression:
where
and
are constant matrices to be estimated from data (as discussed in
Section 7). Model (
3) has been widely used in the literature for estimating a sensor signal as a function of other correlated measurements, as shown, for instance, in [
35,
39,
40,
41,
42]. The linear terms in (
3) provide a linear estimation of the signals that are defined as:
The consistency of the measurements
are monitored through the vector of the primary residuals
that is defined as follows:
Substituting (
4) into (
5) leads to:
where
is the identity matrix and
. Using again (
3) and (
4) in (
5), it is immediate to verify that:
In other words, in fault-free conditions, the vector of the primary residuals is equal to the modeling error.
Sensor Fault Modeling
In this study, an additive (single) failure
on a generic (
i-th) sensor of
is considered. Without any loss of generality, the failure can affect every single sensor. In the presence of a sensor failure, the vector
is replaced by its “faulty version”, that is:
where
is the
i-th column of the identity matrix
.
is an arbitrary scalar, a function of time, modeling the fault shape; thus,
is zero before the fault occurrence and different from zero, starting from the “fault time instant”
. In this study, we consider a step fault:
where
is the fault amplitude associated with the
i-th sensor.
4. Sensor FI and FE Based on Transformed Residuals
Primary residuals are not optimized from an FI point of view. For this reason, they are usually processed by applying transformations to achieve suitable new fault directions that facilitate the FI. An extensive literature on transformed directional residuals techniques is available. One of the first applications is the the Beard–Jones filter [
13], essentially a Luenberger observer whose gains are selected so that the directions of the residuals can be advantageously used to identify faulty sensors. In [
49], taking advantage of the properties of un-observability subspaces, a set of residual transformations that are unaffected by all faults except one was proposed. In this context, the methodology outlined in [
36] is also relevant, where the interaction between directional residuals and fault isolation properties was analyzed.
The FI methodology proposed in [
37] was considered in this effort because it provides optimized robust performance considering the directional properties of the residual noise covariance matrix
. This feature is particularly important when dealing with experimental noisy data. In the approach in [
37], a linear transformation of the primary residual vector
is introduced to provide optimized performance with respect to noise immunity. A transformed residual
with the same number of elements of
is defined as:
where
is the transformation matrix to be computed. Considering (
25), the new fault directions associated with
are the columns
of the matrix:
The covariance of
is by definition:
where the matrix
is computed applying the method proposed in [
37]. Considering this approach, let
and
be two symmetric matrices. Assuming
positive definite, it can be shown that there exists a matrix
such that:
where
and
are the solutions of the generalized eigenvalue problem. Specifically, the columns of
are the eigenvectors of the matrix
, while the columns of
are the corresponding eigenvalues. In the present study, setting
,
, and
, Equations (
28) and (
29) become, respectively:
Relationship (
30) implies that the noise covariance matrix of the transformed residuals in (
27) is spherical, that is
. This property is critical since in the presence of a spherical symmetry noise, the optimal decision line between two fault directions is simply the bisector [
50]. Thus, this property will be exploited for the design of the FI algorithm in
Section 4.1.
As explained in Note 1, the
matrix is estimated using the experimental
in (
24), and the generalized eigenvalues
are derived using commercially available scientific software.
4.1. Transformed Residuals Based on FI and FE
Fault isolation based on the transformed residual
is performed using the same approaches used for the primary residuals in
Section 3.1 and
Section 3.2. Specifically, defining the new transformed residual directions
as the columns of the matrix
, the transformed error matrix
is defined as:
where
is the normalized transformed residual derived from
and
are the new normalized transformed fault directions derived from
. The distance errors associated with the columns
of the matrix
are defined as:
The fault isolation index is determined by applying the same technique introduced in
Section 3.1, that is:
It is observed that the decision method (
34) based on the Euclidean distances (
33) is equivalent to treating as the decision line the bisectors between the directions
in (
32), which, in the case of spherical noise (
), are also optimal for testing fault isolation [
50].
The faulty sensor
is isolated applying (
16) to
derived from (
34). Finally, the fault amplitude is estimated using again (
19), that is:
Note 3: In [
37], it was shown that the best performances are achieved in the case that the transformation matrix
leads to the diagonalization, not only of the noise covariance matrix
, but also of the transformed fault direction matrix
. This may be possible only if the number of residuals is larger than the number of sensors. Alternatively, approximated robust FI methods based on optimality concepts as those in [
35,
51] can be applied.
4.2. Transformed Residuals with Reconstruction-Based FI and FE
Consistent with the approach of
Section 3.2, the reconstruction error for transformed residuals is defined as:
while the reconstructed fault amplitude is:
Fault isolation is again performed by computing the minimum of the errors in (
36); in other words, the fault isolation index is:
Finally, similar to (
23), the estimated fault is:
5. Bayesian Filtering for Online Fault Isolation
The FI approaches described in
Section 3 and
Section 4 are based on a decision method that isolates the faulty sensor as the one providing the minimum of a specific error measure inferred from the residual. This FI logic is based only on information at the current sample time
k and does not take into account the history of the residuals in the previous instants. On the other side, this information is useful for increasing or decreasing the belief of the FI decision over time.
In this paper, we propose a Bayesian Filter (BF) approach for managing the stream of information coming from sensors’ measurements. Specifically, we implemented the so-called “discrete Bayes filter” proposed in [
52]. This filter is essentially a recursive algorithm used to estimate the distribution of a discrete probability function. This type of filter was selected because it builds on a very solid and comprehensible theoretical background; an introduction to the Bayesian decision theory can be found in [
53]. In the present study, the estimated distribution models the probability (belief) that a generic sensor is faulty. The BF infers sensor fault probabilities by processing recursively the error information
defined in (
14), (
20), (
33) and (
36) for the different methods.
Two possible operational statuses are assumed for the sensors. State
indicates the events for which the
i-th sensor is faulty, while state
the event for which it is not faulty. Let
be the likelihood function representing the probability of observing an error
given that the
i-th sensor is faulty; a similar definition holds for
. According to Bayes’ theorem, the posterior fault probabilities
are given by:
where
and
are the a priori fault and non-fault probabilities, respectively, for sensor
i. A key step in the above inference mechanism is the definition of the likelihood functions
. These have to be designed to model the probability of experiencing a distance error
given that the
i-th sensor is faulty; therefore, their distribution needs to be maximum for
and should decrease as
increases. Similar reasoning applies to
. This behavior is captured by the following likelihood functions [
54,
55,
56,
57]:
where the parameters
are used to regulate the shape of the probability functions. At each time step, following the computation of the posterior probabilities (
40), the a priori probabilities are updated recursively using:
to propagate the current probability information to the next time step. In this study, the probabilistic filters are activated immediately after a fault is detected at
. At instant
, it is assumed that all the
sensors have the identical probability to be faulty; in other words, the filters are initialized with:
5.1. Probabilistic (Online) Fault Isolation Method
The recursive BF probabilities are employed for online FI, which is associated with in-flight conditions. Following a fault detection at , the fault is assigned to the sensor whose fault probability first reaches a defined threshold. If exceeds the threshold, the FI scheme has “good confidence” that a fault has occurred on the i-th sensor. Therefore, a failure on that sensor is declared. In this study, the threshold was empirically set at 0.7 (70%); see Note 4.
5.2. Probability Function Tuning
The performance of the BFs depends strictly on the shape of the probability functions in (
42), which, in turn, depend on the values of the parameters
. These values have to be carefully selected to make the filters sensitive to faults while limiting false alarms. Interestingly, a significant difference in the tuning of the filters was found for the distance-based and reconstruction-based techniques. This difference is essential because, while the first method operates with normalized residuals, the second operates with non-normalized residuals.
5.2.1. Distance-Based Methods’ Tuning
For the distance-based techniques, it was relatively simple to calibrate
to limit false alarms. These techniques being based on normalized residuals (
,
), the
values were inferred from the mean value (in fault-free conditions) of the distance between the normalized residual and normalized fault directions. Then, for distances
smaller than the mean value of the distance, the
values of
in (
41) are tuned to be larger than
, so that the BF increases the fault belief with respect to the previous step. Conversely, for larger distances,
is lower than
, resulting in a decrease in the belief. This tuning method was found to be effective since the distance
(independent of the fault size) is always contained in the hyper-ellipsoid (
14).
5.2.2. Reconstruction-Based Methods’ Tuning
For reconstruction-based techniques, the application of the above calibration technique is not possible. This is due to the fact that the errors
in (
20) derive from non-normalized residuals (
and
), and therefore, their values are proportional to the fault amplitude. Thus, the selection of
values that are suitable for any fault amplitude is not trivial. To overcome the problem, we opted for a “forced” normalization of the errors
in (
20) to be used as the input of the BFs. The following normalization method was applied. At each sample instant
k, the 14 errors
are ranked so that
; next, normalized errors
are defined as
. Through this scheme, the new
are such that one normalized error is always less than one; another is exactly equal to one, while all the remaining normalized errors are larger than one. Using the normalized
, it is possible to define a simple tuning strategy for
. Specifically,
are tuned such that the fault belief increases for the (nearest) sensor having
, remains unchanged for the sensor having
, and decreases for all the remaining sensors. It is immediate to verify that
guarantees this behavior. The normalized errors
are then used in the BFs (
40)–(
43) (in place of
) for the reconstruction based methods.
Note 4: An important aspect in the design of a fault diagnosis scheme is the definition of the threshold values to be used for fault detection and isolation. Clearly, the values of these thresholds have a direct impact on the missed alarm rate and false alarm rate. Although several methods have been introduced and tested to compute optimized thresholds [
58,
59], most of the detection methods require a priori knowledge of the signal distribution, changed parameters, and the change amplitude (CUSUM, likelihood ratio test, etc.). Furthermore, these methods assume that modeling errors are Independent and Identically Distributed (IID) random variables. Unfortunately, in our study, we found that the above-mentioned assumptions are not satisfied by experimental residuals and that the application of theoretical thresholds produces very conservative results lacking any practical utility. For this reason, these values were set empirically by trial and error.
Note 5: Since FI algorithms operates in real time, important factors are their computational and memory space requirements. Given that the transformation of fault signatures is performed offline, techniques based on transformed and primary residuals require exactly the same memory space for the storage of the models. As for the computational cost, in reconstruction-based techniques, the computational complexity is
, and the memory space required is
(
to store residuals,
to store estimated fault amplitudes, and
to store errors). In distance-based techniques, the computational complexity, instead, depends on the operations requested to compute the errors in (
20) or (
36). For the technique with primary residuals, the complexity is
because the matrix product involving
in (
14), while in the case of transformed residuals, it is equal to
. The memory space required is quantifiable in
(
to store the residuals,
to store the normalized residuals,
to store
(or
), and
to store the errors). The overall results are summarized in
Table 1. The Bayesian filtering introduces a computational complexity
to calculate the posterior fault probabilities and requires a memory space
(
to store the likelihood probabilities and
to store the posterior fault probabilities).
7. Experimental Models for Sensor FI
The fault isolation techniques introduced in
Section 3 and
Section 4 require the definition of linear multivariate models. Specifically, the definition of the matrices
and
associated with the
linear models in (
4) is required. For each one of the
sensors, the model was identified separately using standard system identification techniques [
3]. From (
3), the resulting models are:
where
and
are the
i-th row of the matrices
and
, respectively. Each of these 14 models depends on 20 potential regressors. It is common practice in model identification to select a subset of regressors that are critical for the estimation of the predicted output
. The regressors’ selection step was partially automated using the algorithm known as the “stepwise regressor selection method”. This is a well-known iterative data-driven algorithm for implementing a linear model by successively adding and/or removing regressors based on their statistical significance in a regression model [
60]. In this effort, the stepwise selection was based on the training data using the ad-hoc procedure available in [
61]. For each model, the selection of the best set of regressors was formulated through the analysis of the Root Mean Squared Error (RMSE) of the prediction error defined as:
Figure 2 shows the evolution of the RMSE for the models of the sensors
,
, and
evaluated both on the training and the validation flight data as a function of the number of regressors included in the model. As expected, while the training data result in a monotone decrease of the RMSE with the increase of the number of regressors in the model, for the validation data, the RMSE reaches a minimum; also, a larger number of regressors induces a decrease of the prediction accuracy. This is a typical example of the well-known modeling overfitting problem. Consequently, for each sensor, the best model was identified as the one that produced the minimum RMSE on the validation data set. The sets of regressors selected by this approach for the
,
, and
models are reported in
Table 3. Without any loss of generality, this procedure was also applied to the other remaining 11 sensors. The number of regressors selected for the 14 models is reported in
Table 4.
Figure 3 compares the RMSE for the 14 models produced by the (normalized) training and validation flight data. It is observed, for all models, that the training and the validation performance are comparable; this implies that the adopted regressor selection procedure is substantially correct and successfully avoids overfitting problems.
8. FI and FE Performance on the Validation Data (Offline Analysis)
For brevity purposes, only the results of the analysis relative to the air data sensors , , and are reported. However, it should be emphasized that the implemented schemes consider the entire set of sensors (residuals); in other words, the FI schemes isolate one among the 14 sensors.
Further, since the main purpose of this research is to compare the performance of the FI and FE techniques, the following analysis was performed assuming an “ideal” failure detection, i.e., the occurrence of a fault is detected as soon as it is injected into a generic time instant . Clearly, in practice, fault detection is not instantaneous, and a fault detection delay is to be expected before the FI and FE algorithms are activated.
The overall evaluation of the FI and FE of the schemes was performed evaluating the average performance provided by the set of four validation flights (approximately 2.05 h) by injecting the faults in the first sample of each validation flight (
). The analysis was then performed considering, for each sensor, 50 equally-spaced fault amplitudes
in (
9) in the range [
;
]. The maximum amplitudes
(see
Table 5) were selected empirically so that, for
, the FI algorithms correctly isolate the fault with a percentage greater than
(see
Section 8.1).
The performance was analyzed using two specific metrics, that is the Fault Isolation Percentage (FIP) and the Relative Fault Reconstruction Error (RFRE). Both metrics are described below.
8.1. Fault Isolation Percentage
Considering a fault on the
i-th sensor of amplitude
in the
j-th validation flight, the Fault Isolation Percentage (FIP) denoted by
is defined as the percent ratio over all the validation flights between the number of samples for which the fault is correctly attributed to the
i-th sensor and the total number of samples:
where:
: number of validation flights.
: number of samples for which the fault isolation index correctly isolates the fault on the i-th sensor, in validation flight j, for fault amplitude .
: total number of samples in validation flight j.
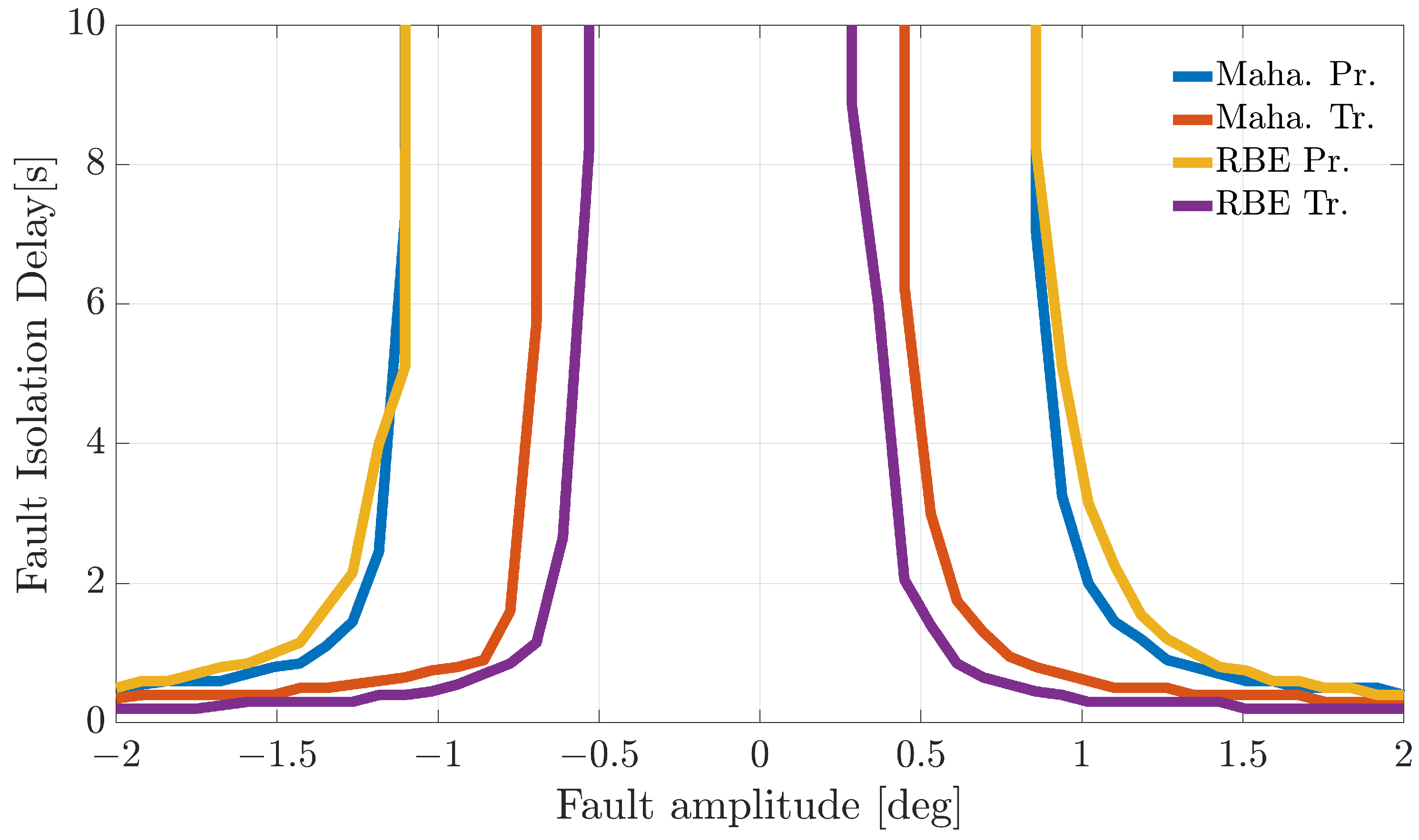
Figure 4,
Figure 5 and
Figure 6 show the FIP for the three sensors as a function of the fault amplitude computed using the
validation flights for each of the considered techniques.
The analysis of the plots reveals that all the techniques can guarantee 100% correct fault isolation for large enough fault amplitudes for all the sensors. On the other side, small amplitude faults are often misinterpreted and misclassified. This is not surprising since small-amplitude faults have amplitudes similar to those of modeling errors, making the FI unreliable. The techniques Maha-Trand RBE-Tr based on transformed residuals provide better performance compared to the techniques based on primary residuals. This highlights the fact that the residual transformation based on the diagonalization of the noise covariance matrix is effective at improving FI performance.
8.2. Relative Fault Reconstruction Error
Considering a fault on the
i-th sensor of amplitude
in the
j-th validation flight, the Relative Fault Reconstruction Error (RFRE) is defined as the percent mean relative amplitude reconstruction error, that is:
where:
: amplitude of the fault on sensor i;
: amplitude of the reconstructed fault at sample time k for the validation flight j.
: set of samples in validation flight j where the fault is correctly attributed to the i-th sensor.
: number of samples in the set .
Figure 7,
Figure 8 and
Figure 9 compare the RFRE as a function of the fault amplitude. From the analysis of the figures, it can be observed that all the techniques accurately estimate the amplitude of either positive or negative faults for a large enough fault amplitude; instead, the estimate is not accurate for small amplitude faults. This is not surprising since when the amplitude of the fault has a magnitude of the same order as the estimator modeling error, the relative fault reconstruction is unreliable and inaccurate. For the
index, it is not possible to identify a clear winning approach. Indeed, the RBE-Pr method provided the best results for the
sensor, the worst for the
sensor, while for the
sensor, the performance was comparable.
10. Conclusions
The purpose of this effort was to compare well-known analytical redundancy-based data-driven techniques for the Fault Isolation (FI) and Fault Estimation (FE) of a set of 14 sensors of a semi-autonomous aircraft. While all these techniques have been shown in the literature to provide close to perfect results using simulated data, only the use of actual experimental data provides the necessary insights and understanding leading to the selection of the best approaches. Specifically, multiple sets of flight data were used to identify linear multivariate models providing a set of primary residuals. Then, residual transformation techniques were applied to generate directional residuals that are robust with respect to the modeling errors. Next, Mahalanobis distance and reconstruction-based methods were used for the FI and the FE. Detailed tests (performed on a set of four validation flights) on the air data sensors showed that the reconstruction-based techniques featuring transformed residuals provide better performance compared to the primary residual-based techniques in terms of the overall fault isolation percentage and fault reconstruction accuracy indices.
In-flight FI was also investigated by applying a bank of recursive Bayesian filters to manage the directional error information online from the 14 sensors. A detailed analysis was conducted by injecting variable amplitude faults at different points throughout the flights. This allowed the estimation of the mean in-flight fault isolation delay. Even for this case, the reconstruction-based methods relying on transformed residuals provided the best performance.
All the considered FI and FE methods are data-driven and were designed based on actual flight data. Therefore, the schemes do not require a priori knowledge of detailed aircraft modeling for their implementation and can be easily returned regularly with updated flight data. Although this is undoubtedly a useful aspect, it is also worth noting, as for any data-based technique, that the reliability of the results depends heavily on the completeness of the available data, which must be representative of all operating conditions. In order to address this issue, all our models were derived by taking multi-flight data rich in maneuvers (as opposed to cruise steady-state conditions), both in the design and validation phases. The quantitative results provide a clear picture of the requested design effort as far as the achievable performance using well-known FI and FE schemes.