A Short Review of Cavity-Enhanced Raman Spectroscopy for Gas Analysis
Abstract
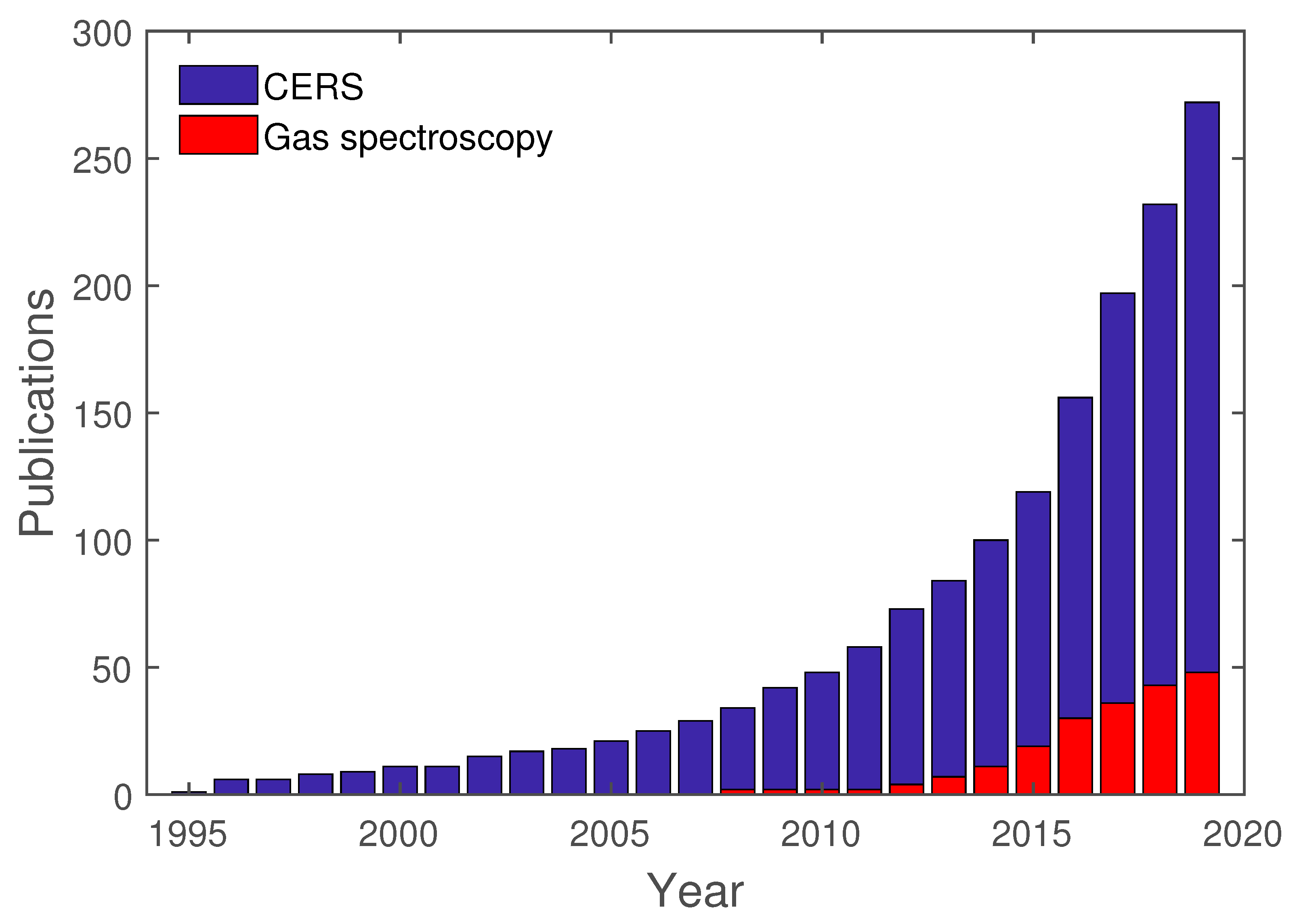
:1. Introduction
2. Raman Theory
3. Raman Enhancement Methods
4. Cavity-Enhanced Raman Spectroscopy
4.1. Basic Cavity Concepts
4.2. Cavities and Locking Methods
4.2.1. CERS Setups
4.2.2. Locking-Methods
4.3. Integrating Cavities and Microcavities
5. Evaluation of Recent CERS Setups
5.1. Enhancement for Different Setups
5.2. Benchmark for CERS Setups
6. Comparison with State of the Art Sensors
7. IoT and Raman Spectroscopy
8. Summary and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| NDIR | Non-dispersive infrared |
| FTIR | Fourier-transform infrared |
| TDLAS | Tune-able laser diode spectroscopy |
| LOD | Limit of detection |
| SERS | Surface-enhanced Raman scattering |
| RR | Resonance Raman |
| CARS | Coherent anti-Stokes Raman scattering |
| CERS | Cavity-enhanced Raman spectroscopy |
| FERS | Fiber-enhanced Raman spectroscopy |
| PBC | Power build-up cavity |
| FWHM | Full width at half maximum |
| PDH | Pound-Drever-Hall |
| OFFL | Optical feedback frequency locking |
| IoT | Internet of Things |
References
- Gebicki, J. Application of electrochemical sensors and sensor matrixes for measurement of odorous chemical compounds. TrAC Trends Anal. Chem. 2016, 77, 1–13. [Google Scholar] [CrossRef]
- Wilson, A.D.; Baietto, M. Applications and advances in electronic-nose technologies. Sensors 2009, 9, 5099–5148. [Google Scholar] [CrossRef] [PubMed]
- Boeker, P. On ‘electronic nose’methodology. Sen. Actuators Chem. 2014, 204, 2–17. [Google Scholar] [CrossRef]
- Munoz, R.; Sivret, E.C.; Parcsi, G.; Lebrero, R.; Wang, X.; Suffet, I.M.; Stuetz, R.M. Monitoring techniques for odour abatement assessment. Water Res. 2010, 44, 5129–5149. [Google Scholar] [CrossRef]
- Dinh, T.V.; Choi, I.Y.; Son, Y.S.; Kim, J.C. A review on non-dispersive infrared gas sensors: Improvement of sensor detection limit and interference correction. Sens. Actuators B Chem. 2016, 231, 529–538. [Google Scholar] [CrossRef]
- Hummelga, C.; Bryntse, I.; Bryzgalov, M.; Martin, H.; Norén, M.; Rödjega, H. Low-cost NDIR based sensor platform for sub-ppm gas detection. Urban Clim. 2015, 14, 342–350. [Google Scholar] [CrossRef]
- Gibson, D.; MacGregor, C. A Novel Solid State Non-Dispersive Infrared CO2 Gas Sensor Compatible with Wireless and Portable Deployment. Sensors 2013, 13, 7079–7103. [Google Scholar] [CrossRef] [Green Version]
- Mendes, L.B.; Ogink, N.W.M.; Edouard, N.; Van Dooren, H.J.C.; Tinôco, I.D.F.F.; Mosquera, J. NDIR Gas Sensor for Spatial Monitoring of Carbon Dioxide Concentrations in Naturally Ventilated Livestock Buildings. Sensors 2015, 15, 11239–11257. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Shi, Y.; Wang, T. Design of a six-gas NDIR gas sensor using an integrated optical gas chamber. Opt. Express 2020, 28, 11451–11462. [Google Scholar] [CrossRef] [PubMed]
- Jacquinot, P. New developments in interference spectroscopy. Rep. Prog. Phys. 1960, 23, 267–312. [Google Scholar] [CrossRef]
- Bak, J.; Clausen, S. FTIR emission spectroscopy methods and procedures for real time quantitative gas analysis in industrial environments. Meas. Sci. Technol. 2001, 13, 150–156. [Google Scholar] [CrossRef]
- Speitel, L.C. Fourier Transform Infrared Analysis of Combustion Gases. J. Fire Sci. 2002, 20, 349–371. [Google Scholar] [CrossRef]
- Werle, P.; Slemr, F.; Maurer, K.; Kormann, R.; Mücke, R.; Jänker, B. Near- and mid-infrared laser-optical sensors for gas analysis. Opt. Lasers Eng. 2002, 37, 101–114. [Google Scholar] [CrossRef]
- Martin, P.A. Near-infrared diode laser spectroscopy in chemical process and environmental air monitoring. Chem. Soc. Rev. 2002, 31, 201–210. [Google Scholar] [CrossRef]
- Lackner, M. Tunable Diode Laser Absorption Spectroscopy (TDLAS) in the Process Industries—A Review. Rev. Chem. Eng. 2007, 23, 65–147. [Google Scholar] [CrossRef]
- Dong, L.; Tittel, F.K.; Li, C.; Sanchez, N.P.; Wu, H.; Zheng, C.; Yu, Y.; Sampaolo, A.; Griffin, R.J. Compact TDLAS based sensor design using interband cascade lasers for mid-IR trace gas sensing. Opt. Express 2016, 24, A528–A535. [Google Scholar] [CrossRef]
- Sur, R.; Sun, K.; Jeffries, J.B.; Hanson, R.K.; Pummill, R.J.; Waind, T.; Wagner, D.R.; Whitty, K.J. TDLAS-based sensors for in situ measurement of syngas composition in a pressurized, oxygen-blown, entrained flow coal gasifier. Appl. Phys. B 2014, 116, 33–42. [Google Scholar] [CrossRef]
- Bell, A.G. On the production and reproduction of sound by light. Am. J. Sci. 1880, s3-20, 305–324. [Google Scholar] [CrossRef] [Green Version]
- Schmid, T. Photoacoustic spectroscopy for process analysis. Anal. Bioanal. Chem. 2006, 384, 1071–1086. [Google Scholar] [CrossRef] [PubMed]
- Haisch, C. Photoacoustic spectroscopy for analytical measurements. Meas. Sci. Technol. 2011, 23, 012001. [Google Scholar] [CrossRef]
- Palzer, S. Photoacoustic-based gas sensing: A review. Sensors 2020, 20, 2745. [Google Scholar] [CrossRef] [PubMed]
- Crawford, T.M. Error Sources In The “Ring Down” Optical Cavity Decay Time Mirror Reflectometer. In Southwest Conf on Optics ’85; Stotlar, S.C., Ed.; International Society for Optics and Photonics: Albuquerque, NM, USA, 1985; Volume 0540, pp. 295–302. [Google Scholar] [CrossRef]
- O’Keefe, A.; Deacon, D.A.G. Cavity ring-down optical spectrometer for absorption measurements using pulsed laser sources. Rev. Sci. Instrum. 1988, 59, 2544–2551. [Google Scholar] [CrossRef] [Green Version]
- Berden, G.; Peeters, R.; Meijer, G. Cavity ring-down spectroscopy: Experimental schemes and applications. Int. Rev. Phys. Chem. 2000, 19, 565–607. [Google Scholar] [CrossRef]
- Wheeler, M.D.; Newman, S.M.; Orr-Ewing, A.J.; Ashfold, M.N.R. Cavity ring-down spectroscopy. J. Chem. Soc. Faraday Trans. 1998, 94, 337–351. [Google Scholar] [CrossRef]
- Scherer, J.J.; Paul, J.B.; O’Keefe, A.; Saykally, R.J. Cavity Ringdown Laser Absorption Spectroscopy: History, Development, and Application to Pulsed Molecular Beams. Chem. Rev. 1997, 97, 25–52. [Google Scholar] [CrossRef]
- Berden, G.; Meijer, G.; Ubachs, W. 2. Spectroscopic applications using ring-down cavities. In Cavity-Enhanced Spectroscopies; Experimental Methods in the Physical Sciences; van Zee, R.D., Looney, J.P., Eds.; Academic Press: Cambridge, MA, USA, 2003; Volume 40, pp. 47–82. [Google Scholar] [CrossRef]
- Kowalski, B.R. Chemometrics. Anal. Chem. 1980, 52, 112–122. [Google Scholar] [CrossRef]
- Frank, I.E.; Kowalski, B.R. Chemometrics. Anal. Chem. 1982, 54, 232–243. [Google Scholar] [CrossRef]
- Sivia, D.S.; Carlile, C.J. Molecular spectroscopy and Bayesian spectral analysis—How many lines are there? J. Chem. Phys. 1992, 96, 170–178. [Google Scholar] [CrossRef]
- Malinowski, E.R. Factor Analysis in Chemistry, 3rd ed.; Wiley: Hoboken, NJ, USA, 2002. [Google Scholar]
- Ehrentreich, F. Wavelet transform applications in analytical chemistry. Anal. Bioanal. Chem. 2002, 372, 115–121. [Google Scholar] [CrossRef] [PubMed]
- Krishna, H.; Majumder, S.K.; Gupta, P.K. Range-independent background subtraction algorithm for recovery of Raman spectra of biological tissue. J. Raman Spectrosc. 2012, 43, 1884–1894. [Google Scholar] [CrossRef]
- Chen, K.; Wei, H.; Zhang, H.; Wu, T.; Li, Y. A Raman peak recognition method based automated fluorescence subtraction algorithm for retrieval of Raman spectra of highly fluorescent samples. Anal. Methods 2015, 7, 2770–2778. [Google Scholar] [CrossRef]
- Otto, M. Chemometrics: Statistics and Computer Application in Analytical Chemistry, 3rd ed.; Wiley: Hoboken, NJ, USA, 2017. [Google Scholar]
- Molstad, L.; Dörsch, P.; Bakken, L.R. Robotized incubation system for monitoring gases (O2, NO, N2O N2) in denitrifying cultures. J. Microbiol. Methods 2007, 71, 202–211. [Google Scholar] [CrossRef]
- Jochum, T.; Fastnacht, A.; Trumbore, S.E.; Popp, J.; Frosch, T. Direct Raman Spectroscopic Measurements of Biological Nitrogen Fixation under Natural Conditions: An Analytical Approach for Studying Nitrogenase Activity. Anal. Chem. 2017, 89, 1117–1122. [Google Scholar] [CrossRef] [Green Version]
- Chow, K.K.; Short, M.; Lam, S.; McWilliams, A.; Zeng, H. A Raman cell based on hollow core photonic crystal fiber for human breath analysis. Med. Phys. 2014, 41, 092701. [Google Scholar] [CrossRef] [PubMed]
- Lourenço, C.; Turner, C. Breath Analysis in Disease Diagnosis: Methodological Considerations and Applications. Metabolites 2014, 4, 465–498. [Google Scholar] [CrossRef] [PubMed]
- Lawal, O.; Ahmed, W.M.; Nijsen, T.M.E.; Goodacre, R.; Fowler, S.J. Exhaled breath analysis: A review of ‘breath-taking’ methods for off-line analysis. Metabolomics 2017, 13, 110. [Google Scholar] [CrossRef] [PubMed]
- Abramczyk, H.; Brozek-Pluska, B.; Jarota, A.; Surmacki, J.; Imiela, A.; Kopec, M. A look into the use of Raman spectroscopy for brain and breast cancer diagnostics: Linear and non-linear optics in cancer research as a gateway to tumor cell identity. Expert Rev. Mol. Diagn. 2020, 20, 99–115. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Herkert, E.; Sterl, F.; Strohfeldt, N.; Walter, R.; Giessen, H. Low-Cost Hydrogen Sensor in the ppm Range with Purely Optical Readout. ACS Sens. 2020, 5, 978–983. [Google Scholar] [CrossRef] [PubMed]
- Ghannoum, A.; Nieva, P.; Yu, A.; Khajepour, A. Development of Embedded Fiber-Optic Evanescent Wave Sensors for Optical Characterization of Graphite Anodes in Lithium-Ion Batteries. ACS Appl. Mater. Interfaces 2017, 9, 41284–41290. [Google Scholar] [CrossRef]
- Cao-Paz, A.M.; Marcos-Acevedo, J.; Del Río-Vázquez, A.; Martínez-Peñalver, C.; Lago-Ferreiro, A.; Nogueiras-Meléndez, A.A.; Doval-Gandoy, J. A Multi-Point Sensor Based on Optical Fiber for the Measurement of Electrolyte Density in Lead-Acid Batteries. Sensors 2010, 10, 2587–2608. [Google Scholar] [CrossRef] [Green Version]
- Sivan, Y.; Dubi, Y. Recent developments in plasmon-assisted photocatalysis—A personal Perspective. Appl. Phys. Lett. 2020, 117, 130501. [Google Scholar] [CrossRef]
- Wackerbarth, H.; Salb, C.; Gundrum, L.; Niederkrüger, M.; Christou, K.; Beushausen, V.; Viöl, W. Detection of explosives based on surface-enhanced Raman spectroscopy. Appl. Opt. 2010, 49, 4362–4366. [Google Scholar] [CrossRef]
- Wieduwilt, F.; Lenth, C.; Ctistis, G.; Plachetka, U.; Möller, M.; Wackerbarth, H. evaluation of an on-site surface enhanced Raman scattering sensor for benzotriazole. Sci. Rep. 2020, 10, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Kneipp, J. Interrogating Cells, Tissues, and Live Animals with New Generations of Surface-Enhanced Raman Scattering Probes and Labels. ACS Nano 2017, 11, 1136–1141. [Google Scholar] [CrossRef]
- Hu, Y.; Cheng, H.; Zhao, X.; Wu, J.; Muhammad, F.; Lin, S.; He, J.; Zhou, L.; Zhang, C.; Deng, Y.; et al. Surface-Enhanced Raman Scattering Active Gold Nanoparticles with Enzyme-Mimicking Activities for Measuring Glucose and Lactate in Living Tissues. ACS Nano 2017, 11, 5558–5566. [Google Scholar] [CrossRef]
- Mosier-Boss, P.A. Review of SERS Substrates for Chemical Sensing. Nanomaterials 2017, 7, 142. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zong, C.; Xu, M.; Xu, L.J.; Wei, T.; Ma, X.; Zheng, X.S.; Hu, R.; Ren, B. Surface-Enhanced Raman Spectroscopy for Bioanalysis: Reliability and Challenges. Chem. Rev. 2018, 118, 4946–4980. [Google Scholar] [CrossRef] [PubMed]
- Begley, R.; Harvey, A.; Byer, R.L. Coherent anti-Stokes Raman spectroscopy. Appl. Phys. Lett. 1974, 25, 387–390. [Google Scholar] [CrossRef] [Green Version]
- Krafft, C.; Dietzek, B.; Popp, J.; Schmitt, M. Raman and coherent anti-Stokes Raman scattering microspectroscopy for biomedical applications. J. Biomed. Opt. 2012, 17, 040801. [Google Scholar] [CrossRef]
- Zheltikov, A.M. Coherent anti-Stokes Raman scattering: from proof-of-the-principle experiments to femtosecond CARS and higher order wave-mixing generalizations. J. Raman Spectrosc. 2000, 31, 653–667. [Google Scholar] [CrossRef]
- Raman, C.V.; Krishnan, K.S. A new type of secondary radiation. Nature 1928, 121, 501. [Google Scholar] [CrossRef]
- Smekal, A. Zur quantentheorie der dispersion. Naturwissenschaften 1923, 11, 873–875. [Google Scholar] [CrossRef]
- Larkin, P. Infrared and Raman Spectroscopy: Principles and Spectral Interpretation; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Long, D.A. The Raman Effect: A Unified Treatment of the Theory of Raman Scattering by Molecules; John Wiley & Sons: New York, NY, USA, 2002. [Google Scholar]
- Parker, F.S. Applications of Infrared, Raman, and Resonance Raman Spectroscopy in Biochemistry; Springer Science & Business Media: Berlin, Germany, 1983. [Google Scholar]
- Robert, B. Resonance Raman spectroscopy. Photosynth. Res. 2009, 101, 147–155. [Google Scholar] [CrossRef] [PubMed]
- Clark, R.J.; Dines, T.J. Resonance Raman spectroscopy, and its application to inorganic chemistry. New analytical methods (27). Angew. Chem. Int. Ed. Engl. 1986, 25, 131–158. [Google Scholar] [CrossRef]
- Tolles, W.M.; Nibler, J.; McDonald, J.; Harvey, A. A review of the theory and application of coherent anti-Stokes Raman spectroscopy (CARS). Appl. Spectrosc. 1977, 31, 253–271. [Google Scholar] [CrossRef]
- Le Ru, E.C.; Etchegoin, P.G. Single-molecule surface-enhanced Raman spectroscopy. Annu. Rev. Phys. Chem. 2012, 63, 65–87. [Google Scholar] [CrossRef] [Green Version]
- Russell, P.S. Photonic-Crystal Fibers. J. Lightwave Technol. 2006, 24, 4729–4749. [Google Scholar] [CrossRef]
- Niklas, C.; Göllner, S.; Müller, F.; Wackerbarth, H.; Ctistis, G. Raman spectroscopy of atmospheric gases using hollow core photonic crystal fibres. In Optical Sensing and Detection VI; SPIE: Bellingham, WA, USA, 2020; Volume 11354, p. 113540O. [Google Scholar]
- Hanf, S.; Keiner, R.; Yan, D.; Popp, J.; Frosch, T. Fiber-enhanced Raman multigas spectroscopy: a versatile tool for environmental gas sensing and breath analysis. Anal. Chem. 2014, 86, 5278–5285. [Google Scholar] [CrossRef]
- Ghenuche, P.; Rammler, S.; Joly, N.Y.; Scharrer, M.; Frosz, M.; Wenger, J.; Russell, P.S.J.; Rigneault, H. Kagome hollow-core photonic crystal fiber probe for Raman spectroscopy. Opt. Lett. 2012, 37, 4371–4373. [Google Scholar] [CrossRef]
- Buric, M.; Chen, K.; Falk, J.; Velez, R.; Woodruff, S. Raman sensing of fuel gases using a reflective coating capillary optical fiber. In Fiber Optic Sensors and Applications VI; SPIE: Bellingham, WA, USA, 2009; Volume 7316, p. 731608. [Google Scholar]
- Weber, A.; Porto, S.P.; Cheesman, L.E.; Barrett, J.J. High-resolution Raman spectroscopy of gases with cw-laser excitation. JOSA 1967, 57, 19–28. [Google Scholar] [CrossRef]
- Hill, R.; Mulac, A.; Hackett, C. Retroreflecting multipass cell for Raman scattering. Appl. Opt. 1977, 16, 2004–2006. [Google Scholar] [CrossRef]
- Lin, H.B.; Campillo, A. Radial profiling of microdroplets using cavity-enhanced Raman spectroscopy. Opt. Lett. 1995, 20, 1589–1591. [Google Scholar] [CrossRef] [PubMed]
- Symes, R.; Sayer, R.M.; Reid, J.P. Cavity enhanced droplet spectroscopy: Principles, perspectives and prospects. Phys. Chem. Chem. Phys. 2004, 6, 474–487. [Google Scholar] [CrossRef]
- Valiunas, J.K.; Tenuta, M.; Das, G. A Gas Cell Based on Hollow-Core Photonic Crystal Fiber (PCF) and Its Application for the Detection of Greenhouse Gas (GHG): Nitrous Oxide (N2O). J. Sens. 2016, 2016, 7678315. [Google Scholar] [CrossRef] [Green Version]
- Saleh, B.E.; Teich, M.C. Fundamentals of Photonics; John Wiley & Sons: New York, NY, USA, 2019. [Google Scholar]
- Bixler, J.N. Integrating Cavity Enhanced Spectroscopy for Liquid and Gas Sensing. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2015. [Google Scholar]
- Moore, T.Z.; Yakovlev, V.V.; Mason, J.D.; Nodurft, D.T.; Tedford, V.; Fry, E.S.; Favela, K.A. Chemical, biological, and trace gas detection and measurement with a newly developed integrating Cavity Enhanced Raman (iCERS) technique. In Next-Generation Spectroscopic Technologies XI; SPIE: Bellingham, WA, USA, 2018; Volume 10657, p. 106570M. [Google Scholar]
- Moore, T.; Yakovlev, V.; Mason, J.; Fry, E.; Nodurft, D.; Tedford, V.; Favela, K. Integrating Cavity Enhanced Raman Spectroscopy of Trace Gases and Bulk Compounds. In CLEO: Applications and Technology; Optical Society of America: San Jose, CA, USA, 2019; p. JTh2A-87. [Google Scholar]
- Moore, T.; Retherford, K.; Davis, M.; Raut, U.; Mandt, K.; Mason, J.; Yakovlev, V. High Sensitivity Planetary Composition Measurements Using Integrating Cavity Enhanced Spectroscopy. In Proceedings of the 3rd International Workshop on Instrumentation for Planetary Mission, Pasadena, CA, USA, 24–27 October 2016; Volume 1980. [Google Scholar]
- Hitz, C.B.; Ewing, J.J.; Hecht, J. Introduction to Laser Technology; John Wiley & Sons: New York, NY, USA, 2012. [Google Scholar]
- Wang, P.; Chen, W.; Wan, F.; Wang, J.; Hu, J. Cavity-enhanced Raman spectroscopy with optical feedback frequency-locking for gas sensing. Opt. Express 2019, 27, 33312–33325. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Chen, W.; Wan, F.; Wang, J.; Hu, J. A review of cavity-enhanced Raman spectroscopy as a gas sensing method. Appl. Spectrosc. Rev. 2020, 55, 393–417. [Google Scholar] [CrossRef]
- Pound, R.V. Electronic frequency stabilization of microwave oscillators. Rev. Sci. Instruments 1946, 17, 490–505. [Google Scholar] [CrossRef]
- Drever, R.; Pugh, J.; Munley, A.; Ford, G.; Ward, H.; Kerr, I.; Robertson, N.; Hough, J. A gravity wave detector using optical cavity sensing. Gen. Relativ. Gravit. 1980, 1983, 265. [Google Scholar]
- Drever, R.; Hall, J.L.; Kowalski, F.; Hough, J.; Ford, G.; Munley, A.; Ward, H. Laser phase and frequency stabilization using an optical resonator. Appl. Phys. B 1983, 31, 97–105. [Google Scholar] [CrossRef]
- Black, E.D. An introduction to Pound–Drever–Hall laser frequency stabilization. Am. J. Phys. 2001, 69, 79–87. [Google Scholar] [CrossRef] [Green Version]
- Elterman, P. Integrating cavity spectroscopy. Appl. Opt. 1970, 9, 2140–2142. [Google Scholar] [CrossRef]
- Purcell, E.M. Spontaneous emission probabilities at radio frequencies. In Confined Electrons and Photons; Springer: Berlin, Germany, 1995; p. 839. [Google Scholar]
- Gérard, J.M.; Sermage, B.; Gayral, B.; Legrand, B.; Costard, E.; Thierry-Mieg, V. Enhanced Spontaneous Emission by Quantum Boxes in a Monolithic Optical Microcavity. Phys. Rev. Lett. 1998, 81, 1110–1113. [Google Scholar] [CrossRef]
- Bayer, M.; Reinecke, T.L.; Weidner, F.; Larionov, A.; McDonald, A.; Forchel, A. Inhibition and Enhancement of the Spontaneous Emission of Quantum Dots in Structured Microresonators. Phys. Rev. Lett. 2001, 86, 3168–3171. [Google Scholar] [CrossRef] [PubMed]
- Xiao-Yun, L.; Yu-Xing, X.; Ju-Ming, H.; Li, Z. Diagnosis of multiple gases separated from transformer oil using cavity-enhanced Raman spectroscopy. Chin. Phys. Lett. 2008, 25, 3326. [Google Scholar] [CrossRef]
- Utsav, K.; Varghese, P.L. Accurate temperature measurements in flames with high spatial resolution using Stokes Raman scattering from nitrogen in a multiple-pass cell. Appl. Opt. 2013, 52, 5007–5021. [Google Scholar] [CrossRef]
- Schlüter, S.; Krischke, F.; Popovska-Leipertz, N.; Seeger, T.; Breuer, G.; Jeleazcov, C.; Schüttler, J.; Leipertz, A. Demonstration of a signal enhanced fast Raman sensor for multi-species gas analyses at a low pressure range for anesthesia monitoring. J. Raman Spectrosc. 2015, 46, 708–715. [Google Scholar] [CrossRef]
- Petrov, D.V. Multipass optical system for a Raman gas spectrometer. Appl. Opt. 2016, 55, 9521–9525. [Google Scholar] [CrossRef] [PubMed]
- Wen, C.; Huang, X.; Wang, W.; Shen, C.; Li, H. Multiple-pass-enhanced Raman spectroscopy for long-term monitoring of hydrogen isotopologues. J. Raman Spectrosc. 2019, 50, 1555–1560. [Google Scholar] [CrossRef]
- Salter, R.; Chu, J.; Hippler, M. Cavity-enhanced Raman spectroscopy with optical feedback cw diode lasers for gas phase analysis and spectroscopy. Analyst 2012, 137, 4669–4676. [Google Scholar] [CrossRef]
- Zaitsu, S.i.; Imasaka, T. Intracavity phase-matched coherent anti-Stokes Raman spectroscopy for trace gas detection. Anal. Sci. 2014, 30, 75–79. [Google Scholar] [CrossRef] [Green Version]
- Thorstensen, J.; Haugholt, K.; Ferber, A.; Bakke, K.; Tschudi, J. Low-cost resonant cavity Raman gas probe for multi-gas detection. J. Eur. Opt.-Soc.-Rapid Publ. 2014, 9. [Google Scholar] [CrossRef] [Green Version]
- Friss, A.J.; Limbach, C.M.; Yalin, A.P. Cavity-enhanced rotational Raman scattering in gases using a 20 mW near-infrared fiber laser. Opt. Lett. 2016, 41, 3193–3196. [Google Scholar] [CrossRef]
- Wang, P.; Chen, W.; Wan, F.; Wang, J.; Teng, L. Simultaneously anayze fault characteristic gases extracted from transformer oil by Raman spectroscopy. In Proceedings of the 2016 IEEE International Conference on High Voltage Engineering and Application (ICHVE), Chengdu, China, 19–22 September 2016; pp. 1–4. [Google Scholar]
- Sandfort, V.; Goldschmidt, J.; Wöllenstein, J.; Palzer, S. Cavity-enhanced Raman spectroscopy for food chain management. Sensors 2018, 18, 709. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, X.; Xia, Y.; Zhan, L.; Huang, J. Near-confocal cavity-enhanced Raman spectroscopy for multitrace-gas detection. Opt. Lett. 2008, 33, 2143–2145. [Google Scholar] [CrossRef]
- Hippler, M. Cavity-enhanced Raman spectroscopy of natural gas with optical feedback cw-diode lasers. Anal. Chem. 2015, 87, 7803–7809. [Google Scholar] [CrossRef] [PubMed]
- Dong, M.; Zheng, C.; Miao, S.; Zhang, Y.; Du, Q.; Wang, Y.; Tittel, F.K. Development and measurements of a mid-infrared multi-gas sensor system for CO, CO2 and CH4 detection. Sensors 2017, 17, 2221. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wong, J.Y. Method for Detecting a Gas Species Using a Super Tube Waveguide. U.S. Patent 7,259,374, 21 August 2007. [Google Scholar]
- Dey, A. Semiconductor metal oxide gas sensors: A review. Mater. Sci. Eng. B 2018, 229, 206–217. [Google Scholar] [CrossRef]
- Sahm, T.; Mädler, L.; Gurlo, A.; Barsan, N.; Pratsinis, S.E.; Weimar, U. Flame spray synthesis of tin dioxide nanoparticles for gas sensing. Sensors Actuators B Chem. 2004, 98, 148–153. [Google Scholar] [CrossRef]
- Guth, U.; Vonau, W.; Zosel, J. Recent developments in electrochemical sensor application and technology—A review. Meas. Sci. Technol. 2009, 20, 042002. [Google Scholar] [CrossRef]
- Sieburg, A.; Jochum, T.; Trumbore, S.E.; Popp, J.; Frosch, T. Onsite cavity enhanced Raman spectrometry for the investigation of gas exchange processes in the Earth’s critical zone. Analyst 2017, 142, 3360–3369. [Google Scholar] [CrossRef]
- Feng, S.; Farha, F.; Li, Q.; Wan, Y.; Xu, Y.; Zhang, T.; Ning, H. Review on smart gas sensing technology. Sensors 2019, 19, 3760. [Google Scholar] [CrossRef] [Green Version]
- Yang, D.; Guo, J.; Liu, Q.; Luo, Z.; Yan, J.; Zheng, R. Highly sensitive Raman system for dissolved gas analysis in water. Appl. Opt. 2016, 55, 7744–7748. [Google Scholar] [CrossRef]
- Keiner, R.; Frosch, T.; Massad, T.; Trumbore, S.; Popp, J. Enhanced Raman multigas sensing—A novel tool for control and analysis of 13 CO2 labeling experiments in environmental research. Analyst 2014, 139, 3879–3884. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Metcalfe, G.D.; Alahmari, S.; Smith, T.W.; Hippler, M. Cavity-Enhanced Raman and Helmholtz Resonator Photoacoustic Spectroscopy to Monitor the Mixed Sugar Metabolism of E. coli. Anal. Chem. 2019, 91, 13096–13104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Petrak, B.J.; Cooper, J.; Konthasinghe, K.; Peiris, M.; Djeu, N.; Hopkins, A.; Muller, A. Isotopic gas analysis through Purcell cavity enhanced Raman scattering. Appl. Phys. Lett. 2016, 108, 091107. [Google Scholar] [CrossRef]
- Petrak, B.J. Microcavity Enhanced Raman Scattering. Ph.D. Thesis, University of South Florida, Tampa, FL, USA, 2016. [Google Scholar]


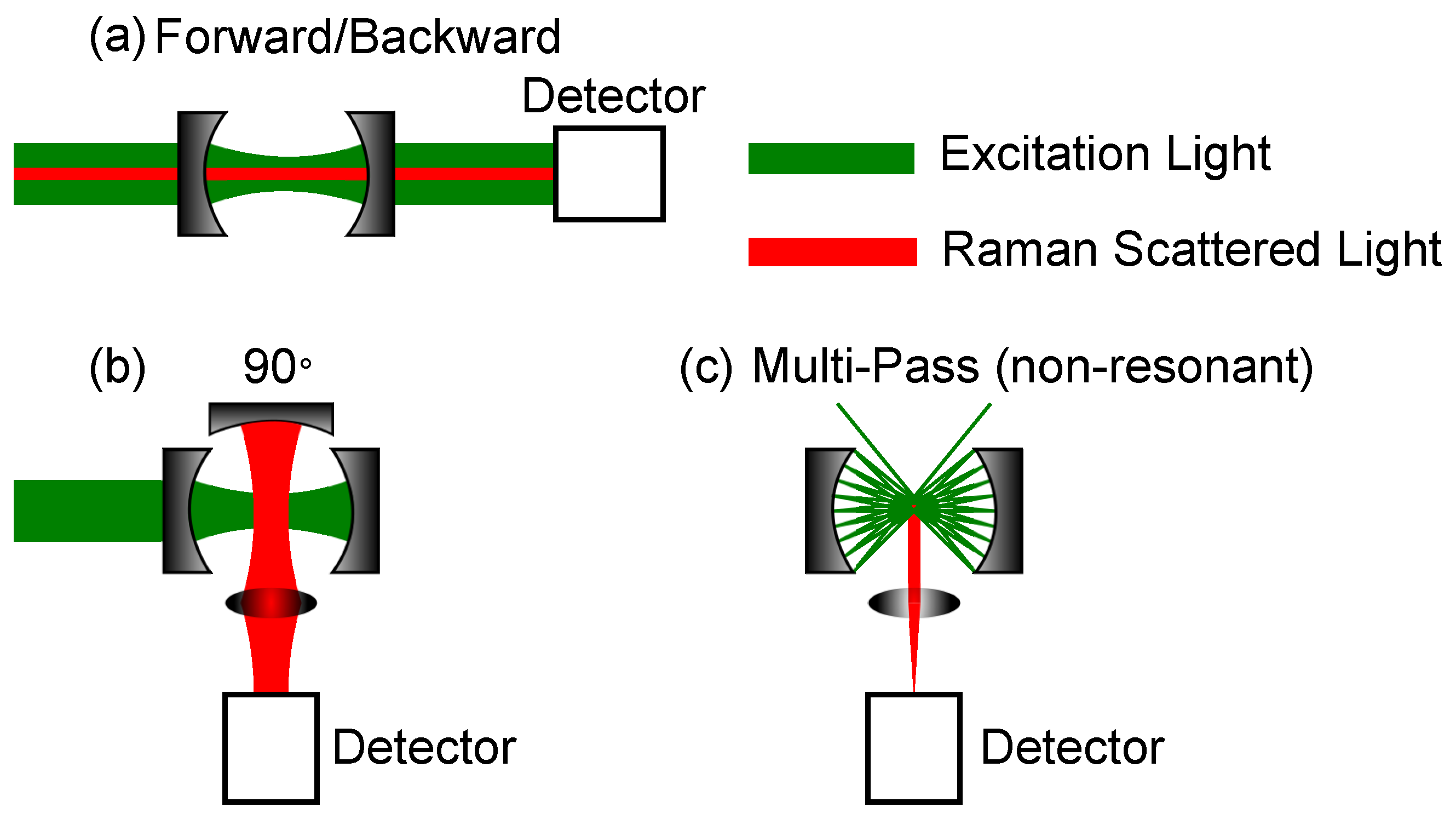

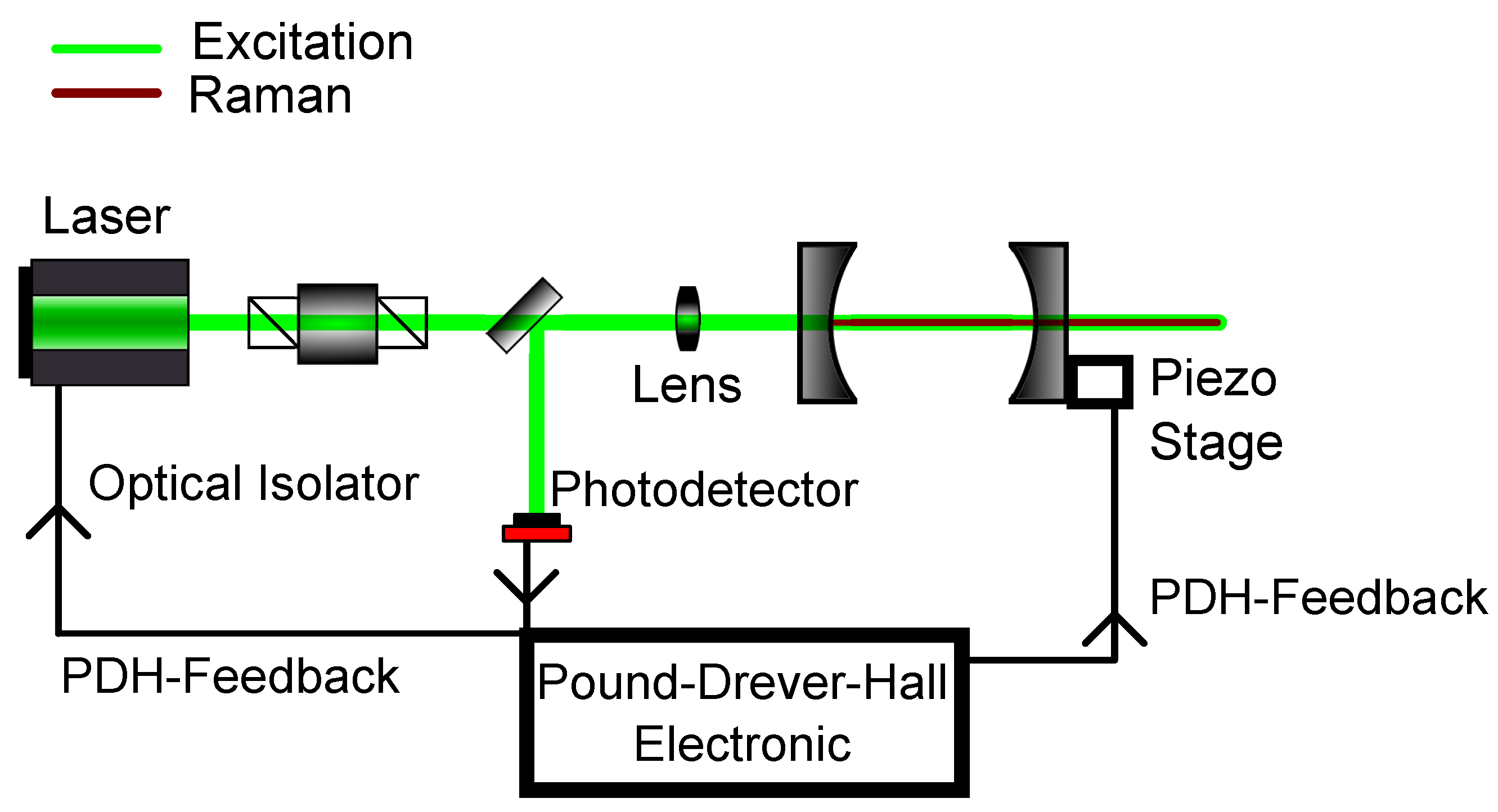
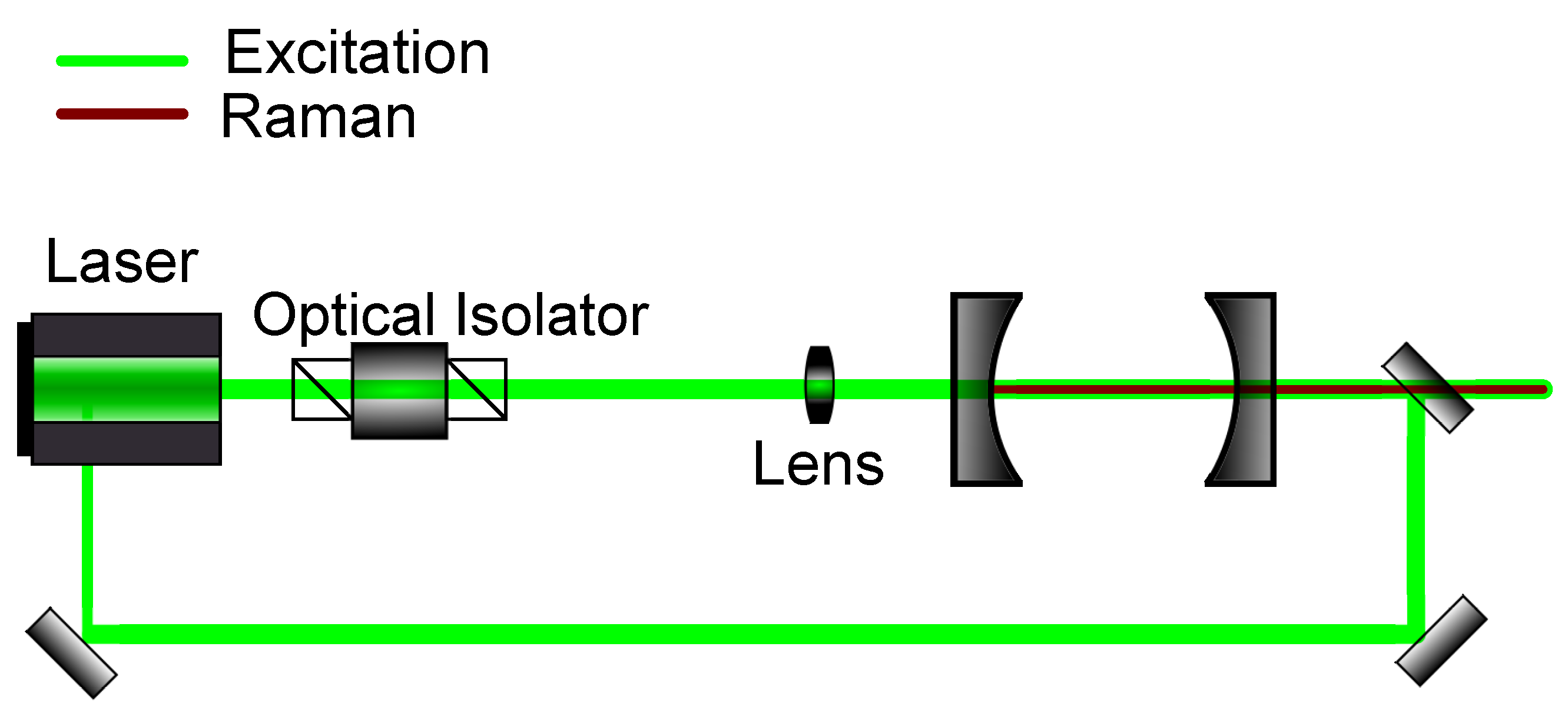
| Enhancement Method | Methodology | Advantages | Disadvantages |
|---|---|---|---|
| Resonance Raman | Electronic transitions of specific analyte are stimulated | Enhancement of up to , mostly used with chromophores | Wavelength-tunable laser (e.g., dye laser) needed |
| Coherent anti-Stokes Raman | Four-wave-mixing | No Fluorescence, also non-Raman active transitions possible | Two laser sources necessary, at least one tunable |
| Surface-enhanced Raman | Plasmonic enhancement | Large enhancement factors, detection down to single molecule level | Distinct nanostructured surface morphology needed, works only when analyte close to surface |
| Fiber-enhanced Raman | Light guiding and confinement | Long interaction lengths (thus enhancements) can be achieved while still compact | Only for gaseous and fluidic analytes |
| Locking Method | Advantages | Disadvantages |
|---|---|---|
| PDH | flexibility to either vary the laser frequency itself or the cavity length | need for high cost electronics |
| Optical feedback frequency locking | easy to implement via back reflection | needs specific semiconductor lasers |
| Group | Geometry | Additional Collection Mirror | Raman Gain |
|---|---|---|---|
| Li et al. [90] | Near confocal | Yes | 45 |
| Utsav et al. [91] | Near confocal | No | 20 |
| Schlüter et al. [92] | Near confocal | Yes | 18.52 |
| Schlüter et al. [92] | Plane Mirror geometry | Yes | 10 |
| Petrov et al. [93] | Near concentric | No | 20 |
| Wen et al. [94] | Four mirror setup | Forward detection | 9 |
| Group | Locking | Raman Detection | Raman Gain |
|---|---|---|---|
| Salter et al. [95] | Optical feedback loop | forward | 833 |
| Zaitsu et al. [96] | Not specified | forward | 6000 |
| Thorstensen et al. [97] | Optical feedback loop | foward | 50 |
| Friss et al. [98] | PDH | 5900 | |
| Wang et al. [99] | Frequency-locking | forward | 11.8 |
| Sandfort et al. [100] | PDH | 851 | |
| Wang et al. [80] | Frequency-locking | forward | 2200 |
| Group | CO | H | O | N |
|---|---|---|---|---|
| Li. et al. [101] | 36 ppm | - | - | - |
| Li et al. [90] | 16 ppm | - | 12 ppm | - |
| Hippler [102] | - | 140 ppm | - | 1000 ppm |
| Wang et al. [99] | 90.6 ppm | 75 ppm | 80.7 ppm | 85 ppm |
| Sandfort et al. [100] | 317 ppm | - | 1412 ppm | 3540 ppm |
| Wang et al. [80] | 17.4 ppm | - | 50.7 ppm | 53.5 ppm |
| Wen et al. [94] | - | 132 ppm | 223 ppm | 213 ppm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niklas, C.; Wackerbarth, H.; Ctistis, G. A Short Review of Cavity-Enhanced Raman Spectroscopy for Gas Analysis. Sensors 2021, 21, 1698. https://doi.org/10.3390/s21051698
Niklas C, Wackerbarth H, Ctistis G. A Short Review of Cavity-Enhanced Raman Spectroscopy for Gas Analysis. Sensors. 2021; 21(5):1698. https://doi.org/10.3390/s21051698
Chicago/Turabian StyleNiklas, Christian, Hainer Wackerbarth, and Georgios Ctistis. 2021. "A Short Review of Cavity-Enhanced Raman Spectroscopy for Gas Analysis" Sensors 21, no. 5: 1698. https://doi.org/10.3390/s21051698
APA StyleNiklas, C., Wackerbarth, H., & Ctistis, G. (2021). A Short Review of Cavity-Enhanced Raman Spectroscopy for Gas Analysis. Sensors, 21(5), 1698. https://doi.org/10.3390/s21051698








