Modeling Capacitive Low-Power Voltage Transformer Behavior over Temperature and Frequency
Abstract
:1. Introduction
2. Low-Power Voltage Transformers: Capacitive Dividers
2.1. Working Principle
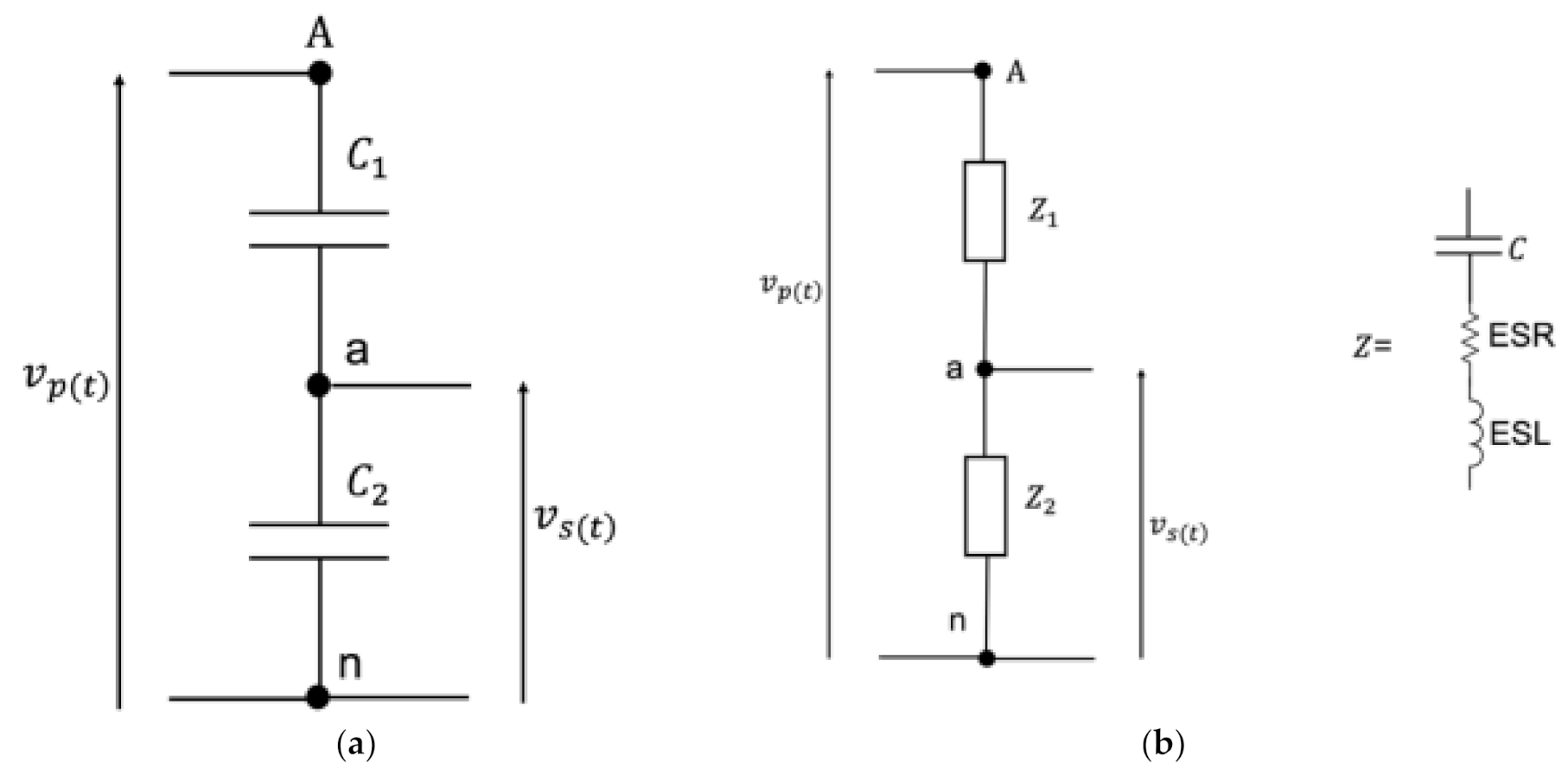
2.2. Modeling
2.3. Influence Factors
2.4. Operation vs. Frequency
3. Test Description for CD Modeling
3.1. Measurements of the Transformation Ratio vs. Temperature and vs. Frequency
3.1.1. Setup
- A Datron Wavetek 4800 multifunction calibrator used as a voltage source. The calibrator is used to supply the LPVTs at a maximum voltage of 200 V for frequencies ranging between 10 Hz and 100 kHz. However, due to limitations of the calibrator itself, a maximum voltage of 20 V can be supplied for frequencies above 100 kHz. For this reason, Table 1 and Table 2 provide the accuracy for the two voltage ranges. The frequency uncertainty is less than 100 ppm for all ranges.
- A thermostatic chamber. It allows to set temperatures in the range from −40 °C to +180 °C.
- A high-voltage differential probe. It features four attenuation ranges at ×100, ×200, ×500, and ×1000, corresponding, respectively, to a maximum rms (root mean square) voltage input of 230 V, 460 V, 1140 V, and 2300 V. The accuracy is ±2% for all attenuation ranges.
- Oscilloscope Tektronix MSO58. It has a bandwidth of 350 MHz, and the ADC (Analog to digital converter) resolution is 12 bits. The input impedance consists of 1 MΩ and 13 pF.
- Two passive off-the-shelf capacitive LPVTs under test whose characteristics are listed in Table 3. Precisely, the following specifications are reported: primary and secondary rated voltages ( and , respectively), accuracy class (AC), rated operating frequency (), and an operating temperature range in °C (). Considering that the aim of this work is not to evaluate the performance of a specific product, the two LPVTs are referred to as A and B from here on.
3.1.2. Test Description
3.2. Impedance Measurement
3.2.1. Setup
- An Agilent 4284A precision LCR meter. It features a frequency range from 20 Hz to 1 MHz, whereas the impedance measurement range spans from 0.01 mΩ to 99.9999 MΩ. The overall accuracy of the instrument is in the range of 0.1%.
- The two capacitive dividers under test are described in Section 3.1.1 and in Table 3.
3.2.2. Test Description
- Short-circuiting the primary terminals (Figure 4a), allowing measuring from the secondary terminals the capacitance obtained from the parallel terminals and .
- Open-circuit measurement from the primary terminals (Figure 4c), allowing measuring from the capacitance obtained from the series of and .
4. Results and Discussion
4.1. Impedance Test Results
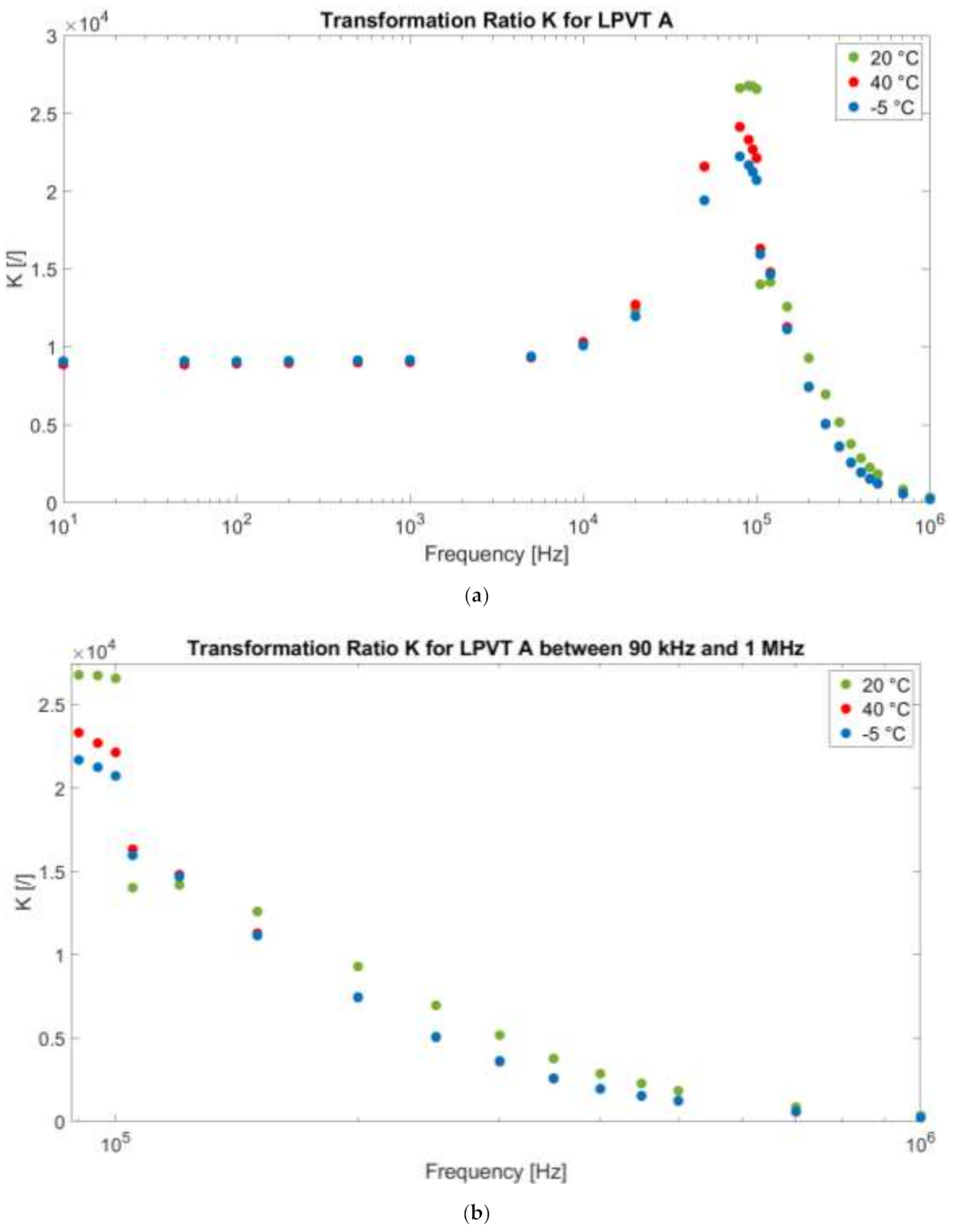
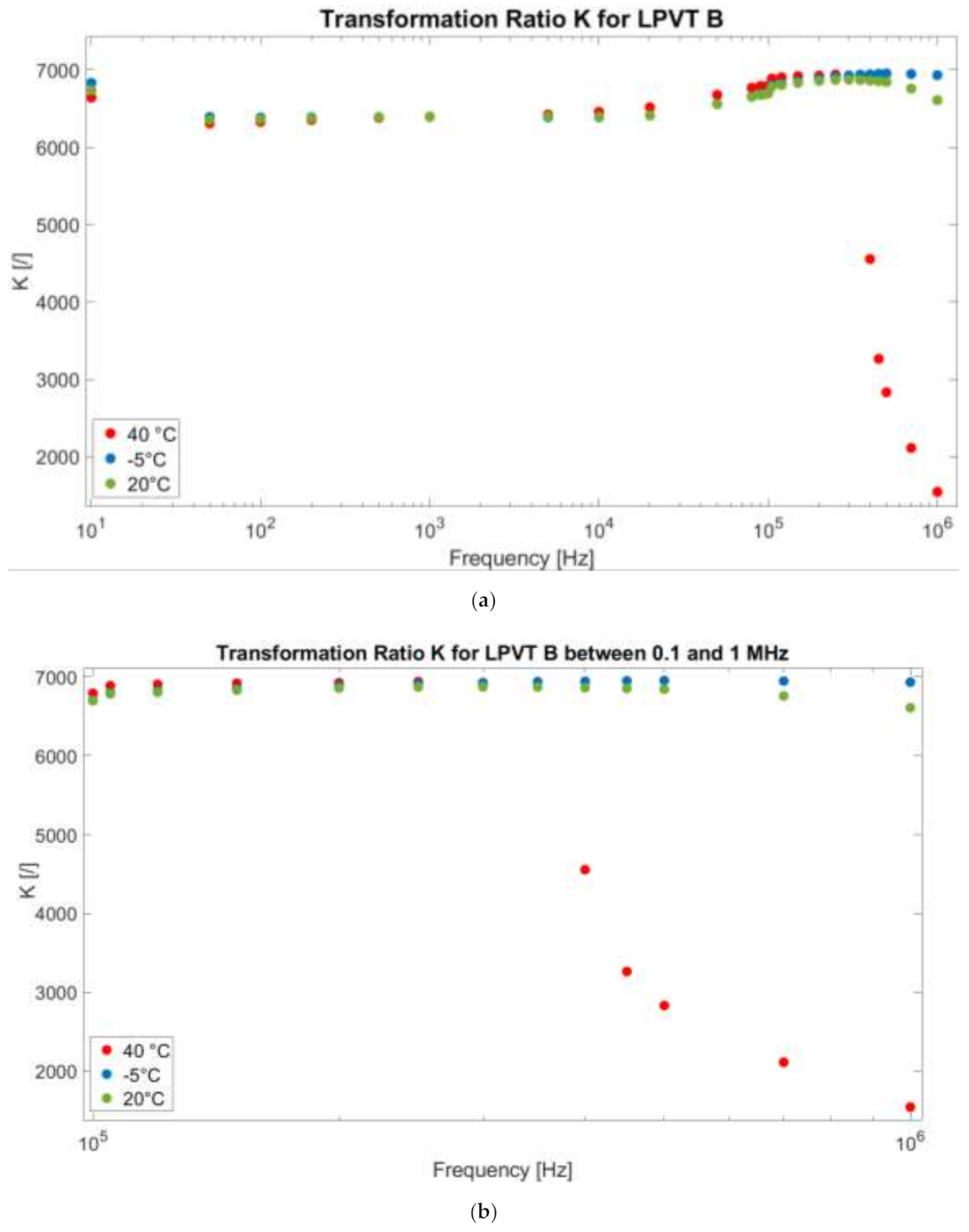
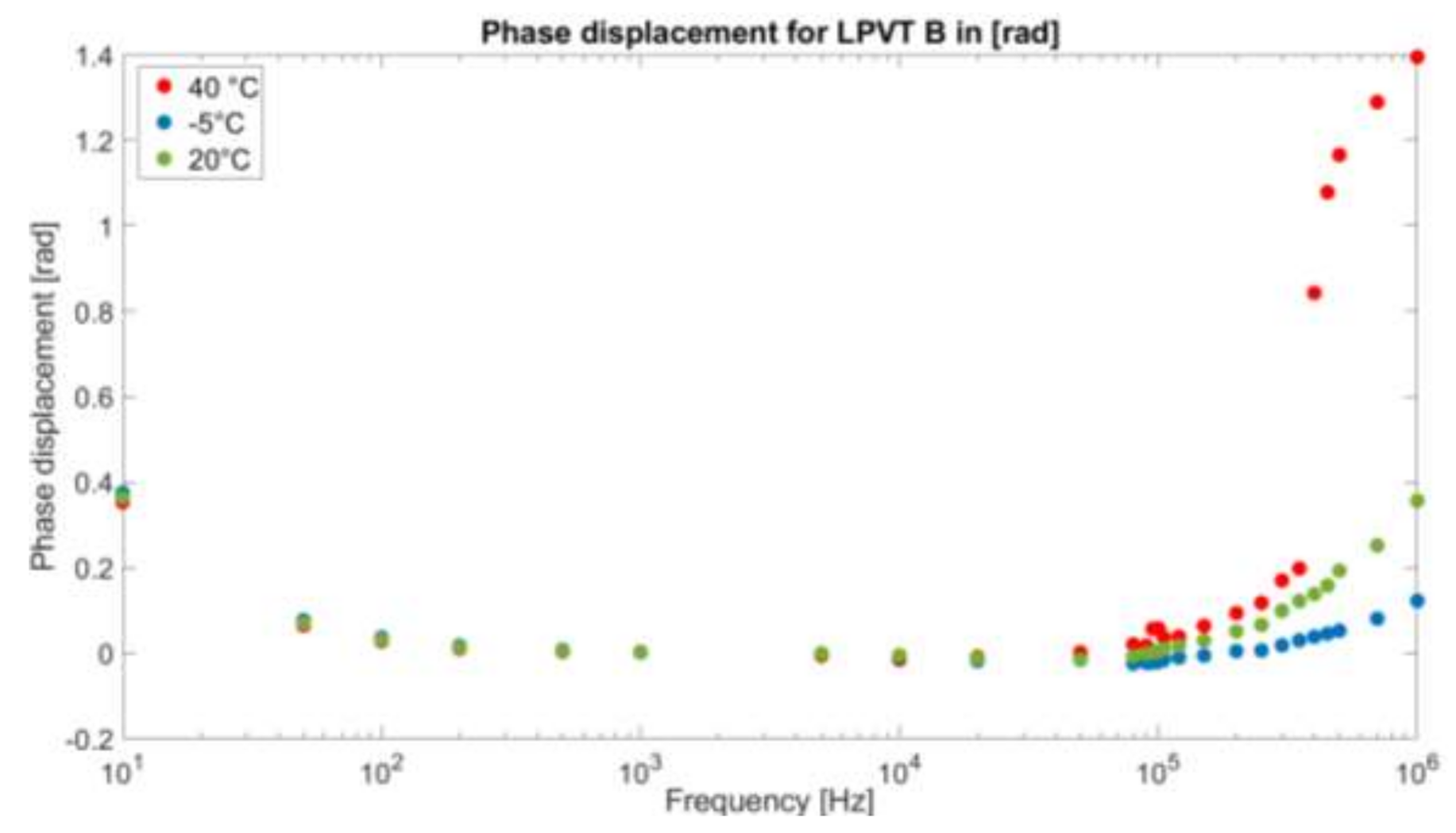
4.2. Transformation Ratio and Phase Displacement Test Results
- Determine the temperature dependencies of the capacitive dividers, helping one to understand how their behavior, and hence their accuracy, changes vs. temperature.
- Determine the frequency dependency of the capacitive dividers. This result is significant for exploiting the measurement capabilities of the dividers outside their design range. In particular, it has been demonstrated whether it is possible to measure high-frequency components according to the divider behavior.
- Determine the combined effect of temperature and frequency. In fact, the simultaneous presence of the two influencing quantities may or may not change, as presented, the accuracy parameters of the capacitive dividers.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- International Standardization Organization. IEC 60044-1: 1996. Instrument Transformers—Part 1: Current Transformers; International Standardization Organization: Geneva, Switzerland, 1996. [Google Scholar]
- International Standardization Organization. IEC 61869-1: 2010. Instrument Transformers—Part 1: General Requirements; International Standardization Organization: Geneva, Switzerland, 2010. [Google Scholar]
- Dadić, M.; Keitoue, S.; Malaric, R.; Gazivoda, S. FIR modeling of voltage instrument transformers with iron core for the study of fast transients. Measurement 2010, 43, 1404–1415. [Google Scholar] [CrossRef]
- Faifer, M.; Laurano, C.; Ottoboni, R.; Toscani, S.; Zanoni, M. Nonlinear behavioral modeling of voltage transform-ers in the frequency domain: Comparing different approaches. IEEE Trans. Instrum. Meas. 2020, 69, 8137–8145. [Google Scholar]
- Jaschke, C.; Schegner, P. A model to compute the resonance effects in high current instrument transformers. In Proceedings of the 2017 IEEE International Magnetics Conference (INTERMAG), Dublin, Ireland, 24–28 April 2017; pp. 1–2. [Google Scholar]
- Sanchez, J.A.; Gonzalez, J.W. SIMTC: Current transformer model. 2010 IEEE ANDESCON 2010, 1–6. [Google Scholar] [CrossRef]
- Torre, F.D.; Faifer, M.; Morando, A.P.; Ottoboni, R.; Cherbaucich, C.; Gentili, M.; Mazza, P. Instrument trans-formers: A different approach to their modeling. In Proceedings of the IEEE International Workshop on Applied Measurements for Power Systems, Aachen, Germany, 28–30 September 2011; pp. 37–41. [Google Scholar]
- Tziouvaras, D.; McLaren, P.; Alexander, G.; Dawson, D.; Esztergalyos, J.; Fromen, C.; Glinkowski, M.; Hasenwinkle, I.; Kezunovic, M.; Kojovic, L.; et al. Mathematical models for current, voltage, and coupling capacitor voltage transformers. IEEE Trans. Power Deliv. 2000, 15, 62–72. [Google Scholar] [CrossRef]
- Paic, I.; Krajtner, D.; Nenadic, Z. A new approach to design and construction process of instrument transformers. IEEE 2005, 1, 527–530. [Google Scholar]
- Crotti, G.; Van Den Brom, H.E.; Mohns, E.; Tinarelli, R.; Luiso, M.; Styblikova, R.; Almutairi, M. Measurement meth-ods and procedures for assessing accuracy of instrument transformers for power quality measurements. In Proceedings of the Conference on Precision Electromagnetic Measurements, Denver, CO, USA, 24–28 August 2020. [Google Scholar]
- Kaczmarek, M.; Stano, E. Proposal for extension of routine tests of the inductive current transformers to evaluation of transformation accuracy of higher harmonics. Int. J. Electr. Power Energy Syst. 2019, 113, 842–849. [Google Scholar] [CrossRef]
- Stiegler, R.; Meyer, J.; Kilter, J.; Konzelmann, S. Assessment of voltage instrument transformers accuracy for har-monic measurements in transmission systems. In Proceedings of the International Conference on Harmonics and Quality of Power, Belo Horizonte, Brazil, 16–19 October 2016; pp. 152–157. [Google Scholar]
- Škundrić, S.; Kovačević, D.; Naumović-Vuković, D. The role and importance of software application in instrument transformers accuracy testing. In Proceedings of the 18th IMEKO World Congress 2006: Metrology for a Sustainable Development, Rio de Janeiro, Brazi, 17–22 September 2006. [Google Scholar]
- Asprou, M.; Kyriakides, E.; Albu, M. Bad data detection considering the accuracy of instrument transformers. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Asprou, M.; Kyriakides, E.; Albu, M. The effect of instrument transformer accuracy class on the WLS state estimator accuracy. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar]
- Mingotti, A.; Peretto, L.; Tinarelli, R. Accuracy Evaluation of an Equivalent Synchronization Method for Assessing the Time Reference in Power Networks. IEEE Trans. Instrum. Meas. 2017, 67, 600–606. [Google Scholar] [CrossRef]
- Murray, R.; De Kock, J. Instrument transformers influence on harmonic measurements for grid code compliance. In Proceedings of the 2018 IEEE 4th Global Electromagnetic Compatibility Conference (GEMCCON), Stellenbosch, South Africa, 7–9 November 2018; pp. 1–5. [Google Scholar]
- Draxler, K.; Stybliková, R. Influence of instrument transformers on quality of electrical power and energy meas-urement. In Proceedings of the IEEE International Symposium on Industrial Electronics, Vigo, Spain, 4–7 June 2007; pp. 1317–1321. [Google Scholar]
- Filipović-Grčić, D.; Filipović-Grčić, B.; Krajtner, D. Frequency response and harmonic distortion testing of inductive voltage transformer used for power quality measurements. Procedia Eng. 2017, 202, 159–167. [Google Scholar] [CrossRef]
- Kaczmarek, M.; Nowicz, R. Application of instrument transformers in power quality assessment. In Proceedings of the International Symposium: Modern Electric Power Systems, Wroclaw, Poland, 20–22 September 2010. [Google Scholar]
- Mingotti, A.; Peretto, L.; Tinarelli, R.; Ghaderi, A. Uncertainty sources analysis of a calibration system for the accu-racy vs. temperature verification of voltage transformers. J. Phys. Conf. Ser. 2018, 1065, 052041. [Google Scholar]
- Litvinov, S.N.; Lebedev, V.D.; Smirnov, N.N.; Tyutikov, V.V.; Makhsumov, I.B. Physical simulation of heat ex-change between 6(10) kV voltage instrument transformer and its environment with natural convection and insolation. MATEC Web Conf. 2018, 194, 1035. [Google Scholar]
- Sivan, V.; Robalino, D.M.; Mahajan, S.M. Measurement of Temperature Gradients Inside a Medium Voltage Current Transformer. In Proceedings of the 2007 39th North American Power Symposium, Las Cruces, NM, USA, 30 September–2 October 2007; pp. 242–245. [Google Scholar]
- Lesniewska, E.; Koszmider, A. Influence of the interaction of voltage and current parts of a combined instrument transformer on its measurement properties. IEEE Proc. Sci. Meas. Technol. 2004, 151, 229–234. [Google Scholar] [CrossRef]
- Xiuke, Y.; Yang, S.; Cunzhan, Y.; Yanli, Q. Analysis of 3D electric field and insulation optimization of oil-immersed inverted current transformer. In Proceedings of the 2011 International Conference on Electrical Machines and Systems, Beijing, China, 20–23 August 2011; pp. 1–4. [Google Scholar]
- Yan, X.; Sun, Y.; Yu, C.; Xie, D. Electric field analysis and optimal design of main insulation for oil-immersed in-verted current transformers. Trans. China Electrotech. Soc. 2014, 29, 37–43. [Google Scholar]
- International Standardization Organization. IEC 61869-2: 2012. Instrument Transformers—Part 2: Additional Requirements for Current Transformers; International Standardization Organization: Geneva, Switzerland, 2012. [Google Scholar]
- International Standardization Organization. IEC 61869-3: 2011. Instrument Transformers—Part 3: Additional Requirements for Inductive Voltage Transformers; International Standardization Organization: Geneva, Switzerland, 2011. [Google Scholar]
- International Standardization Organization. IEC 61869-6: 2016. Instrument Transformers—Part 6: Additional General Requirements for Low-Power Instrument Transformers; International Standardization Organization: Geneva, Switzerland, 2016. [Google Scholar]
- Da Silva, A.M.; Oleskovicz, M.; Fernandes, R.A.S. Comparative analysis between the classic power capacitors model used in simulations and the real power capacitors response tested in a controlled laboratory environment. In Proceedings of the 2014 16th International Conference on Harmonics and Quality of Power (ICHQP), Bucharest, Romania, 25–28 May 2014; pp. 813–817. [Google Scholar]
- Gaur, A.; Agarwal, T.; Asselberghs, I.; Radu, I.; Heyns, M.; Lin, D. A MOS capacitor model for ultra-thin 2D semi-conductors: The impact of interface defects and channel resistance. 2D Mater. 2020, 7, 035018. [Google Scholar]
- Montillet, J. The relativistic capacitor model and the mach-lorentz theory. J. Br. Interplanet. Soc. 2017, 70, 385–393. [Google Scholar]
- Bretterklieber, T.; Neumayer, M.; Flatscher, M. Holistic system modeling of capacitive sensors: From sensor circuitry to calibration. In Proceedings of the 2018 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Houston, TX, USA, 14–17 May 2018; pp. 1–6. [Google Scholar]
- Bolduc, L.; Bouchard, B.; Beaulieu, G. Capacitive divider substation. IEEE Trans. Power Deliv. 1997, 12, 1202–1209. [Google Scholar] [CrossRef]
- Kitak, P.; Ticar, I.; Pihler, J.; Glotic, A.; Popovic, J.; Biro, O.; Preis, K. Application of the hybrid multiobjective opti-mization methods on the capacitive voltage divider. IEEE Trans. Magn. 2009, 45, 1594–1597. [Google Scholar]
- Zong, W.; Li, Y.; Cheng, Y.; Zhang, C.; Xue, Y.; Li, G. The design of a wide-band high-voltage divider. In Proceedings of the 2010 International Conference on Power System Technology: Technological Innovations Making Power Grid Smarter, Hangzhou, China, 24–28 October 2010. [Google Scholar]
- Gonzalez, C.; Weckx, S.; De Rybel, T.; Driesen, J. Dynamic thermal modeling of voltage divider capacitive cou-pling. IEEE Trans. Power Deliv. 2016, 31, 1015–1025. [Google Scholar]
- Hobejogi, T.; Biela, J. Coaxial capacitive voltage divider with high division ratio for high voltage pulses with very fast rise times. In Proceedings of the 2011 IEEE Pulsed Power Conference, Chicago, IL, USA, 19–23 June 2011; pp. 313–318. [Google Scholar]
- Ghaderi, A.; Mingotti, A.; Lama, F.; Peretto, L.; Tinarelli, R. Effects of Temperature on MV Cable Joints Tan Delta Measurements. IEEE Trans. Instrum. Meas. 2019, 68, 3892–3898. [Google Scholar] [CrossRef]
- Peretto, L.; Tinarelli, R.; Ghaderi, A.; Mingotti, A.; Mazzanti, G.; Valtorta, G.; Amoroso, G.; Danesi, S. Monitoring Cable current and Laying Environment Parameters for Assessing the Aging Rate of MV Cable Joint Insulation. In Proceedings of the 2018 IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Cancun, Mexico, 21–24 October 2018; pp. 390–393. [Google Scholar]
- Ma, G.; Xie, Q.; Whittaker, A. Seismic performance assessment of an ultra-high–voltage power transformer. Earthq. Spectra 2019, 55, 423–445. [Google Scholar]
- Ranga, C.; Kumar, A.; Chandel, R. Influence of electrical and thermal ageing on the mineral insulating oil perfor-mance for power transformer applications. Insight Non Destr. Test. Cond. Monit. 2020, 62, 222–231. [Google Scholar]
- Shanker, T.B.; Vaidhyanathan, V.; Mohamed, A.S. Comparison of partial discharge performance of identical gen-erator transformers in a thermal power station by acoustic emission technique-case studies. In Proceedings of the 2019 International Conference on High Voltage Engineering and Technology, Hyderabad, India, 7–8 February 2019. [Google Scholar]
- Batalovic, M.; Matoruga, H.; Berberovic, S.; Matoruga, M. Influence of environmental stresses on high voltage polymer rod type insulator performances. In Proceedings of the 2018 3rd International Conference on Smart and Sustaina-ble Technologies, Split, Croatia, 26–29 June 2018. [Google Scholar]
- Du, B.X.; Liu, Y. High frequency harmonic components of leakage current for monitoring insulator performance in cold fog. In Proceedings of the 2008 IEEE/PES Transmission and Distribution Conference and Exposition, Chicago, IL, USA, 21–24 April 2008; pp. 1–4. [Google Scholar]
- Da Luz, M.V.F.; Molina, F.H.; Arend, E.R. Study of insulator performance under contaminated conditions using a 3D formulation of quasi-static electric fields. In Proceedings of the Digests of the 2010 14th Biennial IEEE Conference on Electromagnetic Field Computation, Chicago, IL, USA, 9–12 May 2010; p. 1. [Google Scholar]
- Wang, P.; Tangyun, X.; Yong, Z.; Shen, Z. Factors affecting performance of cylindrical capacitive ring divider. In Proceedings of the 2018 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Houston, TX, USA, 14–17 May 2018; pp. 1–6. [Google Scholar]
- Elg, A.; Passon, S.; Meisner, J.; Hällström, J. High voltage topologies for very fast transient measurements. In Proceedings of the 21st International Symposium on High Voltage Engineering; Springer: Cham, Switzerland, 2020; pp. 1316–1327. [Google Scholar]
- Rybeland, T.D.; Vandewinckel, E. Guarding Methods for High Voltage Measurements. European Patent 2,508,898, 2012. [Google Scholar]
- Zhu, T.; Nie, Y.; Li, Z.; Lin, X. Parameter estimation method of stray capacitance of capacitive voltage transformer based on improved particle swarm optimization algorithm. Autom. Electr. Power Syst. 2020, 44, 178–186. [Google Scholar]
- Yang, C.; Wu, M.; Jian, C.; Yu, J. The stray capacitance on precision of high-voltage measurement. In Proceedings of the 2009 IEEE Intrumentation and Measurement Technology Conference, Singapore, 5–7 May 2009; pp. 249–253. [Google Scholar]
- Mingotti, A.; Peretto, L.; Tinarelli, R. A Simple Modelling Procedure of Rogowski Coil for Power Systems Applications. In Proceedings of the 2019 IEEE 10th International Workshop on Applied Measurements for Power Systems (AMPS), Aachen, Germany, 25–27 September 2019; pp. 1–5. [Google Scholar]
- Mingotti, A.; Peretto, L.; Tinarelli, R.; Zhang, J. Use of COMTRADE Fault Current Data to Test Inductive Current Transformers. In Proceedings of the 2019 II Workshop on Metrology for Industry 4.0 and IoT (MetroInd4.0&IoT), Naples, Italy, 4–6 June 2019; pp. 103–107. [Google Scholar]
- Jaschke, C.; Schegner, P. Metrological frequency response analysis of a high current instrument transformer. In Proceedings of the 2015 9th International Conference on Sensing Technology (ICST), Auckland, New Zealand, 8–10 December 2015; pp. 640–645. [Google Scholar]
- Makky, A.A.M.; Abo-Zied, H.; Abdelbar, F.N.; Mutschler, P. Design of the instrument current transformer for high frequency high power applications. In Proceedings of the 2008 12th International Middle East Power System Conference, Aswan, Egypt, 12–15 March 2008; pp. 230–233. [Google Scholar]
- Campos, A.C.; Cardoso, K.R.; Cruz, V.P.; Fortes, M.Z. Frequency Response of Capacitive Voltage Dividers for Evaluation of Harmonic Components. In Proceedings of the 2019 IEEE PES Innovative Smart Grid Technologies Conference—Latin America (ISGT Latin America), Gramado, Brazil, 15–18 September 2019; pp. 1–6. [Google Scholar]
- Prochazka, R.; Hlavacek, J.; Knenicky, M.; Mahmoud, R. Determination of frequency characteristics of high voltage di-viders in frequency domain. In Proceedings of the 2016 17th International Scientific Conference on Electric Power Engineering (EPE), Prague, Czech, 16–18 May 2016; pp. 1–4. [Google Scholar]
- Kovačević, U.D.; Stanković, K.Đ.; Kartalović, N.M.; Lončar, B.B. Design of capacitive voltage divider for measuring ultrafast voltages. Int. J. Electr. Power Energy Syst. 2018, 99, 426–433. [Google Scholar] [CrossRef]




| Frequency Band (Hz) | Accuracy (ppm + mV) |
|---|---|
| 10–31 | 135 + 300 |
| 32–330 | 80 + 200 |
| 300–33 k | 80 + 100 |
| 30 k–100 k | 150 + 200 |
| 100 k–330 k | 400 + 1 |
| 300 k–1 M | 0.26% + 5 |
| Frequency Band (Hz) | Accuracy (ppm + mV) |
|---|---|
| 10–31 | 190 + 3 |
| 32–330 | 120 + 2 |
| 300–10 k | 80 + 1 |
| 10 k–33 k | 90 + 2 |
| 30 k–100 k | 300 + 3 |
| 100 k–330 k | 860 + 50 |
| 300 k–1 M | 0.95% + 130 |
| LPVT | AC (/) | ||||
|---|---|---|---|---|---|
| A | 20,000/ | 2/ | 0.5 | 50/60 | −5 to + 40 |
| B | 20,000/ | 3.25/ | 0.5 | 50/60 | −40 to + 80 |
| f (Hz) | N (/) | ||
|---|---|---|---|
| 10 | 1.25 | 200 | 200 |
| 50 | 1.25 | 200 | 200 |
| 100 | 1.25 | 200 | 200 |
| 200 | 1.25 | 200 | 200 |
| 500 | 1.25 | 400 | 200 |
| 1000 | 1.25 | 400 | 200 |
| 5000 | 1.25 | 400 | 200 |
| 10,000 | 1.25 | 400 | 200 |
| 20,000 | 1.25 | 400 | 200 |
| 50,000 | 5 | 400 | 200 |
| 80,000 | 5 | 400 | 200 |
| 90,000 | 5 | 400 | 200 |
| 95,000 | 5 | 400 | 200 |
| 100,000 | 12.5 | 400 | 200 |
| 105,000 | 12.5 | 400 | 20 |
| 120,000 | 12.5 | 400 | 20 |
| 150,000 | 12.5 | 400 | 20 |
| 200,000 | 12.5 | 400 | 20 |
| 250,000 | 12.5 | 400 | 20 |
| 300,000 | 12.5 | 400 | 20 |
| 350,000 | 25 | 400 | 20 |
| 400,000 | 25 | 400 | 20 |
| 450,000 | 25 | 400 | 20 |
| 500,000 | 25 | 400 | 20 |
| 700,000 | 125 | 400 | 20 |
| 1,000,000 | 125 | 400 | 20 |
| 100 | 106.6 | 36.80 | 35.8 |
| 500 | 93.6 | 36.74 | 35.55 |
| 1000 | 67.8 | 36.64 | 35.4 |
| 10,000 | 2.15 | 36.31 | 35.1 |
| 50,000 | 425.1 | 36.07 | 34.9 |
| 100,000 | 370.1 | 35.97 | 34.7 |
| 300,000 | 354.6 | 35.79 | 34.57 |
| 1,000,000 | 364.6 | 35.58 | 34.37 |
| f (Hz) | |||
|---|---|---|---|
| 100 | 39.72 | 10.65 | 8.28 |
| 500 | 39.63 | 10.57 | 8.23 |
| 1000 | 39.58 | 10.56 | 8.16 |
| 10,000 | 39.35 | 10.43 | 8.08 |
| 50,000 | 38.46 | 10.32 | 8.07 |
| 100,000 | 36.3 | 10.29 | 8.06 |
| 300,000 | 21.13 | 10.27 | 7.96 |
| 1,000,000 | 4.607 | 10.19 | 7.91 |
| 100 | 4.325 | 1.494 |
| 500 | 8.664 | 3.402 |
| 1000 | 4.344 | 2.349 |
| 10,000 | 4.383 | 7.530 |
| 50,000 | 8.825 | 8.182 |
| 100,000 | 4.425 | 4.763 |
| 300,000 | 1.482 | 1.664 |
| 1,000,000 | 4.473 | 4.837 |
| 100 | 1.494 | 4.008 |
| 500 | 3.011 | 8.034 |
| 1000 | 1.507 | 4.022 |
| 10,000 | 1.526 | 4.046 |
| 50,000 | 3.084 | 82.79 |
| 100,000 | 1.547 | 43.86 |
| 300,000 | 5.166 | 25.12 |
| 1,000,000 | 1.562 | 34.62 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mingotti, A.; Costa, F.; Pasini, G.; Peretto, L.; Tinarelli, R. Modeling Capacitive Low-Power Voltage Transformer Behavior over Temperature and Frequency. Sensors 2021, 21, 1719. https://doi.org/10.3390/s21051719
Mingotti A, Costa F, Pasini G, Peretto L, Tinarelli R. Modeling Capacitive Low-Power Voltage Transformer Behavior over Temperature and Frequency. Sensors. 2021; 21(5):1719. https://doi.org/10.3390/s21051719
Chicago/Turabian StyleMingotti, Alessandro, Federica Costa, Gaetano Pasini, Lorenzo Peretto, and Roberto Tinarelli. 2021. "Modeling Capacitive Low-Power Voltage Transformer Behavior over Temperature and Frequency" Sensors 21, no. 5: 1719. https://doi.org/10.3390/s21051719
APA StyleMingotti, A., Costa, F., Pasini, G., Peretto, L., & Tinarelli, R. (2021). Modeling Capacitive Low-Power Voltage Transformer Behavior over Temperature and Frequency. Sensors, 21(5), 1719. https://doi.org/10.3390/s21051719









