Practical Model for Energy Consumption Analysis of Omnidirectional Mobile Robot
Abstract
1. Introduction
2. Related Works
3. Energy Modeling
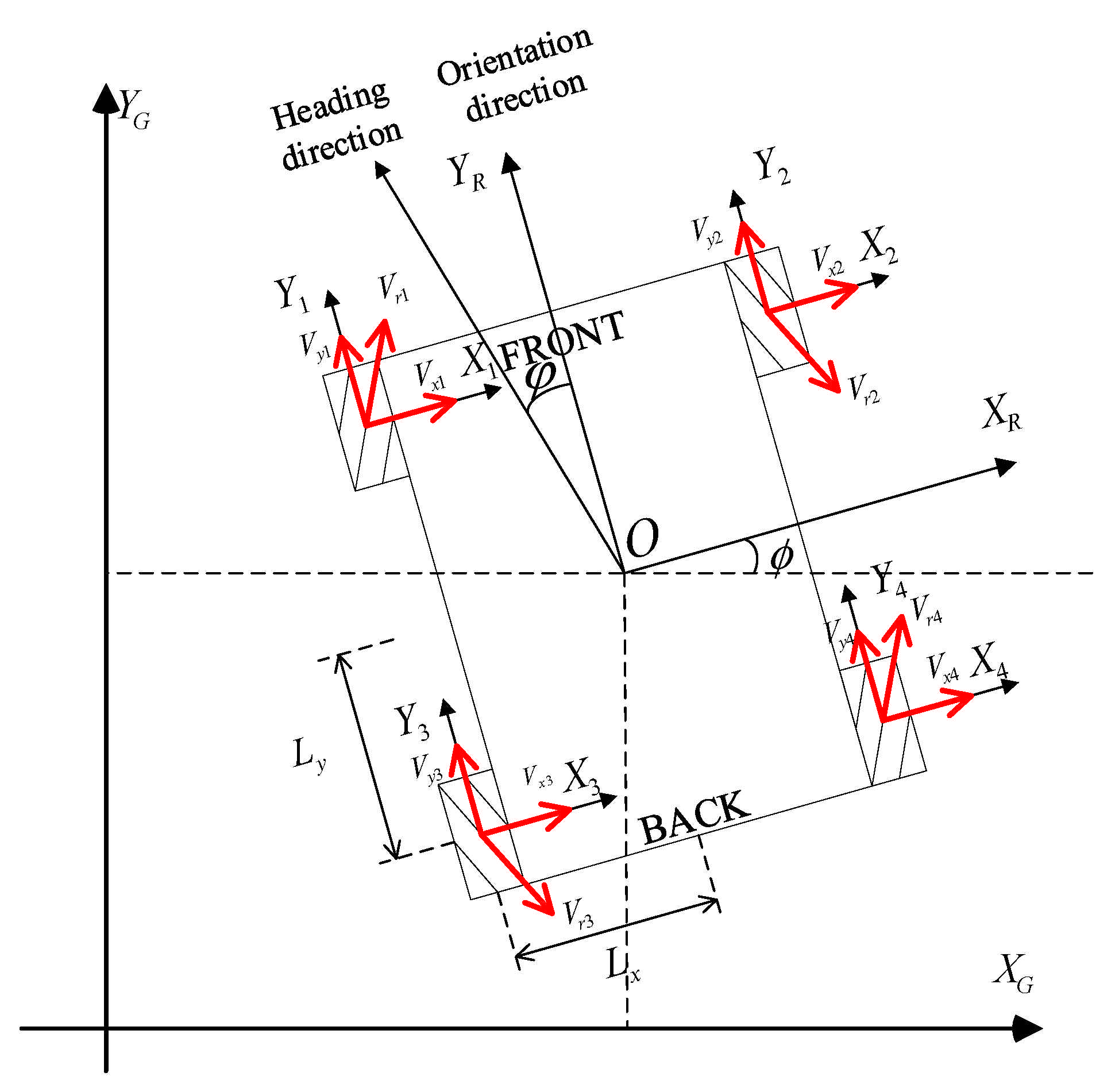
3.1. Motion System
3.2. Control System
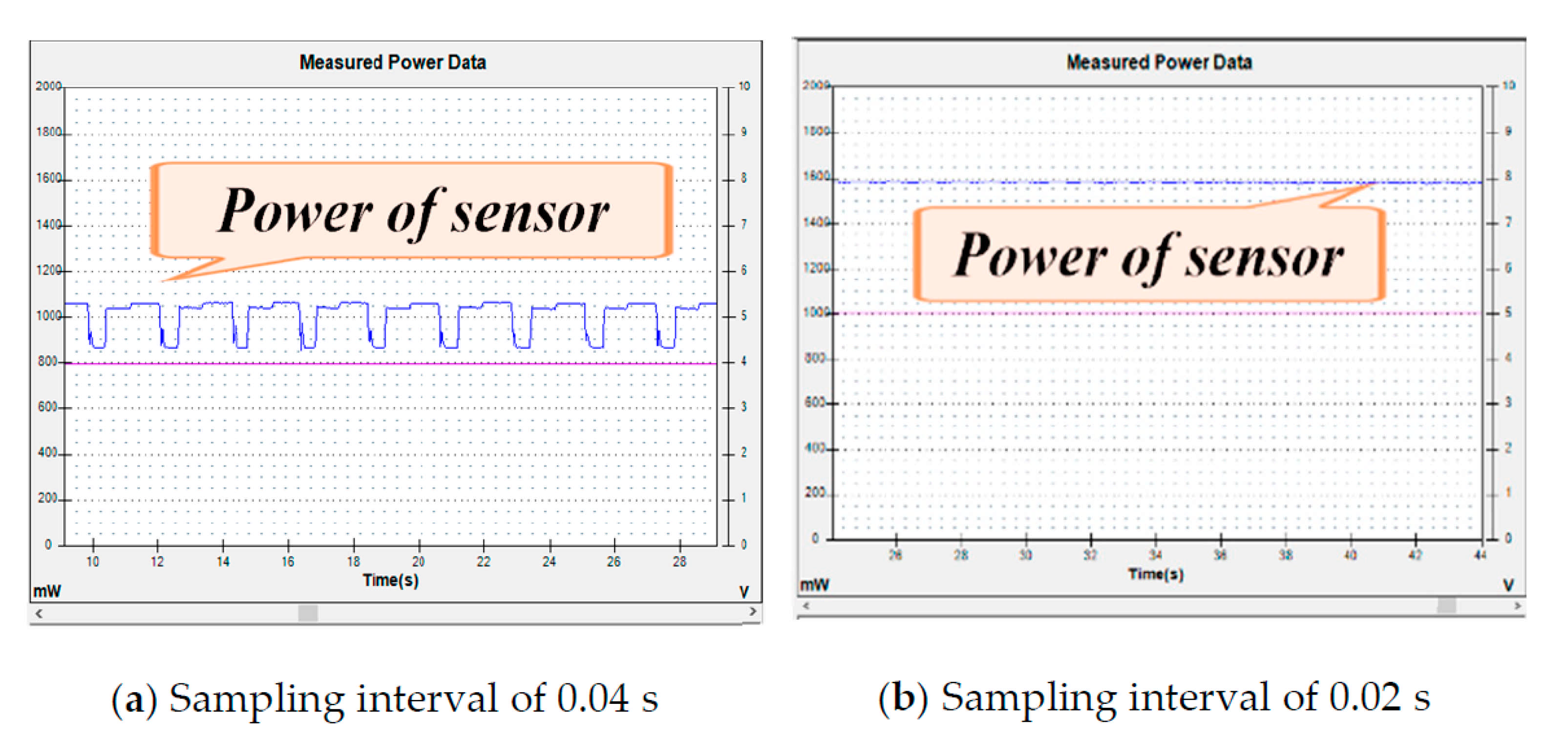
3.3. Sensor System
4. The Influence of Various Factors on the Power Consumption of the Robot
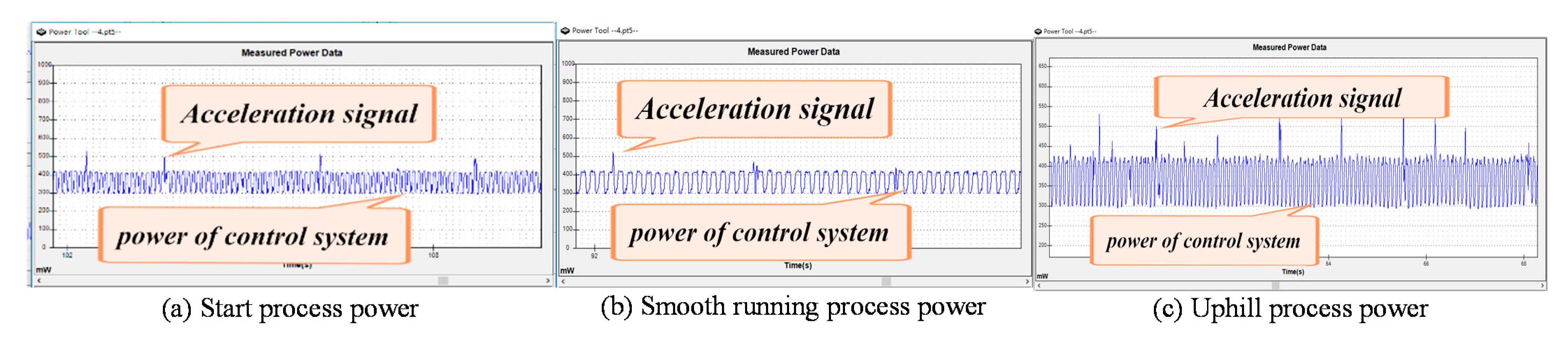
4.1. Research on the Power Consumption of Robots Uphill and Downhill
4.1.1. Power Analysis of Robot Uphill Process
4.1.2. Power Analysis of Robot Downhill Process
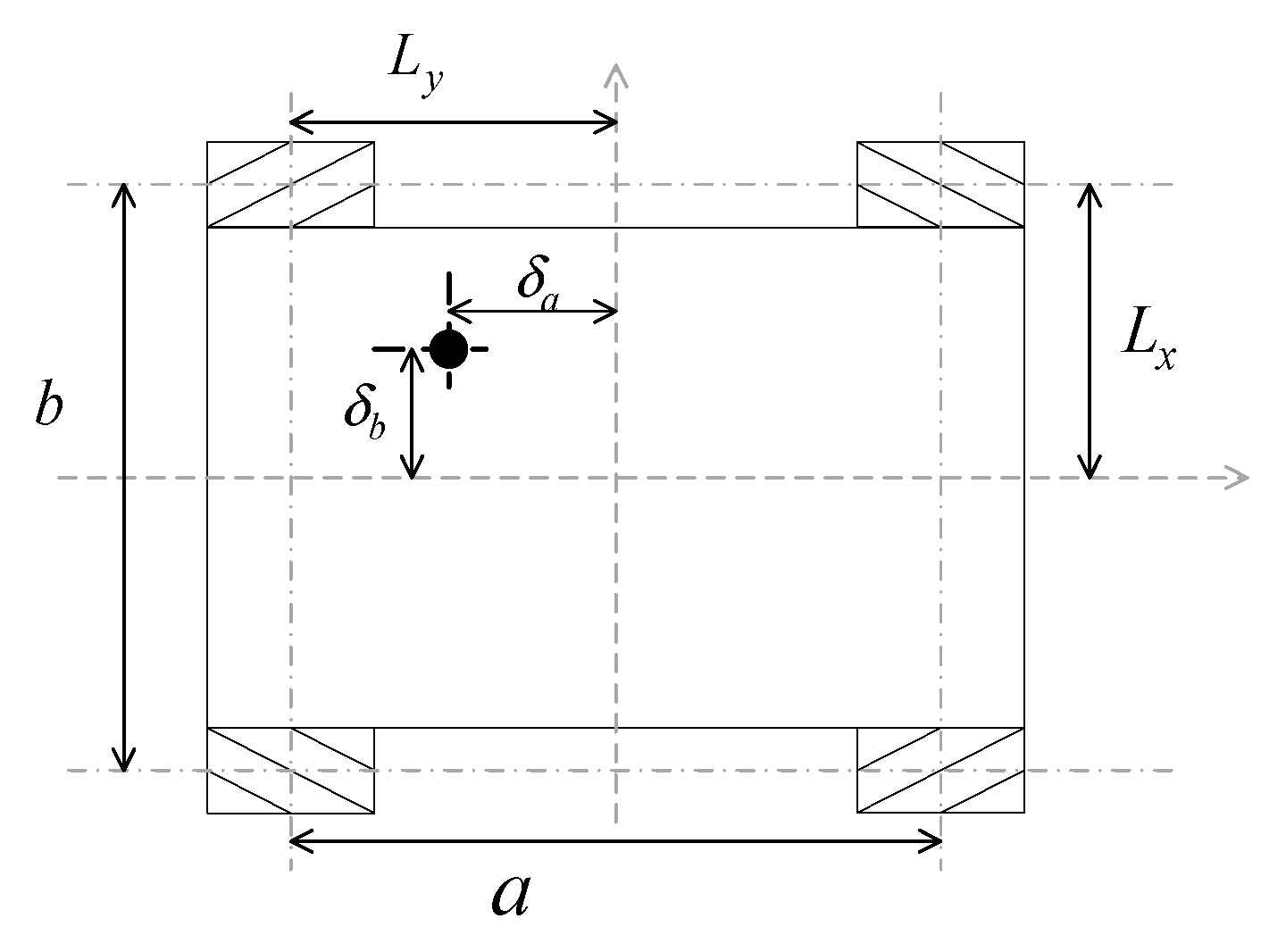
4.2. The Influence of the Center of Gravity on the Power Consumption of the Robot
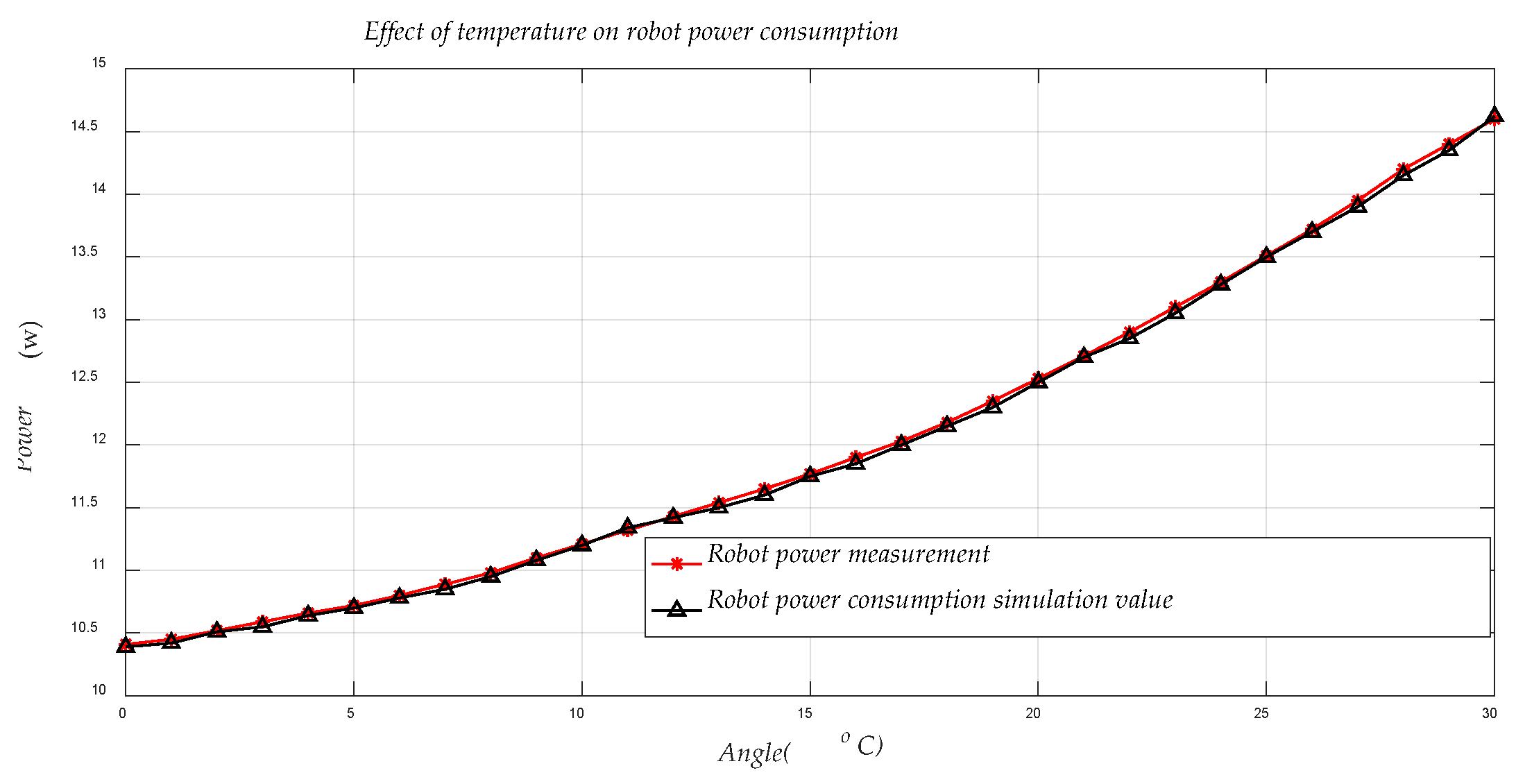
4.3. The Effect of Temperature on the Power Consumption of the Robot
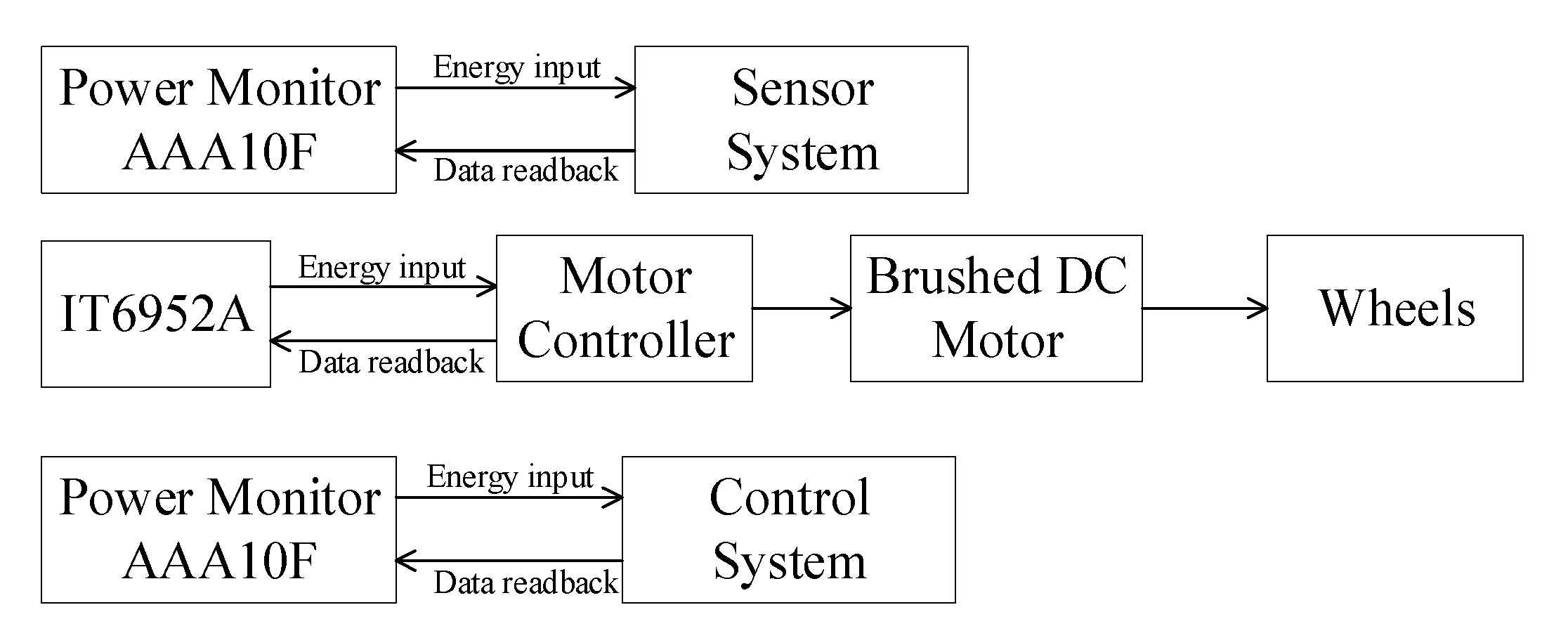
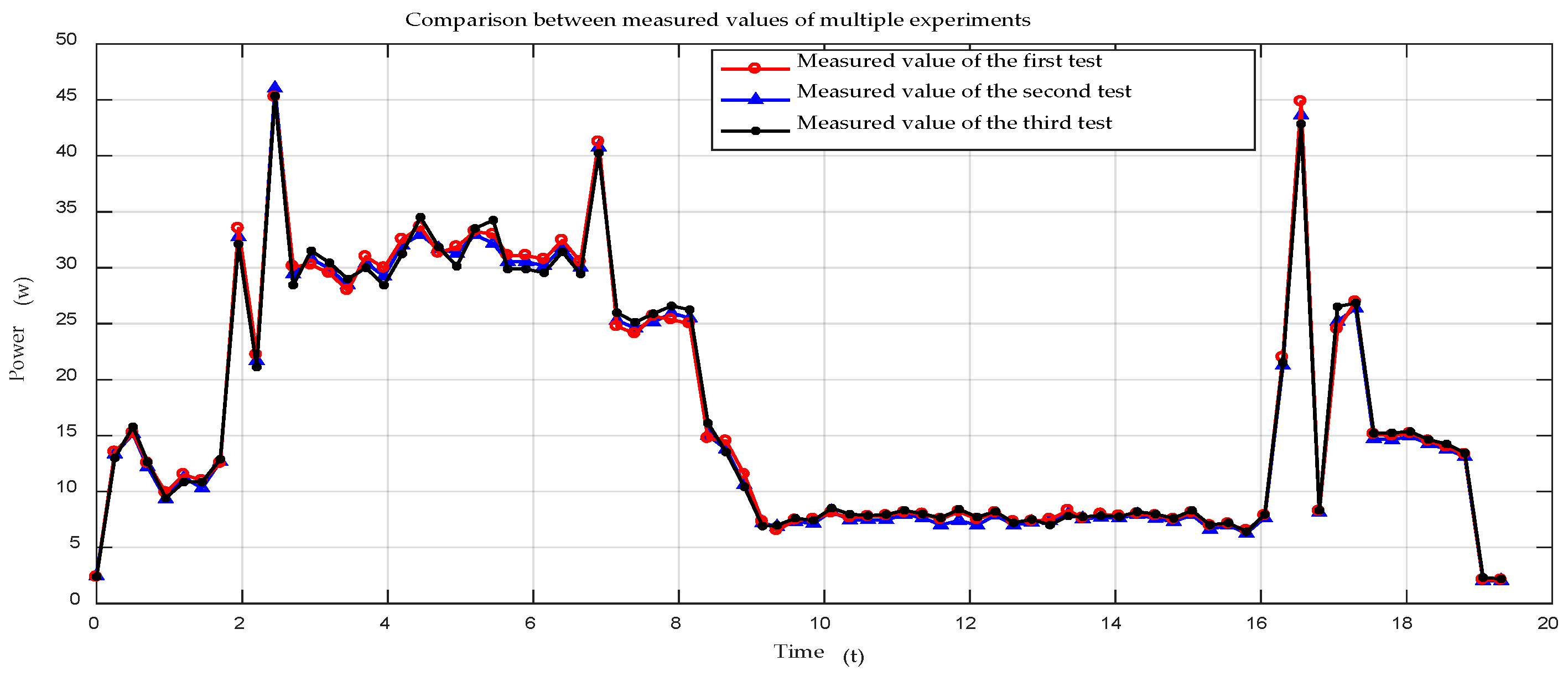
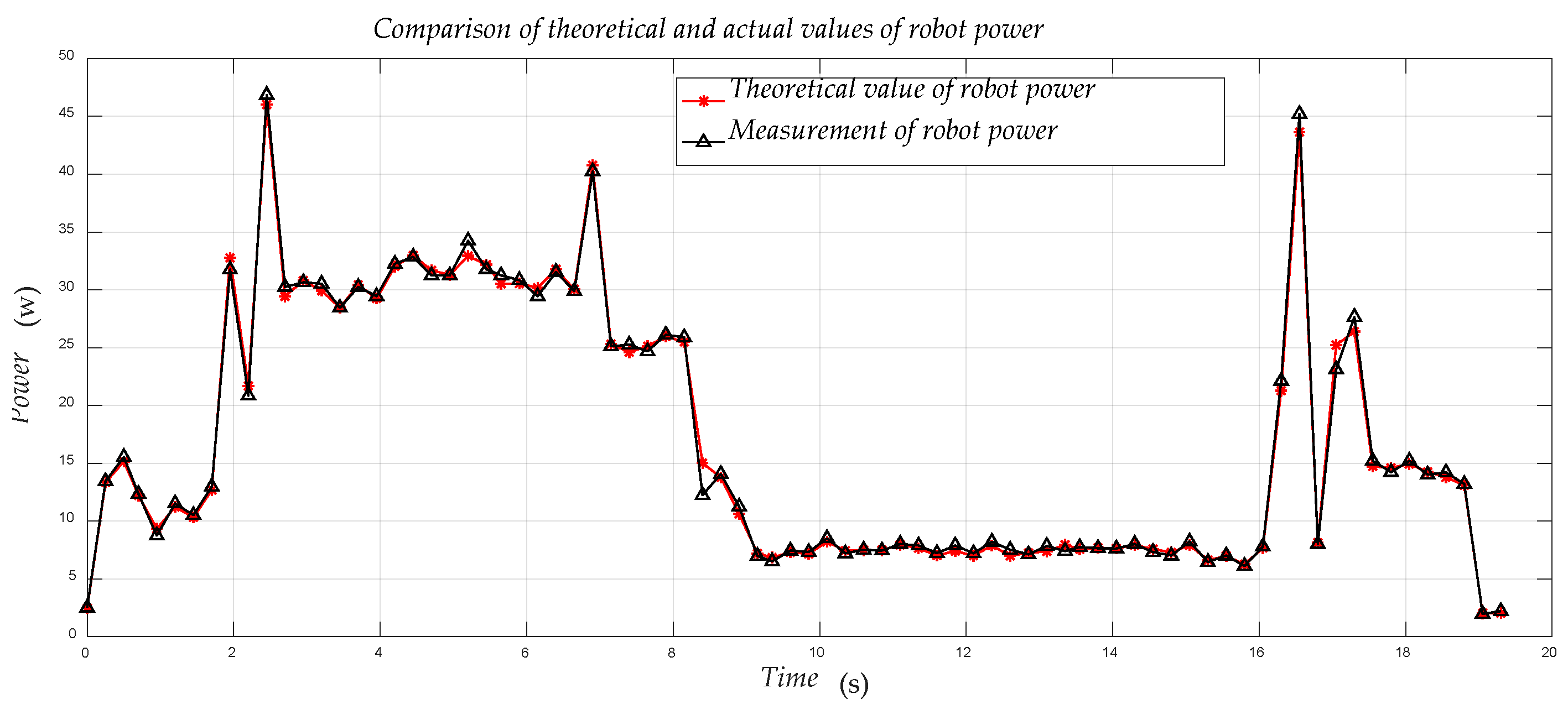
5. Simulation and Experimental Verification
5.1. Motion System
5.2. Control System
5.3. Sensor System
6. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- AdăscăliĠei, F.; Doroftei, I. Practical applications for mobile robots based on Mecanum wheels—A systematic survey. Rom. Rev. Precis. Mech. Opt. Mechatron. 2011, 40, 21–29. [Google Scholar]
- Dogru, S.; Marques, L. A Physics-Based Power Model for Skid-Steered Wheeled Mobile Robots. IEEE Trans. Robot. 2018, 34, 421–433. [Google Scholar] [CrossRef]
- Olaf, D.; Aparna, B.; Glen, B.; Johan, P.; Sylvester, T. Improved Mecanum wheel design for omni-directional robots. In Proceedings of the 2002 Australasian Conference on Robotics and Automation, Auckland, New Zealand, 27–29 November 2002; pp. 117–121. [Google Scholar]
- Xie, C.L.; Scheifele, W.X.; Stol, K.A. Heavy-duty omnidirectional Mecanum-wheeled robot for autonomous navigation: System development and simulation realization. In Proceedings of the 2015 IEEE International Conference on Mechatronics and Automation (ICMA 2015), Beijing, China, 2–5 August 2015; pp. 256–261. [Google Scholar]
- Xie, L.; Herberger, W.; Xu, W.; Stol, K.A. Experimental validation of energy consumption model for the four-wheeled omnidirectional Mecanum robots for energy-optimal motion control. In Proceedings of the 2016 IEEE 14th International Workshop on Advanced Motion Control (AMC), Auckland, New Zealand, 22–24 April 2016; pp. 565–572. [Google Scholar]
- Tampubolon, M.; Pamungkas, L.; Chiu, H.-J.; Liu, Y.-C.; Hsieh, Y.-C. Dynamic Wireless Power Transfer for Logistic Robots. Energies 2018, 11, 527. [Google Scholar] [CrossRef]
- Touzout, W.; Benmoussa, Y.; Benazzouz, D.; Moreac, E.; Diguet, J.-P. Unmanned surface vehicle energy consumption modelling under various realistic disturbances integrated into simulation environment. Ocean Eng. 2021, 222, 108560. [Google Scholar] [CrossRef]
- Kim, H.; Kim, B.K. Online Minimum-Energy Trajectory Planning and Control on a Straight-Line Path for Three-Wheeled Omnidirectional Mobile Robots. IEEE Trans. Ind. Electron. 2013, 61, 4771–4779. [Google Scholar] [CrossRef]
- Phan, D.; Bab-Hadiashar, A.; Lai, C.Y.; Crawford, B.; Hoseinnezhad, R.; Jazar, R.N.; Khayyam, H. Intelligent energy management system for conventional autonomous vehicles. Energy 2020, 191, 116476. [Google Scholar] [CrossRef]
- Tao, Y.; Huang, M.; Chen, Y.; Yang, L. Orderly charging strategy of battery electric vehicle driven by real-world driving data. Energy 2020, 193, 116806. [Google Scholar] [CrossRef]
- Canfield, S.L.; Hill, T.W.; Zuccaro, S.G. Prediction and Experimental Validation of Power Consumption of Skid-Steer Mobile Robots in Manufacturing Environments. J. Intell. Robot. Syst. 2018, 94, 825–839. [Google Scholar] [CrossRef]
- Chuy, O.; Collins, E.G.; Yu, W.; Ordonez, C. Power modeling of a skid steered wheeled robotic ground vehicle. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 4118–4123. [Google Scholar]
- Vepsäläinen, J.; Otto, K.; Lajunen, A.; Tammi, K. Computationally efficient model for energy demand prediction of electric city bus in varying operating conditions. Energy 2019, 169, 433–443. [Google Scholar] [CrossRef]
- Berenz, V.; Tanaka, F.; Suzuki, K. Autonomous battery management for mobile robots based on risk and gain assessment. Artif. Intell. Rev. 2011, 37, 217–237. [Google Scholar] [CrossRef]
- Cai, W.; Zhang, M.; Zheng, Y.R. Task Assignment and Path Planning for Multiple Autonomous Underwater Vehicles Using 3D Dubins Curves. Sensors 2017, 17, 1607. [Google Scholar] [CrossRef]
- Sadrpour, A.; Jin, J.; Ulsoy, A.G. Experimental validation of mission energy prediction model for unmanned ground vehicles. In Proceedings of the 2013 American Control Conference, Washington, DC, USA, 17–19 June 2013; pp. 5960–5965. [Google Scholar]
- Parasuraman, R.; Kershaw, K.; Pagala, P.; Ferre, M. Model Based Online Energy Prediction System for Semi-autonomous Mobile Robots. In Proceedings of the 5th International Conference on Intelligent Systems, Modelling and Simulation, Langkawi, Malaysia, 27–29 January 2014; pp. 411–416. [Google Scholar] [CrossRef]
- Broderick, J.; Hartner, J.; Tilbury, D.M.; Atkins, E.M. Modeling and simulation of an unmanned ground vehicle power system. SPIE Def. Secur. 2014, 9084, 908406. [Google Scholar] [CrossRef]
- Mei, Y.; Lu, Y.-H.; Hu, Y.; Lee, C. A case study of mobile robot’s energy consumption and conservation techniques. In Proceedings of the 12th International Conference on Advanced Robotics, Seattle, WA, USA, 18–20 July 2005; pp. 492–497. [Google Scholar]
- Brateman, J.; Xian, C.; Lu, Y.-H. Energy-efficient scheduling for autonomous mobile robots. In Proceedings of the 2006 IFIP International Conference on Very Large Scale Integration, Nice, France, 16–18 October 2006; pp. 361–366. [Google Scholar]
- Mei, Y.; Lu, Y.-H.; Lee, C.; Hu, Y.C. Energy-efficient mobile robot exploration. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006; pp. 505–511. [Google Scholar]
- Ooi, C.C.; Schindelhauer, C. Minimal Energy Path Planning for Wireless Robots. In Proceedings of the First International Conference on Robot Communication and Coordination, Athens, Greece, 15–17 October 2007; pp. 309–321. [Google Scholar] [CrossRef]
- Sun, Z.; Reif, J. On finding energy-minimizing paths on terrains. IEEE Trans. Robot. 2005, 21, 102–114. [Google Scholar] [CrossRef][Green Version]
- Broderick, J.A.; Tilbury, D.M.; Atkins, E.M. Optimal coverage trajectories for a UGV with tradeoffs for energy and time. Auton. Robot. 2013, 36, 257–271. [Google Scholar] [CrossRef]
- Zhang, L.; Kim, J.; Sun, J. Energy Modeling and Experimental Validation of Four-Wheel Mecanum Mobile Robots for Energy-Optimal Motion Control. Symmetry 2019, 11, 1372. [Google Scholar] [CrossRef]
- Hou, L.; Zhang, L.; Kim, J. Energy Modeling and Power Measurement for Mobile Robots. Energies 2018, 12, 27. [Google Scholar] [CrossRef]
- Kim, C.H.; Kim, B.K. Energy-Saving 3-Step Velocity Control Algorithm for Battery-Powered Wheeled Mobile Robots. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 2375–2380. [Google Scholar]
- Kim, C.H.; Kim, B.K. Minimum-energy translational trajectory generation for differential-driven wheeled mobile robots. J. Intell. Robot. Syst. 2007, 49, 367–383. [Google Scholar] [CrossRef]
- Kim, H.; Kim, B.K. Minimum-energy trajectory planning and control on a straight line with rotation for three-wheeled omni-directional mobile robots. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Algarve, Portugal, 7–12 October 2012; pp. 3119–3124. [Google Scholar]
- Xie, L.; Henkel, C.; Stol, K.; Xu, W. Power-minimization and energy-reduction autonomous navigation of an omnidirectional Mecanum robot via the dynamic window approach local trajectory planning. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418754563. [Google Scholar] [CrossRef]
- Sadrpour, A.; Jin, J.; Ulsoy, A.G. Mission energy prediction for unmanned ground vehicles. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 2229–2234. [Google Scholar]
- Morales, J.; Martínez, J.L.; Mandow, A.; Garcia-Cerezo, A.; Pedraza, S. Power Consumption Modeling of Skid-Steer Tracked Mobile Robots on Rigid Terrain. IEEE Trans. Robot. 2009, 25, 1098–1108. [Google Scholar] [CrossRef]
- Liu, J.; Chou, P.; Bagherzadeh, N.; Kurdahi, F. Power-aware scheduling under timing constraints for mission-critical embedded systems. In Proceedings of the 26th ACM/IEEE Design Automation Conference, Las Vegas, NV, USA, 25–29 June 2001; pp. 840–845. [Google Scholar]
- Iagnemma, K.; Dubowsky, S. Traction Control of Wheeled Robotic Vehicles in Rough Terrain with Application to Planetary Rovers. Int. J. Robot. Res. 2004, 23, 1029–1040. [Google Scholar] [CrossRef]
- Silvaand, F.; Tenreiro-Machado, J. Energy analysis during biped walking. In Proceedings of the 1999 IEEE International Conference on Robotics and Automation, Detroit, MI, USA, 10–15 May 1999; pp. 59–64. [Google Scholar]
- Saito, M.; Fukaya, M.; Iwasaki, T. Serpentine locomotion with robotic snakes. IEEE Control Syst. Mag. 2002, 22, 64–81. [Google Scholar]
- Morales, J.; Martinez, J.L.; Mandow, A.; García-Cerezo, A.J.; Gómez-Gabriel, J.M.; Pedraza, S. Power Analysis for a Skid-Steered Tracked Mobile Robot. In Proceedings of the 2006 IEEE International Conference on Mechatronics, Luoyang, China, 25–28 June 2006; pp. 420–425. [Google Scholar]
- Mei, Y.; Lu, Y.H.; Hu, Y.C.; Lee, C.G. Deployment of mobile robots with energy and timing constraints. IEEE Trans. Robot. 2006, 22, 507–522. [Google Scholar]






| Front | Back | Mean | |
|---|---|---|---|
| M1 (Left motor) | |||
| 0.0019 | 0.0021 | 0.0020 | |
| 1.5223 | 1.5325 | 1.5274 | |
| M2 (Left motor) | |||
| 0.0022 | 0.0026 | 0.0024 | |
| 1.5445 | 1.5326 | 1.5385 |
| Front | Back | Mean | |
|---|---|---|---|
| M1 (Left motor) | |||
| 1.25 | 1.56 | 1.405 | |
| 1.32 | 1.44 | 1.38 | |
| M2 (Left motor) | |||
| 1.35 | 1.37 | 1.36 | |
| 1.38 | 1.35 | 1.365 |
| Parameter | Value |
|---|---|
| 0.15 | |
| 0.08 | |
| 0.01 | |
| 0.2 | |
| 0.05 | |
| 0.3 | |
| 20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, L.; Zhou, F.; Kim, K.; Zhang, L. Practical Model for Energy Consumption Analysis of Omnidirectional Mobile Robot. Sensors 2021, 21, 1800. https://doi.org/10.3390/s21051800
Hou L, Zhou F, Kim K, Zhang L. Practical Model for Energy Consumption Analysis of Omnidirectional Mobile Robot. Sensors. 2021; 21(5):1800. https://doi.org/10.3390/s21051800
Chicago/Turabian StyleHou, Linfei, Fengyu Zhou, Kiwan Kim, and Liang Zhang. 2021. "Practical Model for Energy Consumption Analysis of Omnidirectional Mobile Robot" Sensors 21, no. 5: 1800. https://doi.org/10.3390/s21051800
APA StyleHou, L., Zhou, F., Kim, K., & Zhang, L. (2021). Practical Model for Energy Consumption Analysis of Omnidirectional Mobile Robot. Sensors, 21(5), 1800. https://doi.org/10.3390/s21051800







