Head Pose Estimation through Keypoints Matching between Reconstructed 3D Face Model and 2D Image
Abstract
:1. Introduction
2. Related Work
2.1. Supervised-Learning-Based Methods
2.2. Model-Based Methods
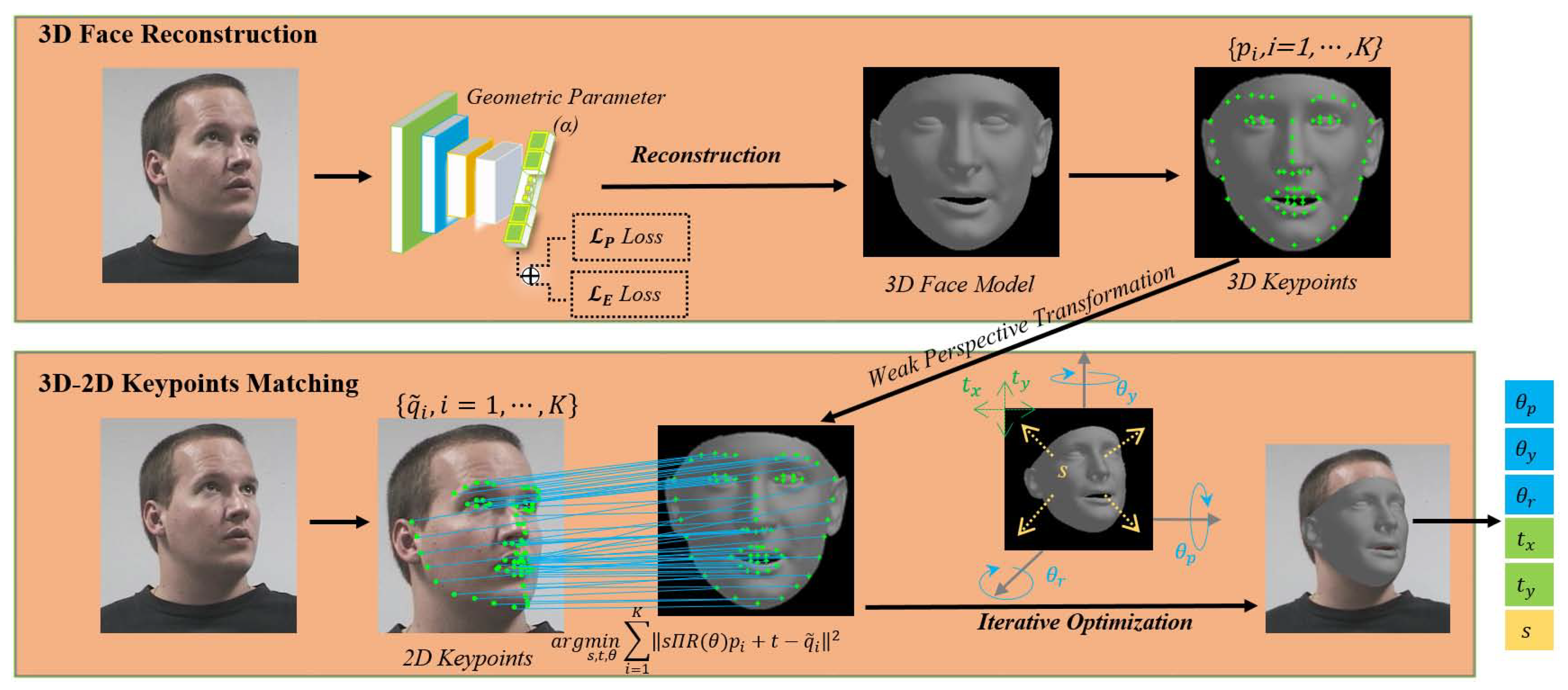
3. Methodology
3.1. Overview
3.2. 3D Face Model Reconstruction
3.2.1. Model Representation
3.2.2. Network Structure
3.2.3. Loss Functions
3.3. Head-Pose Estimation through 3D-2D Keypoints Matching
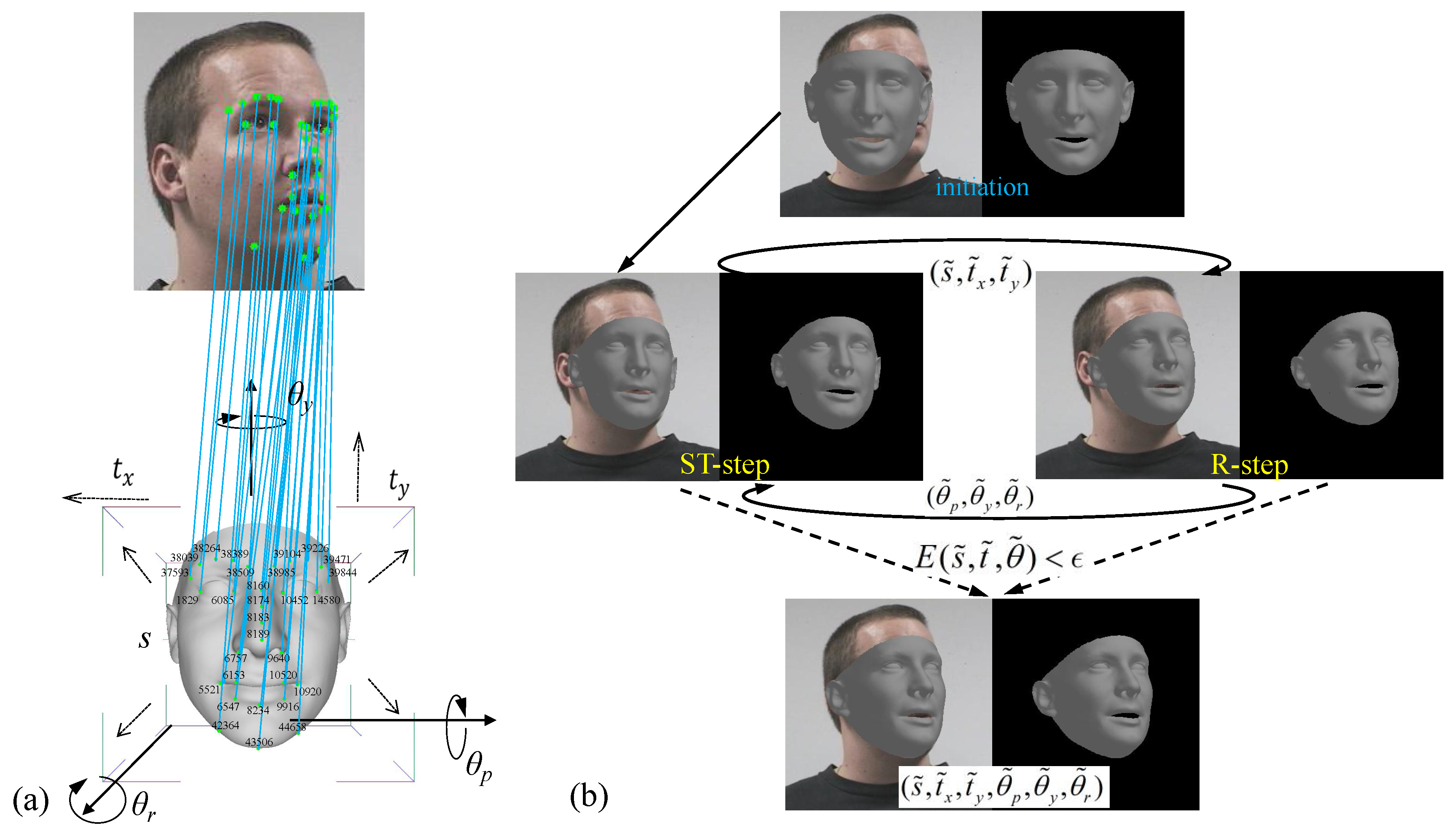
3.3.1. Weak Perspective Transformation
3.3.2. 3D–2D Keypoints Matching
4. Experimental Results
4.1. Implementation Details
4.2. Datasets and Performance Metric
4.3. Performance Analysis of the Proposed Method
4.4. Comparisons with Other Methods
4.5. Cross-Dataset Experiments
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, K.; Zhao, R.; Ji, Q. Human computer interaction with head pose, eye gaze and body gestures. In Proceedings of the 2018 13th IEEE International Conference on Automatic Face & Gesture Recognition (FG), Xi’an, China, 15–19 May 2018; p. 789. [Google Scholar] [CrossRef]
- Kaplan, S.; Guvensan, M.A.; Yavuz, A.G.; Karalurt, Y. Driver behavior analysis for safe driving: A survey. IEEE Trans. Intell. Transp. Syst. 2015, 16, 3017–3032. [Google Scholar] [CrossRef]
- Chen, J.; Luo, N.; Liu, Y.; Liu, L.; Zhang, K.; Kolodziej, J. A hybrid intelligence-aided approach to affect-sensitive e-learning. Computing 2016, 98, 215–233. [Google Scholar] [CrossRef]
- Dantone, M.; Gall, J.; Fanelli, G.; Gool, L.V. Real-time facial feature detection using conditional regression forests. In Proceedings of the 2012 IEEE International Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012; pp. 2578–2585. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, L.; Chen, J. Progressive pose normalization generative adversarial network for frontal face synthesis and face recognition under large pose. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Liu, Y.; Yuan, X.; Gong, X.; Xie, Z.; Fang, F.; Luo, Z. Conditional convolution neural network enhanced random forest for facial expression recognition. Pattern Recognit. 2018, 84, 251–261. [Google Scholar] [CrossRef]
- Liu, L.; Gui, W.; Zhang, L.; Chen, J. Real-time pose invariant spontaneous smile detection using conditional random regression forests. Optik 2019, 182, 647–657. [Google Scholar] [CrossRef]
- Chun, J.; Kim, W. 3d face pose estimation by a robust real time tracking of facial features. Multimed. Tools Appl. 2016, 75, 15693–15708. [Google Scholar] [CrossRef]
- Fanelli, G.; Gall, J.; Gool, L.J.V. Real time head pose estimation with random regression forests. In Proceedings of the 2011 IEEE International Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 20–25 June 2011; pp. 617–624. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, J.; Su, Z.; Luo, Z.; Luo, N.; Liu, L.; Zhang, K. Robust head pose estimation using dirichlet-tree distribution enhanced random forests. Neurocomputing 2016, 173, 42–53. [Google Scholar] [CrossRef]
- Patacchiola, M.; Cangelosi, A. Head pose estimation in the wild using convolutional neural networks and adaptive gradient methods. Pattern Recognit. 2017, 71, 132–143. [Google Scholar] [CrossRef] [Green Version]
- Raza, M.; Chen, Z.; Rehman, S.-U.; Wang, P.; Bao, P. Appearance based pedestrians’ head pose and body orientation estimation using deep learning. Neurocomputing 2018, 272, 647–659. [Google Scholar] [CrossRef]
- Ahn, B.; Choi, D.G.; Park, J.; Kweon, I.S. Real-time head pose estimation using multi-task deep neural network. Robot. Auton. Syst. 2018, 103, 1–12. [Google Scholar] [CrossRef]
- Xu, L.; Chen, J.; Gan, Y. Head pose estimation with soft labels using regularized convolutional neural network. Neurocomputing 2019, 337, 339–353. [Google Scholar] [CrossRef]
- Geng, X.; Xia, Y. Head pose estimation based on multivariate label distribution. In Proceedings of the 2014 IEEE International Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 1837–1842. [Google Scholar] [CrossRef]
- Erik, M.C.; Trivedi, M.M. Head Pose Estimation in Computer Vision: A Survey. TPAMI 2009, 31, 607–626. [Google Scholar] [CrossRef]
- Smith, M.R.; Martinez, T. Improving Classification Accuracy by Identifying and Removing Instances that Should Be Misclassified. In Proceedings of the 2011 International Joint Conference on Neural Networks (IJCNN), San Jose, CA, USA, 31 July–5 August 2011; pp. 2690–2697. [Google Scholar] [CrossRef] [Green Version]
- Gourier, N.; Hall, D.; Crowley, J.L. Estimating face orientation from robust detection of salient facial features. In Proceedings of the ICPR International Workshop on Visual Observation of Deictic Gestures, Cambridge, UK, 23–26 August 2004; pp. 1–9. [Google Scholar]
- Fanelli, G.; Dantone, M.; Gall, J.; Fossati, A.; Gool, L.V. Random forests for real time 3d face analysis. Int. J. Comput. Vis. 2013, 101, 437–458. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.; Zhen, L.; Liu, X.; Shi, H.; Li, S.Z. Face alignment across large poses: A 3d solution. In Proceedings of the 2016 IEEE International Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 146–155. [Google Scholar] [CrossRef] [Green Version]
- Gross, R.; Matthews, I.; Cohn, J.F.; Kanade, T.; Baker, S. Multi-PIE. In Proceedings of the 2008 IEEE International Conference on Automatic Face & Gesture Recognition (FG), Amsterdam, The Netherlands, 17–19 September 2008; pp. 607–626. [Google Scholar] [CrossRef]
- Borghi, G.; Venturelli, M.; Vezzani, R.; Cucchiara, R. POSEidon: Face-from-Depth for Driver Pose Estimation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5494–5503. [Google Scholar] [CrossRef] [Green Version]
- Bao, J.; Ye, M. Head pose estimation based on robust convolutional neural network. Cybern. Inf. Technol. 2016, 16, 133–145. [Google Scholar] [CrossRef] [Green Version]
- Chang, F.; Tran, A.T.; Hassner, T.; Masi, I.; Nevatia, R.; Medioni, G. FacePoseNet: Making a case for landmark-free face alignment. In Proceedings of the 2017 IEEE International Conference on Computer Vision Workshops (ICCVW), Venice, Italy, 22–29 October 2017; pp. 1599–1608. [Google Scholar] [CrossRef] [Green Version]
- Kumar, A.; Alavi, A.; Chellappa, R. KEPLER: Keypoint and pose estimation of unconstrained faces by learning efficient h-cnn regressors. In Proceedings of the 2017 IEEE International Conference on Automatic Face & Gesture Recognition (FG), Washington, DC, USA, 30 May–3 June 2017; pp. 258–265. [Google Scholar] [CrossRef] [Green Version]
- Ruiz, N.; Chong, E.; Rehg, J.M. Fine-Grained head pose estimation without keypoints. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; pp. 2074–2083. [Google Scholar] [CrossRef] [Green Version]
- Yang, T.Y.; Huang, Y.H.; Lin, Y.Y.; Hsiu, P.C.; Chuang, Y.Y. SSR-Net: A compact soft stagewise regression network for age estimation. In Proceedings of the 2018 International Joint Conference on Artifficial Intelligence (IJCAI), Stockholm, Sweden, 13–19 July 2018; pp. 1078–1084. [Google Scholar] [CrossRef] [Green Version]
- Yang, T.Y.; Chen, Y.T.; Lin, Y.Y.; Chuang, Y.Y. FSA-Net: Learning fine-grained structure aggregation for head pose estimation from a single image. In Proceedings of the 2019 IEEE International Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 1087–1096. [Google Scholar] [CrossRef]
- Han, J.; Liu, Y.S. Head posture detection with embedded attention model. In Proceedings of the 2020 International Conference on Internet of People (IoP), Melbourne, Australia, 8–11 December 2020; p. 032003. [Google Scholar] [CrossRef]
- Liu, X.; Liang, W.; Wang, Y.; Li, S.; Pei, M. 3d head pose estimation with convolutional neural network trained on synthetic images. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 1289–1293. [Google Scholar] [CrossRef]
- Sun, W.; Fan, Y.; Min, X.; Peng, S.; Ma, S.; Zhai, G. Lphd: A large-scale head pose dataset for rgb images. In Proceedings of the 2019 IEEE International Conference on Multimedia and Expo (ICME), Shanghai, China, 8–12 July 2019; pp. 1084–1089. [Google Scholar] [CrossRef]
- Feng, Y.; Wu, F.; Shao, X.; Wang, Y.; Zhou, X. Joint 3D Face Reconstruction and Dense Alignment with Position Map Regression Network. In Computer Vision–ECCV 2018. ECCV 2018; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2018; Volume 11218. [Google Scholar] [CrossRef] [Green Version]
- Gecer, B.; Ploumpis, S.; Kotsia, I.; Zafeiriou, S. GANFIT: Generative Adversarial Network Fitting for High Fidelity 3D Face Reconstruction. In Proceedings of the 2019 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 1155–1164. [Google Scholar] [CrossRef] [Green Version]
- Yu, Y.; Mora, K.A.F.; Odobez, J.M. Headfusion: 360∘ head pose tracking combining 3d morphable model and 3d reconstruction. TPAMI 2018, 40, 2653–2667. [Google Scholar] [CrossRef] [Green Version]
- Andrea, F.A.; Barra, P.; Bisogni, C.; Nappi, M.; Ricciardi, S. Near Real-Time Three Axis Head Pose Estimation without Training. IEEE Access 2019, 7, 64256–64265. [Google Scholar] [CrossRef]
- Barra, P.; Barra, S.; Bisogni, C.; Marsico, M.D.; Nappi, M. Web-Shaped Model for Head Pose Estimation: An Approach for Best Exemplar Selection. IEEE Trans. Image Process. 2020, 29, 5457–5468. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, X.; Lei, Z.; Li, S.Z. Face alignment in full pose range: A 3d total solution. TPAMI 2017, 41, 78–92. [Google Scholar] [CrossRef] [Green Version]
- Martin, M.; Stiefelhagen, R. Real Time Head Model Creation and Head Pose Estimation on Consumer Depth Cameras. In Proceedings of the 2014 International Conference on 3D Vision (3DV), Tokyo, Japan, 8–11 December 2014; pp. 641–648. [Google Scholar] [CrossRef]
- Gregory, P.M.; Shalini, G.; Iuri, F.; Dikpal, R.; Jan, K. Robust Model-Based 3D Head Pose Estimation. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 3649–3657. [Google Scholar] [CrossRef]
- Papazov, C.; Marks, T.K.; Jones, M. Real-time 3D head pose and facial landmark estimation from depth images using triangular surface patch features. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 4722–4730. [Google Scholar] [CrossRef]
- Paysan, P.; Knothe, R.; Amberg, B.; Romdhani, S.; Vetter, T. A 3d face model for pose and illumination invariant face recognition. In Proceedings of the 2009 IEEE International Conference on Advanced Video and Signal Based Surveillance (AVSS), Genova, Italy, 2–4 September 2009; pp. 296–301. [Google Scholar] [CrossRef]
- Cao, C.; Weng, Y.L.; Zhou, S.; Tong, Y.Y.; Zhou, K. FaceWarehouse: A 3D Facial Expression Database for Visual Computing. TVCG 2014, 20, 413–425. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- He, K.; Zhang, X.; Ren, S.; Jian, S. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE International Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef] [Green Version]
- Dong, Y.; Zhen, L.; Liao, S.; Li, S.Z. Learning face representation from scratch. Comput. Sci. 2014, arXiv:1411.7923v1. [Google Scholar]
- Guo, Y.; Zhang, J.; Cai, J.; Jiang, B.; Zheng, J. Cnn-based real-time dense face reconstruction with inverse-rendered photo-realistic face images. TPAMI 2019, 41, 1294–1307. [Google Scholar] [CrossRef] [Green Version]
- Tran, A.T.; Hassner, T.; Masi, I.; Medioni, G. Regressing robust and discriminative 3d morphable models with a very deep neural network. In Proceedings of the 2017 IEEE International Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5163–5172. [Google Scholar] [CrossRef] [Green Version]
- More, J.J. The levenberg-marquardt algorithm: Implementation and theory. In Numerical Analysis; Watson, G.A., Ed.; Springer: Berlin/Heidelberg, Germany, 1978; pp. 105–116. [Google Scholar]
- Bulat, A.; Tzimiropoulos, G. How far are we from solving the 2d & 3d face alignment problem? (and a dataset of 230,000 3d facial landmarks). In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 1021–1030. [Google Scholar] [CrossRef] [Green Version]
- Fanelli, G.; Weise, T.; Gall, J.; Gool, L.V. Real time head pose estimation from consumer depth cameras. In Proceedings of the 2011 DAGM Symposium, Frankfurt/Main, Germany, 31 August–2 September 2011; pp. 101–110. [Google Scholar] [CrossRef]
- Kstinger, M.; Wohlhart, P.; Roth, P.M.; Bischof, H. Annotated facial landmarks in the wild: A large-scale, real-world database for facial landmark localization. In Proceedings of the 2011 IEEE International Conference on Computer Vision Workshops (ICCVW), Barcelona, Spain, 6–13 November 2011; pp. 2144–2151. [Google Scholar] [CrossRef]
- Kazemi, V.; Sullivan, J. One millisecond face alignment with an ensemble of regression trees. In Proceedings of the 2014 IEEE International Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 1867–1874. [Google Scholar] [CrossRef] [Green Version]
- Amos, B.; Ludwiczuk, B.; Satyanarayanan, M. Openface: A General-Purpose Face Recognition Library with Mobile Applications; CMU-CS-16-118, Technical Report; CMU School of Computer Science: Pittsburgh, PA, USA, 2016. [Google Scholar]
- Jain, V.; Crowley, J.L. Head pose estimation using multi-scale gaussian derivatives. In Proceedings of the 18th Scandinavian Conference on Image Analysis (SCIA), Espoo, Finland, 17 June 2013; pp. 319–328. [Google Scholar] [CrossRef] [Green Version]
- Ma, B.; Li, A.; Chai, X.; Shan, S. Covga: A novel descriptor based on symmetry of regions for head pose estimation. Neurocomputing 2014, 143, 97–108. [Google Scholar] [CrossRef]
- Lee, S.; Saitoh, T. Head pose estimation using convolutional neural network. In Proceedings of the International Conference on IT Convergence and Security (ICITCS), Seoul, Korea, 31 August 2017; pp. 164–171. [Google Scholar] [CrossRef]
- Sadeghzadeh, A.; Ebrahimnezhad, H. Head pose estimation based on fuzzy systems using facial geometric features. In Proceedings of the 2016 8th International Symposium on Telecommunications (IST), Tehran, Iran, 27–28 September 2016; pp. 777–782. [Google Scholar] [CrossRef]
- Liu, Y.; Xie, Z.; Yuan, X.; Chen, J.; Song, W. Multi-level structured hybrid forest for joint head detection and pose estimation. Neurocomputing 2017, 266, 206–215. [Google Scholar] [CrossRef]
- Vo, M.T.; Nguyen, T.; Le, T. Robust head pose estimation using extreme gradient boosting machine on stacked autoencoders neural network. IEEE Access 2020, 8, 3687–3694. [Google Scholar] [CrossRef]
- Drouard, V.; Horaud, R.; Deleforge, A.; Ba, S.; Evangelidis, G. Robust head-pose estimation based on partially-latent mixture of linear regressions. IEEE Trans. Image Process. 2017, 26, 1428–1440. [Google Scholar] [CrossRef] [Green Version]
- Ahn, B.; Park, J.; Kweon, I.S. Real-time head orientation from a monocular camera using deep neural network. In Proceedings of the Asian Conference on Computer Vision (ACCV), Singapore, 1–5 November 2014; pp. 82–96. [Google Scholar] [CrossRef]
- Drouard, V.; Ba, S.; Evangelidis, G.; Deleforge, A.; Horaud, R. Head pose estimation via probabilistic high-dimensional regression. In Proceedings of the 2015 IEEE International Conference on Image Processing (ICIP), Quebec City, QC, Canada, 27–30 September 2015; pp. 4624–4628. [Google Scholar] [CrossRef] [Green Version]
- Lv, J.; Shao, X.; Xing, J.; Cheng, C.; Zhou, X. A deep regression architecture with two-stage re-initialization for high performance facial landmark detection. In Proceedings of the 2017 IEEE International Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 3691–3700. [Google Scholar] [CrossRef]
- Hsu, H.W.; Wu, T.Y.; Wan, S.; Wong, W.H.; Lee, C.Y. QuatNet: Quaternion-based head pose estimation with multiregression loss. IEEE Trans. Multimed. 2019, 21, 1035–1046. [Google Scholar] [CrossRef]
- Saeed, A.; Al-Hamadi, A.; Ghoneim, A. Head Pose Estimation on Top of Haar-Like Face Detection: A Study Using the Kinect Sensor. Sensors 2015, 15, 20945–20966. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shoja Ghiass, R.; Arandjelovć, O.; Laurendeau, D. Highly Accurate and Fully Automatic 3D Head Pose Estimation and Eye Gaze Estimation Using RGB-D Sensors and 3D Morphable Models. Sensors 2018, 18, 4280. [Google Scholar] [CrossRef] [PubMed] [Green Version]










| Testing Dataset | Without FFP Loss | With FFP Loss | ||||
|---|---|---|---|---|---|---|
| Pitch | Yaw | Pitch + Yaw | Pitch | Yaw | Pitch + Yaw | |
| Pointing’04 [18] | 7.42 | 6.59 | 7.01 | 5.27 | 4.30 | 4.78 |
| BIWI [19] | 9.65 | 6.79 | 8.22 | 7.94 | 5.81 | 6.88 |
| AFLW2000 [20] | 10.46 | 6.86 | 8.66 | 8.49 | 5.60 | 7.05 |
| Multi-PIE [21] | 7.12 | 7.87 | 7.50 | 5.77 | 5.17 | 5.47 |
| Testing Dataset | MAE() without OB | MAE() with OB | ||||
|---|---|---|---|---|---|---|
| Pitch | Yaw | Avg | Pitch | Yaw | Avg | |
| Pointing’04 [18] | 5.27 | 4.30 | 4.78 | 6.32 | 5.85 | 6.09 |
| BIWI [19] | 7.94 | 5.81 | 6.88 | 11.91 | 5.88 | 8.90 |
| AFLW2000 [20] | 8.49 | 5.60 | 7.05 | 12.17 | 7.91 | 9.04 |
| Multi-PIE [21] | 5.77 | 5.17 | 5.47 | 5.12 | 9.83 | 7.48 |
| Pandora [22] | 4.99 | 6.33 | 5.66 | 6.98 | 6.60 | 6.79 |
| Module | Frames per Second |
|---|---|
| 3D face reconstruction(3DFR) | 0.55 |
| 2D keypoints detection | 14.49 |
| 3D-2D keypoints matching | 46.31 |
| Whole system | 0.52 |
| Whole sysem(wo 3DFR) | 11.11 |
| MAE() | |||
|---|---|---|---|
| Yaw | Pitch | Avg | |
| MGD [53] | 6.90 | 8.00 | 7.46 |
| kCovGa [54] | 6.34 | 7.14 | 6.74 |
| CovGA [54] | 7.27 | 8.69 | 7.98 |
| CNN [55] | 5.17 | 5.36 | 5.27 |
| fuzzy [56] | 6.98 | 6.04 | 6.51 |
| MSHF [57] | - | - | 6.60 |
| SAE-XGB [58] | 6.16 | 7.17 | 6.67 |
| hGLLiM [59] | 7.93 | 8.47 | 8.20 |
| Hopenet [26] | 26.61 | 19.59 | 23.10 |
| FSA-Net(FAN) [27] | 25.90 | 18.01 | 21.96 |
| 3DDFA [37] | 6.18 | 7.38 | 6.77 |
| 4C_4S_var4 [36] | 10.63 | 6.34 | 8.49 |
| ours(FAN-30) | 4.30 | 5.27 | 4.78 |
| MAE() | ||||
|---|---|---|---|---|
| Yaw | Pitch | Roll | Avg | |
| CNN-syn [30] | 11.35 | 9.65 | 10.42 | 10.47 |
| DNN [60] | 11.89 | 7.12 | 12.78 | 10.60 |
| regression [61] | 8.85 | 8.70 | - | 8.78 |
| Two-Stage [62] | 9.49 | 11.34 | 6.00 | 10.41 |
| KEPLER [25] | 8.08 | 17.28 | 16.20 | 13.05 |
| QuatNet [63] | 4.01 | 5.49 | 2.94 | 4.15 |
| Dlib [51] | 16.76 | 13.80 | 6.19 | 12.25 |
| FAN [48] | 8.53 | 7.48 | 7.63 | 7.88 |
| 3DDFA [37] | 36.18 | 12.25 | 8.78 | 19.07 |
| QT_PYR [35] | 5.41 | 12.80 | 6.33 | 8.18 |
| QT_PY+R [35] | 6.28 | 14.95 | 4.12 | 8.45 |
| 4C_4S_var4 [36] | 6.21 | 3.95 | 4.16 | 4.77 |
| Haar-Like(LBP) [64] | 9.70 | 11.30 | 7.0 | 9.33 |
| HAFA [65] | 8.95 | 6.80 | - | 7.88 |
| Ours(FAN-30) | 5.81 | 7.94 | 6.74 | 6.83 |
| Methods | Input | Cropping | Fusion | MAE () | |||
|---|---|---|---|---|---|---|---|
| Pitch | Roll | Yaw | Avg | ||||
| SingleCNN [22] | depth | X | - | 8.1 | 6.2 | 11.7 | 8.67 |
| depth | ✔ | - | 6.5 | 5.4 | 10.4 | 7.43 | |
| FfD | ✔ | - | 6.8 | 5.7 | 10.5 | 7.67 | |
| gray-level | ✔ | - | 7.1 | 5.6 | 9.0 | 7.23 | |
| MI | ✔ | - | 7.7 | 5.3 | 10.0 | 7.67 | |
| DoubleCNN [22] | depth + FfD | ✔ | concat | 5.6 | 4.9 | 9.8 | 6.77 |
| depth + MI | ✔ | concat | 6.0 | 4.5 | 9.2 | 6.57 | |
| POSEidon [22] | depth + FfD + MI | ✔ | concat | 6.3 | 5.0 | 10.6 | 7.30 |
| depth + FfD + MI | ✔ | mul + concat | 5.6 | 4.9 | 9.1 | 6.53 | |
| depth + FfD + MI | ✔ | conv + concat | 5.7 | 4.9 | 9.0 | 6.53 | |
| Hopenet [26] | single RGB | X | - | 5.62 | 6.69 | 8.49 | 6.94 |
| FSA-Net [27] | single RGB | X | - | 6.93 | 5.06 | 10.32 | 7.44 |
| 3DDFA [37] | single RGB | X | - | 6.62 | 4.65 | 7.58 | 6.28 |
| Ours(FAN-20) | single RGB | X | - | 4.99 | 3.87 | 6.33 | 5.06 |
| Ours(FAN-30) | single RGB | X | - | 5.21 | 3.88 | 6.27 | 5.12 |
| Ours(FAN-68) | single RGB | X | - | 5.83 | 3.97 | 6.80 | 5.53 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Ke, Z.; Huo, J.; Chen, J. Head Pose Estimation through Keypoints Matching between Reconstructed 3D Face Model and 2D Image. Sensors 2021, 21, 1841. https://doi.org/10.3390/s21051841
Liu L, Ke Z, Huo J, Chen J. Head Pose Estimation through Keypoints Matching between Reconstructed 3D Face Model and 2D Image. Sensors. 2021; 21(5):1841. https://doi.org/10.3390/s21051841
Chicago/Turabian StyleLiu, Leyuan, Zeran Ke, Jiao Huo, and Jingying Chen. 2021. "Head Pose Estimation through Keypoints Matching between Reconstructed 3D Face Model and 2D Image" Sensors 21, no. 5: 1841. https://doi.org/10.3390/s21051841
APA StyleLiu, L., Ke, Z., Huo, J., & Chen, J. (2021). Head Pose Estimation through Keypoints Matching between Reconstructed 3D Face Model and 2D Image. Sensors, 21(5), 1841. https://doi.org/10.3390/s21051841






