Variable Admittance Control Based on Human–Robot Collaboration Observer Using Frequency Analysis for Sensitive and Safe Interaction
Abstract
1. Introduction
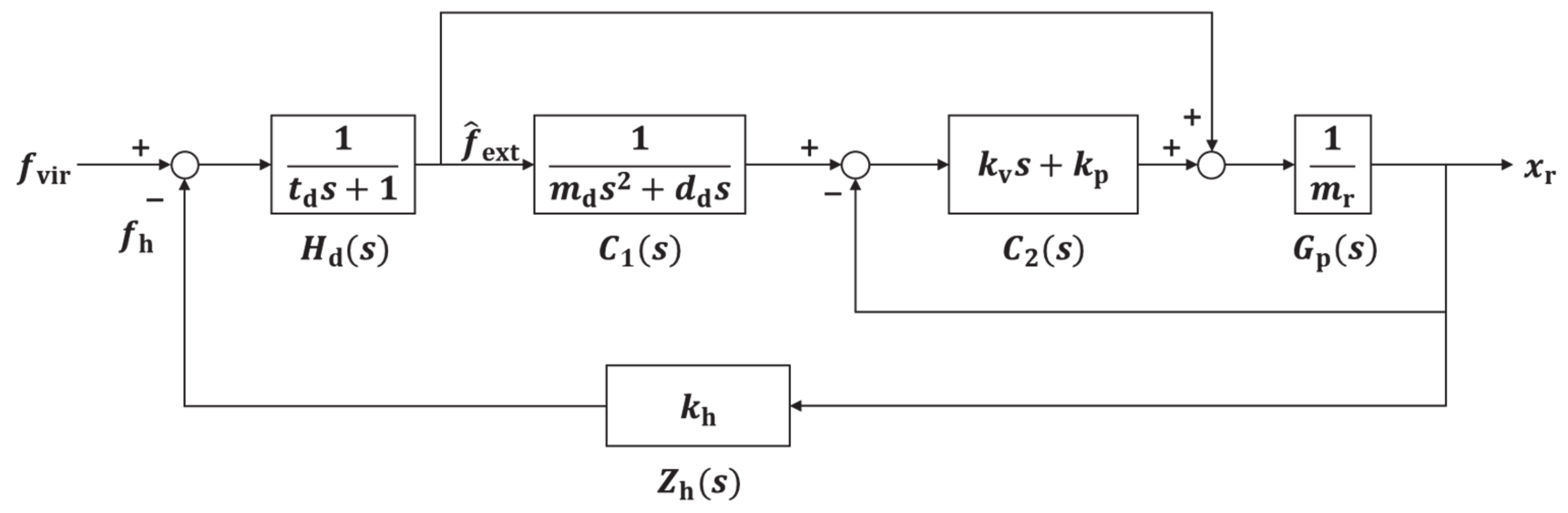
2. The Admittance Control Scheme
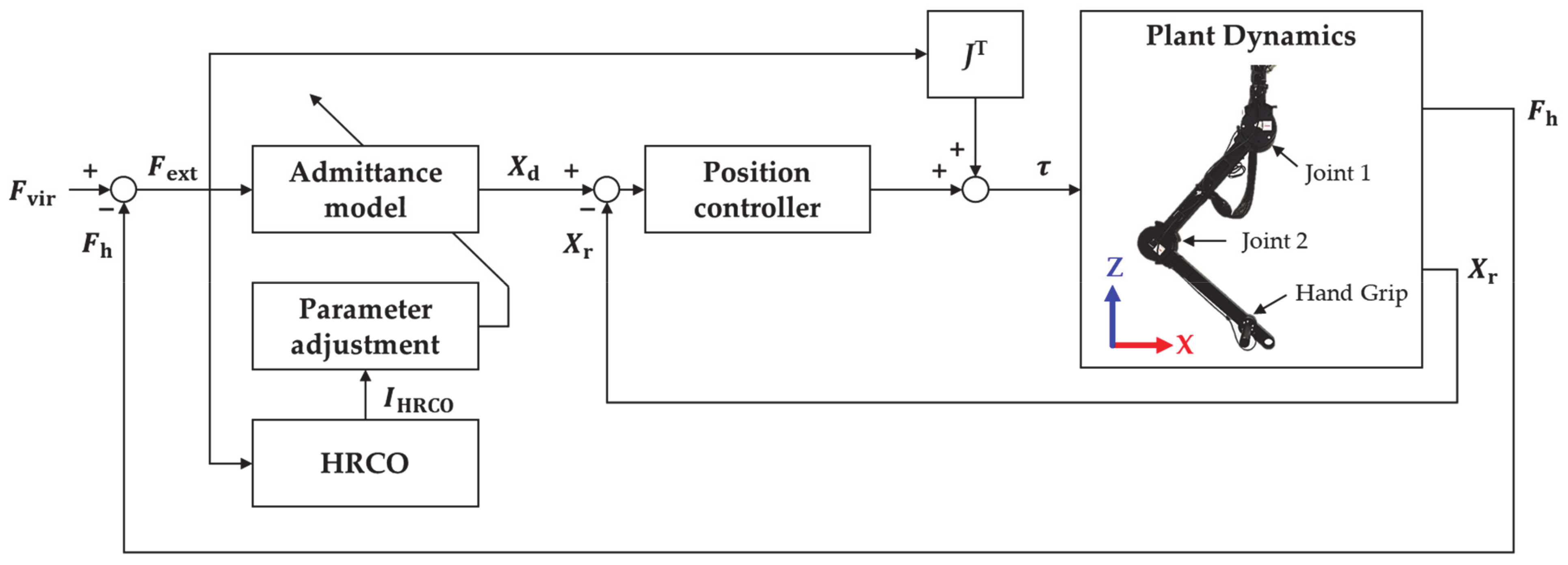
3. Variable Admittance Control Based on HRCO
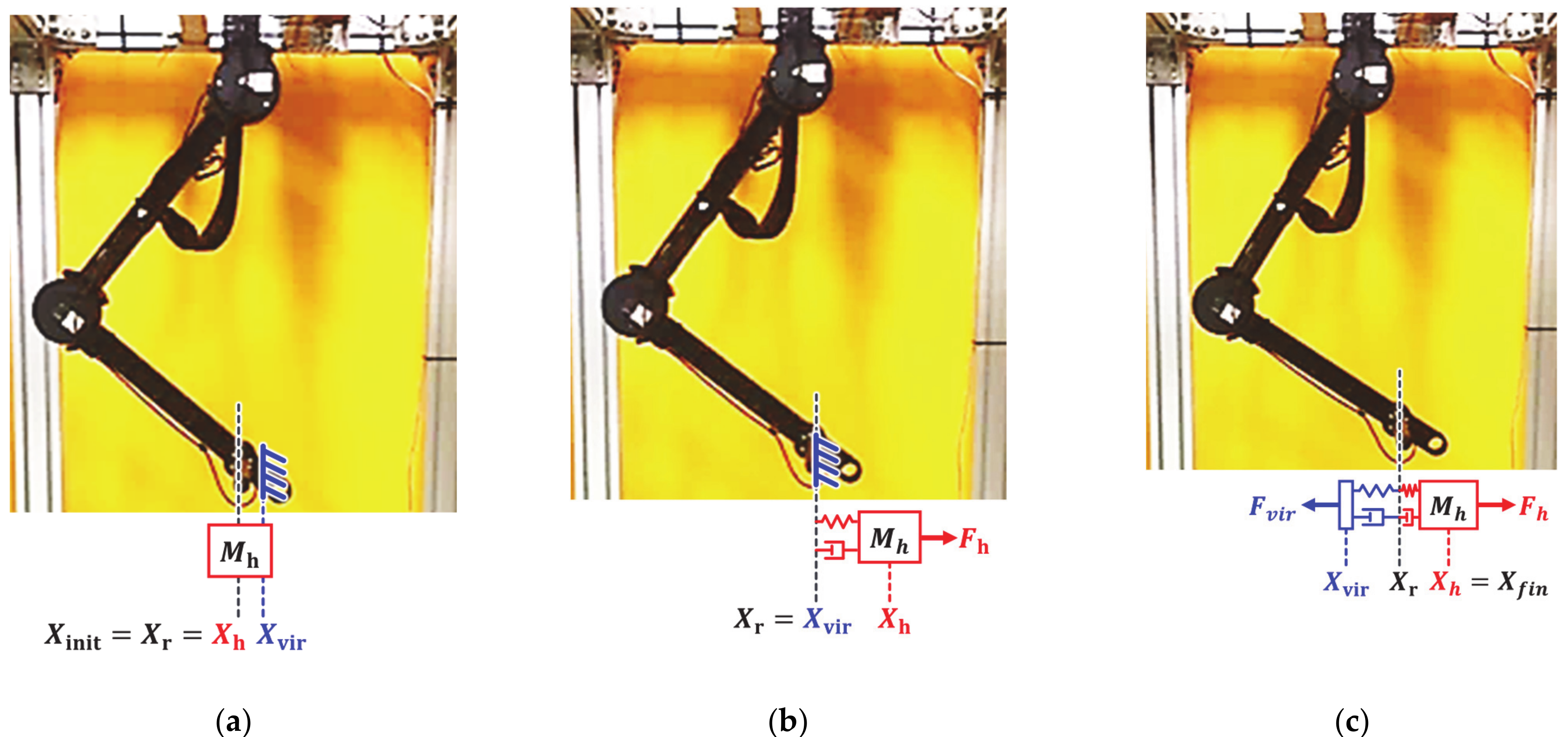
3.1. The Human–Robot Collaboration Observer
3.2. Admittance Adjustment Method Based on HRCO
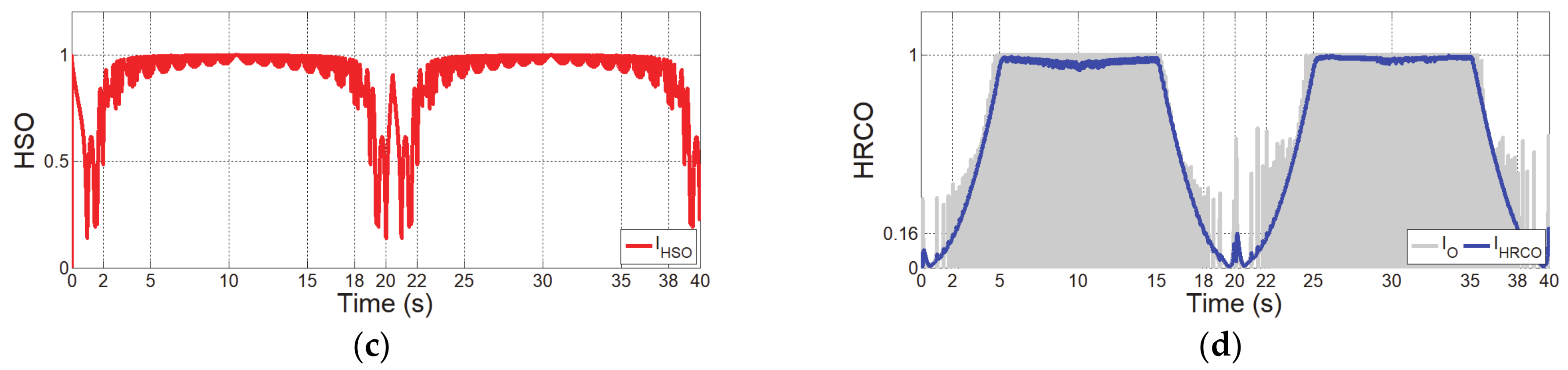
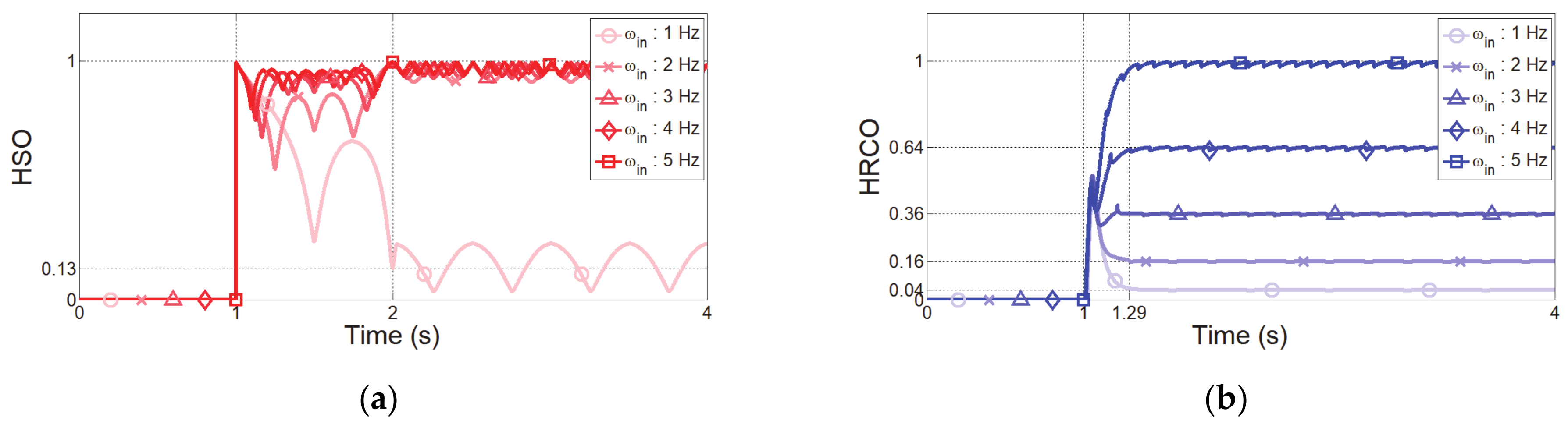
4. Simulation Verification of HRCO
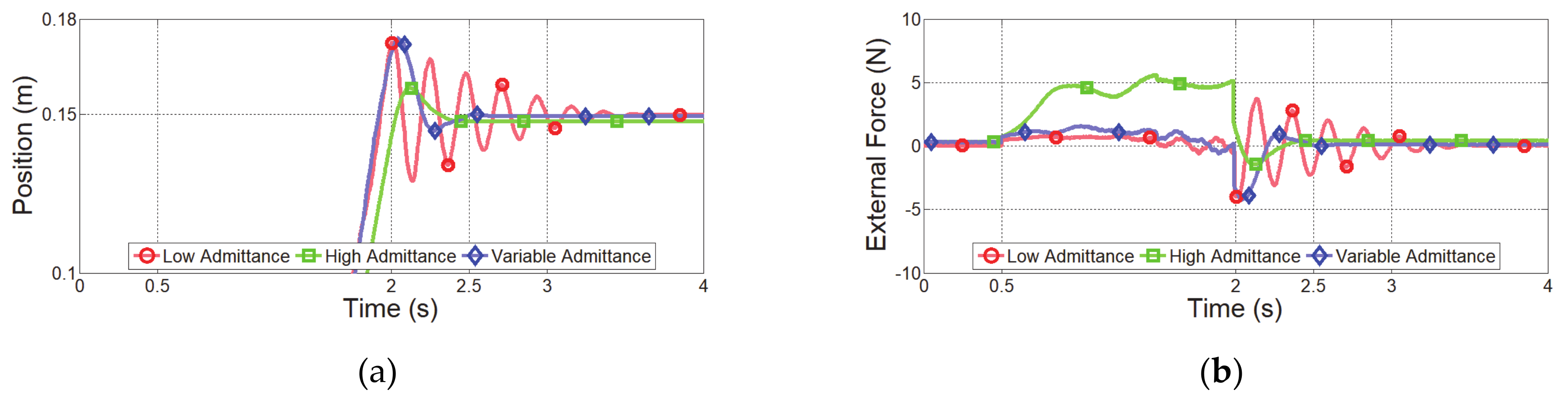
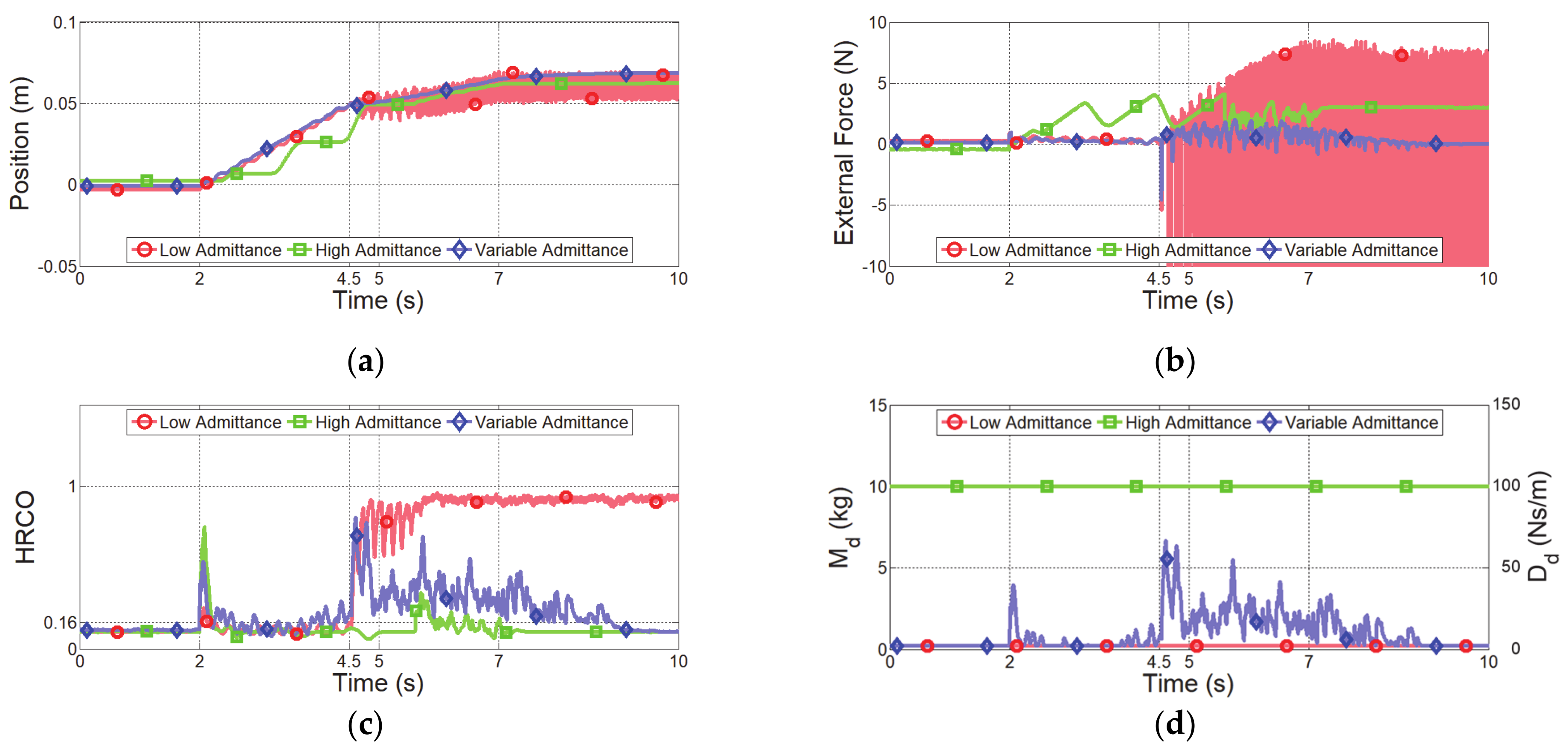
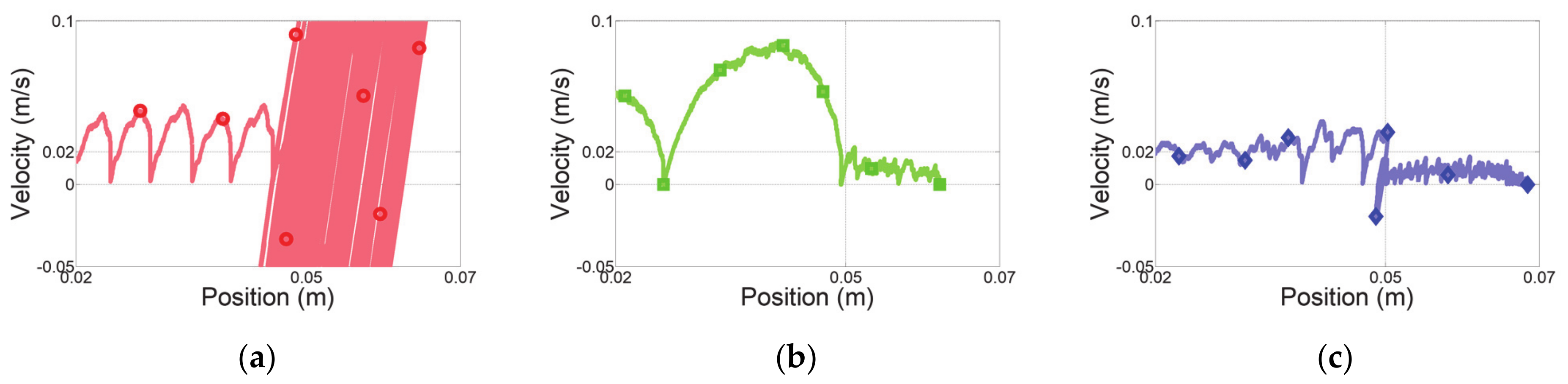
5. Experimental Evaluations of Variable Admittance Control Based on HRCO
5.1. Experimental Setup
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| HSO | haptic stability observer |
| DFT | discrete Fourier transform |
| HRCO | human–robot collaboration observer |
| IIR | infinite impulse response |
| DOF | degree of freedom |
| LPF | low pass filter |
| HPF | high pass filter |
References
- International Federation of Robotics. Executive Summary World Robotics 2016 Industrial Robots; International Federation of Robotics: Frankfurt, Germany, 2016. [Google Scholar]
- Probst, L.; Frideres, L.; Pedersen, B.; Caputi, C. Service Innovation for Smart Industry: Human–Robot Collaboration; European Commission: Luxembourg, 2015. [Google Scholar]
- Villani, V.; Pini, F.; Leali, F.; Secchi, C. Survey on human–robot collaboration in industrial settings: Safety, intuitive interfaces and applications. Mechatronics 2018, 55, 248–266. [Google Scholar] [CrossRef]
- ISO. ISO 10218: Robots and Robotic Devices—Safety Requirements for Industrial Robots—Part 1: Robots; ISO: Geneve, Switzerland, 2011. [Google Scholar]
- ISO. ISO 10218-2: Robots and Robotic Devices—Safety Requirements for Industrial Robots—Part 2: Robot Systems and Integration; ISO: Geneve, Switzerland, 2011. [Google Scholar]
- Bandeira, G.M.; Carmo, M.; Ximenes, B.; Kelner, J. Using Gesture-Based Interfaces to Control Robots; International Conference on Human-Computer Interaction; Springer: Berlin/Heidelberg, Germany, 2015; pp. 3–12. [Google Scholar]
- Gupta, A.K.; Arora, S.K. Industrial Automation and Robotics; Laxmi Publications: New Delhi, India, 2009. [Google Scholar]
- Falco, J.A.; Marvel, J.A.; Norcross, R.J. Collaborative robotics: Measuring blunt force impacts on humans. Chest 2012, 140, 45. [Google Scholar]
- Shahriari, E.; Kramberger, A.; Gams, A.; Ude, A.; Haddadin, S. Adapting to contacts: Energy tanks and task energy for passivity-based dynamic movement primitives. In Proceedings of the 2017 IEEE-RAS 17th International Conference on Humanoid Robotics (Humanoids), Birmingham, UK, 15–17 November 2017; pp. 136–142. [Google Scholar]
- Kramberger, A.; Shahriari, E.; Gams, A.; Nemec, B.; Ude, A.; Haddadin, S. Passivity based iterative learning of admittance-coupled dynamic movement primitives for interaction with changing environments. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 6023–6028. [Google Scholar]
- Raiola, G.; Cardenas, C.A.; Tadele, T.S.; De Vries, T.; Stramigioli, S. Development of a safety-and energy-aware impedance controller for collaborative robots. IEEE Robot. Autom. Lett. 2018, 3, 1237–1244. [Google Scholar] [CrossRef]
- Herrnstadt, G.; McKeown, M.J.; Menon, C. Controlling a motorized orthosis to follow elbow volitional movement: Tests with individuals with pathological tremor. J. Neuroeng. Rehabil. 2019, 16, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Rocon, E.; Belda-Lois, J.; Sanchez-Lacuesta, J.; Pons, J.L. Pathological tremor management: Modelling, compensatory technology and evaluation. Technol. Disabil. 2004, 16, 3–18. [Google Scholar] [CrossRef]
- de Vlugt, E.; Schouten, A.C.; van der Helm, F.C.; Teerhuis, P.C.; Brouwn, G.G. A force-controlled planar haptic device for movement control analysis of the human arm. J. Neurosci. 2003, 129, 151–168. [Google Scholar] [CrossRef]
- Ryu, D.; Song, J.B.; Choi, J.; Kang, S.; Kim, M. Design of a haptic stability observer in frequency domain for stable haptic interaction. In Proceedings of the 2006 SICE-ICASE International Joint Conference, Busan, Korea, 18–21 October 2006; pp. 198–203. [Google Scholar]
- Dimeas, F.; Aspragathos, N. Online stability in human-robot cooperation with admittance control. IEEE Trans. Haptics 2016, 9, 267–278. [Google Scholar] [CrossRef]
- Okunev, V.; Nierhoff, T.; Hirche, S. Human-preference-based control design: Adaptive robot admittance control for physical human-robot interaction. In Proceedings of the 2012 IEEE RO-MAN: The 21st IEEE International Symposium on Robot and Human Interactive Communication, Paris, France, 9–13 September 2012; pp. 443–448. [Google Scholar]
- Ferraguti, F.; Talignani Landi, C.; Sabattini, L.; Bonfè, M.; Fantuzzi, C.; Secchi, C. A variable admittance control strategy for stable physical human–robot interaction. Int. J. Rob. Res. 2019, 38, 747–765. [Google Scholar] [CrossRef]
- Tsumugiwa, T.; Fuchikami, Y.; Kamiyoshi, A.; Yokogawa, R.; Yoshida, K. Stability analysis for impedance control of robot in human-robot cooperative task system. Adv. Mech. Des. Syst. Manuf. 2007, 1, 113–121. [Google Scholar] [CrossRef]
- Keemink, A.Q.; van der Kooij, H.; Stienen, A.H. Admittance control for physical human–robot interaction. Int. J. Rob. Res. 2018, 37, 1421–1444. [Google Scholar] [CrossRef]
- Carignan, C.R.; Cleary, K.R. Closed-loop force control for haptic simulation of virtual environments. Haptics e. 2000, 420, 1. [Google Scholar]
- Ott, C.; Mukherjee, R.; Nakamura, Y. A hybrid system framework for unified impedance and admittance control. J. Intell. Robot. Syst. 2015, 78, 359–375. [Google Scholar] [CrossRef]
- Kim, H.; Kwon, J.; Oh, Y.; You, B.J.; Yang, W. Weighted hybrid admittance-impedance control with human intention based stiffness estimation for human-robot interaction. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1–6. [Google Scholar]
- Duan, J.; Gan, Y.; Chen, M.; Dai, X. Adaptive variable impedance control for dynamic contact force tracking in uncertain environment. Rob. Auton. Syst. 2018, 102, 54–65. [Google Scholar] [CrossRef]
- Koivumäki, J.; Mattila, J. Stability-guaranteed impedance control of hydraulic robotic manipulators. IEEE ASME Trans. Mechatron. 2016, 22, 601–612. [Google Scholar] [CrossRef]
- Tsuji, T.; Morasso, P.G.; Goto, K.; Ito, K. Human hand impedance characteristics during maintained posture. Biol. Cybern. 1995, 72, 475–485. [Google Scholar] [CrossRef]
- Wang, H.; Patota, F.; Buondonno, G.; Haendl, M.; De Luca, A.; Kosuge, K. Stability and variable admittance control in the physical interaction with a mobile robot. Int. J. Adv. Robot. Sys. 2015, 12, 173. [Google Scholar] [CrossRef]
- Du, Z.; Wang, W.; Yan, Z.; Dong, W.; Wang, W. Variable admittance control based on fuzzy reinforcement learning for minimally invasive surgery manipulator. Sensors 2017, 17, 844. [Google Scholar] [CrossRef]
- Tseng, C.C.; Lee, S.L. Closed-form designs of digital fractional order Butterworth filters using discrete transforms. Signal Process. 2017, 137, 80–97. [Google Scholar] [CrossRef]
- Acharya, A.; Das, S.; Pan, I.; Das, S. Extending the concept of analog Butterworth filter for fractional order systems. Signal Process. 2014, 94, 409–420. [Google Scholar] [CrossRef]
- Kang, G.; Oh, H.S.; Seo, J.K.; Kim, U.; Choi, H.R. Variable admittance control of robot manipulators based on human intention. IEEE ASME Trans. Mechatron. 2019, 24, 1023–1032. [Google Scholar] [CrossRef]
- Nishikawa, K.C.; Murray, S.T.; Flanders, M. Do arm postures vary with the speed of reaching? J. Neurophysiol. 1999, 81, 2582–2586. [Google Scholar] [CrossRef] [PubMed]
- Padilla-Garcia, E.A.; Rodriguez-Angeles, A.; ReséNdiz, J.R.; Cruz-Villar, C.A. Concurrent optimization for selection and control of AC servomotors on the powertrain of industrial robots. IEEE Access 2018, 6, 27923–27938. [Google Scholar] [CrossRef]







| Filter Type | |||||
|---|---|---|---|---|---|
| LPF | −1.9556 | 0.9565 | 0.000241 | 0.000483 | 0.000241 |
| HPF | −1.9556 | 0.9565 | 0.978 | −1.9561 | 0.978 |
| HSO | HRCO | |
|---|---|---|
| Frequency Analysis Algorithm | DFT | IIR filter |
| Sampling frequency | 1000 Hz | 1000 Hz |
| Number of sampling data | 1024 ea | 2 ea |
| Frequency resolution | 0.98 Hz |
| Experiment Case | Initial Position (m) | Final Position (m) | Virtual Wall Position (m) | Moving Speed (m/s) | Acceleration (m/s2) | Deceleration (m/s2) |
|---|---|---|---|---|---|---|
| Sudden Human Impedance Change | −0.15 | 0.15 | - | 0.3 | 0.5 | −10.0 |
| Virtual Rigid Wall Collision | 0.0 | 0.1 | 0.05 | 0.02 | 0.5 | 0.5 |
| Comparison Group | (kg) | (Ns/m) | |||
|---|---|---|---|---|---|
| Low Gain Admittance Control | 0.2 | 2 | - | - | - |
| High Gain Admittance Control | 2 | 10 | - | - | - |
| Variable Admittance Control | - | - | 0.2 | 2 | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.; Yang, W. Variable Admittance Control Based on Human–Robot Collaboration Observer Using Frequency Analysis for Sensitive and Safe Interaction. Sensors 2021, 21, 1899. https://doi.org/10.3390/s21051899
Kim H, Yang W. Variable Admittance Control Based on Human–Robot Collaboration Observer Using Frequency Analysis for Sensitive and Safe Interaction. Sensors. 2021; 21(5):1899. https://doi.org/10.3390/s21051899
Chicago/Turabian StyleKim, Hyomin, and Woosung Yang. 2021. "Variable Admittance Control Based on Human–Robot Collaboration Observer Using Frequency Analysis for Sensitive and Safe Interaction" Sensors 21, no. 5: 1899. https://doi.org/10.3390/s21051899
APA StyleKim, H., & Yang, W. (2021). Variable Admittance Control Based on Human–Robot Collaboration Observer Using Frequency Analysis for Sensitive and Safe Interaction. Sensors, 21(5), 1899. https://doi.org/10.3390/s21051899






