The New Trend of State Estimation: From Model-Driven to Hybrid-Driven Methods
Abstract
:1. Introduction
2. State Estimation Based on a Distinct Model
2.1. Kalman Filter Family
2.2. Gaussian Mixture Filter and Random Sampling Filter
2.3. Discussion
3. State Estimation Based on a Blurry Model
3.1. Robust Filter
3.2. IMM and Closed-Loop Adaptive Filter
- (1)
- Multiple system models describe parts of the system and then combine to describe the whole system;
- (2)
- Measurement information is applied to continuously optimize the online system model to make the system model as consistent as possible with the current situation.
4. Data-Driven Modeling by Learning
4.1. Deep Learning Network
4.2. Hyperparameter Optimization
4.3. The Ability to Model System Noise
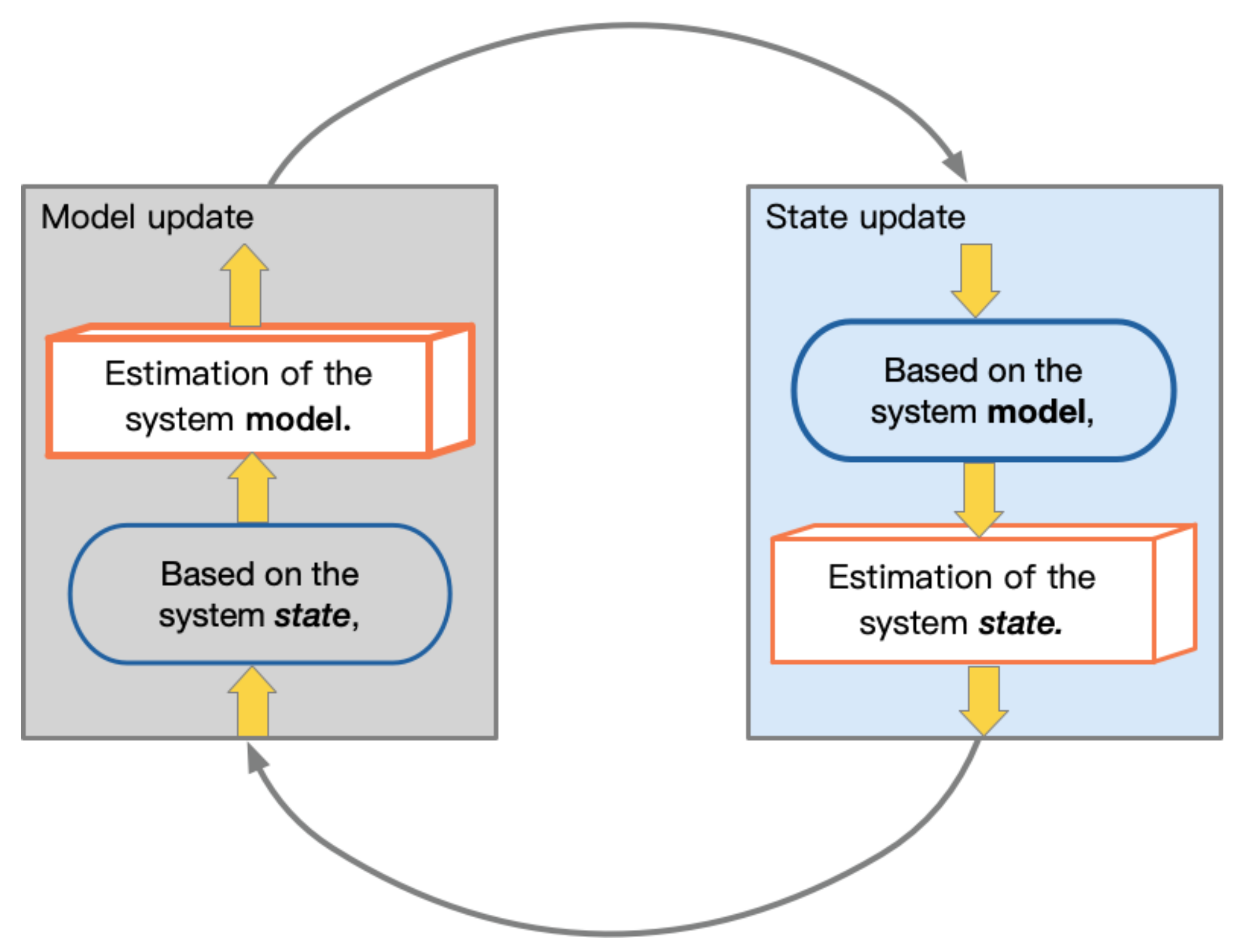
5. State Estimation Based on Hybrid-Driven Methods
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rubio, F.; Valero, F.; Llopis-Albert, C. A review of mobile robots: Concepts, methods, theoretical framework, and applications. Int. J. Adv. Robot. Syst. 2019, 16, 172988141983959. [Google Scholar] [CrossRef] [Green Version]
- Xin, Z.; Pei, L.; Junwei, C. Multi-UAV Cooperative Target Tracking Control Based on Nonlinear Guidance. Command. Inf. Syst. Technol. 2019, 10, 47–54. [Google Scholar]
- Muzammal, M.; Talat, R.; Sodhro, A.H.; Pirbhulal, S. A multi-sensor data fusion enabled ensemble approach for medical data from body sensor networks. Inf. Fusion 2020, 53, 155–164. [Google Scholar] [CrossRef]
- Ma, X.; Guo, R.; Liu, J.; Fang, C.; Zhu, P.; Zhang, Y. State estimation of AC and DC distribution network under three-phase unbalance. Autom. Electr. Power Syst. 2019, 43, 65–71. [Google Scholar]
- Zhang, X.; Zhao, Z.; Wang, Z.; Wang, X. Fault Detection and Identification Method for Quadcopter Based on Airframe Vibration Signals. Sensors 2021, 21, 581. [Google Scholar] [CrossRef]
- Zhao, Z.Y.; Wang, X.Y.; Yao, P.; Bai, Y.T. A health performance evaluation method of multirotors under wind turbulence. Nonlinear Dyn. 2020, 102, 1701–1715. [Google Scholar] [CrossRef]
- Sorenson, H.W. Kalman Filtering: Theory and Application; IEEE Press: New York, NY, USA, 1985. [Google Scholar]
- Wiener, N. Extrapolation, Interpolation, and Smoothing of Stationary Time Series; John Wiley & Sons: New York, NY, USA, 1949. [Google Scholar]
- Kalman, R.E. A new approach to linear filtering and prediction problems. Trans. ASME J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef] [Green Version]
- Qin, Y.Y.; Zhang, H.Y.; Wang, S.H. Principles of Kalman Filtering and Integrated Navigation; Northwestern Polytechnical University Press: Xi’an, China, 1998. [Google Scholar]
- Zorzi, M. Robust Kalman Filtering Under Model Perturbations. IEEE Trans. Autom. Control 2017, 62, 2902–2907. [Google Scholar] [CrossRef] [Green Version]
- Fu, M.; Deng, Z.H.; Zhang, J.W. Kalman Filtering Theory and Its Application in Navigation System; Science Press: Beijing, China, 2010. [Google Scholar]
- Hedayati, M.; Rahmani, M. Robust distributed H∞ filtering over an uncertain sensor network with multiple fading measurements and varying sensor delays. Int. J. Robust Nonlinear Control 2020, 30, 538–566. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K. A new approach for filtering nonlinear system. In Proceedings of the 1995 American Control Conference, Seattle, WA, USA, 21–23 June 1995; pp. 1628–1632. [Google Scholar]
- Julier, S.J.; Uhlmann, J.K. A new method for the nonlinear transformation of means and covariances in filters and estimators. IEEE Trans. Autom. Control 2000, 45, 477–482. [Google Scholar] [CrossRef] [Green Version]
- Norgarrd, M.; Poulsen, N.K.; Ravn, O. New developments in state estimation for nonlinear systems. Automatica 2000, 36, 1627–1638. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J. Reduced sigma point filters for the propagation of means and covariances through nonlinear transformations. In Proceedings of the American Control Conference, Anchorage, AK, USA, 8–10 May 2002; pp. 887–892. [Google Scholar]
- Arasaratnam, I.; Haykin, S. Cubature Kalman smoothers. Automatica 2011, 47, 2245–2250. [Google Scholar] [CrossRef]
- Zhang, P.; Li, B.; Boudaren, M.E.Y.; Yan, J.; Li, M.; Wu, Y. Parameter Estimation of Generalized Gamma Distribution Toward SAR Image Processing. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 3701–3717. [Google Scholar] [CrossRef]
- Jin, Z.; Zhao, J.; Chakrabarti, S.; Ding, L.; Terzija, V. A hybrid robust forecasting-aided state estimator considering bimodal Gaussian mixture measurement errors. Int. J. Electr. Power Energy Syst. 2020, 120, 105962. [Google Scholar] [CrossRef]
- Walia, G.S.; Kumar, A.; Saxena, A. Robust object tracking with crow search optimized multi-cue particle filter. Pattern Anal. Appl. 2020, 23, 1439–1455. [Google Scholar] [CrossRef] [Green Version]
- Jin, X.B.; Sun, S.L.; Wei, H.; Yang, F.B. Advances in multi-sensor information fusion: Theory and applications 2017. Sensors 2018, 18, 1162. [Google Scholar] [CrossRef] [Green Version]
- Bai, Y.T.; Wang, X.Y.; Sun, Q. Spatio-temporal prediction for the monitoring-blind area of industrial atmosphere based on the fusion network. Int. J. Environ. Res. Public Health 2019, 16, 3788. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Zhang, T.; Wang, X.; Jin, X.; Xu, J.; Yu, J.; Zhang, H.; Zhao, Z. An approach of improved multivariate timing-random deep belief net modelling for algal bloom prediction. Biosyst. Eng. 2019, 177, 130–138. [Google Scholar] [CrossRef]
- Hong, J.; Laflamme, S.; Dodson, J.; Joyce, B. Introduction to State Estimation of High-Rate System Dynamics. Sensors 2018, 18, 217. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dehghanpour, K.; Wang, Z.; Wang, J.; Yuan, Y.; Bu, F. A Survey on State Estimation Techniques and Challenges in Smart Distribution Systems. IEEE Trans. Smart Grid 2018, 10, 2312–2322. [Google Scholar] [CrossRef] [Green Version]
- Jin, X.; Yin, G.; Chen, N. Advanced Estimation Techniques for Vehicle System Dynamic State: A Survey. Sensors 2019, 19, 4289. [Google Scholar] [CrossRef] [Green Version]
- Jin, X.B.; Su, T.L.; Kong, J.L.; Bai, Y.T.; Miao, B.B.; Dou, C. State-of-the-art mobile intelligence: Enabling robots to move like humans by estimating mobility with artificial intelligence. Appl. Sci. 2018, 8, 379. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Papageorgiou, M. Real-time freeway traffic state estimation based on extended Kalman filter: A general approach. Transp. Res. Part B Methodol. 2005, 39, 141–167. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, X.; Zhang, W.; Liu, X.; Guo, Y. A Nonlinear Double Model for Multisensor-Integrated Navigation Using the Federated EKF Algorithm for Small UAVs. Sensors 2020, 20, 2974. [Google Scholar] [CrossRef] [PubMed]
- Du, H.; Wang, W.; Xu, C.; Xiao, R.; Sun, C. Real-Time Onboard 3D State Estimation of an Unmanned Aerial Vehicle in Multi-Environments Using Multi-Sensor Data Fusion. Sensors 2020, 20, 919. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Julier, S.J. The scaled unscented transformation. In Proceedings of the American Control Conference, Anchorage, AK, USA, 8–10 May 2002; Volume 6, pp. 4555–4559. [Google Scholar]
- Wang, F.; Su, T.; Jin, X.; Zheng, Y.; Kong, J.; Bai, Y. Indoor tracking by RFID fusion with IMU data. Asian J. Control 2019, 21, 1768–1777. [Google Scholar] [CrossRef]
- Jin, X.B.; Dou, C.; Su, T.L.; Lian, X.F.; Shi, Y. Parallel Irregular Fusion Estimation Based on Nonlinear Filter for Indoor RFID Tracking System. Int. J. Distrib. Sens. Netw. 2016. [Google Scholar] [CrossRef] [Green Version]
- Luo, Z.; Fu, Z.; Xu, Q. An Adaptive Multi-Dimensional Vehicle Driving State Observer Based on Modified Sage-Husa UKF Algorithm. Sensors 2020, 20, 6889. [Google Scholar] [CrossRef]
- Liu, J.; Wang, P.; Zha, F.; Guo, W.; Jiang, Z.; Sun, L. A Strong Tracking Mixed-Degree Cubature Kalman Filter Method and Its Application in a Quadruped Robot. Sensors 2020, 20, 2251. [Google Scholar] [CrossRef]
- Zhang, X.; Shen, Y. Distributed Kalman Filtering Based on the Non-Repeated Diffusion Strategy. Sensors 2020, 20, 6923. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, J.; Hu, G.; Zhong, Y. Set-Membership Based Hybrid Kalman Filter for Nonlinear State Estimation under Systematic Uncertainty. Sensors 2020, 20, 627. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nan, D.; Wang, W.; Wang, K.; Mahfoud, R.J.; Alhelou, H.H.; Siano, P. Dynamic State Estimation for Synchronous Machines Based on Adaptive Ensemble Square Root Kalman Filter. Appl. Sci. 2019, 9, 5200. [Google Scholar] [CrossRef] [Green Version]
- Santos, N.P.; Lobo, V.; Bernardino, A. Unmanned Aerial Vehicle Tracking Using a Particle Filter Based Approach. In Proceedings of the IEEE International Underwater Technology Symposium, UT 2019—Proceedings, Kaohsiung, Taiwan, 16–19 April 2019; pp. 1–10. [Google Scholar]
- Zhao, Z.; Yao, P.; Wang, X.; Xu, J.; Wang, L.; Yu, J. Reliable flight performance assessment of multirotor based on interacting multiple model particle filter and health degree. Chin. J. Aeronaut. 2019, 32, 444–453. [Google Scholar] [CrossRef]
- Arulampalam, M.S.; Maskell, S.; Gordon, N.; Clapp, T. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Trans. Signal Process. 2002, 50, 174–188. [Google Scholar] [CrossRef] [Green Version]
- Leeuwen, P.J.V.; Künsch, H.R.; Nerger, L.; Potthast, R.; Reich, S. Particle filters for high-dimensional geoscience applications: A review. Q. J. R. Meteorol. Soc. 2019, 145, 2335–2365. [Google Scholar] [CrossRef] [PubMed]
- Del Moral, P. Non Linear Filtering: Interacting Particle Solution. Markov Process. Relat. Fields 1996, 2, 555–580. [Google Scholar]
- Stordal, A.S.; Karlsen, H.A.; Nævdal, G.; Skaug, H.J.; Vallès, B. Bridging the ensemble Kalman filter and particle filters: The adaptive Gaussian mixture filter. Comput. Geosci. 2011, 15, 293–305. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.; Liu, S.; Xu, C.; Liu, B.; Yang, M.H. Correlation Particle Filter for Visual Tracking. IEEE Trans. Image Process. 2018, 27, 2676–2687. [Google Scholar] [CrossRef] [PubMed]
- Jing, Y.; Chen, Y. Distributed Color-Based Particle Filter for Target Tracking in Camera Network. In Proceedings of the International Conference on Collaborative Computing: Networking, Applications and Worksharing, Shanghai, China, 16–18 October 2020; pp. 396–406. [Google Scholar]
- Bilik, I.; Tabrikian, J. Maneuvering Target Tracking in the Presence of Glint using the Nonlinear Gaussian Mixture Kalman Filter. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 246–262. [Google Scholar] [CrossRef]
- Bengua, J.A.; Tuan, H.D.; Duong, T.Q.; Poor, H.V. Joint Sensor and Relay Power Control in Tracking Gaussian Mixture Targets by Wireless Sensor Networks. IEEE Trans. Signal Process. 2018, 66, 492–506. [Google Scholar] [CrossRef] [Green Version]
- Ding, F.; Wang, X.H.; Mao, L.; Xu, L. Joint state and multi-innovation parameter estimation for time-delay linear systems and its convergence based on the Kalman filtering. Digit. Signal Process 2017, 62, 211–223. [Google Scholar] [CrossRef]
- Ding, F.; Xu, L.; Zhu, Q. Performance analysis of the generalised projection identification for time-varying systems. IET Control Theory Appl. 2016, 10, 2506–2514. [Google Scholar] [CrossRef] [Green Version]
- Ding, F.; Xu, L.; Meng, D.D. Gradient estimation algorithms for the parameter identification of bilinear systems using the auxiliary model. J. Comput. Appl. Math. 2020, 369, 112575. [Google Scholar] [CrossRef]
- Xu, L. The parameter estimation algorithms based on the dynamical response measurement data. Adv. Mech. Eng. 2017, 9, 1687814017730003. [Google Scholar] [CrossRef]
- Pan, J.; Jiang, X.; Wan, X.K.; Ding, W. A filtering based multi-innovation extended stochastic gradient algorithm for multivariable control systems. Int. J. Control Autom. Syst. 2017, 15, 1189–1197. [Google Scholar] [CrossRef]
- Zhang, X. Recursive parameter estimation and its convergence for bilinear systems. IET Control Theory Appl. 2020, 14, 677–688. [Google Scholar] [CrossRef]
- Li, M.H.; Liu, X.M. The least squares based iterative algorithms for parameter estimation of a bilinear system with autoregressive noise using the data filtering technique. Signal Process 2018, 147, 23–34. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Q.Y. Recursive identification of bilinear time-delay systems through the redundant rule. J. Frankl. Inst. 2020, 257, 726–747. [Google Scholar] [CrossRef]
- Frezzatto, L.; de Oliveira, M.C.; Oliveira, R.C.; Peres, P.L. Robust H∞ filter design with past output measurements for uncertain discrete-time systems. Automatica 2016, 71, 151–158. [Google Scholar] [CrossRef]
- Dehghannasiri, R.; Esfahani, M.S.; Dougherty, E.R. Intrinsically Bayesian Robust Kalman Filter: An Innovation Process Approach. IEEE Trans. Signal Process. 2017, 65, 2531–2546. [Google Scholar] [CrossRef]
- Nishanthi, D.; Banu, L.J.; Balasubramaniam, P. Robust guaranteed cost state estimation for discrete-time systems with random delays and random uncertainties. Int. J. Adapt. Control Signal Process. 2017, 31, 1361–1372. [Google Scholar] [CrossRef]
- Roy, S.; Berry, D.W.; Petersen, I.R.; Huntington, E.H. Robust guaranteed-cost adaptive quantum phase estimation. Phys. Rev. A 2017, 95. [Google Scholar] [CrossRef] [Green Version]
- Ding, D.; Wang, Z.; Dong, H.; Shu, H. Distributed H-infinity state estimation with stochastic parameters and nonlinearities through sensor networks: The finite-horizon case. Automatica 2012, 48, 1575–1585. [Google Scholar] [CrossRef]
- Li, Z.; Chang, X. Robust H∞ control for networked control systems with randomly occurring uncertainties: Observer-based case. ISA Trans. 2018, 83, 13–24. [Google Scholar] [CrossRef]
- Pal, B.C.; Coonick, A.H.; Jaimoukha, I.M.; El-Zobaidi, H. A linear matrix inequality approach to robust damping control design in power systems with superconducting magnetic energy storage device. IEEE Trans. Power Syst. 2000, 15, 356–362. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Fu, Y.; Lin, H.; Liu, J.; Gao, M.; He, Z. A New Constrained State Estimation Method Based on Unscented H∞ Filtering. Appl. Sci. 2020, 10, 8484. [Google Scholar] [CrossRef]
- Daeipour, E.; Bar-Shalom, Y. IMM tracking of maneuvering targets in the presence of glint. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 996–1003. [Google Scholar] [CrossRef]
- Xu, L.; Li, X.R.; Duan, Z. Hybrid grid multiple-model estimation with application to maneuvering target tracking. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 122–136. [Google Scholar] [CrossRef]
- Jin, X.B.; Lian, X.F.; Su, T.L.; Shi, Y.; Miao, B.B. Closed-Loop Estimation for Randomly Sampled Measurements in Target Tracking System. Math. Probl. Eng. 2014, 2014, 315908. [Google Scholar]
- Ouyang, W.; Wu, Y.; Member, S.; Chen, H. INS/Odometer Land Navigation by Accurate Measurement Modeling and Multiple-Model Adaptive Estimation. IEEE Trans. Aerosp. Electron. Syst. 2020, 57, 245–262. [Google Scholar] [CrossRef]
- Bai, Y.; Wang, X.; Jin, X.; Su, T.; Kong, J. Adaptive filtering for MEMS gyroscope with dynamic noise model. ISA Trans. 2020, 101, 430–441. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Ding, F.; Zhu, Q.M. Hierarchical Newton and least squares iterative estimation algorithm for dynamic systems by transfer functions based on the impulse responses. Int. J. Syst. Sci. 2019, 50, 141–151. [Google Scholar] [CrossRef] [Green Version]
- Xu, L. Iterative parameter estimation for signal models based on measured data. Circuits Syst. Signal Process 2018, 37, 3046–3069. [Google Scholar] [CrossRef]
- Gu, Y.; Liu, J.; Li, X.; Chou, Y.; Ji, Y. State space model identification of multirate processes with time-delay using the expectation maximization. J. Frankl. Inst. 2019, 356, 1623–1639. [Google Scholar] [CrossRef]
- Xu, L.; Xiong, W.; Alsaedi, A.; Hayat, T. Hierarchical Parameter Estimation for the Frequency Response Based on the Dynamical Window Data. Int. J. Control Autom. Syst. 2018, 16, 1756–1764. [Google Scholar] [CrossRef]
- Xu, L.; Ding, F.; Lu, X.; Wan, L.; Sheng, J. Hierarchical multi-innovation generalised extended stochastic gradient methods for multivariable equation-error autoregressive moving average systems. IET Control Theory Appl. 2020, 14, 1276–1286. [Google Scholar] [CrossRef]
- Pan, J.B.; Ma, H.; Zhang, X.; Liu, Q.Y. Recursive coupled projection algorithms for multivariable output-error-like systems with coloured noises. IET Signal Process 2020, 14, 455–466. [Google Scholar] [CrossRef]
- Xu, L.; Ding, F.; Wan, L.; Sheng, J. Separable multi-innovation stochastic gradient estimation algorithm for the nonlinear dynamic responses of systems. Int. J. Adapt. Control Signal Process. 2020, 34, 937–954. [Google Scholar] [CrossRef]
- Zhang, X.; Ding, F.; Alsaadi, F.E.; Hayat, T. Recursive parameter identification of the dynamical models for bilinear state space systems. Nonlinear Dyn. 2017, 89, 2415–2429. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, L.; Ding, F.; Hayat, T. Combined state and parameter estimation for a bilinear state space system with moving average noise. J. Frankl. Inst. 2018, 355, 3079–3103. [Google Scholar] [CrossRef]
- Gu, Y.; Zhu, Q.; Nouri, H. Bias compensation-based parameter and state estimation for a class of time-delay non-linear state-space models. IET Control Theory Appl. 2020, 14, 2176–2185. [Google Scholar] [CrossRef]
- Jin, X.B.; Du, J.J.; Bao, J. Target Tracking of a Linear Time Invariant System under Irregular Sampling. Int. J. Adv. Robot. Syst. 2012, 9, 219. [Google Scholar]
- Zhang, X.; Ding, F.; Xu, L.; Yang, E.F. State filtering-based least squares parameter estimation for bilinear systems using the hierarchical identification principle. IET Control Theory Appl. 2018, 12, 1704–1713. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Ji, Y.; Wan, L.; Bu, N. Hierarchical recursive generalized extended least squares estimation algorithms for a class of nonlinear stochastic systems with colored noise. J. Frankl. Inst. 2019, 356, 10102–10122. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Jin, X.B.; Yang, N.X.; Wang, X.Y.; Bai, Y.T.; Su, T.L.; Kong, J.L. Integrated predictor based on decomposition mechanism for PM2.5 long-term prediction. Appl. Sci. 2019, 9, 4533. [Google Scholar] [CrossRef] [Green Version]
- Jin, X.B.; Zheng, W.Z.; Kong, J.L.; Wang, X.Y.; Bai, Y.L.; Su, T.L.; Lin, S. Deep-Learning Forecasting Method for Electric Power Load via Attention-Based Encoder-Decoder with Bayesian Optimization. Energies 2021, 14, 1596. [Google Scholar] [CrossRef]
- Sutskever, I.; Vinyals, O.; Le, Q. Sequence to Sequence Learning with Neural Networks. Adv. Neural Inf. Process. Syst. 2014, 27, 3104–3112. [Google Scholar]
- Chorowski, J.K.; Bahdanau, D.; Serdyuk, D.; Cho, K.; Bengio, Y. Attention-based models for speech recognition. Adv. Neural Inf. Process. Syst. 2015, 28, 577–585. [Google Scholar]
- Pham Luong, M.T.; Manning, C.H. Effective Approaches to Attention-based Neural Machine Translation. arXiv 2015, arXiv:1508.04025. [Google Scholar]
- Wang, Y.; Liu, Z.; Hu, D. Multivariate Time Series Prediction Based on Optimized Temporal Convolutional Networks with Stacked Auto-encoders. Mach. Learn. 2019, 2019, 157–172. [Google Scholar]
- Jin, X.B.; Wang, H.X.; Wang, X.Y.; Bai, Y.T.; Su, T.L.; Kong, J.L. Deep-Learning Prediction Model with Serial Two-Level Decomposition Based on Bayesian Optimization. Complexity 2020, 2020, 4346803. [Google Scholar] [CrossRef]
- Jin, X.B.; Yang, N.X.; Wang, X.; Bai, Y.; Su, T.L.; Kong, J. Deep Hybrid Model Based on EMD with Classification by Frequency Characteristics for Long-Term Air Quality Prediction. Mathematics 2020, 8, 214. [Google Scholar] [CrossRef] [Green Version]
- Jin, X.B.; Yu, X.H.; Wang, X.Y.; Bai, Y.T.; Su, T.L.; Kong, J.L. Deep Learning Predictor for Sustainable Precision Agriculture Based on Internet of Things System. Sustainability 2020, 12, 1433. [Google Scholar] [CrossRef] [Green Version]
- Niu, X.; Li, J.; Sun, J. Dynamic Detection of False Data Injection Attack in Smart Grid using Deep Learning. In Proceedings of the 2019 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 18–21 February 2019; pp. 1–6. [Google Scholar]
- Zhang, C.; Zhang, H.; Qiao, J.; Yuan, D.; Zhang, M. Deep Transfer Learning for Intelligent Cellular Traffic Prediction Based on Cross-Domain Big Data. IEEE J. Sel. Areas Commun. 2019, 37, 1389–1401. [Google Scholar] [CrossRef]
- Al-Sharman, M.; Murdoch, D.; Cao, D.; Lv, C.; Zweiri, Y.; Rayside, D.; Melek, W. A Sensorless State Estimation for A Safety-Oriented Cyber-Physical System in Urban Driving: Deep Learning Approach. IEEE/CAA J. Autom. Sin. 2021, 8, 169–178. [Google Scholar] [CrossRef]
- Jin, X.B.; Yang, N.X.; Wang, X.Y.; Bai, Y.T.; Su, T.L.; Kong, J.L. Hybrid Deep Learning Predictor for Smart Agriculture Sensing Based on Empirical Mode Decomposition and Gated Recurrent Unit Group Model. Sensors 2020, 20, 1334. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jin, X.B.; Yu, X.H.; Su, T.L.; Yang, D.N.; Bai, Y.T.; Kong, J.L.; Wang, L. Distributed Deep Fusion Predictor for a Multi-Sensor System Based on Causality Entropy. Entropy 2021, 23, 219. [Google Scholar] [CrossRef]
- Zhang, K.; Zheng, L.; Liu, Z.; Jia, N. A deep learning based multitask model for network-wide traffic speed predication. Neurocomputing 2020, 396, 438–450. [Google Scholar] [CrossRef]
- Mestav, K.R.; Luengo-Rozas, J.; Tong, L. Bayesian State Estimation for Unobservable Distribution Systems via Deep Learning. IEEE Trans. Power Syst. 2019, 34, 4910–4920. [Google Scholar] [CrossRef] [Green Version]
- Mestav, K.R.; Tong, L. Learning the Unobservable: High-Resolution State Estimation via Deep Learning. In Proceedings of the 2019 57th Annual Allerton Conference on Communication, Control, and Computing, Monticello, IL, USA, 24–27 September 2019; pp. 171–176. [Google Scholar]
- Wang, L.; Zhang, T.; Jin, X.; Xu, J.; Wang, X.; Zhang, H.; Yu, J.; Sun, Q.; Zhao, Z.; Xie, Y. An approach of recursive timing deep belief network for algal bloom forecasting. Neural Comput. Appl. 2020, 32, 163–171. [Google Scholar] [CrossRef]
- Yu, W.; De, E. Deep Boltzmann machine for nonlinear system modelling. Int. J. Mach. Learn. Cybern. 2018, 10, 1705–1716. [Google Scholar] [CrossRef]
- Shi, Z.; Bai, Y.; Jin, X.; Wang, X.; Su, T.; Kong, J. Parallel deep prediction with covariance intersection fusion on non-stationary time series. Knowl. Based Syst. 2021, 2021, 106523. [Google Scholar] [CrossRef]
- Bai, Y.; Jin, X.; Wang, X.; Wang, X.; Xu, J. Dynamic correlation analysis method of air pollutants in spatio-temporal analysis. Int. J. Environ. Res. Public Health 2020, 17, 360. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bergstra, J.S.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for hyper-parameter optimization. Adv. Neural Inf. Process. Syst. 2011, 24, 2546–2554. [Google Scholar]
- Zamzam, A.S.; Fu, X.; Sidiropoulos, N.D. Data-Driven Learning-Based Optimization for Distribution System State Estimation. IEEE Trans. Power Syst. 2019, 34, 4796–4805. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Li, Y.; Quevedo, D.E.; Lau, V.; Shi, L. Data-driven power control for state estimation: A Bayesian inference approach. Automatica 2015, 54, 332–339. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Wang, Z.; Xu, M. DeepMTT: A deep learning maneuvering target-tracking algorithm based on bidirectional LSTM network. Inf. Fusion 2020, 53, 289–304. [Google Scholar] [CrossRef]
- Shaukat, N.; Ali, A.; Iqbal, M.J.; Moinuddin, M.; Otero, P. Multi-Sensor Fusion for Underwater Vehicle Localization by Augmentation of RBF Neural Network and Error-State Kalman Filter. Sensors 2021, 21, 1149. [Google Scholar] [CrossRef] [PubMed]
- Khuntia, P.; Hazra, R. An efficient Deep reinforcement learning with extended Kalman filter for device-to-device communication underlaying cellular network. Trans. Emerg. Telecommun. Technol. 2019, 30, e3671. [Google Scholar] [CrossRef]
- Zhang, L.; Mao, D.; Niu, J.; Wu, Q.M.; Ji, Y. Continuous tracking of targets for stereoscopic HFSWR based on IMM filtering combined with ELM. Remote Sens. 2020, 12, 272. [Google Scholar] [CrossRef] [Green Version]
- Zhao, C.; Sun, L.; Yan, Z.; Neumann, G.; Duckett, T.; Stolkin, R. Learning Kalman Network: A deep monocular visual odometry for on-road driving. Robot. Auton. Syst. 2019, 121, 103234. [Google Scholar] [CrossRef]
- Li, Q.; Wu, Z.Y.; Rahman, A. Evolutionary Deep Learning with Extended Kalman Filter for Effective Prediction Modeling and Efficient Data Assimilation. J. Comput. Civ. Eng. 2019, 33, 04019014. [Google Scholar] [CrossRef]
- Gao, C.; Yan, J.; Zhou, S.; Varshney, P.K.; Liu, H. Long short-term memory-based deep recurrent neural networks for target tracking. Inf. Sci. 2019, 502, 279–296. [Google Scholar] [CrossRef]
- Bai, Y.; Wang, X.; Jin, X.; Zhao, Z.; Zhang, B. A neuron-based Kalman filter with nonlinear auto-regressive model. Sensors 2020, 20, 299. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sharman, M.K.S.A. Deep Learning-Based Neural Network Training for State Estimation Enhancement: Application to Attitude Estimation. IEEE Trans. Instrum. Meas. 2019, 69, 24–34. [Google Scholar] [CrossRef] [Green Version]
- Yu, Y.; Liu, Q.; Chambon, S.; Hamzah, M. Using deep Kalman filter to predict drilling time series. In Proceedings of the International Petroleum Technology Conference, Beijing, China, 26–28 March 2019. [Google Scholar] [CrossRef]





| Filter | Requirements for the System | Accuracy for a Practical System | Calculation Cost | Description |
|---|---|---|---|---|
| Kalman filter | Linear, with Gaussian white noise | Low | Low | The requirements for the system are very high, so it is difficult to achieve high accuracy in the actual application system. |
| EKF | Nonlinear, with Gaussian noise | Medium | Low | The performance of UKF and CKF is better than that of EKF, but their calculation amount is slightly larger than that of EKF. |
| UKF | Nonlinear, with Gaussian noise | Medium | Medium | |
| CKF | Nonlinear, with Gaussian noise | Medium | Medium | |
| Gaussian mixture filters | Nonlinear, with non-Gaussian noise | Medium | Medium | These filters have low requirements for the system. However, the amount of calculation is large. |
| Particle filters | Nonlinear, with non-Gaussian noise | High | High |
| References | Network Cell | Hyperparameter Optimization | Type of Network | Purpose |
|---|---|---|---|---|
| [84] | Long short-term memory (LSTM) | Not mentioned | Classic deep learning network | Classify sequence |
| [85] | Gated recurrent unit (GRU) | Not mentioned | Classic deep learning network | Forecasting time-series data |
| [86,87,88] | Recurrent neural network (RNN) | Not mentioned | Classic deep learning network | Machine translation |
| [89] | Attention-based LSTM | Not mentioned | Classic deep learning network | Machine translation |
| [90] | Convolution network | Bayesian optimization | Classic deep learning network | Prediction |
| [91,92,93] | GRU | Bayesian optimization | Classic deep learning network | Prediction |
| [94] | Bidirectional RNN | Not mentioned | Classic deep learning network | Detection |
| [95] | ConvLSTM | Not mentioned | Classic deep learning network | Prediction |
| [96] | RNN | Not mentioned | Classic deep learning network | State estimation |
| [97] | GRU | Manual search | Classic deep learning network | Prediction |
| [98] | LSTM | Manual search | Bayesian deep learning network | Prediction |
| [99] | GRU | Bayesian optimization | Classic deep learning network | Prediction |
| [100,101] | Multi-layer forward neural network | Not mentioned | Bayesian deep learning network | State estimation |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, X.-B.; Robert Jeremiah, R.J.; Su, T.-L.; Bai, Y.-T.; Kong, J.-L. The New Trend of State Estimation: From Model-Driven to Hybrid-Driven Methods. Sensors 2021, 21, 2085. https://doi.org/10.3390/s21062085
Jin X-B, Robert Jeremiah RJ, Su T-L, Bai Y-T, Kong J-L. The New Trend of State Estimation: From Model-Driven to Hybrid-Driven Methods. Sensors. 2021; 21(6):2085. https://doi.org/10.3390/s21062085
Chicago/Turabian StyleJin, Xue-Bo, Ruben Jonhson Robert Jeremiah, Ting-Li Su, Yu-Ting Bai, and Jian-Lei Kong. 2021. "The New Trend of State Estimation: From Model-Driven to Hybrid-Driven Methods" Sensors 21, no. 6: 2085. https://doi.org/10.3390/s21062085
APA StyleJin, X.-B., Robert Jeremiah, R. J., Su, T.-L., Bai, Y.-T., & Kong, J.-L. (2021). The New Trend of State Estimation: From Model-Driven to Hybrid-Driven Methods. Sensors, 21(6), 2085. https://doi.org/10.3390/s21062085








