An Automated High-Accuracy Detection Scheme for Myocardial Ischemia Based on Multi-Lead Long-Interval ECG and Choi-Williams Time-Frequency Analysis Incorporating a Multi-Class SVM Classifier
Abstract
1. Introduction
2. Methodology
2.1. Data Sources
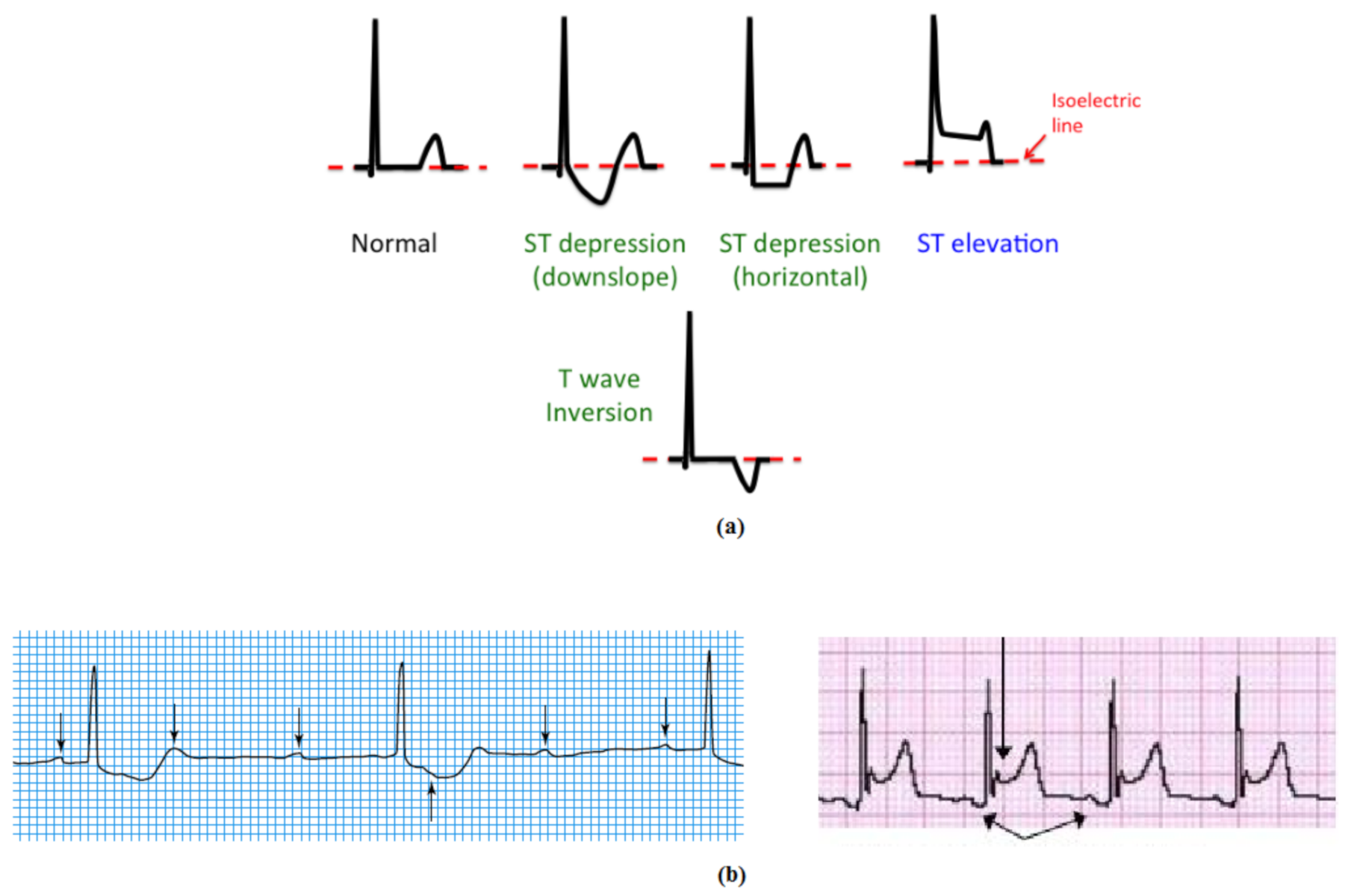
2.2. ECG Data Pre-Processing
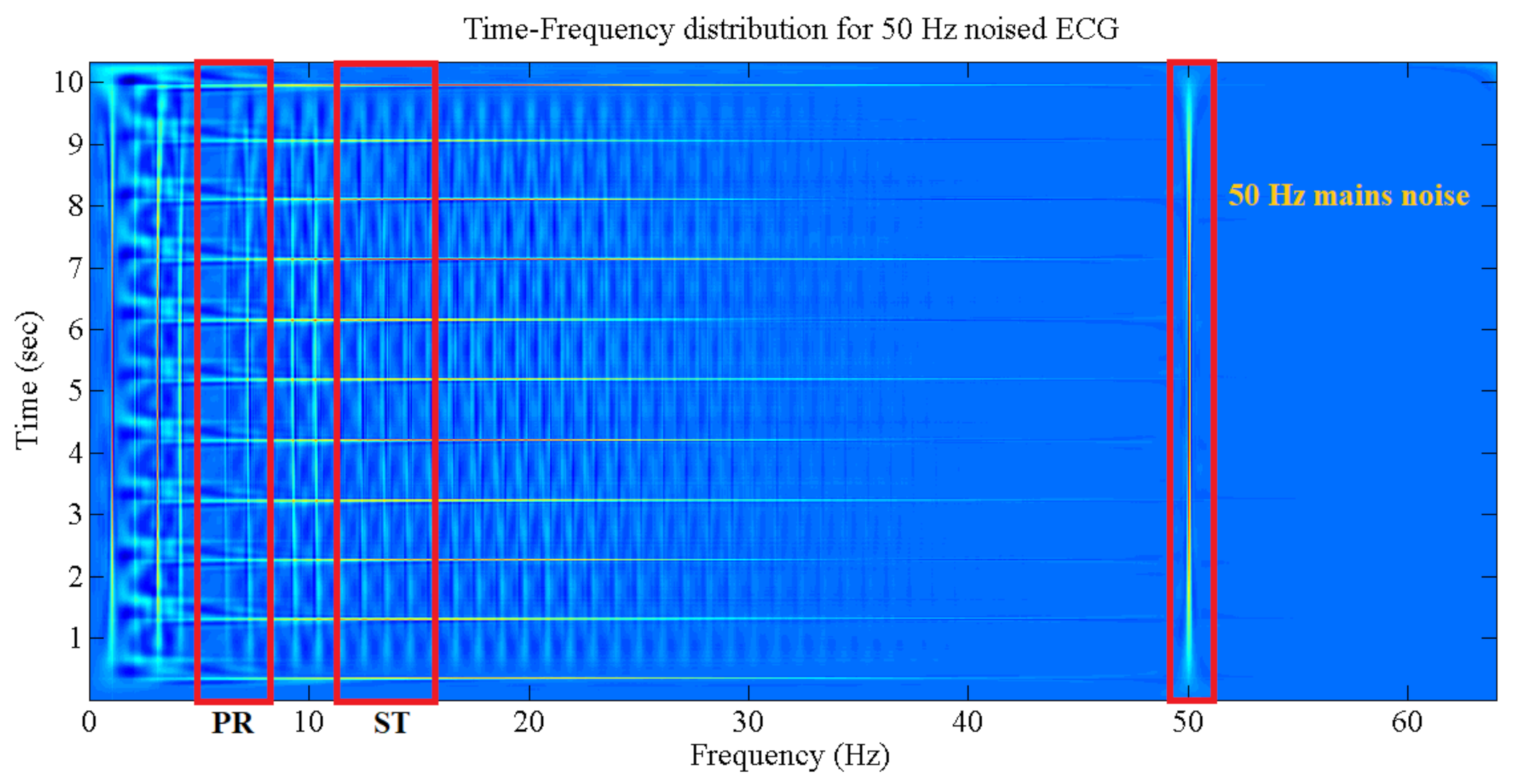
2.3. Choi-Williams Time-Frequency Distribution (CWD)
2.4. The Multi-Class SVM Classifier
2.5. Classifier Structure
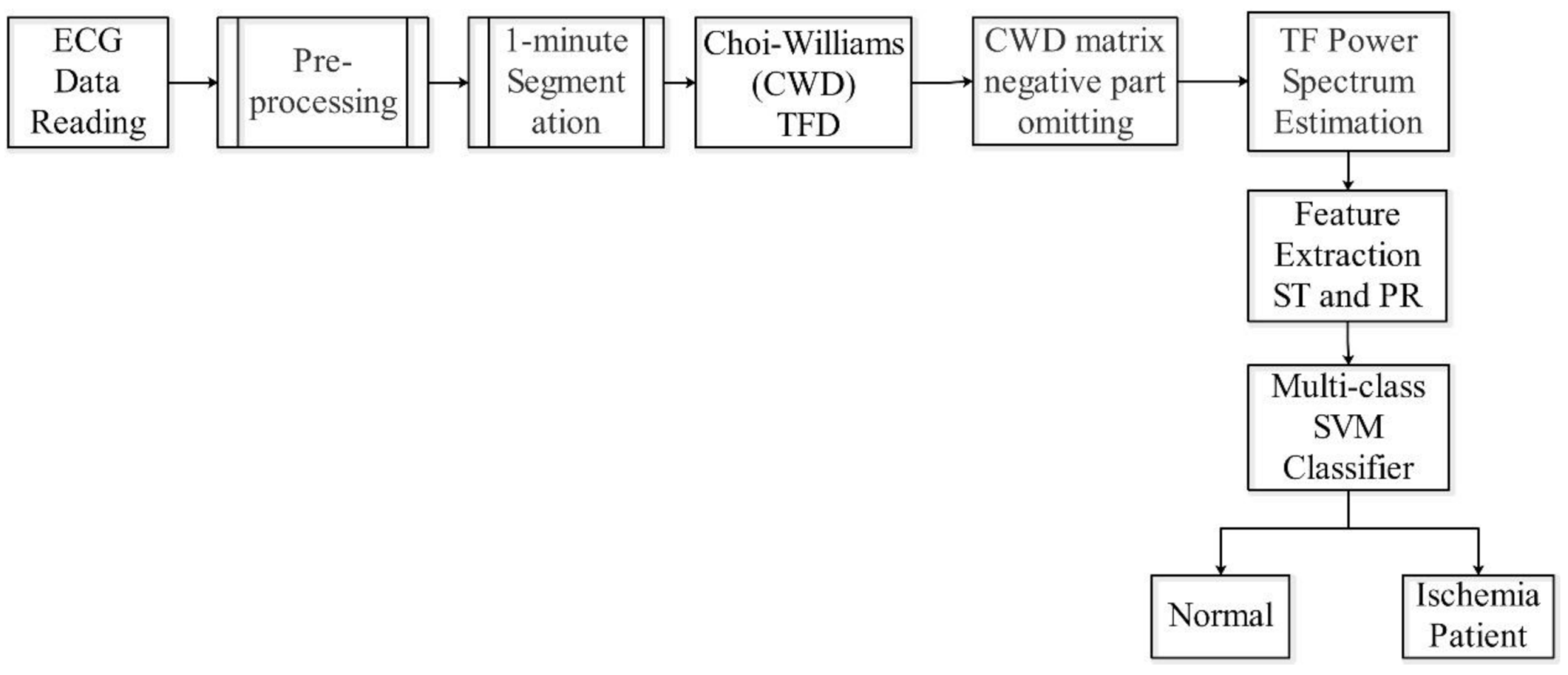
2.6. Algorithm
- Step 1: Pre-processing of raw ECG data from the PTB database. During this pre-processing exercise, raw ECG data are prepared for analysis. The ECG data are re-sampled, filtered, and scaled to remove unwanted artifacts, which may affect the classification results.
- Step 2: The output data from step 1 are segmented into 1 min slots. This segmentation is performed for all ECG data used in this study.
- Step 3: The ECG 1 min data are decomposed with the use of CWD in the time and frequency slots. Each slot contains the relative components which describe the instantaneous heart activity condition according to its electrical changes. The CWD is applied to each ECG lead individually.
- Step 4: The negative elements are omitted from the CWD main matrix. If is the CWD matrix element, then:
- Step 5: Feature extractions are performed by estimating the CWD ST and PR components using the mean values of certain frequency bands, as portrayed below:
- Step 6: The indicator factor (F) is computed by mapping the results from (5) into the multi-class SVM classifier for potential patients. This facilitates the identification of learned margins for the classification of unknown input data.
- Step 1: Repeat the process of part one from step 1 to step 5, except for the use of input data for testing instead of training data.
- Step 2: The result from step 5 is fed into the ex-trained multi-class SVM.
- Step 3: The data are classified according to decision-making in Equation (16).
3. Results
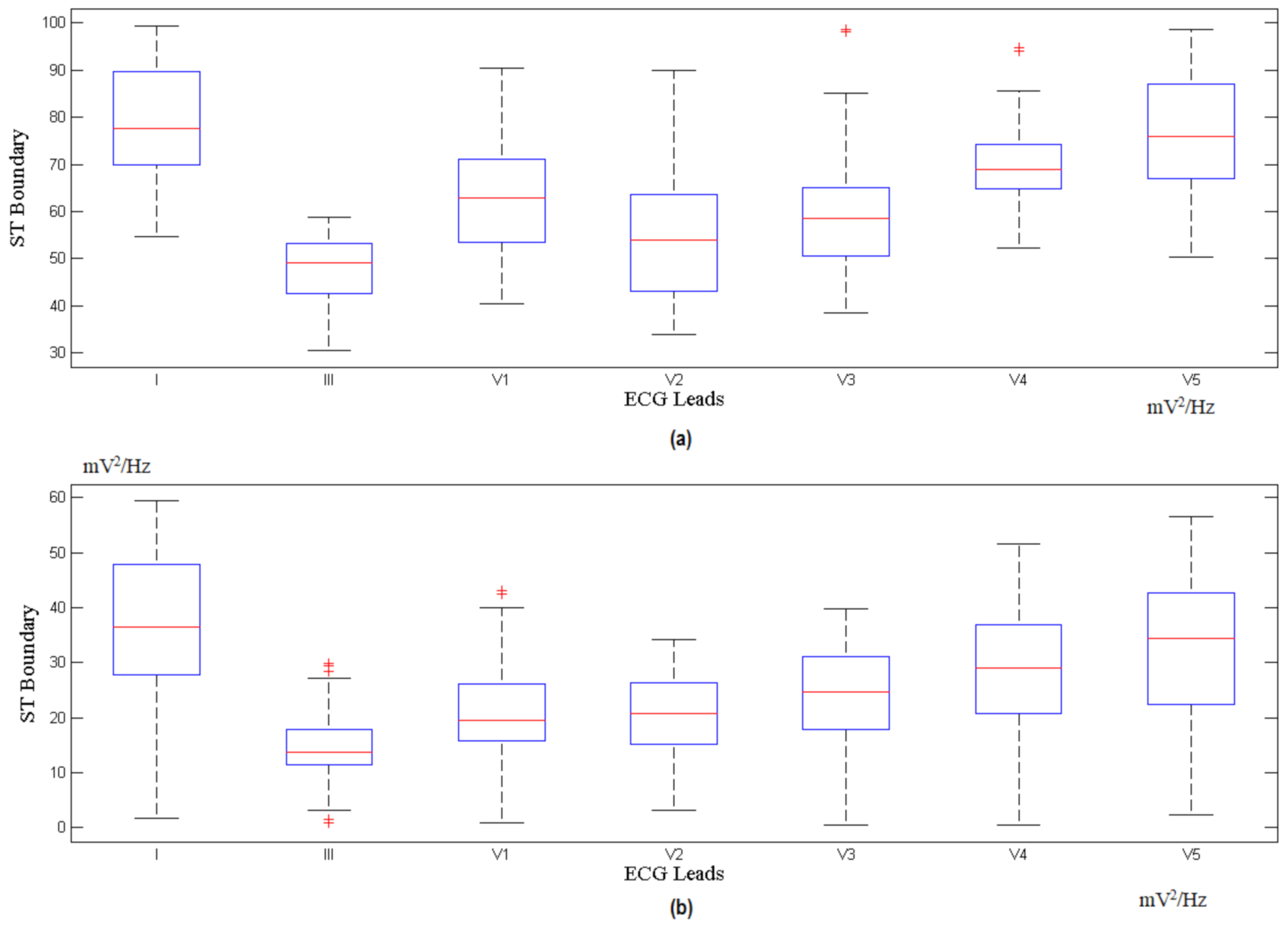
3.1. The Choi-Williams Feature Extraction Process
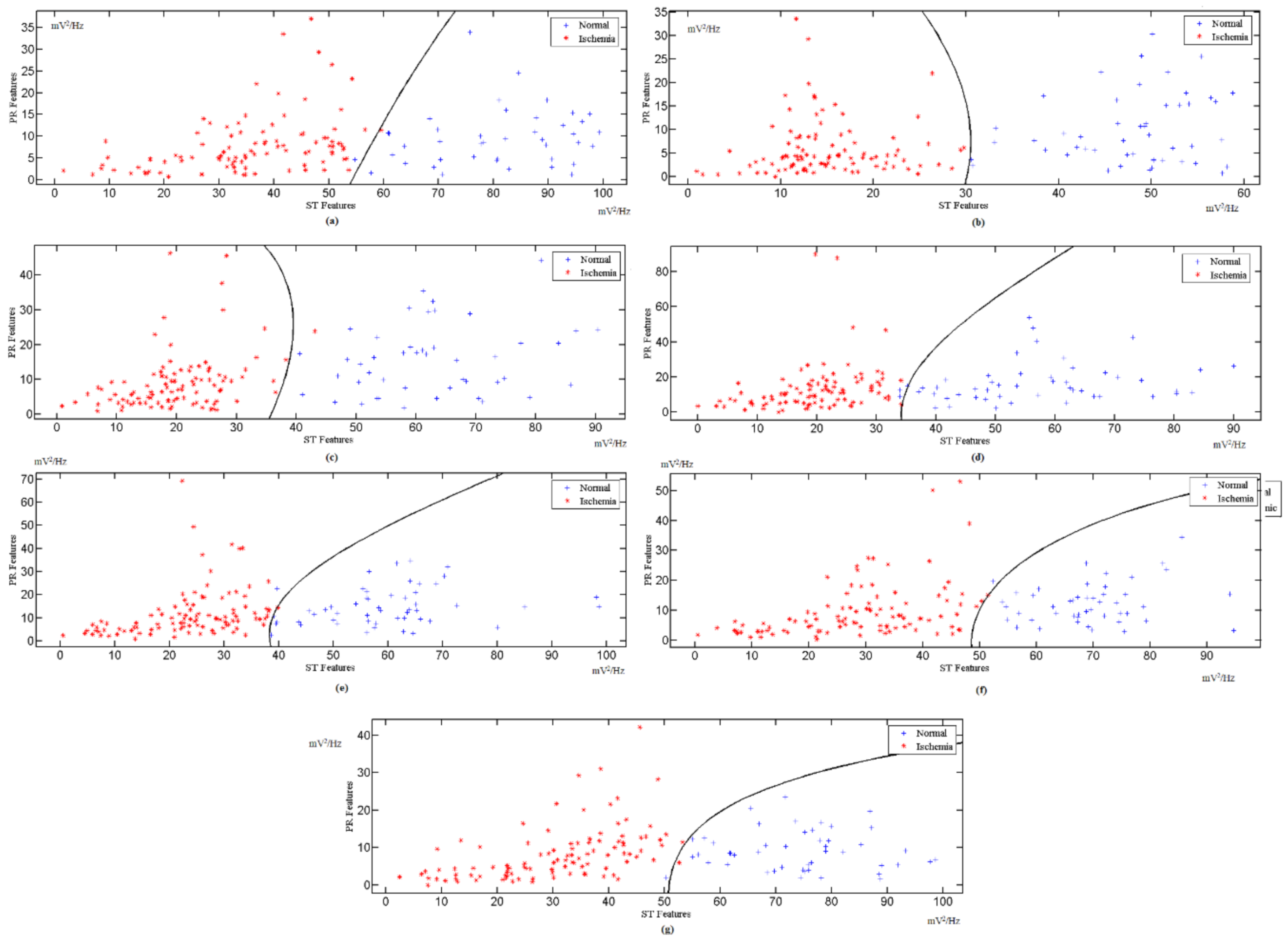
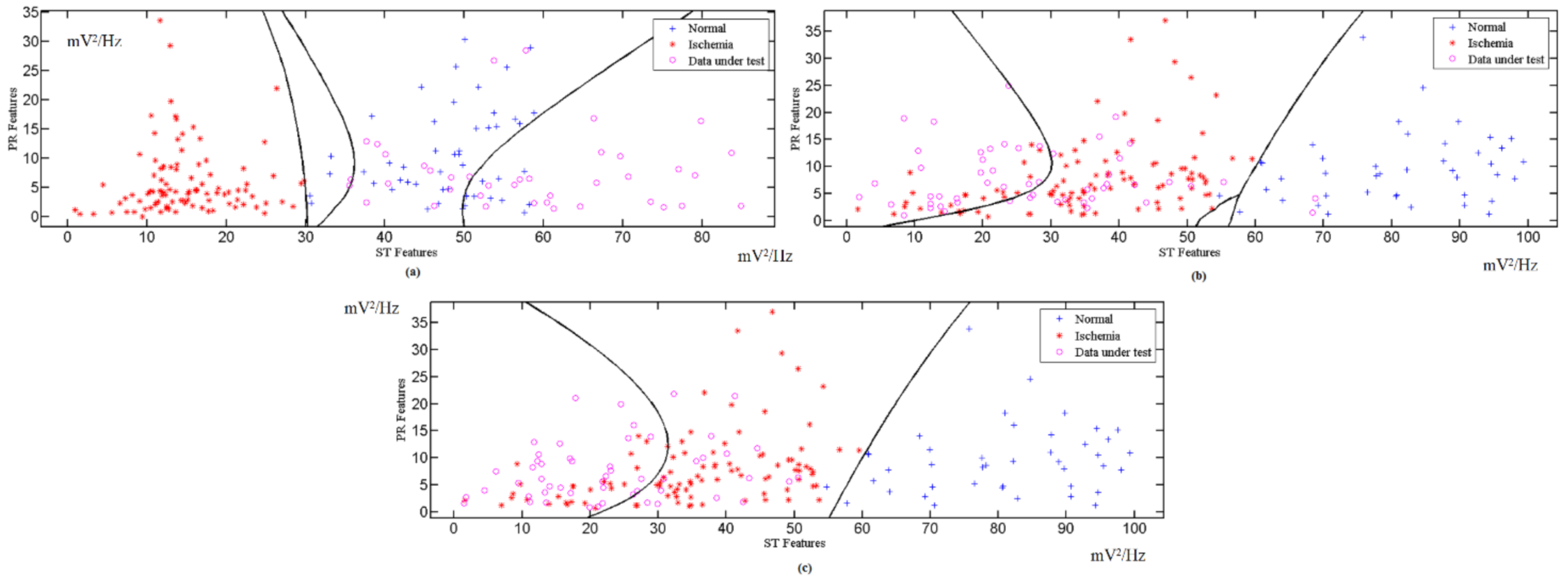
3.2. Indicator Factor (F) Calculation
3.3. Classified Unknown Input Data
4. Discussion
- It comes with a high level of accuracy and sensitivity for the detection of MI cases.
- It excludes the need for ECG morphological detection.
- Its automated feature selection and extraction are combined in a single module.
- Its ten-fold cross validation ensures reliability and robustness.
- It does not require intricate computational machinery.
- The drawbacks of our scheme are listed as follows:
- Its detection of MI cases bypasses other heart problems such as arrhythmia.
- Due to the complexity of time time-frequency calculations, it is currently performed on computers. More efforts should be made to render the proposed scheme available on mobile phones.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Mendis, S.; Davis, S.; Norrving, B. Organizational update: The world health organization global status report on noncommunicable diseases 2014; one more landmark step in the combat against stroke and vascular disease. Stroke 2015, 46, e121–e122. [Google Scholar] [CrossRef]
- Lin, X.; Green, J.C.; Xian, H.; Cai, M.; Skrzypek, J.; Tao, H. Holiday and weekend effects on mortality for acute myocardial infarction in Shanxi, China: A cross-sectional study. Int. J. Public Health 2020, 65, 847–857. [Google Scholar] [CrossRef] [PubMed]
- Acharya, U.R.; Fujita, H.; Adam, M.; Lih, O.S.; Sudarshan, V.K.; Hong, T.J.; Koh, J.E.; Hagiwara, Y.; Chua, C.K.; Poo, C.K. Automated characterization and classification of coronary artery disease and myocardial infarction by decomposition of ECG signals: A comparative study. Inf. Sci. 2017, 377, 17–29. [Google Scholar] [CrossRef]
- Pławiak, P. Novel methodology of cardiac health recognition based on ECG signals and evolutionary-neural system. Expert Syst. Appl. 2018, 92, 334–349. [Google Scholar] [CrossRef]
- Hussein, A.; Hashim, S.; Aziz, A.A.; Rokhani, F.; Adnan, W.W. Automated and high accuracy out-of-hospital heart diseases early detection system. Int. J. Cardiol. 2017, 249, S9–S10. [Google Scholar] [CrossRef]
- Barmpoutis, P.; Dimitropoulos, K.; Apostolidis, A.; Grammalidis, N. Multi-lead ECG signal analysis for myocardial infarction detection and localization through the mapping of Grassmannian and Euclidean features into a common Hilbert space. Biomed. Signal Process. Control 2019, 52, 111–119. [Google Scholar] [CrossRef]
- Ghosh, S.K.; Ponnalagu, R.; Tripathy, R.; Acharya, U.R. Automated detection of heart valve diseases using chirplet transform and multiclass composite classifier with PCG signals. Comput. Biol. Med. 2020, 118, 103632. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, M. Ischemia detection using isoelectric energy function. Comput. Biol. Med. 2016, 68, 76–83. [Google Scholar] [CrossRef] [PubMed]
- Arif, M.; Malagore, I.A.; Afsar, F.A. Detection and localization of myocardial infarction using k-nearest neighbor classifier. J. Med. Syst. 2012, 36, 279–289. [Google Scholar] [CrossRef] [PubMed]
- Madden, A.; Ivulich, S.; Paraskeva, M.; Snell, G.; Dooley, M. Do Your Patients Take Their Tablets? High Prevalence of Non-Adherence to Immunosuppression in Lung Transplant Recipients (LTR). J. Heart Lung Transplant. 2016, 35, S124. [Google Scholar] [CrossRef]
- Lenis, G.; Pilia, N.; Loewe, A.; Schulze, W.H.; Dössel, O. Comparison of baseline wander removal techniques considering the preservation of ST changes in the ischemic ECG: A simulation study. Comput. Math. Methods Med. 2017, 2017, 9295029. [Google Scholar] [CrossRef] [PubMed]
- Madden, A.; Ivulich, S.; Snell, G. The switch between Tacrolimus and Everolimus in a Lung Transplant Recipient (LTR) with Renal Impairment. Hemoglobin (g/L) 2010, 94, 80. [Google Scholar]
- Sun, L.; Lu, Y.; Yang, K.; Li, S. ECG analysis using multiple instance learning for myocardial infarction detection. IEEE Trans. Biomed. Eng. 2012, 59, 3348–3356. [Google Scholar] [CrossRef] [PubMed]
- Safdarian, N.; Dabanloo, N.J.; Attarodi, G. A new pattern recognition method for detection and localization of myocardial infarction using T-wave integral and total integral as extracted features from one cycle of ECG signal. J. Biomed. Sci. Eng. 2014, 2014, 48523. [Google Scholar] [CrossRef]
- Kaveh, A.; Chung, W. Automated classification of coronary atherosclerosis using single lead ECG. In Proceedings of the 2013 IEEE Conference on Wireless Sensor (ICWISE), Penang Island, Malaysia, 19–21 November 2019; pp. 108–113. [Google Scholar]
- Liu, B.; Liu, J.; Wang, G.; Huang, K.; Li, F.; Zheng, Y.; Luo, Y.; Zhou, F. A novel electrocardiogram parameterization algorithm and its application in myocardial infarction detection. Comput. Biol. Med. 2015, 61, 178–184. [Google Scholar] [CrossRef]
- Murthy, H.N.; Meenakshi, M. Efficient Algorithm for Early Detection of Myocardial Ischemia using PCA based Features. Indian J. Sci. Technol. 2016, 9, 1–13. [Google Scholar] [CrossRef]
- Sharma, L.; Tripathy, R.; Dandapat, S. Multiscale energy and eigenspace approach to detection and localization of myocardial infarction. IEEE Trans. Biomed. Eng. 2015, 62, 1827–1837. [Google Scholar] [CrossRef]
- Hsu, C.-C.; Lin, B.-S.; He, K.-Y.; Lin, B.-S. Design of a wearable 12-lead noncontact electrocardiogram monitoring system. Sensors 2019, 19, 1509. [Google Scholar] [CrossRef] [PubMed]
- Tan, J.H.; Hagiwara, Y.; Pang, W.; Lim, I.; Oh, S.L.; Adam, M.; San Tan, R.; Chen, M.; Acharya, U.R. Application of stacked convolutional and long short-term memory network for accurate identification of CAD ECG signals. Comput. Biol. Med. 2018, 94, 19–26. [Google Scholar] [CrossRef]
- Acharya, U.R.; Fujita, H.; Lih, O.S.; Hagiwara, Y.; Tan, J.H.; Adam, M. Automated detection of arrhythmias using different intervals of tachycardia ECG segments with convolutional neural network. Inf. Sci. 2017, 405, 81–90. [Google Scholar] [CrossRef]
- Sudarshan, V.K.; Acharya, U.R.; Oh, S.L.; Adam, M.; Tan, J.H.; Chua, C.K.; Chua, K.P.; San Tan, R. Automated diagnosis of congestive heart failure using dual tree complex wavelet transform and statistical features extracted from 2 s of ECG signals. Comput. Biol. Med. 2017, 83, 48–58. [Google Scholar] [CrossRef]
- Hlawatsch, F.; Auger, F. Time-Frequency Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- “Treatment_of_Angina”, Pharmwiki, Tulane University School of Medicine. Available online: https://tmedweb.tulane.edu/pharmwiki/doku.php/treatment_of_angina?rev=1486134671 (accessed on 25 November 2020).
- Rangayyan, R.M. Biomedical Signal Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Villani, V.; Sabattini, L.; Riggio, G.; Secchi, C.; Minelli, M.; Fantuzzi, C. A natural infrastructure-less human–robot interaction system. IEEE Robot. Autom. Lett. 2017, 2, 1640–1647. [Google Scholar] [CrossRef]
- Zhang, J.; Tian, J.; Cao, Y.; Yang, Y.; Xu, X. Deep time–frequency representation and progressive decision fusion for ECG classification. Knowl. -Based Syst. 2020, 190, 105402. [Google Scholar] [CrossRef]
- Reljin, N.; Lazaro, J.; Hossain, M.B.; Noh, Y.S.; Cho, C.H.; Chon, K.H. Using the redundant convolutional encoder–decoder to denoise QRS complexes in ECG signals recorded with an armband wearable device. Sensors 2020, 20, 4611. [Google Scholar] [CrossRef]
- Zhang, M.-L.; Zhou, Z.-H. A review on multi-label learning algorithms. IEEE Trans. Knowl. Data Eng. 2014, 26, 1819–1837. [Google Scholar] [CrossRef]
- Choi, H.-I.; Williams, W.J. Improved time-frequency representation of multicomponent signals using exponential kernels. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 862–871. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, L.; Diao, M. LPI radar waveform recognition based on time-frequency distribution. Sensors 2016, 16, 1682. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Hu, L.; Chen, K.; Li, E. Time-frequency analysis of nonstationary complex magneto-hydro-dynamics in fusion plasma signals using the Choi-Williams distribution. Fusion Eng. Des. 2013, 88, 2767–2772. [Google Scholar] [CrossRef]
- Pereira, G.R.; De Oliveira, L.F.; Nadal, J. Reducing cross terms effects in the Choi-Williams transform of mioelectric signals. Comput. Methods Programs Biomed. 2013, 111, 685–692. [Google Scholar] [CrossRef] [PubMed]
- Boashash, B. Time-Frequency Signal Analysis and Processing: A Comprehensive Reference; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Hussein, A.F.; Hashim, S.J.; Aziz, A.F.A.; Rokhani, F.Z.; Adnan, W.A.W. Performance evaluation of time-frequency distributions for ECG signal analysis. J. Med. Syst. 2018, 42, 15. [Google Scholar] [CrossRef] [PubMed]
- Kavzoglu, T.; Colkesen, I. A kernel functions analysis for support vector machines for land cover classification. Int. J. Appl. Earth Obs. Geoinf. 2009, 11, 352–359. [Google Scholar] [CrossRef]
- Hejazi, M.; Al-Haddad, S.; Hashim, S.J.; Aziz, A.F.A.; Singh, Y.P. Non-fiducial based ECG biometric authentication using one-class support vector machine. In Proceedings of the 2017 Signal Processing: Algorithms, Architectures, Arrangements, and Applications (SPA), Poznan, Poland, 20–22 September 2017; pp. 190–194. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Khandait, P.; Bawane, N.; Limaye, S. Features Extraction of ECG Signal for detection of cardiac arrhythmias. Int. J. Comput. Appl. 2012, 2, 520–525. [Google Scholar]
- Vretos, N.; Tefas, A.; Pitas, I. Using robust dispersion estimation in support vector machines. Pattern Recognit. 2013, 46, 3441–3451. [Google Scholar] [CrossRef]
- Weston, J.; Watkins, C. Multi-Class Support Vector Machines; Citeseer: Princeton, NJ, USA, 1998. [Google Scholar]
- Gillani, Z.; Akash, M.S.H.; Rahaman, M.M.; Chen, M. CompareSVM: Supervised, Support Vector Machine (SVM) inference of gene regularity networks. BMC Bioinform. 2014, 15, 1–7. [Google Scholar] [CrossRef]
- Li, H.; Feng, X.; Cao, L.; Li, E.; Liang, H.; Chen, X. A new ECG signal classification based on WPD and ApEn feature extraction. Circuits Syst. Signal Process. 2016, 35, 339–352. [Google Scholar] [CrossRef]
- Li, S.; Fang, H.; Liu, X. Parameter optimization of support vector regression based on sine cosine algorithm. Expert Syst. Appl. 2018, 91, 63–77. [Google Scholar] [CrossRef]
- Xiang, Y.; Lin, Z.; Meng, J. Automatic QRS complex detection using two-level convolutional neural network. Biomed. Eng. Online 2018, 17, 13. [Google Scholar] [CrossRef] [PubMed]
- Burns, N. Cardiovascular Physiology; School of Medicine, Trinity College: Dublin, Ireland, 2013. [Google Scholar]
- Zhang, G.; Si, Y.; Yang, W.; Wang, D. A Robust Multilevel DWT Densely Network for Cardiovascular Disease Classification. Sensors 2020, 20, 4777. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.P.; Chen, Y.; Huang, P. Application of Deep Learning Algorithm in Clinical Analysis of Patients with Serum Electrolyte Disturbance. IEEE Access 2020, 8, 124646–124660. [Google Scholar] [CrossRef]
- Kim, W.-S.; Jin, S.-H.; Park, Y.; Choi, H.-M. A study on development of multi-parametric measure of heart rate variability diagnosing cardiovascular disease. In Proceedings of the World Congress on Medical Physics and Biomedical Engineering 2006, Seoul, Korea, 27 August–1 September 2006; pp. 3480–3483. [Google Scholar]
- Jayachandran, E. Analysis of myocardial infarction using discrete wavelet transform. J. Med. Syst. 2010, 34, 985–992. [Google Scholar] [CrossRef]
- Toole, J.O.; Boashash, B. Fast and memory-efficient algorithms for computing quadratic time—Requency distributions. Appl. Comput. Harmon. Anal. 2013, 35, 350–358. [Google Scholar] [CrossRef]
- Al-Kindi, S.G.; Ali, F.; Farghaly, A.; Nathani, M.; Tafreshi, R. Towards real-time detection of myocardial infarction by digital analysis of electrocardiograms. In Proceedings of the 2011 1st Middle East Conference on Biomedical Engineering, Sharjah, UAE, 22–25 February 2011; pp. 454–457. [Google Scholar]
- Murugan, S.; Radhakrishnan, S. Rule Based Classification Of Ischemic Ecg Beats Using Antminer. Int. J. Eng. Sci. Technol. 2010, 1, 3929–3935. [Google Scholar]
- Park, J.; Pedrycz, W.; Jeon, M. Ischemia episode detection in ECG using kernel density estimation, support vector machine and feature selection. Biomed. Eng. Online 2012, 11, 1. [Google Scholar] [CrossRef] [PubMed]
- Jafarian, K.; Vahdat, V.; Salehi, S.; Mobin, M. Automating detection and localization of myocardial infarction using shallow and end-to-end deep neural networks. Appl. Soft Comput. 2020, 93, 106383. [Google Scholar] [CrossRef]


| Database | Number of Subjects | Number of Records | Length (min) Per Record | Leads | Sampling Frequency | Total Used Data Length (min)/Lead | Training Used Data 80% | Validating Used Data 10% | Testing Used Data 10% |
|---|---|---|---|---|---|---|---|---|---|
| European ST-T database | 78 | 88 | 120 | 2 | 250 | 21,600 | 17,280 | 2160 | 2160 |
| Fantasia Normal database | 40 | 40 | 120 | 1 | 250 | 4800 | 3840 | 480 | 480 |
| Collected data from IBN-AL-NAFEES Hospital | 30 | 30 | 30 | 7 | 133 | 180 | 144 | 18 | 18 |
| Database | Accuracy (%) | Sensitivity (%) | Specificity (%) |
|---|---|---|---|
| European ST-T database | 99.31 | 99.33 | 96.31 |
| Fantasia Normal database | 99.19 | 99.49 | 99.61 |
| Collected data from IBN-AL-NAFEES Hospital | 98.78 | 99.65 | 99.42 |
| Total | 99.09 | 99.49 | 98.44 |
| Method | Accuracy % | Sensitivity % | Specificity % | Database/ Remark | Subjects/ Records Number | Approach |
|---|---|---|---|---|---|---|
| Murugan [53] | NA | 92.30 | 94.30 | European ST-T/Beat | 90 records | Ant-Miner algorithm |
| Jinhopark [54] | NA | 95.70 | 95.30 | European ST-T/Beat | 90 records | Kernel density estimation (DWT based) with SVM |
| Safdarian [14] | 94.00 | NA | NA | PTB/Beat | 290 subjects | T wave integral with KNN, PNN and ANN |
| B. Liu [16] | 94.40 | NA | NA | PTB/Beat | 52 Normal 148 MI | ECG polynomial fitting algorithm PolyFit-based ECG |
| Jian Wang [48] | 89.00 | 91.70 | 81.50 | Hospital data collection | 167 patients | Deep learning-based scheme |
| L. Sun [13] | NA | 91.00 | 85.00 | PTB/Beat | 52 Normal 238 MI | ST segment, Polynomial fitting with KNN |
| Acharya U.R. [3] | 98.50 | 99.70 | 98.50 | PTB/Beat | 52 Normal 148 CAD | DCT features based |
| Murthy [17] | 90.51 | 96.19 | NA | European ST-T/Beat | 16 MI | Statistical analysis with PCA and SVM |
| M. Arif [9] | 98.30 | 97.00 | 99.60 | PTB/Beat | 52 Normal 148 MI | KNN, Time domain feature extraction |
| J.H. Tan [20] | 99.85 | 99.84 | 99.85 | Fantasia, PTB Single lead | 52 Normal 238 MI | 8-layers stacked CNN-LSTM with Blindfold |
| P. Barmpoutis [6] | 99.70 | - | - | PTB/Beat | 290 subjects | mapping of Grassmannian and Euclidean features into a Hilbert space |
| V.K. Sudarshan [22] | 99.86 | 99.78 | 99.94 | MIT-BIH Normal, Fantasia, and BIDMC/2-s Frame | 73 subjects | Dual tree complex WT coefficients features with KNN |
| W.S. Kim [49] | NA | 84.60 | 91.50 | Collected data/HRV | 20 Normal 64 Patients | HRV time and frequency measurements |
| E.S. Jayachan-dran [50] | 95.00 | NA | NA | MIT-BIH/Beat | 6 Normal 2 MI | Time domain analysis |
| S.G. Al-Kindi [52] | 93.70 | 85.00 | 100.00 | PTB/ST-segments | 20 Normal 20 MI | ST segment analysis by DWT |
| L.N. Sharma [18] | 96.00 | 93.00 | 99.00 | PTB/Frame | 52 Normal 238 MI | ST segment analysed by DWT, KNN and SVM |
| Kamal Jafarian [55] | 98.43 | 98.50 | 98.37 | PTB/ST-segments | 52 Normal 148 MI | CNN scheme used with DWT and PCA based features |
| This work | 99.09 | 99.49 | 98.44 | European ST-T, Fantasia, and Collected data/minute | 92 Normal 266 MI | PR and ST feature extraction by using Choi-Williams and classified by Multi-Class SVM |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussein, A.F.; Hashim, S.J.; Rokhani, F.Z.; Wan Adnan, W.A. An Automated High-Accuracy Detection Scheme for Myocardial Ischemia Based on Multi-Lead Long-Interval ECG and Choi-Williams Time-Frequency Analysis Incorporating a Multi-Class SVM Classifier. Sensors 2021, 21, 2311. https://doi.org/10.3390/s21072311
Hussein AF, Hashim SJ, Rokhani FZ, Wan Adnan WA. An Automated High-Accuracy Detection Scheme for Myocardial Ischemia Based on Multi-Lead Long-Interval ECG and Choi-Williams Time-Frequency Analysis Incorporating a Multi-Class SVM Classifier. Sensors. 2021; 21(7):2311. https://doi.org/10.3390/s21072311
Chicago/Turabian StyleHussein, Ahmed Faeq, Shaiful Jahari Hashim, Fakhrul Zaman Rokhani, and Wan Azizun Wan Adnan. 2021. "An Automated High-Accuracy Detection Scheme for Myocardial Ischemia Based on Multi-Lead Long-Interval ECG and Choi-Williams Time-Frequency Analysis Incorporating a Multi-Class SVM Classifier" Sensors 21, no. 7: 2311. https://doi.org/10.3390/s21072311
APA StyleHussein, A. F., Hashim, S. J., Rokhani, F. Z., & Wan Adnan, W. A. (2021). An Automated High-Accuracy Detection Scheme for Myocardial Ischemia Based on Multi-Lead Long-Interval ECG and Choi-Williams Time-Frequency Analysis Incorporating a Multi-Class SVM Classifier. Sensors, 21(7), 2311. https://doi.org/10.3390/s21072311






