Correcting Susceptibility Artifacts of MRI Sensors in Brain Scanning: A 3D Anatomy-Guided Deep Learning Approach
Abstract
:1. Introduction
- We design a deep convolutional network to estimate the 3D displacement field. The deep network is designed to make TS-Net robust to different sizes, resolutions, and modalities of the input image by using batch normalization (BN) layers and size-normalized layers.
- We estimate the displacement field in all three dimensions instead of only along the phase-encoding direction. In other words, TS-Net predicts the displacement field that captures the 3D displacements for every voxel. This, to our knowledge, is a significant improvement compared to most existing SAC methods [10,16], which estimate the distortions only along the PE direction and ignore the distortions along with the other two directions.
- We introduce a learning method that leverages images in the training of TS-Net. The motivation is that the image is widely considered as a gold standard representation of a subject’s brain anatomy [17], and it is readily available in brain studies [18]. To make TS-Net more applicable for general use, the image is used only in training for network regularization, but not in the inference phase.
- We provide an extensive evaluation of the proposed TS-Net on four large public datasets from the Human Connectome Project (HCP) [19]. First, an ablation study is conducted to analyze the effects of using different similarity measures to train TS-Net, the effects of various components in the TS-Net framework, and the effects of using a pre-trained TS-Net when training a new dataset. Second, TS-Net is compared with three state-of-the-art SAC methods, i.e., TOPUP [10], TISAC [15], and S-Net [16], in terms of correction accuracy and processing time.
2. Materials and Methods
2.1. EPI Datasets
2.2. The Proposed TS-Net Method
2.3. Experimental Methods
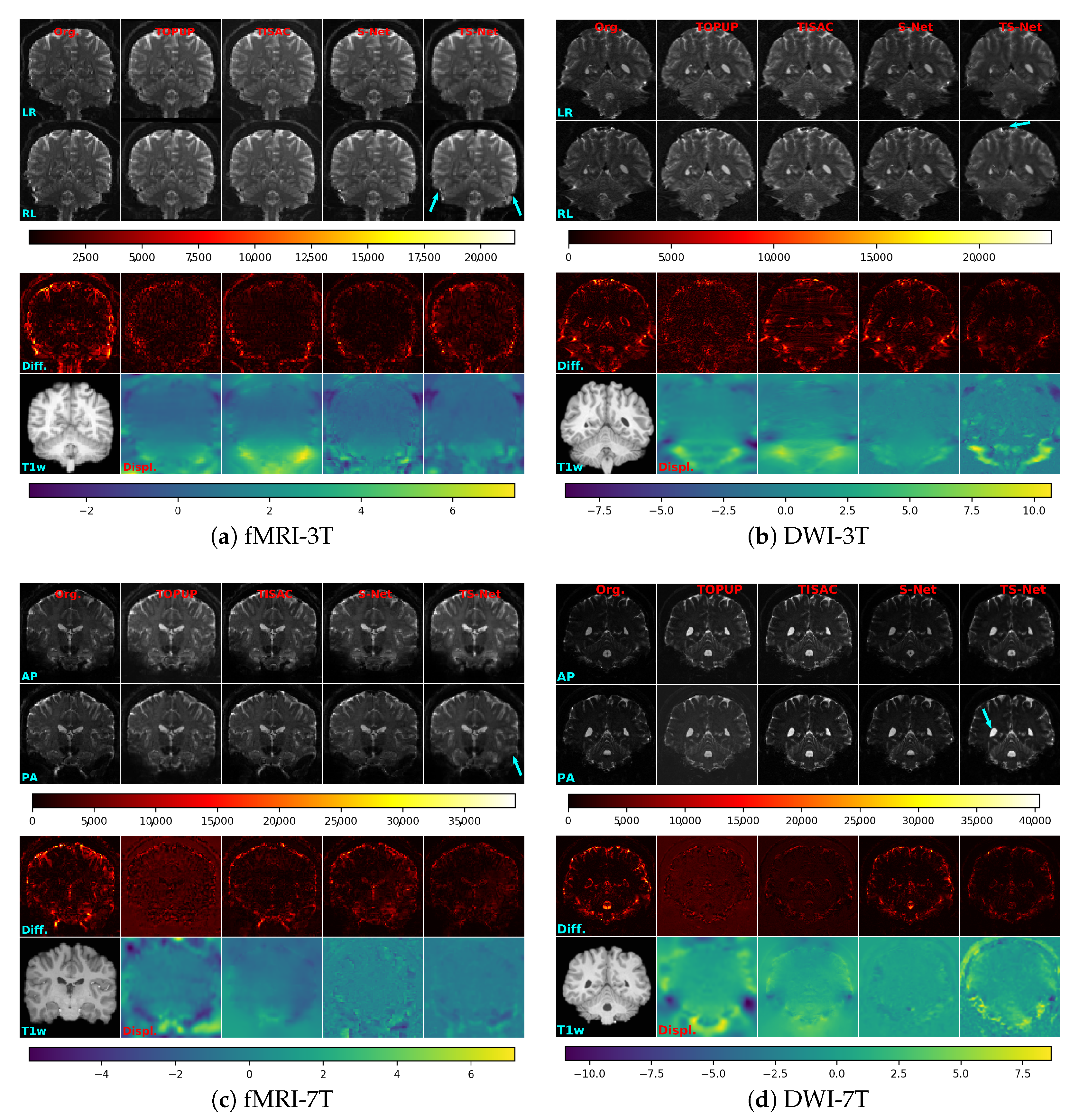
3. Results
3.1. Ablation Study of the Proposed Method
3.2. Comparison with Other Methods
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Similarity Metrics
Appendix A.1. Mean Squared Error
Appendix A.2. Local Cross-Correlation
Appendix A.3. Local Normalized Cross-Correlation
Appendix B. Supplementary Figure

References
- Poustchi-Amin, M.; Mirowitz, S.A.; Brown, J.J.; McKinstry, R.C.; Li, T. Principles and applications of echo-planar imaging: A review for the general radiologist. Radiographics 2001, 21, 767–779. [Google Scholar] [CrossRef]
- Matthews, P.M.; Honey, G.D.; Bullmore, E.T. Applications of fMRI in translational medicine and clinical practice. Nat. Rev. Neurosci. 2006, 7, 732–744. [Google Scholar] [CrossRef]
- Baars, B.J.; Gage, N.M. Brain imaging. In Fundamentals of Cognitive Neuroscience; Book Section 5; Academic Press: San Diego, CA, USA, 2013; pp. 109–140. [Google Scholar]
- Chang, H.; Fitzpatrick, J.M. A technique for accurate magnetic resonance imaging in the presence of field inhomogeneities. IEEE Trans. Image Process. 1992, 11, 319–329. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schmitt, F. Echo-Planar Imaging. In Brain Mapping—An Encyclopedic Reference; Book Section 6; Academic Press: Cambridge, MA, USA, 2015; Volume 1, pp. 53–74. [Google Scholar]
- Chan, R.W.; von Deuster, C.; Giese, D.; Stoeck, C.T.; Harmer, J.; Aitken, A.P.; Atkinson, D.; Kozerke, S. Characterization and correction of Eddy-current artifacts in unipolar and bipolar diffusion sequences using magnetic field monitoring. J. Magn. Reson. 2014, 244, 74–84. [Google Scholar] [CrossRef] [Green Version]
- Irfanoglu, M.O.; Sarlls, J.; Nayak, A.; Pierpaoli, C. Evaluating corrections for Eddy-currents and other EPI distortions in diffusion MRI: Methodology and a dataset for benchmarking. Magn. Reson. Med. 2019, 81, 2774–2787. [Google Scholar] [CrossRef]
- Jezzard, P.; Balaban, R.S. Correction for geometric distortion in echo planar images from B0 field variations. Magn. Reson. Med. 1995, 34, 65–73. [Google Scholar] [CrossRef]
- Holland, D.; Kuperman, J.M.; Dale, A.M. Efficient correction of inhomogeneous static magnetic field-induced distortion in echo planar imaging. NeuroImage 2010, 50, 175–184. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Andersson, J.L.R.; Skare, S.; Ashburner, J. How to correct susceptibility distortions in spin-echo echo-planar images: Application to diffusion tensor imaging. NeuroImage 2003, 20, 870–888. [Google Scholar] [CrossRef]
- Ruthotto, L.; Kugel, H.; Olesch, J.; Fischer, B.; Modersitzki, J.; Burger, M.; Wolters, C.H. Diffeomorphic susceptibility artifact correction of diffusion-weighted magnetic resonance images. Phys. Med. Biol. 2012, 57, 5715–5731. [Google Scholar] [CrossRef] [PubMed]
- Hedouin, R.; Commowick, O.; Bannier, E.; Scherrer, B.; Taquet, M.; Warfield, S.K.; Barillot, C. Block-matching distortion correction of echo-planar images with opposite phase encoding directions. IEEE Trans. Med. Imaging 2017, 36, 1106–1115. [Google Scholar] [CrossRef] [Green Version]
- Irfanoglu, M.O.; Modia, P.; Nayaka, A.; Hutchinson, E.B.; Sarllsc, J.; Pierpaoli, C. DR-BUDDI (diffeomorphic registration for blip-up blip-down diffusion imaging) method for correcting echo planar imaging distortions. NeuroImage 2015, 106, 284–299. [Google Scholar] [CrossRef] [Green Version]
- Duong, S.T.M.; Schira, M.M.; Phung, S.L.; Bouzerdoum, A.; Taylor, H.G.B. Anatomy-guided inverse-gradient susceptibility artefact correction method for high-resolution fMRI. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 786–790. [Google Scholar]
- Duong, S.T.M.; Phung, S.L.; Bouzerdoum, A.; Taylor, H.G.B.; Puckett, A.M.; Schira, M.M. Susceptibility artifact correction for sub-millimeter fMRI using inverse phase encoding registration and T1 weighted regularization. J. Neurosci. Methods 2020, 336, 108625. [Google Scholar] [CrossRef]
- Duong, S.T.M.; Phung, S.L.; Bouzerdoum, A.; Schira, M.M. An unsupervised deep learning technique for susceptibility artifact correction in reversed phase-encoding EPI mages. Magn. Reson. Imaging 2020, 71, 1–10. [Google Scholar] [CrossRef]
- Howarth, C.; Hutton, C.; Deichmann, R. Improvement of the image quality of T1-weighted anatomical brain scans. NeuroImage 2006, 29, 930–937. [Google Scholar] [CrossRef] [PubMed]
- Polimeni, J.R.; Renvall, V.; Zaretskaya, N.; Fischl, B. Analysis strategies for high-resolution UHF-fMRI data. NeuroImage 2018, 168, 296–320. [Google Scholar] [CrossRef]
- Essen, D.C.V.; Ugurbil, K.; Auerbach, E.; Barch, D.; Behrens, T.E.J.; Bucholz, R.; Chang, A.; Chen, L.; Corbetta, M.; Curtiss, S.W.; et al. The human connectome project: A data acquisition perspective. NeuroImage 2012, 62, 2222–2231. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Essen, D.C.V.; Smith, S.M.; Barch, D.M.; Behrens, T.E.J.; Yacoub, E.; Ugurbil, K. The WU-Minn human connectome project: An overview. NeuroImage 2013, 80, 62–79. [Google Scholar] [CrossRef] [Green Version]
- Ugurbil, K.; Xu, J.; Auerbach, E.J.; Moeller, S.; Vu, A.T.; Duarte-Carvajalino, J.M.; Lenglet, C.; Wu, X.; Schmitter, S.; Moortele, P.F.V.D.; et al. Pushing spatial and temporal resolution for functional and diffusion MRI in the Human Connectome Project. NeuroImage 2013, 80, 80–104. [Google Scholar] [CrossRef] [Green Version]
- Balakrishnan, G.; Zhao, A.; Sabuncu, M.R.; Guttag, J.; Dalca, A.V. VoxelMorph: A learning framework for deformable medical image registration. IEEE Trans. Med. Imaging 2019, 38, 1788–1800. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional networks for biomedical image segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Nguyen, T.N.A.; Phung, S.L.; Bouzerdoum, A. Hybrid deep learning-Gaussian process network for pedestrian lane detection in unstructured scenes. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 5324–5338. [Google Scholar] [CrossRef] [PubMed]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Avants, B.B.; Epstein, C.L.; Grossman, M.; Gee, J.C. Symmetric diffeomorphic image registration with cross-correlation: Evaluating automated labeling of elderly and neurodegenerative brain. Med. Image Anal. 2008, 12, 26–41. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baig, A.; Chaudhry, M.A.; Mahmood, A. Local normalized cross correlation for geo-registration. In Proceedings of the 2012 9th International Bhurban Conference on Applied Sciences & Technology (IBCAST), Islamabad, Pakistan, 9–12 January 2012; pp. 70–74. [Google Scholar]
- Chollet, F. Keras. Available online: https://github.com/fchollet/keras (accessed on 1 April 2020).
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kegl, B. Algorithms for hyper-parameter optimization. In Proceedings of the 25th Annual Conference on Neural Information Processing Systems (NIPS 2011), Granada, Spain, 12–14 December 2011; pp. 2546–2554. [Google Scholar]
- Bergstra, J.; Yamins, D.; Cox, D.D. Making a science of model search: Hyperparameter optimization in hundreds of dimensions for vision architectures. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. I-115–I-123. [Google Scholar]
- Bergstra, J.; Komer, B.; Eliasmith, C.; Yamins, D.; Cox, D.D. Hyperopt: A Python library for model selection and hyperparameter optimization. Comput. Sci. Discov. 2015, 8, 014008. [Google Scholar] [CrossRef]
- Ulyanov, D.; Vedaldi, A.; Lempitsky, V. Instance normalization: The missing ingredient for fast stylization. arXiv 2016, arXiv:1607.08022. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Neyshabur, B.; Bhojanapalli, S.; McAllester, D.; Srebro, N. Exploring generalization in deep learning. In Proceedings of the International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–7 December 2017; pp. 5949–5958. [Google Scholar]
- Finn, C.; Abbeel, P.; Levine, S. Model-agnostic meta-learning for fast adaptation of deep networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 11–15 August 2017; Volume 70, pp. 1126–1135. [Google Scholar]
- Nichol, A.; Achiam, J.; Schulman, J. On first-order meta-learning algorithms. arXiv 2018, arXiv:1803.02999v3. [Google Scholar]






| Datasets | No. Subjs. | Gender Distribution | Age Distribution | Image Size (Voxels) | Resolution (mm) | Acquisition Sequences | BW Hz/P | Field Strength | PE Directions | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| fMRI-3T | 182 | Males: | 72 | 22–25 years: | 24 | 90 × 104 × 72 | 2 × 2 × 2 | Multi-band 2D gradient-echo EPI, factor of 8 | 2290 | 3T | LR and RL |
| 26–30 years: | 85 | ||||||||||
| Females: | 110 | 31–35 years: | 71 | ||||||||
| over 36 years: | 2 | ||||||||||
| DWI-3T | 180 | Males: | 71 | 22–25 years: | 23 | 144 × 168 × 111 | 1.25 × 1.25 × 1.25 | Multi-band 2D spin-echo EPI, factor of 3 | 1488 | 3T | LR and RL |
| 26–30 years: | 84 | ||||||||||
| Females: | 109 | 31–35 years: | 71 | ||||||||
| over 36 years: | 2 | ||||||||||
| fMRI-7T | 184 | Males: | 72 | 22–25 years: | 24 | 130 × 130 × 85 | 1.6 × 1.6 × 1.6 | Multi-band 2D gradient-echo EPI, factor of 5 | 1924 | 7T | AP and PA |
| 26–30 years: | 85 | ||||||||||
| Females: | 112 | 31–35 years: | 73 | ||||||||
| over 36 years: | 2 | ||||||||||
| DWI-7T | 178 | Males: | 69 | 22–25 years: | 21 | 200 × 200 × 132 | 1.05 × 1.05 × 1.05 | Multi-band 2D spin-echo EPI, factor of 2 | 1388 | 7T | AP and PA |
| 26–30 years: | 85 | ||||||||||
| Females: | 109 | 31–35 years: | 70 | ||||||||
| over 36 years: | 2 | ||||||||||
| Datasets | Training Set | Validation Set | Test Set | |||
|---|---|---|---|---|---|---|
| No. Subjects | No. Pairs | No. Subjects | No. Pairs | No. Subjects | No. Pairs | |
| fMRI-3T | 140 | 1685 | 16 | 187 | 26 | 1395 |
| DWI-3T | 135 | 392 | 15 | 44 | 30 | 90 |
| fMRI-7T | 138 | 2890 | 15 | 322 | 31 | 1269 |
| DWI-7T | 133 | 140 | 15 | 15 | 30 | 60 |
| Params | fMRI-3T | DWI-3T | fMRI-7T | DWI-7T |
|---|---|---|---|---|
| 0.1771 | 0.002 | 0.9323 | 0.025 | |
| 0.01 | 0.01 | 0.01 | 0.01 | |
| Batch size | 4 | 1 | 1 | 1 |
| Datatypes | fMRI-3T | DWI-3T | fMRI-7T | DWI-7T |
|---|---|---|---|---|
| mean ± std | mean ± std | mean ± std | mean ± std | |
| Uncorrected | 0.335 * ± 0.023 | 0.142 * ± 0.020 | 0.229 * ± 0.023 | 0.120 * ± 0.018 |
| TOPUP | 0.753 * ± 0.024 | 0.468 * ± 0.031 | 0.583 * ± 0.024 | 0.371 * ± 0.025 |
| TISAC | 0.674 * ± 0.036 | 0.436 * ± 0.058 | 0.427 * ± 0.036 | 0.364 * ± 0.048 |
| S-Net | 0.608 * ± 0.027 | 0.242 * ± 0.039 | 0.412 * ± 0.027 | 0.182 * ± 0.025 |
| TS-Net | 0.692 ± 0.022 | 0.571 ± 0.034 | 0.648 ± 0.022 | 0.398 ± 0.031 |
| Methods | Processor | fMRI-3T 90 × 104 × 72 | DWI-3T 144 × 168 × 111 | fMRI-7T 130 × 130 × 85 | DWI-7T200 × 200 × 132 |
|---|---|---|---|---|---|
| (Mean ± std) | (Mean ± std) | (Mean ± std) | (Mean ± std) | ||
| TOPUP | CPU | 252.55 ± 3.61 | 997.39 ± 9.04 | 535.71 ± 44.29 | 1944.65 ± 18.72 |
| TISAC | 25.76 ± 11.81 | 57.73 ± 12.03 | 28.48 ± 5.14 | 126.13 ± 26.25 | |
| S-Net | 0.63 ± 0.03 | 2.21 ± 0.03 | 1.36 ± 0.03 | 4.55 ± 0.04 | |
| TS-Net | 0.65 ± 0.04 | 2.30 ± 0.05 | 1.45 ± 0.04 | 4.92 ± 0.06 | |
| S-Net | GPU | 0.13 ± 0.14 | 0.42 ± 0.18 | 0.22 ± 0.16 | 0.72 ± 0.25 |
| TS-Net | 0.14 ± 0.16 | 0.43 ± 0.21 | 0.23 ± 0.18 | 0.80 ± 0.26 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duong, S.T.M.; Phung, S.L.; Bouzerdoum, A.; Ang, S.P.; Schira, M.M. Correcting Susceptibility Artifacts of MRI Sensors in Brain Scanning: A 3D Anatomy-Guided Deep Learning Approach. Sensors 2021, 21, 2314. https://doi.org/10.3390/s21072314
Duong STM, Phung SL, Bouzerdoum A, Ang SP, Schira MM. Correcting Susceptibility Artifacts of MRI Sensors in Brain Scanning: A 3D Anatomy-Guided Deep Learning Approach. Sensors. 2021; 21(7):2314. https://doi.org/10.3390/s21072314
Chicago/Turabian StyleDuong, Soan T. M., Son Lam Phung, Abdesselam Bouzerdoum, Sui Paul Ang, and Mark M. Schira. 2021. "Correcting Susceptibility Artifacts of MRI Sensors in Brain Scanning: A 3D Anatomy-Guided Deep Learning Approach" Sensors 21, no. 7: 2314. https://doi.org/10.3390/s21072314
APA StyleDuong, S. T. M., Phung, S. L., Bouzerdoum, A., Ang, S. P., & Schira, M. M. (2021). Correcting Susceptibility Artifacts of MRI Sensors in Brain Scanning: A 3D Anatomy-Guided Deep Learning Approach. Sensors, 21(7), 2314. https://doi.org/10.3390/s21072314








