Design of a New 1D Halbach Magnet Array with Good Sinusoidal Magnetic Field by Analyzing the Curved Surface
Abstract
:1. Introduction
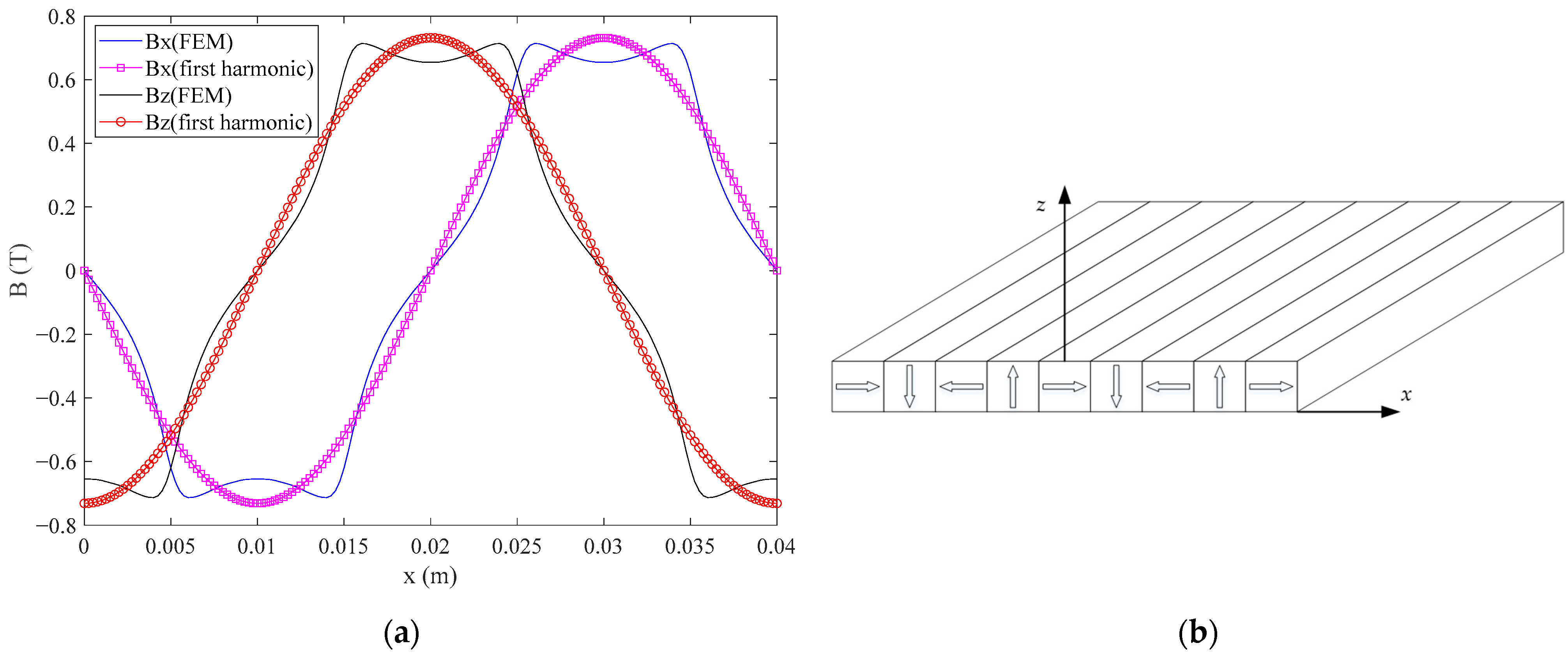
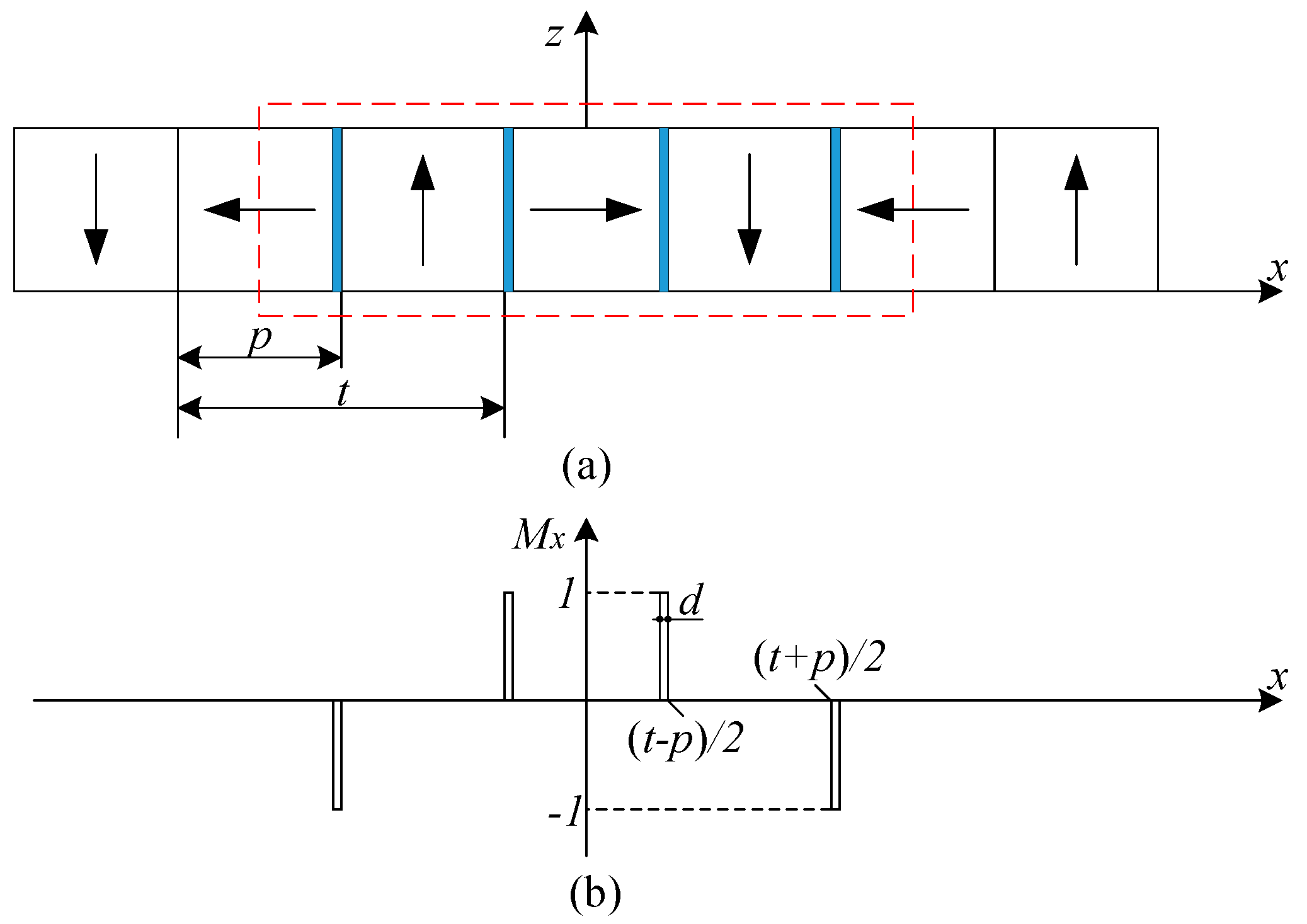
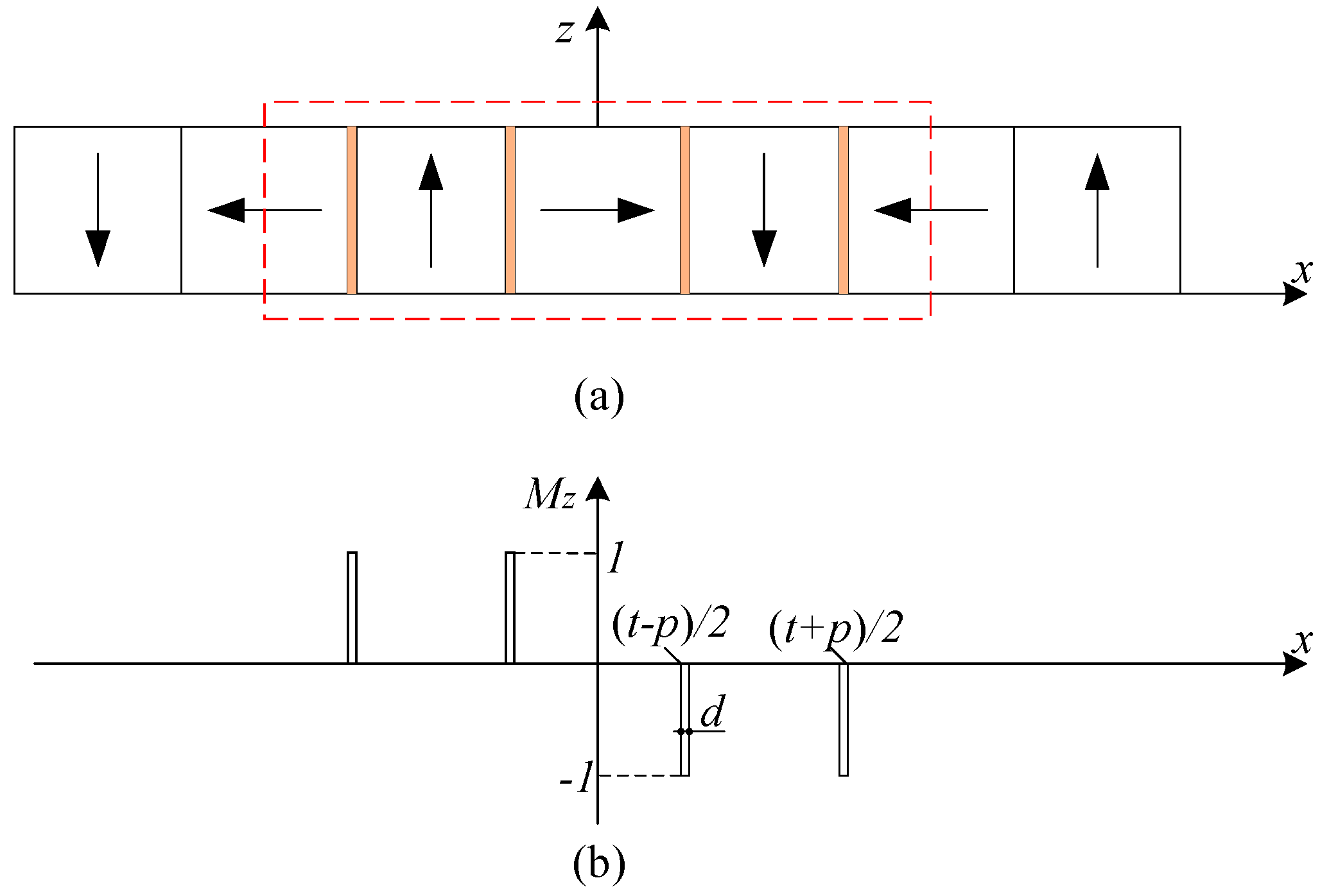
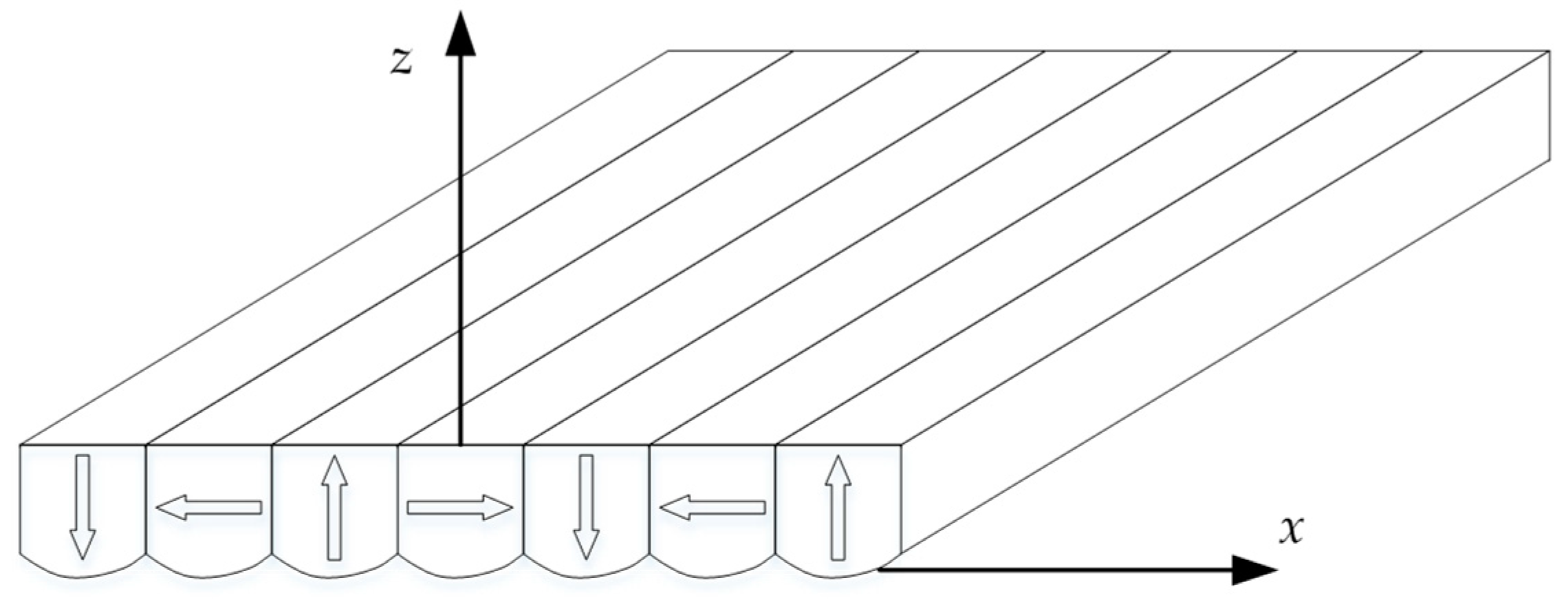
2. Modeling of the New Magnet Array
3. Design of New Magnet Array
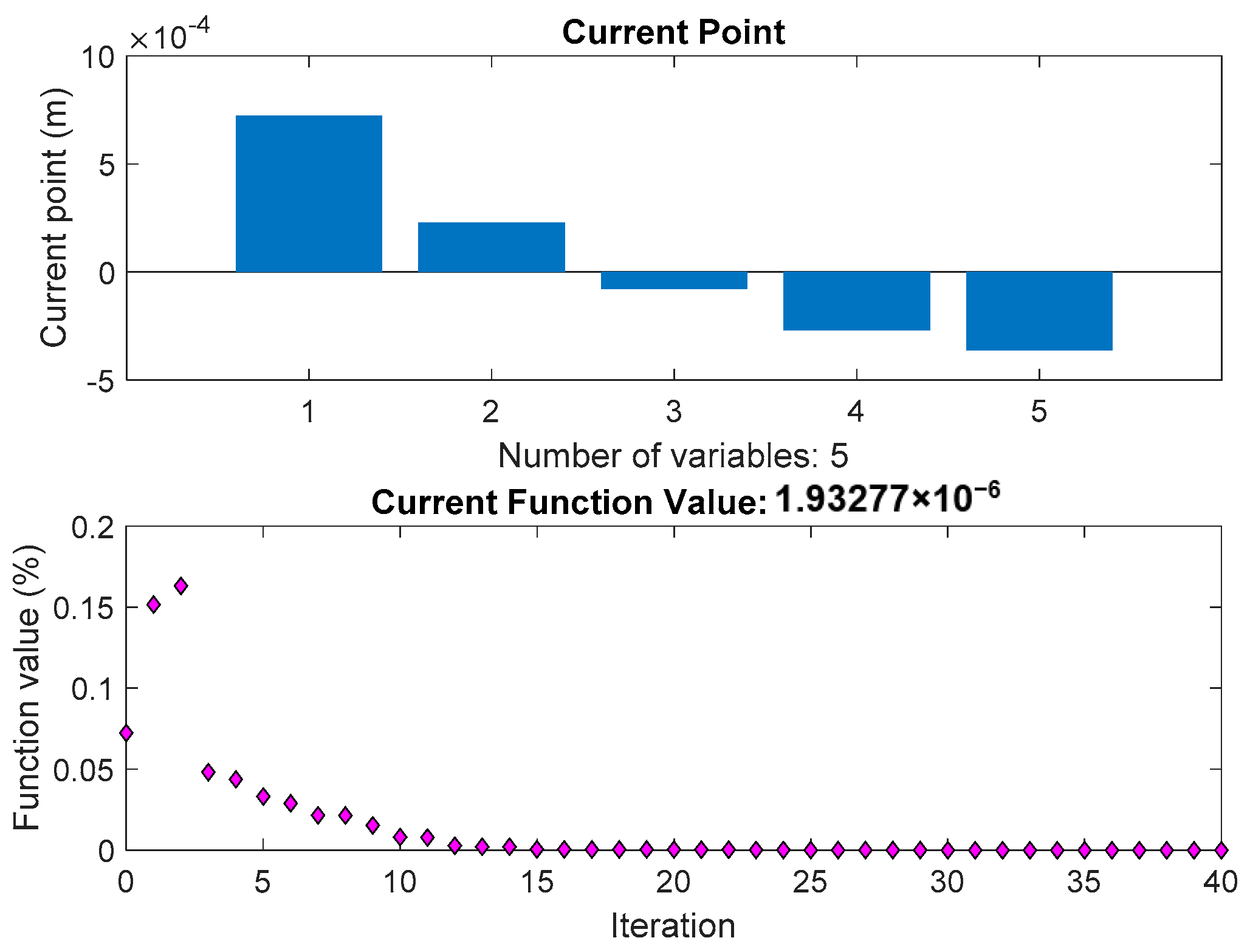
3.1. Optimization
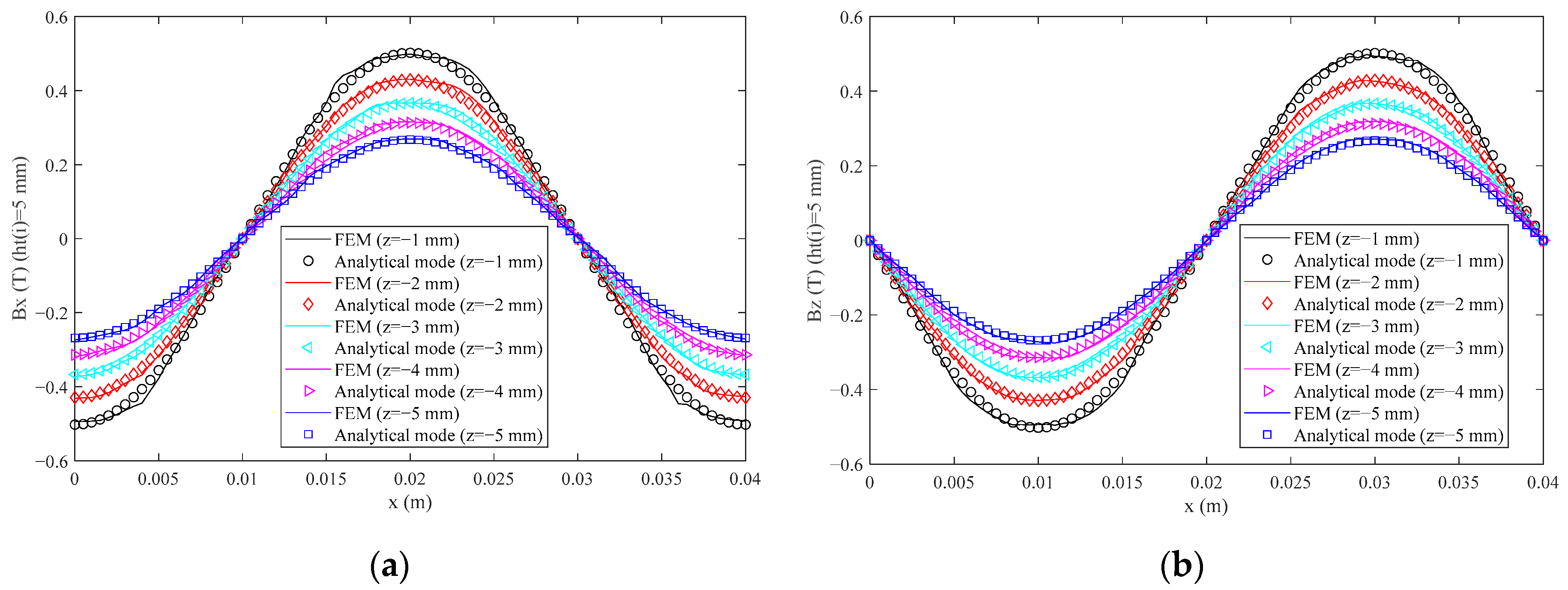
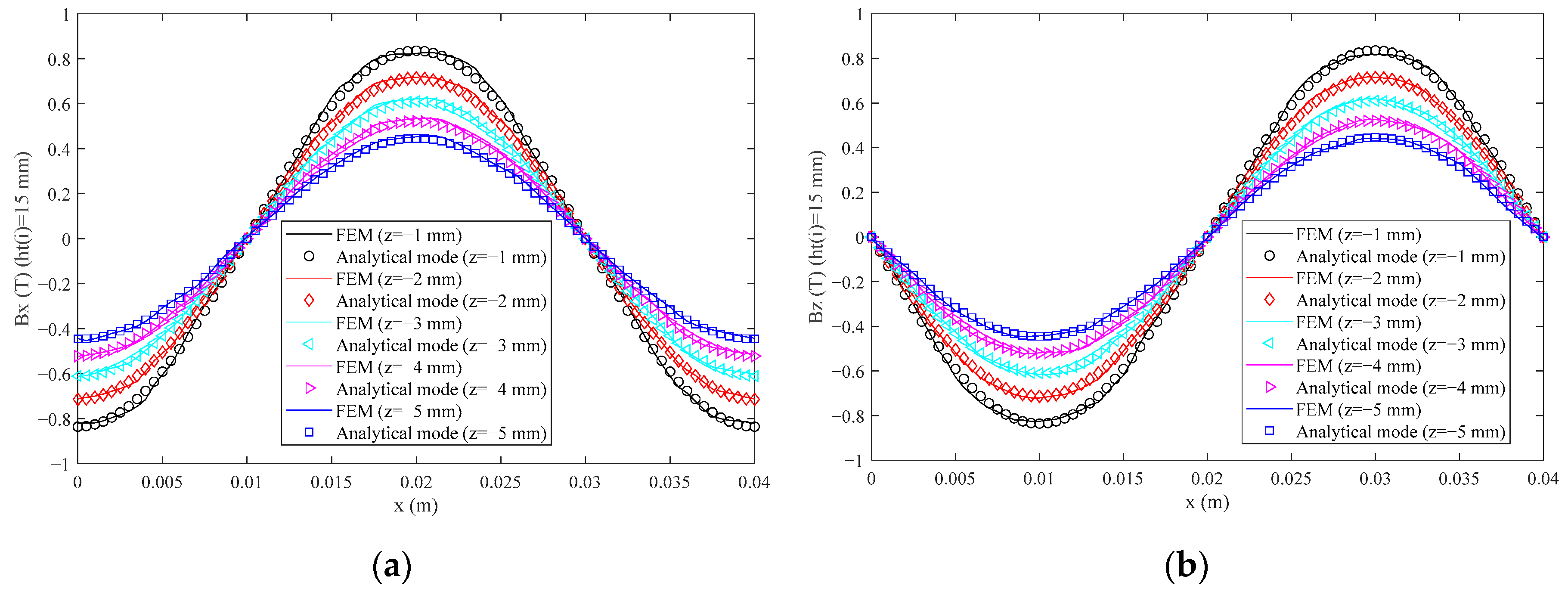
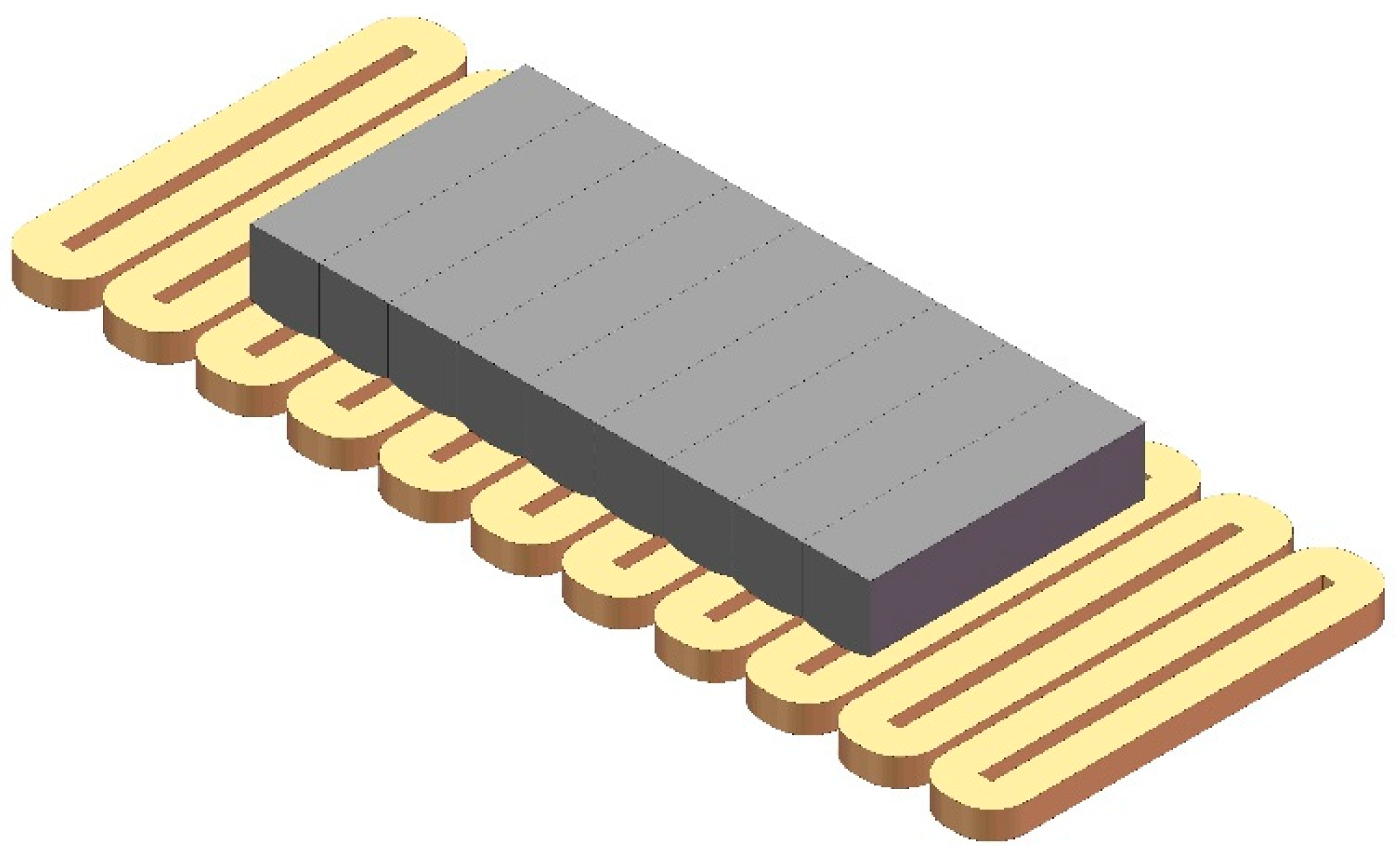
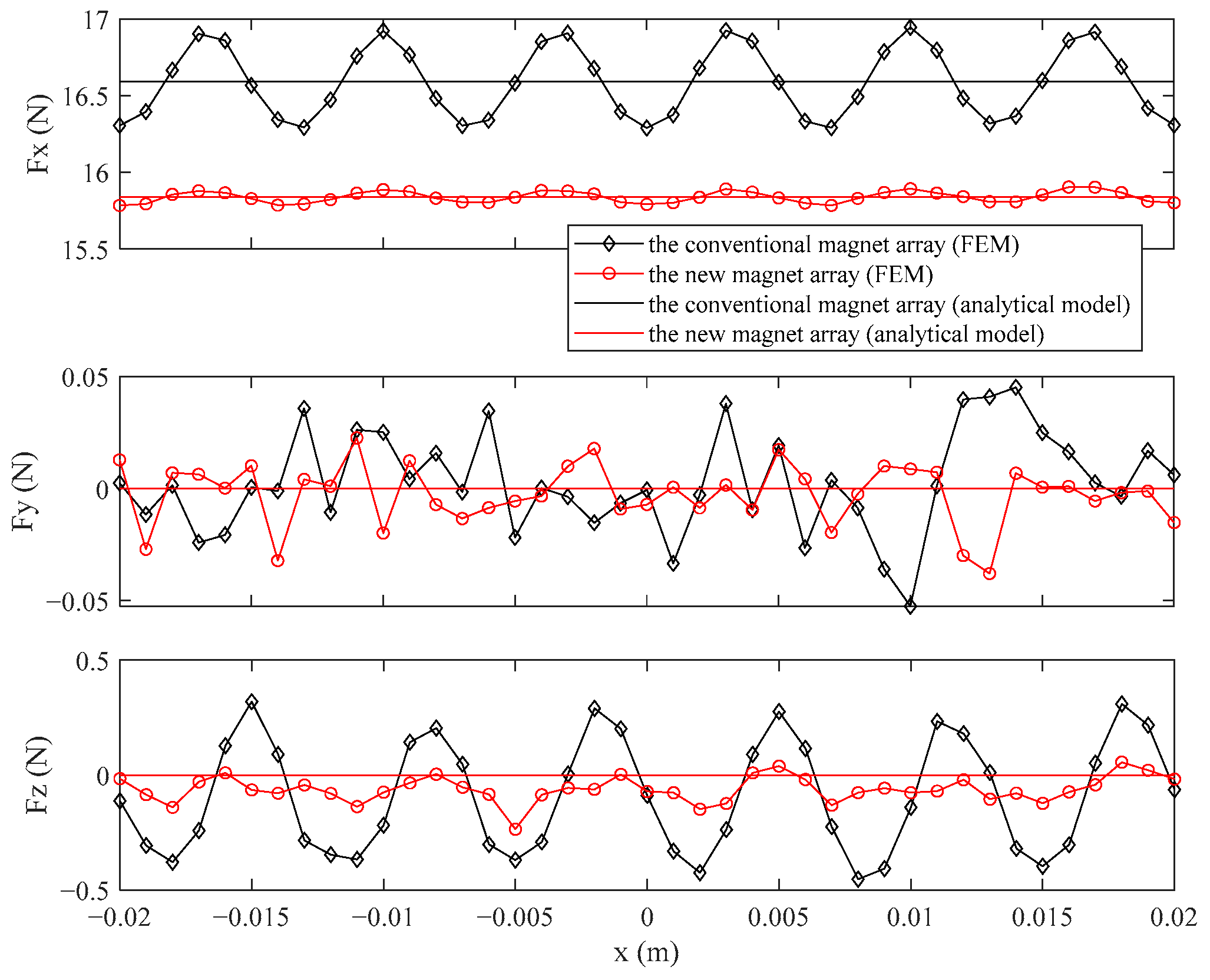
3.2. Verification with FEM
4. Discussion
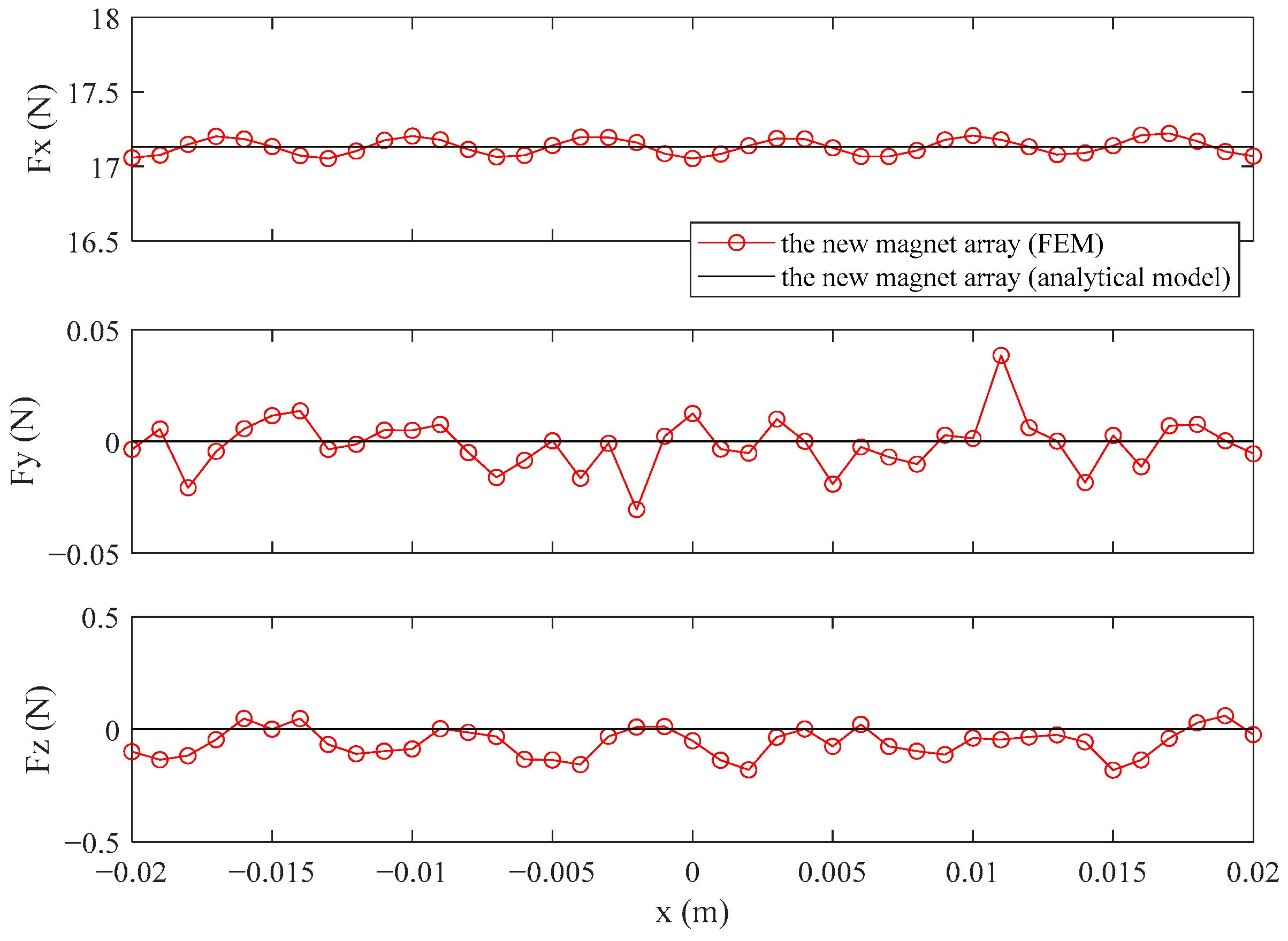
4.1. The Applicability of Optimization Results
4.1.1. Different Lengths of Permanent Magnet
4.1.2. Different Heights of Permanent Magnet
4.2. The Effect on the Mass
4.3. The Effect on the Air Gap
4.4. The Effect on the Force
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rahideh, A.; Ghaffari, A.; Barzegar, A.; Mahmoudi, A. Analytical Model of Slotless Brushless PM Linear Motors Considering Different Magnetization Patterns. IEEE Trans. Energy Conver. 2018, 33, 1797–1804. [Google Scholar] [CrossRef]
- Kim, W.J.; Trumper, D.L. High-precision magnetic levitation stage for photolithography. Precis. Eng. 1998, 22, 66–77. [Google Scholar]
- Guo, L.; Zhang, H.; Galea, M.; Li, J.; Gerada, C. Multiobjective Optimization of a Magnetically Levitated Planar Motor with Multilayer Windings. IEEE Trans. Ind. Electron. 2016, 63, 3522–3532. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Chen, X.; Luo, X.; Zeng, L. Analysis and Optimization of a Novel 2-D Magnet Array with Gaps and Staggers for a Moving-Magnet Planar Motor. Sensors 2018, 18, 124. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, F.; Lv, Y.; Xu, X.; Dinavahi, V. FPGA-Based Real-Time Wrench Model of Direct Current Driven Magnetic Levitation Actuator. IEEE Trans. Ind. Electron. 2018, 65, 9635–9645. [Google Scholar] [CrossRef]
- Yoon, J.Y.; Lang, J.H.; Trumper, D.L. Double-Sided Linear Iron-Core Fine-Tooth Motor for Low Acoustic Noise and High Acceleration. IEEE-ASME Trans. Mech. 2019, 24, 2161–2170. [Google Scholar] [CrossRef]
- Chi, S.; Yan, J.; Shan, L.; Wang, P. Detent Force Minimizing for Moving-Magnet-Type Linear Synchronous Motor. IEEE Trans. Magn. 2019, 55, 8102005. [Google Scholar] [CrossRef]
- Eckert, P.R.; Flores Filho, A.F.; Perondi, E.; Ferri, J.; Goltz, E. Design Methodology of a Dual-Halbach Array Linear Actuator with Thermal-Electromagnetic Coupling. Sensors 2016, 16, 360. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Trumper, D.L.; Kim, W.J.; Williams, M.E. Design and analysis framework for linear permanent-magnet machines. IEEE Trans. Ind. Appl. 1996, 32, 371–379. [Google Scholar] [CrossRef]
- Kim, W.J.; Trumper, D.L.; Lang, J.H. Modeling and vector control of planar magnetic levitator. IEEE Trans. Ind. Appl. 1998, 34, 1254–1262. [Google Scholar]
- Lee, M.G.; Gweon, D.G. Optimal design of a double-sided linear motor with a multi-segmented trapezoidal magnet array for a high precision positioning system. J. Magn. Magn. Mater. 2004, 281, 336–346. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, B.; Ding, Y.; Ding, H. Field analysis of a sinusoidal-edged Halbach magnet array using the differential quadrature finite element method. Int. J. Appl. Electrom. 2016, 50, 63–80. [Google Scholar] [CrossRef]
- Usman, I.U.R.; Lu, X. Force Ripple Attenuation of 6-DOF Direct Drive Permanent Magnet Planar Levitating Synchronous Motors. IEEE Trans. Magn. 2015, 51, 1–8. [Google Scholar] [CrossRef]
- Rui, C. A New Type of Magnet Array for Planar Motor. Master’s Thesis, The University of British Columbia, Vancouver, BC, Canada, 2016. [Google Scholar]
- Boduroglu, A.; Gulec, M.; Demir, Y.; Yolacan, E.; Aydin, M. A New Asymmetric Planar V-Shaped Magnet Arrangement for A Linear PM Synchronous Motor. IEEE Trans. Magn. 2019, 55, 1–5. [Google Scholar] [CrossRef]
- Zhang, Y.; Martínez-García, M.; Kalawsky, R.S.; Latimer, A. Grey-box Modelling of the Swirl Characteristics in Gas Turbine Combustion System. Measurement 2020, 151, 107266. [Google Scholar] [CrossRef]
- Mai, H.C.M.; Dubas, F.; Chamagne, D.; Espanet, C. Optimal design of a surface mounted permanent magnet in-wheel motor for an urban hybrid vehicle. In Proceedings of the IEEE Vehicle Power and Propulsion Conference, Dearborn, MI, USA, 7–10 September 2009. [Google Scholar]
- Dong, H.K.; Hirota, K. Vector control for loss minimization of induction motor using GA–PSO. Appl. Soft. Comput. 2008, 8, 1692–1702. [Google Scholar]
- Gangl, P.; Amstutz, S.; Langer, U. Topology Optimization of Electric Motor Using Topological Derivative for Nonlinear Magnetostatics. IEEE Trans. Magn. 2015, 52, 7201104. [Google Scholar] [CrossRef]
- Shiri, A.; Shoulaie, A. Design Optimization and Analysis of Single-Sided Linear Induction Motor, Considering All Phenomena. IEEE Trans. Energy Conver. 2012, 27, 516–525. [Google Scholar] [CrossRef]
- Zhang, Y.; Martínez-García, M.; Serrano-Cruz, J.R.; Latimer, A. Multi-region System Modelling by using Genetic Programming to Extract Rule Consequent Functions in a TSK Fuzzy System. In Proceedings of the IEEE 4th International Conference on Advanced Robotics and Mechatronics (ICARM), Toyonaka, Japan, 3–5 July 2019. [Google Scholar]
- Xue, X.D.; Cheng, K.W.E.; Ho, S.L.; Sutanto, D. Precise analytical modelling magnetic characteristics of switched reluctance motor drives using two-dimensional least squares. In Proceedings of the IEEE 34th Annual Conference on Power Electronics Specialist, Acapulco, Mexico, 15–19 June 2003. [Google Scholar]
- Milan, S.; Aidar, Z.; Tohid, A.; Yakov, L.; Gabriele, G.; Alex, R. Simultaneous Selective Harmonic Elimination and THD Minimization for a Single-Phase Multilevel Inverter with Staircase Modulation. IEEE Trans. Ind. Appl. 2017, 54, 1532–1541. [Google Scholar]




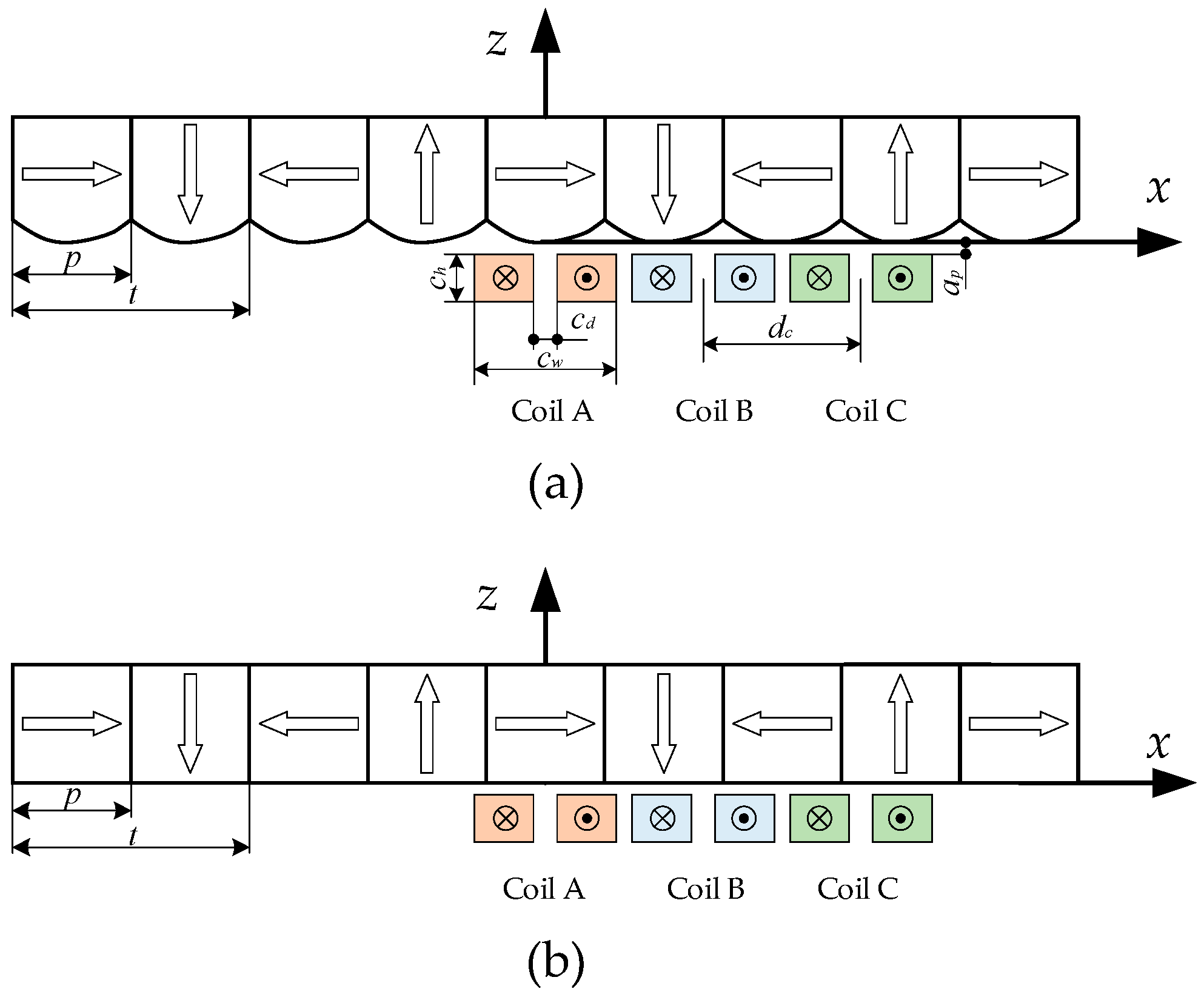
| Parameters | Symbol | Value | Unit |
|---|---|---|---|
| pole pitch | t | 20 | mm |
| the side length of the magnets | p | 10 | mm |
| remanence of the permanent magnets | Br | 1.2 | T |
| the number of pieces of half of one permanent magnet | n | 5 | - |
| the positions of the top surface of each piece | ht(1)~ht(5) | 10 | mm |
| Optimization variables | Constraints | Unit |
|---|---|---|
| hp(1)~hp(5) | [−2,10] | mm |
| z (mm) | RMS (∆Bx) (T) | Ratio of Peak Value of Bx of FEM (%) | THD (Bx) (%) | RMS (∆Bz) (T) | Ratio of Peak Value of Bz of FEM (%) | THD (Bz) (%) |
|---|---|---|---|---|---|---|
| −1 | 0.0159 | 2.19 | 2.69 | 0.0154 | 2.14 | 2.69 |
| −2 | 0.0094 | 1.50 | 1.43 | 0.0075 | 1.20 | 1.43 |
| −3 | 0.0075 | 1.40 | 0.76 | 0.0058 | 1.08 | 0.76 |
| −4 | 0.0063 | 1.38 | 0.41 | 0.0059 | 1.28 | 0.41 |
| −5 | 0.0060 | 1.52 | 0.22 | 0.0051 | 1.29 | 0.22 |
| Parameters | Symbol | Value | Unit |
|---|---|---|---|
| air gap | ap | 1 | mm |
| the length of the magnet array in the y-direction | ml | 40 | mm |
| the height of the coil | ch | 4 | mm |
| the width of the coil | cw | 12 | mm |
| the width of the air core of the coil | cd | 2 | mm |
| the distance between two coil centers | dc | 13.33 | mm |
| the number of coil turns | N | 100 | - |
| Magnet Array | Fx (N) | RMS (∆Fx)(N) | Fy (N) | RMS (∆Fy) (N) | Fz (N) | RMS (∆Fz) (N) |
|---|---|---|---|---|---|---|
| Theconventional magnet array | 16.5901 | 0.2280 | 0 | 0.0244 | 0 | 0.2611 |
| The newmagnet array | 15.8390 | 0.0365 | 0 | 0.0138 | 0 | 0.0829 |
| Magnet Array | Fx (N) | RMS(∆Fx)(N) | Fy (N) | RMS(∆Fy) (N) | Fz (N) | RMS(∆Fz) (N) |
|---|---|---|---|---|---|---|
| The new magnet array | 17.1322 | 0.0527 | 0 | 0.0116 | 0 | 0.0857 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Hou, S.; Xu, X.; Xiao, W. Design of a New 1D Halbach Magnet Array with Good Sinusoidal Magnetic Field by Analyzing the Curved Surface. Sensors 2021, 21, 2522. https://doi.org/10.3390/s21072522
Liu G, Hou S, Xu X, Xiao W. Design of a New 1D Halbach Magnet Array with Good Sinusoidal Magnetic Field by Analyzing the Curved Surface. Sensors. 2021; 21(7):2522. https://doi.org/10.3390/s21072522
Chicago/Turabian StyleLiu, Guangdou, Shiqin Hou, Xingping Xu, and Wensheng Xiao. 2021. "Design of a New 1D Halbach Magnet Array with Good Sinusoidal Magnetic Field by Analyzing the Curved Surface" Sensors 21, no. 7: 2522. https://doi.org/10.3390/s21072522
APA StyleLiu, G., Hou, S., Xu, X., & Xiao, W. (2021). Design of a New 1D Halbach Magnet Array with Good Sinusoidal Magnetic Field by Analyzing the Curved Surface. Sensors, 21(7), 2522. https://doi.org/10.3390/s21072522





