Designing Mid-Infrared Gold-Based Plasmonic Slot Waveguides for CO2-Sensing Applications
Abstract
:1. Introduction
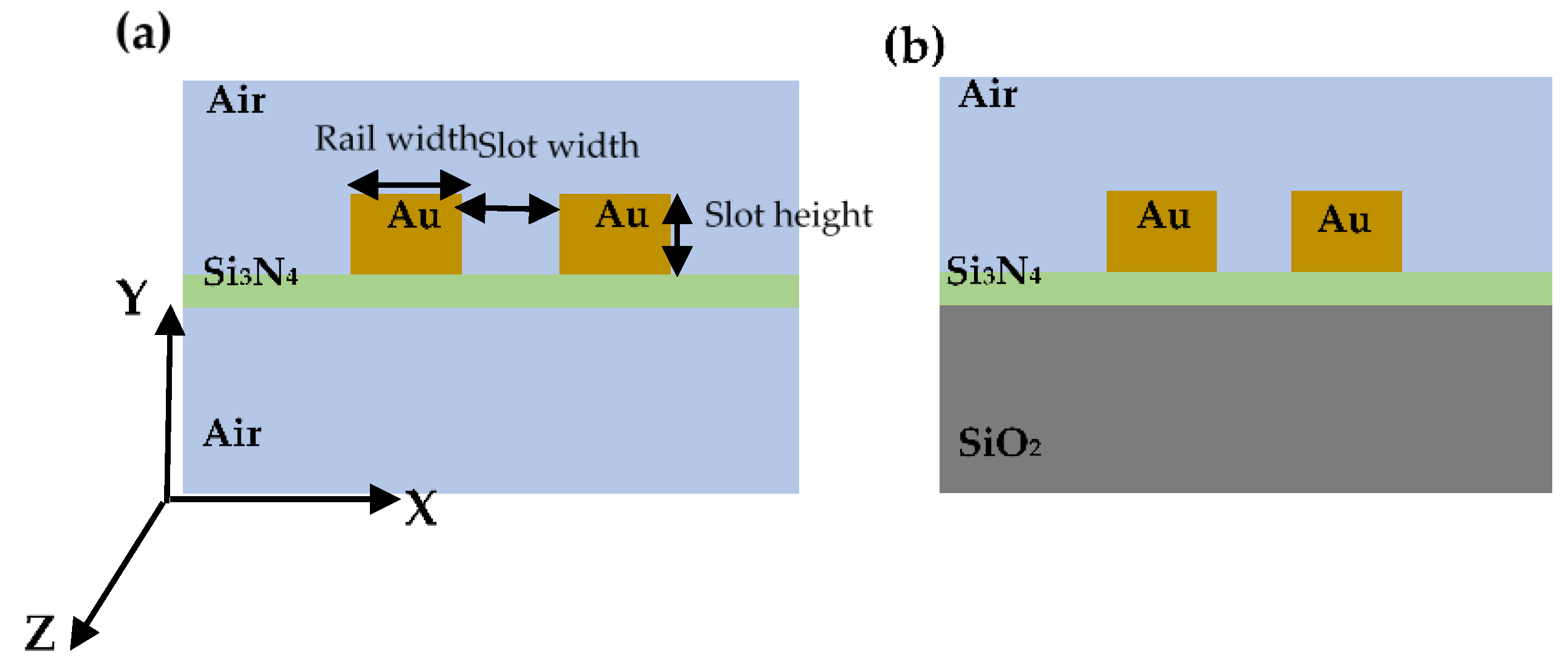
2. Materials and Methods
3. Results and Discussion
3.1. Theoretical Concepts
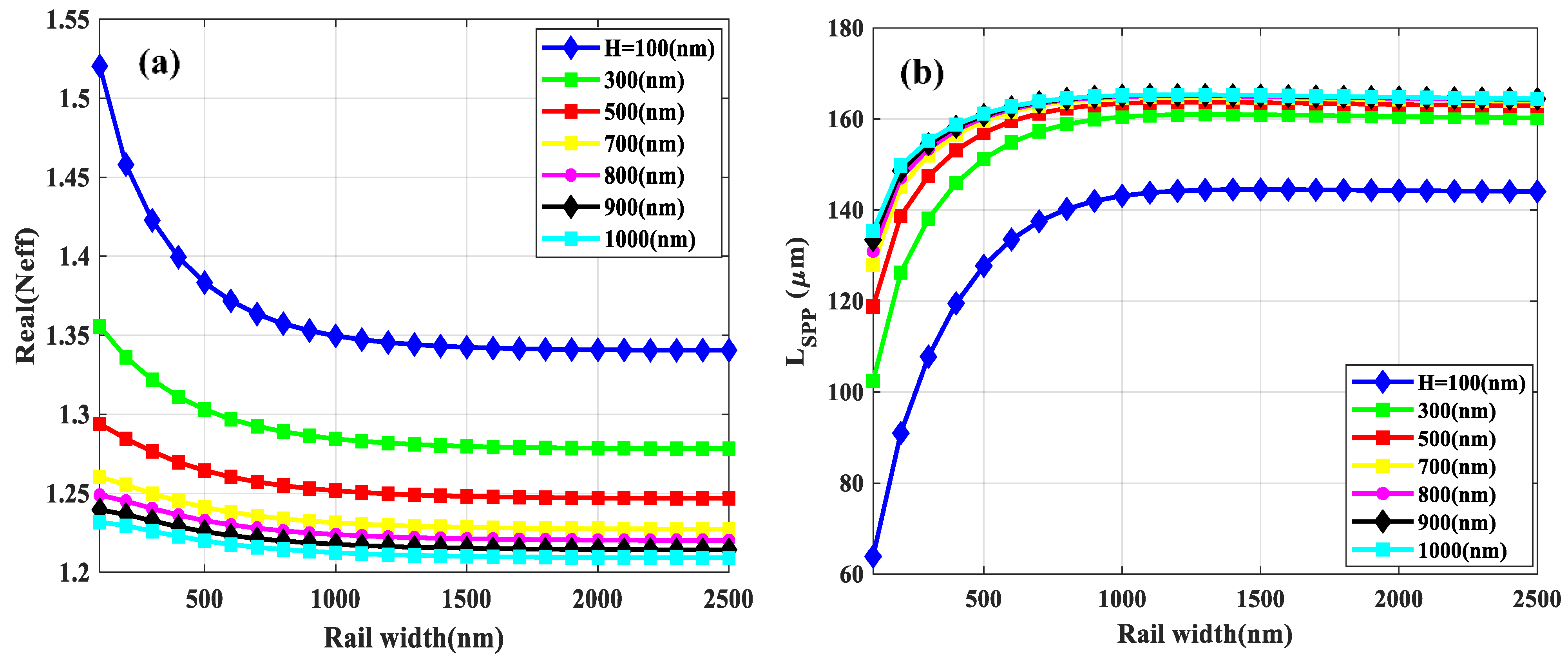
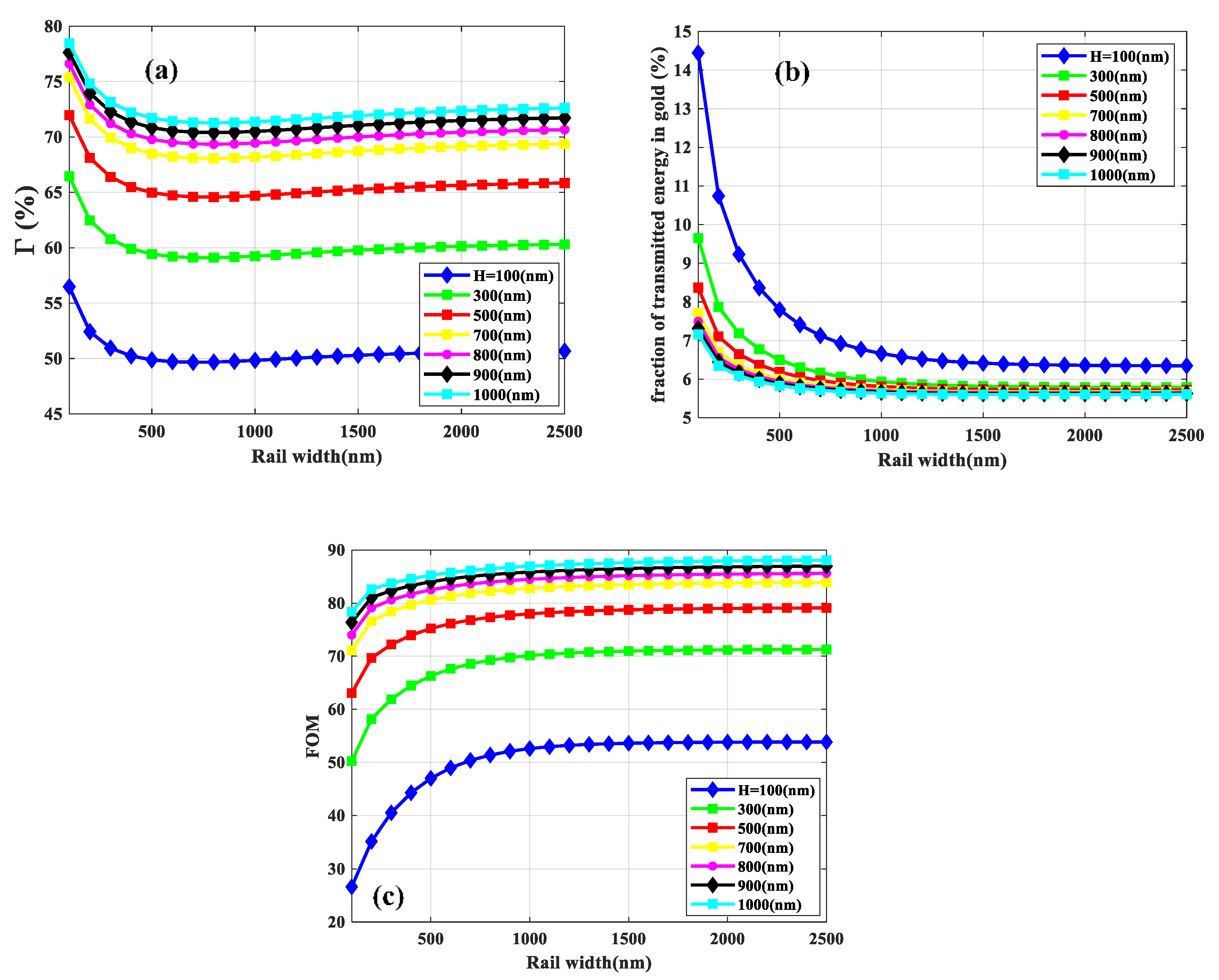
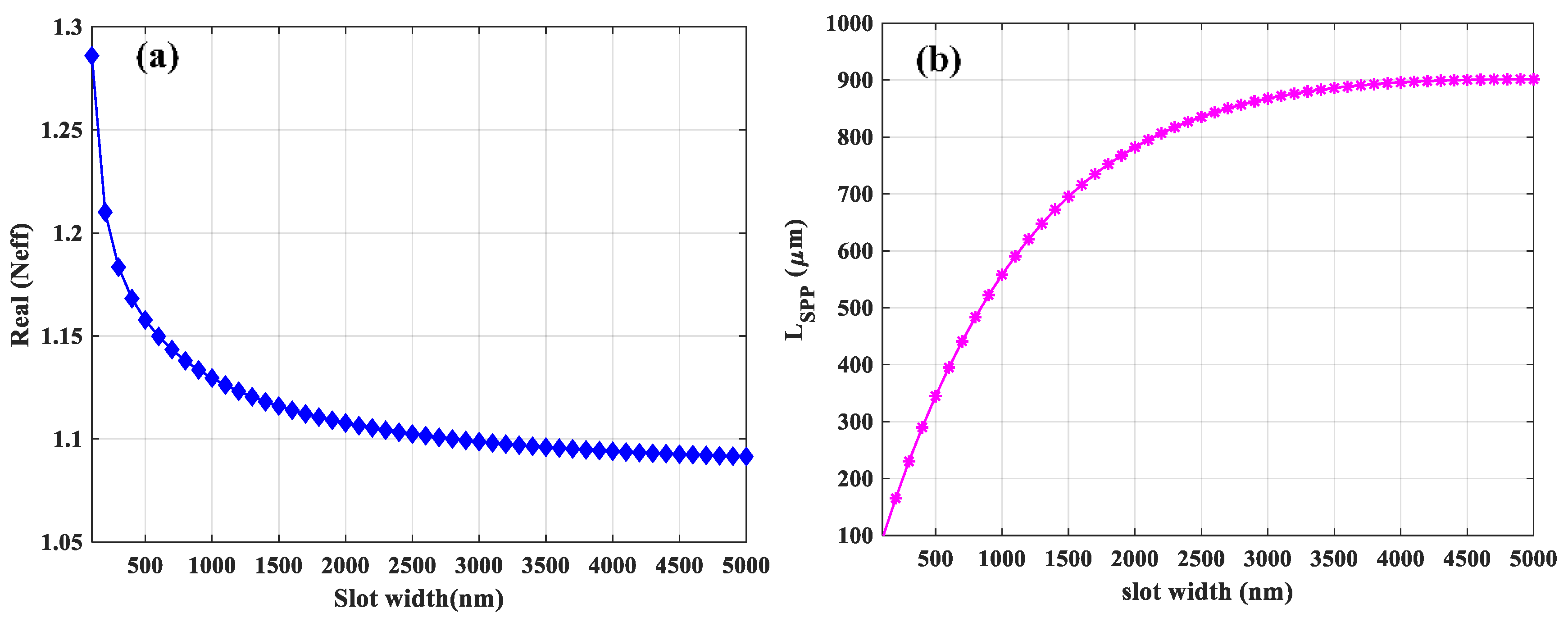
3.1.1. Confinement Factor (Γ)
3.1.2. Propagation Length
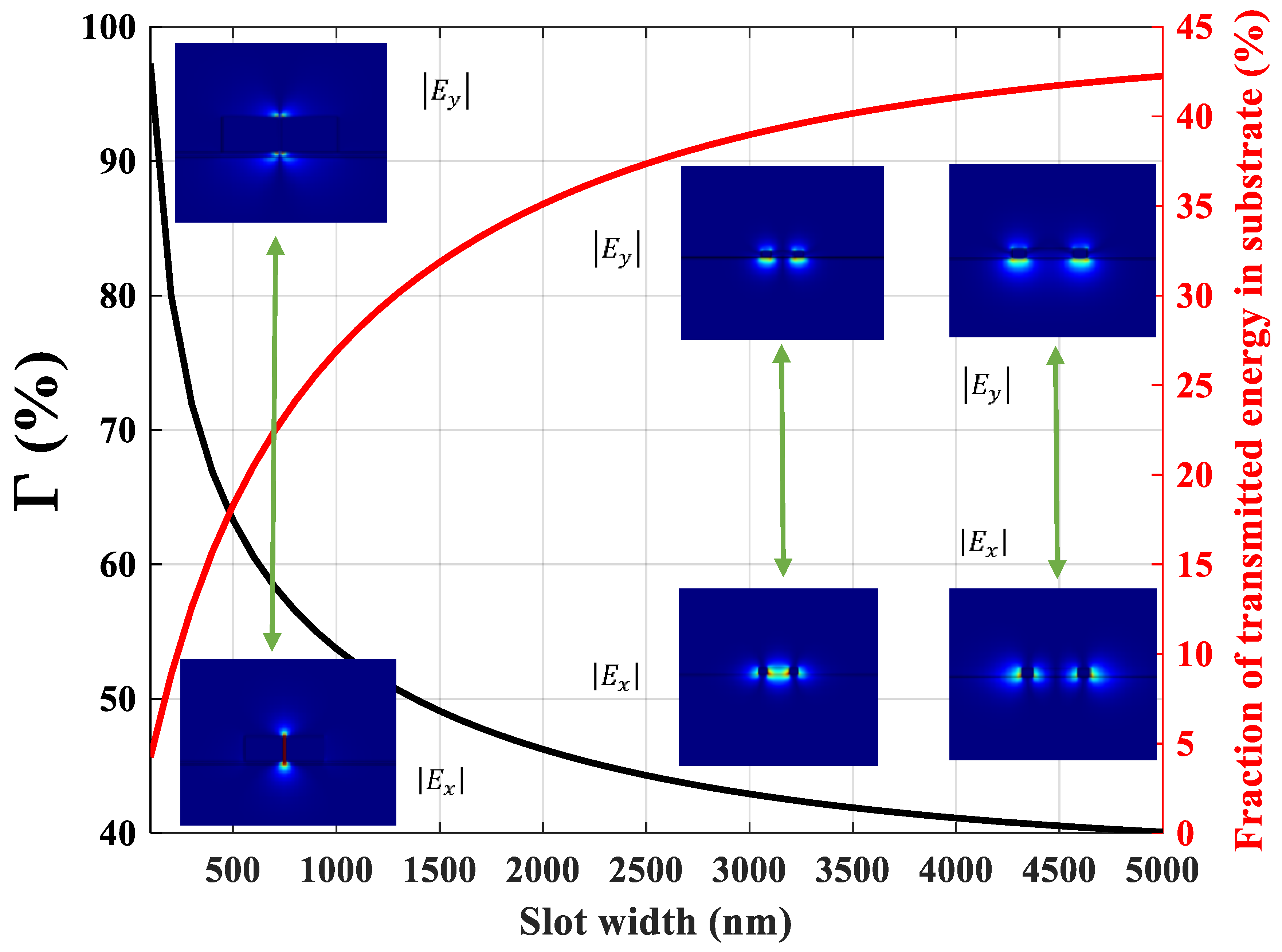
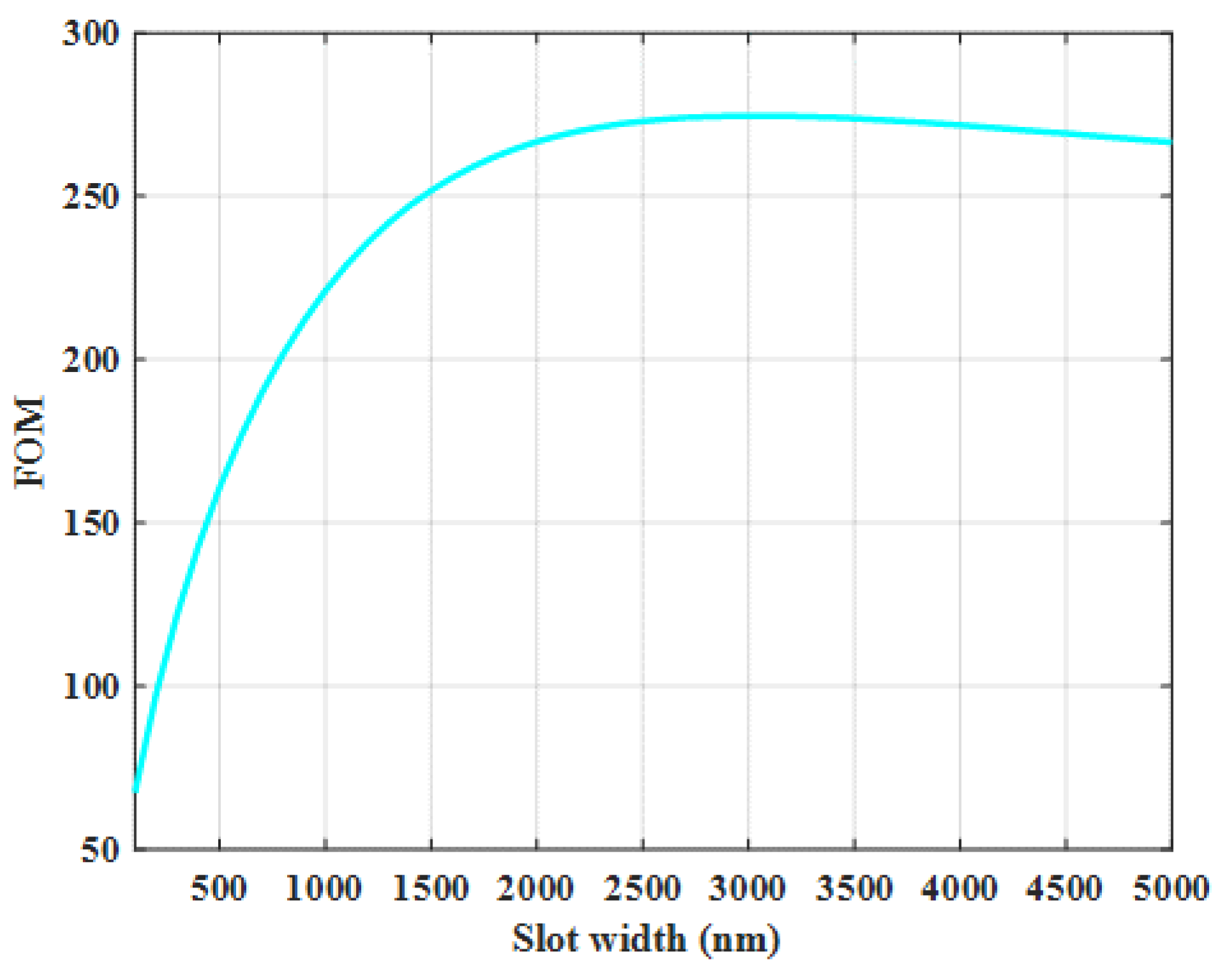
3.2. Free-Standing Structure
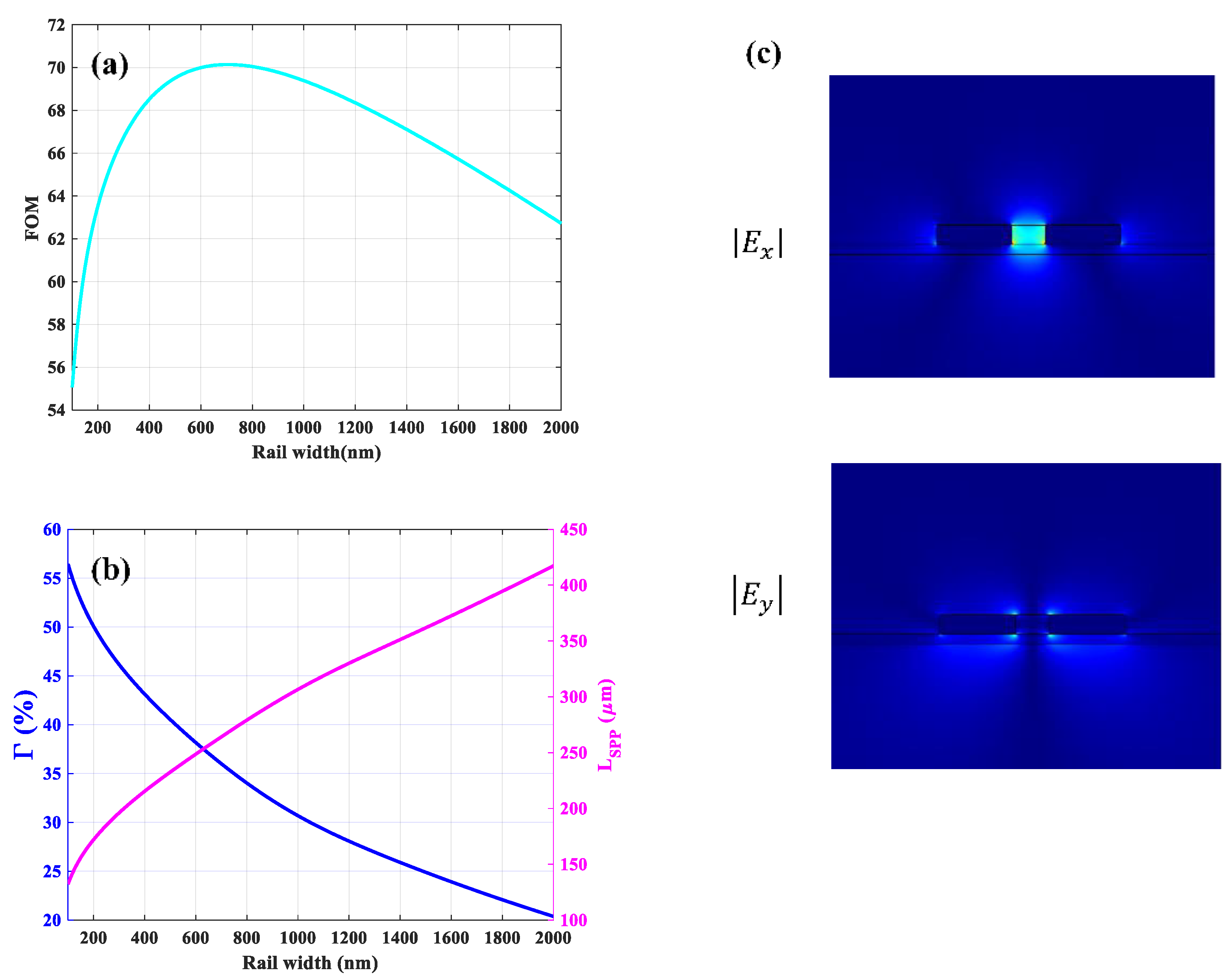
3.3. Asymmetric Structure
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Feng, N.N.; Brongersma, M.L.; Dal Negro, L. Metal–dielectric slot-waveguide structures for the propagation of surface plasmon polaritons at 1.55. IEEE J. Quantum Electron. 2007, 43, 479–485. [Google Scholar] [CrossRef]
- Jannesari, R.; Pühringer, G.; Grille, T.; Jakoby, B. Using an optimized grating as a mid-IR surface plasmon gas sensor utilizing highly doped silicon. IEEE Sens. 2019. [Google Scholar] [CrossRef]
- Prämassing, M.; Liebtrau, M.; Schill, H.J.; Irsen, S.; Linden, S. Interferometric near-field characterization of plasmonic slot waveguides in single and poly-crystalline gold films. Opt. Express 2020, 28, 12998–13007. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dionne, J.A.; Sweatlock, L.A.; Atwater, H.A.; Polman, A. Plasmon slot waveguides: Towards chip-scale propagation with subwavelength-scale localization. Phys. Rev. B 2006, 73, 035407. [Google Scholar] [CrossRef] [Green Version]
- Barnes, W.L.; Dereux, A.; Ebbesen, T.W. Surface plasmon subwavelength optics. Nature 2003, 424, 824–830. [Google Scholar] [CrossRef]
- Ozbay, E. Plasmonics: Merging photonics and electronics at nanoscale dimensions. Science 2006, 311, 189–193. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, H.; Raza, A.; Clemmen, S.; Baets, R. Surface-enhanced Raman spectroscopy based on plasmonic slot waveguides with free-space oblique illumination. IEEE J. Quantum Electron. 2019, 56, 1–8. [Google Scholar] [CrossRef]
- Chen, C.; Mohr, D.A.; Choi, H.K.; Yoo, D.; Li, M.; Oh, S.H. Waveguide-integrated compact plasmonic resonators for on-chip mid-infrared laser spectroscopy. Nano Lett. 2018, 18, 7601–7608. [Google Scholar] [CrossRef]
- Wei, Q.; Xiao, J.; Chen, S.; Wang, Q.; Cai, M.; Yang, D.; Qin, H. Asymmetric long-range surface plasmon polariton waveguides for sensing applications. IEEE Photonics J. 2019, 11, 1–9. [Google Scholar] [CrossRef]
- Singh, L.; Sharma, T.; Kumar, M. Controlled hybridization of plasmonic and optical modes for low-loss nano-scale optical confinement with ultralow dispersion. IEEE J. Quantum Electron. 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Rajput, S.; Kaushik, V.; Jain, S.; Kumar, M. Slow light enhanced phase shifter based on low-loss silicon-ITO hollow waveguide. IEEE Photonics J. 2019, 11, 1–8. [Google Scholar] [CrossRef]
- Singh, L.; Jain, S.; Kumar, M. Optical slot waveguide with grating-loaded cladding of silicon and titanium dioxide for label-free bio-sensing. IEEE Sens. J. 2019, 19, 6126–6133. [Google Scholar]
- Hong, Y.S.; Kim, J.; Sung, H.K. Characterization of a functional hydrogel layer on a silicon-based grating waveguide for a biochemical sensor. Sensors 2016, 16, 914. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barrios, C.A.; Banuls, M.J.; Gonzalez-Pedro, V.; Gylfason, K.B.; Sanchez, B.; Griol, A.; Maquieira, A.; Sohlström, H.; Holgado, M.; Casquel, R. Label-free optical biosensing with slot-waveguides. Opt. Lett. 2008, 33, 708–710. [Google Scholar] [CrossRef] [Green Version]
- Kita, D.M.; Michon, J.; Johnson, S.G.; Hu, J. Are slot and sub-wavelength grating waveguides better than strip waveguides for sensing? Optica 2018, 5, 1046–1054. [Google Scholar] [CrossRef] [Green Version]
- Jannesari, R.; Pühringer, G.; Grille, T.; Jakoby, B. Design and analysis of a slot photonic crystal waveguide for highly sensitive evanescent field absorption sensing in fluids. Micromachines 2020, 11, 781. [Google Scholar] [CrossRef]
- Sun, X.; Alam, M.Z.; Mojahedi, M.; Aitchison, J.S. Confinement and integration density of plasmonic waveguides. IEEE J. Sel. Top. Quantum Electron. 2014, 21, 268–275. [Google Scholar] [CrossRef]
- West, P.R.; Ishii, S.; Naik, G.V.; Emani, N.K.; Shalaev, V.M.; Boltasseva, A. Searching for better plasmonic materials. Laser Photonics Rev. 2010, 4, 795–808. [Google Scholar] [CrossRef] [Green Version]
- Chen, K.; Guo, P.; Dao, T.D.; Li, S.Q.; Ishii, S.; Nagao, T.; Chang, R.P. Protein-functionalized indium-tin oxide nanoantenna arrays for selective infrared biosensing. Adv. Opt. Mater. 2017, 5, 1700091. [Google Scholar] [CrossRef]
- Popa, D.; Udrea, F. Towards integrated mid-infrared gas sensors. Sensors 2019, 19, 2076. [Google Scholar] [CrossRef] [Green Version]
- Nicoletti, S.; Fédéli, J.M.; Fournier, M.; Labeye, P.; Barritault, P.; Marchant, A.; Glière, A.; Teulle, A.; Coutard, J.G.; Duraffourg, L. Miniaturization of mid-IR sensors on Si: Challenges and perspectives. In Silicon Photonics; International Society for Optics and Photonics: San Francisco, CA, USA, 2019; Volume 10923, p. 109230. [Google Scholar]
- Khonina, S.N.; Kazanskiy, N.L.; Butt, M.A. Evanescent field ratio enhancement of a modified ridge waveguide structure for methane gas sensing application. IEEE Sens. J. 2020, 20, 8469–8476. [Google Scholar] [CrossRef]
- Stewart, G.; Culshaw, B. Optical waveguide modelling and design for evanescent field chemical sensors. Opt. Quantum Electron. 1994, 26, S249–S259. [Google Scholar] [CrossRef]
- Huang, Y.; Kalyoncu, S.K.; Zhao, Q.; Torun, R.; Boyraz, O. Silicon-on-sapphire waveguides design for mid-IR evanescent field absorption gas sensors. Opt. Commun. 2014, 313, 186–194. [Google Scholar] [CrossRef]
- Ottonello-Briano, F.; Errando-Herranz, C.; Rödjegård, H.; Martin, H.; Sohlström, H.; Gylfason, K.B. Carbon dioxide absorption spectroscopy with a mid-infrared silicon photonic waveguide. Opt. Lett. 2020, 45, 109–112. [Google Scholar] [CrossRef] [Green Version]
- Zhou, T.; Wu, T.; Wu, Q.; Chen, W.; Wu, M.; Ye, C.; He, X. Real-time monitoring of 13C-and 18O-isotopes of human breath CO2 using a mid-infrared hollow waveguide gas sensor. Anal. Chem. 2020, 92, 12943–12949. [Google Scholar] [CrossRef] [PubMed]
- Wilk, A.; Seichter, F.; Kim, S.S.; Tütüncü, E.; Mizaikoff, B.; Vogt, J.A.; Wachter, U.; Radermacher, P. Toward the quantification of the 13CO2/12CO2 ratio in exhaled mouse breath with mid-infrared hollow waveguide gas sensors. Anal. Bioanal. Chem. 2012, 402, 397–404. [Google Scholar] [CrossRef]
- Osowiecki, G.D.; Barakat, E.; Naqavi, A.; Herzig, H.P. Vertically coupled plasmonic slot waveguide cavity for localized biosensing applications. Opt. Express 2014, 22, 20871–20880. [Google Scholar] [CrossRef]
- El Sherif, M.H.; Ahmed, O.S.; Bakr, M.H.; Swillam, M.A. Polarization-controlled excitation of multilevel plasmonic nano-circuits using single silicon nanowire. Opt. Express 2012, 20, 12473–12486. [Google Scholar] [CrossRef]
- Sederberg, S.; Firby, C.J.; Greig, S.R.; Elezzabi, A.Y. Integrated nanoplasmonic waveguides for magnetic, nonlinear, and strong-field devices. Nanophotonics 2017, 6, 235–257. [Google Scholar] [CrossRef]
- Bozhevolnyi, S.I.; Volkov, V.S.; Devaux, E.; Ebbesen, T.W. Channel plasmon-polariton guiding by subwavelength metal grooves. Phys. Rev. Lett. 2005, 95, 046802. [Google Scholar] [CrossRef] [Green Version]
- Veronis, G.; Fan, S. Modes of subwavelength plasmonic slot waveguides. J. Lightwave Technol. 2007, 25, 2511–2521. [Google Scholar] [CrossRef]
- Babar, S.; Weaver, J.H. Optical constants of Cu, Ag, and Au revisited. Appl. Opt. 2015, 54, 477–481. [Google Scholar] [CrossRef]
- Ranacher, C.; Consani, C.; Tortschanoff, A.; Jannesari, R.; Bergmeister, M.; Grille, T.; Jakoby, B. Mid-infrared absorption gas sensing using a silicon strip waveguide. Sens. Actuators A Phys. 2018, 277, 117–123. [Google Scholar] [CrossRef]
- Vlk, M.; Datta, A.; Alberti, S.; Yallew, H.D.; Mittal, V.; Murugan, G.S.; Jágerská, J. Extraordinary evanescent field confinement waveguide sensor for mid-infrared trace gas spectroscopy. Light Sci. Appl. 2021, 10, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Robinson, J.T.; Preston, K.; Painter, O.; Lipson, M. First-principle derivation of gain in high-index-contrast waveguides. Opt. Express 2008, 16, 16659–16669. [Google Scholar] [CrossRef]
- Parriaux, O.; Lambeck, P.V.; Hoekstra, H.J.W.M.; Veldhuis, G.J.; Pandraud, G. Evanescent wave sensor of sensitivity larger than a free space wave. Opt. Quantum Electron. 2000, 32, 909–921. [Google Scholar] [CrossRef]
- Iqbal, T. Propagation length of surface plasmon polaritons excited by a 1D plasmonic grating. Curr. Appl. Phys. 2015, 15, 1445–1452. [Google Scholar] [CrossRef]
- Xiang, C.; Wang, J. Long-range hybrid plasmonic slot waveguide. IEEE Photonics J. 2013, 5, 4800311. [Google Scholar] [CrossRef]
- Spettel, J.; Stocker, G.; Dao, T.D.; Jannesari, R.; Tortschanoff, A.; Saeidi, P.; Pühringer, G.; Dubois, F.; Fleury, C.; Consani, C.; et al. Aluminium, gold-tin and titanium-tungsten alloys for mid-infrared plasmonic gratings. Opt. Mater. Express 2021, 11, 1058–1069. [Google Scholar] [CrossRef]
- Butt, M.A.; Khonina, S.N.; Kazanskiy, N.L. Numerical analysis of a miniaturized design of a Fabry–Perot resonator based on silicon strip and slot waveguides for bio-sensing applications. J. Mod. Opt. 2019, 66, 1172–1178. [Google Scholar] [CrossRef]
- Butt, M.A.; Khonina, S.N.; Kazanskiy, N.L. Modelling of Rib channel waveguides based on silicon-on-sapphire at 4.67 μm wavelength for evanescent field gas absorption sensor. Optik 2018, 168, 692–697. [Google Scholar] [CrossRef]
- Kazanskiy, N.L.; Khonina, S.N.; Butt, M.A. Plasmonic sensors based on Metal-insulator-metal waveguides for refractive index sensing applications: A brief review. Phys. E Low-Dimens. Syst. Nanostruct. 2020, 117, 113798. [Google Scholar] [CrossRef]
- Ranacher, C.; Consani, C.; Vollert, N.; Tortschanoff, A.; Bergmeister, M.; Grille, T.; Jakoby, B. Characterization of evanescent field gas sensor structures based on silicon photonics. IEEE Photonics J. 2018, 10, 1–14. [Google Scholar] [CrossRef]
- Liu, L.; Han, Z.; He, S. Novel surface plasmon waveguide for high integration. Opt. Express 2005, 13, 6645–6650. [Google Scholar] [CrossRef] [PubMed]
- Wu, K.; Poon, A.W. Stress-released Si3N4 fabrication process for dispersion-engineered integrated silicon photonics. Opt. Express 2020, 28, 17708–17722. [Google Scholar] [CrossRef]
- Shafikov, A.; Schurink, B.; van de Kruijs, R.W.; Benschop, J.; van den Beld WT, E.; Houweling, Z.S.; Bijkerk, F. Strengthening ultrathin Si3N4 membranes by compressive surface stress. Sens. Actuators A Phys. 2021, 317, 112456. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saeidi, P.; Jakoby, B.; Pühringer, G.; Tortschanoff, A.; Stocker, G.; Dubois, F.; Spettel, J.; Grille, T.; Jannesari, R. Designing Mid-Infrared Gold-Based Plasmonic Slot Waveguides for CO2-Sensing Applications. Sensors 2021, 21, 2669. https://doi.org/10.3390/s21082669
Saeidi P, Jakoby B, Pühringer G, Tortschanoff A, Stocker G, Dubois F, Spettel J, Grille T, Jannesari R. Designing Mid-Infrared Gold-Based Plasmonic Slot Waveguides for CO2-Sensing Applications. Sensors. 2021; 21(8):2669. https://doi.org/10.3390/s21082669
Chicago/Turabian StyleSaeidi, Parviz, Bernhard Jakoby, Gerald Pühringer, Andreas Tortschanoff, Gerald Stocker, Florian Dubois, Jasmin Spettel, Thomas Grille, and Reyhaneh Jannesari. 2021. "Designing Mid-Infrared Gold-Based Plasmonic Slot Waveguides for CO2-Sensing Applications" Sensors 21, no. 8: 2669. https://doi.org/10.3390/s21082669
APA StyleSaeidi, P., Jakoby, B., Pühringer, G., Tortschanoff, A., Stocker, G., Dubois, F., Spettel, J., Grille, T., & Jannesari, R. (2021). Designing Mid-Infrared Gold-Based Plasmonic Slot Waveguides for CO2-Sensing Applications. Sensors, 21(8), 2669. https://doi.org/10.3390/s21082669





